Medición de formas de modo Chladni con un método de palanca óptica

Resumen

Se propone un método simple de medición de la forma del modo Chladni en una placa elástica por el principio de una palanca óptica.

Resumen

Determinar cuantitativamente el patrón Chladni de una placa elástica es de gran interés tanto en la ciencia física como en las aplicaciones de ingeniería. En este artículo, se propone un método de medición de formas de modo de una placa vibratoria basada en un método de palanca óptica. En la medición se emplearon tres placas de acrílico circular bajo diferentes excitaciones armónicas centrales. A diferencia de un método tradicional, sólo un lápiz láser ordinario y una pantalla de luz hecha de vidrio de tierra se emplean en este enfoque novedoso. El enfoque es el siguiente: el lápiz láser proyecta un haz a la placa vibratoria perpendicularmente, y luego el haz se refleja en la pantalla de luz en la distancia, en la que se forma un segmento de línea hecho del punto reflejado. Debido al principio de persistencia de la visión, el punto de luz podría leerse como una línea recta brillante. La relación entre la pendiente de la forma del modo, la longitud del punto de luz y la distancia de la placa vibratoria y la pantalla de luz se puede obtener con operaciones algebraicas. A continuación, la forma del modo se puede determinar integrando la distribución de talud con las condiciones de contorno adecuadas. Las formas de modo de campo completo de la placa Chladni también podrían determinarse más de una manera tan sencilla.

Introducción

Las formas del modo Chladni son de gran interés tanto en aplicaciones de ciencia como de ingeniería. Los patrones de Chladni son reacciones de ondas físicas, y uno puede ilustrar el patrón de onda con varios métodos. Es un método bien conocido para mostrar los diversos modos de vibración en una placa elástica delineando las líneas nodales. Las partículas pequeñas siempre se emplean para mostrar los patrones Chladni, ya que pueden detenerse en los nodos donde la amplitud de vibración relativa de la placa es cero, y las posiciones de los nodos varían con el modo resonante para formar varios patrones Chladni.

Muchos investigadores han prestado atención a varios patrones chladni, pero sólo muestran las líneas nodales de las formas de modo, las formas de modo (es decir, amplitud de vibración) entre las líneas nodales no se ilustran. Waller investigó las vibraciones libres de un círculo¹, un cuadrado², un isósceles triángulos en ángulo recto³, un rectangular⁴, elíptica⁵ placas, y diferentes patrones Chladni se ilustran en él. Reconstruido diferentes patrones Chladni a través de enfoques experimentales y teóricos, y la ecuación inhomogénea Helmholtz se adopta durante el modelado teórico^6,7. Es un método popular de uso de Láser Doppler Vibrometer (LDV) o Interferometría electrónica de patrón de espectro (ESPI) para medir cuantitativamente las formas de modo de los patrones Chladni^8,9,10. Aunque LDV permite la resolución de amplitud del femtómetro y rangos de frecuencia muy altos, por desgracia, el precio de LDV también es un poco caro para la demostración en el aula y / o la educación física de la universidad. Con esta consideración, el presente documento propuso un enfoque simple para determinar cuantitativamente las formas de modo de un patrón Chladni con bajo costo, ya que aquí sólo se necesita un lápiz láser adicional y una pantalla ligera.

El presente método de medición se ilustra en la Figura 1¹¹. La placa vibratoria tiene tres posiciones diferentes: la posición de reposo, la posición 1 y la posición 2. Las posiciones 1 y 2 representan los dos lugares vibratorios máximos de la placa. Un lápiz láser proyecta un haz recto en la superficie de la placa, y si la placa se encuentra en la posición de reposo, el rayo láser se reflejará directamente en la pantalla de luz. Mientras que la placa se encuentra en las posiciones 1 y 2, entonces el rayo láser se reflejará en el punto A y B en la pantalla de luz, respectivamente. Debido al efecto de la persistencia de la visión, habrá una línea recta brillante en la pantalla de luz. La longitud de la luz brillante L está relacionada con la distancia D entre la pantalla de luz y la ubicación del punto láser. Diferentes puntos en la placa tienen diferentes pendientes, que podrían ser determinados por la relación entre L y D. Después de obtener la pendiente de la forma de modo en diferentes puntos de la placa, el problema se convierte en una integral definida. Con la ayuda de la amplitud de vibración límite de la placa y los datos de pendiente discretos, la forma de modo de la placa vibratoria se puede obtener fácilmente. Toda la configuración experimental se indica en la Figura 2¹¹.

Este documento describe la configuración experimental y el procedimiento para el método de palanca óptica para medir las formas del modo Chladni. También se ilustran algunos resultados experimentales típicos.

Protocolo

1. Configuración y procedimientos experimentales

NOTA: Configure el sistema experimental como se muestra en la Figura 2.

1. Preparación del sistema de vibración
   1. Prepare tres placas acrílicas circulares espejadas de 1,0 mm de espesor con diámetro de 150 mm, 200 mm y 250 mm respectivamente. Taladre un agujero de 3 mm de diámetro en el centro de cada placa. Marque varios puntos negros cada 5 mm a lo largo de un radio arbitrario.
   2. Fije cada placa a la barra de accionamiento del vibrador con un perno en el punto medio. Conduzca el vibrador con una onda sinusoidal utilizando un generador de forma de onda, y la configuración predeterminada será suficiente para el experimento de resonancia.
      NOTA: La dirección de excitación del vibrador es horizontal para la comodidad de mover la pantalla después.
   3. Adquisición de la frecuencia de resonancia
      1. Coloque el lápiz láser para proyectar el rayo láser a la placa vibratoria perpendicularmente de tal manera que el haz se refleje en la pantalla de luz en la distancia. Las distancias entre el lápiz láser y la placa y la pantalla de luz son de 120 mm y 500 mm, respectivamente.
         NOTA: Cuanto más lejos esté la distancia entre la pantalla de luz y la placa vibratoria, más obvio aparecerá el fenómeno. También se observa que el método actual se puede utilizar para medir formas de modo axisimétrico o no axisimétrico. Debido a la consideración de la simplicidad y la conveniencia, el presente manuscrito sólo demuestra la aplicación en la determinación de formas de modo axisymmetric de tres placas circulares. Entonces sólo tenemos que medir la amplitud de vibración a lo largo de cualquier dirección radial para reconstruir la forma de modo bidimensional de la placa.
      2. Mueva el lápiz láser a lo largo de la dirección perpendicular a su dirección de longitud para hacer que el punto de incidente escanee sobre un diámetro mientras el generador de señal cambia su frecuencia continuamente. Hálo rápidamente hasta que la longitud del punto se estire significativamente a lo largo del diámetro al escanear en un cierto rango de frecuencia, y aparecen algunos puntos con casi ninguna expansión. Para la placa con un diámetro de 150 mm, 200 mm y 250 mm, los rangos de frecuencia barridos son 200-400 Hz, 100-300 Hz y 50-250 Hz, respectivamente.
      3. Escanee este cierto rango de frecuencia lentamente y elija la frecuencia a la que el punto se expande más obviamente. Se encuentra que para la placa con un diámetro de 150 mm, 200 mm y 250 mm, las frecuencias de resonancia son 346 Hz, 214 Hz y 150 Hz, respectivamente.
2. Preparación de la trayectoria de la luz y el sistema de medición
   1. Coloque la pantalla de luz paralela a la placa vibratoria. Marque la distancia con una regla de medidor y utilice 500 mm como distancia inicial.
   2. Coloque el lápiz láser para proyectar el haz perpendicularmente en la placa de tal manera que el haz se refleje en la pantalla de luz en la distancia. Asegúrese de que la marca realizada antes se puede escanear mientras el lápiz láser se está moviendo.
      NOTA: La luz del rayo láser debe proyectarse perpendicularmente en la placa.
3. Medición experimental
   1. Encienda el generador de señal y establezca la frecuencia de excitación para que sea la misma que la frecuencia de resonancia obtenida en el paso 1.1.3.3. La intensidad de la señal debe ser lo más pequeña posible una vez que el punto de luz en la pantalla de luz es lo suficientemente grande como para ser grabado.
   2. Ajuste el lápiz láser para que el punto de incidente coincida con el primer marcador, que es el marcador más cercano al punto fijo de la placa.
   3. Mueva la pantalla de una distancia D de 500 mm a 1000 mm y mida la longitud del punto L en la pantalla cada 50 mm. Registrar datos en forma tabular.
   4. Ajuste el lápiz láser para hacer el punto de incidente adyacente al siguiente marcador a su vez y repita el paso 1.3.3 hasta que se hayan medido todos los marcadores.
      NOTA: Dado que las placas de acrílico se deforman fácilmente plásticamente bajo excitación, el proceso de medición experimental de una placa no se puede pausar durante mucho tiempo.
   5. Sustituya la placa anterior por la siguiente y repita los pasos 1.3.1 a 1.3.4.

2. Procesamiento de datos

1. Determinar el ángulo entre el incidente y la luz reflejada con la relación:
   
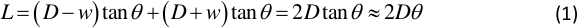
   donde D es la distancia entre la posición de reposo de la placa vibratoria y la pantalla de luz, w es la amplitud vibratoria de la placa, y L es la longitud del punto de luz en la pantalla de luz. Varios pares de D y L se obtienen en el paso 1.3.3.
2. Determine la pendiente 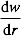de la forma del modo mediante:
   
   NOTA: La pendiente obtenida siempre es positiva con Eqs. (1) y (2).
3. Utilice un signo menos entre dos puntos cero para obtener la distribución de talud verdadera.
   NOTA: No importa si la revisión comienza desde el primer o el segundo punto cero.
4. Integre la distribución de pendiente de cada placa y determine la constante integral por los nodos para obtener la forma de modo con:
   
   NOTA: Los nodos corresponden a la pendiente más grande de la forma de modo. es una constante determinada por la ubicación de las líneas nodales del patrón Chladni que se muestra en la Figura 2.
5. Calcular la incertidumbre de la pendiente¹² con:
   
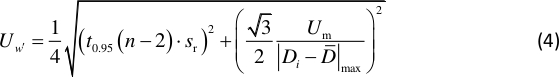
   NOTA: t_0.95(n – 2) es el factor de distribución t con 95% de confianza y grados de libertad n-2, y es alrededor de 2 aquí. S_r es el error estándar de la regresión lineal con D y L, U_m denota la incertidumbre de la distancia medida D_i, y es 0,5 mm aquí. La distancia media medida se define por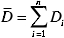 , y n denota el número total de D_{i medidos.}

Resultados

La frecuencia de excitación que puede excitar el patrón de Chladni axisymmétrico se determina a través de la prueba de barrido de frecuencia. Se prueban tres placas de acrílico circular con diámetros de 150 mm, 200 mm y 250 mm, y los resultados muestran que las frecuencias de resonancia axisimétrica de primer orden son 346 Hz, 214 Hz y 150 Hz para las tres placas respectivamente. Se concluye que con un diámetro más grande, la placa es más flexible, y la frecuencia de resonancia correspondiente será más peque?...

Discusión

El método de palanca óptica se adopta en este papel para determinar la forma de modo de una placa, ya que el patrón Chladni sólo puede mostrar las líneas nodales de una placa vibratoria. Para determinar la forma de modo de la placa, la relación entre la pendiente y la distancia de la pantalla de luz y la longitud del punto debe obtenerse de antemano. A continuación, a través del cálculo de integración definido, la forma del modo del patrón Chladni podría determinarse cuantitativamente.

Materiales

Name	Company	Catalog Number	Comments
Acrylic plates	Dongguan Jinzhu Lens Products Factory		Three 1.0-mm-thickness mirrored circular acrylic plates with diameter of 150 mm, 200 mm and 250 mm respectively. They are easily deformed.
Laser pen	Deli Group	2802	Red laser is more friendly to the viewer. The finer the laser beam, the better.
Light screen	Northern Tempered Glass Custom Taobao Store		Several layers of frosted stickers can be placed on the glass to achieve the effect of frosted glass.
Ruler	Deli Group	DL8015	The length is 1m and the division value is 1mm.
Signal generator	Dayang Science Education Taobao Store	TFG6920A	Common ones in university laboratories are available.
Vibrator	Dayang Science Education Taobao Store		The maximum amplitude is 1.5cm.The power is large enough to cause a noticeable phenomenon when the board vibrates. Otherwise, add a power amplifier.