מדידה של צורות מצב כלדני בשיטת מנוף אופטי

Summary

שיטה פשוטה למדידת צורת מצב כלדני על לוח אלסטי על ידי העיקרון של ידית אופטית מוצעת.

Abstract

קביעת כמות דפוס כלדני של צלחת אלסטית היא עניין רב הן במדע פיזי והן ביישומים הנדסיים. בנייר זה מוצעת שיטה למדידת צורות מצב של לוח רוטט המבוסס על שיטת ידית אופטית. שלוש צלחות אקריליות מעגליות הועסקו במדידה תחת רגשות הרמוניים מרכז שונים. שונה משיטה מסורתית, רק עט לייזר רגיל ומ מסך אור עשוי זכוכית טחון מועסקים בגישה חדשנית זו. הגישה היא כדלקמן: עט הלייזר מקרין קרן לצלחת רוטטת בניצב, ואז הקרן משתקפת למסך האור במרחק, שבו נוצר קטע קו עשוי מהמקום ההשתקף. בשל עקרון ההתמדה בראייה, ניתן לקרוא את נקודת האור כקו ישר בהיר. ניתן להשיג את הקשר בין השיפוע של צורת המצב, אורך נקודת האור לבין המרחק של הלוח הרטט ומסך האור באמצעות פעולות אלגבריות. לאחר מכן ניתן לקבוע את צורת המצב על-ידי שילוב התפלגות המדרון עם תנאי גבול מתאימים. צורות מצב שדה מלא של צלחת Chladni יכול גם להיקבע עוד יותר בדרך פשוטה כזו.

Introduction

צורות מצב כלדני הן עניין רב הן יישומים מדעיים והנדסיים. דפוסי כלדני הם תגובות של גלים פיזיים, ואחד יכול להמחיש את דפוס הגל בשיטות שונות. זוהי שיטה ידועה כדי להראות את מצבי רטט שונים על לוח אלסטי על ידי התוויית קווי nodal. חלקיקים קטנים מועסקים תמיד כדי להראות את דפוסי כלדני, שכן הם יכולים לעצור בצמתים שבהם משרעת רוטטת יחסית של הצלחת היא אפס, ואת תנוחות של צמתים להשתנות עם מצב מהדהד כדי ליצור דפוסי כלדני שונים.

חוקרים רבים שמו לב לתבניות Chladni שונות, אבל הם מראים רק את קווי nodal של צורות המצב, את צורות המצב (כלומר, משרעת רטט) בין קווי nodal אינם מאוירים. וולר חקר את התנודות^{החופשיות של מעגל 1},^{ריבוע 2}, משולשים^{בזווית ישרה 3},^{מלבני 4},^{אליפטי 5} צלחות, ודפוסי כלדני שונים מאוירים בו. טואן ואח' שיחזרו דפוסי כלדני שונים באמצעות גישות ניסיוניות ותיאורטיות, ומשוואה הלמהולץ לא-הומוצאנית מאומצת במהלך הדוגמנות^{התיאורטית 6,7}. זוהי שיטה פופולרית של שימוש לייזר דופלר Vibrometer (LDV) או אלקטרונית ספקל דפוס אינטרפרומטריה (ESPI) כדי למדוד באופן כמותי את צורות המצב של דפוסי כלדני^8,9,10. למרות LDV מאפשר רזולוציית משרעת femtometer טווחי תדר גבוה מאוד, למרבה הצער, המחיר של LDV הוא גם קצת יקר עבור הדגמה בכיתה ו / או השכלה בפיזיקה במכללה. עם שיקול זה, הנייר הנוכחי הציע גישה פשוטה כדי לקבוע באופן כמותי את צורות המצב של תבנית Chladni עם עלות נמוכה, מאז רק עט לייזר נוסף ומ מסך אור נדרשים כאן.

שיטת המדידה הנוכחית מאוירת באות 111. לצלחת הרטטת יש שלוש תנוחות שונות: תנוח המנוחה, מיקום 1 ומיקום 2. מיקום 1 ו- 2 מייצג את שני המקומות הרטטים המרביים של הצלחת. עט לייזר מקרין קרן ישרה על פני השטח של הלוח, ואם הלוח מאתר במיקום המנוחה, קרן הלייזר תשתקף ישירות למסך האור. בעוד הצלחת מאתרת בעמדה 1 ו-2, קרן הלייזר תשתקף כדי להצביע A ו-B על המסך הקל, בהתאמה. בשל ההשפעה של התמדה של חזון, יהיה קו ישר בהיר על מסך האור. אורך האור הבהיר L קשור למרחק D בין מסך האור לבין המיקום של נקודת הלייזר. נקודות שונות על הצלחת יש מדרונות שונים, אשר יכול להיקבע על ידי מערכת היחסים בין L ו D. לאחר קבלת המדרון של צורת המצב בנקודות שונות על הלוח, הבעיה הופכת אינטגרלי מובהק. בעזרת משרעת רטט הגבול של הלוח ונתוני המדרון הדיסקרטי, ניתן להשיג בקלות את צורת המצב של הלוח הרטט. כל ההתקנה הניסיונית ניתנת בדמות 211.

מאמר זה מתאר את ההתקנה וההליך הניסיוניים של שיטת המנוף האופטי כדי למדוד את צורות מצב כלדני. כמה תוצאות ניסיוניות טיפוסיות מאוירות גם.

Protocol

1. התקנה ניסיונית והליכים

הערה: הגדר את המערכת הניסיונית כפיצג באות 2.

1. הכנת מערכת הרטט
   1. הכן שלוש לוחות אקריליק עגולים בעובי 1.0 מ"מ בקוטר של 150 מ"מ, 200 מ"מ ו-250 מ"מ בהתאמה. לקדוח חור של 3 מ"מ קוטר במרכז כל צלחת. סמן מספר נקודות שחורות כל 5 מ"מ ברדיוס שרירותי.
   2. חבר כל צלחת לרף האקטואט של הויברטור עם בורג בנקודת האמצע. הניעו את הויברטור עם גל סינוס באמצעות מחולל צורות גל, והגדרות ברירת המחדל יספיקו לניסוי התהודה.
      הערה: כיוון העירור של הויברטור הוא אופקי לנוחות הזזת המסך לאחר מכן.
   3. רכישת תדירות התהודה
      1. מקם את עט הלייזר כדי להקרין את קרן הלייזר על הלוח הרוטט בניצב כך שהקרן תשתקף למסך האור במרחק. המרחקים בין עט הלייזר לצלחת ומ מסך האור הם 120 מ"מ ו-500 מ"מ, בהתאמה.
         הערה: ככל שהמרחק בין מסך האור לצלחת הרוטטת, כך מופיעה התופעה ברורה יותר. כמו כן, יום לב כי ניתן להשתמש בשיטה הנוכחית כדי למדוד צורות מצב צירי או לא-צירי. בשל השיקול של פשטות ונוחות, כתב היד הנוכחי מדגים את היישום רק בקביעת צורות מצב צירי של שלוש לוחות עגולים. אז אנחנו רק צריכים למדוד את משרעת הרטט לאורך כל כיוון רדיאלי כדי לשחזר את צורת המצב הדו מימדי של הלוח.
      2. הזז את עט הלייזר לאורך הכיוון בניצב לכיוון האורך שלו כדי לגרום לנקודת האירוע לסרוק על קוטר בזמן שגנרטור האות משנה את התדר שלו ברציפות. עשה זאת במהירות עד שאורך הספוט נמתח באופן משמעותי לאורך הקוטר בעת סריקה בטווח תדרים מסוים, ונקודות מסוימות ללא התרחבות כמעט מופיעות. עבור הלוח בקוטר של 150 מ"מ, 200 מ"מ ו-250 מ"מ, טווחי התדרים שנסחפו הם 200-400 הרץ, 100-300 הרץ ו-50-250 הרץ, בהתאמה.
      3. סרוק את טווח התדרים הזה באיטיות ובחר את התדירות שבה הנקודה מתרחבת באופן ברור ביותר. נמצא כי עבור הלוח בקוטר של 150 מ"מ, 200 מ"מ ו-250 מ"מ, תדרי התהודה הם 346 הרץ, 214 הרץ ו-150 הרץ, בהתאמה.
2. הכנת נתיב האור ומערכת המדידה
   1. מקם את מסך האור במקביל לצלחת הרטטת. סמן את המרחק בסרגל מטר והשתמש ב- 500 מ"מ כמרחק ההתחלה.
   2. מניחים את עט הלייזר כדי להקרין את הקרן בניצב על הצלחת כך שהקרן תשתקף למסך האור במרחק. ודא שניתן לסרוק את הסימן שנעשה לפני כן בזמן שמכלאת הלייזר זזה.
      הערה: יש להקרין את אור קרן הלייזר בניצב על הלוח.
3. מדידה ניסיונית
   1. הפעל את מחולל האותות והגדר את תדירות העירור כך שתהיה זהה לתדירות התהודה שהושגה בשלב 1.1.3.3. עוצמת האות צריכה להיות קטנה ככל האפשר ברגע שאור האור במסך האור גדול מספיק כדי להיות מוקלט.
   2. כוונן את עט הלייזר כדי להפוך את נקודת האירוע חופפת עם הסמן הראשון, שהוא הסמן הקרוב ביותר לנקודה הקבועה של הלוח.
   3. הזז את המסך ממרחק D של 500 מ"מ ל- 1000 מ"מ ומדד את אורך הספוט L על המסך כל 50 מ"מ. רכך נתונים בצורה טבלאית.
   4. כוונן את עט הלייזר כדי להפוך את נקודת האירוע בסמוך לסמן הבא בתורו וחזור על שלב 1.3.3 עד שכל סמנים נמדדו.
      הערה: מאז צלחות אקרילי הם מעוותים בקלות פלסטיק תחת העירה, תהליך המדידה הניסיוני של צלחת אחת לא ניתן להשהות במשך זמן רב.
   5. החלף את הלוחית הקודמת בצלחת הבאה וחזור על שלבים 1.3.1 עד 1.3.4.

2. עיבוד נתונים

1. לקבוע את הזווית בין האירוע לאור משתקף עם קשר גומלין:
   
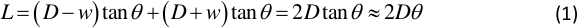
   כאשר D הוא המרחק בין מיקום המנוחה של הלוח רוטט למסך האור, w רוטט משרעת של הצלחת, ו- L הוא אורך נקודת האור על מסך האור. מספר זוגות של D ו- L מתקבלים בשלב 1.3.3.
2. קבע א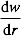ת השיפוע של צורת המצב על-ידי:
   
   הערה: המדרון שהושג הוא תמיד חיובי עם Eqs. (1) ו-(2).
3. השתמש בסימן חיסור בין שתי נקודות אפס כדי להשיג את התפלגות המדרון האמיתית.
   הערה: אין זה משנה אם המהדורה מתחילה מנקודת האפס הראשונה או השנייה.
4. שלב את התפלגות המדרון של כל לוח וקבוע את הקבוע האינטגרלי על-ידי צמהים כדי להשיג את צורת המצב עם:
   
   הערה: צמהים תואמים למדרון הגדול ביותר של צורת המצב. הוא קבוע שנקבע על-ידי המיקום של השורות nodal של תבנית כלדני המוצגת באות 2.
5. חשב את אי הוודאות של המדרון¹² עם:
   
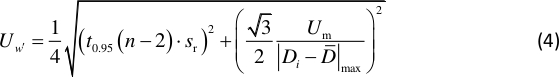
   הערה: t_0.95(n – 2) הוא גורם ההפצה t עם 95% ביטחון ודרגות של חופש n-2, וזה בערך 2 כאן. S_{r היא} השגיאה הסטנדרטית של הרגרסיה ליניארית עם D ו- L, U_m מציין את חוסר הוודאות של המרחק נמדד D_i, והוא 0.5 מ"מ כאן. המרחק הנמדד הממוצע מוגדר על-ידי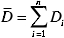 , ו- n מציין את המספר הכולל של D_{i שנמדד}.

תוצאות

תדירות העירור שיכולה לעורר דפוס כלדני צירי נקבע באמצעות בדיקת התדירות הגורפת. שלוש לוחות אקריליק עגולים בקוטרים של 150 מ"מ, 200 מ"מ ו-250 מ"מ נבדקים, והתוצאות מראות כי תדרי התהודה הציריים של הסדר הראשון הם 346 הרץ, 214 הרץ ו-150 הרץ עבור שלוש הלוחות בהתאמה. הוא הגיע למסקנה כי בקוטר גדול יותר, הצלחת גמיש...

Discussion

שיטת הידית האופטית מאומצת בנייר זה כדי לקבוע את צורת המצב של צלחת, שכן תבנית כלדני יכולה להראות רק את קווי הנודאל של לוח רוטט. כדי לקבוע את צורת המצב של הלוח, יש להשיג מראש את הקשר בין המדרון והמרחק של מסך האור ואורך הספוט. לאחר מכן, באמצעות חישוב אינטגרציה מוחלט, צורת המצב של תבנית כלדני יכול...

Materials

Name	Company	Catalog Number	Comments
Acrylic plates	Dongguan Jinzhu Lens Products Factory		Three 1.0-mm-thickness mirrored circular acrylic plates with diameter of 150 mm, 200 mm and 250 mm respectively. They are easily deformed.
Laser pen	Deli Group	2802	Red laser is more friendly to the viewer. The finer the laser beam, the better.
Light screen	Northern Tempered Glass Custom Taobao Store		Several layers of frosted stickers can be placed on the glass to achieve the effect of frosted glass.
Ruler	Deli Group	DL8015	The length is 1m and the division value is 1mm.
Signal generator	Dayang Science Education Taobao Store	TFG6920A	Common ones in university laboratories are available.
Vibrator	Dayang Science Education Taobao Store		The maximum amplitude is 1.5cm.The power is large enough to cause a noticeable phenomenon when the board vibrates. Otherwise, add a power amplifier.