Measurement of Chladni Mode Shapes with an Optical Lever Method

Summary

A simple method of measuring the Chladni mode shape on an elastic plate by the principle of an optical lever is proposed.

Abstract

Quantitatively determining the Chladni pattern of an elastic plate is of great interest in both physical science and engineering applications. In this paper, a method of measuring mode shapes of a vibrating plate based on an optical lever method is proposed. Three circular acrylic plates were employed in the measurement under different center harmonic excitations. Different from a traditional method, only an ordinary laser pen and a light screen made of ground glass are employed in this novel approach. The approach is as follows: the laser pen projects a beam to the vibrating plate perpendicularly, and then the beam is reflected to the light screen in the distance, on which a line segment made of the reflected spot is formed. Due to the principle of vision persistence, the light spot could be read as a bright straight line. The relationship between the slope of the mode shape, length of the light spot and the distance of the vibrating plate and the light screen can be obtained with algebraic operations. Then the mode shape can be determined by integrating the slope distribution with suitable boundary conditions. The full-field mode shapes of Chladni plate could also be determined further in such a simple way.

Introduction

Chladni mode shapes are of great interest in both science and engineering applications. Chladni patterns are reactions of physical waves, and one can illustrate the wave pattern with various methods. It is a well-known method to show the various modes of vibration on an elastic plate by outlining the nodal lines. Small particles are always employed to show the Chladni patterns, since they can stop at the nodes where the relative vibrating amplitude of the plate is zero, and the positions of the nodes vary with resonant mode to form various Chladni patterns.

Many researchers have paid attention to various Chladni patterns, but they only show the nodal lines of the mode shapes, the mode shapes (i.e., vibration amplitude) between the nodal lines are not illustrated. Waller investigated the free vibrations of a circle¹, a square², an isosceles right angled triangles³, a rectangular⁴, elliptical⁵ plates, and different Chladni patterns are illustrated therein. Tuan et al. reconstructed different Chladni patterns through both experimental and theoretical approaches, and the inhomogeneous Helmholtz equation is adopted during the theoretical modeling^6,7. It is a popular method of using Laser Doppler Vibrometer (LDV) or Electronic Speckle Pattern Interferometry (ESPI) to quantitatively measure the mode shapes of the Chladni patterns^8,9,10. Although LDV enables femtometer amplitude resolution and very high frequency ranges, unfortunately, the price of LDV is also a little expensive for classroom demonstration and/or college physics education. With this consideration, the present paper proposed a simple approach to quantitatively determine the mode shapes of a Chladni pattern with low cost, since only an extra laser pen and a light screen are needed here.

The present measurement method is illustrated in Figure 1¹¹. The vibrating plate has three different positions: the rest position, position 1 and position 2. Position 1 and 2 represent the two maximum vibrating places of the plate. A laser pen projects a straight beam on the surface of the plate, and if the plate locates at the rest position, the laser beam will be directly reflected to the light screen. While the plate locates at position 1 and 2, then the laser beam will be reflected to point A and B on the light screen, respectively. Due to the effect of persistence of vision, there will be a bright straight line on the light screen. The length of the bright light L is related to the distance D between the light screen and the location of the laser point. Different points on the plate have different slopes, which could be determined by the relationship between L and D. After obtaining the slope of the mode shape at different points on the plate, the problem turns into a definite integral. With the help of the boundary vibration amplitude of the plate and the discrete slope data, the mode shape of the vibrating plate can be obtained easily. The whole experimental setup is given in Figure 2¹¹.

This paper describes the experimental setup and procedure for the optical lever method to measure the Chladni mode shapes. Some typical experimental results are also illustrated.

Protocol

1. Experimental setup and procedures

NOTE: Set up the experimental system as shown in Figure 2.

1. Preparation of the vibration system
   1. Prepare three 1.0-mm-thickness mirrored circular acrylic plates with diameter of 150 mm, 200 mm and 250 mm respectively. Drill a hole of 3 mm in diameter at the center of each plate. Mark several black points every 5 mm along an arbitrary radius.
   2. Attach each plate to the actuate bar of the vibrator with a bolt in the middle point. Drive the vibrator with a sine wave using a waveform generator, and default settings will be enough for the resonance experiment.
      NOTE: The excitation direction of the vibrator is horizontal for the convenience of moving the screen afterwards.
   3. Acquisition of the resonance frequency
      1. Place the laser pen to project the laser beam to the vibrating plate perpendicularly such that the beam is reflected to the light screen in the distance. The distances between the laser pen and the plate and the light screen are 120 mm and 500 mm, respectively.
         NOTE: The farther the distance between the light screen and the vibrating plate, the more obvious the phenomenon appears. It is also noted that the present method can be used to measure either axisymmetric or non-axisymmetric mode shapes. Due to the consideration of simplicity and convenience, the present manuscript only demonstrates the application in determining axisymmetric mode shapes of three circular plates. Then we just need to measure the vibration amplitude along any radial direction to reconstruct the two-dimensional mode shape of the plate.
      2. Move the laser pen along the direction perpendicular to its length direction to make the incident point scan over a diameter while the signal generator changing its frequency continuously. Do it quickly until the spot length is significantly stretched along the diameter when scanning in a certain frequency range, and some spots with almost no expansion appear. For the plate with a diameter of 150 mm, 200 mm and 250 mm, the frequency ranges swept are 200-400 Hz, 100-300 Hz and 50-250 Hz, respectively.
      3. Scan this certain frequency range slowly and pick out the frequency at which the spot expands most obviously. It is found that for the plate with a diameter of 150 mm, 200 mm and 250 mm, the resonance frequencies are 346 Hz, 214 Hz and 150 Hz, respectively.
2. Preparation of the light path and measurement system
   1. Place the light screen parallel to the vibrating plate. Mark the distance with a meter ruler, and use 500 mm as the starting distance.
   2. Place the laser pen to project the beam perpendicularly on the plate such that the beam is reflected to the light screen in the distance. Make sure that the mark made before can be scanned while the laser pen is moving.
      NOTE: The laser beam light must be projected perpendicularly on the plate.
3. Experimental measurement
   1. Turn on the signal generator and set the excitation frequency to be the same as the resonance frequency obtained in step 1.1.3.3. The signal intensity should as small as possible once the light spot on the light screen is large enough to be recorded.
   2. Adjust the laser pen to make the incident point coincide with the first marker, which is the nearest marker to the fixed point of the plate.
   3. Move the screen from a distance D of 500 mm to 1000 mm and measure the spot length L on the screen every 50 mm. Record data in tabular form.
   4. Adjust the laser pen to make the incident point adjacent to the next marker in turn and repeat step 1.3.3 until all the markers have been measured.
      NOTE: Since acrylic plates are easily deformed plastically under excitation, the experimental measurement process of one plate cannot be paused for a long time.
   5. Replace the former plate with the next one and repeat steps 1.3.1 to 1.3.4.

2. Data processing

1. Determine the angle θ between the incident and reflected light with relationship:
   
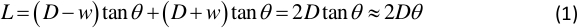
   where D is the distance between the rest position of the vibrating plate and the light screen, w is vibrating amplitude of the plate, and L is the length of the light spot on the light screen. Several pairs of D and L are obtained in step 1.3.3.
2. Determine the slope 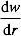of the mode shape by:
   
   NOTE: The obtained slope is always positive with Eqs.(1) and (2).
3. Use a minus sign between two zero points to obtain the true slope distribution.
   NOTE: It does not matter whether the revision begins from the first or the second zero point.
4. Integrate the slope distribution of each plate and determine the integral constant by the nodes to obtain the mode shape with:
   
   NOTE: Nodes correspond to the largest slope of the mode shape. is a constant determined by the location of the nodal lines of the Chladni pattern shown in Figure 2.
5. Compute the uncertainty of the slope¹² with:
   
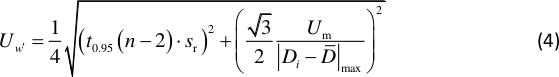
   NOTE: t_0.95(n – 2) is the t distribution factor with 95% confidence and degrees of freedom n-2, and it is about 2 here. S_r is the standard error of the linear regression with D and L, U_m denotes the uncertainty of the measured distance D_i, and is 0.5 mm here. The average measured distance is defined by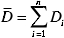 , and n denotes the total number of measured D_i.

Results

The excitation frequency that can excite axisymmetric Chladni pattern is determined through the frequency sweeping test. Three circular acrylic plates with diameters of 150 mm, 200 mm and 250 mm are tested, and results show that the first order axisymmetric resonance frequencies are 346 Hz, 214 Hz and 150 Hz for the three plates respectively. It is concluded that with larger diameter, the plate is more flexible, and the corresponding resonance frequency will be smaller. The Chladni patterns of the acrylic plate with diff...

Discussion

The optical lever method is adopted in this paper to determine the mode shape of a plate, since the Chladni pattern can only show the nodal lines of a vibrating plate. To determine the mode shape of the plate, the relationship between the slope and distance of the light screen and spot length should be obtained in advance. Then through definite integration calculation, the mode shape of the Chladni pattern could be quantitatively determined.

Generally, the whole process of the present approach...

Materials

Name	Company	Catalog Number	Comments
Acrylic plates	Dongguan Jinzhu Lens Products Factory		Three 1.0-mm-thickness mirrored circular acrylic plates with diameter of 150 mm, 200 mm and 250 mm respectively. They are easily deformed.
Laser pen	Deli Group	2802	Red laser is more friendly to the viewer. The finer the laser beam, the better.
Light screen	Northern Tempered Glass Custom Taobao Store		Several layers of frosted stickers can be placed on the glass to achieve the effect of frosted glass.
Ruler	Deli Group	DL8015	The length is 1m and the division value is 1mm.
Signal generator	Dayang Science Education Taobao Store	TFG6920A	Common ones in university laboratories are available.
Vibrator	Dayang Science Education Taobao Store		The maximum amplitude is 1.5cm.The power is large enough to cause a noticeable phenomenon when the board vibrates. Otherwise, add a power amplifier.