光レバー法によるクラドニモード形状の測定

要約

光レバーの原理により弾性板上のクラドニモード形状を測定する簡単な方法が提案されている。

要約

弾性プレートのクラドニパターンを定量的に決定することは、物理科学と工学の両方のアプリケーションに大きな関心を持っています。本論文では、光学レバー法に基づく振動板の形状を測定する方法を提案する。3つの円形アクリル板を異なる中心高調波励起下で測定に採用した。従来の方法とは異なり、この新しいアプローチでは、普通のレーザーペンとグラウンドガラスで作られた光スクリーンのみが採用されています。アプローチは次の通りです:レーザーペンは振動板にビームを垂直に投影し、その後、ビームは反射されたスポットから成る線分が形成される遠くの光スクリーンに反射されます。ビジョン持続性の原理により、ライトスポットは明るい直線として読み取ることができる。モード形状の傾き、光スポットの長さと振動板と光スクリーンの距離との関係は、代数演算で得ることができる。次に、適当な境界条件で傾斜分布を統合することにより、モード形状を決定することができる。Chladniプレートのフルフィールドモード形状も、このような簡単な方法でさらに決定することができます。

概要

クラドニモード形状は、科学と工学の両方のアプリケーションに大きな関心を持っています。クラドニパターンは物理波の反応であり、波のパターンを様々な方法で示すことができます。節点線を概説することで、弾性プレートに様々な振動モードを表示する方法としてよく知られています。小さな粒子は、プレートの相対的な振動振幅がゼロであるノードで停止することができ、ノードの位置は共鳴モードによって変化してさまざまなクラドニパターンを形成するため、常にクラドニパターンを示すために採用されます。

多くの研究者は、様々なクラドニパターンに注意を払っていますが、それらは、モード形状の節点線のみを示し、節点線間のモード形状(すなわち、振動振幅)は図示されていません。ウォーラーは円^1、正方形^2、正角三角形³のアイソセッセ、長方形^4、楕円形^の5プレート、および異なるクラドニパターンの自由振動を調査した。Tuan et al. は、実験と理論の両方のアプローチを通じて異なるクラドニパターンを再構築し、理論モデリング^6,7の間に不均一なヘルムホルツ方程式が採用される。これは、レーザードップラーバイブロメータ(LDV)または電子スペックルパターン干渉法(ESPI)を使用して、クラドニパターン^8、9、10のモード形状を定量的に測定する一般的な方法である。LDVは、フェムトメーターの振幅分解能と非常に高い周波数範囲を可能にしますが、残念ながら、LDVの価格は教室のデモンストレーションや大学の物理学教育のために少し高価です。この点を考慮して、本論文は、追加のレーザーペンとライトスクリーンのみが必要であるため、低コストでクラドニパターンのモード形状を定量的に決定する簡単なアプローチを提案した。

本測定方法は 、図1¹¹に示す。振動板は3つの異なる位置を有する:残りの位置、位置1および位置2。位置 1 と 2 は、プレートの最大振動場所を表します。レーザーペンはプレートの表面にまっすぐなビームを投影し、プレートが残りの位置に位置する場合、レーザービームは直接光スクリーンに反射されます。プレートが位置 1 と 2 に位置している間、レーザービームはライトスクリーン上の点 A と B にそれぞれ反射されます。ビジョンの持続性の効果により、ライトスクリーン上に明るい直線が表示されます。明るい光 L の長さは、光スクリーンとレーザー点の位置との間の距離 D に関連する。プレート上の異なる点は 、L と Dの関係によって決定することができる異なる斜面を有する。プレート上の異なる点でモード形状の勾配を得た後、問題は明確な積分に変わる。プレートの境界振動振幅と離散傾斜データの助けを借りて、振動板のモード形状を容易に得ることができます。実験のセットアップ全体を図 2¹¹に示します。

本論文では、クラドニモード形状を測定する光レバー法の実験設定と手順について説明する。いくつかの典型的な実験結果も示される。

プロトコル

1. 実験的なセットアップと手順

注: 図 2に示すように、実験システムをセットアップします。

1. 振動システムの準備
   1. 直径150mm、200mm、250mmの3枚の1.0mm-厚さのミラー円形アクリルプレートを用意します。各プレートの中心に直径3mmの穴を開けます。任意の半径に沿って、5 mm ごとに複数の黒い点をマークします。
   2. 各プレートを、中間点のボルトでバイブレーターのアクチュエートバーに取り付けます。波形発生器を使用して正位波でバイブレーターを駆動し、デフォルト設定は共振実験のために十分です。
      注:振動子の励起方向は、その後画面を移動する利便性のために水平です。
   3. 共振周波数の獲得
      1. レーザーペンを配置して、レーザービームを振動板に垂直に投影し、遠くに光スクリーンに反射するようにします。レーザーペンとプレートとライトスクリーンの距離はそれぞれ120mmと500mmです。
         注: ライトスクリーンと振動プレートの距離が遠いほど、現象がより明白に現れます。また、本方法は、軸対称または非軸対称モード形状の測定に使用できることにも留意した。簡便さと利便性を考慮して、本稿は3つの円形プレートの軸対称モード形状を決定する際の適用のみを示している。次に、プレートの2次元モード形状を再構築するために、任意の半径方向に沿った振動振幅を測定する必要があります。
      2. レーザーペンを長さ方向に垂直に移動して、信号発生器が連続して周波数を変化させながら、入射点を直径をスキャンします。特定の周波数範囲でスキャンする場合、スポット長が直径に沿って大幅に伸縮し、膨張がほとんどないスポットが現れるまで、素早くそれを行います。直径150mm、200mm、250mmのプレートの場合、周波数範囲はそれぞれ200-400 Hz、100-300 Hz、50-250 Hzです。
      3. この特定の周波数範囲をゆっくりとスキャンし、スポットが最も明らかに拡大する周波数を選びます。直径150mm、200mm、250mmのプレートの場合、共振周波数はそれぞれ346Hz、214Hz、150Hzであることがわかりました。
2. 光路・測定システムの準備
   1. 照明スクリーンを振動板に平行に配置します。距離をメーター定規でマークし、開始距離として 500 mm を使用します。
   2. レーザーペンを配置して、ビームが遠くの光スクリーンに反射するように、ビームをプレート上に垂直に投影します。レーザーペンの動きの間に前に作られたマークがスキャンできることを確認してください。
      メモ: レーザー光はプレートに垂直に射出する必要があります。
3. 実験測定
   1. 信号発生器をオンにし、励起周波数をステップ1.1.3.3で得た共振周波数と同じに設定します。信号強度は、ライトスクリーンのライトスポットが記録できるほど大きければ、できるだけ小さくする必要があります。
   2. レーザーペンを調整して、入射点がプレートの固定点に最も近いマーカーである最初のマーカーと一致するようにします。
   3. 画面を500mmから1000mmまでの距離 D から移動し、50mmごとに画面のスポット長 L を測定します。表形式でデータを記録します。
   4. レーザーペンを調整して次のマーカーに隣接する入射点を作り、すべてのマーカーが測定されるまでステップ1.3.3を繰り返します。
      注:アクリル板は励起下で容易に塑性に変形するので、1つの版の実験的測定プロセスは長い間一時停止することができません。
   5. 前のプレートを次のプレートに置き換え、手順 1.3.1 ~ 1.3.4 を繰り返します。

2. データ処理

1. リレーションを持つインシデントと反射光の間の角度 θ を決定します。
   
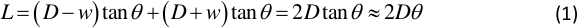
   ここで Dは振動板の残り位置とライトスクリーンの間の距離、wはプレートの振動振幅、Lはライトスクリーン上のライト スポットの長さです。DとLのいくつかのペアがステップ1.3.3で得られます。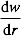
2. モードシェイプの勾配を次の方法で決定します。
   
   注: 取得した傾斜は、Eqs では常に正です。(1)および(2)。
3. 2 つのゼロ点の間にマイナス記号を使用して、真の勾配分布を取得します。
   注: リビジョンが最初のゼロポイントから始まるか、2 番目のゼロポイントから始まるかは関係ありません。
4. 各プレートの勾配分布を統合し、ノードによって積分定数を決定し、モード形状を次の値で取得します。
   
   注: 節点は、モード形状の最大勾配に対応します。は図 2に示す Chladni パターンの節点線の位置によって決まる定数です。
5. 次の値を使用して、傾斜^{角 12} の不確実性を計算します。
   
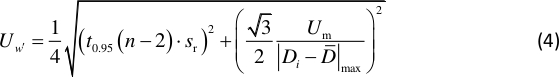
   注: t_0.95(n – 2) は 95% の信頼度と自由度n-2 のt分布係数であり、ここでは約 2 です。S_rは、DおよびLを使用した線形回帰の標準誤差であり、U_mは測定距離D_iの不確実性を示し、ここでは 0.5 mm です。平均測定距離は で定義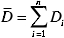 され、nは測定された D _iの総数を示します。

結果

軸対称クラドニパターンを励起できる励起周波数は、周波数スイープ試験を通じて決定されます。直径150mm、200mm、250mmの3つの円形アクリルプレートがテストされ、その結果、3つのプレートに対して、第1次軸対称共振周波数が346Hz、214Hz、150Hzであることを示しています。大きな直径でプレートがより柔軟になり、対応する共振周波数が小さくなると結論付けられます。異なる直径を有するア?...

ディスカッション

この論文では、クロドニパターンは振動板の節線しか示せないため、プレートのモード形状を決定するために光学レバー法を採用しています。プレートのモード形状を決定するために、ライトスクリーンの傾きと距離とスポット長との関係は、事前に得られるべきである。次に、明確な積分計算を通じて、Chladniパターンのモード形状を定量的に決定することができた。

?...

資料

Name	Company	Catalog Number	Comments
Acrylic plates	Dongguan Jinzhu Lens Products Factory		Three 1.0-mm-thickness mirrored circular acrylic plates with diameter of 150 mm, 200 mm and 250 mm respectively. They are easily deformed.
Laser pen	Deli Group	2802	Red laser is more friendly to the viewer. The finer the laser beam, the better.
Light screen	Northern Tempered Glass Custom Taobao Store		Several layers of frosted stickers can be placed on the glass to achieve the effect of frosted glass.
Ruler	Deli Group	DL8015	The length is 1m and the division value is 1mm.
Signal generator	Dayang Science Education Taobao Store	TFG6920A	Common ones in university laboratories are available.
Vibrator	Dayang Science Education Taobao Store		The maximum amplitude is 1.5cm.The power is large enough to cause a noticeable phenomenon when the board vibrates. Otherwise, add a power amplifier.