Misurazione delle forme in modalità Chladni con un metodo a leva ottica

Riepilogo

Viene proposto un metodo semplice per misurare la forma in modalità Chladni su una piastra elastica secondo il principio di una leva ottica.

Abstract

Determinare quantitativamente il modello Chladni di una piastra elastica è di grande interesse sia per le scienze fisiche che per le applicazioni ingegneristiche. In questo documento viene proposto un metodo di misurazione delle forme in modalità di una piastra vibrante basato su un metodo a leva ottica. Tre piastre acriliche circolari sono state impiegate nella misurazione sotto diverse eccitazioni armoniche al centro. Diverso da un metodo tradizionale, in questo nuovo approccio vengono impiegati solo una normale penna laser e uno schermo luminoso in vetro macinato. L'approccio è il seguente: la penna laser proietta un fascio alla piastra vibrante perpendicolarmente, e quindi il fascio viene riflesso sullo schermo luminoso in lontananza, su cui si forma un segmento di linea fatto del punto riflesso. A causa del principio di persistenza della vista, il punto luce potrebbe essere letto come una linea retta brillante. La relazione tra la pendenza della forma della modalità, la lunghezza del punto luce e la distanza della piastra vibrante e dello schermo luminoso può essere ottenuta con operazioni algebriche. Quindi la forma della modalità può essere determinata integrando la distribuzione della pendenza con condizioni limite adeguate. Anche le forme in modalità full-field della piastra di Chladni potrebbero essere ulteriormente determinate in modo così semplice.

Introduzione

Le forme in modalità Chladni sono di grande interesse sia per le applicazioni scientifiche che ingegneristiche. I modelli di Chladni sono reazioni di onde fisiche, e si può illustrare il modello d'onda con vari metodi. È un metodo ben noto per mostrare le varie modalità di vibrazione su una piastra elastica delineando le linee nodali. Piccole particelle sono sempre utilizzate per mostrare i modelli di Chladni, poiché possono fermarsi ai nodi in cui l'ampiezza vibrante relativa della piastra è zero, e le posizioni dei nodi variano con la modalità risonante per formare vari modelli di Chladni.

Molti ricercatori hanno prestato attenzione a vari modelli chladni, ma mostrano solo le linee nodali delle forme del modo, le forme di modalità (cioè l'ampiezza delle vibrazioni) tra le linee nodali non sono illustrate. Waller ha studiato le vibrazioni libere di^{un cerchio 1,un quadrato 2,}un isoscele triangoli angolati a^{destra 3,un rettangolare 4,ellittiche 5} piastre e diversi motivi Chladni sono illustrati in esso. Ha ricostruito diversi modelli di Chladni attraverso approcci sia sperimentali che teorici, e l'equazione di Helmholtz disomogenea viene adottata durante la modellazione^{teorica 6,7}. È un metodo popolare per utilizzare laser Doppler Vibrometer (LDV) o Electronic Speckle Pattern Interferometry (ESPI) per misurare quantitativamente le forme di modalità dei modelli Chladni^8,9,10. Sebbene LDV consenta una risoluzione dell'ampiezza del femtometro e intervalli di frequenza molto elevati, sfortunatamente, il prezzo della LDV è anche un po 'costoso per la dimostrazione in classe e / o l'educazione fisica universitaria. Con questa considerazione, il presente documento ha proposto un approccio semplice per determinare quantitativamente le forme di modalità di un modello Chladni a basso costo, poiché qui sono necessari solo una penna laser extra e uno schermo luminoso.

Il presente metodo di misurazione è illustrato nella figura 1¹¹. La piastra vibrante ha tre diverse posizioni: la posizione di riposo, la posizione 1 e la posizione 2. Le posizioni 1 e 2 rappresentano i due punti massimi di vibrazione della piastra. Una penna laser proietta un fascio dritto sulla superficie della piastra e, se la piastra si trova nella posizione di riposo, il raggio laser verrà riflesso direttamente sullo schermo luminoso. Mentre la piastra si trova in posizione 1 e 2, il raggio laser verrà riflesso rispettivamente al punto A e B sullo schermo luminoso. A causa dell'effetto della persistenza della vista, ci sarà una linea retta brillante sullo schermo luminoso. La lunghezza della luce intensa L è correlata alla distanza D tra lo schermo luminoso e la posizione del punto laser. Diversi punti sul piatto hanno pendenze diverse, che potrebbero essere determinate dal rapporto tra L e D. Dopo aver ottenuto la pendenza della forma della modalità in diversi punti della piastra, il problema si trasforma in un integrale definito. Con l'aiuto dell'ampiezza delle vibrazioni limite della piastra e dei dati di pendenza discreti, è possibile ottenere facilmente la forma in modalità della piastra vibrante. L'intera configurazione sperimentale è fornita nella figura 2¹¹.

In questo documento vengono descritte la configurazione sperimentale e la procedura per il metodo della leva ottica per misurare le forme in modalità Chladni. Vengono illustrati anche alcuni risultati sperimentali tipici.

Protocollo

1. Allestimento e procedure sperimentali

NOTA: Impostare il sistema sperimentale come illustrato nella figura 2.

1. Preparazione del sistema di vibrazioni
   1. Preparare tre piastre acriliche circolari specchiate dello spessore di 1,0 mm con diametro rispettivamente di 150 mm, 200 mm e 250 mm. Praticare un foro di 3 mm di diametro al centro di ogni piastra. Contrassegnare diversi punti neri ogni 5 mm lungo un raggio arbitrario.
   2. Attaccare ogni piastra alla barra di azionamento del vibratore con un bullone nel punto centrale. Guida il vibratore con un'onda sina usando un generatore di forme d'onda e le impostazioni predefinite saranno sufficienti per l'esperimento di risonanza.
      NOTA: La direzione di eccitazione del vibratore è orizzontale per la comodità di spostare lo schermo in seguito.
   3. Acquisizione della frequenza di risonanza
      1. Posizionare la penna laser per proiettare il raggio laser sulla piastra vibrante perpendicolarmente in modo che il fascio si rifletta sullo schermo luminoso in lontananza. Le distanze tra la penna laser e la piastra e lo schermo luminoso sono rispettivamente di 120 mm e 500 mm.
         NOTA: Più lontana è la distanza tra lo schermo luminoso e la piastra vibrante, più evidente appare il fenomeno. Si noti inoltre che il metodo presente può essere utilizzato per misurare forme in modalità assimmetrica o non assimmetrica. A causa della considerazione della semplicità e della convenienza, il presente manoscritto dimostra solo l'applicazione nella determinazione delle forme in modalità assimmetrica di tre lastre circolari. Quindi dobbiamo solo misurare l'ampiezza delle vibrazioni lungo qualsiasi direzione radiale per ricostruire la forma bidimensionale della piastra.
      2. Spostare la penna laser lungo la direzione perpendicolare alla sua direzione di lunghezza per fare la scansione del punto incidente su un diametro mentre il generatore di segnale cambia continuamente la sua frequenza. Fallo rapidamente fino a quando la lunghezza del punto non è significativamente allungata lungo il diametro durante la scansione in un certo intervallo di frequenza e appaiono alcuni punti senza quasi alcuna espansione. Per la piastra con un diametro di 150 mm, 200 mm e 250 mm, le gamme di frequenza sweep sono rispettivamente di 200-400 Hz, 100-300 Hz e 50-250 Hz.
      3. Scansiona lentamente questo certo intervallo di frequenza e scegli la frequenza con cui il punto si espande più ovviamente. Si scoprì che per la piastra con un diametro di 150 mm, 200 mm e 250 mm, le frequenze di risonanza sono rispettivamente di 346 Hz, 214 Hz e 150 Hz.
2. Preparazione del percorso luminoso e del sistema di misurazione
   1. Posizionare lo schermo luminoso parallelo alla piastra vibrante. Contrassegnare la distanza con un righello del misuratore e utilizzare 500 mm come distanza di partenza.
   2. Posizionare la penna laser per proiettare il fascio perpendicolarmente sulla piastra in modo che il fascio si rifletta sullo schermo luminoso in lontananza. Assicurarsi che il segno fatto prima possa essere scansionato mentre la penna laser è in movimento.
      NOTA: La luce del raggio laser deve essere proiettata perpendicolarmente sulla piastra.
3. Misurazione sperimentale
   1. Accendere il generatore di segnale e impostare la frequenza di eccitazione come la stessa frequenza di risonanza ottenuta nel passaggio 1.1.3.3. L'intensità del segnale dovrebbe essere il più piccola possibile una volta che il punto luce sullo schermo luminoso è abbastanza grande da essere registrato.
   2. Regolare la penna laser per far coincidere il punto incidente con il primo marcatore, che è il marcatore più vicino al punto fisso della piastra.
   3. Spostare lo schermo da una distanza D da 500 mm a 1000 mm e misurare la lunghezza spot L sullo schermo ogni 50 mm. Registrare i dati in forma tabellare.
   4. Regolare la penna laser per rendere il punto incidente adiacente al marcatore successivo a turno e ripetere il passaggio 1.3.3 fino a quando tutti i marcatori non sono stati misurati.
      NOTA: Poiché le piastre acriliche sono facilmente deformate plasticamente sotto eccitazione, il processo di misurazione sperimentale di una piastra non può essere messo in pausa a lungo.
   5. Sostituire la piastra precedente con quella successiva e ripetere i passaggi da 1.3.1 a 1.3.4.

2. Trattamento dei dati

1. Determinare l'angolo θ tra l'incidente e la luce riflessa con la relazione:
   
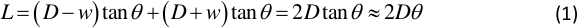
   dove D è la distanza tra la posizione di riposo della piastra vibrante e lo schermo luminoso, w è l'ampiezza vibrante della piastra, e L è la lunghezza del punto luce sullo schermo luminoso. Diverse coppie di D e L sono ottenute nel passaggio 1.3.3.
2. Determinare la 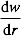pendenza della forma modalità:
   
   NOTA: La pendenza ottenuta è sempre positiva con Eqs. (1) e (2).
3. Utilizzare un segno meno tra due punti zero per ottenere la distribuzione della pendenza reale.
   NOTA: non importa se la revisione inizia dal primo o dal secondo punto zero.
4. Integrare la distribuzione della pendenza di ogni piastra e determinare la costante integrale da parte dei nodi per ottenere la forma della modalità con:
   
   NOTA: i nodi corrispondono alla pendenza più grande della forma della modalità. è una costante determinata dalla posizione delle linee nodali del modello di Chladni mostrata nella figura 2.
5. Calcola l'incertezza della pendenza¹² con:
   
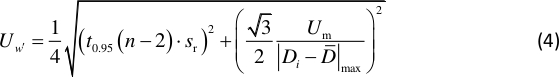
   NOTA: t_0,95(n – 2) è il fattore di distribuzione t con il 95% di fiducia e gradi di libertà n-2, ed è di circa 2 qui. S_r è l'errore standard della regressione lineare con D e L, U_m denota l'incertezza della distanza misurata D_i, ed è 0,5 mm qui. La distanza media misurata è definita da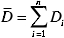 e n indica il numero totale di D_{i misurati.}

Risultati

La frequenza di eccitazione che può eccitare il modello di Chladni assimmetrico è determinata attraverso il test di spazzamento della frequenza. Vengono testate tre piastre acriliche circolari con diametri di 150 mm, 200 mm e 250 mm e i risultati mostrano che le frequenze di risonanza assimmetrica di primo ordine sono rispettivamente di 346 Hz, 214 Hz e 150 Hz per le tre piastre. Si conclude che con un diametro maggiore, la piastra è più flessibile e la corrispondente frequenza di risonanza sarà più piccola. I moti...

Discussione

Il metodo della leva ottica viene adottato in questa carta per determinare la forma della modalità di una piastra, poiché il modello Chladni può mostrare solo le linee nodali di una piastra vibrante. Per determinare la forma della modalità della piastra, la relazione tra la pendenza e la distanza dello schermo luminoso e la lunghezza del punto deve essere ottenuta in anticipo. Quindi, attraverso il calcolo dell'integrazione definita, la forma della modalità del modello di Chladni potrebbe essere determinata quantita...

Materiali

Name	Company	Catalog Number	Comments
Acrylic plates	Dongguan Jinzhu Lens Products Factory		Three 1.0-mm-thickness mirrored circular acrylic plates with diameter of 150 mm, 200 mm and 250 mm respectively. They are easily deformed.
Laser pen	Deli Group	2802	Red laser is more friendly to the viewer. The finer the laser beam, the better.
Light screen	Northern Tempered Glass Custom Taobao Store		Several layers of frosted stickers can be placed on the glass to achieve the effect of frosted glass.
Ruler	Deli Group	DL8015	The length is 1m and the division value is 1mm.
Signal generator	Dayang Science Education Taobao Store	TFG6920A	Common ones in university laboratories are available.
Vibrator	Dayang Science Education Taobao Store		The maximum amplitude is 1.5cm.The power is large enough to cause a noticeable phenomenon when the board vibrates. Otherwise, add a power amplifier.