Jusqu'à présent, la loi du gaz parfait, PV = nRT, a été appliquée à une grande variété de différents types de problèmes, allant de la stœchiométrie d'une réaction ou des problèmes de formule empirique et moléculaire à la détermination de la densité et de la masse molaire d'un gaz. Cependant, le comportement d'un gaz est souvent non idéal, ce qui signifie que les relations observées entre sa pression, son volume et sa température ne sont pas décrites avec exactitude par les lois sur les gaz.  

Selon la théorie cinétique des gaz, les particules d'un gaz parfait n'exercent pas de forces d'attraction ni de répulsion les unes sur les autres. On suppose qu'elles ont un volume négligeable par rapport à celui du récipient. À température ambiante et à 1 atm ou moins, les gaz adoptent le comportement idéal, tel qu'il est impliqué par l'équation des gaz parfaits.

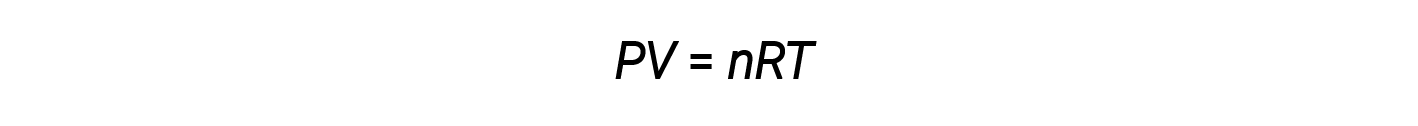
Toutefois, à des pressions plus élevées ou à des températures plus basses, des écarts par rapport à la loi du gaz parfait se produisent, ce qui signifie que les relations observées entre sa pression, son volume et sa température ne sont pas suivies avec exactitude.

La réorganisation de l'équation des gaz parfaits à résoudre pour n donne :

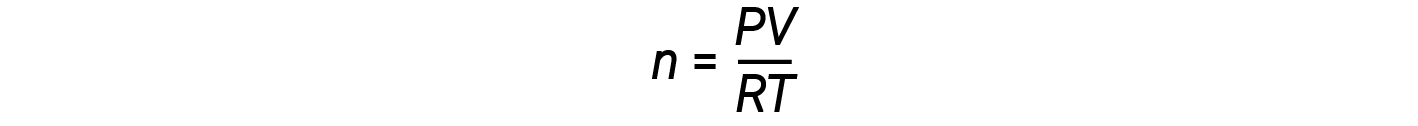
Pour 1 mole d'un gaz parfait, le rapport PV/RT = 1, quelle que soit la pression. Tout écart de ce rapport de 1 indique un comportement non idéal.

La loi du gaz parfait ne décrit pas bien le comportement des gaz à des pressions relativement élevées. Ce qui signifie que le rapport est égal à 1 uniquement à des pressions basses. Mais à mesure que la pression augmente, PV/RT commence à s'écarter de 1, et les écarts ne sont pas uniformes. À des pressions élevées, l'écart par rapport au comportement idéal est important et différent pour chaque gaz. En d'autres termes, les gaz réels ne se comportent pas idéalement à une pression élevée. Cependant, à des pressions plus faibles (généralement inférieures à 10 atm), l'écart par rapport au comportement idéal est faible et nous pouvons utiliser l'équation des gaz parfaits.

Les particules d'un gaz parfait hypothétique n'ont pas de volume significatif et ne s'attirent pas ou ne se repoussent pas l'une l'autre. En général, les gaz réels se rapprochent de ce comportement à des pressions relativement basses et des températures relativement élevées. Cependant, à des pressions élevées, les molécules d'un gaz sont tassées plus près l'une de l'autre et la quantité d'espace vide entre les molécules est réduite. À ces pressions plus élevées, le volume des molécules de gaz elles-mêmes devient considérable par rapport au volume total occupé par le gaz. Le gaz devient donc moins compressible à ces pressions élevées, et bien que son volume continue de diminuer avec l’élévation de la pression, cette diminution n’est pas proportionnelle à la loi de Boyle-Mariotte.

À des pressions relativement faibles, les molécules de gaz n'ont pratiquement aucune attraction les unes pour les autres parce qu'elles sont (en moyenne) si éloignées, et elles se comportent presque comme les particules d'un gaz parfait. Toutefois, à des pressions plus élevées, la force d'attraction n'est plus négligeable elle non plus. Cette force rapproche légèrement les molécules entre elles, diminuant légèrement la pression (si le volume est constant) ou diminuant le volume (à pression constante). Ce changement est plus prononcé à basse température parce que les molécules ont moins d'Éc par rapport aux forces d'attraction, et donc elles surmontent ces attractions moins efficacement après qu'elles soient entrées en collision les unes avec l'autres.

Il existe plusieurs équations différentes qui se rapprochent mieux du comportement des gaz que la loi du gaz parfait. La première, et la plus simple, a été proposée par le scientifique néerlandais Johannes Van der Waals en 1879. L'équation de Van der Waals améliore la loi du gaz parfait en y ajoutant deux termes : l'un pour tenir compte du volume des molécules de gaz et l'autre pour les forces d'attraction entre elles.

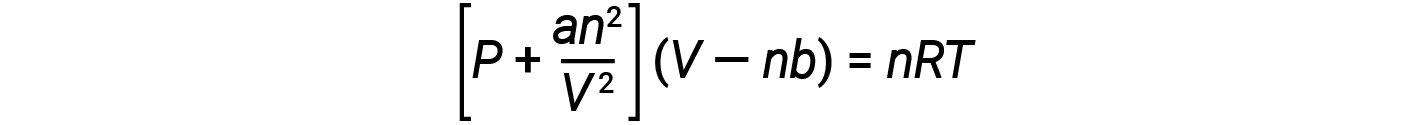
La constante a correspond à la force de l'attraction entre les molécules d'un gaz particulier, et la constante b correspond à la taille des molécules d'un gaz particulier. La “ rectification ” apportée au terme de pression dans la loi du gaz parfait est an²/V², et la “ rectification ” du volume est nb. Notez que lorsque V est relativement grand et n relativement petit, ces deux rectifications deviennent négligeables et l'équation de Van der Waals se résume à la loi du gaz parfait, PV = nRT. Une telle condition correspond à un gaz dans lequel un nombre relativement faible de molécules occupe un volume relativement important, c'est-à-dire un gaz à une pression relativement basse.

À basse pression, la rectification de l'attraction intermoléculaire, a, est plus importante que celle du volume moléculaire, b. À des pressions élevées et à des petits volumes, la rectification du volume des molécules devient importante parce que les molécules elles-mêmes sont incompressibles et constituent une fraction considérable du volume total. À une certaine pression intermédiaire, les deux rectifications ont des influences opposées, et le gaz semble suivre la relation donnée par PV = nRT sur une petite plage de pressions.

À proprement parler, l'équation du gaz parfait fonctionne bien lorsque les attractions intermoléculaires entre les molécules de gaz sont négligeables et que les molécules de gaz n'occupent pas elles-mêmes une part considérable du volume entier. Ces critères sont remplis dans des conditions de basse pression et de température élevée. Dans de telles conditions, on dit que le gaz se comporte idéalement, et les écarts par rapport aux lois sur les gaz sont suffisamment faibles pour qu'ils puissent être ignorés, mais ce n'est souvent pas le cas.

Ce texte est adapté de Openstax, Chimie 2e, Section 9.2 : Gaz au comportement non-idéal.