Finora, la legge del gas ideale, PV = nRT, è stata applicata a una varietà di diversi tipi di problemi, che vanno dalla stechiometria di reazione e problemi di formula empirica e molecolare alla determinazione della densità e della massa molare di un gas. Tuttavia, il comportamento di un gas è spesso non ideale, il che significa che le relazioni osservate tra la sua pressione, volume e temperatura non sono descritte con precisione dalle leggi sul gas.

Secondo la teoria molecolare cinetica, le particelle di un gas ideale non mostrano forze attraenti o repulsive l'una sull'altra. Si presume che abbiano un volume trascurabile rispetto a quello del contenitore. A temperatura ambiente e 1 atm o meno, i gas seguono il comportamento ideale, come implica l'equazione del gas ideale.

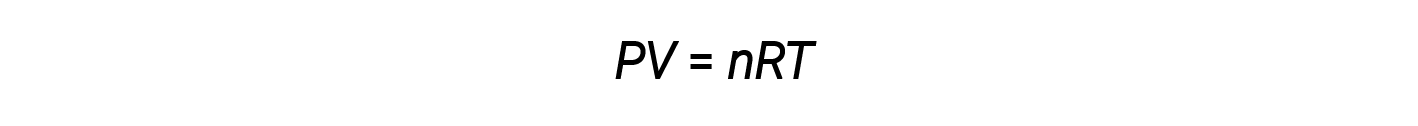
A pressioni più elevate o temperature più basse, tuttavia, si verificano deviazioni dalla legge del gas ideale, il che significa che le relazioni osservate tra la sua pressione, volume e temperatura non sono seguite con precisione.

Riorganizzare l'equazione del gas ideale per risolvere per n dà:

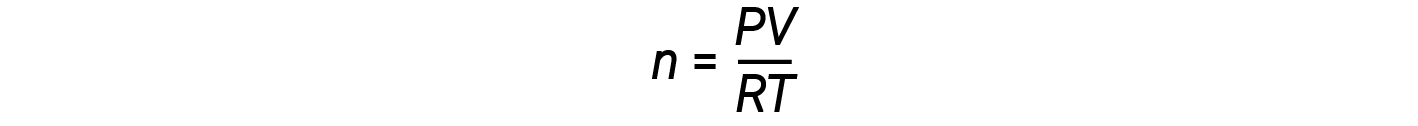
Per 1 talpa di un gas ideale, il rapporto PV/RT = 1, indipendentemente dalla pressione. Qualsiasi deviazione di questo rapporto da uno è un'indicazione di comportamento non ideale.

La legge ideale sul gas non descrive bene il comportamento del gas a pressioni relativamente elevate. Ciò significa che il rapporto è uguale a 1 solo a basse pressioni. Ma man mano che la pressione aumenta, PV / RT inizia a deviare da 1 e le deviazioni non sono uniformi. Ad alte pressioni, la deviazione dal comportamento ideale è grande e diversa per ogni gas. I gas reali, in altre parole, non si comportano idealmente ad alta pressione. A pressioni più basse (di solito sotto i 10 atm), tuttavia, la deviazione dal comportamento ideale è piccola, e possiamo usare l'equazione del gas ideale.

Le particelle di un ipotetico gas ideale non hanno volume significativo e non si attraggono o si respingono a vicenda. In generale, i gas reali approssimano questo comportamento a pressioni relativamente basse e alte temperature. Tuttavia, ad alte pressioni, le molecole di un gas sono affollate più vicine tra loro, e la quantità di spazio vuoto tra le molecole è ridotta. A queste pressioni più elevate, il volume delle molecole di gas stesse diventa apprezzabile rispetto al volume totale occupato dal gas. Il gas, quindi, diventa meno comprimibile a queste alte pressioni, e sebbene il suo volume continui a diminuire con l'aumentare della pressione, questa diminuzione non è proporzionale come previsto dalla legge di Boyle.

A pressioni relativamente basse, le molecole di gas non hanno praticamente alcuna attrazione l'una per l'altra perché sono (in media) così distanti, e si comportano quasi come particelle di un gas ideale. A pressioni più elevate, tuttavia, anche la forza di attrazione non è più insignificante. Questa forza avvicina leggermente le molecole, diminuendo leggermente la pressione (se il volume è costante) o diminuendo il volume (a pressione costante). Questo cambiamento è più pronunciato a basse temperature perché le molecole hanno ke più basse rispetto alle forze attrattive, e quindi sono meno efficaci nel superare queste attrazioni dopo essersi scontrate l'una con l'altra.

Ci sono diverse equazioni che approssimano meglio il comportamento del gas rispetto alla legge del gas ideale. Il primo, e il più semplice di questi, fu sviluppato dallo scienziato olandese Johannes van der Waals nel 1879. L'equazione di van der Waals migliora la legge del gas ideale aggiungendo due termini: uno per tenere conto del volume delle molecole di gas e un altro per le forze attrattive tra di loro.

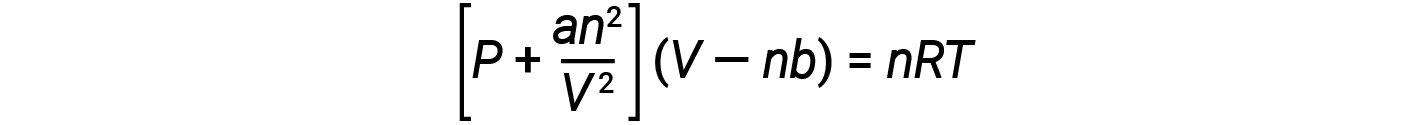
La costante a corrisponde alla forza dell'attrazione tra molecole di un particolare gas, e la costante b corrisponde alla dimensione delle molecole di un particolare gas. La "correzione" al termine di pressione nella legge del gas ideale è un²/V², e la "correzione" al volume è nb. Si noti che quando V è relativamente grande e n è relativamente piccolo, entrambi questi termini di correzione diventano trascurabili, e l'equazione di van der Waals si riduce alla legge del gas ideale, PV = nRT. Tale condizione corrisponde ad un gas in cui un numero relativamente basso di molecole occupa un volume relativamente grande, cioè un gas a pressione relativamente bassa.

A basse pressioni, la correzione per l'attrazione intermolecolare, a, è più importante di quella per il volume molecolare, b. Ad alte pressioni e piccoli volumi, la correzione del volume delle molecole diventa importante perché le molecole stesse sono incomprimibili e costituiscono una frazione apprezzabile del volume totale. Ad una certa pressione intermedia, le due correzioni hanno influenze opposte, e il gas sembra seguire la relazione data da PV = nRT su una piccola gamma di pressioni.

A rigor di termini, l'equazione del gas ideale funziona bene quando le attrattive intermolecolari tra molecole di gas sono trascurabili e le molecole di gas stesse non occupano una parte apprezzabile dell'intero volume. Questi criteri sono soddisfatti in condizioni di bassa pressione e alta temperatura. In tali condizioni, si dice che il gas si comporti idealmente, e le deviazioni dalle leggi sul gas sono abbastanza piccole da poter essere ignorate — questo, tuttavia, molto spesso non è il caso.

Questo testo è adattato da Openstax, Chimica 2e, Sezione 9.2: Comportamento gassoso non ideale.