Determinazione delle forze di impingement su una piastra piana con il metodo del volume di controllo

Fonte: Ricardo Mejia-Alvarez e Hussam Hikmat Jabbar, Dipartimento di Ingegneria Meccanica, Michigan State University, East Lansing, MI

Lo scopo di questo esperimento è quello di dimostrare le forze sui corpi come risultato di cambiamenti nel momento lineare del flusso intorno a loro usando una formulazione del volume di controllo [1, 2]. L'analisi del volume di controllo si concentra sull'effetto macroscopico del flusso sui sistemi di ingegneria, piuttosto che sulla descrizione dettagliata che potrebbe essere ottenuta con un'analisi differenziale. Ognuna di queste due tecniche ha un posto nella cassetta degli attrezzi di un analista di ingegneria e dovrebbero essere considerate approcci complementari piuttosto che concorrenti. In generale, l'analisi del volume di controllo darà all'ingegnere un'idea dei carichi dominanti in un sistema. Questo darà a lei / lui una sensazione iniziale su quale percorso perseguire quando si progettano dispositivi o strutture, e dovrebbe idealmente essere il passo iniziale da fare prima di perseguire qualsiasi progettazione o analisi dettagliata tramite formulazione differenziale.

Il principio principale alla base della formulazione del volume di controllo è quello di sostituire i dettagli di un sistema esposto a un flusso di fluido con un diagramma semplificato del corpo libero definito da una superficie chiusa immaginaria soprannominata volume di controllo. Questo diagramma dovrebbe contenere tutte le forze di superficie e del corpo, il flusso netto di quantità di moto lineare attraverso i confini del volume di controllo e la velocità di variazione del momento lineare all'interno del volume di controllo. Questo approccio implica la definizione intelligente del volume di controllo in modi che semplificano l'analisi allo stesso tempo che catturano gli effetti dominanti sul sistema. Questa tecnica sarà dimostrata con un jet aereo che impatta su una piastra piana a diverse angolazioni. Utilizzeremo l'analisi del volume di controllo per stimare il carico aerodinamico sulla piastra e confronteremo i nostri risultati con le misurazioni effettive della forza risultante ottenuta con un equilibrio aerodinamico.

Un volume di controllo (CV) è definito da una superficie chiusa immaginaria, soprannominata superficie di controllo (CS), definita arbitrariamente per studiare l'effetto del flusso intorno a oggetti e sistemi. La Figura 1 mostra un esempio di volume di controllo contenente una regione di flusso che circonda un oggetto solido. Il flusso nelle immediate vicinanze dell'oggetto è molto complesso e vorremmo evitare tale complessità per stimare l'effetto globale del flusso sull'elemento di supporto. Una volta definito, il CV diventa un diagramma a corpo libero che cattura le interazioni tra il flusso e l'oggetto racchiuso che danno origine a carichi nel sistema di supporto. A tal fine, equipariamo le forze superficiali e corporee sul CV con il cambiamento di momento lineare del flusso che attraversa il CV. Le forze superficiali sono la pressione, il taglio indotto dal flusso e le eventuali reazioni dei solidi "tagliati" dal volume di controllo. Le forze corporee sono fondamentalmente il peso di tutto ciò che è contenuto nel volume di controllo, compresi solidi e fluidi, e qualsiasi altra forza indotta da effetti volumetrici come i campi elettromagnetici. La variazione della quantità di moto lineare del flusso è l'effetto aggiunto del flusso netto di quantità di moto attraverso il CS e il tasso di variazione della quantità di moto contenuto nel CV. Tutti questi effetti possono essere riassunti nell'equazione per la conservazione del momento lineare in forma integrale:

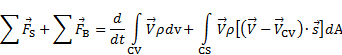(1)

Qui, 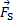ci sono le forze di superficie e sono le forze del 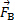corpo. Il primo termine sul lato destro dell'equazione (1) rappresenta il tasso di variazione della quantità di moto all'interno del volume di controllo, mentre il secondo termine rappresenta il flusso netto di quantità di moto attraverso la superficie di controllo. La differenza vettoriale 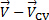è la velocità relativa tra il CV e il flusso, e il vettore 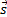è l'unità verso l'esterno normale al differenziale di area. Il punto prodotto tra la velocità relativa e 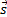rappresenta la componente di velocità che attraversa il CS, e d'ora in poi contribuisce allo scambio di quantità di moto lineare. Il segno di questo prodotto punto è negativo dove il flusso di quantità di moto è diretto nel CV e positivo dove è diretto lontano dal CV. In questa forma, l'equazione (1) è l'equilibrio del momento lineare in relazione a un sistema di riferimento inerziale. Si noti che (1) è un'equazione vettoriale, il che significa che in generale ha tre componenti indipendenti. Con questo in mente, l'analista deve fare attenzione a stabilire l'insieme di forze che bilanciano i cambiamenti nel momento lineare per ogni coordinata.

Per la presente dimostrazione, abbiamo la configurazione mostrata nella Figura 1, in cui un CV fisso racchiude una piastra esposta a un jet aereo. Poiché il flusso del getto è costante, non vi è alcun cambiamento di quantità di moto all'interno del CV, quindi il primo termine sul lato destro dell'equazione (1) svanisce. Inoltre, il CV non si muove, quindi . Quindi, la somma delle forze sul CV si bilancia con il flusso netto di slancio attraverso il CS.

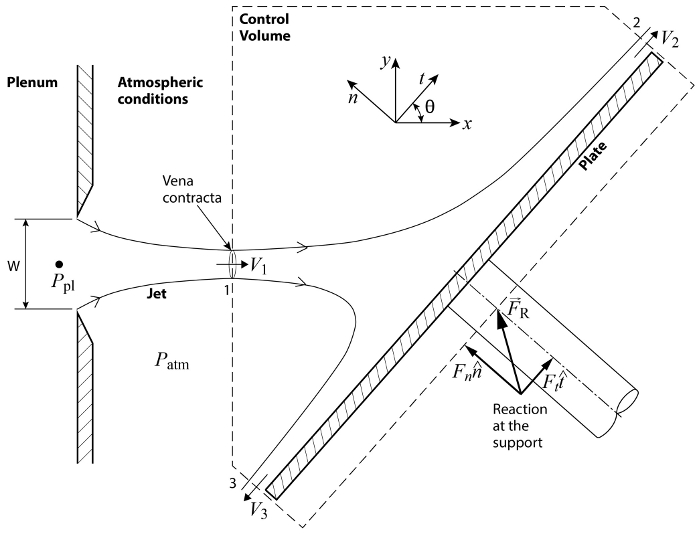
Figura 1. Schema della configurazione di base. Un getto aereo esce dal plenum attraverso una fessura di larghezza W. Il getto impatta su una piastra inclinata e viene deviato mentre esercita un carico sulla superficie.

Considerando la configurazione nella Figura 1, il momentum fluisce nel CV attraverso la porta 1 e lascia il CV attraverso le porte 2 e 3. Il CV attraversa il getto in entrata alla vena contracta , (per ulteriori informazioni, si veda il video "L'interazione di pressione e velocità: il getto impinging su una piastra inclinata")che è il primo posto in cui le linee di flusso diventano parallele e, di conseguenza, la pressione statica attraverso il getto diventa omogenea e corrisponde al valore della pressione circostante, cioè, pressione atmosferica 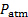. Allo stesso modo, le porte 2 e 3 si trovano abbastanza lontane dalla regione di impinging per consentire alle linee di flusso di diventare parallele e alla pressione di corrispondere a quella dell'ambiente circostante. Di conseguenza, la pressione ovunque sul CS è uguale alla pressione atmosferica, 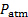. Di conseguenza, dato che la pressione è distribuita in modo omogeneo attorno al CS, la sua forza netta sul volume di controllo è zero. Inoltre, poiché il CS è stato disegnato perpendicolarmente ai flussi di ingresso e di uscita, non vi è alcun carico di taglio indotto dal flusso sul CS. In sintesi, l'equazione (1) semplifica la seguente relazione per il caso illustrato nella Figura 1

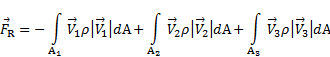(2)

Ecco, 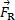la reazione del sistema di supporto risultante dalla trasmissione del carico aerodinamico che il getto esercita sulla piastra. Come mostrato nella Figura 1, questa reazione si trova nella porzione del volume di controllo che "taglia" attraverso il sistema di supporto della piastra. Questa è considerata una forza superficiale nel senso che questo taglio immaginario farebbe parte della superficie di controllo. Poiché 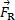è l'unica interazione con il volume di controllo non associata al flusso di quantità di moto, è l'unico termine sul lato sinistro delle equazioni (1) e (2). Si noti dal confronto tra queste equazioni che i prodotti a punti all'interno degli integrali risultano semplicemente nelle grandezze dei corrispondenti vettori di velocità perché sono allineati con i vettori di area. Inoltre, come detto prima, il loro segno indica se il flusso di quantità di moto è diretto nel CV (-) o lontano da esso (+). Se assumiamo inoltre che la velocità alle porte sia approssimativamente omogenea e che il flusso sia incomprimibile, le velocità e la densità possono essere prese al di fuori degli integrali e l'equazione (2) diventa:

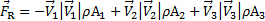(3)

Rigorosamente parlando, il profilo di velocità non è mai perfettamente omogeneo, e questa semplificazione richiede una moltiplicazione per un coefficiente di correzione, 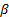, il cui valore dipende dai dettagli del profilo di velocità. In una data porta di flusso, questo coefficiente è definito come il rapporto tra il flusso di quantità di moto esatto e il flusso di quantità di moto stimato dalla velocità media:

(4)

Nei flussi turbolenti questo coefficiente è molto vicino a 1 perché il profilo di velocità tende ad essere quasi omogeneo. Poiché questo è il caso del presente esperimento, l'equazione (3) è un'approssimazione ragionevole per le misurazioni correnti. Ma se la portata dovesse essere ridotta o la posizione della piastra spostata più a valle fino a raggiungere condizioni di flusso laminare, sarebbe necessario risolvere gli integrali sul lato destro dell'equazione (2) senza approssimazione. Basato sulla Figura 1, 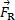può essere scomposto nelle sue coordinate normali e tangenti alla piastra 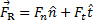. Dove 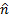e sono i vettori unitari in ogni 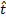coordinata e e sono le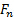 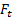grandezze delle proiezioni di in ogni 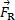coordinata. Quindi, l'equazione (3) può essere scomposa come:

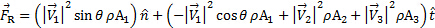(5)

Si noti che il segno meno sul componente normale scompare perché la proiezione di 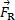sull'asse normale è negativa. Vogliamo determinare il carico normale sulla piastra con questo studio perché tende ad essere il componente più rilevante dal punto di vista strutturale. Dall'equazione (4), otteniamo il carico normale sulla piastra:

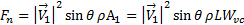(6)

Qui, 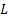è la campata della piastra ed è 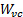la larghezza del getto alla vena contracta. In generale, il rapporto di contrazione tra la larghezza di uscita del getto 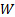e la vena contracta è molto vicino a [2, 3, 4]:

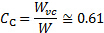(7)

In sintesi, la forza normale sulla piastra può essere stimata dalla seguente relazione:

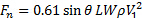(8)

Qui, definiamo 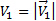per semplicità. D'altra parte, il valore del termine 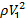è determinato usando l'equazione di Bernoulli tra il plenum e la vena contracta (vedi Figura 2 per riferimento). La velocità all'interno del plenum è considerata trascurabile, e dato che il getto è orizzontale, i cambiamenti di altezza tra il plenum e la vena contracta svaniscono. Quindi, l'equazione di Bernoulli diventa:

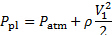(9)

Ricordiamo che la pressione alla vena contracta corrisponde alla pressione circostante, che è atmosferica. Quindi, la pressione dinamica alla vena contracta segue:

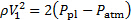(10)

Sostituendo l'equazione (9) nell'equazione (7) si ottiene il risultato finale per stimare la forza normale sulla piastra in base alle caratteristiche del getto aereo:

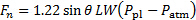(11)

Questo risultato deriva dall'analisi del volume di controllo della conservazione del momento lineare. Per avere una valutazione della sua accuratezza, confronteremo queste stime con misurazioni dirette della forza. A tal fine, le componenti orizzontali ( 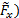e verticali ( 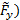della forza totale raffigurata nella Figura 2 sono catturate da un equilibrio aerodinamico. Per determinare i componenti di questa forza misurata sul sistema di coordinate, utilizziamo la seguente trasformazione di coordinate:

(12)

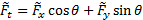(13)

Dove è stata aggiunta una tilde per sottolineare che queste forze sono ottenute mediante misurazione diretta con un equilibrio aerodinamico.

1. Impostazione della struttura

1. Assicurati che non ci sia flusso nella struttura.
2. Collegare la porta positiva del trasduttore di pressione al rubinetto di pressione plenum ( ).
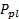3. Lasciare la porta negativa del trasduttore di pressione aperta all'atmosfera ( ).
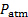4. Registrare il fattore di conversione del trasduttore da Volt a Pascal ( ).
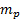5. Registrare la larghezza di uscita del getto.
6. Registrare l'estensione della piastra.
7. Registrare le costanti di conversione del bilancio di forza da Volt a Newton (forza orizzontale: 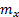; forza verticale: ).
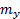8. Impostare il sistema di acquisizione dati per campionare ad una velocità di 100 Hz per un totale di 1000 campioni (cioè 10 secondi di dati).
9. Montare la piastra di impatto sul bilanciamento della forza e regolare le sue uscite a zero.

2. Registrazione dei dati

1. Impostare l'angolo della piastra a 90^o (vedere la Figura 2 per riferimento).
2. Accendere la struttura di flusso.
3. Registrare la lettura del trasduttore di pressione in Volt, che corrisponde alla differenza di pressione tra il Plenum e l'atmosfera ( ).
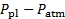4. Registrare i dati di forza utilizzando il sistema di acquisizione dati.
5. Moltiplicare i valori acquisiti (in Volt) per i fattori di conversione della forza ( 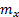e ) e inserire i risultati nella tabella 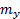1.
6. Spegnere la struttura di flusso.
7. Modificare l'angolo della piastra.
8. Ripetete i passaggi da 2.2 a 2.6 per i seguenti angoli:

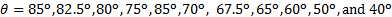
Figura 2 . Impostazione sperimentale. (A): Dettaglio del sistema di aspirazione per pressurizzare il plenum a pressione 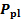. (B): lato di scarico con piastra di impingement. (C): Dettaglio della fessura di scarico. Fare clic qui per visualizzare una versione più grande di questa figura.

3. Analisi dei dati

1. Calcolare la forza normale misurata dalla bilancia usando l'equazione(11) e registrarla nella tabella 1.
2. Determinare il valore teorico della forza normale dall'equazione (10) e registrarlo nella tabella 1.
3. Calcola il disaccordo tra i due valori come percentuale.

Tabella 1 . Parametri di base per lo studio sperimentale.

Parametro	Valore
Larghezza dell'ugello agetto( W )	19,05 mm
Span della piastra (L)	110,49 cm
Costante di calibrazione del trasduttore (m_p)	141,3829 Pa/V
Coefficiente orizzontale di bilanciamento (m_x)	22,2411 N/V
Coefficiente verticale di bilanciamento (m_y)	4,4482 N/V

La Figura 3 mostra un confronto tra il carico normale sulla piastra piana misurato direttamente da un equilibrio aerodinamico e stimato dalla conservazione della quantità di moto lineare. In generale, l'analisi del momento lineare ha catturato la tendenza dominante delle misurazioni dirette al variare dell'angolo di impingement. Le discrepanze in queste misurazioni variavano in modo non monotono con l'angolo di impingement. Per gli angoli di impingement nell'intervallo e per , le 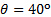discrepanze sono inferiori al 6%. Sono più alti per gli altri angoli, ma mai superiori al 12,5%. Sembra esserci un crossover intorno , in cui la tendenza delle discrepanze si inverte: le misurazioni mostrano carichi normali più elevati rispetto all'analisi del momento lineare per 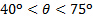e inferiore per 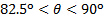. Queste differenze nelle tendenze potrebbero essere dovute al fatto che l'analisi del momento lineare assume cambiamenti inviscidi, non dissipativi, nel momento lineare, mentre le misurazioni dirette non possono evitare l'effetto della viscosità sul flusso. Per l'intervallo, 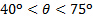la componente di taglio diventa dominante e quindi gli effetti turbolenti dello strato limite potrebbero essere importanti. In questo caso, le fluttuazioni di velocità normali della parete dovute alla turbolenza potrebbero essere responsabili dell'aumento del carico normale. D'altra parte, la velocità assiale del getto subisce una significativa riduzione della portata 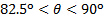mentre si trasforma per diventare prevalentemente tangente alla parete. È probabile che questo effetto consenta alla viscosità di dissipare la viscosità a causa di una riduzione dei valori locali del numero di Reynolds e ciò comporterebbe valori ridotti del carico normale.

Tabella 2. Risultati rappresentativi.

θ	F ̃_x(N)	F ̃_y (N)	F ̃_n (N)	F_n (N)	ε (%)
90o	15.257	9.034	15.257	16.773	9.9
85o	15.151	9.831	15.950	16.709	4.8
82,5o	15.035	10.231	16.242	16.630	2.4
80o	15.929	10.498	17.510	16.518	5.7
75o	14.248	10.453	16.468	16.202	1.6
70o	13.518	11.405	16.604	15.762	5.1
67,5o	13.100	11.294	16.425	15.496	5.7
65o	12.771	11.579	16.468	15.202	7.7
60o	11.881	11.863	16.221	14.526	10.5
50o	9.746	11.241	14.691	12.849	12.5
40o	6.357	9.444	11.320	10.782	4.8

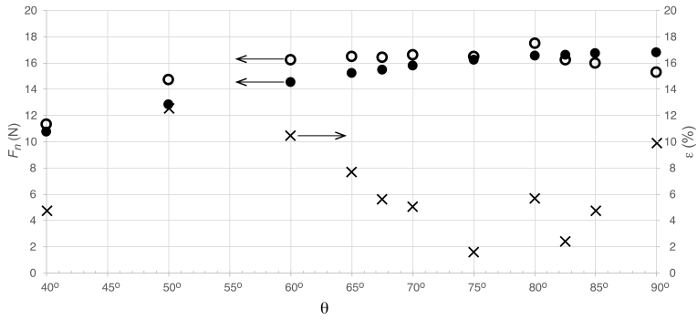
Figura 3. Risultati rappresentativi. Carico sulla piastra a causa del getto di impinging. I simboli rappresentano: : misurazione diretta del carico; : stima dalla conservazione della quantità di moto lineare; : errore percentuale tra misure sperimentali e stima teorica. 

Abbiamo dimostrato l'applicazione dell'analisi del volume di controllo della conservazione del momento lineare per determinare le forze esercitate da un getto che impatta su una piastra piana. Questa analisi si è rivelata semplice da applicare e ha fornito una stima soddisfacente dei carichi senza richiedere una conoscenza dettagliata del modello di flusso attorno alla piastra. Sebbene ci fossero alcune discrepanze (sia in grandezza che in tendenza) dovute all'assunzione di base della trasformazione inviscida della quantità di moto, questa tecnica offre un mezzo per ottenere una rapida stima del comportamento del sistema senza approfondire uno studio dettagliato del flusso del fluido. Quindi, questo è un potente strumento per l'analista di ingegneria per, ad esempio, prevedere la fattibilità dello sviluppo di un determinato sistema di ingegneria con un investimento minimo di tempo e risorse. Una volta condotta questa prima analisi per determinare la fattibilità, l'ingegnere può passare a un'analisi di flusso più dettagliata utilizzando, ad esempio, la fluidodinamica computazionale.

L'analisi del volume di controllo della conservazione della quantità di moto lineare è un potente strumento per l'ingegneria dei fluidi. Trova applicazione in un'ampia varietà di problemi per aggirare metodi più coinvolti come l'analisi differenziale. Alcuni esempi di questa analisi possono essere descritti:

Progettazione della pala della turbina Pelton: in generale, una pala della turbina Pelton dovrebbe essere progettata per convertire la massima quantità di quantità di moto lineare in coppia. Ciò si ottiene determinando la geometria della lama che massimizza il cambiamento nel momento lineare dei getti d'acqua. A tal fine, il risultato tipico dell'analisi del volume di controllo è che il getto dovrebbe essere fatto girare su se stesso, cioè 180^o. Questa è in generale una sfida tecnica per un dispositivo rotante, ma fornisce all'analista una guida iniziale per un'analisi più dettagliata utilizzando altri strumenti.

Trascina il carico sulle strutture civili: una delle sfide dell'ingegneria civile è progettare strutture che sopportino il carico del vento. Per prevedere gli effetti del vento su una struttura di dimensioni reali, è possibile condurre esperimenti con un modello in scala ridotta in gallerie del vento o dell'acqua. A tal fine, è possibile utilizzare l'analisi del volume di controllo della conservazione del momento lineare basata su misurazioni della velocità a monte e a valle del modello per determinare il carico effettivo sul prototipo. Questo metodo semplifica la campagna sperimentale e consente di risparmiare tempo, fatica e denaro in preparazione alla costruzione di una struttura su scala reale.