気液平衡
概要
ソース: マイケル g. ベントンとケリー ・ m ・ ドゥーリー、工業化学科、ルイジアナ州立大学、バトン ルージュ, ルイジアナ
気液平衡は、一般的なプロセス設計環境のモデル化、蒸留などのエンジニア リングに最も重要です。混合物の成分の相互作用を理解することは非常に重要なこのような区切り記号を解析、設計、運用です。活量係数は、関連混合物組成と分子間相互作用のための優れたツールです。分子間相互作用パラメーターの検索には、予測モデルを用いた混合物の活量係数のすることができます。
気液平衡蒸留などの化学業界での一般的なプロセスで重要な要因であります。蒸留は、液体をその沸点に区切ってのプロセスです。液体混合物は蒸留装置または列に供給し、煮します。気液平衡データは決定か液体混合物を分離するのに便利です。液体の沸点が異なるため 1 つの液体は蒸気に沸騰し、他は液体として滞在し、ユニットを介してドレインしながら列に上昇します。プロセスは非常に様々 な業界で重要です。
この実験では気液平衡装置およびガスクロマト グラフを使用して様々 な組成の脱イオン水、イソプロパノール、メタノールの混合物の活量係数を取得します。さらに、システムのバイナリの相互作用パラメーターは、ウィルソンの方程式と活量係数を使用して決定されます。
原則
気液平衡状態は、純粋なコンポーネントまたは混合物が液体および蒸気相と機械的・熱的平衡と 2 つのフェーズの間は純の大量転送で存在するのです。気体と液体は重力と熱 (図 1) によって区切られます。液体混合物は、真空ポンプで真空状態に置かれるシステムに挿入されます。蒸気を凝縮、沸騰の商工会議所に戻されますし、液体と混合する返されました。混合物のいくつかの分離の沸点差。揮発性成分が蒸発し始めるので、水の沸点は追加の部品のより高いです。

図 1: 装置の描写
活量係数は、同じ組成の最適なソリューションのフガシティーを実際混合物の成分のフガシティーの比率として定義されます。フガシティーは、標準状態の化学ポテンシャルの相違点の表示に使用するプロパティです。気相雰囲気はフガシティー係数の面で表現できます [φ: f私V = φ私y私f私0 v ]、y は私と私のモル分数を気相と f私0 v = = 蒸気標準状態フガシティー (T と P で純粋な成分蒸気のフガシティー)。この実験は、φ は私のように、低圧力のため = 1 と f私0 v = p. 液体相の雰囲気、活動係数 γ私の面で表現できます: f私L = γi 私f私x0 L x を私= 液相中の i と f私0 Lのモル分数液体標準状態フガシティーを =。
この T の飽和蒸気圧力 (P私s) で純粋な成分の液体フガシティーは、平衡の純粋な気体と液体は、Pis、でしょう。液体雰囲気は圧力の弱い機能だけなので、P私sと P の差が大きくない限り、P私とsT と P (f私0 L) 純粋な成分の液体フガシティーを近似できること私たち。この近似は通常「ポインティング補正無視」と呼ばれます。実験者は、平衡状態にある気体と液体の組成を測定する VLE 装置を使用する場合、実験者もメジャー P に活量係数を計算することが直接、P私S を決定する t. T を測定する必要があります。すべての私。
混合物の組成を決定するこの実験で使用される VLE デバイスの中心部は、「つばを吐く「沸騰液体を平衡チャンバーの断熱、コットレル ポンプです。2 つの磁気式サンプリング バルブ液体及び凝縮蒸気のサンプルの回収を可能にします。大きな貯水池は、オン ・ オフ制御バルブ スイッチとは電気ポンプによって引き起こされる変動システムの圧力パルスを湿らせるのに役立ちます。遅いリークは、必要に応じて空気の回収率、一定の圧力を維持するために空気の入力の率間のバランスを作成する使用できます。
気液平衡の解決に匹敵する方法は、さまざまなモデルを使用します。ラウールの法則、ドルトンの法則やヘンリーの法則は、気液平衡濃度データを見つけることができますすべての理論です。すべての 3 つのモデルは、分圧、全圧および物質のモル分率の比例に関連しています。ウィルソンの方程式は、過度に複雑なされていないながら混和性液体の正確であること実証されています。また、ウィルソンのモデルには、理想的な値からのずれを考慮しての活量係数が組み込まれています。
手順
1. プライミング システム
- 通気装置のフレームにマウントされているベント/制御三方弁を用いた VLE (必要な) 場合廃棄物のフラスコにシステムから液体を排出することによって。
- サンプル チューブを削除し、(必要な場合) クリーン チューブと置き換えます。液体は、システムから完全に排出されません。
- 実験の最初の実行のための混合物で入力のバルブを介して補充約 (vol %)50% メタノール、イソプロパノール 30%、水 20%。2 週目の約 25% メタノール、45% イソプロパノール 30% の水と補充します。3 週目の詰替液体を繰り返しする必要があります。液体容量の合計は約 130 cm3です。
- 電気ポンプと真空ジャケットと交わるスポットの真下に液体で満たしなさい。ほんのわずかの液体を「吐き出す」(液体を激しくない沸騰中ポップ) するときに十分な液体を取得する非常に高い沸騰料金を必要とするシステムとなります。
- ビーカーを使用し、平衡室の上部に追加ポートに液体を注ぐ。ポートを閉じます。
- 壁に水銀圧力計と気圧の圧力をチェックします。(必要な場合) に一致するデジタル圧力計の「ゼロ」を調整します。
- 「制御」する三方弁を切り替え、真空ポンプと圧力コント ローラーを起動します。
- いくつかの回転圧力コント ローラーのスロットル バルブを開き、ドロップ急速に圧力を観察します。デジタル圧力計の圧力を見る。
- 取得する圧力コント ローラーに制御圧力のセット ポイントを設定 〜 700 mm hg 制御弁のクリックをリッスンします。コントロール ポイントに達すると、真空ポンプからのノイズは聞こえるように異なるになります。
- この時点で、スロットル バルブとコントロール バルブが開き、真空ポンプにあまりにも多くの空気を捨てて、圧力が徐々 に回復する前に 700 mm 以下ディップするたびに、いくつかのターンを開いた。完全に、スロットル バルブを閉じるし、½ ターンについてそれを開きます。
- コントロール バルブをもう一度、クリックを開始するを待つし、少しずつ圧力変動だけ ~0.5 mmHg までまたは以下のバルブが開いているときにスロットル バルブを閉じます。700 mmHg 近く非常に維持するために必要に応じてコントロール ポイントまたはリーク弁にマイナーな調整を行います。
- 混合物は 700 mmhg ± 10 mmHg では、一度は、マントル パワー、凝縮水と磁気攪拌加熱ヒーター電源を入れます。25-30% ヒーター電力と 1.5-2 ターン マントル パワーを開始するしてみてください。装置は 20 分を必要とする以下のアプローチの平衡へ。この時間の間に圧力を調整してください。
2. 実験の実行
- 沸騰、電気ポンプは液体を吐き出すし始めます、沸騰の商工会議所に滴り落ちる液体を見ることができます。凝縮蒸気もはや表示する必要になります。平衡に達すると、実験者がわかります凝縮蒸気の安定した点滴 (2 - 3 滴/秒)、液体を返される (2 - 3 滴/秒)。温度は ± 0.03 ° C に安定する必要があります、圧力は 700.0 ± 0.5 mmHg で安定しているはずです。これらの条件は、少なくとも 2 分間 (ほど) に設けられて、均衡が達成されます。
- (「1」と「2」コント ローラー上) 4 または 5 回マーク各長時間磁気のバルブを開く約 0.5 cm3各サンプル管の液の収集およびチューブを終了するのに十分な。バルブがボタンに応答しない場合に、オフ コント ローラーの電源スイッチを反転しようと。この最初のサンプル チューブと配信システムを洗浄に使用して破棄されます。テストの構成には影響しませんので、洗濯によって、チューブの両側に任意の残りの化学物質が、サンプリング対象と同じ化学物質で置き換えられます。
- 一瞬治まる、ベント/弁 3 ウェイのシステムを発散し沸騰を待つ 30 s ヒーターの電源を切ります。サンプル チューブを削除、数回を旋回し、廃棄物の鍋にそれらをダンプします。
- システムのサンプル チューブを修理、ベント弁を「コントロール」し、ヒーターに電源を再確立する平衡を待つ引き返します。装置は冷却しない場合にこの手順は数分だけかかります。平衡が再確立されたとき、温度のわずかな違いを観察することがあります。これはサンプリングのための全体的な組成のわずかな障害によりすることができます。
- 平衡が再確立されると、2 つの新しいサンプルを取る。準備ができて新しい隔壁を有する 2 つのラベル付きバイアルがあります。
- サンプルを取って ~0.5 cm3各チューブに再度後ヒーターをオフにシステムをぶちまける、サンプル チューブを削除し、バイアルにそれらを注ぐ。バイアルのキャップ、必要に応じてクリーン チューブにサンプル チューブを置き換えます。
- サンプルを分析しながら、新しいサンプルを準備します。ビーカーやフラスコに 〜 15 cm3の液体を排出する.純粋なメタノールのサンプル ポートを介してメタノール/イソプロパノール 50/50 〜 20 cm3を追加します。これは新しい全体の構成を与えます。
- 必ずサンプル チューブが完全に空、システムを閉鎖、ベント弁を切り替える「制御」,、ヒーターの電源を入れます。すぐに働いて場合、平衡再設立される急速に。メモ前の例から温度差があります。
- 平衡およびサンプリング前に洗浄し、1 つのサンプルを取ることを記憶としてプロシージャを繰り返し、最後のサンプルを取る。コンポーネントを追加して、実験を続けます。12 個のデータ ポイントで活量係数と (ほぼ) バイナリの相互作用係数を決定するために十分です。
3. システムをシャット ダウンします。
- ヒーターをオフにします。クール、攪拌機及び復水器の水を遮断する装置を開始する場合
- システムを大気圧に戻すコント ローラーを設定 > 1020 mbar、スロットル バルブを閉め、タンクのバルブを開くし、通気孔を三方バルブを設定。
- 大気圧に達すると、一度ポンプをオフ シャット ダウンします。貯水池からの液体を排水弁のレベルに到達するまでが、貯蔵所の液体の残りの部分を残します。3 方向バルブを閉じます。
4. 分析
- 非線形回帰分析と残差二乗目的関数の標準的な金額を使用して、このシステムのため (後述)、三ウィルソン方程式 6 定数を逆行するのに raw データから計算された活量係数を使用します。グラフィカルな方法で適合の品質を評価し、エラー x 100 を合わせて平均である平均パーセントの相対偏差 (千葉大学) を計算します。

- 初期の推測の階乗のメソッドを使用して応答パラメーター空間内のいくつかの異なる方向から真の最適値に収束します。十分に t 統計によると相対精度を決定するための 1 つの GC サンプルを複製することによって GC 測定の精度を計算し、受容・適切な特定の GC 測定を拒否するかどうかを決定するため、精度を使ってください仮説のテスト。
- APRDs を GC 測定の相対精度を比較し、議論します。また圧力および温度のゲージの絶対精度を報告 - 一日あたり一度これらを決定します。
結果
データの活量係数には、(表 1) をコンポーネントごとに平均値からの有意な偏差は表示されません。これは、中間コンポーネントの組成が大きく変動しているいないため、期待どおりです。ただし、1 の近くのコンポーネントは、γ の近く 1 を持っています。低構成コンポーネント高 γ があります。コンポーネントが減らされた偏差である混合物中の濃度の高い、したがってそれに接近するだろう理想的な (γ = 1)。混合物に低濃度とコンポーネントがある高い偏差の γ は 1 よりも大きくなります。
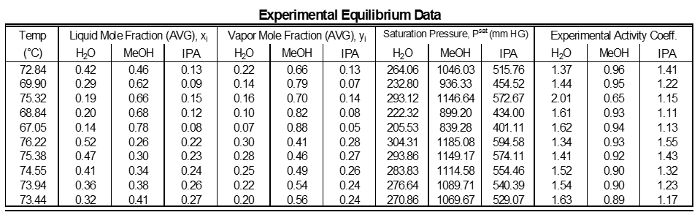
表 1: 実験データの各サンプルの結果。
データはウィルソン モデル パラメーターにピッタリだったし、係数を算出した (表 2)。実験間の二乗残差の合計の単純な削減とウィルソン式 (1) の活量係数が使用されました。これは、Excel のソルバー機能を使用して達成されました。パリティのプロットを示すは、ウィルソンの方程式モデル活量係数を実験的発見の活量係数に関連します。実験的活量係数を算出し、算出係数と比較してグラフィカルに。

表 2: ウィルソン モデル パラメーターにデータをフィッティングの結果。
 (1)
(1)
パラメーターの値は、(表 3) にベスト フィットでした。理想的には相関関係は、y 軸に沿って = x;ただし、有意な相関関係の理想的なシナリオに似ている (図 2) が見つかりました。期待どおりに、データの活量係数は各コンポーネントの平均値からの有意な偏差を表示されませんでした。実験間の二乗残差の合計の削減とウィルソン式活量係数は Excel のソルバー機能を使用します。パリティのプロットは、ウィルソンの方程式モデル活量係数を実験的発見の活量係数に関連します。
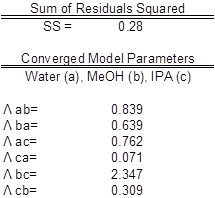
テーブル 3: モデル ・水 (a)、メタノール (b)、IPA (c) パラメーター。実験値が予期される値と比較した。

図 2: 実験的活量係数とモデル活動係数との相関の描写。
申請書と概要
この実験を示した定数 P メタノール - イソプロパノール - 水の気液混合物の平衡 = 700 mm Hg、温度と組成を測定、活量係数を計算する方法。期待どおりに、各コンポーネントの平均値から大幅データの活量係数を逸脱することしていません。実験間の二乗残差の合計の削減とウィルソン式活量係数は Excel のソルバー機能を使用します。パリティのプロットは、ウィルソンの方程式モデル活量係数を実験的発見の活量係数に関連します。
石油業界で蒸留、石油製品の分離の主なプロセスです。多くの石油精製所は原油1蒸留を使用します。軽質炭化水素は、重い粒子、沸点1に基づいて分離から分離されます。ガスのプロパン、ブタン1上がるような軽い材料中の低い板でオイルを収集のような重い材料です。ガソリン、ジェット、ディーゼル燃料などの炭化水素は、区切られた1。このプロセスは、完全に分離し、製品1を精製する多くの時間を繰り返しが多い。製油所は、ので効率はキー1最大容量で新製品を作成する常に安定した状態でこれらのプロセスを実行します。これらの過程における化学エンジニアは生産1の効率を最適化に焦点を当てます。
トレイ蒸留カラムは、別の様々 な化学製品にも使用されます。エタノールはこのような製品です。密接に関連するプロセスを通じてさまざまな製品は、燃料用エタノール、ビール、酒はすべてできるよう蒸留2をします。特定の量のアルコールは、特定の証明書2を作成するために水から分離できます。このプロセスは、製品内の水分の割合を減らすことに制限されてが完全にそれの2を除去できません。共沸蒸留が必要、水を完全に除去するためにエタノール2から水を分離する抽出化学物質を使用しています。
参考文献
- About the Refinery." Processing & Refining Crude Oil. Chevron.com, n.d. Web. 17 Nov. 2016.
- Madson, PW. Ethanol Distillation: The Fundamentals. Cincinnati: Katzen International, n.d. Print. Accessed from Web. 01 Oct. 2016.
タグ
スキップ先...
このコレクションのビデオ:

Now Playing
気液平衡
Chemical Engineering
89.2K 閲覧数

フィンドチューブ熱交換器の熱伝達効率のテスト
Chemical Engineering
17.9K 閲覧数

トレイを使用して対流および伝導性の熱伝達を調査するドライヤー
Chemical Engineering
44.0K 閲覧数

プロピレング リコール溶液の粘度
Chemical Engineering
32.9K 閲覧数

シリカ アルミナ粉末のポロシ メーター
Chemical Engineering
9.6K 閲覧数

押し出しによる力法律モデルのデモ
Chemical Engineering
10.1K 閲覧数

ガス吸収
Chemical Engineering
36.8K 閲覧数

トレイ蒸留効率に還流比の影響
Chemical Engineering
77.8K 閲覧数

液-液抽出の効率
Chemical Engineering
48.5K 閲覧数

液相反応: しょ糖
Chemical Engineering
9.7K 閲覧数

化学修飾によるサリチル酸の結晶化
Chemical Engineering
24.3K 閲覧数

充填層反応器内の単相および流れ
Chemical Engineering
19.0K 閲覧数

ポリジメチルシロキサンを付加重合の動力学
Chemical Engineering
16.1K 閲覧数

エチレンの触媒反応: 水素化
Chemical Engineering
30.4K 閲覧数

スピンと寒さ
Chemical Engineering
7.4K 閲覧数
Copyright © 2023 MyJoVE Corporation. All rights reserved