Equilibrio vapore-liquido
Panoramica
Fonte: Michael G. Benton e Kerry M. Dooley,Dipartimento di Ingegneria Chimica, Louisiana State University, Baton Rouge, LA
L'equilibrio vapore-liquido è fondamentale nelle applicazioni ingegneristiche come la distillazione, la modellazione ambientale e la progettazione generale dei processi. Comprendere le interazioni dei componenti in una miscela è molto importante nella progettazione, nel funzionamento e nell'analisi di tali separatori. Il coefficiente di attività è uno strumento eccellente per mettere in relazione le interazioni molecolari con la composizione della miscela. La ricerca dei parametri di interazione molecolare consente una previsione futura dei coefficienti di attività per una miscela utilizzando un modello.
L'equilibrio vapore-liquido è un fattore critico nei processi comuni nell'industria chimica, come la distillazione. La distillazione è il processo di separazione dei liquidi dal loro punto di ebollizione. Una miscela liquida viene alimentata in un'unità o colonna di distillazione, quindi bollita. I dati di equilibrio vapore-liquido sono utili per determinare come le miscele liquide si separeranno. Poiché i liquidi hanno diversi punti di ebollizione, un liquido bolle in un vapore e sale nella colonna, mentre l'altro rimarrà come liquido e drenerà attraverso l'unità. Il processo è molto importante in una varietà di settori.
In questo esperimento, i coefficienti di attività di miscele di varie composizioni di metanolo, isopropanolo e acqua deionizzata saranno ottenuti utilizzando un apparato di equilibrio vapore-liquido e gascromatografo. Inoltre, i parametri di interazione binaria del sistema saranno determinati utilizzando l'equazione di Wilson e i coefficienti di attività.
Principi
L'equilibrio vapore-liquido è uno stato in cui esiste un componente o una miscela pura in fase liquida e vapore, con equilibrio meccanico e termico e nessun trasferimento di massa netta tra le due fasi. Vapore e liquido sono separati dalla gravità e dal calore (Figura 1). La miscela liquida viene inserita nel sistema, che viene messo in uno stato di vuoto con una pompa per vuoto. Il vapore viene condensato e restituito per mescolarsi con il liquido, che viene quindi riportato alla camera di ebollizione. Le differenze nel punto di ebollizione provocano una certa separazione della miscela. Il punto di ebollizione dell'acqua è superiore a quello dei componenti aggiunti, quindi i componenti volatili iniziano ad evaporare.

Figura 1: Una rappresentazione dell'apparato
Un coefficiente di attività è definito come il rapporto tra la fugacità di un componente in una miscela reale e la fugacità di una soluzione ideale della stessa composizione. La fugacità è una proprietà utilizzata per mostrare le differenze tra i potenziali chimici a stati standard. Le fugacità in fase vapore possono essere espresse in termini di coefficiente di fugacità [φ: fiV = φi yi fi0V ], con yi = frazione mol di i nella fase vapore, e fi0V = fugacità allo stato standard del vapore (la fugacità del vapore componente puro a T e P). Per le basse pressioni, come in questo esperimento, φi = 1 e fi0V = P. Le fugacità in fase liquida possono essere espresse in termini di coefficiente di attività γi: fiL = γi xi fi0L , con xi = frazione mol di i nella fase liquida e fi0L = fugacità allo stato standard liquido.
Alla pressione di saturazione (Pis) di questo T, la fugacità liquida della componente pura sarebbe Pis, perché il vapore puro e il liquido sono in equilibrio. Poiché le fugacità liquide sono solo funzioni deboli di pressione, possiamo approssimare la fugacità liquida della componente pura a T e P (fi0L) come Pis, purché la differenza tra Pis e P non sia grande. Questa approssimazione è solitamente chiamata "trascurare la correzione di Poynting". Se gli sperimentatori usano un apparecchio VLE per misurare le composizioni del vapore e del liquido che sono in equilibrio, gli sperimentatori possono calcolare direttamente i coefficienti di attività forniti per misurare anche P e T. T deve essere misurato per determinare PiS per tutti i.
Il cuore del dispositivo VLE, utilizzato in questo esperimento per determinare le composizioni delle miscele, è una pompa Cottrell che "sputa" liquido bollente in una camera di equilibrio ben isolata. Due valvole di campionamento ad azionamento magnetico consentono il prelievo di campioni di vapore liquido e condensato. Un grande serbatoio aiuta a smorzare gli impulsi di pressione nel sistema mentre la valvola di controllo on-off cambia e dalle fluttuazioni causate dalla pompa Cottrell. Una perdita lenta può essere utilizzata per creare un equilibrio tra la velocità di prelievo dell'aria e la velocità di ingresso dell'aria per mantenere una pressione costante, se necessario.
Un modo comparabile per risolvere l'equilibrio vapore-liquido è quello di utilizzare una varietà di modelli. La legge di Raoult, la legge di Dalton e la legge di Henry sono tutti modelli teorici che possono trovare i dati di concentrazione di equilibrio vapore-liquido. Tutti e tre i modelli sono correlati alla proporzionalità delle pressioni parziali, della pressione totale e delle frazioni moli delle sostanze. L'equazione di Wilson ha dimostrato di essere accurata per i liquidi miscibili, pur non essendo eccessivamente complessa. Inoltre, il modello di Wilson incorpora coefficienti di attività per tenere conto della deviazione dai valori ideali.
Procedura
1. Innesco del sistema
- Sfiatare il sistema VLE utilizzando la valvola a 3 vie di sfiato/controllo montata sul telaio dell'apparecchio e (se necessario) drenando il liquido dal sistema in un pallone di scarico.
- Rimuovere le provette campione e sostituirle con provette pulite (se necessario). Il liquido non scaricherà completamente dal sistema.
- Per la prima serie di esperimenti, riempire attraverso la valvola di ingresso con una miscela di circa (vol%) 50% metanolo, 30% isopropanolo e 20% acqua. Per la seconda settimana, riempire con circa il 25% di metanolo, il 45% di isopropanolo e il 30% di acqua. Per la terza settimana, riempi con qualsiasi liquido che devi ripetere. La capacità totale del liquido è di circa 130 cm3.
- Riempire di liquido appena sotto il punto in cui la pompa Cottrell si interseca con la camicia del vuoto. Troppo poco liquido farà sì che il sistema richieda tassi di ebollizione molto elevati per ottenere abbastanza liquido da "sputare" (quando il liquido scoppia mentre bolle intensamente).
- Utilizzare un becher e versare il liquido nella porta di addizione nella parte superiore della camera di equilibrio. Chiudere la porta.
- Controllare la pressione barometrica con il manometro a mercurio sulla parete. Regolare lo "zero" sul manometro digitale in modo che corrisponda (se necessario).
- Commutare la valvola di sfiato a tre vie per "controllare" e avviare la pompa per vuoto e il regolatore di pressione.
- Aprire la valvola a farfalla sul regolatore di pressione a diversi giri e osservare la pressione scendere rapidamente. Guarda la pressione sul manometro digitale.
- Impostare il set-point della pressione di controllo sul regolatore di pressione per ottenere ~ 700 mm Hg. Ascoltare per fare clic sulla valvola di controllo. Una volta raggiunto il punto di controllo, il rumore della pompa per vuoto sarà udibilmente diverso.
- A questo punto, con la valvola a farfalla aperta a più giri, ogni volta che la valvola di controllo si apre, troppa aria viene scaricata nella pompa per vuoto e la pressione scende sotto i 700 mm prima di riprendersi lentamente. Chiudere completamente la valvola a farfalla, quindi aprirla per circa 1/2 giro.
- Attendere che la valvola di controllo inizi a fare clic di nuovo, quindi chiudere la valvola a farfalla con piccoli incrementi fino a quando la pressione fluttua solo ~ 0,5 mmHg o meno quando la valvola è aperta. Apportare piccole regolazioni al punto di controllo o alla valvola di tenuta, se necessario, per mantenere molto vicino a 700 mmHg.
- Una volta che la miscela è entro ±10 mmHg di 700 mmHg, accendere la potenza del riscaldatore, la potenza del mantello di riscaldamento, l'acqua del condensatore e l'agitatore magnetico. Prova il 25-30% di potenza del riscaldatore e l'1,5-2 giri di potenza del mantello per iniziare. L'apparato richiederà 20 minuti o meno per avvicinarsi all'equilibrio. Continua a regolare la pressione durante questo periodo.
2. Esecuzione dell'esperimento
- Al momento dell'ebollizione, la pompa Cottrell inizierà a sputare liquido e il liquido può essere visto gocciolare di nuovo nella camera di ebollizione. Il vapore condensato richiederà più tempo per apparire. Quando viene raggiunto l'equilibrio, gli sperimentatori dovrebbero vedere gocciolamenti costanti di vapore condensato (2 - 3 gocce / s) e liquido restituito (2 - 3 gocce / s). La temperatura dovrebbe essere stabile a ± 0,03 ºC e la pressione dovrebbe essere stabile a 700,0 ± 0,5 mmHg. Quando queste condizioni sono state stabilite per almeno 2 minuti (o giù di lì), si raggiunge l'equilibrio.
- Aprire le valvole magnetiche (contrassegnate "1" e "2" sul controller) 4 o 5 volte ciascuna per un tempo sufficiente a raccogliere circa 0,5 cm3 di liquido in ciascuna provetta del campione e chiudere le provette. Se una valvola non risponde al suo pulsante, prova a spegnere e riaccendi l'interruttore di alimentazione del controller. Questo primo campione verrà utilizzato per lavare i tubi e il sistema di consegna e verrà scartato. Il lavaggio sostituisce qualsiasi sostanza chimica rimanente sui lati dei tubi con la stessa sostanza chimica che viene campionata, quindi non influirà sulla composizione del test.
- Spegnere momentaneamente l'alimentazione al riscaldatore, attendere 30 s affinché l'ebollizione si plachi, quindi sfiatare il sistema con la valvola a 3 vie di sfiato / controllo. Rimuovere i tubi del campione, ruotare un paio di volte, quindi scaricarli nella discarica.
- Rimontare le provette campione sul sistema, riportare la valvola di sfiato al "controllo", riaccendere l'alimentazione al riscaldatore e attendere che l'equilibrio venga ristabilito. Questo richiederà solo pochi minuti se l'apparecchio non si raffredda. Una leggera differenza di temperatura può essere osservata quando l'equilibrio viene ristabilito. Ciò può essere dovuto a un leggero disturbo della composizione complessiva dovuto al campionamento.
- Una volta ristabilito l'equilibrio, prendi due nuovi campioni. Avere due flaconcini etichettati con nuovi setti pronti.
- Dopo aver prelevato di nuovo ~ 0,5 cm3 campioni in ciascun tubo, spegnere il riscaldatore, sfiatare il sistema, rimuovere i tubi campione e versarli nelle fiale. Chiudere i flaconcini e sostituire le provette con provette pulite, se necessario.
- Durante l'analisi dei campioni, preparare un nuovo campione. Scolare ~ 15 cm3 di liquido in un becher o in un pallone. Aggiungere ~ 20 cm3 di metanolo puro o 50/50 metanolo / isopropanolo attraverso la porta del campione. Questo darà una nuova composizione complessiva.
- Assicurarsi che le provette del campione siano completamente vuote, quindi chiudere il sistema, accendere la valvola di sfiato su "controllo" e riaccendere il riscaldatore. Se si lavora rapidamente, l'equilibrio sarà ristabilito rapidamente. Si noti che dovrebbe esserci una differenza di temperatura rispetto al campione precedente.
- Ripetere la procedura di equilibratura e campionamento come prima, ricordando di prendere un campione da lavare, quindi prendere il campione finale. Continuare gli esperimenti aggiungendo componenti. Dodici punti dati sono sufficienti per determinare i coefficienti di attività e (approssimativamente) i coefficienti di interazione binaria.
3. Spegnimento del sistema
- Spegnere i riscaldatori. Quando l'apparecchio inizia a raffreddarsi, spegnere l'agitatore e l'acqua del condensatore.
- Riportare il sistema alla pressione atmosferica; impostare il controller >1020 mbar, chiudere la valvola a farfalla, impostare la valvola a tre vie per lo sfiato e aprire la valvola sul serbatoio.
- Una volta raggiunta la pressione atmosferica, spegnere la pompa. Scaricare il liquido dal serbatoio fino a raggiungere il livello della valvola, ma lasciare il resto del liquido nel serbatoio. Chiudere la valvola a 3 vie.
4. Analisi
- Usando la regressione non lineare e una somma standard di funzioni oggettive residue al quadrato, usa i coefficienti di attività calcolati dai dati grezzi per regredire le 6 costanti per l'equazione di Wilson ternaria (sotto), per questo sistema. Valutare la qualità dell'adattamento con metodi grafici e calcolare le deviazioni relative percentuali medie (APRD), che sono errori di adattamento medio x 100.

- Convergere sui valori ottimali reali da diverse direzioni nello spazio dei parametri di risposta utilizzando un metodo fattoriale per le ipotesi iniziali. Calcolare la precisione delle misurazioni GC replicando sufficientemente un campione GC per determinare le precisioni relative in base alla t-statistica e utilizzare le precisioni per determinare se accettare / rifiutare una particolare misurazione GC mediante un test di ipotesi appropriato.
- Confronta le precisioni relative della misurazione GC con gli APRD e discuti. Segnala anche le precisioni assolute dei manometri di pressione e temperatura - determinali una volta al giorno.
Risultati
I coefficienti di attività dei dati non mostrano deviazioni significative da un valore medio per ciascun componente (Tabella 1). Questo è come previsto perché per le composizioni di componenti intermedi non ci sono grandi variazioni. Tuttavia, i componenti vicini a 1 hanno γ è vicino a 1. I componenti a bassa composizione hanno γ elevate. Componenti più alti in concentrazione in una miscela che avrà una deviazione ridotta, quindi sarà più vicino all'ideale (γ = 1). I componenti con concentrazioni più basse in una miscela avranno deviazioni più elevate, quindi i loro γ saranno maggiori di 1.
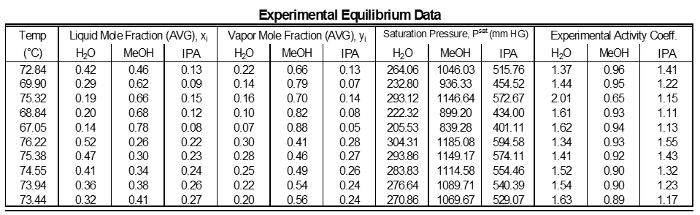
Tabella 1: Risultati di ciascun campionamento dei dati sperimentali.
I dati erano adatti ai parametri del modello Wilson e i coefficienti sono stati calcolati (Tabella 2). È stata utilizzata una semplice riduzione della somma dei residui al quadrato tra i coefficienti di attività sperimentali e quelli dell'equazione di Wilson (1). Ciò è stato ottenuto utilizzando la funzione risolutore di Excel. Il grafico di parità mostrato mette in relazione i coefficienti di attività del modello dell'equazione di Wilson con i coefficienti di attività trovati sperimentalmente. I coefficienti di attività sperimentale sono stati calcolati e confrontati graficamente con i coefficienti del modello calcolati.

Tabella 2: Risultati dell'adattamento dei dati ai parametri del modello Wilson.
 (1)
(1)
I valori dei parametri trovati erano i più adatti (Tabella 3). Idealmente la correlazione è lungo la linea y=x; tuttavia, è stata trovata una correlazione significativa simile allo scenario ideale (Figura 2). I coefficienti di attività dei dati non hanno mostrato deviazioni significative da un valore medio per ciascun componente, come previsto. Una riduzione della somma dei residui al quadrato tra i coefficienti di attività dell'equazione sperimentale e di Wilson è stata utilizzata con la funzione risolutore di Excel. Il grafico di parità mette in relazione i coefficienti di attività del modello dell'equazione di Wilson con i coefficienti di attività trovati sperimentalmente.
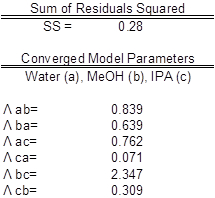
Tabella 3: Parametri del modello con acqua (a), MeOH (b) e IPA (c). I valori sperimentali vengono confrontati con i valori attesi.

Figura 2: Rappresentazione della correlazione tra i coefficienti di attività sperimentale e i coefficienti di attività del modello.
Applicazione e Riepilogo
Questo esperimento ha dimostrato l'equilibrio delle miscele metanolo - isopropanolo - vapore acqueo-liquido a una costante P = 700 mm Hg e come misurare la temperatura e la composizione e calcolare i coefficienti di attività. I coefficienti di attività dei dati non si sono discostati in modo significativo da un valore medio per ciascun componente, come previsto. Una riduzione della somma dei residui al quadrato tra i coefficienti di attività dell'equazione sperimentale e di Wilson è stata utilizzata con la funzione risolutore di Excel. Il grafico di parità mette in relazione i coefficienti di attività del modello dell'equazione di Wilson con i coefficienti di attività trovati sperimentalmente.
Nell'industria petrolifera, la distillazione è il processo principale per la separazione dei prodotti petroliferi. Molte raffinerie di petrolio utilizzano la distillazione per il petrolio greggio1. Gli idrocarburi leggeri sono separati dalle particelle più pesanti, separandosi in base ai punti diebollizione 1. Materiali pesanti come i gasoli si raccolgono nelle piastre inferiori, mentre i materiali leggeri come propano e butano salgono di1. Gli idrocarburi, come benzina, jet e gasolio, sono separati1. Questo processo viene spesso ripetuto molte volte per separare e perfezionare completamente i prodotti1. Le raffinerie eseguono questi processi allo stato stazionario, creando costantemente nuovi prodotti alla massima capacità, quindi l'efficienza è la chiave1. Gli ingegneri chimici che lavorano su questi processi si concentrano sull'ottimizzazione dell'efficienza della produzione1.
Le colonne di distillazione del vassoio vengono utilizzate anche per separare una varietà di prodotti chimici. L'etanolo è uno di questi prodotti. Attraverso processi strettamente correlati, una varietà di prodotti come etanolo per uso combustibile, birra e liquori possono essere distillati2. Quantità specifiche di alcol possono essere separate dall'acqua al fine di creare una prova specifica2. Questo processo si limita a ridurre la percentuale di acqua nel prodotto, ma non può eliminarlo completamente2. Per rimuovere completamente l'acqua, è necessaria la distillazione azeotropica, che utilizza sostanze chimiche di estrazione per separare l'acqua dall'etanolo2.
Riferimenti
- About the Refinery." Processing & Refining Crude Oil. Chevron.com, n.d. Web. 17 Nov. 2016.
- Madson, PW. Ethanol Distillation: The Fundamentals. Cincinnati: Katzen International, n.d. Print. Accessed from Web. 01 Oct. 2016.
Vai a...
Video da questa raccolta:

Now Playing
Equilibrio vapore-liquido
Chemical Engineering
89.4K Visualizzazioni

Verifica dell'efficienza del trasferimento di calore di uno scambiatore di calore a tubi alettati
Chemical Engineering
17.9K Visualizzazioni

Utilizzo di un essiccatore a vassoio per studiare il trasferimento di calore convettivo e conduttivo
Chemical Engineering
44.0K Visualizzazioni

Viscosità delle soluzioni di glicole propilenico
Chemical Engineering
33.1K Visualizzazioni

Porosimetria della polvere di silicato di alluminio
Chemical Engineering
9.6K Visualizzazioni

Dimostrazione del modello Power Law per estrusione
Chemical Engineering
10.3K Visualizzazioni

Assorbitore di gas
Chemical Engineering
36.8K Visualizzazioni

L'effetto del rapporto di riflusso sull'efficienza della distillazione dei vassoi
Chemical Engineering
77.9K Visualizzazioni

Efficienza di estrazione liquido-liquido
Chemical Engineering
48.6K Visualizzazioni

Reattore in fase liquida: inversione del saccarosio
Chemical Engineering
9.7K Visualizzazioni

Cristallizzazione dell'acido salicilico mediante modificazione chimica
Chemical Engineering
24.3K Visualizzazioni

Flusso monofase e bifase in un reattore a letto impaccato
Chemical Engineering
19.0K Visualizzazioni

Cinetica di polimerizzazione per addizione al polidimetilsilossano
Chemical Engineering
16.4K Visualizzazioni

Reattore catalitico: Idrogenazione dell'etilene
Chemical Engineering
30.5K Visualizzazioni

Valutazione del trasferimento di calore di uno Spin-and-Chill
Chemical Engineering
7.4K Visualizzazioni