Method Article
Morphology-Based Distinction Between Healthy and Pathological Cells Utilizing Fourier Transforms and Self-Organizing Maps
* These authors contributed equally
In This Article
Summary
Here, we provide a workflow that allows the identification of healthy and pathological cells based on their 3-dimensional shape. We describe the process of using 2D projection outlines based on the 3D surfaces to train a Self-Organizing Map that will provide objective clustering of the investigated cell populations.
Abstract
The appearance and the movements of immune cells are driven by their environment. As a reaction to a pathogen invasion, the immune cells are recruited to the site of inflammation and are activated to prevent a further spreading of the invasion. This is also reflected by changes in the behavior and the morphological appearance of the immune cells. In cancerous tissue, similar morphokinetic changes have been observed in the behavior of microglial cells: intra-tumoral microglia have less complex 3-dimensional shapes, having less-branched cellular processes, and move more rapidly than those in healthy tissue. The examination of such morphokinetic properties requires complex 3D microscopy techniques, which can be extremely challenging when executed longitudinally. Therefore, the recording of a static 3D shape of a cell is much simpler, because this does not require intravital measurements and can be performed on excised tissue as well. However, it is essential to possess analysis tools that allow the fast and precise description of the 3D shapes and allows the diagnostic classification of healthy and pathogenic tissue samples based solely on static, shape-related information. Here, we present a toolkit that analyzes the discrete Fourier components of the outline of a set of 2D projections of the 3D cell surfaces via Self-Organizing Maps. The application of artificial intelligence methods allows our framework to learn about various cell shapes as it is applied to more and more tissue samples, whilst the workflow remains simple.
Introduction
Timely, simple and precise determination of the pathological status of biological tissue is of the highest interest in biomedical research. Mouse models provide the means to study a range of pathological conditions, such as immune reactions or cancer development, in combination with complex 3D and 4D (3 spatial dimensions and time) microscopy techniques. Microscopy studies can be performed via intravital or excised-tissue 2-photon microscopy, light-sheet microscopy, and -to a limited tissue depth of approximately 100 µm- by confocal microscopy. In order to have time-related information about the cells' behavior under physiological or pathological conditions, it is necessary to monitor the tissue for an extended period of time, which usually requires intravital imaging1,2. Naturally, the applicability of this technique is limited to animal models due to its invasiveness. Non-invasive techniques are also available for human applications, including a variety of tomography methods (MSOT, CT, etc.), but these methods all lack the necessary spatial -and often temporal- resolution to study behavior at the cellular level.
Static information regarding the appearance of cells may be accessible more easily via various 3D imaging techniques executed on excised tissue samples. Here, the kinetic behavior of the cells is not measured, thus it is necessary to adopt novel analysis techniques that are able to determine the pathogenic status of the examined cells based solely on their morphology3. Such an approach was used to link cell shapes and tissue textures to pathological behavior4,5,6.
In the new technique described here, the cells are reconstructed as 3D surfaces and their shapes are characterized via 3D-to-2D projections and successive Fourier-based periphery-shape analysis7,8. By reducing the dimensions from 3 to 2, the problem is simplified. It is also possible to characterize the cell surfaces in 3D by applying spherical harmonics analysis, as it has been done for medical images9. However, spherical harmonics do not handle sharp and rugged shapes well, requiring a multi-scale grid to be established on the unit sphere. In addition, the number of necessary spherical harmonics components can be large (50-70), with the underlying calculations very demanding and the results hard to interpret10,11,12.
With our newly proposed method, the task is reduced to a series of 2D shape descriptions, where the number of the 2D projections is up to the analyst and can be adjusted according to the complexity of the 3D shape. The projections are generated automatically via a Python script that runs inside a 3D animation tool. The 2D projections are described by the discrete Fourier transform (DFT) components of their periphery, calculated by a Fiji13 plugin that is provided here as part of our software package. The DFT is applied here in order to decompose the complex outline of the cell into a series of sin and cos functions. In this way, we can describe the outline with a relatively small number of DFT components, thus reducing the complexity of the problem (for further details see Equations section). The DFT components are put into a trained Self-Organizing Map (SOM14), where the existence of shape clusters can be objectively tested8. SOMs provide a competitive and unsupervised learning tool from the field of artificial intelligence. They consist of a linked array of artificial neurons which communicate with each other via a weighted neighborhood distance function. The neuronal system responds to the first element of the input dataset and the neurons whose response is the strongest are "grouped" nearer to each other. As the neural system receives more and more input, data neurons that repeatedly respond strongly start to form well defined cluster within the system. After proper training on a large dataset that contains 2D shape information in form of a set of DFT components, any individual cell's DFT components can be put into the trained SOM and reveal whether the cell likely belongs to the healthy or the pathogenic cell group. We expect such tool to become a great addition to the methods of scientific and clinical diagnostics.
Protocol
1. Protocol Requirements
- Obtain high-resolution deconvolved three-dimensional (3D) microscopy data deconvolved in compliance with the Nyquist criterion with a sampling interval at least twice the highest spatial frequency of the specimen to obtain a high resolution image.
- Use 3D rendering software for the surface reconstruction and export.
- Use 3D animation software capable of running Python scripts (the Python script can be downloaded from the github repository: https://github.com/zcseresn/ShapeAnalysis) to create 2D projections.
- Use Fiji13 to analyze 2D projections and extract the DFT components.
- Use the current Fiji distribution. If there already exists an installed version of Fiji, make sure that the installed version is the latest. This can be easily achieved by running the Help |Update option.
- Use the Active Contour plugin15, which can be downloaded from http://imagejdocu.tudor.lu/doku.php?id=plugin:segmentation:active_contour:start and should be copied into the plugins folder.
- Download the SHADE Fiji plugin from the github repository and copy into the plugins folder.
- Use computational mathematics software capable of calculating Self-Organizing Maps.
2. Reconstruct the 3D Image.
NOTE: For testing purposes, an example dataset is provided in the github repository (see above).
- Start the 3D reconstruction software and open the 3D image data.
- Create a 3D Surface of (all) object(s).
- Select the 3D view option and click on Surfaces. Click on the Next button (blue circle with a white triangle) to proceed with the surface creation wizard.
- Select the image channel for the surface reconstruction.
- Apply a smoothing function to avoid porous surfaces.
- Choose a smoothing value that does not hide the details of the surface but avoids porous surfaces.
- Select a thresholding method to find the surfaces.
- Use an absolute intensity threshold when the objects are well-separated from the background and have an approximately uniform brightness level.
- Apply a local contrast threshold when the objects vary in their intensity but can still be separated from the local background and from the other objects surrounding them. Set the local threshold search area according to the value of the expected diameter of the reconstructed objects.
- Filter the reconstructed surfaces according to morphological parameters of interest, e.g., volume, sphericity, surface-to-volume ratio, etc., and finish the surface reconstruction.
- Save and export the generated surfaces in a format that is compatible with the 3D animation software that will be used in the next step.
3. Transform the 3D reconstructed surfaces into 2D projections
- Start Blender and go to the output tab in the right-side window. Select the TIFF format from the dropdown menu and set the color depth to 8 bit RGBA.
- Switch into Scripting Mode and open the provided script file "GUI_AutoRotate.py" from the repository provided with this work (https://github.com/zcseresn/ShapeAnalysis).
- Click on Run Script. Choose the folder of the wrl files when prompted for input.
- If needed, create more rotations when working with more complex surfaces: go to the GUI and set the box Rotations to a value above 6.
NOTE: A rotation of 6 different angles can be sufficient to distinguish the different cell populations. It is not recommended to create less than six rotations per surface, because of potential information loss. - Run the script by clicking on the Rotate button in the GUI. Save the projections of the individual surfaces in the same folder that was used as the input folder (step 2.3). By default, the images are saved in an 8 bit Tiff format (see step 2.1), which is the format required by the Fiji plugin SHADE.
4. Find the periphery and calculate the Fourier components using Fiji.
- Open Fiji and select SHADE in the Plugins menu. Start with the default values and fine-tune the parameters later on. Click OK when ready to run the program.
- Choose a Gradient Threshold value for the thresholding of the input image.
- Choose the Number of Iterations. The higher the Number of Iterations value, the more precise the reconstruction of the periphery. For simpler shapes, a lower number is usually sufficient.
- Use the Number of Dilations parameter to determine how much larger the starting mask is compared to the actual cell. Usually more complex shapes need more dilation steps for proper periphery finding.
- Check the Dark Background checkbox if the projected shapes are brighter than the background.
- Activate the Show Intermediate Results checkbox only when using a small test dataset to determine the performance of SHADE. Activating this option for larger datasets lowers the computational efficiency and could possibly halt a system with low video memory.
- Check the Save Result Tables checkbox to use the results of SHADE as an input for step 5. If the box is checked, all results are saved in individual csv files. A summary of the output data is always generated in a file called "Result_collection_of_all_DFT_calculations.csv".
- Select the input data folder that contains the TIFF files that were created in step 3.
- Provide the output data folder.
- Click OK to start the plugin.
5. Self-Organizing Maps
NOTE: SOM networks are only able to classify data when they are trained on a large dataset which contains input from all expected cell types and conditions. For demonstration purposes, such a dataset is provided and can be found in our repository (“AllCells_summary_normalised.csv” from https://github.com/zcseresn/ShapeAnalysis
- Follow these guidelines if there is no trained SOM available yet for the input data; otherwise proceed to step 5.2.
- Start a computational mathematical software capable of performing neural network classifications.
- Select a data file to be used for training the SOM network. This dataset should contain all experimental conditions in order to train the SOM on the particular cell types and experimental conditions.
NOTE: It is also possible to use the provided AllCells_summary_normalised.csv for testing the system. - Start the training and wait till the training is completed before proceeding. By default, the script is set to run 2000 iterations ("Epochs").
NOTE: The number of iterations depends on the learning rate of the SOM. Depending on the input data it is advisable to test both higher and lower number of epochs and observe the stability of the pattern of the SOM. When using the script provided, the number of iterations can be changed under line 32. The network size can be changed in line 34 (by default it is set to 12 by 12). - After the training is finished, examine the network’s topology (neighbor distances, input planes, sample hits, etc.). The network is now trained and can be saved for future use.
- Load in the SOM, when using an already trained map (this can come either from Step 5.1 or from other sources) in order to cluster a dataset.
- Import the csv file that is to be tested with the preloaded trained SOM. Select the csv output of the SHADE Plugin from step 4 when using data prepared by the SHADE plugin.
NOTE: It is also possible to use the example data files “InteractingCells_summary_normalised.csv”, “MobileCells_summary_normalised.csv” or “PhagocytosingCells_summary_normalised.csv” that are provided via github. - After the classification is finished, evaluate the results of the SOM as in step 5.1.5.
- Examine the hitmap generated from the csv file. Each cell of the map shows how many times the dataset "hits" that particular cell of the trained SOM. When a group of cells are clustered in a small area of this map, this indicates that the dataset is fairly homogenous. Multiple clusters will indicate that subgroups likely exist in the dataset.
- Examine the neighborhood weight distances. Areas of this map that are well separated correspond to groups of objects that behave very differently from the SOM's point of view. With DFT components as input data, this means that these cell groups have very dissimilar shapes of the corresponding 3D surfaces.
- Examine the weight planes for information about the contribution by each element of the feature vector. In case of using the 20 DFT components as described earlier, 19 maps will appear here. When using the provided example dataset, the first 5 or 6 weight planes will be different, but the rest of them will appear fairly similar. In this case it can be concluded that it would be enough to use approximately 7 DFT components.
- Import the csv file that is to be tested with the preloaded trained SOM. Select the csv output of the SHADE Plugin from step 4 when using data prepared by the SHADE plugin.
Results
We applied a DFT to calculate the main components of the shape corresponding to the cell projections. The Fourier descriptors were obtained by applying the DFT algorithm to the xy-coordinate pairs of the fitted periphery of the cell projections, obtained as the output of the AbSnake part of our workflow. These xycoordinate pairs can be handled as a complex-valued 2D vector "g":
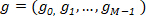
From the vector "g", we use DFT to calculate the complex-valued Fourier spectrum:
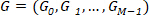
Based on well-known formulas of the discrete Fourier spectrum, and using the complex-number labeling of "g" as:
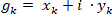
We get:
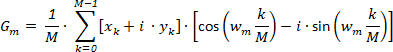 (1)
(1)
We can calculate the real ("A") and imaginary ("B") components of 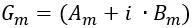 :
:
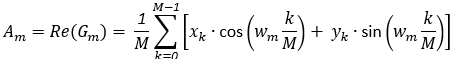 (2)
(2)
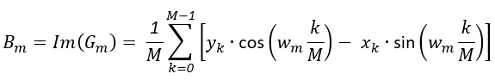 (3)
(3)
Here, the first DFT component G0 corresponds to m = 0, which gives:
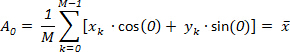 (4)
(4)
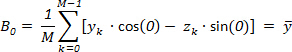 (5)
(5)
Consequently, this component describes the geometrical center of the original object.
The second element of the DFT forward spectrum, G1, corresponds to m = 1:
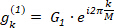
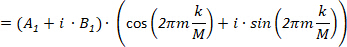 (6)
(6)
From Eq.6 we conclude that these points form a circle with a radius of 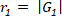 and starting angle
and starting angle 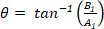 , where the circle describes one complete revolution while the shape is traced once. The center of the circle is located at the origin (0, 0), the radius is |G1| and the starting point is:
, where the circle describes one complete revolution while the shape is traced once. The center of the circle is located at the origin (0, 0), the radius is |G1| and the starting point is:
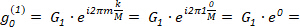
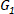 (7)
(7)
In general, for a single Fourier coefficient 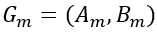 , the coordinates are described as:
, the coordinates are described as:
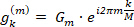
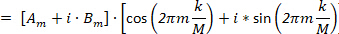 (8)
(8)
Similarly to Eq.6, Eq.8 also describes a circle, but with a radius of Rm=|Gm|, a starting angle 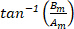 and a starting point at
and a starting point at 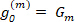 , where the contour is traced once whilst the circle runs through "m" full orbits16,17.
, where the contour is traced once whilst the circle runs through "m" full orbits16,17.
Shape parameters as SOM input
The workflow, as described in Figure 1, was applied to a deconvolved (using a measured Point Spread Function) intravital multi-photon microscopy dataset of microglial cells to characterize their morphological changes in healthy or cancerous cortical tissue18. Twenty DFT components were calculated for each 2D projection of the reconstructed 3D surfaces and the results were used as an input for the SOM training. Under physiological conditions, the microglia presented a rather complex shape with multiple, highly branched processes (Figure 2a). When placed in a cancerous environment (cortical tumor model), the microglia changed to a simpler, more spindle-like shape (Figure 2b).
The trained SOM was tested in order to evaluate its ability to distinguish between healthy and cancerous cells. The healthy cell population was projected onto a single area of the SOM (Figure 2c). The SOM responded to the cancerous microglia dataset with a dumbbell-shaped active region (Figure 2d). A blindly mixed input data set that consisted of DFT shape components from both the healthy and the cancerous group was projected by the SOM into two distinct groups, whilst keeping the shape of their individual contours similar to those of the separated groups (Figure 2e; compare with 2c and 2d). It can be concluded that the mixed dataset was successfully clustered by the SOM.
We tested the performance of the SOM by comparing its projections with the manual analysis of the same data by a medical expert, who classified the dataset based on their spatio-temporal behavior. The expert identified four distinct cell groups (resting cells, phagocytosing cells, interacting cells, and mobile cells18), which were reconstructed and used to train a 12x12 SOM. The trained network (Figure 3a) shows groups of high hit-value artificial neurons, especially in the bottom left and the middle areas of the SOM. The response of the trained network was also tested with four randomly selected subsets (which were not part of the training dataset) of images from the four different groups identified by the expert18. These image subsets resulted in four well-defined responses by the SOM, as shown in Figure 3b. The resting cells exhibit the most complex shape and showed the highest separation level within the neural network (Figure 3b "resting" panel). The other three identified cell types shared a common area of the SOM in the bottom left corner, but were otherwise separated by the SOM. The bottom left corner SOM area thus corresponds to the lower-index DFT values.
The robustness of the SOM approach was tested by using the trained SOM with three random subsets of the same -resting- cell type (not part of the training dataset). The response of the SOM to this input exhibits a very similar response (Figure 3c, subsets 1-3), demonstrating the robustness of our approach.
Time-dependent cell shape changes are precisely characterized by DFT
In order to examine the effect of time-dependent changes of the cell shape on the DFT components, one to three cells per subgroup (see Figure 3b) were tracked for 13 to 28 time points. Figure 4 shows the first ten DFT components of a mobile cell (Figure 4a) and an interacting cell (Figure 4b), which were plotted as a function of time. The mobile cell exhibits a permanently altering shape (see Supplementary Video 4 in 8), which is reflected by a rougher DFT surface. The bursts of the DFT amplitude in the first third of the time course for the interacting cell coincide with the fast and vast cell shape changes as shown in Supplementary Video 5 in 8.
The time course of all 19 DFT components was also characterized for these two cells at three separate time points during the tracking of a mobile cell (Figure 5a) and of an interacting cell (Figure 5b). The perpendicular axes represent hereby the six rotation angles and indicate that all projections are equally important for the characterization of the shape for both cell types.
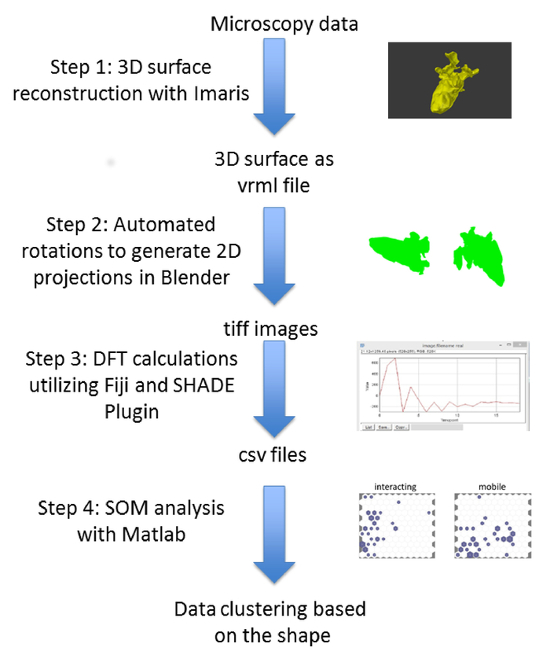
Figure 1. Step by step workflow of the data processing to identify cell clustering based on the shape of cells. Surfaces reconstructed in 3D were used as input to Blender for automated 3D-to-2D projections. The periphery of each projection was located and the DFT components were calculated. The components served as an input either to a trained SOM in Matlab, or to train a new SOM. Please click here to view a larger version of this figure.
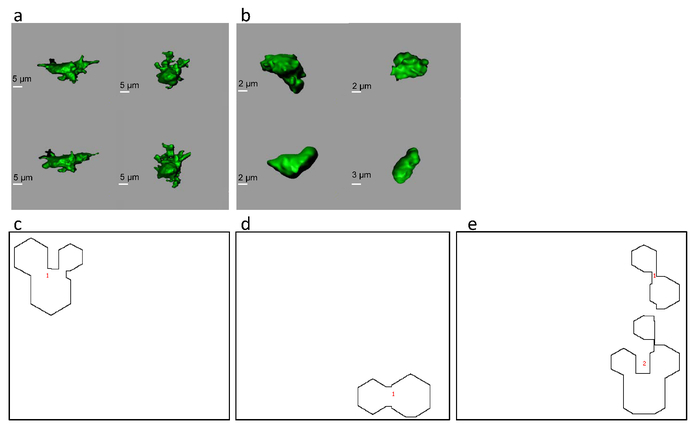
Figure 2. Typical appearance of mouse cortical microglia cells under control conditions (a) and in cancerous tissue (b) Screenshots of reconstructed microglia surfaces. SOM projections were created from the three groups of microglia samples from the mouse cortex: control (non-tumorous) cells (c), tumor cells (d), and a mixed population of cells (e). This figure has been modified with permission8. Please click here to view a larger version of this figure.
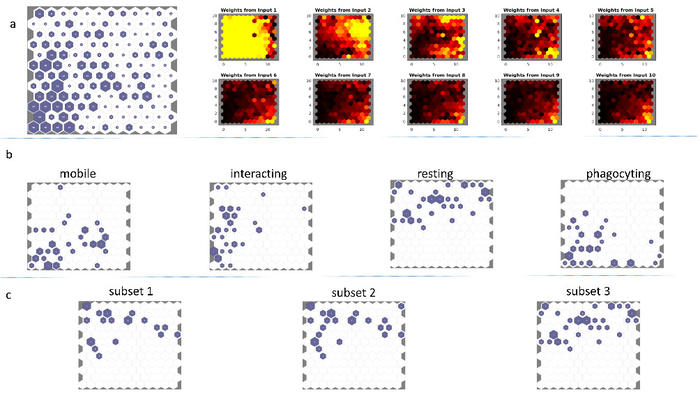
Figure 3. (a, left) Self-Organizing Map of a mouse microglia dataset consisting of 768 input feature vectors. The dataset was used to train a 12x12 artificial neural network, using hexagonal neighborhood geometry, random initialization and 2000 epochs. (a, right) The corresponding SOM input planes of the first 10 DFT components (b) The responses of the SOM depicted in (a), to one random VRML file subset each from the four cell types "mobile," "interacting," "resting," and "phagocytic" as first described in Figure 5 of Bayerl et al.18. (c) The response of the same SOM as in (a, left) to three random subsets of the entire dataset (which were thus not part of the training dataset) of the "resting cells"-type 3D surfaces. The similarity amongst the three responses is notable. This figure has been modified with permission8. Please click here to view a larger version of this figure.
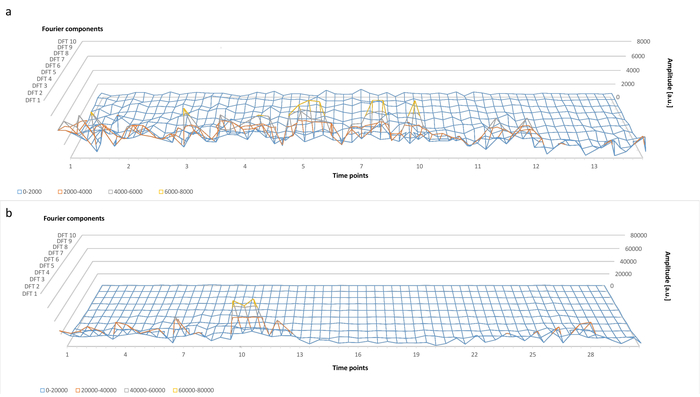
Figure 4. (a) Time dependence of the first 10 DFT components during an intravital imaging experiment of mouse microglia. This panel shows data for a cell of the "Mobile Cells" type. The x-axis corresponds to time points of the experiment at 60 s time resolution, the y-axis shows the amplitude of the DFT components in arbitrary units (a.u.), whereas the z-axis corresponds to the DFT component from 1 to 10. (b) As in (a) but for a cell of the "Interacting Cells" type. This figure has been modified with permission8. Please click here to view a larger version of this figure.
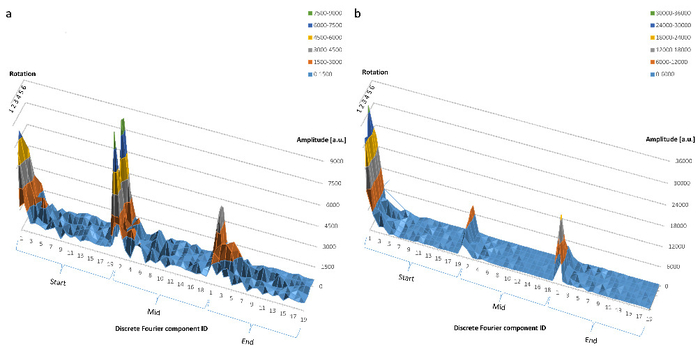
Figure 5. (a) The behavior of all 19 DFT components of a cell of the "Mobile Cells" type at the beginning, at the middle and at the end of the experiment. The numbers on the x-axis correspond to the DFT component ID from 1 to 19. The y-axis shows the DFT component amplitude in arbitrary units (a.u.), whilst the z -axis marks the six random rotation angles. (b) Same as in (a) but for a cell of the "Interacting Cells" type. This figure has been modified with permission8. Please click here to view a larger version of this figure.
Discussion
The identification of potentially pathological conditions using small, intact tissue samples is of high importance. Such techniques will assure a timely response to infectious diseases and aggressive types of cancer. The kinetic and morphological responses of various immune cells, e.g., microglia and macrophages, are characteristic of the immune response of the body. Although in most cases it is not practical or even possible to monitor the kinetic behavior of these cells, it is fairly straightforward to acquire 3-dimensional images to retrieve their shape. Typically, immune cells assume a complex shape in healthy tissue and a much simpler form under inflamed or cancerous conditions18. Whilst the time-dependent characteristics of such shape change would add to our understanding of the development of the immune response, using only the 3D shape of a representative group of cells can also be sufficient to determine the healthy or pathological nature of the tissue.
Characterizing the 3-dimensional surface of a cell is not a simple task. The application of spherical harmonics is a way to represent a 3D surface with a relatively large number (50-70) of components11,12. In addition, determining the spherical harmonics is computationally expensive; projecting very complex shapes onto the unit sphere is either impossible or very difficult due to the need to apply multiple grids of various fineness on the unit sphere; finally, the meaningful interpretation of the spectra of the spherical harmonics components is far from being trivial.
In our work presented here, we replace the difficult task of direct 3D surface analysis with the much simpler approach of using 2D projections of the original surface to gain sufficient morphological information to identify pathologic conditions. We demonstrated every step of this workflow by using 3D microscopy data from myeloid cells, whilst clearly pointing out that all steps were simple to complete, and the resulting 2-dimensional maps were easy to interpret.
Naturally, a 3D-to-2D projection will lead to information loss about the structure of the surface. In our example dataset of microglia in a mouse cortical tumor model, it was enough to use six angles when creating the 2D projections. However, more complex shapes, or less prominent morphological changes may require that a larger number of projections are created so as to be able to reliably identify cell subgroups with the SOM. For this reason, our approach is designed to be able to generate and analyze any number of projections. Simply by choosing a higher number of projections for more complex shapes, it is possible to scale the information loss to a tolerable minimum. As an example, the interacting cell type in Figure 4a and 4b would require a larger number of projections in order to represent the complex surface properly.
As any approximate method, the hereby proposed workflow had to be tested against the results of a manual classification process of microglia18. The results presented earlier confirmed the reliability of the automated workflow. Furthermore, the workflow is more time efficient compared to conventional analysis. The medical expert who classified the microglia cells manually needed approximately 4 weeks for his analysis of the dataset, whereas our workflow needed only about 1 day. The robustness of our approach was also clearly proven by the reproducibility of the trained SOM to a subset of data that belonged to the same cell type but was not used to train the SOM, as show in Figure 3c.
Even though our approach did not consider kinetic information, we examined the effect of timing on the DFT-based shape analysis. The most typical example for time-dependent behavior was found amongst the mobile cell population, where the contribution from the higher indexed DFT components was clearly observable, as in Figure 4a. This calls attention to the importance of utilizing a high enough number of DFT components when dealing with cell types that are likely to behave in a very time-dependent manner. Due to the automated nature and high execution speed of our software tools, the increased number of DFT components and projections will increase the precision and reliability of the results, whilst they will not appreciably hinder the computational performance.
Disclosures
The authors declare that they have no competing financial interests.
Acknowledgements
The authors thank Benjamin Krause for the fruitful discussion and his support. The authors further thank Robert Günther for his assistance with the live cell microscopy.
The work was supported by the DFG financial support NI1167/3-1 (JIMI) to R.N. and Z.C., DFG financial support CRC 1278 PolyTarget Project Z01 for Z.C., C01 in TRR130 to R.N. and SFB633, TRR130, Exc257 to A.E.H. and J.B.S. The BfR provided intramural support SFP1322-642 for F.L.K and A.L.
Materials
| Name | Company | Catalog Number | Comments |
| Imaris 9.1.2, software | Bitplane, Zürich, Switzerland | v.9.1.2 | 3D image reconstruction and surface generation; this was used by us! |
| Blender 2.75a, software | https://www.blender.org/ | v.2.75a | 3D and 4D open source animation software; 2.75a is the required version for this Python |
| Fiji /ImageJ, software | https://fiji.sc/ | ImageJ v.1.52b | Open source multi-D image analysis toolkit |
| MATLAB | MathWorks, www.mathworks.com | R2017b | General computational mathematical software |
| MATLAB Machine Learning kit | MathWorks, www.mathworks.com | R2017b | Can only be used together with MATLAB |
| Fiji plugins: SHADE | https://github.com/zcseresn/ShapeAnalysis | v.1.0 | |
| Fiji plugins: ActiveContour | http://imagejdocu.tudor.lu/doku.php? id=plugin:segmentation:active_contour:start | absnake2 | |
| Computer | Any | NA | See Imaris instructions for minimum computer requirements |
References
- Masedunskas, A., et al. Intravital microscopy: a practical guide on imaging intracellular structures in live animals. Bioarchitecture. 2 (5), 143-157 (2012).
- Niesner, R. A., Hauser, A. E. Recent advances in dynamic intravital multi-photon microscopy. Cytometry A. 79 (10), 789-798 (2011).
- Ho, S. Y., et al. NeurphologyJ: an automatic neuronal morphology quantification method and its application in pharmacological discovery. BMC Bioinformatics. 12, 230 (2011).
- Yin, Z., et al. A screen for morphological complexity identifies regulators of switch-like transitions between discrete cell shapes. Nature Cell Biology. 15 (7), 860 (2013).
- Yu, H. Y., Lim, K. P., Xiong, S. J., Tan, L. P., Shim, W. Functional Morphometric Analysis in Cellular Behaviors: Shape and Size Matter. Advanced Healthcare Materials. 2 (9), (2013).
- Johnson, G. R., Buck, T. E., Sullivan, D. P., Rohde, G. K., Murphy, R. F. Joint modeling of cell and nuclear shape variation. Molecular Biology of the Cell. 26 (22), 4046-4056 (2015).
- Wang, S. -. H., Cheng, H., Phillips, P., Zhang, Y. -. D. Multiple Sclerosis Identification Based on Fractional Fourier Entropy and a Modified Jaya Algorithm. Entropy. 20 (4), 254 (2018).
- Kriegel, F. L., et al. Cell shape characterization and classification with discrete Fourier transforms and self-organizing maps. Cytometry Part A. 93 (3), 323-333 (2017).
- Styner, M., et al. Framework for the Statistical Shape Analysis of Brain Structures using SPHARM-PDM. Insight Journal. (1071), 242-250 (2006).
- El-Baz, A., et al. 3D shape analysis for early diagnosis of malignant lung nodules. Medical Image Computing and Computer Assisted Intervention. 14 (Pt 3), 175-182 (2011).
- Williams, E. L., El-Baz, A., Nitzken, M., Switala, A. E., Casanova, M. F. Spherical harmonic analysis of cortical complexity in autism and dyslexia. Translational Neuroscience. 3 (1), 36-40 (2012).
- Kruggel, F. Robust parametrization of brain surface meshes. Medical Image Analysis. 12 (3), 291-299 (2008).
- Schindelin, J., et al. Fiji: an open-source platform for biological-image analysis. Nature Methods. 9 (7), 676-682 (2012).
- Kohonen, T. Essentials of the self-organizing map. Neural Networks. 37, 52-65 (2013).
- Andrey, P., Boudier, T. Adaptive Active Contours. ImageJ user and developer conference. , (2006).
- Burger, W., Burge, M. J. . Principles of Digital Image Processing. , (2013).
- Lestrel, P. E. . Fourier Descriptors and their Applications in Biology. , (2008).
- Bayerl, S. H., et al. Time lapse in vivo microscopy reveals distinct dynamics of microglia-tumor environment interactions-a new role for the tumor perivascular space as highway for trafficking microglia. Glia. 64 (7), 1210-1226 (2016).
Reprints and Permissions
Request permission to reuse the text or figures of this JoVE article
Request PermissionThis article has been published
Video Coming Soon
Copyright © 2025 MyJoVE Corporation. All rights reserved