Method Article
Estimation of Contact Regions Between Hands and Objects During Human Multi-Digit Grasping
In This Article
Summary
When we grasp an object, multiple regions of the fingers and hand typically make contact with the object's surface. Reconstructing such contact regions is challenging. Here, we present a method for approximately estimating the contact regions by combining marker-based motion capture with existing deep learning-based hand mesh reconstruction.
Abstract
To grasp an object successfully, we must select appropriate contact regions for our hands on the surface of the object. However, identifying such regions is challenging. This paper describes a workflow to estimate the contact regions from marker-based tracking data. Participants grasp real objects, while we track the 3D position of both the objects and the hand, including the fingers' joints. We first determine the joint Euler angles from a selection of tracked markers positioned on the back of the hand. Then, we use state-of-the-art hand mesh reconstruction algorithms to generate a mesh model of the participant's hand in the current pose and the 3D position.
Using objects that were either 3D printed or 3D scanned-and are, thus, available as both real objects and mesh data-allows the hand and object meshes to be co-registered. In turn, this allows the estimation of approximate contact regions by calculating the intersections between the hand mesh and the co-registered 3D object mesh. The method may be used to estimate where and how humans grasp objects under a variety of conditions. Therefore, the method could be of interest to researchers studying visual and haptic perception, motor control, human-computer interaction in virtual and augmented reality, and robotics.
Introduction
The capacity to grasp and manipulate objects is a key ability that allows humans to reshape the environment to their wants and needs. However, controlling multi-jointed hands effectively is a challenging task that requires a sophisticated control system. This motor control system is guided by several forms of sensory input, amongst which vision is paramount. Through vision, individuals can identify the objects in the environment and estimate their position and physical properties and can then reach, grasp, and manipulate those objects with ease. Understanding the complex system that links the input at the retinae with the motor commands that control the hands is a key challenge of sensorimotor neuroscience. To model, predict, and understand how this system works, we must first be able to study it in detail. This requires high-fidelity measurements of both visual inputs and hand motor outputs.
Past motion-tracking technology has imposed a number of limitations on the study of human grasping. For example, systems requiring cables attached to the participants' hands1,2 tend to restrict the range of finger motions, potentially altering the grasping movements or the measurements themselves. Despite such limitations, previous research has been able to identify several factors that influence visually guided grasping. Some of these factors include object shape3,4,5,6, surface roughness7,8,9, or the orientation of an object relative to the hand4,8,10. However, to overcome previous technological limitations, the majority of this prior research has employed simple stimuli and highly constrained tasks, thus predominantly focusing on individual factors3,4,6,7,10, two-digit precision grips3,4,6,9,11,12,13,14,15,16,17,18, single objects19, or very simple 2D shapes20,21. How previous findings generalize beyond such reduced and artificial lab conditions is unknown. Additionally, the measurement of hand-object contact is often reduced to the estimation of digit contact points22. This simplification may be appropriate to describe a small subset of grasps in which only the fingertips are in contact with an object. However, in the majority of real-world grasps, extensive regions of the fingers and palm come in contact with an object. Further, a recent study23 has demonstrated, using a haptic glove, that objects can be recognized by how their surface impinges on the hand. This highlights the importance of studying the extended contact regions between the hands and the objects grasped, not just the contact points between the objects and the fingertips22.
Recent advances in motion capture and 3D hand modeling have allowed us to move past previous limitations and to study grasping in its full complexity. Passive marker-based motion tracking is now available with millimeter-sized markers that can be attached to the back of the participant's hands to track joint movements24. Further, automatic marker identification algorithms for passive marker systems are now sufficiently robust to almost eliminate the need for the extensive manual postprocessing of marker data25,26,27. Markerless solutions are also reaching impressive levels of performance at tracking animal body parts in videos28. These motion-tracking methods, thus, finally allow reliable and non-invasive measurements of complex multi-digit hand movements24. Such measurements can inform us about joint kinematics and enable us to estimate the contact points between the hand and an object. Additionally, in recent years, the computer vision community has been tackling the problem of constructing models of the human hands that can replicate the soft tissue deformations during object grasping and even during self-contact between hand parts29,30,31,32. Such 3D mesh reconstructions can be derived from different types of data, such as video footage33,34, skeletal joints (derived from marker-based35 or markerless tracking36), and depth images37. The first key advance in this domain was provided by Romero et al.38, who derived a parametric hand model (MANO) from over 1,000 hand scans from 31 subjects in various poses. The model contains parameters for both the pose and shape of the hand, facilitating regression from different sources of data to a full hand reconstruction. The more recent DeepHandMesh29 solution builds on this approach by constructing a parametrized model through deep learning and by adding penetration avoidance, which more accurately replicates physical interactions between hand parts. By combining such hand mesh reconstructions with 3D tracked object meshes, it is, thus, now possible to estimate contact regions not just on the surface of objects32 but also on the surface of the hand.
Here, we propose a workflow that brings together the high-fidelity 3D tracking of objects and hand joints with novel hand mesh reconstruction algorithms. The method yields detailed maps of hand-object contact surfaces. These measurements will assist sensorimotor neuroscientists in extending our theoretical understanding of human visually guided grasping. Further, the method could be useful to researchers in adjacent fields. For example, human factor researchers may use this method to construct better human-machine interface systems in virtual and augmented reality18. High-fidelity measurements of human grasping behaviors can also assist roboticists in designing human-inspired robotic grasping systems based on the principles of interactive perception39,40,41,42,43. We, thus, hope that this method will help advance grasping research across neuroscience and engineering fields from sparse descriptions of highly constrained tasks to fuller characterizations of naturalistic grasping behaviors with complex objects and real-world tasks. The overall approach is outlined in Figure 1.
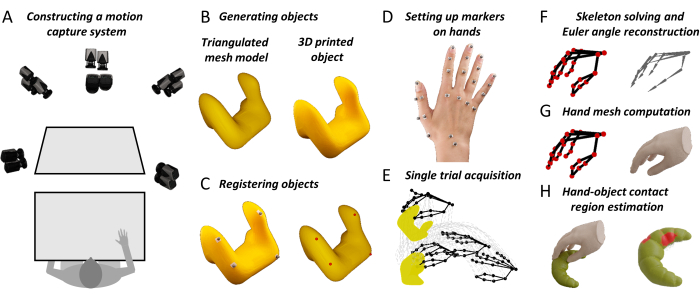
Figure 1: Key steps in the proposed method. (A) Motion capture cameras image a workbench from multiple angles. (B) A stimulus object is 3D printed from a triangulated mesh model. (C) Four spherical reflective markers are glued to the surface of the real object. A semi-automated procedure identifies four corresponding points on the surface of the mesh object. This correspondence allows us to roto-translate the mesh model to the 3D tracked position of the real object. (D) Reflective markers are attached to different landmarks on the back of a participant's hand using double-sided tape. (E) The motion capture system acquires the trajectories in 3D space of the tracked object and hand markers during a single trial. (F) A participant-specific hand skeleton is constructed using 3D computer graphics software. Skeletal joint poses are then estimated for each frame of each trial in an experiment through inverse kinematics. (G) Joint poses are input to a modified version of DeepHandMesh29, which outputs an estimated 3D hand mesh in the current 3D pose and position. (H) Finally, we use mesh intersection to compute the hand-object contact regions. Please click here to view a larger version of this figure.
Protocol
Prior to beginning an experiment, the participants must provide informed consent in accordance with the institutional guidelines and the Declaration of Helsinki. All the protocols described here have been approved by the local ethics committee of Justus Liebig University Giessen (LEK-FB06).
1. Installation of all the necessary software
- Download the project repository at Data and Code Repository.
- Install the software listed in the Table of Materials (note the software versions and follow the links for purchase options and instructions).
- Within the Data and Code Repository, open a command window, and run the following command:
conda env create -f environment.yml - Download and install the pretrained DeepHandMesh29 instantiation following the instructions provided at https://github.com/facebookresearch/DeepHandMesh.
- Place DeepHandMesh in the folder "deephandmesh" of the Data and Code Repository. Replace the file "main/model.py" with the model.py file contained in the Data and Code Repository.
2. Preparing the motion capture system
- Position a workbench within a tracking volume imaged from multiple angles by motion-tracking cameras arranged on a frame surrounding the workspace (Figure 1A). Prepare reflective markers by attaching double-sided adhesive tape to the base of each marker.
- Execute Qualisys Track Manager (QTM) as an Administrator.
NOTE: Executing QTM as an Administrator is necessary for the Python SDK to take control of the QTM interface. We advise always running QTM as an Administrator.
3. Calibrating the cameras
- Place the L-shaped calibration object within the tracking volume.
- Within the QTM, click on Calibrate in the Capture menu, or press the wand icon in the Capture toolbar. Wait for a calibration window to open. Select the duration of the calibration, and press OK.
- Wave the calibration wand across the tracking volume for the duration of the calibration. Press the Export button, and specify a file path in which to export the calibration as a text file. Accept the calibration by pressing OK.
4. Creating a stimulus object
- Construct a virtual 3D object model in the form of a polygon mesh. Use a 3D printer to construct a physical replica of the object model.
NOTE: The data repository in step 1.1 provides example objects in STL and Wavefront OBJ file formats. Objects in STL format are manifold and ready for 3D printing.
5. Preparing the stimulus object
- Attach four non-planar reflective markers to the surface of the real object. Place the object within the tracking volume.
- In the project repository, execute the Python script "Acquire_Object.py". Follow the instructions provided by the script to perform a 1 s capture of the 3D position of the object markers.
- Select all the markers of the rigid body. Right-click on and select Define Rigid Body (6DOF) | Current Frame. Enter the name of the rigid body, and press OK.
- In the File menu, select Export | To TSV. In the new window, check the boxes 3D, 6D, and Skeleton in the Data Type settings. Check all the boxes in the General settings. Press OK and then Save.
6. Co-registering real and mesh model versions of the stimulus object
- Open Blender, and navigate to the Scripting workspace. Open the file "Object_CoRegistration.py", and press Run. Navigate to the Layout workspace, and press n to toggle the sidebar. Within the sidebar, navigate to the Custom tab.
- Select the .obj file to be co-registered, and press the Load Object button.
- Select the trajectory file that was exported in step 3.3, and specify the names of the markers attached to the rigid object separated by semicolons. In the Marker header, specify the line in the trajectory file that contains the column names of the data (counting starts at 0).
- Select the corresponding rigid body file with the 6D suffix, and specify the name of the rigid body defined in step 4.1. In the 6D header, specify the line in the rigid body file that contains the column names of the data.
- Press Load Markers. Translate and rotate the Markers object and/or the Object object to align them. Specify a mesh output file, and press Run Coregistration. This will output an .obj file that contains the co-registered stimulus mesh.
7. Setting up markers on the hands
- Attach 24 spherical reflective markers on different landmarks of a participant's hand using double-sided tape.
NOTE: The specific positioning of the markers is demonstrated in Figure 2.- Position the markers centrally on top of the respective fingertips, as well as the distal interphalangeal joints, proximal interphalangeal joints, and metacarpophalangeal joints of the index finger, middle finger, ring finger, and small finger.
- For the thumb, position one marker each on the fingertip and the basal carpometacarpal joint, as well as a pair of markers each on the metacarpophalangeal and the interphalangeal joints.
NOTE: These marker pairs need to be displaced in opposite directions perpendicular to the thumb's main axis and are necessary to estimate the thumb's orientation. - Finally, place markers at the center of the wrist and on the scaphotrapeziotrapezoidal joint.
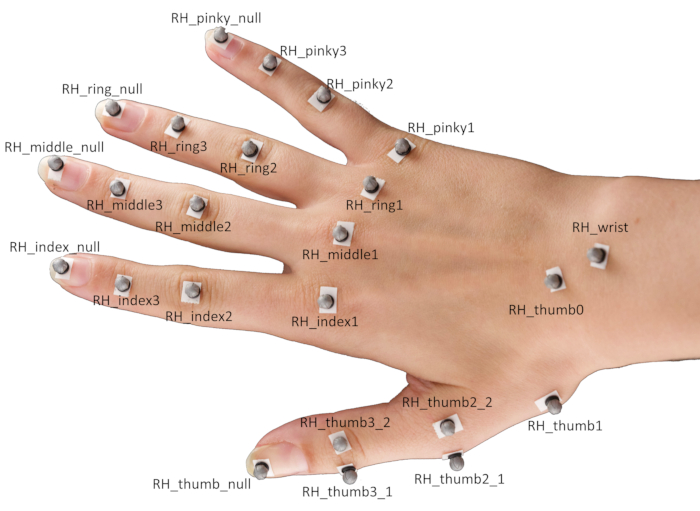
Figure 2: Marker placement on a participant's hand. Abbreviation: RH = right hand. Please click here to view a larger version of this figure.
8. Acquiring a single trial
- Ask the participant to place their hand flat on the workbench with the palm facing downward and to close their eyes. Place the stimulus object on the workbench in front of the participant.
- While the QTM is running, execute the Python script "Single_Trial_Acquisition.py" in the project repository. Follow the instructions provided by the script to capture a single trial of the participant grasping the stimulus object.
NOTE: The script will produce an auditory cue. This will signal to the participant to open their eyes and execute the grasp. In our demonstrations, the task is to reach and grasp the target object, lift it vertically by approximately 10 cm, set it down, and return the hand to its starting position.
9. Labeling the markers
- Within the QTM, drag and drop the individual marker trajectories from Unidentified trajectories to Labeled trajectories, and label them according to the naming convention in Figure 2.
- Select all the markers attached to the hand, and right-click on and select Generate AIM model from selection. In the new window, select Create new model based on Marker connections from existing AIM model and press the Next button.
- Select the RH_FH model definition, and press Open. Press Next, enter a name for the AIM model, and press OK. Finally, press Finish to create an AIM model for the participant's hand, which will be used to automatically identify markers in successive trials from the same participant.
10. Creating a personalized skeleton definition for the participant
- In the QTM, navigate to the Play menu, and select Play with Real-Time Output.
- Open Maya. Navigate to the QTM Connect shelf, and press the Connect to QTM icon. In the new window, check Markers, and press Connect. Now, press the Play icon in the QTM Connect shelf.
- Shift-select all the hand markers and press the Wash Locators icon. Select the washed hand markers, and press Ctrl + G. This will create a group node. Name the group Markers.
- Select all the hand markers. In the Modify menu, click Search and Replace Names. Search for the RH_ prefix, and delete the prefix for the markers.
- Press the Import Solver icon in the QTM Connect shelf. Load the skeleton definition "RH_FH.xml".
- In the Windows menu, navigate to General Editors | Namespace Editor. Within the new window, click on :(root), and press New to create a new namespace, RH. Click on the RH namespace, press New, and name the new namespace ModelPose.
- Select all the markers, click on the RH namespace, and press Add Selected to add the markers to the RH namespace.
- Select the skeleton bones, click on the ModelPose namespace, and press Add Selected to add the skeleton bones to the ModelPose namespace.
- Rotate, translate, and scale the skeleton to fit the marker data. Next, for each skeleton joint individually, Shift + Select the skeleton joint and its associated markers, and press the Add Attachments icon. Finally, press the Export Solver icon to export the new skeleton definition to an XML file that can be loaded in the QTM (see next step).
NOTE: This step is not strictly necessary, but it is useful to increase the accuracy of the skeleton fit to the marker data. Read the QSolverQuickstartGuide on https://github.com/qualisys/QTM-Connect-For-Maya for more information.
11. Reconstruct the joint skeletal joint poses
- Within the QTM, open the project settings by pressing the gearwheel icon. In the sidebar, navigate to Skeleton Solver, and press Load to select a skeleton definition file. Adjust the Scale Factor to 100%, and press Apply.
- Navigate to TSV Export, and check the boxes 3D, 6D, and Skeleton in the Data Type settings. Check all the boxes in the General settings. Press Apply, and close the project settings.
- Press the Reprocess icon, check the boxes Solve Skeletons and Export to TSV file, and press OK.
12. Generating hand mesh reconstructions
- Open a command window in the project repository, and activate the conda environment by executing the command:
conda activate contact-regions - Then, execute the following command, and follow the instructions provided by the script to generate, for each frame of the trial, a hand mesh reconstructing the current hand pose.
python Hand_Mesh_Reconstruction.py --gpu 0 --test_epoch 4
NOTE: These mesh reconstructions are generated automatically using a modified version of the open-source and pretrained hand mesh generation tool, DeepHandMesh29.
13. Generating hand-object contact region estimates
- Open a command window in the project repository, execute the following command, and follow the instructions provided by the script to generate hand and object contact region estimates by computing the intersection between the hand and object meshes.
blender --background --python "Contact_Region_Estimation.py"
Results
The first requirement for the proposed method is a system to accurately track the position of 3D objects and hands. The specific setup is shown in Figure 1A and uses hardware and software produced by the motion capture company Qualisys. We position a workbench within a tracking volume (100 cm x 100 cm x 100 cm), which is imaged from multiple angles by eight tracking cameras and six video cameras arranged on a cubical frame surrounding the workspace. The tracking cameras track the 3D position of the reflective markers within the tracking volume at 180 frames/s and with sub-millimeter 3D spatial resolution. We employ 4 mm reflective markers, which are attached to the objects and hands using skin-friendly double-sided adhesive tape. The 3D marker positions are processed by the motion capture software. The discussion section also reviews alternative motion capture systems that could be employed with the proposed method.
To obtain accurate 3D reconstructions of real objects being grasped and manipulated, we propose two options. The first, which is the one adopted here, is to start from a virtual 3D object model in the form of a polygon mesh. Such 3D models can be constructed using appropriate software (e.g., Blender 3D44) and then 3D printed (Figure 1B). The second option is to take an existing, real 3D object and use 3D scanning technology to construct a mesh model replica of the object. Whichever the strategy, the end goal is to obtain both a real 3D object and the corresponding virtual 3D object mesh model. Of note, the approach described here works only with rigid (i.e., non-deformable) objects.
Once the 3D surface of an object is available as a mesh model, its position must be tracked and co-registered (Figure 1C). To do so, four non-planar reflective markers are attached to the surface of the real object, and the object is placed within the tracking volume. The 3D positions of the object markers are then briefly captured. This capture is used to establish the correspondence between the four markers and four vertices of the object mesh model. This is done using a simple ad hoc software route written in Blender’s Python API. Within Blender’s Viewport, the program presents the virtual object together with the marker positions which are represented as a single mesh object comprised of one sphere for each marker. The user can then rotate and translate the object and/or the markers to align them such that they co-align with the real markers placed on the real object. The program will register the rotations and translation that are applied to calculate a single roto-translation that is finally applied to the original object mesh, providing an object mesh that is co-registered with the rigid body definition in QTM.
Having established correspondence, whenever the real object is moved within the tracking volume, the virtual object can be placed in the new position by computing the roto-translation between the tracked markers and the four corresponding mesh vertices. To record the dynamics of the grasp instead, a total of 24 spherical reflective markers are attached on different landmarks of the hand using double-sided tape (Figure 1D and Figure 2).
At the beginning of a trial (Figure 1E), a participant places their hand flat on the workbench with the palm facing downward and closes their eyes. The experimenter places a target object on the workbench in front of the participant. Next, an auditory cue signals to the participant to open their eyes and execute the grasp. In our demonstrations, the task is to reach and grasp the target object, lift it vertically by approximately 10 cm, set it down, and return the hand to its starting position. A script written in Python 3.7 controls the experiment. On each trial, the script selects and communicates the current condition settings to the experimenter (e.g., object identity and positioning). The script also controls the trial timing, including auditory cues and the start and stop of the motion capture recordings.
Limbs are not only characterized by their position in 3D space but also by their pose. Thus, to obtain a complete 3D reconstruction of a human hand executing a real grasp, we require not only the positions of each joint in 3D space but also the relative pose (translation and rotation) of each joint with respect to its parent joint (Figure 1F). Skeletal joint positions and orientations can be inferred from marker positions using inverse kinematics. To do so, here we employ the skeleton solver provided by the QTM software. For the solver to work, we must first provide a skeleton definition that links the position and orientation of each joint to multiple marker positions. A skeleton definition is, thus, constructed, and the skeleton rig is linked to the marker data using the QTM Connect plugin for Maya. We create personalized skeleton definitions for each participant to maximize the accuracy of the skeleton fits to the marker data. For each participant, we manually fit a hand skeleton to a single frame of motion capture data. Having obtained a participant-specific skeleton definition, we then run the skeleton solver to estimate the skeletal joint poses for each frame of each trial in the experiment.
For each frame of each trial in an experiment, we generate a hand mesh that reconstructs the current hand pose using the open-source and pretrained hand mesh generation tool, DeepHandMesh28 (Figure 1G). DeepHandMesh is a deep encoder-decoder network that generates personalized hand meshes from images. First, the encoder estimates the pose of a hand within an image (i.e., the joint Euler angles). Then, the estimated hand pose and a personalized ID vector are input to the decoder, which estimates a set of three additive correctives to a rigged template mesh. Finally, the template mesh is deformed according to the estimated hand pose and correctives using linear blend skinning. The first corrective is an ID-dependent skeleton corrective through which the skeletal rig is adjusted to incorporate the person-specific joint positions. The other two correctives are mesh correctives through which the mesh vertices are adjusted to better represent the hand surface of the participant. One of the mesh correctives is an ID-dependent mesh corrective that accounts for the surface structure of an individual participant's hand. The final mesh corrective instead is a pose-dependent vertex corrective that accounts for hand surface deformations due to the current hand pose.
DeepHandMesh is trained using weak supervision with 2D joint key points and scene depth maps. Here, we use only the pretrained DeepHandMesh decoder to generate hand mesh reconstructions, modified in the following ways (Figure 3). First, as the network is not trained on specific participants, the generic ID-dependent mesh corrective provided with the pretrained model is employed (Figure 3A). Further, the ID-dependent skeleton corrective is derived using the QTM skeleton solver as described above (Figure 3B). Proportional scaling of the hand with the skeleton length is assumed, and the mesh thickness is uniformly scaled by a factor derived from the relative scaling of the skeleton such that the mesh better approximates the participant's hand size (Figure 3C). This modified mesh is input to the decoder, together with the current hand pose (derived from the marker data) and the 3D position and orientation of the wrist. The decoder, thus, computes the current pose-dependent corrective, applies all the correctives and roto-translations, and outputs a 3D hand mesh reconstruction of the current hand pose in the same coordinate frame as the 3D tracked object mesh (Figure 3D).
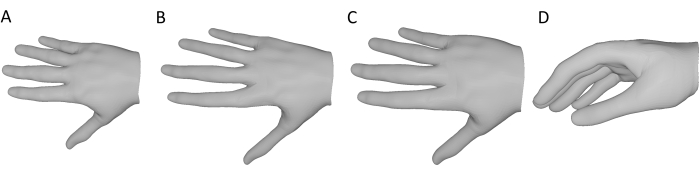
Figure 3: Modifications to the pretrained DeepHandMesh decoder. (A) Fixed, generic ID-dependent mesh corrective. (B) ID-dependent skeleton corrective derived through inverse kinematics in step 10. (C) The size of the hand mesh is scaled by the same factor as the skeletal joints. (D) Final 3D hand mesh reconstruction of the current hand pose. Please click here to view a larger version of this figure.
Having reconstructed 3D mesh models for both a participant's hand and a grasped object, hand-object contact regions can be estimated by computing the intersection between the hand and object meshes (Figure 1H). The assumption behind this is that the real hand is deformed by contact with the surface, meaning the skeleton can come closer to the surface than would be possible if the hand were rigid, which allows portions of the hand mesh to pass through the object mesh. As a result, the contact areas can be approximated as the regions of overlap between the two meshes.
Specifically, to compute these regions of overlap, we define object mesh vertices that are contained within the 3D volume of the hand mesh as being in contact with the hand. These vertices are identified using a standard raytracing approach45. For each vertex of the object mesh, a ray is cast from that vertex to an arbitrary 3D point outside the hand mesh. We then assess the number of intersections that occur between the cast ray and the triangles composing the hand's surface. If the number of intersections is odd, the object vertex is contained inside the hand mesh. If the number of intersections is even, then the object vertex is outside the hand mesh. The contact regions on the surface of the object can, thus, be approximated as the set of triangle faces whose vertices are all contained within the hand mesh. We can apply the same rationale to the hand mesh vertices contained in the 3D volume of the object mesh to estimate the contact regions on the surface of the hand. Notably, more advanced approaches to Boolean mesh operations could also be used31.
Video 1 shows a video of a hand, tracked points, and co-registered mesh all moving side-by-side during a single grasp to a 3D-printed cat figurine. Figure 4A instead shows a single frame at the time of hand-object contact from a grasp to a 3D-printed croissant, together with the hand-object mesh reconstructions (Figure 4B) and the estimated contact regions on the surface of the croissant (Figure 4C).
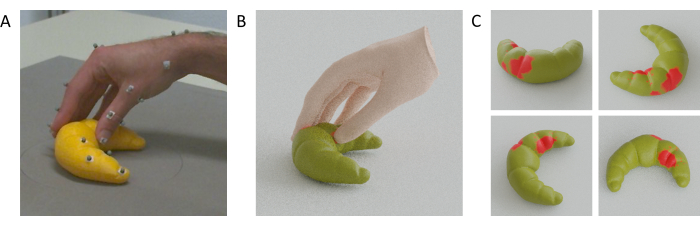
Figure 4: Estimated hand-object contact regions. (A) Tracked hand and object viewed from one of the tracking cameras during a grasp. (B) Reconstructed hand mesh and tracked object mesh rendered from the same viewpoint as the tracking camera. (C) Contact regions on the surface of the object seen from multiple viewpoints. Please click here to view a larger version of this figure.
Video 1: Mesh reconstructions of the hand and object. Gif animation of the hand, tracked markers, and the hand and object mesh reconstructions during a single grasp viewed from the same camera viewpoint. Please click here to download this Video.
Discussion
We propose a method that enables the estimation of contact regions for hand-object interactions during multi-digit grasps. As full tracking of the whole surface of a hand is currently intractable, we propose using a reconstruction of a hand mesh whose pose is determined by sparse key points on the hand. To track these sparse key points, our solution employs a research-grade motion capture system based on passive marker tracking. Of course, other motion capture systems could also be employed with the proposed method, granted that they yield sufficiently accurate 3D position data. We advise against active marker motion capture systems (such as the popular but discontinued Optotrak Certus), since these require attaching cables and/or electronic devices to the participants' hands, which may restrict movements or at least yield less typical grasps as participants are made more consciously aware of the pose of their hands. Motion-tracking gloves using inertial measurement units may be a possibility, even though these systems are known to suffer from drift, may also restrict hand movements, and do not allow for the surface of the hand to come into full and direct contact with the object surfaces. Commercial markerless hand-tracking solutions (e.g., the Leap Motion46,47,48) may also be a possibility, although it may not be possible to track object positions with these systems alone. The most promising alternative option to a research-grade motion capture system is given by open-source, markerless tracking solutions (e.g., Mathis et al.28). If used with multiple co-registered cameras49, such systems could potentially track hand joint positions and object positions in 3D without the need of markers, gloves, or cables. These solutions, as well as this marker-based system, may suffer, however, from data loss issues due to occlusions.
Limitations and future directions
As the hand reconstructions obtained through this method will not be fully accurate, there are some limitations to the types of experiments for which the method should be used. Deviations in hand mesh reconstructions from ground truth will manifest themselves in deviations in the estimated hand/object contact regions. Thus, applying this method to derive absolute measures would require assessing the fidelity of the contact region estimates. However, even approximate estimates can still be useful in within-participant experimental designs because the potential biases of the method are likely to affect different experimental conditions within a participant in a similar way. Therefore, statistical analyses and inferences should be performed only on measures such as the differences in contact area between conditions, where the direction of an effect will correlate with the respective ground truth. In future research, we plan to further validate our approach, for example by comparing contact region estimates to thermal fingerprints on objects covered in thermochromic paint.
Most processing steps from the data collection to the final contact region estimation are fully automated and, thus, offer important contributions toward a standardized procedure for hand-object contact region estimation. However, an initial fit of the individualized skeletons to the 3D positions of the tracked markers must still be performed manually to obtain a skeleton definition for each participant. As the number of participants for an experiment increases, so does the number of manual fits, and this is currently the most time-consuming step in the procedure and requires some familiarity with manual rigging in the Autodesk Maya Software. In the future, we aim to automate this step to avoid human influence on the procedure by adding an automatic skeleton calibration procedure.
The workflow described here relies on the Qualisys hardware and software (e.g., the QTM skeleton solver). This currently limits the accessibility of our method to laboratories that have a similar setup. In principle, however, the method can be applied to any source of motion capture data. To expand the accessibility, in ongoing work, we are exploring alternatives that should generalize our workflow and make it less reliant on specific hardware and software licenses.
Another important limitation of the method is that, in its current form, it can only be applied to rigid (non-deformable) objects. In the future, this limitation could be overcome using methods for recording the surface shape of the grasped object as it deforms. Additionally, due to its approximate nature, the method is not currently well suited to very small or thin objects.
In conclusion, by integrating state-of-the-art motion tracking with high-fidelity hand surface modeling, we provide a method to estimate hand-object contact regions during grasping and manipulation. In future research, we plan to deploy this method to investigate and model visually guided grasping behavior in humans16. We further plan to integrate these tools with eye tracking46, 50,51,52 and virtual/augmented reality systems53,54,55 to investigate visually guided hand and eye movement motor control in real and virtual naturalistic environments18,46,56,57. For these reasons, the proposed method could be of interest to researchers studying haptic perception58, motor control, and human-computer interaction in virtual and augmented reality. Finally, accurate measurements of human grasping abilities could inform the design of robust robotic systems based on the principles of interactive perception39,40,41,42,43 and may have translational applications for upper limb prosthetics.
Disclosures
The authors declare that no competing interests exist.
Acknowledgements
This research was funded by Deutsche Forschungsgemeinschaft (DFG, German Research Foundation: project No. 222641018-SFB/TRR 135 TP C1 and IRTG-1901 "The Brain in Action") and by the Research Cluster "The Adaptive Mind" funded by the Excellence Program of the Hessian Ministry of Higher Education, Science, Research, and Art. The authors thank the Qualisys support team, including Mathias Bankay and Jeffrey Thingvold, for assistance in developing our methods. The authors also thank Michaela Jeschke for posing as the hand model. All data and analysis scripts to reproduce the method and the results presented in the manuscript are available on Zenodo (doi: 10.5281/zenodo.7458911).
Materials
| Name | Company | Catalog Number | Comments |
| Anaconda Python distribution | (Anaconda 5.3.1 or later); https://repo.anaconda.com/archive/ | scripts and functions were generated in Python version 3.7 | |
| Autodesk Maya | Autodesk, Inc. | Maya2022; https://www.autodesk.com/products/maya/overview | 3D computer graphics application. |
| Blender | Blender Foundation | Blender 2.92; https://download.blender.org/release/ | 3D computer graphics application. |
| Computer Workstation | N/A | N/A | OS: Windows 10 or higher. |
| DeepHandMesh | Meta Platforms, Inc. (Meta Open Source) | https://github.com/facebookresearch/DeepHandMesh | Pre-trained hand mesh generation tool. |
| Miqus M5 | Qualisys Ab | https://www.qualisys.com/cameras/miqus/ | Passive marker motion tracking camera (8 units). |
| Miqus video camera | Qualisys Ab | https://www.qualisys.com/cameras/miqus-video/ | Color video camera, synchronized with Miquis M5 tracking cameras (6 units). |
| Project repository | N/A | Data and Code Repository | Data and code to replicate the current project. The repository is currently under construction, but we provide a private link where reviewers can download the current and most up-to-date version of the repository. The final repository will be made publicly available upon acceptance. |
| Python 3 | Python Software Foundation | Python Version 3.7 | Python3 and associated built-in libraries. |
| QTM Connect for Maya | Qualisys Ab | https://github.com/qualisys/QTM-Connect-For-Maya | Stream skeleton, rigid bodies and marker data from QTM to Maya |
| QTM Qualisys Track Manager | Qualisys Ab | Qualisys Track Manager 2021.2; https://www.qualisys.com/software/qualisys-track-manager/ | Motion capture software |
| Qualisys SDK for Python | Qualisys Ab | https://github.com/qualisys/qualisys_python_sdk | Implements communication between QTM and Python |
References
- Derzsi, Z., Volcic, R. MOTOM toolbox: MOtion Tracking via Optotrak and Matlab. Journal of Neuroscience Methods. 308, 129-134 (2018).
- Franz, V. H. Optotrak Toolbox. The Optotrak Toolbox: Control your Optotrak from within Matlab. , Available from: http://www.ecogsci.cs.uni-tuebingen.de/OptotrakToolbox/ (2004).
- Eloka, O., Franz, V. H. Effects of object shape on the visual guidance of action. Vision Research. 51 (8), 925-931 (2011).
- Lederman, S. J., Wing, A. M. Perceptual judgement, grasp point selection and object symmetry. Experimental Brain Research. 152 (2), 156-165 (2003).
- Schettino, L. F., Adamovich, S. V., Poizner, H. Effects of object shape and visual feedback on hand configuration during grasping. Experimental Brain Research. 151 (2), 158-166 (2003).
- Chen, Z., Saunders, J. A. Online processing of shape information for control of grasping. Experimental Brain Research. 233 (11), 3109-3124 (2015).
- Burstedt, M. K., Flanagan, J. R., Johansson, R. S. Control of grasp stability in humans under different frictional conditions during multidigit manipulation. Journal of Neurophysiology. 82 (5), 2393-2405 (1999).
- Paulun, V. C., Gegenfurtner, K. R., Goodale, M. A., Fleming, R. W. Effects of material properties and object orientation on precision grip kinematics. Experimental Brain Research. 234 (8), 2253-2265 (2016).
- Klein, L. K., Maiello, G., Fleming, R. W., Voudouris, D. Friction is preferred over grasp configuration in precision grip grasping. Journal of Neurophysiology. 125 (4), 1330-1338 (2021).
- Mamassian, P. Prehension of objects oriented in three-dimensional space. Experimental Brain Research. 114 (2), 235-245 (1997).
- Paulun, V. C., Kleinholdermann, U., Gegenfurtner, K. R., Smeets, J. B. J., Brenner, E. Center or side: biases in selecting grasp points on small bars. Experimental Brain Research. 232 (7), 2061-2072 (2014).
- Goodale, M. A., et al. Separate neural pathways for the visual analysis of object shape in perception and prehension. Current Biology. 4 (7), 604-610 (1994).
- Kleinholdermann, U., Franz, V. H., Gegenfurtner, K. R. Human grasp point selection. Journal of Vision. 13 (8), 23(2013).
- Maiello, G., Paulun, V. C., Klein, L. K., Fleming, R. W. Object visibility, not energy expenditure, accounts for spatial biases in human grasp selection. i-Perception. 10 (1), 204166951982760-20 (2019).
- Maiello, G., Schepko, M., Klein, L. K., Paulun, V. C., Fleming, R. W. Humans can visually judge grasp quality and refine their judgments through visual and haptic feedback. Frontiers in Neuroscience. 14, 591898(2021).
- Klein, L. K., Maiello, G., Paulun, V. C., Fleming, R. W. Predicting precision grip grasp locations on three-dimensional objects. PLoS Computational Biology. 16 (8), 1008081(2020).
- Maiello, G., Paulun, V. C., Klein, L. K., Fleming, R. W. The sequential-weight illusion. i-Perception. 9 (4), 204166951879027(2018).
- Chessa, M., Maiello, G., Klein, L. K., Paulun, V. C., Solari, F. Grasping objects in immersive Virtual Reality. 2019 IEEE Conference on Virtual Reality and 3D User Interfaces (VR). , 1749-1754 (2019).
- Crajé, C., Lukos, J. R., Ansuini, C., Gordon, A. M., Santello, M. The effects of task and content on digit placement on a bottle). Experimental Brain Research. 212 (1), 119-124 (2011).
- Lukos, J., Ansuini, C., Santello, M. Choice of contact points during multidigit grasping: Effect of predictability of object center of mass location. Journal of Neuroscience. 27 (14), 3894-3903 (2007).
- Gilster, R., Hesse, C., Deubel, H. Contact points during multidigit grasping of geometric objects. Experimental Brain Research. 217 (1), 137-151 (2012).
- Schot, W. D., Brenner, E., Smeets, J. B. J. Robust movement segmentation by combining multiple sources of information. Journal of Neuroscience Methods. 187 (2), 147-155 (2010).
- Sundaram, S., et al. Learning the signatures of the human grasp using a scalable tactile glove. Nature. 569 (7758), 698-702 (2019).
- Yan, Y., Goodman, J. M., Moore, D. D., Solla, S. A., Bensmaia, S. J. Unexpected complexity of everyday manual behaviors. Nature Communications. 11 (1), 3564(2020).
- Han, S., et al. Online optical marker-based hand tracking with deep labels. ACM Transactions on Graphics. 37 (4), 1-10 (2018).
- Clouthier, A. L., et al. Development and validation of a deep learning algorithm and open-source platform for the automatic labelling of motion capture markers. IEEE Access. 9, 36444-36454 (2021).
- Qualisys AB Qualisys Track Manager User Manual (Version 2022.1). , Available from: https://www.qualisys.com/ (2022).
- Mathis, A., et al. DeepLabCut: Markerless pose estimation of user-defined body parts with deep learning. Nature Neuroscience. 21 (9), 1281-1289 (2018).
- Moon, G., Shiratori, T., Lee, K. M. DeepHandMesh: A weakly-supervised deep encoder-decoder framework for high-fidelity hand mesh modeling. ECCV 2020. , (2020).
- Smith, B., et al. Constraining dense hand surface tracking with elasticity. ACM Transactions on Graphics. 39 (6), 219(2020).
- Taheri, O., Ghorbani, N., Black, M. J., Tzionas, D. GRAB: A dataset of whole-body human grasping of objects. Computer Vision - ECCV 2020: 16th European Conference. , Glasgow, UK. 581-600 (2020).
- Brahmbhatt, S., Tang, C., Twigg, C. D., Kemp, C. C., Hays, J. ContactPose: A dataset of grasps with object contact and hand pose. Computer Vision - ECCV 2020. , 361-378 (2020).
- Wang, J., et al. RGB2Hands: Real-time tracking of 3D hand interactions from monocular RGB video. ACM Transactions on Graphics. 39 (6), 218(2020).
- Zhang, X., Li, Q., Mo, H., Zhang, W., Zheng, W. End-to-end hand mesh recovery from a monocular RGB image. 2019 IEEE/CVF International Conference on Computer Vision (ICCV). , 2354-2364 (2019).
- Endo, Y., Tada, M., Mochimaru, M. Reconstructing individual hand models from motion capture data). Journal of Computational Design and Engineering. 1 (1), 1-12 (2014).
- Mueller, F., et al. GANerated hands for real-time 3D hand tracking from monocular RGB. 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. , 49-59 (2018).
- Mueller, F., et al. Real-time pose and shape reconstruction of two interacting hands with a single depth camera. ACM Transactions on Graphics. 38 (4), 49(2019).
- Romero, J., Tzionas, D., Black, M. J. Embodied hands: Modeling and capturing hands and bodies together. ACM Transactions on Graphics. 36 (6), 245(2017).
- Kappler, D., Bohg, J., Schaal, S. Leveraging big data for grasp planning. 2015 IEEE International Conference on Robotics and Automation (ICRA). , 4304-4311 (2015).
- Kokic, M., Kragic, D., Bohg, J. Learning task-oriented grasping from human activity datasets). IEEE Robotics and Automation Letters. 5 (2), 3352-3359 (2020).
- Shao, L., et al. UniGrasp: Learning a unified model to grasp with multifingered robotic hands. IEEE Robotics and Automation Letters. 5 (2), 2286-2293 (2020).
- Shao, L., Migimatsu, T., Zhang, Q., Yang, K., Bohg, J. Concept2Robot: Learning manipulation concepts from instructions and human demonstrations. Robotics: Science and Systems XVI. , (2020).
- Bohg, J. Interactive perception: Leveraging action in perception and perception in action. IEEE Transactions on Robotics. 33 (6), 1273-1291 (2017).
- Blender Foundation. , Available from: https://www.blender.org (2022).
- Roth, S. D. Ray casting for modeling solids. Computer Graphics and Image Processing. 18 (2), 109-144 (1982).
- Maiello, G., Kwon, M., Bex, P. J. Three-dimensional binocular eye-hand coordination in normal vision and with simulated visual impairment. Experimental Brain Research. 236 (3), 691-709 (2018).
- Weichert, F., Bachmann, D., Rudak, B., Fisseler, D. Analysis of the accuracy and robustness of the leap motion controller. Sensors. 13 (5), 6380-6393 (2013).
- Guna, J., Jakus, G., Pogačnik, M., Tomažič, S., Sodnik, J. An analysis of the precision and reliability of the leap motion sensor and its suitability for static and dynamic tracking. Sensors. 14 (2), 3702-3720 (2014).
- Sheshadri, S., Dann, B., Hueser, T., Scherberger, H. 3D reconstruction toolbox for behavior tracked with multiple cameras. Journal of Open Source Software. 5 (45), 1849(2020).
- Maiello, G., Harrison, W. J., Bex, P. J. Monocular and binocular contributions to oculomotor plasticity. Scientific Reports. 6, 31861(2016).
- Caoli, A., et al. A dichoptic feedback-based oculomotor training method to manipulate interocular alignment. Scientific Reports. 10, 15634(2020).
- Gibaldi, A., Vanegas, M., Bex, P. J., Maiello, G. Evaluation of the Tobii EyeX eye tracking controller and Matlab toolkit for research. Behavior Research Methods. 49 (3), 923-946 (2017).
- Chessa, M., Maiello, G., Borsari, A., Bex, P. J. The Perceptual quality of the Oculus Rift for immersive virtual reality. Human-Computer Interaction. 34 (1), 51-82 (2016).
- Maiello, G., Chessa, M., Bex, P. J., Solari, F. Near-optimal combination of disparity across a log-polar scaled visual field. PLoS Computational Biology. 16 (4), 1007699(2020).
- Maiello, G., Chessa, M., Solari, F., Bex, P. J. The (in)effectiveness of simulated blur for depth perception in naturalistic images. PLoS One. 10 (10), 0140230(2015).
- Maiello, G., Chessa, M., Solari, F., Bex, P. J. Simulated disparity and peripheral blur interact during binocular fusion. Journal of Vision. 14 (8), 13(2014).
- Maiello, G., Kerber, K. L., Thorn, F., Bex, P. J., Vera-Diaz, F. A. Vergence driven accommodation with simulated disparity in myopia and emmetropia. Experimental Eye Research. 166, 96-105 (2018).
- Moscatelli, A., et al. The change in fingertip contact area as a novel proprioceptive cue. Current Biology. 26 (9), 1159-1163 (2016).
Reprints and Permissions
Request permission to reuse the text or figures of this JoVE article
Request PermissionThis article has been published
Video Coming Soon
Copyright © 2025 MyJoVE Corporation. All rights reserved