29.14 : Magnetic Vector Potential
In electrostatics, the electric field can be written as the negative gradient of the potential. In magnetostatics, the zero divergence of the magnetic field ensures that the magnetic field can be expressed as the curl of a vector potential. This potential is known as the magnetic vector potential.
Consider an ideal solenoid with n turns per unit length and radius R. If I is the current through the solenoid, the magnetic field inside the solenoid is expressed as the product of vacuum permeability, the number of turns per unit length, and the current. Conversely, the magnetic field outside the solenoid is zero. Considering this, what is the vector potential for an ideal solenoid?
The magnetic flux through the solenoid is given by
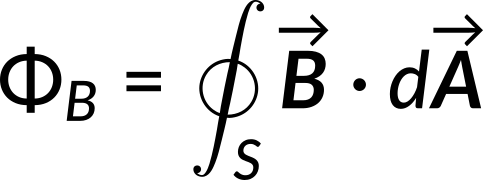
Since the magnetic field equals the curl of the vector potential, the magnetic flux can be rewritten in terms of the vector potential.
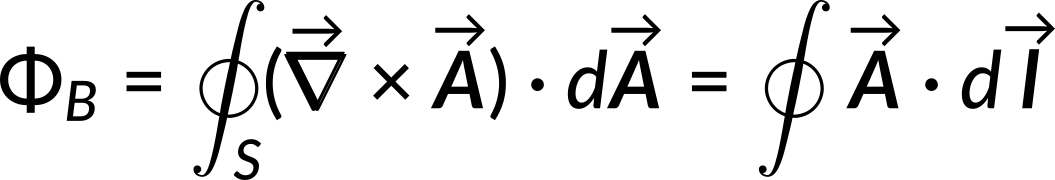
Thus, the line integral of the magnetic vector potential equals the surface integral of the magnetic field.
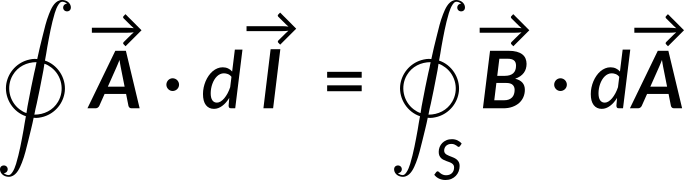
Now consider a circular Amperian loop of radius r inside the solenoid. The magnetic flux through this loop is given by
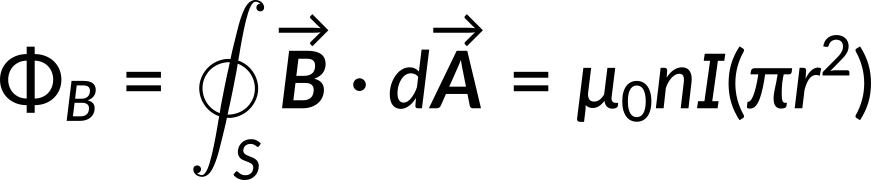
Equating the magnetic flux to the line integral of the magnetic vector potential, the expression for the vector potential can be obtained.
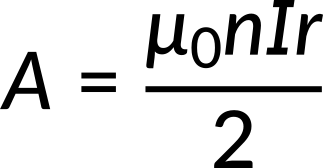
The vector potential mimics the magnetic field and acts along the circumference.
Aus Kapitel 29:

Now Playing
29.14 : Magnetic Vector Potential
Sources of Magnetic Fields
512 Ansichten

29.1 : Magnetfeld durch bewegte Ladungen
Sources of Magnetic Fields
8.2K Ansichten

29.2 : Biot-Savart-Gesetz
Sources of Magnetic Fields
5.7K Ansichten

29.3 : Biot-Savart-Gesetz: Problemlösung
Sources of Magnetic Fields
2.4K Ansichten

29.4 : Magnetfeld aufgrund eines dünnen geraden Drahtes
Sources of Magnetic Fields
4.7K Ansichten

29.5 : Magnetfeld durch zwei gerade Drähte
Sources of Magnetic Fields
2.3K Ansichten

29.6 : Magnetische Kraft zwischen zwei parallelen Strömen
Sources of Magnetic Fields
3.4K Ansichten

29.7 : Magnetfeld einer Stromschleife
Sources of Magnetic Fields
4.3K Ansichten

29.8 : Divergenz und Krümmung des Magnetfeldes
Sources of Magnetic Fields
2.7K Ansichten

29.9 : Das Amperesche Gesetz
Sources of Magnetic Fields
3.6K Ansichten

29.10 : Amperes Gesetz: Problemlösung
Sources of Magnetic Fields
3.5K Ansichten

29.11 : Magnetspulen
Sources of Magnetic Fields
2.4K Ansichten

29.12 : Magnetfeld eines Magneten
Sources of Magnetic Fields
3.7K Ansichten

29.13 : Ringkerne
Sources of Magnetic Fields
2.8K Ansichten

29.15 : Potential durch ein magnetisiertes Objekt
Sources of Magnetic Fields
248 Ansichten
See More
Copyright © 2025 MyJoVE Corporation. Alle Rechte vorbehalten