29.14 : Magnetic Vector Potential
In electrostatics, the electric field can be written as the negative gradient of the potential. In magnetostatics, the zero divergence of the magnetic field ensures that the magnetic field can be expressed as the curl of a vector potential. This potential is known as the magnetic vector potential.
Consider an ideal solenoid with n turns per unit length and radius R. If I is the current through the solenoid, the magnetic field inside the solenoid is expressed as the product of vacuum permeability, the number of turns per unit length, and the current. Conversely, the magnetic field outside the solenoid is zero. Considering this, what is the vector potential for an ideal solenoid?
The magnetic flux through the solenoid is given by
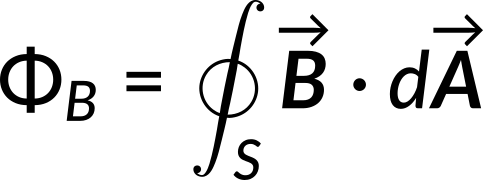
Since the magnetic field equals the curl of the vector potential, the magnetic flux can be rewritten in terms of the vector potential.
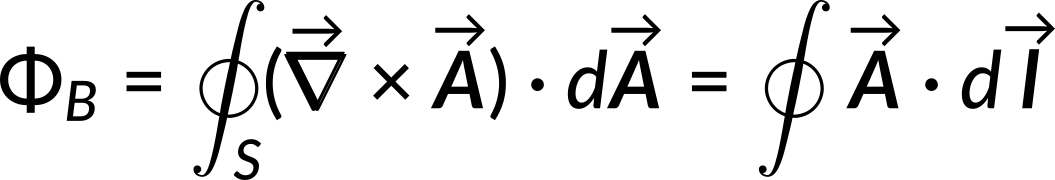
Thus, the line integral of the magnetic vector potential equals the surface integral of the magnetic field.
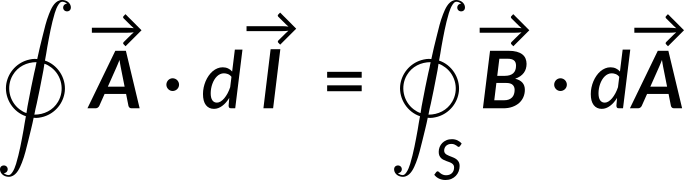
Now consider a circular Amperian loop of radius r inside the solenoid. The magnetic flux through this loop is given by
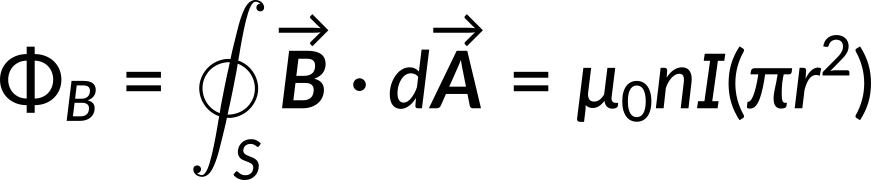
Equating the magnetic flux to the line integral of the magnetic vector potential, the expression for the vector potential can be obtained.
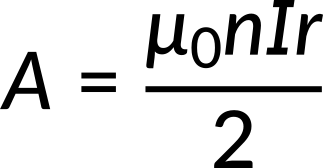
The vector potential mimics the magnetic field and acts along the circumference.
Из главы 29:

Now Playing
29.14 : Magnetic Vector Potential
Sources of Magnetic Fields
514 Просмотры

29.1 : Магнитное поле из-за движущихся зарядов
Sources of Magnetic Fields
8.2K Просмотры

29.2 : Закон Био-Савара
Sources of Magnetic Fields
5.7K Просмотры

29.3 : Закон Био-Савара: решение проблем
Sources of Magnetic Fields
2.4K Просмотры

29.4 : Магнитное поле благодаря тонкому прямому проводу
Sources of Magnetic Fields
4.7K Просмотры

29.5 : Магнитное поле благодаря двум прямым проводам
Sources of Magnetic Fields
2.3K Просмотры

29.6 : Магнитная сила между двумя параллельными токами
Sources of Magnetic Fields
3.4K Просмотры

29.7 : Магнитное поле токовой петли
Sources of Magnetic Fields
4.3K Просмотры

29.8 : Дивергенция и закручивание магнитного поля
Sources of Magnetic Fields
2.7K Просмотры

29.9 : Закон Ампера
Sources of Magnetic Fields
3.6K Просмотры

29.10 : Закон Ампера: решение проблем
Sources of Magnetic Fields
3.5K Просмотры

29.11 : Соленоиды
Sources of Magnetic Fields
2.4K Просмотры

29.12 : Магнитное поле соленоида
Sources of Magnetic Fields
3.7K Просмотры

29.13 : Тороиды
Sources of Magnetic Fields
2.8K Просмотры

29.15 : Потенциал из-за намагниченного объекта
Sources of Magnetic Fields
249 Просмотры
See More
Авторские права © 2025 MyJoVE Corporation. Все права защищены