Explosion Quantifizierung Mit Hopkinson Pressure Bars

Zusammenfassung

This protocol details the use of Hopkinson pressure bars to measure reflected blast loading from near-field explosive events. It is capable of interpolating a pressure-time history at any point on a reflective boundary and as such can be used to fully characterize the spatial and temporal variations in loading produced.

Zusammenfassung

Nahfeld-Hochlastmessung stellt ein Problem für viele Sensortypen, da sie sehr aggressive Umgebungen ertragen müssen und in der Lage sein, Druck zu messen, bis zu vielen hundert Megapascal. In dieser Hinsicht hat die Einfachheit des Hopkinson Druck bar einen großen Vorteil, dass während der Messung Ende des Hopkinson Bar aushalten kann und zu harten Bedingungen ausgesetzt werden, kann der DMS-an der Stange montiert in einiger Entfernung angebracht werden. Dies ermöglicht Schutzgehäuse verwendet werden, welche die Dehnungsmesser schützen, aber nicht mit der Messwerterfassung stören. Die Verwendung einer Anordnung von Druckstangen ermöglicht es, die Druckzeitverläufe an diskreten bekannten Punkten gemessen werden. Dieser Artikel beschreibt auch die Interpolation Routine verwendet, um Druck-Zeitverläufe an un-instrumentierten Stellen auf der Ebene von Interesse abzuleiten. Derzeit ist die Technik wurde in der freien Luft und begraben seicht in verschiedenen Böden zu messen Laden von Sprengstoffen verwendet.

Einleitung

Charakterisieren die Ausgabe von Sprengladungen hat viele Vorteile, sowohl militärische (Verteidigung gegen Sprengkörper in aktuellen Konfliktzonen improvisierten vergrabene) und zivilen (Gestaltung Strukturkomponenten). In der letzten Zeit hat sich dieses Thema große Aufmerksamkeit erhalten. Ein Großteil des gesammelten Wissens wurde bei der Quantifizierung der Ausgabe von Ladungen zum Ziel, die Gestaltung wirksamer Schutzstrukturen zu ermöglichen. Das Hauptproblem dabei ist, dass, wenn die Messungen nicht von hoher Genauigkeit sind dann die Mechanismen der Lastübertragung in diesen explosiven Ereignisse unklar bleiben. Dies wiederum führt zu Problemen Validieren numerischen Modellen, die für die Validierung dieser Messungen verlassen.

Der Begriff Nahfeld verwendet Blasten mit skalierten Entfernungen, Z, weniger als ca. 1 m / kg ^1/3, wobei Z = R / W ^1/3, R der Abstand vom Zentrum des Sprengstoffes zu beschreiben und W die Ladung Masse ausgedrücktals äquivalente Masse von TNT. In diesem Bereich wird die Beladung der Regel durch eine extrem hohe Größe gekennzeichnet, hoch räumlich und zeitlich ungleichmäßigen Belastungen. Robuste Instrumentierung ist daher die extremen Drücke erforderlich, um mit Nahfeld-Belastung zu bemessen. Bei skalierten Entfernungen Z <0,4 m / kg ^1/3, direkte Messungen der Strahlparameter sind entweder nicht vorhanden oder nur sehr wenige ¹ und die semi-empirischen Prognosedaten für diesen Bereich wird auf Parameterstudien basiert fast ausschließlich. Dabei werden die semi-empirischen Vorhersagen über die angegebenen durch Kingery und Bulmash ^2, die außerhalb des Autors beabsichtigten Umfang ist. Während auf diesen Prognosen basierten Tools ^3,4 für exzellente erster Ordnung Schätzungen der Belastung erlauben sie erfassen nicht die Funktionsweise der Nahfeld-Veranstaltungen, die im Mittelpunkt der aktuellen Forschung sind.

Nahfeld-Explosion Messungen haben in der letzten Zeit konzentrierte sich auf die Quantifizierung der Ausgut von vergrabene Ladungen. Die Methoden variieren , von der Beurteilung der zu einer strukturellen Ziel verursachte Verformung ^{5-7 8-13} globalen Impulsmessung zu lenken. Diese Methoden liefern wertvolle Informationen für die Validierung von Schutzsystemkonstruktionen sind aber nicht in der Lage die Funktionsweise der Lastübertragung zu untersuchen. Die Prüfung kann an beiden Laborwaagen (1/10 full scale), oder in der Nähe des Skalenendwerts (> 1/4), mit pragmatischen Gründen wie Controlling Eingrabtiefe oder Gewährleistung keine inhärente Form der Stoßfront wird durch die erzeugte erfolgen Verwendung von Zündern und nicht bloßen Kosten ^14. Mit vergrabenen Ladungen müssen die Bodenbedingungen sehr gesteuert werden , um die Wiederholbarkeit des Tests ¹⁵ zu gewährleisten.

Unabhängig von der, ob die Ladung in der freien Luft platziert ist oder vergraben ist, ist die grundlegende Frage der resultierenden Explosion bei der Messung der Gültigkeit der Messungen durch die Instrumentierung deplo Gewährleistungyed. In der vorgesehenen Testvorrichtung ¹⁶ eine feste 'starren' Zielplatte wird verwendet , um die Hopkinson Druckstäbe abzuschirmen ¹⁷ (HDU) , während gleichzeitig sichergestellt wird, dass die Enden der Balken nur die vollständig reflektiert Drücke aufzeichnen kann. Die Autoren haben bereits entschieden, dass eine Messung reflektierten Druck gezeigt aus einem starren Ziel genauer und wiederholbarer als einfällt, oder "Freifeld" Messungen ^18-20. Die Geometrie dieser Platte ist , so daß jede Druckentlastungs erzeugt durch Löschen oder Umströmung der Zielkante ²¹ vernachlässigbar wäre. Diese neue Testvorrichtung wurde bei 1/4 Maßstab gebaut. Bei diesem Maßstab eine strenge Kontrolle über den Grabbedingungen und den Sprengstoff sichergestellt werden kann, mit dem vollen Umfang der Füllmenge von 5 kg bis 78 g verkleinert, bei einer Grabtiefe von 25 mm.

Protokoll

1. Starre Reaktionsrahmen

1. Bestimmen Sie skalierte Entfernung , bei der Prüfung stattfinden wird unter Verwendung der Gleichung 1, wobei R der Abstand von der Mitte des Sprengstoffs ist, und W ist die Ladungsmasse als eine äquivalente Masse von TNT ausgedrückt.
   Z = R / W ^1/3 (1)
2. Berechnen ungefähre maximale Impuls diese Anordnung wird über die numerische Modellierung erzeugen (siehe Anhang A) oder spezielle Werkzeuge wie ConWep ^3.
   Hinweis: Die Verwendung von ConWep ³ für freie Luft Explosion ist nur gültig, wenn eine Schätzung der von vergrabene Ladungen erzeugten Drücke erforderlich ist die erweiterte numerische Modellierung erforderlich ist.
3. Überprüfen der geschätzten Belastung aus der Modellierung wird nicht in der Ebene erzeugen Auslenkungen von mehr als 0,5 mm in der Zielplatte.
4. Erhöhen Sie die um einen Faktor von 10 berechnet Belastung für Ungenauigkeiten bei der Modellierung zu berücksichtigen und die Flexibilität zur für zukünftige testing.
5. Entwerfen Sie einen starren Reaktions Rahmen der Lage sein , die maximale Belastung zu widerstehen ¹⁶ berechnet. In einer Abteilung Engineering, führen diese Berechnungen im Haus; suchen auf die Dienste von einem Statiker.
   1. Procure starren Reaktionsrahmen, Vertrag eine Fachfirma zu fertigen und die Rahmen zu den Entwürfen der Statiker installieren.
6. Procure Zielplatte, Vertrag einen Spezialisten Stahlbauer.
   Beachten Sie, dass die Platte auf Wägezellen montiert werden muss (falls verwendet) und die Löcher für die HPBS (entworfen in Abschnitt 3) müssen vor der Montage durch die Platte gebohrt werden.

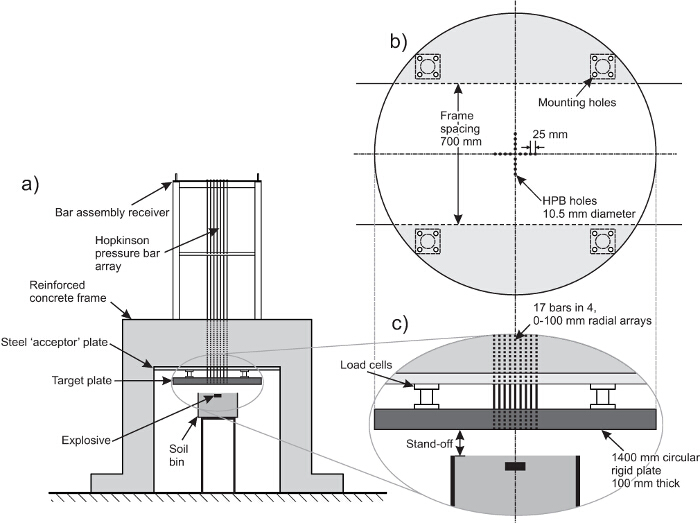
Abbildung 1. Schematische Darstellung des Testrahmens. (A) Gesamtanordnung, (B) Plan der Zielscheibe, (C) Nahansicht der Zielscheibe. Ter Hopkinson Druckstäbe werden von der Stangenanordnung Empfänger aufgehängt, so dass sie mit dem Gesicht der Zielplatte bündig sitzen. Dies ermöglicht die vollständig reflektiert Druck auf die Zielplatte wirkende aufgezeichnet werden. Bitte hier klicken , um eine größere Version dieser Figur zu sehen.

2. Laden-Cell-Design

1. Beschaffen oder Lastzellen herzustellen (falls verwendet). Diese können entweder off-the-shelf universal (Druck / Zug) DMS-Kanister Modelle oder eingebaut in-house mit Abschnitten von dickwandigen mild Stahlrohr verschweißt Montageplatten mit Dehnmessstreifen in einer Wheatstone'schen Brückenbildung befestigt , wie in Abbildung gezeigt 2.
2. Wenn die Lastzellen haben im Haus hergestellt worden, um sie zu einem externen Auftragnehmer für die Kalibrierung senden.

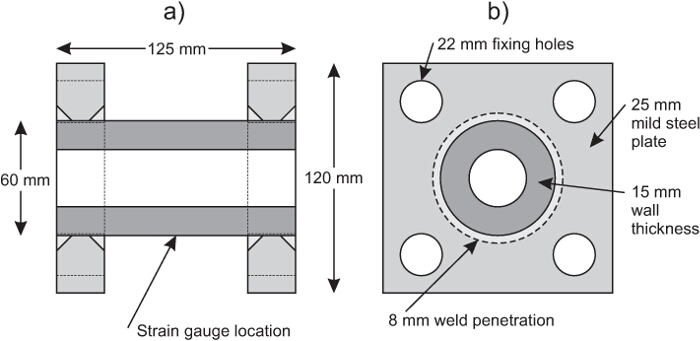
Abbildung 2. Schematische Darstellung der in-house gefertigt Wägezellen. (A) Seitenansicht (B) Ende Höhe. Der dunkelgraue Zylinder ist eine dicke Wand Stahlrohr, das unter Belastung belastet. Dieser Stamm wird aufgezeichnet einen einzelnen Dehnmessstreifen unter Verwendung als keine Rotation während des Ladens erlebt wird. Von der Kalibrierung der Wägezelle kann die Belastung auf den Stress zurück angewendet bezogen werden. Bitte hier klicken , um eine größere Version dieser Figur zu sehen.

3. Hopkinson Pressure Bar Design

1. Bestimmen Sie die Dauer der Aufnahme, , Erforderlich, um die volle Beladung von der Explosion zu erfassen. Die Mindestdauer erforderlich ist die Zeit, in der numerischen Modell (Abschnitt 1.2) für den Druck auf Null zurück genommen, nach der anfänglichen Druckspitze. Hier verwenden 1,2 ms.
2. Decide auf das Material der Wahl für die HPBS. Dies wirkt sich auf die elastische Wellengeschwindigkeit, 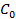, In der Bar, die gegeben ist durch 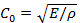woher ist der Young-Modul und 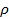ist die Dichte. Für einen hohen Druckstoß zu messen, verwenden steifen Materialien wie Stahl; wo, wie wenn eine schwächere Stoß erwartet wird, weniger steifen Materialien, wie beispielsweise einer Magnesiumlegierung oder Nylon.
3. Wählen, um die Position auf der HPB, dass der Dehnungsmesser positioniert wird, so nah wie möglich an die geladene Fläche der HPB sein Dispersion zu minimieren. In der aktuellen Aufstellung der Dicke der Zielplatte und der Wendigkeit erforderlich, um die Stangen an Ort und Stelle zu passen dazu geführt, dass die Messgeräte nur 250 mm von der geladenen Fläche installiert werden konnte.
4. Berechnen Sie die HPB Länge erforderlich unter Verwendung von 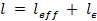, woher 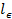ist der Abstand von der geladenen Fläche des HPB auf dem Dehnungsmesser und (3,25 m).
5. Bestimmen erforderlich HPB Radius ausreichende Bandbreite haben, um die Veranstaltung zu erfassen mit: kHz, wobei 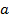in mm ^22,23 (5 mm) ist die HPB Radius.
6. Entscheiden Sie sich für die räumliche Auflösung erforderlich, um die Druckverteilung über die Platte zu erfassen. Dies ist im Allgemeinen so nahe wie möglich, während die strukturelle Integrität der Zielplatte gehalten wird. In der aktuellen Arbeit, verwenden 25 mm.
7. Bohrungen in der Targetplatte die HPBS montiert (dies kann ein Teil des Herstellungsprozesses sein). Eine enge Passung erforderlich without die HPBS in Kontakt mit der Platte zu sein. Hier verwenden 0,5 mm Toleranz mit 17 Löchern in einer Kreuzform (Abbildung 1b) gebohrt wird.
8. Beschaffen Sie die HPBS (17), um sicherzustellen , die distalen Enden haben Gewinde für die Aufhängung in der Stangenanordnung Empfänger (3A) zu ermöglichen.

4. Versuchsaufbau und Datenerfassung

Hinweis: Bei der Reaktion Rahmen, Zielplatte, Wägezellen und HPBS entworfen und hergestellt, die Montage beginnen kann , wie in Abbildung 1 gezeigt , und in Protokollabschnitt 1 ausgelegt.

1. Befestigen Halbleiter Dehnmessstreifen HPBS (3B) und Wägezellen mit Sekunden wobei darauf geachtet , die Kontinuität der Erde durch alle Verkabelung zu gewährleisten. Ein Beispiel für die Wheatstone - Brücke für die HPBS verwendet wird in 3C gezeigt.
   1. Überprüfen Sie, ob alle Erdungskabel angeschlossen sind Kontinuität der Erde zu gewährleisten. Gut geerdet Testvorrichtung verbessertSignalqualität vor allem.
2. Stellen Sie sicher, Verdrahtung ausreichend lang ist das Oszilloskop lokalisierbar ist in einem Hoch freien Bereich (geschirmte Verkabelung verwendet werden, die ausreichend Signalbandbreite hat), um sicherzustellen.
3. Setzen Sie die Zielplatte mit dem starren Reaktionsrahmen unter Verwendung der optionalen Wägezellen , falls vorhanden (Abbildung 1C).
4. Hang HBPs von der Stangenanordnung Empfänger, die geladene Ende durch das richtige Loch in der Platte Ziel vorbei. Hängen die HPBS frei von einer Mutter auf den Gewinde distalen Ende des HPB verschraubt.
5. Stellen Sie sicher, Bars sind vertikal mit einer Wasserwaage (Einstellung des Empfängers entsprechend).
6. Überprüfen Sie die Gesichter der HPBS sind Ebene mit der Zielplatte, entsprechend der Stellmutter.
7. Stellen Sie den Rand an dem veränderlichen Widerstand in der Aufbereitungsschaltung (3C) Spannung zu halten , innerhalb der Grenzen des Oszilloskops während des Testens. Tun Sie dies durch Versuch und Irrtum darauf abzielt, die aus dem Gleichgewicht zu setzen für jeden Kanalwie auf Null auf der Digitalanzeige auf den Verstärkerboxen gesehen.
8. Schließen Sie das verstärkte Messer Ausgang an einen geeigneten Digital-Oszilloskop. Konfigurieren einer Abtastfrequenz zu haben (1,56 MHz), Aufnahmezeit (28,7 msec) mit einem Pre-Trigger Dauer von 3,3 msec.
   1. Stellen Sie die Aufzeichnung auslösen, wenn die Spannung in der Pause Kabelkanal (die selbst in das Oszilloskop verdrahtet ist) überschreitet ein "out-Fenster '. Nehmen Sie Spannung für jeden angeschlossenen Messgerät (insgesamt 22, 17 HPBS, 4 Wägezellen und der Pause Draht) und Zeit.

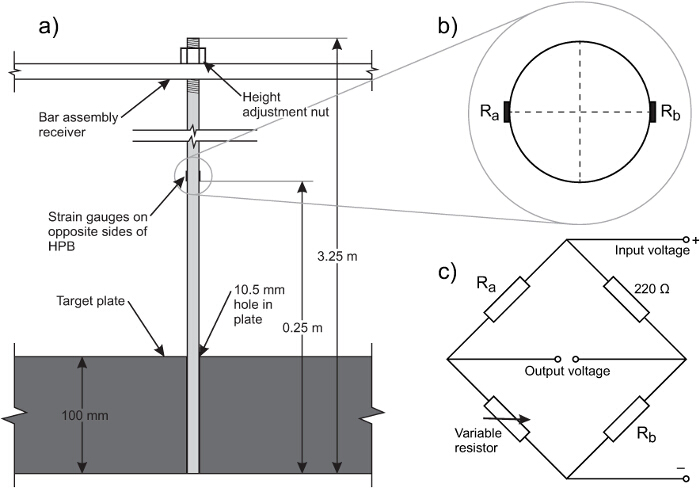
Abbildung 3. (A) Schematische Darstellung eines HPB in die Zielplatte versehen, (B) Schnitt durch HPB bei Spur Lage, (C) Beispiel Wheatstone'schen Brückenschaltung. Zwei Dehnmessstreifen sind in der Wheatstone-Brücke, so dass verwendet und Biegen des Hopkinson-Bar ist cancelled aus. Bitte hier klicken , um eine größere Version dieser Figur zu sehen.

5. Explosive Vorbereitung

1. Entscheiden Sie sich für die Sprengladung Masse und Stand-off in den Tests verwendet werden (100 g PE4 bei 75 mm).
2. Entscheiden Sie, ob die Gebühren in der freien Luft zu detoniert sind oder in einem anderen Medium (Boden, Wasser etc.). Für freie Luft testet eine kugelförmige Ladung Form normalerweise verwendet wird , während mit vergrabenen Kosten der Standard eine 3: 1 Hocke Zylinder ^24,25.
3. Für freie Lufttests:
   1. Hängen Sie die Ladung unter der Zielplatte an der richtigen Stand-off (75 mm). Sie erreichen dies mit einem dünnen Holzstreifen oder auf einem Blatt polythene die Ladung platzieren.
   2. Legen Sie die Ladung koaxial mit der Messanordnung, um gültige Messwerte zu gewährleisten.
   3. Für freie Lufttests einen elektrischen Zünder verwenden, mit dem Detonator auf halbem Weg gebracht werden indie Ladung von der Basis. Tun Sie dies im letzten Moment vor dem Brennen und wenn der Bereich wurde bereits sichergestellt.
4. Für begraben Tests:
   1. Fabrizieren einen geeigneten Behälter für das Medium. Bei Böden verwendet die Stromprüfung 1/4 Skala Behälter ^23.
   2. Entscheiden Sie über die Bodenart genutzt und den geotechnischen Bedingungen werden: Feuchtigkeitsgehalt und Trockendichte des Bodens, siehe Lit. ¹⁵ für weitere Details..
   3. Entscheiden Sie sich für die Grabtiefe bei der Prüfung zu verwenden. Dies ist in der Regel 100 mm in einem vollen Skala-Test, wie die aktuellen Tests bei ¼ Skala fertig sind dies bedeutet eine 25 mm Grabtiefe.
   4. Mischen Sie den Boden gründlich mit einem geeignet dimensionierten Bau Mischer mit dem Soll-Feuchtigkeitsgehalt zu erreichen. Für Sanden erforderliche Mischzeit ist 10 min.
      1. Überprüfen, um den Feuchtigkeitsgehalt der Mischung durch eine kleine Menge entfernt und gewogen, die Gesamtmasse zu berechnen, 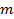. Trockendie entfernt Boden und erneut wiegen die Wassermasse zu berechnen, . Geotechnische Feuchtigkeitsgehalte sind in Form von gravimetrischen Feuchtigkeitsgehalt angegeben, .
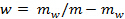      2. Wenn der Feuchtigkeitsgehalt innerhalb der Toleranz fortsetzen, remixen sonst den Boden. Eine Toleranz von ± 0,05 bis 0,1% wurde in der aktuellen Arbeit erreicht.
   5. Wiegen Sie die leeren Bodenbehälter und berechnen Sie die Volumenberechnung der Bodendichte zu ermöglichen, einmal voll ist (Schritt 5.4.7).
   6. Verdichten des Bodens in Schichten, dünn genug, um die Zieldichte zu gewährleisten, um sicherzustellen, dass die Masse des Bodens des Behälters eintritt bekannt ist. Für Leighton Buzzard Sand ¹⁵ wird dies in zwei Ebenen durchgeführt.
   7. Sobald der Behälter voll ist, prüfen Sie, dass die Dichte des Bodens innerhalb der Toleranz (± 0,2%). Die Zieltrockendichte in allen Tests mit Leighton Buzzard Sand betrug 1,6Mg / m ^3. Berechnen Trockendichte, unter Verwendung von 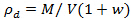, Wobei ρ _d der Trockenrohdichte ist, M die Gesamtmasse des Bodens zu dem Behälter hinzugefügt wird , ist V das Volumen des Bodenbehälters und w ist der Feuchtigkeitsgehalt.
   8. Ausgraben ein kleines Loch ≈50 mm die Ladung zu ermöglichen, an der richtigen Grabtiefe (25 mm) mit der Oberfläche platziert werden.
   9. Legen Sie eine nicht-elektrische Sprengzünder in die Basis der Ladung und raben einen geeigneten Kanal zu der Seite des Behälters die obere Oberfläche des Behälters, um sicherzustellen, ununterbrochenen, sobald der Boden ersetzt.
   10. Legen Ladung und Zünder in das ausgehobene Loch, die Überprüfung der Grabtiefe korrekt ist. Zurück füllen das Loch mit dem Aushubmaterial.

6. Zündfolge

Hinweis: Es gibt eine kleine Menge an Überlappung mit Protokollabschnitt 5 aufgrund der nature des Tests. Die Zündfolge sollte darauf abzielen, das Risiko zu minimieren und sollte nur von entsprechend geschultem Personal durchgeführt werden.

1. Für freie Lufttests:
   1. Vereinbaren Sie kostenlosen Support unter der Zielplatte an der richtigen Stand-off (75 mm).
   2. Schließen Sie den Bereich. Bereitstellen von Wachen, um sicherzustellen, Bereich während des Brennens ist klar.
   3. Platzieren Ladung auf dem Träger co-axial zur Instrumentierung. Bringen Sie den Bruch Draht an den Zünder und legen Sie die Zünder in der Ladung.
2. Für begraben Tests:
   1. Platzieren Bodenbehälter, so dass die Ladungs ​​koaxial zur HPB-Array angeordnet ist.
   2. Schließen Sie den Bereich. Bereitstellen von Wachen, um sicherzustellen, Bereich während des Brennens ist klar.
   3. Schließen Sie den Break-Draht, sicherstellen, dass er sich um den Umfang der Ladung gewickelt wird (dies ergibt eine wiederholbare Zeit der Detonation in begraben Gebühren).
3. Bewegen Sie Punkt zu Brennen und bestätigen Instrumentierung ausgeführt wird.
4. Versorgen Sie den Bruch Draht. Prüfen Sie mit Wächteres ist sicher, mit dem Brennen, um fortzufahren.
5. Initiieren Sprengstoff. Machen Sie den Testbereich sicher.
6. Laden und Sichern von Daten.
7. Re-open Testbereich.

7. Numerische Interpolation für ein Array 1D HPB

1. Importieren Sie die Daten aus den Rohdaten-Dateien in Matlab.
2. Zeitverschiebungs alle Daten in der radialen Richtung , so dass der Spitzendruck für jeden Takt gleichzeitig kommt als der Spitzendruck des zentralen bar unter Verwendung von Gleichung 2 (4B).
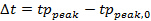   (2)
3. Interpolieren der Druck an jeder radialen Abstand von 4B.
4. Zeichnen Sie die Ankunftszeiten ( 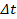) Verwendet , um die Spitzendrücke und passen eine kubische Gleichung durch die Daten (4C) auszurichten.
5. Time-Shift die interpolierten Daten der Ankunftszeiten zu passen, Gattungenting eine kontinuierliche Stoßfront (4D).
6. Wiederholen Sie dies für jeden einzelnen Satz von Testdaten.

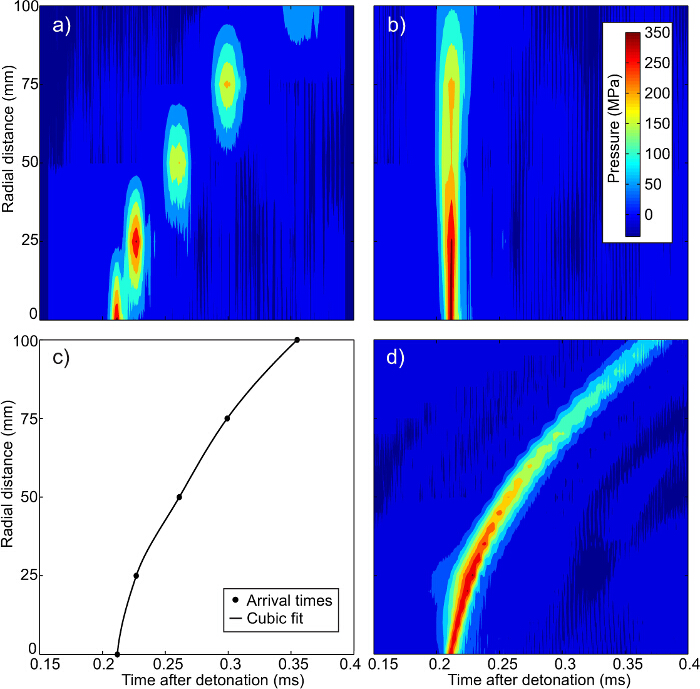
Abbildung 4. Interpolation Sequenz für 1D HPB - Array. (A) Original - Daten, (B) zeitverschobene Daten, (C) vorne Ankunftszeiten schocken, und (D) endgültig interpoliert Druckzeitdaten ^16. Die diskrete Natur der Druckzeitverläufe deutlich in (A) zu sehen ist mit dort an jeder der fünf Positionen Gauge keine Kontinuität zwischen den Spitzendrücke zu sein. Wenn durch Spitzendruck , wie in (B) die Interpolation der Druck an jedem radialen Abstand (unter der Annahme der gleichen Ankunftszeit) ausgerichtet ist möglich. Durch die Aufnahme der Zeitverschiebung erforderlich die Spitzendrücke, die Ankunftszeit der Stoßfront auszurichten als sh berechnet werdenSelbst in (C). Auf diese Weise können dann die Ankunftszeit und die Geschichte Druckzeit für jede radiale Abstand sein Interpolation des Drucks von (B) und die Zeit von (C) , was den endgültigen interpoliert Druck , wie in (D) berechnet werden. Bitte klicken Sie hier um ein , um zu vergrößern Version dieser Figur.

8. Numerische Interpolation für ein Array 2D HPB

Hinweis: Der Code verwendet, um die Interpolation in Matlab zu laufen, zusammen mit einer Beispielergebnisdatei zur Verfügung gestellt worden, die in diesem Abschnitt Bezug genommen wird.

1. Importieren Sie die Daten aus den Rohdaten-Dateien in Matlab. Für die beispielhafte Testdaten, doppelklicken Sie auf die test_data.mat-Datei, und klicken Sie dann auf "Fertig stellen" in den Import-Assistenten.
2. Öffnen Sie das interpolation2d.m Matlab-Skript.
3. Definieren Sie ein regelmäßiges Gitter, über die die Interpolationlaufen durch das Netz zu verändern. Stellen Sie sicher , das die gleiche Auflösung wie das Netz in einer zukünftigen numerischen Modellierung ^26,27 ist. Dies wird in der '% Mesh-Details "des Code festgelegt.
4. Führen Sie das interpolation2d.m Matlab-Skript. Beachten Sie die folgenden Schritte in der Code implementiert werden und sind hier für Klarheit aufgeführt.
   1. Time-Shift alle HPB Druckspuren durch 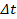(Gleichung 2). Originaldaten gezeigt für 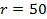mm in 5B mit der gleichen Daten zeitverschoben in 5C.
      Hinweis: Die Zeitverschiebung ist erforderlich, die Interpolationsroutine zu ermöglichen, erfolgreich die Stoßfront zu einem gegebenen Zeitpunkt zu lokalisieren. Dies beinhaltet im Wesentlichen die Daten für jeden radialen Anordnung ausgerichtet, so dass alle Maximaldrücke auszurichten.
   2. Berechnen Sie den Radius, Und ang le, 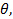für einen gegebenen Punkt von Interesse auf dem Gitter, wie in 5A gezeigt.
   3. Tragen Sie die 1D-Interpolation auf die beiden HPB-Arrays am nächsten zu dem Punkt von Interesse für den aktuellen Radius (für 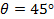die Interpolation verwenden würde die 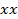und 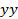Arrays).
   4. Interpolieren linear zwischen den zwei Drücken basierend auf 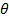(Wieder für ein 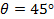die Gewichtung würde 50% der sein 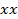und 50% der 12eq30.jpg "/> Array berechnet Drücke).
   5. Berechnen Sie die momentane Belastung durch die interpolierte Druck durch den Gitterabstand (Fläche) multipliziert wird, die Last zu geben.
   6. Multiplizieren, um die Last, die durch den Zeitschritt der Abtastung des momentanen Impuls zu erhalten.
   7. Wiederholen Sie dies für alle Standorte und Zeiten (die momentane Impuls Addition der Gesamtimpuls zu geben).
   8. Time-Shift die Druckzeithistorie für jeden Standort basierend auf kubische Interpolation der Schock Ankunftszeit (5D).

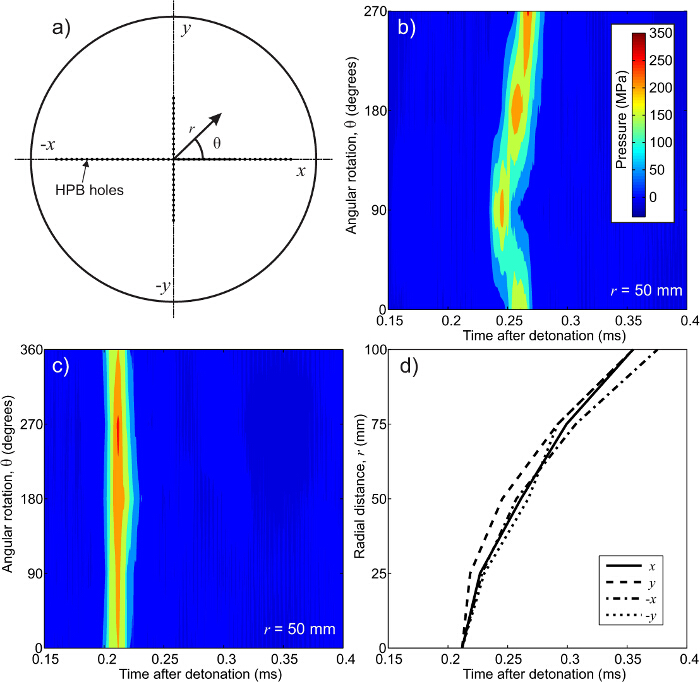
Abbildung 5. Interpolation Sequenz für 2D - HPB - Array. (A) Sign Konventionen verwendet, (B) Originaldaten 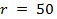mm, (C) zeitverschobene Daten412 / 53412eq36.jpg "/> mm, und (D) Ankunftszeiten für jede radiale Richtung ^16. Für eine 2D - Anordnung von Stäben der Druckzeitverlauf an einer beliebigen Stelle auf beiden radialen Abstand abhängig ist und welchem ​​Quadranten der Punkt von Interesse liegt . Wenn die Explosion vollkommen symmetrisch waren dann die Drücke in (B) würde vertikale Linien bilden , wie in (C) gezeigt. in (B), dass die Stoßfront ist die 50 mm Position zu sehen ist erreicht auf 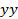Achse zuerst.
Bitte klicken Sie hier , um eine größere Version dieser Figur zu sehen.

Ergebnisse

Ein effektiv starr braucht Reaktionsrahmen zur Verfügung gestellt werden. In der aktuellen insgesamt verliehenen Impuls von mehreren hundert Newton-Sekunden Prüfung muss mit minimaler Ablenkung widerstanden werden. Eine Abbildung des starren Reaktionsrahmen verwendet wird , in Abbildung 1 wiedergegeben. In jedem Rahmen ein 50 mm Stahl "Akzeptor" Platte in die Basis der Querträger gegossen wurde. Auch wenn es nicht ausdrücklich gefordert, ermöglicht dies ei...

Diskussion

Mit dem Protokoll über den Autoren dargelegt haben gezeigt, dass es möglich ist, High-Fidelity-Messungen der stark variierenden Belastung von einer Sprengladung zu erhalten, eine Reihe von Hopkinson Druckstangen verwendet wird. Mit Hilfe der Interpolation Routine skizzierte die diskreten Druck-Zeitverläufe können in einem kontinuierlichen Schockfront umgewandelt werden, die für die Ausgabe solcher Modelle direkt als Ladefunktion in der numerischen Modellierung oder als Validierungsdaten verwendbar ist.

Materialien

Name	Company	Catalog Number	Comments
Load Cell	RDP	RSL0960	This is only indicative, the exact load cell should be able to resolve the required loading
Steel target plate / HPBs	Garratts		Fabricated to order
Strain gauge	Kyowa	KSP-2-120-E4	To use with steel HPBs
Cyanoacrylate	Kyowa	CC-33-A	Check with manufacturer depending on mar material to be used
Digital Oscilloscope	TiePie	HS4 16-bit Handyscopes	6 used in parallel in current testing
Leighton Buzzard sand	Garside sands	Garside 14/25	Uniform silica sand