JoVE 비디오를 활용하시려면 도서관을 통한 기관 구독이 필요합니다. 전체 비디오를 보시려면 로그인하거나 무료 트라이얼을 시작하세요.
Method Article
폭발 정량화는 홉 킨슨 압력 막대를 사용하여
요약
This protocol details the use of Hopkinson pressure bars to measure reflected blast loading from near-field explosive events. It is capable of interpolating a pressure-time history at any point on a reflective boundary and as such can be used to fully characterize the spatial and temporal variations in loading produced.
초록
그들은 매우 공격적인 환경을 견딜과 메가 파스칼의 수백까지 압력을 측정 할 수 있어야로 근거리 폭발 하중 측정은 여러 센서 유형에 대한 문제를 제시한다. 이 점에서, 홉 킨슨 압력 바의 단순성은 홉 킨슨 바의 측정 끝이 견딜 수 및 가혹한 조건에 노출되는 동안, 스트레인 게이지가 약간의 거리에 부착 할 수있는 막대에 장착한다는 점에서 큰 장점이있다. 이 보호 틀은 스트레인 게이지를 보호하지만, 측정 수집을 방해하지 않은 이용 될 수있다. 압박 막대의 어레이의 사용은 공지 된 이산 지점에서 압력의 시간 이력을 측정 할 수있다. 이 문서는 또한 관심의 평면에 미 계측 위치에서 압력 - 시간 이력을 유도하는 데 사용되는 보간 루틴을 설명합니다. 현재이 기술은 자유 공기 내의 높은 폭발물의 로딩을 측정하기 위해 사용 된 다양한 토양에 얕게 매장.
서문
폭발물의 출력을 특성화하는 것은 두 (현재 분쟁 지역에서 폭발 장치를 즉석에서 매립형 방어) 군사 및 민간 (구조 구성 요소를 설계), 많은 혜택이 있습니다. 최근에이 주제에 상당한 관심을 받고있다. 수집 된 지식의 대부분은보다 효과적인 보호 구조의 설계를 가능하게 전하의 출력 정량 대상으로하고있다. 여기에 주요 문제는 만든 측정이 높은 충실도의하지 않은 경우 다음이 폭발 사건의 하중 전달의 메커니즘 불분명 남아 있습니다. 이것은 차례로 검증을위한 이러한 측정에 의존하는 수치 모델을 검증하는 문제로 이어집니다.
근접장 용어는 스케일링 거리, Z, 이하 1 ~ M / Z = R / W 1/3, R은 폭발성의 중심으로부터의 거리이다 1/3 kg 미만, W와 폭발을 설명하는 데 사용되는 전하 대량 발현TNT의 등가 질량있다. 이 정권에서로드는 일반적으로 높은 공간 및 시간적으로 비 균일 부하 매우 높은 크기, 특징입니다. 강력한 기기는 이에 근접장 로딩과 관련된 극도의 압력을 측정 할 필요가있다. 스케일 거리 Z에서 <0.4 m는 / 1/3 kg의 폭발 매개 변수를 직접 측정 존재 또는 거의 1이 범위에 대한 반 경험적 예측 데이터가 파라 메트릭 연구에 거의 전적으로 기반 중 하나입니다. 이것은 저자의 의도 된 범위를 벗어나 Kingery 및 Bulmash 2에 의해 주어진 반 경험적 예측을 사용하는 것입니다. 이러한 예측 3,4에 기반 도구가로드의 우수한 일차 추정을 허용하는 동안 그들은 완전히 현재의 연구의 초점이다 근접장 이벤트의 역학을 캡처하지 않습니다.
근거리 폭발 측정이 최근에이은 OUTP을 정량화에 초점을 맞춘매몰 비용에서 유타. 사용 된 방법은 글로벌 임펄스 측정 8-13을 직접 구조 대상 5-7로 인한 변형을 평가 다릅니다. 이러한 방법은 보호 시스템 설계의 검증을위한 유용한 정보를 제공 할 수 있지만 완전히 하중 전달의 메커니즘을 조사 할 수 없습니다. 시험은에 의해 생성되는 등의 매장 깊이를 제어하거나 충격 전면에는 고유의 모양을 보장하지 않습니다 같은 실제적인 이유와 함께, 또는 주변의 풀 스케일 (> 1/4)에 양쪽 실험실 저울 (1/10 풀 스케일)에서 할 수 있습니다 뇌관보다는 베어 요금 (14)의 사용. 매립 전하 토양 조건은 높은 테스트 (15)의 재현성을 보장하기 위해 제어 될 필요가있다.
전하가없는 공기에 배치 또는 매설 여부 독립적 얻어진 폭발 측정에서 가장 근본적인 문제는 계측 deplo 의한 측정의 유효성을 보장하는 것이다YED. 설계된 시험 장치 (16)에 고정 된 '강성'타겟 플레이트는 바의 단부에만 완전히 반영 압력을 기록 할 수 있음을 보장하는 동시에 하다니 홉 킨슨 압력 바 (17) (HPBs)를 보호하기 위해 사용된다. 단단한 목표는 '자유 필드'측정 18-20보다 정확하고 사건보다 반복, 또는이다에서 저자는 이전에 반사 된 압력의 측정을 보여 주었다. 이 판의 형상은 타겟 에지 (21) 주위에 삭제 또는 유동에 의해 생성 된 압력 릴리프 무시할 것이라고 예이다. 이 새로운 시험 장치는 1/4 규모로 건설되고있다. 매장 조건과 폭발물을 통해이 규모 엄격한 제어에서 25mm의 매장 깊이에서 78g으로 축소 5kg의 풀 스케일 충전 크기, 확보 할 수있다.
프로토콜
1. 엄밀한 반응 프레임
- 테스트 R은 폭발성의 중심으로부터의 거리를 수학 식 1을 이용하여 열린다되는 스케일링 된 거리를 결정하고, W는 질량 TNT의 등가 질량 표현 전하이다.
Z = R / W 1/3 (1) - 이 배열은 수치 모델링을 통해 생성됩니다 대략적인 최대 충격을 계산합니다 (부록 A 참조) 또는 ConWep 3과 같은 특정 도구를 제공합니다.
참고 : 매몰 비용에서 발생하는 압력의 추정은 고급 수치 모델링이 필요 필요한 경우 ConWep 3의 사용, 무료 송풍에만 유효합니다. - 대상 접시에 0.5 mm의 면내 변위를 생성하지 않습니다 모델링에서 추정 된로드를 확인합니다.
- 모델링 부정확성을 고려하기 위해 (10)의 인자에 의해 계산 된 하중을 증가시키고 향후 TES 유연성을 추가 할팅.
- 16 계산 된 최대 하중에 저항 할 수 있도록 강성 반응 프레임 디자인. 엔지니어링 부서에서, 집에서 이러한 계산을 수행; 그렇지 않으면 구조 엔지니어의 서비스를 추구합니다.
- 단단한 반응 프레임을 조달 제조 및 구조 엔지니어의 디자인에 프레임을 설치하는 전문가 계약자 계약.
- , 타겟 판을 조달 전문 강철 제작자 계약.
(사용하는 경우) 플레이트로드 셀에 장착 될 필요가 있고 (3 절 설계)을 HPBs을위한 구멍을 설치하기 전에 판을 드릴 될 필요가 있습니다.
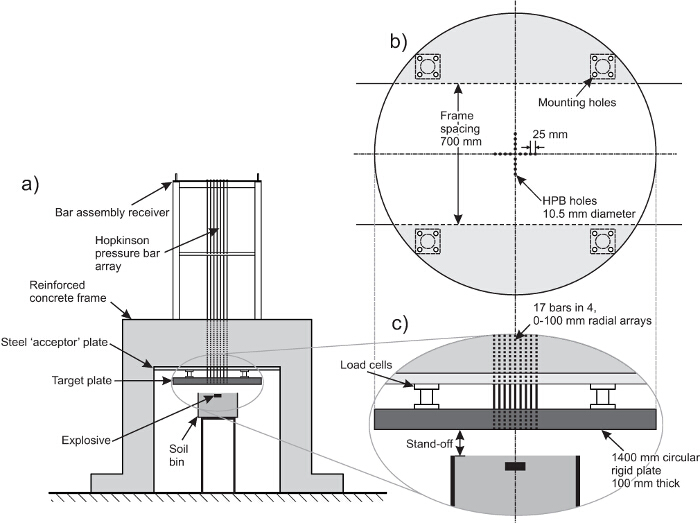
테스트 프레임의 그림 1. 도식. (A) 전체 배열, (B) 표적 판의 계획, (C) 표적 판의 확대보기. 티그들이 표적 판의 표면과 같은 높이 앉아 있도록 그 홉 킨슨 압력 바는 바 어셈블리 수신기로부터 걸려있다. 이 표적 판에 작용하는 완전히 반영 압력을 기록 할 수 있습니다. 이 그림의 더 큰 버전을 보려면 여기를 클릭하십시오.
2.로드 셀 디자인
- 또는 조달 (사용 된 경우) 부하 셀을 제조. 이들은 사내 휘트 스톤 브리지 형성에 부착 된 스트레인 게이지와 플레이트를 장착 용접 두께의 벽 연강 튜브의 섹션을 사용하여 그림과 같이 보편적 인 (압축 / 인장) 스트레인 게이지 용기 모델 - 선반 - 오프 또는 내장 될 중 하나를 수 2.
- 로드 셀은 자체 제작 한 경우, 교정을위한 외부 계약자에게 보낼 수 있습니다.
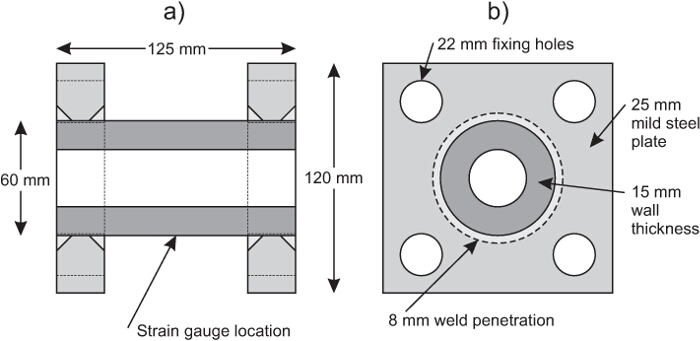
사내 제작로드 셀을. (A) 측면도, (B) 최종 높이 그림 2. 다이어그램. 짙은 회색 실린더로드 아래 균주 두꺼운 벽 강관이다. 이 균주는 더 회전이로드하는 동안 경험하지 된 바와 같이 하나의 스트레인 게이지를 사용하여 기록한다. 변형이 가해지는 스트레스에 다시 관련 될 수 로드셀의 교정에서. 이 그림의 더 큰 버전을 보려면 여기를 클릭하십시오.
3. 홉 킨슨 압력 바 디자인
- 기록 기간을 결정
 , 폭발의 전체로드를 캡처해야합니다. 필요한 최소 기간은 초기 압력 스파이크 후, 제로로 돌아갑니다 압력 수치 모델 (1.2 절)에 걸리는 시간입니다. 여기에 1.2 밀리 초를 사용합니다.
, 폭발의 전체로드를 캡처해야합니다. 필요한 최소 기간은 초기 압력 스파이크 후, 제로로 돌아갑니다 압력 수치 모델 (1.2 절)에 걸리는 시간입니다. 여기에 1.2 밀리 초를 사용합니다. - DeciHPBs에 대한 선택의 재료에 드. 이 탄성 표면파의 속도에 영향
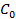 에 의해 주어진 바에서
에 의해 주어진 바에서 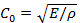 어디에
어디에  인 영률
인 영률 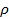 밀도이다. 고압 충격을 측정하기위한, 강철과 같은 단단한 재료를 사용; 여기서 약한 충격이 예상되는 경우로서는, 마그네슘 합금 또는 나일론 덜 단단한 재료를 사용한다.
밀도이다. 고압 충격을 측정하기위한, 강철과 같은 단단한 재료를 사용; 여기서 약한 충격이 예상되는 경우로서는, 마그네슘 합금 또는 나일론 덜 단단한 재료를 사용한다. - 스트레인 게이지 분산을 최소화 HPB의 적재면에 가능한 한 가깝게되고, 위치 될 것이라는 HPB의 위치를 선택한다. 표적 판의 현재 셋업 두께 대신 바를 맞게 필요한 기동성에 게이지에만 적재면으로부터 250mm가 설치 될 수 있음을 의미한다.
- 는 HP를 계산B 길이하여 필요한
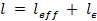 여기서
여기서 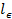 인 스트레인 게이지에 HPB의로드 단면으로부터의 거리 및
인 스트레인 게이지에 HPB의로드 단면으로부터의 거리 및  (3.25 m).
(3.25 m). - 를 사용하여 이벤트를 캡처 할 수있는 충분한 대역폭이 요구 HPB 반경을 결정합니다 :
 kHz에서,
kHz에서, 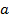 mm (22, 23) (5 mm)의 HPB 반경이다.
mm (22, 23) (5 mm)의 HPB 반경이다. - 플레이트 전체 압력의 분포를 캡처하는데 요구되는 공간 분해능을 결정한다. 표적 판의 구조적 무결성을 유지하면서, 이는 일반적으로 가능한 한 근접한다. 현재 작업에서 25mm를 사용합니다.
- HPBs 탑재하는 표적 판 드릴 구멍 (이는 제조 공정의 일부가 될 수있다). 닫기를 맞는이 witho 필요플레이트와 접촉되는 HPBs을 유타. 여기에 17 홀이 십자가 모양 (그림 1b)에 드릴 된 0.5 mm의 허용 오차를 사용합니다.
- 막대 조립체 수신기 (도 3A)에서 정지 가능하도록 나사 말단부를 확실하게 상기 HPBs (17) 조달.
4. 실험 설정 및 데이터 수집
참고 : 그림 1 및 프로토콜 부 (1) 디자인으로 설계 및 제조 된 반응 프레임, 표적 판,로드 셀 및 HPBs으로 조립을 시작할 수 있습니다.
- HPBs (그림 3B)과로드 셀, 시아 노 아크릴 레이트를 사용하는 모든 케이블을 통해 땅의 연속성을 보장하기 위해 조심에 반도체 스트레인 게이지를 부착합니다. HPBs 사용되는 휘트 스톤 브리지의 일례가도 3c에 도시된다.
- 확인 모든 접지 케이블은 땅의 연속성을 보장하기 위해 부착된다. 그런데 접지 시험 장치는 개선특히 신호 품질.
- 배선이 확인 오실로스코프가 폭발 자유 영역 (차폐 배선은 충분한 신호 대역폭을 갖는 사용해야합니다)에 위치 될 것입니다 수 있도록 충분히 긴 있는지 확인하십시오.
- 본 (도 1C)의 경우 선택적인로드 셀을 사용하여, 강성 반응 프레임 표적 판을 장착한다.
- 표적 판의 구멍을 통해 정확한로드 단부를 통과하는 바 조립체 수신기에서 끊기 HBPs. HPB의 나사 선단에 나사 너트에서 자유롭게 HPBs을 끊습니다.
- 확인 바는 정신 수준 (그에 따라 수신기를 조정)을 사용하여 수직이다.
- 이에 따라 너트를 조정의 HPBs의 얼굴이 목표 플레이트 수준입니다 확인합니다.
- 테스트하는 동안 오실로스코프의 범위 내에서 전압을 유지하기 위해 조절 회로 (그림 3C)의 가변 저항에 트림을 설정합니다. 재판을 통해이 작업을 수행하고 각 채널에 대한 균형 아웃을 설정하는 것을 목표로 오류제로 증폭기 박스의 디지털 판독 볼있다.
- 적합한 디지털 오실로스코프에 증폭 된 계기 출력을 연결합니다. 3.3 밀리의 사전 트리거 기간이 샘플링 주파수 (1.56 메가 헤르츠), 기록 시간 (28.7 밀리 초)을 가지고 구성합니다.
- (자체 오실로스코프에 연결되어) 브레이크 와이어 채널의 전압이 '아웃 창'을 초과하는 경우 트리거 녹화를 설정합니다. 연결된 각 게이지 (총 22, 17 HPBs, 4로드 셀 및 휴식 와이어) 시간 녹음 전압.
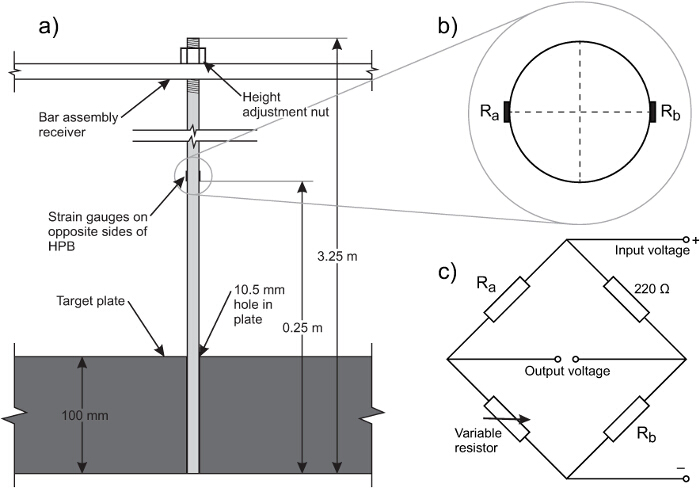
도 3 (A)도 표적 판 게이지 위치 HPB 내지 (B) 부 (C) 실시 예 휘트 스톤 브리지 회로에 장착 된 HPB의. 두 스트레인 게이지가되도록 휘트 스톤 브리지에 사용하고 홉 킨슨 막대의 휨는 C되고아웃 ancelled. 이 그림의 더 큰 버전을 보려면 여기를 클릭하십시오.
5. 폭발 준비
- 폭발적인 충전 질량을 결정하고 스탠드 - 오프 시험에 사용되는 (75mm에 100g의 PE4).
- 요금 무료 공기 또는 다른 매체 (토양, 물 등) 내에서 폭발할지 여부를 결정합니다. 1 스쿼트 실린더 (24, 25) : 무료 공기 매장 비용과 표준이 3 반면 구형 충전 형상이 일반적으로 사용된다 테스트합니다.
- 무료 공기 테스트의 경우 :
- 올바른 스탠드 오프 (75mm)의 표적 판 아래의 요금을 일시 중단합니다. 얇은 목재 스트립 또는 폴리에틸렌의 시트에 요금을 배치하여이를 달성.
- 유효한 측정을 위해 상기 측정 배열 동축 전하를 놓는다.
- 무료 공기 시험은 기폭 장치와 전기 뇌관을 사용하십시오로 절반 방법 배치되는기지에서 충전. 발사 때 범위가 이미 안전했다되기 전에 마지막 순간에이 작업을 수행합니다.
- 매장 시험의 경우 :
- 매체에 적합한 용기를 제작. 토양 들어, 현재 테스트 1/4 스케일 용기 (23)를 사용한다.
- 이용 될 수있는 토양 유형 및 지반 조건에 따라 결정 : 수분 함량과 토양의 건조 밀도는 참조 심판 (15) 자세한 내용은..
- 테스트에 사용하기 위해 매장 깊이를 결정합니다. 현재 시험 ¼ 규모로 완료 이것은 이것은 25mm 매장 깊이를 의미하며, 일반적으로 전체 규모의 시험 100 mm입니다.
- 완전히 목표 수분 함량을 달성하기 위해 적절한 크기 건설 믹서 토양 섞는다. 샌즈 필요한 혼합 시간은 10 분이다.
- 소량을 제거하여 혼합물의 수분 함량을 확인하고 총 질량을 계산하여, 무게
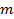 . 마른제거 된 토양 및 물의 질량을 계산하는 재 - 계량
. 마른제거 된 토양 및 물의 질량을 계산하는 재 - 계량  . 지반 수분 함량은 중량 수분 함량의 관점에서 지정된
. 지반 수분 함량은 중량 수분 함량의 관점에서 지정된 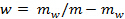 .
. - 공차 계속 내 수분 함량이, 그렇지 않으면 토양 리믹스. ± 0.05-0.1 %의 허용 오차는 현재 작업에 달성되었다.
- 소량을 제거하여 혼합물의 수분 함량을 확인하고 총 질량을 계산하여, 무게
- 빈 토양 컨테이너를 달아 토양 밀도의 계산 회 전체 (단계 5.4.7)를 활성화하기 위해 볼륨을 계산합니다.
- 용기를 입력 토양의 중량이 알려진 것을 보장 대상 밀도를 보장하기에 충분히 얇은 층에서 토양을 컴팩트. 레이튼 Buzzard의 모래 (15)이 두 개의 층으로 이루어집니다.
- 컨테이너가 가득 차면, 토양의 밀도가 내 (0.2 % ±) 허용에 있는지 확인합니다. 레이튼 Buzzard의 모래와 모든 테스트의 대상 건조 밀도는 1.6이었다마그네슘 / m 3. , 건조 밀도를 계산 사용
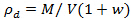 ρ (D)가 건조 밀도이고, M은 상기 용기에 첨가 토양의 총 질량이고, V는 토양 용기의 용적이며, w는 수분량이다.
ρ (D)가 건조 밀도이고, M은 상기 용기에 첨가 토양의 총 질량이고, V는 토양 용기의 용적이며, w는 수분량이다. - 전하 정확한 매몰 깊이 (25mm)의 상면에 배치 될 수 있도록 작은 구멍을 ≈50 mm 발굴.
- 전하의베이스로 비 전기 뇌관을 배치하고, 토양이 교체되면 용기의 상면은 중단 보장하기 위해, 용기의 측면에 적합한 채널을 발굴.
- 매장 깊이를 확인하는 것이 정확, 굴착 구멍에 충전 및 기폭 장치를 놓습니다. 위로 발굴 재료로 구멍을 채우십시오.
6. 소성 시퀀스
주 : 프로토콜 부 (5)와 중첩 소량 인해 NAT에 존재테스트의 URE. 발사 순서는 위험을 최소화하는 것을 목표로한다 만 적절히 훈련 된 직원에 의해 수행되어야한다.
- 무료 공기 테스트의 경우 :
- 올바른 스탠드 오프 (75mm)의 표적 판 아래 요금 지원을 정렬합니다.
- 범위를 닫습니다. 범위를 발사하는 동안 분명 보장하기 위해 보초를 배포합니다.
- 계측에 지원 동축에 요금을 놓습니다. 기폭 장치로 브레이크 와이어를 연결하고 충전에 기폭 장치를 배치합니다.
- 매장 시험의 경우 :
- 충전이 HPB 배열에 동축 배치되도록 토양 컨테이너를 배치합니다.
- 범위를 닫습니다. 범위를 발사하는 동안 분명 보장하기 위해 보초를 배포합니다.
- , 휴식 와이어 연결이 전하의 주변 (이 매몰 비용에 폭발 더 반복 시간을 제공) 주위에 싸여 보장한다.
- 포인트를 발사로 이동 및 계측가 실행 확인합니다.
- 브레이크 와이어에 전원을 공급한다. 보초 확인소성을 진행하는 것이 안전합니다.
- 폭발물을 시작합니다. 테스트 영역이 안전하게.
- 다운로드 및 데이터를 백업합니다.
- 다시 열고 시험 범위.
1 차원 HPB 배열 7. 수치 보간
- matlab에에 원시 데이터 파일에서 데이터를 가져옵니다.
- 각 바의 피크 압력은 수학 식 (2) (도 4b)을 이용하여, 중앙 바의 최대 압력과 동시에 도착하도록 반경 방향으로 모든 데이터를 시간 시프트.
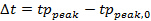 (2)
(2) - 도 4b에서 어떤 반경 방향 거리에서의 압력 보간.
- (도착 시간을 플롯
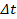 ) 피크를 정렬 압력 데이터 (도 4C)을 통해 차 방정식에 맞게 사용된다.
) 피크를 정렬 압력 데이터 (도 4C)을 통해 차 방정식에 맞게 사용된다. - 도착 시간을 맞추기 위해 보간 된 데이터를 타임 - 시프트 속은팅 연속 충격 앞 (그림 4D).
- 테스트 데이터의 각 세트에 대해 반복합니다.
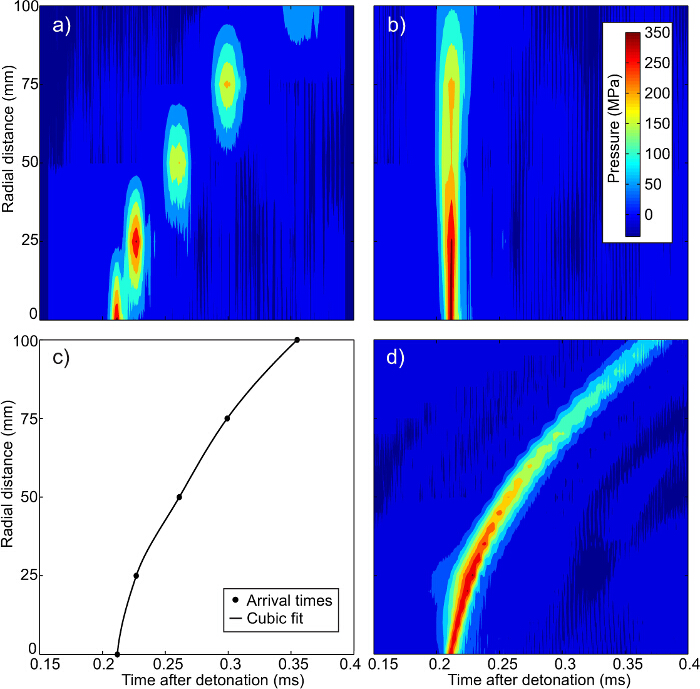
1D HPB 배열에 대한도 4 보간 서열. (A) 원래의 데이터 (B)의 시간 시프트 된 데이터 (C) 앞에 도달 시간을 충격 및 (D), 최종 보간 압력 타임 데이터 (16). 압력의 시간 이력의 개별 특성이 명확 다섯 게이지 위치 각각에서의 피크 압력 사이에 연속성이없는 인로 (A)에서 볼 수있다. (B) (동일한 도달 시간을 가정하여) 어떤 반경 방향 거리에서 압력의 보간과 피크 압력에 의해 배향 가능한 경우이다. 피크 압력을 충격 앞에 도달 시간을 정렬하는 데 필요한 시간의 변화를 기록함으로써, SH 같이 계산 될 수있다(C)에서 자신의. 이 후, 도착 시간 및 압력의 시간 이력 (B) 및 (C) (D)에 도시 된 바와 같이 최종 보간 압력.주고 때때로 압력 보간 될 수있는 반경 방향 거리에 대해 계산 될 수 있도록 크게 보려면 여기를 클릭하세요 이 그림의 버전입니다.
2 차원 HPB 배열 8. 수치 보간
참고 : 매트랩 보간을 실행하는 데 사용되는 코드는이 절에서 언급 될 것이다 예를 들어 결과 파일과 함께 제공되었습니다.
- matlab에에 원시 데이터 파일에서 데이터를 가져옵니다. 다음 예제 테스트 데이터의 test_data.mat 파일을 더블 클릭하고 들어 오기 마법사에서 '마침'을 클릭합니다.
- interpolation2d.m matlab에 스크립트를 엽니 다.
- 일반 그리드를 정의하는 보간 것 이상메쉬를 변경하여 실행. 이 미래의 수치 모델링 (26, 27)에서 메시와 동일한 해상도를 확인하십시오. 이것은 코드의 '% 메쉬 정보'섹션에서 설정됩니다.
- interpolation2d.m 매트랩 스크립트를 실행합니다. 다음 단계는 코드에서 구현 및 명확성을 위해 여기에 나열되어 있습니다.
- 모든 HPB 압력 흔적을 시간 이동
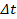 (수학 식 2). 원본 데이터에 대해 표시됩니다
(수학 식 2). 원본 데이터에 대해 표시됩니다 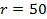 동일한 데이터를 타임 - 쉬프트도 5c에서와도 5b에 mm.
동일한 데이터를 타임 - 쉬프트도 5c에서와도 5b에 mm.
주 : 타임 시프트 보간 루틴이 성공적으로 임의의 주어진 시간에 충격 전면을 찾을 수 있도록 할 필요가있다. 이것은 본질적으로 모든 최대 압력이 정렬되도록 각각 방사 방향 어레이의 데이터를 정렬하는 것을 포함한다. - 반경을 계산,
 및 중앙 르,
및 중앙 르, 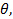 도 5a에 도시 된 바와 같이 그리드에 관심의 특정 지점에 대한.
도 5a에 도시 된 바와 같이 그리드에 관심의 특정 지점에 대한. - 현재 반경에 대한 관심 지점에 가장 가까운 두 HPB 배열에 1D 보간을 적용
 (에 대한
(에 대한 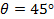 보간은을 사용
보간은을 사용 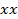 과
과 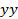 배열).
배열). - 에 기초하여,이 압력 사이의 선형 보간
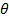 (다시에 대한
(다시에 대한 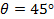 가중치가 50 %가 될 것이다
가중치가 50 %가 될 것이다 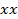 및 50 % 12eq30.jpg "/> 배열 산출 압력).
및 50 % 12eq30.jpg "/> 배열 산출 압력). - 부하를주는 격자 간격 (영역)에 의한 보간 압력을 곱하여 순간 부하를 계산합니다.
- 순간적인 임펄스를 얻기 위해 샘플링 시간 간격으로 부하를 곱한다.
- (총 충격을주는 순간적인 충동을 합산) 모든 위치와 시간에 대해 반복합니다.
- 충격 도착 시간 (도 5d)의 차 보간에 기초하여 각각의 위치에 대한 압력의 시간 이력을 타임 시프트.
- 모든 HPB 압력 흔적을 시간 이동
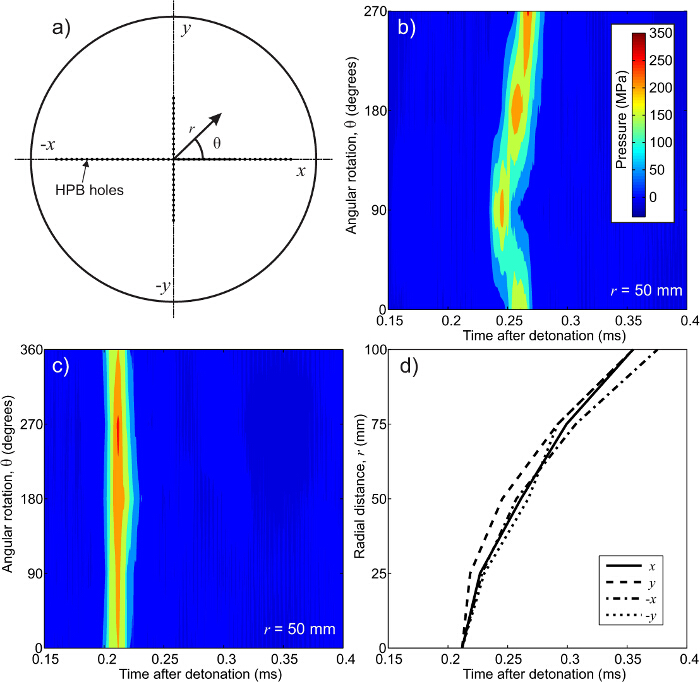
2D HPB 배열 그림 5. 보간 순서. 사용 (A) 로그인 규칙, (B) 원본 데이터 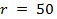 mm (C)의 시간 - 시프트 된 데이터412 / 53412eq36.jpg "/> mm, 각 반경 방향 16 (D) 도착 시간. 임의의 지점에서의 압력의 시간 이력을 모두 반경 방향 거리에 의존하고 막대 차원 어레이의 관심 지점이 위치한 사분면 블래스트 완벽 대칭 인 경우. (C)에 도시 된 바와 같이 쇼크 프론트 것을 알 수있다 (B)에서, 후 (B) 내의 압력은. 수직 라인을 형성하는 것에서 50mm의 위치에 도달
mm (C)의 시간 - 시프트 된 데이터412 / 53412eq36.jpg "/> mm, 각 반경 방향 16 (D) 도착 시간. 임의의 지점에서의 압력의 시간 이력을 모두 반경 방향 거리에 의존하고 막대 차원 어레이의 관심 지점이 위치한 사분면 블래스트 완벽 대칭 인 경우. (C)에 도시 된 바와 같이 쇼크 프론트 것을 알 수있다 (B)에서, 후 (B) 내의 압력은. 수직 라인을 형성하는 것에서 50mm의 위치에 도달 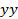 제 1 축.
제 1 축.
이 그림의 더 큰 버전을 보려면 여기를 클릭하십시오.
결과
실효 적 반응 강성 프레임을 제공 할 필요가있다. 현재는 수백 뉴턴 초 총 부과 된 충격 테스트에서 최소 편향에 저항해야합니다. 사용되는 경질 반응 프레임의 그림은 그림 1에 제시되어있다. 각 프레임에서 50mm 스틸 '수용체'판은 크로스 빔의 바닥에 던져되었습니다. 명시 적으로 요구되지 동안,이로드 셀 / 표적 판 쉽게 고정 가능 콘크리트 빔의면에 ?...
토론
저자 위에 설명 된 프로토콜을 사용하는 것이 홉 킨슨 압력 바의 배열을 사용하여 폭약에서 매우 다양한 로딩의 높은 정확도 측정치를 얻을 수 있음을 보여 주었다. 이산 감압 시간 이력을 보간 루틴을 사용하는 것이 가능 약술 수치 모델링 또는 모델의 출력을위한 검증 데이터로서로드 함수로서 직접 사용할 수있다 연속 충격 앞쪽으로 변형 될 수있다.
매립 된 전하를 사용?...
공개
The authors have nothing to disclose.
감사의 말
The authors wish to thank the Defence Science and Technology Laboratory for funding the published work.
자료
| Name | Company | Catalog Number | Comments |
| Load Cell | RDP | RSL0960 | This is only indicative, the exact load cell should be able to resolve the required loading |
| Steel target plate / HPBs | Garratts | Fabricated to order | |
| Strain gauge | Kyowa | KSP-2-120-E4 | To use with steel HPBs |
| Cyanoacrylate | Kyowa | CC-33-A | Check with manufacturer depending on mar material to be used |
| Digital Oscilloscope | TiePie | HS4 16-bit Handyscopes | 6 used in parallel in current testing |
| Leighton Buzzard sand | Garside sands | Garside 14/25 | Uniform silica sand |
참고문헌
- Esparza, E. Blast measurements and equivalency for spherical charges at small scaled distances. Int. J. Impact Eng. 4 (1), 23-40 (1986).
- Kingery, C. N., Bulmash, G. ARBRL-TR-02555. Airblast parameters from TNT spherical air burst and hemispherical surface burst. , (1984).
- Hyde, D. W. . Conventional weapons program (ConWep). , (1991).
- Randers-Pehrson, G., Bannister, K. A. ARL-TR-1310. Airblast loading model for DYNA2D and DYNA3D. , (1997).
- Neuberger, A., Peles, S., Rittel, D. Scaling the response of circular plates subjected to large and close-range spherical explosions. Part II: Buried charges. Int. J. Impact Eng. 34 (5), 874-882 (2007).
- Xu, S., et al. An inverse approach for pressure load identification. Int. J. Impact Eng. 37 (7), 865-877 (2010).
- Pickering, E. G., Chung Kim Yuen, S., Nurick, G. N., Haw, P. The response of quadrangular plates to buried charges. Int. J. Impact Eng. 49, 103-114 (2012).
- Bergeron, D. M., Trembley, J. E. Canadian research to characterize mine blast output. , (2000).
- Hlady, S. L. Effect of soil parameters on landmine blast. , (2004).
- Fourney, W. L., Leiste, U., Bonenberger, R., Goodings, D. J. Mechanism of loading on plates due to explosive detonation. Int. J. on Blasting and Fragmentation. 9 (4), 205-217 (2005).
- Anderson, C. E., Behner, T., Weiss, C. E. Mine blast loading experiments. Int. J. Impact Eng. 38 (8-9), 697-706 (2011).
- Fox, D. M., et al. The response of small scale rigid targets to shallow buried explosive detonations. Int. J. Impact Eng. 38 (11), 882-891 (2011).
- Ehrgott, J. Q., Rhett, R. G., Akers, S. A., Rickman, D. D. Design and fabrication of an impulse measurement device to quantify the blast environment from a near-surface detonation in soil. Experimental Techniques. 35 (3), 51-62 (2011).
- Pope, D. J., Tyas, A. Use of hydrocode modelling techniques to predict loading parameters from free air hemispherical explosive charges. , (2002).
- Clarke, S. D., et al. Repeatability of buried charge testing. , (2014).
- Clarke, S. D., et al. A large scale experimental approach to the measurement of spatially and temporally localised loading from the detonation of shallow-buried explosives. Meas Sci Technol. 26, 015001 (2015).
- Hopkinson, B. A Method of Measuring the Pressure Produced in the Detonation of High Explosives or by the Impact of Bullets. Philos. Trans. R. Soc. (London) A. 213, 437-456 (1914).
- Rigby, S. E., Tyas, A., Fay, S. D., Clarke, S. D., Warren, J. A. Validation of semi-empirical blast pressure predictions for far field explosions - is there inherent variability in blast wave parameters?. , (2014).
- Rigby, S. E., Tyas, A., Bennett, T., Clarke, S. D., Fay, S. D. The negative phase of the blast load. Int. J. of Protective Structures. 5 (1), 1-20 (2014).
- Rigby, S. E., Fay, S. D., Tyas, A., Warren, J. A., Clarke, S. D. Angle of incidence effects on far-field positive and negative phase blast parameters. Int. J. of Protective Structures. 6 (1), 23-42 (2015).
- Tyas, A., Warren, J., Bennett, T., Fay, S. Prediction of clearing effects in far-field blast loading of finite targets. Shock Waves. 21 (2), 111-119 (2011).
- Tyas, A., Watson, A. J. A study of the effect of spatial variation of load in the pressure bar. Meas Sci Technol. 11 (11), 1539-1551 (2000).
- Tyas, A., Watson, A. J. An investigation of frequency domain dispersion correction of pressure bar signals. Int. J. Impact Eng. 25 (1), 87-101 (2001).
- NATO Standardisation Agency. Procedures for evaluating the protection level of logistic and light armoured vehicles. Allied Engineering Publication (AEP) 55. 2, (2011).
- Elgy, I. D., et al. . UK ministry of defence technical authority instructions for testing the protection level of vehicles against buried blast mines. , (2014).
- Clarke, S. D., et al. Finite element simulation of plates under non-uniform blast loads using a point-load method: Buried explosives. , (2015).
- Rigby, S. E., et al. Finite element simulation of plates under non-uniform blast loads using a point-load method: Blast wave clearing. , (2015).
- Hallquist, J. O. . LS-DYNA theory manual. , (2006).
- Fay, S. D., et al. Capturing the spatial and temporal variations in impulse from shallow buried charges. , (2013).
- Fay, S. D., et al. Measuring the spatial and temporal pressure variation from buried charges. , (2014).
재인쇄 및 허가
JoVE'article의 텍스트 или 그림을 다시 사용하시려면 허가 살펴보기
허가 살펴보기This article has been published
Video Coming Soon
Copyright © 2025 MyJoVE Corporation. 판권 소유