Explosão Quantificação Usando barras de pressão Hopkinson

Resumo

This protocol details the use of Hopkinson pressure bars to measure reflected blast loading from near-field explosive events. It is capable of interpolating a pressure-time history at any point on a reflective boundary and as such can be used to fully characterize the spatial and temporal variations in loading produced.

Resumo

Perto de campo de medição de carga explosão apresenta um problema para muitos tipos de sensores como eles devem suportar ambientes muito agressivos e ser capaz de medir pressões até muitas centenas de MPa. A este respeito, a simplicidade da barra de pressão de Hopkinson tem uma grande vantagem na medida em que, enquanto a extremidade de medição da barra de Hopkinson pode suportar e ser exposto a condições adversas, o aferidor de tensão montado para a barra pode ser afixada a uma certa distância. Isto permite que invólucros de protecção para ser utilizada que proteger o medidor de tensão, mas não interferir com a aquisição de medição. O uso de uma matriz de barras de pressão permite que as variações no tempo a pressão nos pontos discretos conhecidos a ser medido. Este artigo também descreve a rotina de interpolação utilizados para obter variações no tempo de pressão em locais instrumentado-un no plano de interesse. Atualmente, a técnica tem sido utilizada para medir a carga de explosivos de alta potência no ar livre e enterrado superficialmente em vários solos.

Introdução

Caracterizando a saída de cargas explosivas tem muitos benefícios, tanto militar (defesa contra enterrado dispositivos explosivos improvisados ​​em zonas de conflito atuais) e civis (concepção de componentes estruturais). Nos últimos tempos, este tema tem recebido atenção considerável. Grande parte do conhecimento reunido foi destinado à quantificação da produção de cargas para permitir a concepção de estruturas de protecção mais eficaz. O principal problema aqui é que, se as medições efectuadas não são de alta fidelidade, em seguida, os mecanismos de transferência de carga nestes acontecimentos explosivos permanecem obscuros. Isto por sua vez leva a problemas na validação de modelos numéricos que dependem dessas medições para validação.

O termo de campo próximo é usado para descrever blastos com distâncias dimensionado, Z, inferior a 1 m ~ / kg ^1/3, em que Z = R / W ^1/3, R é a distância desde o centro do explosivo, e W é a carga expressa em massacomo uma massa equivalente de TNT. Neste regime, o carregamento é normalmente caracterizada por extremamente elevada magnitude, temporalmente cargas não uniformes e altamente espacial. instrumentação robusta é, portanto, necessária para medir as pressões extremas associadas com o carregamento de campo próximo. No escalado distâncias Z <0,4 m / kg ^1/3, medições diretas dos parâmetros de explosão ou são inexistentes ou muito poucos ¹ e os dados preditivos semi-empíricos para esta faixa é baseada quase inteiramente em estudos paramétricos. Isso envolve o uso das previsões semi-empíricos dadas por Kingery e Bulmash ^2, que está fora do escopo pretendido pelo autor. Enquanto ferramentas com base nestas previsões ^3,4 permitir excelentes estimativas de primeira ordem de carregamento não capturar totalmente a mecânica de eventos de campo próximo, que são o foco da pesquisa atual.

Medições de campo próximo explosão tem nos últimos tempos focada na quantificação do output do pagamento de taxas enterrados. As metodologias empregadas variam de avaliar a deformação causada a um alvo estrutural ^5-7 para dirigir medição impulso global de ^8-13. Esses métodos fornecem informações valiosas para a validação de projetos de proteção do sistema, mas não são capazes de investigar plenamente os mecanismos de transferência de carga. O teste pode ser feito em ambas as escalas de laboratório (1/10 escala total), ou pelo próximo grande escala (> 1/4), com razões pragmáticas, tais como controle de profundidade de enterramento ou a assegurar nenhuma forma inerente da frente de choque é gerada pelo uso de detonadores em vez de encargos nuas ^14. Com taxas enterradas as condições do solo precisam ser altamente controlado para garantir a repetibilidade do teste ^15.

Independente do se a carga é colocada no ar livre ou é enterrado, a questão mais fundamental para medir a explosão resultante é assegurar a validade das medições feitas pela deplo instrumentaçãoyed. No aparelho de teste destinado ¹⁶ uma placa-alvo 'rígida' fixo é usado para proteger as barras de pressão Hopkinson ¹⁷ (HPBs), enquanto, ao mesmo tempo, assegurar que as extremidades das barras só pode gravar as pressões totalmente refletida. Os autores têm mostrado anteriormente que a medida da pressão refletida de uma meta rígida é mais preciso e repetível de incidente, ou medições de 'free-campo' ^18-20. A geometria desta placa é de tal forma que qualquer descarga de pressão gerado pela compensação ou de fluxo em torno da borda alvo ²¹ seria negligenciável. Este novo aparelho de teste foi construído em 1/4 escala. Neste controlo apertado escala sobre as condições de enterro e os explosivos pode ser assegurada, com o tamanho de carga escala de 5 kg escalados até 78 g, a uma profundidade de enterramento de 25 mm.

Protocolo

1. Quadro Reacção rígida

1. Determinar distância à escala em que o teste será realizado através da Equação 1, em que R é a distância desde o centro do explosivo, e W é a carga de massa expressa como uma massa equivalente de TNT.
   Z = R / W ^1/3 (1)
2. Calcule impulso máximo aproximado este acordo irá gerar através de modelagem numérica (ver Anexo A) ou ferramentas específicas, tais como ConWep ^3.
   Nota: O uso de ConWep ³ só é válida para jato de ar livre, se é necessária uma estimativa das pressões geradas pelas taxas enterrado a modelagem numérica mais avançado é necessário.
3. Verifique a carga estimada a partir da modelação não irá gerar deslocamentos no plano de mais do que 0,5 mm na placa alvo.
4. Aumentar a carga calculada por um fator de 10 para contabilizar imprecisões na modelagem e para adicionar flexibilidade para futuras testing.
5. Projetar uma estrutura de reacção rígida para ser capaz de resistir à carga máxima calculada ^16. Em um departamento de engenharia, realizar estes cálculos em casa; caso contrário, procurar os serviços de um engenheiro estrutural.
   1. Adquirir quadros de reação rígidas, contratar um empreiteiro especialista para fabricar e instalar os quadros para os desenhos do engenheiro estrutural.
6. Adquirir uma placa-alvo, contratar um fabricante de aço especialista.
   Note-se que a placa terá que ser montada sobre células de carga (se usado) e para que os furos (HPBs concebidos na secção 3) terão de ser perfurado através da placa antes da montagem.

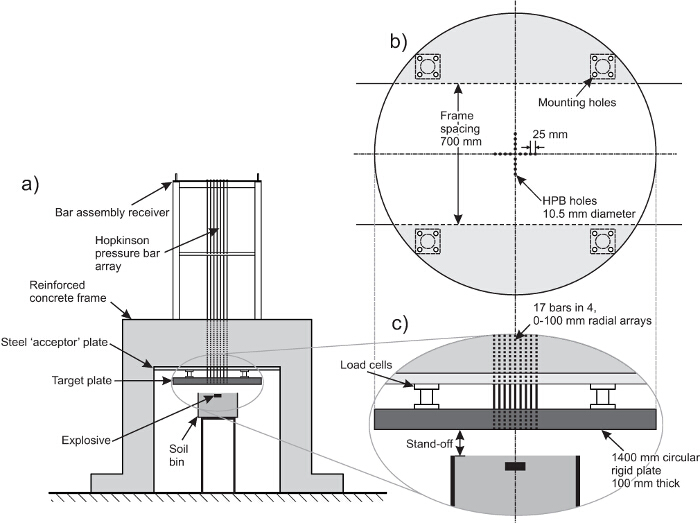
Figura 1. Esquema do quadro de teste. (A) arranjo geral, (B) Plano de placa alvo, (C) close-up vista da placa-alvo. Tbarras de pressão ele Hopkinson são pendurados a partir do receptor conjunto da barra de modo que fiquem alinhadas com a face da placa-alvo. Isso permite que a pressão totalmente reflectido actua sobre a placa alvo a ser gravado. Por favor clique aqui para ver uma versão maior desta figura.

Projeto celular 2. Coloque

1. Adquirir ou fabricar células de carga (se usado). Estes podem ser off-the-shelf universal (compressão / tensão) modelos da vasilha de bitola tensão ou construídos in-house usando seções de tubos de aço leve parede de espessura soldadas a montagem de placas com medidores de tensão apostas de formação de ponte de Wheatstone como mostrado na Figura 2.
2. Se as células de carga foram fabricadas em casa, enviá-los para um contratante externo para a calibração.

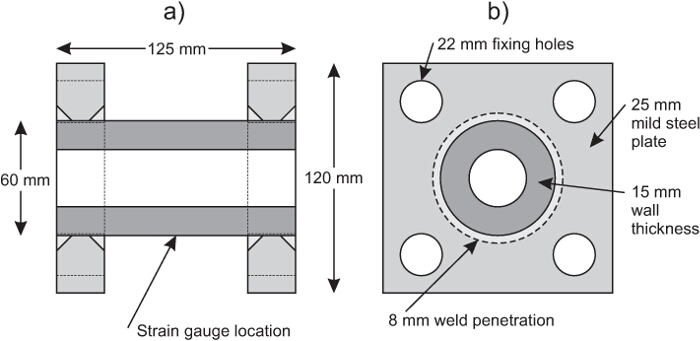
Figura 2. Diagrama do. (A) em alçado lateral, (B) em alçado da extremidade, internamente fabricado células de carga. O cilindro cinza escuro é um tubo de aço parede espessa que tensiona sob carga. Esta estirpe é gravada usando um único medidor de tensão como nenhuma rotação é experimentada durante o carregamento. A partir da calibração da célula de carga a tensão pode ser relacionada de volta para a tensão aplicada. Por favor clique aqui para ver uma versão maior desta figura.

3. Hopkinson Bar pressão de projeto

1. Determinar a duração de gravação, , Necessário para capturar o carregamento completo da explosão. A duração mínima necessária é o tempo gasto no modelo numérico (secção 1.2) para que a pressão voltar a zero, depois do pico de pressão inicial. Aqui, usar 1,2 mseg.
2. DeciDE sobre o material de escolha para os HPBs. Isso afeta a velocidade da onda elástica, 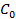, No bar, que é dada pela 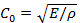Onde é o módulo de Young e 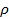é a densidade. Para a medição de um choque de alta pressão, utilizar materiais duros tais como aço; onde, como se um choque mais fraca é esperado, utilizar materiais menos rígidos, tais como uma liga de magnésio ou mesmo nylon.
3. Escolha da posição sobre o HPB que o medidor de tensão irá ser posicionado, sendo o mais próximo possível para o rosto carregado da HPB para minimizar a dispersão. Na configuração de corrente a espessura da placa do alvo e a maneabilidade necessária para ajustar as barras no lugar significava que os calibres só poderia ser instalado 250 mm a partir da cara carregada.
4. Calcular o HPcomprimento B necessário utilizando 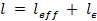, Onde 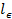é a distância a partir da face da HPB carregado para o medidor de tensão e (3,25 m).
5. Determinar necessário raio HPB ter largura de banda suficiente para capturar o evento usando: kHz, onde 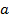HPB é o raio em mm ^22,23 (5 mm).
6. Decidir sobre a resolução espacial necessária para capturar a distribuição de pressão através da placa. Isto é, geralmente, tão próximo quanto possível, mantendo a integridade estrutural da placa do alvo. No trabalho atual, use 25 mm.
7. Faça furos na placa-alvo para montar os HPBs (isso pode ser parte do processo de fabricação). Um bom ajuste é necessário without os HPBs estejam em contacto com a placa. Aqui, utilizar tolerância 0,5 milímetros com 17 furos a ser perfurada em forma de cruz (Figura 1b).
8. Adquirir a HPBs (17), certificando-se de que as extremidades distais roscados para permitir a suspensão em que o receptor de barra (Figura 3A).

4. Configuração Experimental & Aquisição de Dados

Nota: Com a estrutura de reacção, a placa de destino, as células de carga e HPBs concebido e fabricado, a montagem pode começar como mostrado na Figura 1, e concebido na secção protocolo 1.

1. Fixar os extensómetros de semicondutores para HPBs (Figura 3B) e células de carga, utilizando cianoacrilato, tendo o cuidado de assegurar a continuidade da terra através de todo o cabeamento. Um exemplo de ponte de Wheatstone utilizado para os HPBs é mostrado na Figura 3C.
   1. Verifique se todos os cabos de terra estão ligados a garantir a continuidade da terra. aparelho de teste bem ligado à terra vai melhorarnomeadamente a qualidade do sinal.
2. Certifique-se de fiação é suficientemente longo para garantir que o osciloscópio é localizável em uma área livre de explosão (fiação blindado deve ser usado que tem largura de banda suficiente do sinal).
3. Montar a placa de destino para o quadro rígido de reacção, usando as células de carga opcionais, se presentes (Figura 1C).
4. Pendure HBPs do receptor de montagem de barra, passando o fim carregado através do orifício na placa-alvo. Pendurar as HPBs livremente de uma porca enroscada na extremidade distal roscada da HPB.
5. Garantir barras são verticais utilizando um nível de bolha (ajustar o receptor em conformidade).
6. Verifique os rostos dos HPBs são de nível com a placa-alvo, ajustando a porca em conformidade.
7. Definir a guarnição sobre a resistência variável no circuito de condicionamento (Figura 3C) para manter a tensão dentro dos limites de osciloscópio durante o teste. Fazer isso através de tentativa e erro, com o objetivo de definir o fora de equilíbrio para cada canalcomo pode ser visto no visor digital, nas caixas do amplificador para zero.
8. Ligue a saída de calibre amplificado para um osciloscópio digital adequado. Configurar a ter uma frequência de amostragem (1,56 MHz), a duração da gravação (28,7 ms) com uma duração pré-disparador de 3,3 ms.
   1. Definir a gravação para disparar quando a tensão no canal de quebra de fio (que é em si conectado ao osciloscópio) excede um "out-janela". tensão de registro para cada medidor ligado (22 no total, 17 HPBs, 4 células de carga eo fio break) e tempo.

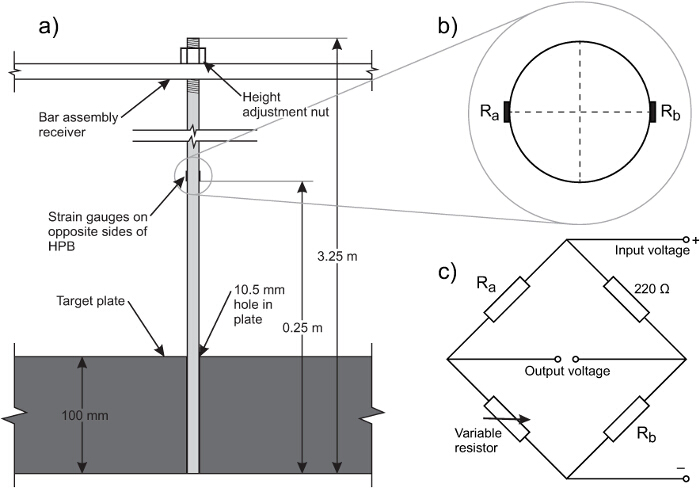
Figura 3. (A) Diagrama de uma HPB montado na placa do alvo, a secção (B) através de HPB no local calibre, (C) circuito de ponte de Wheatstone exemplo. Dois extensómetros são usados ​​na ponte de Wheatstone e de modo que a dobragem da barra de Hopkinson é Cancelled fora. Por favor clique aqui para ver uma versão maior desta figura.

5. preparação Explosivo

1. Decidir sobre a massa e carga explosiva stand-off para ser utilizado nos ensaios (100 g PE4 a 75 mm).
2. Decidir se as acusações devem ser detonada no ar livre ou dentro de outro meio (solo, água etc.). Para ar livre testa uma forma esférica carga é normalmente utilizada enquanto que com encargos enterrado o padrão é de 3: 1 cilindro de agachamento ^24,25.
3. Para os testes de ar livre:
   1. Suspender a carga abaixo da placa-alvo no stand-off correta (75 mm). Conseguir isso com uma tira de madeira fina ou colocando a carga em uma folha de polietileno.
   2. Coloque a carga de co-axialmente com a matriz de medição para assegurar as leituras válidas.
   3. Para os testes de ar livre usar um detonador elétrico, com o detonador de serem colocados no meio do caminho paraa carga a partir da base. Faça isso no último momento antes de disparar e quando o intervalo já foi feito seguro.
4. Para os testes enterrado:
   1. Fabricar um recipiente adequado para o meio. Para solos, o teste atual usa 1/4 recipientes escala ^23.
   2. Decidir sobre o tipo de solo a ser utilizado e as condições geotécnicas: teor de umidade e densidade seca do solo, ver ref ¹⁵ para mais detalhes..
   3. Decidir sobre a profundidade de enterramento para usar no ensaio. Este é geralmente 100 mm em um teste de grande escala, como os testes atuais são feitos em ¼ escala, isto significa uma profundidade de enterramento 25 mm.
   4. Misture o solo completamente usando um misturador de construção de tamanho adequado para atingir o teor de humidade alvo. Para areias o tempo de mistura necessário é de 10 min.
      1. Verificação do teor de humidade da mistura através da remoção de uma pequena quantidade e pesá-lo para calcular a massa total, 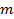. Secoo solo removido e re-pesar para calcular a massa de água, . teores de umidade geotécnicas são especificadas em termos de teor de umidade gravimétrica, .
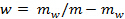      2. Se o teor de humidade está dentro da tolerância continuar, caso contrário, recombinar o solo. A tolerância de ± 0,05-0,1% foi alcançado no trabalho atual.
   5. Pesar o recipiente vazio do solo e calcular o volume para permitir o cálculo da densidade do solo, uma vez completa (passo 5.4.7).
   6. Compactar o solo em camadas, suficientemente fino para garantir a densidade alvo, garantindo que a massa de solo entra no recipiente é conhecido. Para Leighton Buzzard Areia ¹⁵ isso é feito em duas camadas.
   7. Uma vez que o recipiente está cheio, verificar que a densidade do solo dentro da tolerância é (± 0,2%). A densidade seca-alvo em todos os testes com Leighton Buzzard areia foi de 1,6Mg / m ^3. Calcular a densidade seca, usando 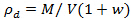, Onde ρ _d é a densidade em seco, M é a massa total do solo adicionado ao recipiente, V é o volume do recipiente do solo e W é o teor de humidade.
   8. Escavar um buraco pequeno ≈50 mm para permitir que a carga a ser colocado com a superfície superior à profundidade de enterro correcta (25 mm).
   9. Coloque um detonador não eléctrica para a base da carga, e escavar um canal adequado para o lado do recipiente, para assegurar que a superfície de topo do recipiente não é interrompido, uma vez que o solo é substituído.
   10. Coloque carga e detonador para o buraco escavado, verificando a profundidade de enterramento é correto. Voltar preencher o furo com o material escavado.

6. sequência Firing

Nota: há uma pequena quantidade de sobreposição com a secção protocolo 5 devido ao nature do teste. A sequência de disparo deve ter por objectivo minimizar o risco e só deve ser realizada por pessoal devidamente treinado.

1. Para os testes de ar livre:
   1. Organizar o apoio de carga abaixo da placa-alvo no stand-off correta (75 mm).
   2. Fechar o intervalo. Implantar sentinelas para garantir a gama é clara durante a queima.
   3. Coloque carga sobre a co-axial de apoio para a instrumentação. Fixe o fio de pausa para o detonador, e coloque o detonador na carga.
2. Para os testes enterrado:
   1. Coloque recipiente solo de modo que a carga é colocada co-axial para array HPB.
   2. Fechar o intervalo. Implantar sentinelas para garantir a gama é clara durante a queima.
   3. Ligue o fio de ruptura, garantindo que é enrolado em torno da periferia da carga (o que dá um tempo mais repetível da detonação dos encargos enterrados).
3. Mova o ponto de disparar e confirmar a instrumentação está em execução.
4. Fornecer energia para a quebra de fio. Verifique com sentinelasé seguro para prosseguir com a queima.
5. Iniciado explosivos. Tornar a área de teste seguro.
6. Faça o download e backup de dados.
7. Re-aberto gama de teste.

7. interpolação numérica para uma matriz 1D HPB

1. Importe os dados dos arquivos de dados brutos em Matlab.
2. Time-shift todos os dados na direcção radial de modo que a pressão de pico para cada barra chega ao mesmo tempo que o pico de pressão da barra central, utilizando a Equação 2 (Figura 4B).
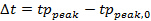   (2)
3. Interpolar a pressão em qualquer distância radial a partir da Figura 4B.
4. Traçar os tempos de chegada ( 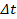) Utilizado para alinhar as pressões de pico e encaixar uma equação cúbica através dos dados (Figura 4C).
5. Time-shift os dados interpolados para ajustar os tempos de chegada, gênerosting uma frente de choque contínuo (Figura 4D).
6. Repita para cada conjunto individual de dados de teste.

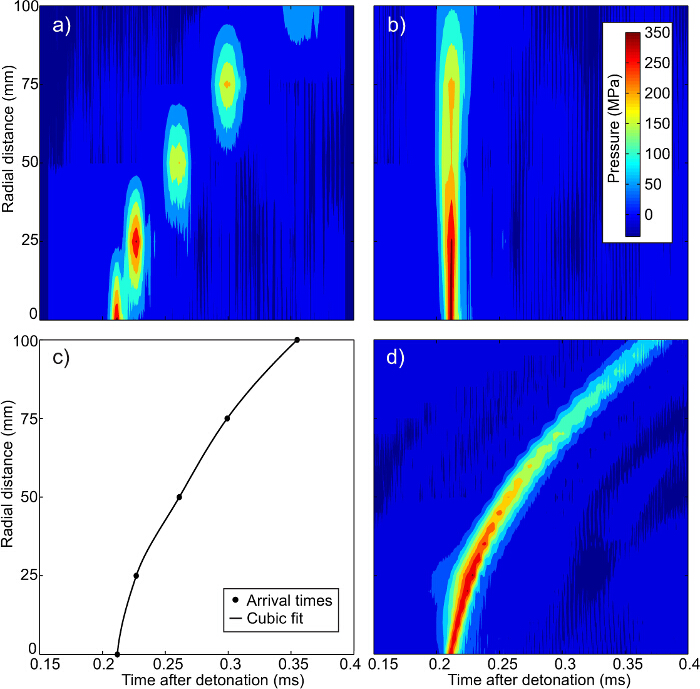
Figura 4. A sequência de interpolação para a matriz 1D HPB. (A) Dados originais, (B) dados deslocadas no tempo, (C) chocar tempos de chegada da frente, e os dados de tempo de pressão interpolados final de ¹⁶ (D). A natureza discreta das funções temporais pressão pode claramente ser visto em (A) com a existência de nenhuma continuidade entre os picos de pressão em cada um dos cinco locais de calibre. Quando alinhados por pico de pressão como em (B) a interpolação de pressão em qualquer distância radial (assumindo o mesmo tempo de chegada) é possível. Ao registrar a mudança de tempo necessário para alinhar as pressões de pico o tempo de chegada da frente de choque pode ser calculado como shprópria em (C). Isso, então, permite que o tempo de chegada e história tempo a pressão deve ser calculada para qualquer distância radial ser interpolação da pressão da (B) e tempo de (C) dando a pressão final interpolados como visto em (D). Por favor clique aqui para ver uma maior versão desta figura.

8. interpolação numérica para uma matriz 2D HPB

Nota: O código usado para executar a interpolação em Matlab foi fornecido juntamente com um exemplo de arquivo de resultados que será referido nesta seção.

1. Importe os dados dos arquivos de dados brutos em Matlab. Para os dados de exemplo de teste, clique duas vezes no arquivo test_data.mat e clique em "Concluir" no Assistente de importação.
2. Abra o script Matlab interpolation2d.m.
3. Definir uma grade regular sobre a qual a interpolação serárodar mudando a malha. Garantir isso é a mesma resolução que as malhas de qualquer futuro ^26,27 modelagem numérica. Isso é definido na seção do código dos detalhes% malha '.
4. Execute o script Matlab interpolation2d.m. Observe as seguintes etapas são implementadas no código e são listadas aqui para maior clareza.
   1. Time-shift todos os vestígios de pressão HPB por 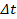(Equação 2). dados originais é mostrado para 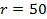mm na Figura 5B, com a mesma na Figura 5C deslocou-tempo dados.
      Nota: O deslocamento de tempo é necessário para permitir que a rotina de interpolação para localizar com sucesso a frente de choque num dado momento. Isso envolve, essencialmente, alinhando os dados para cada matriz radial assim todas as pressões máximas alinhar.
   2. Calcular o raio, E ang le, 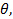para um determinado ponto de interesse sobre a grelha, como mostrado na Figura 5A.
   3. Aplique a interpolação 1D para as duas matrizes HPB mais próximos ao ponto de interesse para o raio atual (para 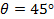a interpolação usaria o 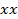e 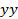matrizes).
   4. Interpolar linearmente entre as pressões 2 com base em 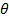(Mais uma vez para uma 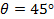o seu peso será 50% do 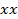e 50% do 12eq30.jpg "/> array pressões calculadas).
   5. Calcula-se a carga instantânea pela multiplicação da pressão interpolado pelo espaçamento da grade (área) a dar a carga.
   6. Multiplicar a carga por o passo de tempo de amostragem para obter o impulso instantânea.
   7. Repita o procedimento para todos os locais e horários (somando o impulso instantânea para dar o impulso total).
   8. Tempo diferido a evolução temporal da pressão para cada local com base no interpolação cúbico de chegada a hora de choque (Figura 5D).

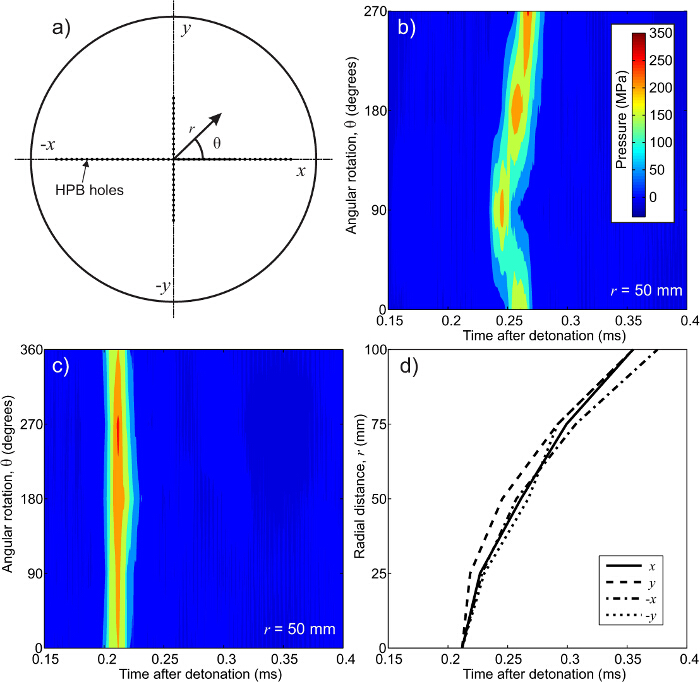
Figura 5. A sequência de interpolação para a matriz 2D HPB. Convenções de sinal (A) utilizados, (B) de dados original 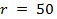mm, (c) dados deslocadas no tempo412 / 53412eq36.jpg "/> mm e horários de chegada (D) para cada sentido radial ^16. Para uma matriz 2D de bares a evolução temporal da pressão em qualquer ponto é dependente tanto distância radial e que quadrante o ponto de interesse está localizado . Se a explosão foram perfeitamente simétrica, em seguida, as pressões em (B) que formam linhas verticais como mostrado em (C). em (B), pode ser visto que a frente de choque atinge a localização é 50 milímetros sobre 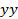primeiro eixo.
Por favor clique aqui para ver uma versão maior desta figura.

Resultados

Um quadro de reação efetivamente rígida deve ser fornecida. No actual testar um impulso Comunicados total de várias centenas de Newton-segundos necessitam de ser resistido com uma deflexão mínima. Uma ilustração da estrutura de reacção rígida utilizada é dada na Figura 1. Em cada quadro de um aço placa 50 mm »aceitador 'foi molde para a base das vigas transversais. Embora não explicitamente exigida, este permite a fácil fixação do células de carga ...

Discussão

Usando o protocolo acima delineado, os autores demonstraram que é possível obter medições de alta fidelidade da carga altamente variando de uma carga explosiva, usando uma matriz de barras de pressão Hopkinson. Utilizando a rotina de interpolação delineou as variações no tempo das pressões discretas pode ser transformado em uma frente de choque contínuo que é utilizável diretamente como a função de carregamento na modelagem numérica ou como dados de validação para a produção de tais modelos.

Materiais

Name	Company	Catalog Number	Comments
Load Cell	RDP	RSL0960	This is only indicative, the exact load cell should be able to resolve the required loading
Steel target plate / HPBs	Garratts		Fabricated to order
Strain gauge	Kyowa	KSP-2-120-E4	To use with steel HPBs
Cyanoacrylate	Kyowa	CC-33-A	Check with manufacturer depending on mar material to be used
Digital Oscilloscope	TiePie	HS4 16-bit Handyscopes	6 used in parallel in current testing
Leighton Buzzard sand	Garside sands	Garside 14/25	Uniform silica sand