Zum Anzeigen dieser Inhalte ist ein JoVE-Abonnement erforderlich. Melden Sie sich an oder starten Sie Ihre kostenlose Testversion.
Method Article
Experimentelle Methoden zur Erforschung der menschlichen Posturalkontrolle
In diesem Artikel
Zusammenfassung
Dieser Artikel stellt einen experimentellen/analytischen Rahmen zur Untersuchung der menschlichen Haltungskontrolle vor. Das Protokoll bietet Schritt-für-Schritt-Verfahren für die Durchführung von Standexperimenten, die Messung von Körperkinematik und Kinetiksignale und die Analyse der Ergebnisse, um Einblicke in die Mechanismen zu geben, die der menschlichen Haltungskontrolle zugrunde liegen.
Zusammenfassung
Viele Komponenten des Nerven- und Bewegungsapparates wirken gemeinsam, um eine stabile, aufrechte menschliche Haltung zu erreichen. Kontrollierte Experimente, begleitet von geeigneten mathematischen Methoden, sind erforderlich, um die Rolle der verschiedenen Subsysteme zu verstehen, die an der menschlichen Haltungskontrolle beteiligt sind. Dieser Artikel beschreibt ein Protokoll für die Durchführung von gestörten stehenden Experimenten, die Erfassung experimenteller Daten und die Durchführung der nachfolgenden mathematischen Analyse mit dem Ziel, die Rolle des Bewegungsapparates und der zentralen Kontrolle im Menschlichen zu verstehen. aufrechte Haltung. Die Ergebnisse dieser Methoden sind wichtig, weil sie Einblicke in die gesunde Gleichgewichtskontrolle geben, die Grundlage für das Verständnis der Ätiologie des gestörten Gleichgewichts bei Patienten und älteren Menschen bilden und bei der Gestaltung von Interventionen zur Verbesserung der Haltungskontrolle und Stabilität. Diese Methoden können verwendet werden, um die Rolle des somatosensorischen Systems, der intrinsischen Steifigkeit des Sprunggelenks und des visuellen Systems bei der Haltungskontrolle zu untersuchen, und können auch erweitert werden, um die Rolle des vestibulären Systems zu untersuchen. Die Methoden sind im Falle einer Knöchelstrategie anzuwenden, bei der sich der Körper in erster Linie um das Sprunggelenk bewegt und als invertiertes Pendel mit nur einem Glied gilt.
Einleitung
Die menschliche Haltungskontrolle wird durch komplexe Wechselwirkungen zwischen dem zentralen Nervensystem und dem Bewegungsapparat1realisiert. Der menschliche Körper im Stehen ist von Natur aus instabil, unterliegt einer Vielzahl von inneren (z.B. Atmung, Herzschlag) und äußeren (z.B. Schwerkraft) Störungen. Stabilität wird durch einen verteilten Regler mit zentralen, reflexiven und intrinsischen Komponenten erreicht (Abbildung 1).
Die Haltungskontrolle wird erreicht durch: einen aktiven Controller, der durch das Zentralnervensystem (ZNS) und das Rückenmark vermittelt wird, was die Muskelaktivierung verändert; und ein intrinsischer Steifigkeitsregler, der Gelenkbewegungen ohne Änderung der Muskelaktivierung widersteht (Abbildung 1). Der zentrale Controller verwendet sensorische Informationen, um absteigende Befehle zu erzeugen, die korrigierende Muskelkräfte erzeugen, um den Körper zu stabilisieren. Sensorische Informationen werden durch die visuellen, vestibulären und somatosensorischen Systeme transduziert. Insbesondere erzeugt das somatosensorische System Informationen über die Stützfläche und gelenkswinkel; Vision liefert Informationen über die Umwelt; und das vestibuläre System erzeugt Informationen über die Kopfwinkelgeschwindigkeit, die lineare Beschleunigung und die Ausrichtung in Bezug auf die Schwerkraft. Der zentrale, geschlossene Controller arbeitet mit langen Verzögerungen, die destabilisierend sein können2. Das zweite Element des aktiven Reglers ist die Reflexsteifigkeit, die bei kurzer Latenz Muskelaktivität erzeugt und Drehmomente erzeugt, die der Gelenkbewegung widerstehen.
Es ist eine Latenz mit beiden Komponenten des aktiven Controllers verbunden. folglich spielt die Gelenksteifigkeit, die ohne Verzögerung wirkt, eine wichtige Rolle bei der Haltungskontrolle3. Die intrinsische Steifigkeit wird durch passive viskoelastische Eigenschaften von kontrahierenden Muskeln, Weichteilen und Trägheitseigenschaften der Gliedmaßen erzeugt, die widerstandsive Drehmomente sofort als Reaktion auf jede Gelenkbewegung erzeugt4. Die Rolle der Gelenksteifigkeit (intrinsische und Reflexsteifigkeit) bei der Haltungskontrolle ist nicht klar zu verstehen, da sie sich mit Denkbedingungen ändert, definiert durch Muskelaktivierung4,5,6 und Gelenkposition 4 , 7 , 8, die sich beide mit dem Körper schwanken, dem Stehen inhärent.
Die Identifizierung der Rollen des zentralen Reglers und der Gelenksteifigkeit bei der Haltungskontrolle ist wichtig, da sie die Grundlage für die Diagnose der Ätiologie von Gleichgewichtsbeeinträchtigungen bildet; die Gestaltung gezielter Interventionen für Patienten; Bewertung des Sturzrisikos; Entwicklung von Strategien zur Sturzprävention bei älteren Menschen; und das Design von Hilfsgeräten wie Orthesen und Prothesen. Es ist jedoch schwierig, da die verschiedenen Subsysteme zusammen wirken und nur die gesamte resultierende Körperkinematik, Gelenkdrehmomente und Muskelelektromyographie gemessen werden können.
Daher ist es wichtig, experimentelle und analytische Methoden zu entwickeln, die die messbaren Haltungsvariablen verwenden, um den Beitrag jedes Subsystems zu bewerten. Eine technische Schwierigkeit besteht darin, dass die Messung von Haltungsvariablen im geschlossenen Kreislauf erfolgt. Infolgedessen sind die Ein- und Ausgänge (Ursache und Wirkung) miteinander verknüpft. Folglich ist es notwendig, a) externe Störungen (als Eingänge) anzuwenden, um Haltungsreaktionen in Antworten (als Ausgänge) hervorzurufen, und b) spezialisierte mathematische Methoden anzuwenden, um Systemmodelle zu identifizieren und Ursache und Wirkung zu entwirren9.
Der vorliegende Artikel konzentriert sich auf die Haltungskontrolle, wenn eine Knöchelstrategie verwendet wird, d.h. wenn die Bewegungen in erster Linie über das Sprunggelenk auftreten. In diesem Zustand bewegen sich Oberkörper und untere Gliedmaßen zusammen, so dass der Körper als invertiertes Einzelglied pendel in sagittaler Ebene10modelliert werden kann. Die Knöchelstrategie wird verwendet, wenn die Stützfläche fest ist und die Störungen klein sind1,11.
In unserem Labor12wurde ein stehendes Gerät entwickelt, das in der Lage ist, geeignete mechanische (propriozeptive) und visuelle sensorische Störungen anzuwenden und die Körperkinematik, Kinetik und Muskelaktivitäten aufzuzeichnen. Das Gerät bietet die experimentelle Umgebung, die benötigt wird, um die Rolle der Knöchelsteifigkeit, zentrale Kontrollmechanismen und ihre Wechselwirkungen zu untersuchen, indem posturale Reaktionen mit visuellen oder/und somatosensorischen Reizen erzeugt werden. Es ist auch möglich, das Gerät zu erweitern, um die Rolle des vestibulären Systems durch die Anwendung der direkten elektrischen Stimulation auf die Mastoid-Prozesse zu untersuchen, die ein Gefühl der Kopfgeschwindigkeit erzeugen und haltungsreaktionen evozieren können12,13 .
Andere haben auch ähnliche Geräte entwickelt, um menschliche Haltungssteuerung zu studieren, wo lineare Piezo elektrische Aktuatoren11, rotierende Elektromotoren14,15und lineare elektrische Motoren16,17 , 18 wurden verwendet, um mechanische Störungen auf knöchelim Stehen anzuwenden. Komplexere Geräte wurden auch entwickelt, um Multi-Segment-Haltungskontrolle zu studieren, wo es möglich ist, mehrere Störungen auf Knöchel- und Hüftgelenke gleichzeitig anzuwenden19,20.
Stehgerät
Zwei servogesteuerte elektrohydraulische Drehantriebe bewegen zwei Pedale, um kontrollierte Störungen der Knöchelposition anzuwenden. Die Aktuatoren können große Drehmomente (>500 Nm) erzeugen, die für die Haltungssteuerung benötigt werden; dies ist besonders wichtig in Fällen wie vorwärts schlank, wo das Körperzentrum der Masse ist weit (vorder) von Knöchel-Achse der Rotation, was zu großen Werten des Knöcheldrehmoments für die Haltungskontrolle.
Jeder Drehantrieb wird über ein separates proportionales Servoventil gesteuert, das pedalpositionsrückmeldungn, gemessen durch ein Hochleistungspotentiometer an der Aktorwelle (Materialtabelle). Der Controller wird über ein MATLAB-basiertes xPC-Echtzeit-Digitalsignalverarbeitungssystem implementiert. Der Aktuator/Servoventil zusammen haben eine Bandbreite von mehr als 40 Hz, viel größer als die Bandbreite des gesamten Haltungskontrollsystems, Knöchelgelenksteifigkeit und der Zentralsteuerung21.
Virtual-Reality-Gerät und -Umgebung
Ein Virtual-Reality-Headset (VR)(Tabelle der Materialien) wird verwendet, um die Vision zu stören. Das Headset enthält einen LCD-Bildschirm (dualAMOLED 3.6'' Bildschirm mit einer Auflösung von 1080 x 1200 Pixel pro Auge), der dem Benutzer eine stereoskopische Ansicht der an das Gerät gesendeten Medien bietet und eine dreidimensionale Tiefenwahrnehmung bietet. Die Bildwiederholrate beträgt 90 Hz, ausreichend, um den Benutzern einen soliden virtuellen Sinn zu bieten22. Das Sichtfeld des Bildschirms ist 110°, genug, um visuelle Störungen ähnlich wie reale Situationen zu erzeugen.
Das Headset verfolgt die Drehung des Kopfes des Benutzers und ändert die virtuelle Ansicht entsprechend, sodass der Benutzer vollständig in die virtuelle Umgebung eingetaucht ist. daher kann es das normale visuelle Feedback liefern; und es kann auch das Sehen stören, indem es das Gesichtsfeld in der sagittalen Ebene dreht.
Kinetische Messungen
Die vertikale Reaktionskraft wird durch vier Wägezellen gemessen, die zwischen zwei Platten unter dem Fuß eingeklemmt sind (Materialtabelle). Das Knöcheldrehmoment wird direkt an Drehmomentwandlern mit einer Leistung von 565 Nm und einer Torsionssteifigkeit von 104 kNm/rad gemessen; es kann auch indirekt von den vertikalen Kräften gemessen werden, die von den Wägezellen transduziert werden, unter Verwendung ihrer Abstände zur Knöchelachse der Rotation23, vorausgesetzt, dass die horizontalen Kräfte, die auf die Füße im Stehen angewendet werden, klein sind2,24. Der Druckmittelpunkt (COP) wird in der sagittalen Ebene gemessen, indem das Knöcheldrehmoment durch die gesamte vertikale Kraft dividiert wird, gemessen von den Wägezellen23.
Kinematische Messungen
Der Fußwinkel ist derselbe wie der Pedalwinkel, denn wenn eine Knöchelstrategie verwendet wird, bewegt sich der Fuß des Motivs mit dem Pedal. Der Schaftwinkel in Bezug auf die Vertikale wird indirekt aus der linearen Verschiebung des Schafts, gemessen durch einen Laser-Entfernungsmesser (Materialtabelle) mit einer Auflösung von 50 m und einer Bandbreite von 750 Hz25erhalten. Knöchelwinkel ist die Summe des Fuß- und Schaftwinkels. Der Körperwinkel in Bezug auf die vertikale wird indirekt aus der linearen Verschiebung des Mittelpunkts zwischen der linken und rechten hinteren iliac Stachel (PSIS) erhalten, gemessen mit einem Laser-Entfernungsmesser (Tabelle der Materialien) mit einer Auflösung von 100 m und Bandbreite von 750 Hz23. Kopfposition und Drehung werden in Bezug auf das globale Koordinatensystem der VR-Umgebung von den VR-System-Basisstationen gemessen, die zeitgesteuerte Infrarotimpulse (IR) mit 60 Impulsen pro Sekunde aussenden, die vom Headset-IR-Sensoren mit Submillimeter aufgenommen werden. genauigkeit.
Datenerfassung
Alle Signale werden mit einem Anti-Aliasing-Filter mit einer Eckfrequenz von 486,3 gefiltert und dann bei 1000 Hz mit leistungsstarkem 24-Bit/8-Kanal, simultaner Probenahme, dynamischer Signalerfassungskarten (Tabelle der Materialien) mit einer dynamischen Reichweite von 20 V.
Sicherheitsmechanismen
Sechs Sicherheitsmechanismen wurden in das stehende Gerät eingebaut, um Verletzungen von Personen zu verhindern; die Pedale werden separat gesteuert und stören sich nie gegenseitig. (1) Die Aktuatorwelle verfügt über eine Nocke, die mechanisch ein Ventil aktiviert, das den hydraulischen Druck abschaltet, wenn die Wellendrehung 20° von ihrer horizontalen Position überschreitet. (2) Zwei einstellbare mechanische Stopps begrenzen den Bewegungsbereich des Aktuators; diese werden vor jedem Experiment auf den Bewegungsumfang jedes Subjekts festgelegt. (3) Sowohl das Subjekt als auch der Experimentator halten einen Panikknopf; Durch Drücken der Taste wird die hydraulische Leistung von den Aktuatoren getrennt und sie lösen, so dass sie manuell bewegt werden können. (4) Handläufe auf beiden Seiten des Themas stehen zur Verfügung, um im Falle einer Instabilität Unterstützung zu leisten. (5) Der Betreff trägt einen Ganzkörpergurt(Materialtabelle), der an starren Querträgern in der Decke befestigt ist, um sie im Falle eines Sturzes zu stützen. Der Gurt ist schwach und stört nicht das normale Stehen, es sei denn, das Subjekt wird instabil, wo der Gurt verhindert, dass das Subjekt fällt. Im Falle des Sturzes werden die Pedalbewegungen manuell entweder vom Motiv, mit dem Panikknopf oder vom Experimentator gestoppt. (6) Die Servoventile stoppen die Drehung der Aktuatoren mit ausfallsicheren Mechanismen bei Unterbrechung der Stromversorgung.
Access restricted. Please log in or start a trial to view this content.
Protokoll
Alle experimentellen Methoden wurden von der McGill University Research Ethics Board genehmigt und Probanden unterzeichnen informierte Zustimmungen vor der Teilnahme.
1. Experimente
HINWEIS: Jedes Experiment umfasst die folgenden Schritte.
- Vortest
- Bereiten Sie einen bestimmten Überblick über alle durchzuführenden Versuche vor, und erstellen Sie eine Checkliste für die Datenerfassung.
- Geben Sie dem Betreffenden ein Zustimmungsformular mit allen notwendigen Informationen, bitten Sie ihn, es gründlich zu lesen, alle Fragen zu beantworten und dann das Formular unterschreiben zu lassen.
- Zeichnen Sie das Gewicht, die Größe und das Alter des Motivs auf.
- Themenvorbereitung
- Elektromyographie-Messung
- Verwenden Sie einzelne Differentialelektroden (Materialtabelle) mit einem Zwischenelektrodenabstand von 1 cm für die Messung der Elektromyographie (EMG) der Knöchelmuskulatur.
- Verwenden Sie einen Verstärker (Tabelle der Materialien) mit einer Gesamtverstärkung von 1000 und einer Bandbreite von 20 bis 2000 Hz.
- Um ein hohes Signal-Rausch-Verhältnis (SNR) und minimales Quergespräch zu gewährleisten, können Sie die Elektrodenaufsatzbereiche nach den Richtlinien des Seniam-Projekts26lokalisieren und markieren, wie unten: (1) für den medialen Gastrocnemius (MG), die markanteste Ausbuchtung der Muskel; (2) für den seitlichen Gastrocnemius (LG), 1/3 der Linie zwischen dem Kopf der Fibel und der Ferse; (3) für Soleus (SOL), 2/3 der Linie zwischen den medialen Kondylen des Oberschenkelknochens und dem medialen Malleolus; (4) für tibialis anterior (TA), 1/3 der Linie zwischen der Spitze der Fibel und der Spitze des medialen Malleolus.
- Rasieren Sie die markierten Bereiche mit einem Rasiermesser und reinigen Sie die Haut mit Alkohol. Lassen Sie die Haut gründlich trocknen.
- Rasieren Sie einen knöchernen Bereich auf der Patella für die Referenzelektrode, und reinigen Sie mit Alkohol.
- Lassen Sie das Thema in einer entspannten Supine-Position liegen.
- Legen Sie die Referenzelektrode auf den rasierten Bereich der Patella.
- Befestigen Sie die Elektroden nacheinander an den rasierten Bereichen der Muskeln, mit doppelseitigem Klebeband, wobei darauf geachtet wird, dass die Elektroden sicher an der Haut befestigt werden.
- Bitten Sie nach dem Platzieren jeder Elektrode den Betreffenden, eine plantarflexing/dorsiflexing Kontraktion gegen Widerstand durchzuführen, und untersuchen Sie die Wellenformen auf einem Oszilloskop, um sicherzustellen, dass das EMG-Signal einen hohen SNR hat. Wenn das Signal SNR schlecht ist, bewegen Sie die Elektroden, bis eine Position mit einem hohen SNR gefunden ist.
- Stellen Sie sicher, dass die Bewegungen des Motivs nicht durch die EMG-Kabel behindert werden.
- Kinematische Messungen
- Befestigen Sie einen reflektierenden Marker am Schaft mit einem Gurt, der für die Shankwinkelmessung verwendet werden kann.
HINWEIS: Platzieren Sie den Schaftmarker so hoch wie möglich auf dem Schaft, um die größtmögliche lineare Verschiebung für eine bestimmte Drehung zu erzeugen, wodurch die Winkelauflösung verbessert wird. - Lassen Sie das Thema auf den Körpergurt legen.
- Befestigen Sie einen Reflexionsmarker an der Taille des Motivs mit einem Gurt, der für die Messung des Oberkörperwinkels verwendet werden soll. Stellen Sie sicher, dass der reflektierende Taillenmarker in der Mitte zwischen dem linken und rechten PSIS platziert wird und dass die Kleidung des Motivs die reflektierende Oberfläche der Taille nicht bedeckt.
- Lassen Sie das Thema auf den stehenden Apparat zu bekommen.
- Passen Sie die Fußposition des Motivs an, um die seitlichen und medialen Malleoli jedes Beins an der Drehachse des Pedals auszurichten.
- Umreißen Sie die Fußpositionen des Motivs mit einem Marker und weisen Sie sie an, ihre Füße während der Experimente an den gleichen Stellen zu halten. Dadurch wird sichergestellt, dass die Drehachsen der Knöchel und Aktoren während der Experimente ausgerichtet bleiben.
- Passen Sie die vertikale Position der Laser-Entfernungsmesser so an, dass sie auf die Mitte der reflektierenden Marker zeigen. Passen Sie den horizontalen Abstand zwischen dem Laser-Entfernungsmesser und den reflektierenden Markern so an, dass die Entfernungsfinder im mittleren Bereich arbeiten und im stillen Stehen nicht sättigen.
- Lassen Sie das Motiv um den Knöchel nach vorne und rückwärts lehnen und sicherstellen, dass die Laser in ihrem Arbeitsbereich bleiben.
- Messen Sie die Höhe der Laser-Entfernungsmesser in Bezug auf die Knöchelachse der Rotation.
HINWEIS: Diese Höhen werden verwendet, um lineare Verschiebungen in Winkel umzuwandeln.
- Befestigen Sie einen reflektierenden Marker am Schaft mit einem Gurt, der für die Shankwinkelmessung verwendet werden kann.
- Experimentelle Protokolle
- Informieren Sie das Thema darüber, was sie für jede Versuchsbedingung erwartet.
- Weisen Sie das Subjekt an, still mit den Händen an der Seite zu stehen, während es nach vorne schaut, und ihr Gleichgewicht zu wahren, wie sie es tun, wenn es den realen Störungen gegenübersteht.
- Bei gestörten Versuchen beginnen Sie die Störung und lassen Sie das Subjekt sich daran anpassen.
- Starten Sie die Datenerfassung, sobald der Betreff ein stabiles Verhalten festgestellt hat.
- Geben Sie dem Betreffenden nach jeder Studie eine ausreichende Ruhezeit, um Ermüdung zu vermeiden. Kommunizieren Sie mit ihnen, um zu sehen, ob sie mehr Zeit benötigen.
- Führen Sie die folgenden Tests durch.
- Führen Sie für den Gerätetest einen 2-min-Test durch, um die Sensordaten 2 h vor der Ankunft des Probanden zu untersuchen. Suchen Sie in den aufgezeichneten Sensordaten nach unregelmäßig großen Geräuschen oder Offsets. Wenn es Probleme gibt, lösen Sie sie, bevor das Thema eintrifft.
- Für leises Stehen, führen Sie eine 2-min ruhige Standprüfung ohne Störungen durch.
HINWEIS: Diese Studie bietet eine Referenz, die erforderlich ist, um zu bestimmen, ob/wie sich Haltungsvariablen als Reaktion auf Störungen ändern. - Für gestörte Experimente führen Sie die Störung aus und erfassen Sie Daten für 2 x 3 min. Tragen Sie Pedalstörungen auf, wenn das Ziel darin besteht, die Rolle des somatosensorischen Systems/Knöchelsteifigkeit im Stehen zu untersuchen. Wenden Sie visuelle Störungen an, wenn das Ziel darin besteht, die Rolle des Sehens bei der Haltungskontrolle zu untersuchen. Wenden Sie visuelle und Pedalstörungen gleichzeitig an, wenn das Ziel darin besteht, die Wechselwirkung der beiden Systeme in der Haltungskontrolle zu untersuchen.
HINWEIS: Pedalstörungen werden als Drehung der stehenden Gerätepedale angewendet. In ähnlicher Weise werden visuelle Störungen angewendet, indem das virtuelle Gesichtsfeld mithilfe des VR-Headsets rotiert wird. Der Winkel des Pedal-/Gesichtsfeldes folgt einem Signal, das je nach Studienziel ausgewählt wird. Der Diskussionsabschnitt enthält Einzelheiten zu den Störungsarten, die für die Untersuchung der Haltungskontrolle verwendet werden, und die Vorzüge jeder Störung.
- Führen Sie mindestens 3 Versuche für jede spezifische Störung durch.
ANMERKUNG: Es werden mehrere Versuche durchgeführt, um die Zuverlässigkeit der Modelle bei der Analyse der gesammelten Daten zu gewährleisten. z.B. ist es möglich, die Modelle zu validieren. - Führen Sie die Versuche in einer zufälligen Reihenfolge durch, um sicherzustellen, dass die Probanden nicht lernen, auf eine bestimmte Störung zu reagieren; dies ermöglicht es auch, auf zeitveränderndes Verhalten zu überprüfen.
- Überprüfen Sie die Daten nach jeder Testversion visuell, um sicherzustellen, dass die erfassten Signale von hoher Qualität sind.
- Elektromyographie-Messung
2. Identifizierung der menschlichen Haltungskontrolle
- Nicht-parametrische Identifizierung des dynamischen Verhältnisses des Körperwinkels zu visuellen Störungen
- versuch
- Erwerben Sie visuell gestörte Versuche für 2 min gemäß den Schritten in den Abschnitten 1.1 und 1.2.
- Verwenden Sie ein Trapezsignal (TrapZ) mit einer Peak-to-Peak-Amplitude von 0,087 rad und einer Geschwindigkeit von 0,105 rad/s.
- Halten Sie die Pedalposition konstant im Nullwinkel.
- analyse
HINWEIS: Die Datenanalyse in den Abschnitten 2.1.2 und 2.2.2 wird mit MATLAB durchgeführt.- Dezimieren Sie den rohen Körperwinkel und visuelle Störungssignale (z. B. dass die höchste beobachtbare Frequenz 10 Hz ist), mit den folgenden Befehlen:

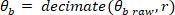
wo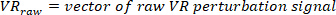
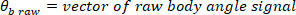
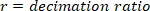
HINWEIS: Bei einer Abtastrate von 1 kHz muss das Dezimierungsverhältnis 50 betragen, um eine höchste Frequenz von 10 Hz zu haben. - Wählen Sie die niedrigste Zinshäufigkeit aus, die die Fensterlänge für die Leistungsschätzung bestimmt.
HINWEIS: Hier wird eine Mindestfrequenz von 0,1 Hz gewählt, so dass die Fensterlänge für die Leistungsschätzung 1/0,1 Hz = 10 s beträgt. Die Frequenzauflösung ist die gleiche wie die minimale Frequenz, und daher werden die Berechnungen für 0.1, 0.2, 0.3, ..., 10 Hz durchgeführt. - Wählen Sie den Fenstertyp und den Überlappungsgrad aus, um die Leistungsspektren zu finden.
HINWEIS: Bei einer Versuchslänge von 120 s ergeben 10 s Hanning-Fenster mit 50% Überlappung eine Mittelung von 23 Segmenten für die Leistungsspektrumschätzung. Da wir die Daten auf 20 Hz dezimiert haben, hat ein 10 s Fenster eine Länge von 200 Proben. - Verwenden
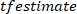 Sie die Funktion, um den Frequenzgang (FR) des Systems zu finden:
Sie die Funktion, um den Frequenzgang (FR) des Systems zu finden: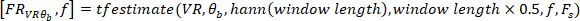
wo

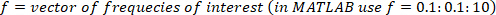
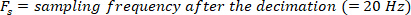
ANMERKUNG: Die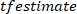 vorgestellte Funktion berechnet das Kreuzspektrum zwischen der dezimierten VR-Störung und
vorgestellte Funktion berechnet das Kreuzspektrum zwischen der dezimierten VR-Störung und 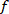 dem Körperwinkel in den von
dem Körperwinkel in den von 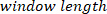 angegebenen Frequenzen mithilfe eines Hanning-Fensters mit der angegebenen Länge und der Anzahl der Überlappungen
angegebenen Frequenzen mithilfe eines Hanning-Fensters mit der angegebenen Länge und der Anzahl der Überlappungen 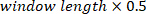 (d. h. 50% Überlappung). In ähnlicher Weise berechnet es das auto-Spektrum des VR-Eingangs. Anschließend berechnet es anhand des geschätzten Kreuzspektrums und des Auto-Spektrums die FR des Systems.
(d. h. 50% Überlappung). In ähnlicher Weise berechnet es das auto-Spektrum des VR-Eingangs. Anschließend berechnet es anhand des geschätzten Kreuzspektrums und des Auto-Spektrums die FR des Systems. - Suchen Sie die Verstärkung und Phase der geschätzten FR in Schritt 2.1.2.4 mit den folgenden Befehlen:
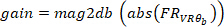
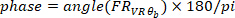
wo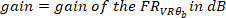
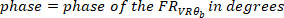
- Berechnen Sie die Kohärenzfunktion mit dem folgenden Befehl:
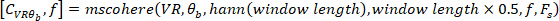
wo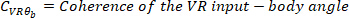
ANMERKUNG: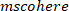 Die Funktion folgt
Die Funktion folgt 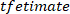 einem ähnlichen
einem ähnlichen 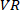 Verfahren, um die Kohärenz zwischen und
Verfahren, um die Kohärenz zwischen und 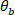 zu finden.
zu finden. - Zeichnen Sie die Verstärkung, Phase und Kohärenz als Funktion der Frequenz.
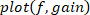
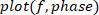
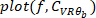
ANMERKUNG: Die vorgestellte Methode kann auf den Fall ausgedehnt werden, in dem sowohl visuelle als auch mechanische Störungen angewendet werden, bei denen eine MIMO-Identifikationsmethode mit mehreren Eingaben und mehreren Ausgängen (MIMO) verwendet werden muss9. Die Identifizierung kann auch mit der Subspace-Methode (die sich inhärent mit MIMO-Systemen befasst)27 oder mit parametrischen Übertragungsfunktionsmethoden wie MIMO Box-Jenkins28erfolgen. Sowohl Subspace als auch Box-Jenkins (und andere Methoden) werden in der MATLAB Systemidentifikations-Toolbox implementiert.
- Dezimieren Sie den rohen Körperwinkel und visuelle Störungssignale (z. B. dass die höchste beobachtbare Frequenz 10 Hz ist), mit den folgenden Befehlen:
- versuch
- Parametrische Identifizierung der intrinsischen Steifigkeit des Knöchels im Stehen
- versuch
- Führen Sie mechanisch gestörte Versuche für 2 min. Verwenden Sie eine pseudo-zufällige binäre Sequenzen (PRBS) Störung mit einer Peak-to-Peak-Amplitude von 0,02 rad und einem Schaltintervall von 200 ms. Stellen Sie sicher, dass der Mittlere Winkel des Pedals Null ist.
- analyse
- Unterscheiden Sie das Fußsignal einmal, um Fußgeschwindigkeit zu erhalten ( ,
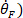 zweimal, um Fußbeschleunigung zu erhalten (
zweimal, um Fußbeschleunigung zu erhalten ( und dreimal, um seinen Ruck zu erhalten (
und dreimal, um seinen Ruck zu erhalten (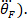 Ähnlich unterscheiden Sie das Drehmoment, um seine Geschwindigkeit und Beschleunigung zu erhalten, mit den folgenden befehlen:
Ähnlich unterscheiden Sie das Drehmoment, um seine Geschwindigkeit und Beschleunigung zu erhalten, mit den folgenden befehlen: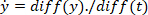
wo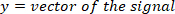
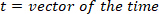
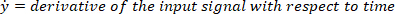
- Berechnen Sie die Position der lokalen Maxima und lokalen Minima der Fußgeschwindigkeit, um Impulse zu lokalisieren, mit dem folgenden Befehl:
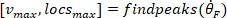
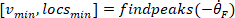
wo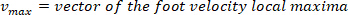
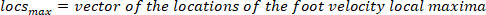
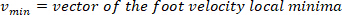
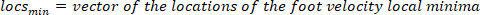
HINWEIS: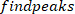 Funktion findet alle lokalen Maxima (positive Fußgeschwindigkeit) und ihre Positionen. Um die lokale Minima zu finden, wird die gleiche Funktion verwendet, aber das Zeichen der Fußwinkelgeschwindigkeit muss umgekehrt werden.
Funktion findet alle lokalen Maxima (positive Fußgeschwindigkeit) und ihre Positionen. Um die lokale Minima zu finden, wird die gleiche Funktion verwendet, aber das Zeichen der Fußwinkelgeschwindigkeit muss umgekehrt werden. - Entwerfen Sie einen8. Butterworth Tiefpassfilter mit einer Eckfrequenz von 50 Hz mit dem folgenden Befehl:
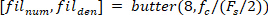

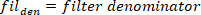
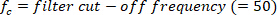
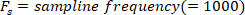
- Filtern Sie alle Signale mit Nullphasenverschiebung mit dem Butterworth-Filter:
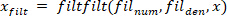
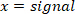
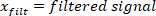
HINWEIS: "filtfilt" Funktion verursacht keine Verschiebung des gefilterten Signals. Verwenden Sie nicht die Funktion "Filter", da sie eine Verschiebunggeneriert. - Zeichnen Sie die Fußgeschwindigkeit, und finden Sie visuell eine Schätzung des Zeitraums zwischen dem Extrem a der Fußgeschwindigkeit und dem Beginn des Pulses (der erste Punkt mit Null-Fuß-Geschwindigkeit vor der Spitzengeschwindigkeit ist). Für die Störung in dieser Studie trat dieser Punkt 25 ms vor der Geschwindigkeitsextrema in Schritt 2.2.2.2 auf.
- Berechnen Sie für jeden Impuls das Knöchelhintergrunddrehmoment als Mittelwert des Knöcheldrehmoments von 25 ms vor Dem Start des Impulses, d.h. dem Mittelwert des Drehmoments im Segment, das 50 ms bis 25 ms vor der Geschwindigkeitsextrema beginnt. Tun Sie dies für den kth Puls mit einer positiven Geschwindigkeit mit dem folgenden Befehl:
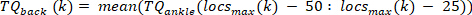
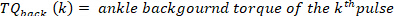
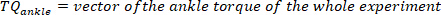
HINWEIS: Dies geschieht sowohl für maximale als auch für minimale Geschwindigkeiten (negative Fußgeschwindigkeit), die in Schritt 2.2.2.2 gefunden werden. - Finden Sie das Minimum und Maximum aller Hintergrunddrehmomente für alle Impulse mit dem folgenden Befehl:
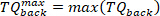
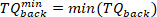
- Extrahieren Sie für jeden Impuls die Drehmomentdaten von 65 ms nach dem Impulsstart (als intrinsisches Drehmomentsegment) mit folgendem Befehl:
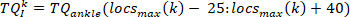
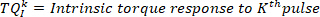
HINWEIS: Dies geschieht auch für die erste und zweite Ableitung des Knöcheldrehmoments (um die erste und zweite Ableitung des intrinsischen Drehmoments bereitzustellen), sowie für Fußwinkel, Fußgeschwindigkeit, Fußbeschleunigung und Fußruck. - Berechnen Sie die Änderung des k th-Initius-Drehmomentsegments anhand des Anfangswerts mit dem folgenden Befehl:
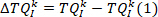
HINWEIS: Dies geschieht ähnlich für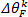 Fußwinkel zu erhalten.
Fußwinkel zu erhalten. - Teilen Sie den Drehmomentbereich (in Schritt 2.2.2.7) in 3 Nm breite Behälter und finden Sie die Impulse mit Hintergrunddrehmoment in jedem Behälter.
HINWEIS: Dies geschieht mit der"Find"-Funktion und der Indizierung. Es wird angenommen, dass die intrinsische Steifigkeit in jedem Behälter konstant ist, da sich das Knöchelhintergrunddrehmoment nicht wesentlich ändert. - Schätzen Sie die intrinsischen Steifigkeitsparameter des erweiterten intrinsischen Modells (EIM)29, für den jth bin mit den Impulsen in Gruppe j ( ).
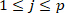
- Verketten Sie alle intrinsischen Drehmomentantworten im
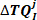 j th bin, um den Vektor zu bilden:
j th bin, um den Vektor zu bilden: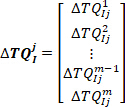
wobei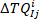 die i
die i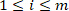 th ( ) intrinsische Drehmomentantwort in Gruppe j ist.
th ( ) intrinsische Drehmomentantwort in Gruppe j ist.
ANMERKUNG: In ähnlicher Weise verketten Fußwinkel, Geschwindigkeit und Beschleunigung sowie erste und zweite Ableitungen des intrinsischen Drehmoments derj. Gruppe, die in Schritt 2.2.2.11.2 verwendet werden sollen. - Setzen Sie den Fußwinkel, die Geschwindigkeit, die Beschleunigung und den Ruck sowie die erste und zweite Ableitung des Drehmoments der Gruppe j zusammen, um die Regressionsmatrix zu bilden:
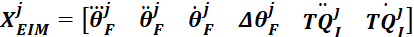
- Suchen Sie die intrinsischen Steifigkeitsparameter für die jth-Gruppe mithilfe des umgekehrten Schrägstrichs:
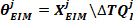
- Extrahieren Sie das
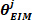 vierte Element der
vierte Element der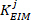 niederfrequenten intrinsischen Steifigkeit .
niederfrequenten intrinsischen Steifigkeit .
- Verketten Sie alle intrinsischen Drehmomentantworten im
- Führen Sie Schritte in Abschnitt 2.2.2.11 für alle Gruppen (Bins) aus, und schätzen Sie die entsprechende niederfrequente Intrinsische Steifigkeit.
- Teilen Sie alle geschätzten Niedrigfrequenzsteifigkeitswerte durch die kritische Steifigkeit des Motivs:
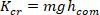
wobei m die Masse des Subjekts ist, g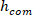 die Gravitationsbeschleunigung und die Höhe des Körpermittelpunkts über der Knöchelachse der Rotation, abgeleitet von anthropometrischen Daten30. Dies ergibt die normalisierte Steifigkeit (
die Gravitationsbeschleunigung und die Höhe des Körpermittelpunkts über der Knöchelachse der Rotation, abgeleitet von anthropometrischen Daten30. Dies ergibt die normalisierte Steifigkeit (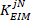 ).
). - Konvertieren Sie das Knöchelhintergrunddrehmoment in
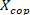 die COP-Position des Knöchelhintergrunds ( ), indem Sie die Knöchelhintergrunddrehmomente mit den entsprechenden gemessenen vertikalen Kräften dividieren.
die COP-Position des Knöchelhintergrunds ( ), indem Sie die Knöchelhintergrunddrehmomente mit den entsprechenden gemessenen vertikalen Kräften dividieren. - Plot
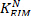 als Funktion des Druckzentrums.
als Funktion des Druckzentrums.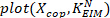
wo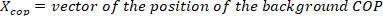
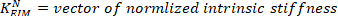
- Unterscheiden Sie das Fußsignal einmal, um Fußgeschwindigkeit zu erhalten ( ,
- versuch
Access restricted. Please log in or start a trial to view this content.
Ergebnisse
Pseudo-Random-Ternary-Sequenz (PRTS) und TrapZ-Signale
Abbildung 2A zeigt ein PRTS-Signal, das durch die Integration eines Pseudo-Zufallsgeschwindigkeitsprofils erzeugt wird. Für jede 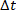 Probezeit kann die Signalgeschwindigkeit gleich Null sein oder einen vordefinierten positiven oder negativen Wert erfassen.
Probezeit kann die Signalgeschwindigkeit gleich Null sein oder einen vordefinierten positiven oder negativen Wert erfassen.
Access restricted. Please log in or start a trial to view this content.
Diskussion
Mehrere Schritte sind entscheidend bei der Durchführung dieser Experimente, um die menschliche Haltungskontrolle zu untersuchen. Diese Schritte sind mit der korrekten Messung der Signale verbunden und umfassen: 1) Korrekte Ausrichtung der Schaftknöchel-Drehungsachse an der der Pedale, für die korrekte Messung der Knöchelmomente. 2) Korrekte Einrichtung der Entfernungsmesser, um sicherzustellen, dass sie in ihrem Bereich arbeiten und während der Experimente nicht gesättigt sind. 3) Messung von EMG mit guter Qualitä...
Access restricted. Please log in or start a trial to view this content.
Offenlegungen
Die Autoren haben nichts zu verraten.
Danksagungen
Dieser Artikel wurde durch NPRP-Stipendium #6-463-2-189 von der Qatar National Research und MOP Grant #81280 von den Canadian Institutes of Health Research ermöglicht.
Access restricted. Please log in or start a trial to view this content.
Materialien
| Name | Company | Catalog Number | Comments |
| 5K potentiometer | Maurey | 112P19502 | Measures actuator shaft angle |
| 8 channel Bagnoli surface EMG amplifiers and electrodes | Delsys | Measures the EMG of ankle muscles | |
| AlienWare Laptop | Dell Inc. | P69F001-Rev. A02 | VR-ready PC laptop |
| Data acquisition card | National instruments | 4472 | Samples the analogue signals from the sensors |
| Directional valve | REXROTH | 4WMR10C3X | Bypasses the flow if the angle of actuator shaft goes beyond ±20° |
| Full body harness | Jelco | 740 | Protect the subjects from falling |
| Laser range finder | Micro-epsilon 1302-100 | 1507307 | Measures shank linear displacement |
| Laser range finder | Micro-epsilon 1302-200 | 1509074 | Measures body linear displacement |
| Load cell | Omega | LC302-100 | Measures vertical reaction forces |
| Proportional servo-valve | MOOG | D681-4718 | Controls the hydraulic flow to the rotary actuators |
| Rotary actuator | Rotac | 26R21VDEISFTFLGMTG | Applies mechanical perturbations |
| Torque transducer | Lebow | 2110-5k | Measures ankle torque |
| Virtual Environment Motion Trackers | HTC inc. | 1551984681 | Tracks the head motion |
| Virtual Reality Headset | HTC inc. | 1551984681 | Provides visual perturbations |
Referenzen
- Horak, F. B. Postural orientation and equilibrium: what do we need to know about neural control of balance to prevent falls? Age and Ageing. 35, 7-11 (2006).
- Morasso, P. G., Schieppati, M. Can muscle stiffness alone stabilize upright standing? Journal of Neurophysiology. 82 (3), 1622-1626 (1999).
- Kearney, R. E., Hunter, I. W. System identification of human joint dynamics. Critical Reviews in Biomedical Engineering. 18 (1), 55-87 (1990).
- Mirbagheri, M. M., Barbeau, H., Kearney, R. E. Intrinsic and reflex contributions to human ankle stiffness: variation with activation level and position. Experimental Brain Research. 135 (4), 423-436 (2000).
- Weiss, P. L., Hunter, I. W., Kearney, R. E. Human ankle joint stiffness over the full range of muscle activation levels. Journal of Biomechanics. 21 (7), 539-544 (1988).
- Golkar, M. A., Sobhani Tehrani, E., Kearney, R. E. Linear Parameter Varying Identification of Dynamic Joint Stiffness during Time-Varying Voluntary Contractions. Frontiers in Computational Neuroscience. 11, 35(2017).
- Weiss, P. L., Kearney, R. E., Hunter, I. W. Position dependence of ankle joint dynamics--I. Passive mechanics. Journal of Biomechanics. 19 (9), 727-735 (1986).
- Weiss, P. L., Kearney, R. E., Hunter, I. W. Position dependence of ankle joint dynamics--II. Active mechanics. Journal of Biomechanics. 19 (9), 737-751 (1986).
- Engelhart, D., Boonstra, T. A., Aarts, R. G. K. M., Schouten, A. C., van der Kooij, H. Comparison of closed-loop system identification techniques to quantify multi-joint human balance control. Annual Reviews in Control. 41, 58-70 (2016).
- Kiemel, T., Elahi, A. J., Jeka, J. J. Identification of the plant for upright stance in humans: multiple movement patterns from a single neural strategy. Journal of Neurophysiology. 100 (6), 3394-3406 (2008).
- Loram, I. D., Lakie, M. Direct measurement of human ankle stiffness during quiet standing: the intrinsic mechanical stiffness is insufficient for stability. Journal of Physiology-London. 545 (3), 1041-1053 (2002).
- Fitzpatrick, R., Burke, D., Gandevia, S. C. Loop gain of reflexes controlling human standing measured with the use of postural and vestibular disturbances. Journal of Neurophysiology. 76 (6), 3994-4008 (1996).
- Dakin, C. J., Son, G. M. L., Inglis, J. T., Blouin, J. S. Frequency response of human vestibular reflexes characterized by stochastic stimuli. The Journal of Physiology. 583 (3), 1117-1127 (2007).
- Vlutters, M., Boonstra, T. A., Schouten, A. C., vander Kooij, H. Direct measurement of the intrinsic ankle stiffness during standing. Journal of Biomechanics. 48 (7), 1258-1263 (2015).
- Casadio, M., Morasso, P. G., Sanguineti, V. Direct measurement of ankle stiffness during quiet standing: implications for control modelling and clinical application. Gait and Posture. 21 (4), 410-424 (2005).
- Sakanaka, T. E. Causes of Variation in Intrinsic Ankle Stiffness and the Consequences for Standing. , University of Birmingham. Doctoral dissertation (2017).
- Sakanaka, T. E., Lakie, M., Reynolds, R. F. Sway-dependent changes in standing ankle stiffness caused by muscle thixotropy. Journal of Physiology. 594 (3), 781-793 (2016).
- Peterka, R. J., Murchison, C. F., Parrington, L., Fino, P. C., King, L. A. Implementation of a Central Sensorimotor Integration Test for Characterization of Human Balance Control During Stance. Frontiers in Neurology. 9, 1045(2018).
- Engelhart, D., Schouten, A. C., Aarts, R. G., van der Kooij, H. Assessment of Multi-Joint Coordination and Adaptation in Standing Balance: A Novel Device and System Identification Technique. IEEE Transactions on Neural Systems and Rehabilitation Engineering. 23 (6), 973-982 (2015).
- Boonstra, T. A., Schouten, A. C., van der Kooij, H. Identification of the contribution of the ankle and hip joints to multi-segmental balance control. Journal of Neuroengineering and Rehabilitation. 10, 23(2013).
- Forster, S. M., Wagner, R., Kearney, R. E. A bilateral electro-hydraulic actuator system to measure dynamic ankle joint stiffness during upright human stance. Proceedings of the 25th Annual International Conference of the IEEE Engineering in Medicine and Biology Society. , Cancun, Mexico. (2003).
- Davis, J., Hsieh, Y. -H., Lee, H. -C. Humans perceive flicker artifacts at 500 Hz. Scientific Reports. 5, 7861(2015).
- Amiri, P., Kearney, R. E. Ankle intrinsic stiffness changes with postural sway. Journal of Biomechanics. 85, 50-58 (2019).
- van der Kooij, H., van Asseldonk, E., van der Helm, F. C. Comparison of different methods to identify and quantify balance control. Journal of Neuroscience Methods. 145 (1-2), 175-203 (2005).
- Amiri, P., MacLean, L. J., Kearney, R. E. Measurement of shank angle during stance using laser range finders. International Conference of the IEEE Engineering in Medicine and Biology. , Orlando, FL. (2016).
- The SENIAM project. , Available from: http://www.seniam.org/ (2019).
- Jalaleddini, K., Tehrani, E. S., Kearney, R. E. A Subspace Approach to the Structural Decomposition and Identification of Ankle Joint Dynamic Stiffness. IEEE Transactions on Biomedical Engineering. 64 (6), 1357-1368 (2017).
- Amiri, P., Kearney, R. E. A Closed-loop Method to Identify EMG-Ankle Torque Dynamic Relation in Human Balance Control. Conference Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society. , Berlin, Germany. (2019).
- Sobhani Tehrani, E., Jalaleddini, K., Kearney, R. E. Ankle Joint Intrinsic Dynamics is More Complex than a Mass-Spring-Damper Model. IEEE Transactions on Neural Systems and Rehabilitation Engineering. 25 (9), 1568-1580 (2017).
- NASA. Anthropometry and biomechanics. , Available from: http://msis.jsc.nasa.gov/sections/section03.htm (1995).
- Peterka, R. J. Sensorimotor integration in human postural control. Journal of Neurophysiology. 88 (3), 1097-1118 (2002).
- Amiri, P., Kearney, R. E. Ankle intrinsic stiffness is modulated by postural sway. Conference Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society. , Seogwipo, South Korea. (2017).
- Jeka, J. J., Allison, L. K., Kiemel, T. The dynamics of visual reweighting in healthy and fall-prone older adults. Journal of Motor Behavior. 42 (4), 197-208 (2010).
- Jilk, D. J., Safavynia, S. A., Ting, L. H. Contribution of vision to postural behaviors during continuous support-surface translations. Experimental Brain Research. 232 (1), 169-180 (2014).
- Winter, D. A., Patla, A. E., Prince, F., Ishac, M., Gielo-Perczak, K. Stiffness control of balance in quiet standing. Journal of Neurophysiology. 80 (3), 1211-1221 (1998).
- Pasma, J. H., Boonstra, T. A., van Kordelaar, J., Spyropoulou, V. V., Schouten, A. C. A Sensitivity Analysis of an Inverted Pendulum Balance Control Model. Frontiers in Computational Neuroscience. 11, 99(2017).
- Pasma, J. H., et al. Changes in sensory reweighting of proprioceptive information during standing balance with age and disease. Journal of Neurophysiology. 114 (6), 3220-3233 (2015).
- Pasma, J. H., et al. Impaired standing balance: The clinical need for closing the loop. Neuroscience. , 157-165 (2014).
- Engelhart, D., et al. Impaired Standing Balance in Elderly: A New Engineering Method Helps to Unravel Causes and Effects. Journal of the American Medical Directors Association. 15 (3), (2014).
- Pasma, J. H., Boonstra, T. A., Campfens, S. F., Schouten, A. C., Van der Kooij, H. Sensory reweighting of proprioceptive information of the left and right leg during human balance control. Journal of Neurophysiology. 108 (4), 1138-1148 (2012).
- Goodworth, A. D., Peterka, R. J. Sensorimotor integration for multisegmental frontal plane balance control in humans. Journal of Neurophysiology. 107 (1), 12-28 (2012).
- Kiemel, T., Zhang, Y., Jeka, J. J. Identification of neural feedback for upright stance in humans: stabilization rather than sway minimization. Journal of Neuroscience. 31 (42), 15144-15153 (2011).
- van der Kooij, H., van Asseldonk, E. H. F., Geelen, J., van Vugt, J. P. P., Bloem, B. R. Detecting asymmetries in balance control with system identification: first experimental results from Parkinson patients. Journal of Neural Transmission. 114 (10), 1333(2007).
- Fujisawa, N., et al. Human standing posture control system depending on adopted strategies. Medical and Biological Engineering and Computing. 43 (1), 107-114 (2005).
- Johansson, R., Magnusson, M., Fransson, P. A., Karlberg, M. Multi-stimulus multi-response posturography. Mathematical Biosciences. 174 (1), 41-59 (2001).
- Jeka, J., Oie, K., Schöner, G., Dijkstra, T., Henson, E. Position and Velocity Coupling of Postural Sway to Somatosensory Drive. Journal of Neurophysiology. 79 (4), 1661-1674 (1998).
- Peterka, R. J., Benolken, M. S. Role of somatosensory and vestibular cues in attenuating visually induced human postural sway. Experimental Brain Research. 105 (1), 101-110 (1995).
- Maki, B. E., Fernie, G. R. A system identification approach to balance testing. Progress in Brain Research. 76, 297-306 (1988).
- Johansson, R., Magnusson, M., Akesson, M. Identification of human postural dynamics. IEEE Transactions on Biomedical Engineering. 35 (10), 858-869 (1988).
- Maki, B. E., Holliday, P. J., Fernie, G. R. A Posture Control Model and Balance Test for the Prediction of Relative Postural Stability. IEEE Transactions on Biomedical Engineering. BME-34. 10 (10), 797-810 (1987).
- Werness, S. A., Anderson, D. J. Parametric analysis of dynamic postural responses. Biological Cybernetics. 51 (3), 155-168 (1984).
- Hwang, S., Agada, P., Kiemel, T., Jeka, J. J. Identification of the Unstable Human Postural Control System. Frontiers in Systems Neuroscience. 10, 22(2016).
- Ishida, A., Imai, S., Fukuoka, Y. Analysis of the posture control system under fixed and sway-referenced support conditions. IEEE Transactions on Biomedical Engineering. 44 (5), 331-336 (1997).
- Ishida, A., Miyazaki, S. Maximum likelihood identification of a posture control system. IEEE Transactions on Biomedical Engineering. 34 (1), 1-5 (1987).
- Ljung, L. System Identification: Theory for the User. , Prentice-Hall, Inc. Upper Saddle River, NJ. (1986).
- Forssell, U., Ljung, L. Closed-loop identification revisited. Automatica. 35 (7), 1215-1241 (1999).
- Horak, F. B., Nashner, L. M. Central programming of postural movements: adaptation to altered support-surface configurations. Journal of Neurophysiology. 55 (6), 1369-1381 (1986).
Access restricted. Please log in or start a trial to view this content.
Nachdrucke und Genehmigungen
Genehmigung beantragen, um den Text oder die Abbildungen dieses JoVE-Artikels zu verwenden
Genehmigung beantragenThis article has been published
Video Coming Soon
Copyright © 2025 MyJoVE Corporation. Alle Rechte vorbehalten