É necessária uma assinatura da JoVE para visualizar este conteúdo. Faça login ou comece sua avaliação gratuita.
Method Article
Métodos experimentais para estudar o controle postural humano
Neste Artigo
Resumo
Este artigo apresenta um quadro experimental/analítico para o estudo do controle postural humano. O protocolo fornece procedimentos passo-a-passo para a realização de experimentos permanentes, medindo cinemática corporal e sinais de cinética, e analisando os resultados para fornecer insights sobre os mecanismos subjacentes ao controle postural humano.
Resumo
Muitos componentes dos sistemas nervoso e musculoesquelético atuam em concerto para alcançar a postura humana estável e vertical. Experimentos controlados acompanhados de métodos matemáticos apropriados são necessários para compreender o papel dos diferentes subsistemas envolvidos no controle postural humano. Este artigo descreve um protocolo para a realização de experimentos permanentes perturbados, adquirindo dados experimentais e realizando a subsequente análise matemática, com o objetivo de compreender o papel do sistema musculoesquelético e do controle central em humanos postura vertical. Os resultados gerados por esses métodos são importantes, pois fornecem insights sobre o controle do equilíbrio saudável, formam a base para a compreensão da etiologia do comprometimento do equilíbrio em pacientes e idosos, e auxiliam na elaboração de intervenções para melhorar controle postural e estabilidade. Esses métodos podem ser utilizados para estudar o papel do sistema somatossensorial, rigidez intrínseca da articulação do tornozelo e sistema visual no controle postural, podendo também ser estendido para investigar o papel do sistema vestibular. Os métodos são para ser usado no caso de uma estratégia de tornozelo, onde o corpo se move principalmente sobre a articulação do tornozelo e é considerado um único link-pêndulo invertido.
Introdução
O controle postural humano é realizado através de interações complexas entre os sistemas nervoso central e músculo-esqueléticos1. O corpo humano em pé é inerentemente instável, sujeito a uma variedade de perturbações internas (por exemplo, respiração, batimento cardíaco) e externas (por exemplo, gravidade). A estabilidade é alcançada por um controlador distribuído com componentes centrais, reflexos e intrínsecos (Figura 1).
O controle postural é conseguido por: um controlador ativo, mediado pelo sistema nervoso central (CNS) e pela medula espinal, que muda a ativação do músculo; e um controlador de rigidez intrínseca que resiste à movimentação articular sem alteração na ativação muscular (Figura 1). O controlador central usa informações sensoriais para gerar comandos descendentes que produzem forças musculares corretivas para estabilizar o corpo. A informação sensorial é transada pelos sistemas Visual, vestibular e somatossensorial. Especificamente, o sistema somatossensorial gera informações sobre a superfície de suporte e os ângulos articulares; visão fornece informações sobre o meio ambiente; e o sistema vestibular gera informações sobre a velocidade angular da cabeça, aceleração linear e orientação em relação à gravidade. O controlador de circuito fechado central opera com longos atrasos que podem ser desestabilizadores2. O segundo elemento do controlador ativo é a rigidez reflexa, que gera atividade muscular com latência curta e produz torques resistentes ao movimento articular.
Há uma latência associada a ambos os componentes do controlador ativo; Consequentemente, a rigidez intrínseca articular, que atua sem demora, desempenha um papel importante no controle postural3. A rigidez intrínseca é gerada por Propriedades visco-elásticas passivas de músculos contratantes, tecidos moles e propriedades inerciais dos membros, o que gera torques resistivos instantaneamente em resposta a qualquer movimento articular4. O papel da rigidez articular (rigidez intrínseca e reflexa) no controle postural não é claramente compreendido, uma vez que se modifica com as condições de operação, definidas pela ativação muscular4,5,6 e posição articular 4. º , 7 anos de , 8, ambos os quais mudam com a oscilação do corpo, inerente à posição.
Identificar os papéis do controlador central e a rigidez articular no controle postural é importante, pois fornece a base para: diagnosticar a etiologia das deficiências de equilíbrio; a conceção de intervenções orientadas para os doentes; avaliação do risco de quedas; o desenvolvimento de estratégias de prevenção de quedas em idosos; e o design de dispositivos assistivos, como Ortopedia e próteses. Entretanto, é difícil, porque os subsistemas diferentes actuam junto e somente a cinemática resultante total do corpo, os torques da junção, e a electromiografia do músculo podem ser medidos.
Portanto, é imprescindível o desenvolvimento de métodos experimentais e analíticos que utilizem as variáveis posturais mensuráveis para avaliar a contribuição de cada subsistema. Uma dificuldade técnica é que a mensuração das variáveis posturais é feita em circuito fechado. Como resultado, as entradas e saídas (causa e efeito) estão inter-relacionadas. Conseqüentemente, é necessário: a) aplicar perturbações externas (como insumos) para evocar reações posturais em respostas (como saídas), e b) empregar métodos matemáticos especializados para identificar modelos de sistema e desentangular causa e efeito9.
O presente artigo centra-se no controle postural quando uma estratégia de tornozelo é usada, ou seja, quando os movimentos ocorrem principalmente sobre a articulação do tornozelo. Nesta condição, o corpo superior e os membros inferiores movem-se juntos, conseqüentemente, o corpo pode ser modelado como um pêndulo invertido de ligação única no plano sagital10. A estratégia do tornozelo é usada quando a superfície de suporte é firme e as perturbações são pequenas1,11.
Um instrumento ereto capaz de aplicar as perturbações sensoriais mecânicas (proprioceptive) e visuais apropriadas e registrar a cinemática do corpo, a cinética, e as atividades do músculo foram desenvolvidas em nosso laboratório12. O dispositivo fornece o ambiente experimental necessário para estudar o papel da rigidez do tornozelo, mecanismos de controle central e suas interações, gerando respostas posturais usando estímulos visuais ou/e somatossensoriais. Também é possível estender o dispositivo para estudar o papel do sistema vestibular pela aplicação da estimulação elétrica direta aos processos mastoides, que podem gerar uma sensação de velocidade da cabeça e evocar respostas posturais12,13 .
Outros também desenvolveram dispositivos semelhantes para estudar o controle postural humano, onde atuadores elétricos piezo lineares11, motores elétricos rotativos14,15e motores elétricos lineares16,17 , 18 foram utilizados para aplicar perturbações mecânicas ao tornozelo em pé. Dispositivos mais complexos também foram desenvolvidos para estudar o controle postural multisegmento, onde é possível aplicar múltiplas perturbações às articulações do tornozelo e quadril simultaneamente19,20.
Aparelho permanente
Dois atuadores rotativos eletrohidráulicos servo-controlados movem dois pedais para aplicar perturbações controladas da posição do tornozelo. Os atuadores podem gerar grandes torques (> 500 nanômetro) necessários para o controle postural; Isso é especialmente importante em casos como Lean Forward, onde o centro de massa do corpo é muito (anterior) do eixo do tornozelo de rotação, resultando em grandes valores de torque do tornozelo para controle postural.
Cada atuador giratório é controlado por uma válvula servo proporcional separada, usando o gabarito da posição do pedal, medido por um potenciómetro de capacidade elevada no eixo do atuador (tabela dos materiais). O controlador é implementado usando um sistema de processamento de sinal digital em tempo real baseado em MATLAB xPC. O atuador/servo-válvula juntos têm uma largura de banda de mais de 40 Hz, muito maior do que a largura de banda do sistema de controle postural global, rigidez da articulação do tornozelo, e o controlador central21.
Dispositivo de realidade virtual e ambiente
Um headset de realidade virtual (VR) (tabela de materiais) é usado para perturbar a visão. O auricular contém uma tela LCD (Dual AMOLED 3,6 ' ' tela com uma resolução de 1080 x 1200 pixels por olho) que fornece ao usuário uma visão estereoscópica dos meios de comunicação enviados para o dispositivo, oferecendo a percepção de profundidade tridimensional. A taxa de atualização é 90 Hz, suficiente para fornecer um sentido virtual sólido para os usuários22. O campo de visão da tela é 110 °, o suficiente para gerar perturbações visuais semelhantes às situações do mundo real.
O headset rastreia a rotação da cabeça do usuário e altera a exibição virtual de acordo para que o usuário esteja totalmente imerso no ambiente virtual; Conseqüentemente, pode fornecer o gabarito visual normal; e também pode perturbar a visão girando o campo visual no plano sagital.
Medições cinéticas
A força de reação vertical é medida por quatro células de carga, imprensadas entre duas placas abaixo do pé (tabela de materiais). O torque do tornozelo é medido diretamente por transdutores de torque com uma capacidade de 565 nm e uma rigidez torcional de 104 kNm/RAD; Ele também pode ser medido indiretamente a partir das forças verticais transcorridas pelas células de carga, usando suas distâncias para o eixo do tornozelo de rotação23, assumindo que as forças horizontais aplicadas aos pés em pé são pequenas2,24. O centro de pressão (COP) é medido no plano sagital dividindo o torque do tornozelo pela força vertical total, medida pelas células de carga23.
Medições cinemáticas
O ângulo do pé é o mesmo que o ângulo do pedal, porque quando uma estratégia do tornozelo é usada, o pé do assunto move-se com o pedal. O ângulo da pata com respeito ao vertical é obtido indiretamente do deslocamento linear do Shank, medido por um inventor da escala do laser (tabela dos materiais) com uma definição do μm 50 e da largura de faixa de 750 Hertz25. O ângulo do tornozelo é a soma dos ângulos do pé e da pata. O ângulo do corpo em relação ao vertical é obtido indiretamente do deslocamento linear do ponto médio entre as espinhas ilíacas superiores esquerdas e direitas (PSIS), medidos usando um localizador de laser (tabela de materiais) com uma resolução de 100 μm e largura de banda de 750 Hz23. A posição e a rotação da cabeça são medidas em relação ao sistema de coordenadas global do ambiente VR pelas estações base do sistema VR que emitem pulsos infravermelhos (IR) cronometrados em 60 pulsos por segundo que são captado pelos sensores de infravermelho do headset com submilímetro Precisão.
Aquisição de dados
Todos os sinais são filtrados com um filtro anti-aliasing com uma frequência de canto de 486,3 e, em seguida, amostrados em 1000 Hz com alto desempenho de 24 bits/8 canais, amostragem simultânea, cartões de aquisição de sinal dinâmico (tabela de materiais) com uma dinâmica intervalo de 20 V.
Mecanismos de segurança
Seis mecanismos de segurança foram incorporados no aparelho de pé para evitar lesões em indivíduos; os pedais são controlados separadamente e nunca interferem uns com os outros. (1) o eixo do atuador tem uma came, que ative mecanicamente uma válvula que desconecta a pressão hidráulica se a rotação do eixo excede ± 20 ° de sua posição horizontal. (2) duas paradas mecânicas ajustáveis limitam a amplitude de movimento do atuador; Estes são ajustados à escala de cada assunto do movimento antes de cada experimentação. (3) tanto o assunto eo experimentador segurar um botão de pânico; pressionando o botão desliga a energia hidráulica dos atuadores e faz com que eles fiquem soltos, para que eles possam ser movidos manualmente. (4) os corrimão situados em cada lado do assunto estão disponíveis para fornecer o apoio em caso da instabilidade. (5) o sujeito usa um arnês de corpo inteiro (tabela de materiais), anexado a barras transversais rígidas no teto para apoiá-los em caso de queda. O arnês é frouxo e não interfere com a posição normal, a menos que o sujeito se torne instável, onde o arnês impede que o sujeito caia. No caso de queda, os movimentos do pedal serão interrompidos manualmente quer pelo sujeito, usando o botão de pânico ou pelo experimentador. (6) as servo-válvulas param a rotação dos atuadores usando mecanismos à prova de falhas em caso da interrupção elétrica da fonte.
Access restricted. Please log in or start a trial to view this content.
Protocolo
Todos os métodos experimentais foram aprovados pelo Conselho de ética em pesquisa da Universidade McGill e os sujeitos assinam consenditos informados antes de participarem.
1. experiências
Observação: cada experimento envolve as seguintes etapas.
- Pré-teste
- Prepare um contorno definitivo de todos os ensaios a serem realizados e faça uma lista de verificação para a coleta de dados.
- Fornecer o assunto com um formulário de consentimento com todas as informações necessárias, pedir-lhes para lê-lo completamente, responder a quaisquer perguntas, e depois tê-los assinar o formulário.
- Registre o peso, a altura e a idade do sujeito.
- Preparação do assunto
- Medição de eletromiografia
- Use eletrodos diferenciais únicos (tabela de materiais) com uma distância entre eletrodos de 1 cm para a medição da eletromiografia (EMG) dos músculos do tornozelo.
- Use um amplificador (tabela de materiais) com um ganho total de 1000 e uma largura de banda de 20 − 2000 Hz.
- Para garantir uma alta relação sinal/ruído (SNR) e mínima conversa cruzada, localize e marque as áreas de fixação do eletrodo de acordo com as diretrizes fornecidas pelo projeto seniam26, como abaixo: (1) para o gastrocnêmio medial (mg), a protuberância mais proeminente do muscular (2) para o gastrocnêmio lateral (LG), 1/3 da linha entre a cabeça da fíbula e o calcanhar; (3) para o sóleo (SOL), 2/3 da linha entre os côndilos mediais do fêmur e o maléolo medial; (4) para tibial anterior (ta), 1/3 da linha entre a ponta da fíbula e a ponta do maléolo medial.
- Raspar as áreas marcadas com uma navalha e limpar a pele com álcool. Deixe a pele secar completamente.
- Raspar uma área óssea na patela para o eletrodo de referência, e limpar com álcool.
- Tenha o assunto deitado em uma posição supina relaxado.
- Coloque o eletrodo de referência na área raspada da patela.
- Anexar os eletrodos um por um para as áreas raspadas dos músculos, usando fita dupla face, tendo o cuidado de garantir que os eletrodos são fixados para a pele de forma segura.
- Depois de colocar cada eletrodo, peça ao sujeito que realize uma contração plantarflexing/dorsiflexing contra a resistência e examine as formas de onda em um osciloscópio para garantir que o sinal EMG tenha um SNR alto. Se o sinal SNR é pobre, mova os elétrodos até que uma posição com um SNR elevado esteja encontrada.
- Certifique-se de que os movimentos do sujeito não são prejudicado pelos cabos EMG.
- Medições cinemáticas
- Prenda um marcador reflexivo à haste com uma cinta, para ser usado para a medida do ângulo da pata.
Nota: Coloque o marcador da haste tão alto quanto possível na haste para gerar o maior deslocamento linear possível para uma determinada rotação, portanto, melhorando a resolução angular. - Tenha o assunto põr sobre o chicote de fios do corpo.
- Anexar um marcador de reflexão para a cintura do sujeito com uma cinta, para ser usado para a medição do ângulo do corpo superior. Assegure-se de que o marcador reflexivo da cintura esteja coloc no mid-point entre os PSISs esquerdos e direito e que a roupa do assunto não cobre a superfície reflexiva da cintura.
- Tenha o assunto começ no instrumento ereto.
- Ajuste a posição do pé do sujeito para alinhar os maléolos laterais e medial de cada perna ao eixo de rotação do pedal.
- Delinear as posições do pé do sujeito com um marcador e instruí-los a manter os pés nos mesmos locais durante os experimentos. Isso garante que os eixos de rotação dos tornozelos e atuadores permaneçam alinhados ao longo dos experimentos.
- Ajuste a posição vertical dos Finders da escala do laser para apontar ao centro dos marcadores reflexivos. Ajuste a distância horizontal entre o inventor da escala do laser e os marcadores reflexivos, de modo que os Finders da escala trabalhem em seu mid-range e não saturar durante a posição quieta.
- Tenha o assunto inclinar-se para a frente e para trás sobre o tornozelo e assegurar-se de que os lasers permaneçam dentro de sua escala de trabalho.
- Meça a altura dos Finders da escala do laser com respeito ao eixo de rotação do tornozelo.
Observação: essas alturas são usadas para converter deslocamentos lineares em ângulos.
- Prenda um marcador reflexivo à haste com uma cinta, para ser usado para a medida do ângulo da pata.
- Protocolos experimentais
- Informe o assunto do que esperar para cada condição experimental.
- Instrua o assunto a permanecer quietamente com as mãos no lado ao olhar para a frente, e para manter seu contrapeso como fazem, quando enfrentado as perturbações do mundo real.
- Para julgamentos perturbados, iniciar a perturbação e permitir que o sujeito se adaptar a ele.
- Iniciar a aquisição de dados uma vez que o assunto estabeleceu um comportamento estável.
- Forneça o assunto com período de descanso suficiente após cada experimentação para evitar a fatiga. Comunique-se com eles para ver se eles precisam de mais tempo.
- Realize as seguintes tentativas.
- Para o teste do instrumento, realize um teste de 2 min para examinar os dados do sensor 2 h antes da chegada do sujeito. Procure ruídos ou deslocamentos irregularmente grandes nos dados gravados do sensor. Se houver problemas, resolvê-los antes que o assunto chegue.
- Para a posição quieta, realize um teste ereto quieto de 2 min sem perturbações.
Nota: esta avaliação fornece uma referência, necessária para determinar se/como as variáveis posturais mudam em resposta a perturbações. - Para experimentos perturbados, execute a perturbação e adquira dados por 2 − 3 min. Aplique perturbações do pedal se o objetivo é investigar o papel da rigidez do sistema somatosensorial/tornozelo na posição. Aplicar perturbações visuais se o objetivo é examinar o papel da visão no controle postural. Aplique perturbações visuais e de pedal simultaneamente se o objetivo é examinar a interação dos dois sistemas no controle postural.
Nota: as perturbações do pedal são aplicadas como a rotação dos pedais do dispositivo ereto. Da mesma forma, as perturbações visuais são aplicadas girando o campo visual virtual, usando o headset VR. O ângulo do pedal/campo visual segue um sinal, selecionado de acordo com os objetivos do estudo. A seção de discussão fornece detalhes sobre os tipos de perturbação, utilizados para o estudo do controle postural e os méritos de cada perturbação.
- Realize um mínimo de 3 ensaios para cada perturbação específica.
Observação: vários testes são feitos para garantir a confiabilidade dos modelos ao executar a análise nos dados coletados; por exemplo, é possível cruzar validar os modelos. - Realize os ensaios em uma ordem aleatória para garantir que os sujeitos não aprendam a reagir a uma perturbação específica; Isso também torna possível verificar o comportamento de variação de tempo.
- Verifique os dados visualmente após cada teste para garantir que os sinais adquiridos são de alta qualidade.
- Medição de eletromiografia
2. identificação do controle postural humano
- Identificação não-paramétrica da relação dinâmica do ângulo do corpo com as perturbações visuais
- Experiência
- Adquira testes visualmente perturbados por 2 min de acordo com as etapas nas seções 1,1 e 1,2.
- Use um sinal trapezoidal (TrapZ) com uma amplitude Peak-to-Peak de 0, 87 RAD e uma velocidade de 0,105 rad/s.
- Segure a posição do pedal constante no ângulo zero.
- Análise
Nota: a análise dos dados nas secções 2.1.2 e 2.2.2 é efectuada utilizando o MATLAB.- Dizate o ângulo do corpo cru e os sinais de perturbação Visual (de tal forma que a maior frequência observável é de 10 Hz), utilizando os seguintes comandos:

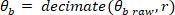
Onde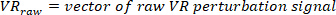
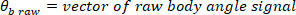
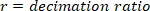
Nota: para uma taxa de amostragem de 1 kHz, a razão de decimação deve ser 50 para ter uma frequência mais alta de 10 Hz. - Escolha a menor frequência de juros, que determinará o comprimento da janela para estimativa de potência.
Nota: aqui, uma frequência mínima de 0,1 Hz é escolhida, de modo que o comprimento da janela para estimativa de potência é 1/0.1 Hz = 10 s. A resolução de frequência é a mesma que a frequência mínima e, portanto, os cálculos são feitos para 0,1, 0,2, 0,3,..., 10 Hz. - Escolha o tipo de janela e o grau de sobreposição para encontrar os espectros de potência.
Nota: para um período experimental de 120 s, 10 s janelas Hanning com 50% sobreposição resulta em média de 23 segmentos para estimativa de espectro de potência. Uma vez que dizimos os dados para 20 Hz, uma janela de 10 s tem um comprimento de 200 amostras. - Use a
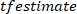 função para encontrar a resposta de frequência (FR) do sistema:
função para encontrar a resposta de frequência (FR) do sistema: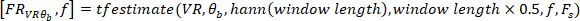
Onde

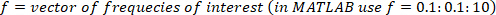
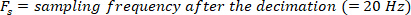
Nota: a função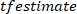 apresentada calcula o espectro cruzado entre a perturbação de VR dizreada e o ângulo do corpo nas frequências especificadas por
apresentada calcula o espectro cruzado entre a perturbação de VR dizreada e o ângulo do corpo nas frequências especificadas por 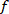 , usando uma janela de Hanning com o comprimento especificado
, usando uma janela de Hanning com o comprimento especificado 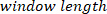 e o número de sobreposições igual a
e o número de sobreposições igual a 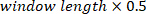 (ou seja, 50% de sobreposição). Da mesma forma, ele calcula o espectro automático da entrada VR. Em seguida, usando o espectro cruzado e o espectro automático estimados, ele calcula o FR do sistema.
(ou seja, 50% de sobreposição). Da mesma forma, ele calcula o espectro automático da entrada VR. Em seguida, usando o espectro cruzado e o espectro automático estimados, ele calcula o FR do sistema. - Encontre o ganho e a fase do FR estimado na etapa 2.1.2.4, usando os seguintes comandos:
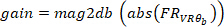
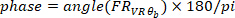
Onde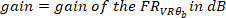
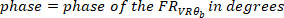
- Calcule a função de coerência utilizando o seguinte comando:
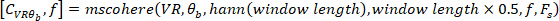
Onde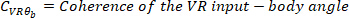
Nota: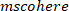 a função segue um procedimento semelhante
a função segue um procedimento semelhante 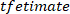 a encontrar a coerência entre
a encontrar a coerência entre 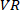 e
e 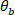 .
. - Plotar o ganho, a fase e a coerência em função da frequência.
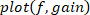
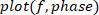
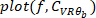
Nota: o método apresentado pode ser estendido para o caso em que as perturbações visuais e mecânicas são aplicadas, onde um método de identificação de múltiplas entradas e múltiplas saídas (MIMO) FR deve ser usado9. A identificação também pode ser feita usando o método subespacial (que inerentemente lida com sistemas MIMO)27 ou usando métodos de função de transferência paramétrica, como mimo Box-Jenkins28. Tanto o subespaço quanto o Box-Jenkins (e outros métodos) são implementados na caixa de ferramentas de identificação do sistema MATLAB.
- Dizate o ângulo do corpo cru e os sinais de perturbação Visual (de tal forma que a maior frequência observável é de 10 Hz), utilizando os seguintes comandos:
- Experiência
- Identificação paramétrica da rigidez intrínseca do tornozelo em pé
- Experiência
- Realize ensaios mecanicamente perturbados por 2 min. Use uma perturbação pseudoaleatória de sequências binárias (PRBS) com uma amplitude de pico a pico de 0, 2 RAD e um intervalo de comutação de 200 ms. Assegure-se de que o ângulo médio do pedal seja zero.
- Análise
- Diferencie o sinal do pé uma vez para obter
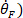 a velocidade do pé (, duas
a velocidade do pé (, duas vezes para obter a aceleração do pé (
vezes para obter a aceleração do pé (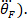 e três vezes para obter seu empurrão (similarmente diferencie o torque para obter sua velocidade e aceleração, usando o seguinte Comando:
e três vezes para obter seu empurrão (similarmente diferencie o torque para obter sua velocidade e aceleração, usando o seguinte Comando: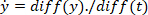
Onde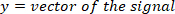
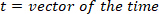
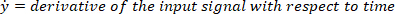
- Calcule a localização dos máximos locais e mínimos locais da velocidade do pé para localizar pulsos, usando o seguinte comando:
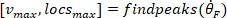
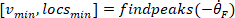
Onde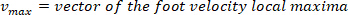
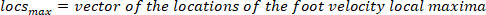
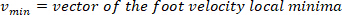
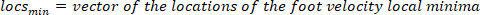
Nota: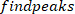 a função encontra todos os máximos locais (velocidade positiva do pé) e seus locais. Para encontrar a minima local, a mesma função é usada, mas o sinal da velocidade do ângulo do pé deve ser revertido.
a função encontra todos os máximos locais (velocidade positiva do pé) e seus locais. Para encontrar a minima local, a mesma função é usada, mas o sinal da velocidade do ângulo do pé deve ser revertido. - Projetar um 8ª ordem Butterworth filtro passa-baixa com uma frequência de canto de 50 Hz, usando o seguinte comando:
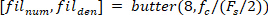

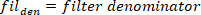
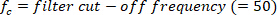
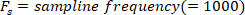
- Filtre todos os sinais com deslocamento de fase zero usando o filtro Butterworth:
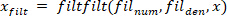
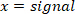
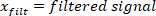
Nota: a função "filtfilt" não causa qualquer deslocamento no sinal filtrado. Não use o "filtro" função, porque ele gera uma mudança. - Plotar a velocidade do pé, e visualmente encontrar uma estimativa do período de tempo entre a extrema da velocidade do pé e o início do pulso (que é o primeiro ponto com a velocidade do pé zero antes da velocidade de pico). Para a perturbação neste estudo, este ponto ocorreu 25 MS antes da velocidade extrema encontrada na etapa 2.2.2.2.
- Para cada pulso, calcule o torque de fundo do tornozelo como a média do torque do tornozelo de 25 MS antes do início do pulso, ou seja, a média do torque no segmento a partir de 50 MS até 25 MS antes da velocidade extrema. Faça isso para o pulso kth com uma velocidade positiva usando o seguinte comando:
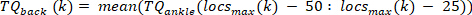
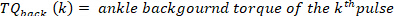
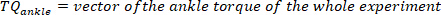
Nota: isto é feito para velocidades máximas e mínimas (velocidade negativa do pé) encontradas na etapa 2.2.2.2. - Encontre o mínimo e o máximo de todos os torques de fundo para todos os pulsos, usando o seguinte comando:
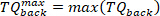
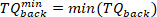
- Para cada pulso, extraia os dados do torque de 65 MS após o começo do pulso (como o segmento intrínseco do torque), usando o seguinte comando:
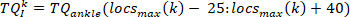
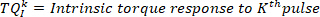
Nota: isto também é feito para o primeiro e segundo derivado do torque do tornozelo (para fornecer o primeiro e segundo derivados do torque intrínseco), bem como, o ângulo do pé, a velocidade do pé, pé de aceleração, e pé empurrão. - Calcule a alteração no segmento de torque intrínseco do kth de seu valor inicial, usando o seguinte comando:
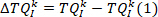
Nota: isto é feito similarmente para que o ângulo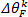 do pé obtenha.
do pé obtenha. - Divida a faixa de torque (obtida na etapa 2.2.2.7) em 3 escaninhos de largura nm e encontre os pulsos com torque de fundo em cada compartimento.
Observação: isso é feito usando a função "Find" e a indexação. Supõe-se que a rigidez intrínseca é constante em cada escaninho, desde que o torque do fundo do tornozelo não muda significativamente. - Estimar os parâmetros de rigidez intrínseca do modelo intrínseco estendido (EIM)29, para o jth bin usando os pulsos no grupo j
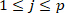 ().
().- Concatenar todas as respostas de torque intrínsecas na bin jth para formar o
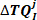 vetor:
vetor: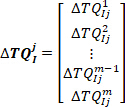
onde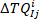 está a resposta de torque
está a resposta de torque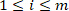 intrínseco ith () no grupo j.
intrínseco ith () no grupo j.
Nota: similarmente, concatenar o ângulo do pé, a velocidade, e a aceleração, e os primeiros e segundos derivados do torque intrínseco do grupo do jth a ser usados na etapa 2.2.2.11.2. - Coloque o ângulo do pé, velocidade, aceleração e empurrão, bem como a primeira e segunda derivada do torque do grupo j juntos para formar a matriz regressor:
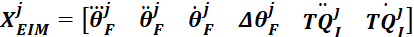
- Encontre os parâmetros de rigidez intrínseca para ogrupo j usando o operador de barra invertida (\):
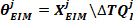
- Extraia o quarto elemento de
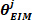 como a rigidez
como a rigidez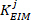 intrínseca de baixa frequência.
intrínseca de baixa frequência.
- Concatenar todas as respostas de torque intrínsecas na bin jth para formar o
- Execute as etapas na seção 2.2.2.11 para todos os grupos (Bins) e estimar a rigidez intrínseca de baixa frequência correspondente.
- Divida todos os valores estimados da rigidez da baixa freqüência pela rigidez crítica do assunto:
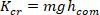
onde m é a massa do sujeito, g é a aceleração gravitacional,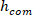 e é a altura do centro de massa do corpo acima do eixo de rotação do tornozelo, derivado dos dados antropométricos30. Isto dá a rigidez normalizada
e é a altura do centro de massa do corpo acima do eixo de rotação do tornozelo, derivado dos dados antropométricos30. Isto dá a rigidez normalizada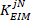 ().
(). - Converta o torque do fundo do tornozelo no fundo do tornozelo
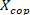 posição Cop () dividindo os torques de fundo do tornozelo com as forças verticais medidas correspondentes.
posição Cop () dividindo os torques de fundo do tornozelo com as forças verticais medidas correspondentes. - Plotar
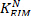 como uma função do centro de pressão.
como uma função do centro de pressão.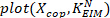
Onde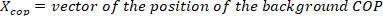
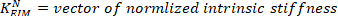
- Diferencie o sinal do pé uma vez para obter
- Experiência
Access restricted. Please log in or start a trial to view this content.
Resultados
Pseudo seqüência ternária aleatória (PRTS) e sinais TrapZ
A Figura 2a mostra um sinal de PRTs, que é gerado integrando um perfil pseudo da velocidade aleatória. Para cada tempo 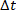 de amostragem, a velocidade do sinal pode ser igual a zero, ou adquirir um valor positivo ou negativo pré-definido
de amostragem, a velocidade do sinal pode ser igual a zero, ou adquirir um valor positivo ou negativo pré-definido
Access restricted. Please log in or start a trial to view this content.
Discussão
Várias etapas são críticas na realização desses experimentos para estudar o controle postural humano. Estas etapas são associadas com a medida correta dos sinais e incluem: 1) alinhamento correto do eixo do tornozelo da pata da rotação àquele dos pedais, para a medida correta de torques do tornozelo. 2) ajuste correto dos Finders da escala para assegurar-se de que trabalhem em sua escala e não sejam saturados durante os experimentos. 3) medida do EMG com boa qualidade e conversa transversal mínima. 4) aplicaç...
Access restricted. Please log in or start a trial to view this content.
Divulgações
Os autores não têm nada a revelar.
Agradecimentos
Este artigo foi tornado possível pela concessão de NPRP #6-463-2-189 da pesquisa nacional de Qatar e da concessão do espanador #81280 dos institutos canadenses da pesquisa da saúde.
Access restricted. Please log in or start a trial to view this content.
Materiais
| Name | Company | Catalog Number | Comments |
| 5K potentiometer | Maurey | 112P19502 | Measures actuator shaft angle |
| 8 channel Bagnoli surface EMG amplifiers and electrodes | Delsys | Measures the EMG of ankle muscles | |
| AlienWare Laptop | Dell Inc. | P69F001-Rev. A02 | VR-ready PC laptop |
| Data acquisition card | National instruments | 4472 | Samples the analogue signals from the sensors |
| Directional valve | REXROTH | 4WMR10C3X | Bypasses the flow if the angle of actuator shaft goes beyond ±20° |
| Full body harness | Jelco | 740 | Protect the subjects from falling |
| Laser range finder | Micro-epsilon 1302-100 | 1507307 | Measures shank linear displacement |
| Laser range finder | Micro-epsilon 1302-200 | 1509074 | Measures body linear displacement |
| Load cell | Omega | LC302-100 | Measures vertical reaction forces |
| Proportional servo-valve | MOOG | D681-4718 | Controls the hydraulic flow to the rotary actuators |
| Rotary actuator | Rotac | 26R21VDEISFTFLGMTG | Applies mechanical perturbations |
| Torque transducer | Lebow | 2110-5k | Measures ankle torque |
| Virtual Environment Motion Trackers | HTC inc. | 1551984681 | Tracks the head motion |
| Virtual Reality Headset | HTC inc. | 1551984681 | Provides visual perturbations |
Referências
- Horak, F. B. Postural orientation and equilibrium: what do we need to know about neural control of balance to prevent falls? Age and Ageing. 35, 7-11 (2006).
- Morasso, P. G., Schieppati, M. Can muscle stiffness alone stabilize upright standing? Journal of Neurophysiology. 82 (3), 1622-1626 (1999).
- Kearney, R. E., Hunter, I. W. System identification of human joint dynamics. Critical Reviews in Biomedical Engineering. 18 (1), 55-87 (1990).
- Mirbagheri, M. M., Barbeau, H., Kearney, R. E. Intrinsic and reflex contributions to human ankle stiffness: variation with activation level and position. Experimental Brain Research. 135 (4), 423-436 (2000).
- Weiss, P. L., Hunter, I. W., Kearney, R. E. Human ankle joint stiffness over the full range of muscle activation levels. Journal of Biomechanics. 21 (7), 539-544 (1988).
- Golkar, M. A., Sobhani Tehrani, E., Kearney, R. E. Linear Parameter Varying Identification of Dynamic Joint Stiffness during Time-Varying Voluntary Contractions. Frontiers in Computational Neuroscience. 11, 35(2017).
- Weiss, P. L., Kearney, R. E., Hunter, I. W. Position dependence of ankle joint dynamics--I. Passive mechanics. Journal of Biomechanics. 19 (9), 727-735 (1986).
- Weiss, P. L., Kearney, R. E., Hunter, I. W. Position dependence of ankle joint dynamics--II. Active mechanics. Journal of Biomechanics. 19 (9), 737-751 (1986).
- Engelhart, D., Boonstra, T. A., Aarts, R. G. K. M., Schouten, A. C., van der Kooij, H. Comparison of closed-loop system identification techniques to quantify multi-joint human balance control. Annual Reviews in Control. 41, 58-70 (2016).
- Kiemel, T., Elahi, A. J., Jeka, J. J. Identification of the plant for upright stance in humans: multiple movement patterns from a single neural strategy. Journal of Neurophysiology. 100 (6), 3394-3406 (2008).
- Loram, I. D., Lakie, M. Direct measurement of human ankle stiffness during quiet standing: the intrinsic mechanical stiffness is insufficient for stability. Journal of Physiology-London. 545 (3), 1041-1053 (2002).
- Fitzpatrick, R., Burke, D., Gandevia, S. C. Loop gain of reflexes controlling human standing measured with the use of postural and vestibular disturbances. Journal of Neurophysiology. 76 (6), 3994-4008 (1996).
- Dakin, C. J., Son, G. M. L., Inglis, J. T., Blouin, J. S. Frequency response of human vestibular reflexes characterized by stochastic stimuli. The Journal of Physiology. 583 (3), 1117-1127 (2007).
- Vlutters, M., Boonstra, T. A., Schouten, A. C., vander Kooij, H. Direct measurement of the intrinsic ankle stiffness during standing. Journal of Biomechanics. 48 (7), 1258-1263 (2015).
- Casadio, M., Morasso, P. G., Sanguineti, V. Direct measurement of ankle stiffness during quiet standing: implications for control modelling and clinical application. Gait and Posture. 21 (4), 410-424 (2005).
- Sakanaka, T. E. Causes of Variation in Intrinsic Ankle Stiffness and the Consequences for Standing. , University of Birmingham. Doctoral dissertation (2017).
- Sakanaka, T. E., Lakie, M., Reynolds, R. F. Sway-dependent changes in standing ankle stiffness caused by muscle thixotropy. Journal of Physiology. 594 (3), 781-793 (2016).
- Peterka, R. J., Murchison, C. F., Parrington, L., Fino, P. C., King, L. A. Implementation of a Central Sensorimotor Integration Test for Characterization of Human Balance Control During Stance. Frontiers in Neurology. 9, 1045(2018).
- Engelhart, D., Schouten, A. C., Aarts, R. G., van der Kooij, H. Assessment of Multi-Joint Coordination and Adaptation in Standing Balance: A Novel Device and System Identification Technique. IEEE Transactions on Neural Systems and Rehabilitation Engineering. 23 (6), 973-982 (2015).
- Boonstra, T. A., Schouten, A. C., van der Kooij, H. Identification of the contribution of the ankle and hip joints to multi-segmental balance control. Journal of Neuroengineering and Rehabilitation. 10, 23(2013).
- Forster, S. M., Wagner, R., Kearney, R. E. A bilateral electro-hydraulic actuator system to measure dynamic ankle joint stiffness during upright human stance. Proceedings of the 25th Annual International Conference of the IEEE Engineering in Medicine and Biology Society. , Cancun, Mexico. (2003).
- Davis, J., Hsieh, Y. -H., Lee, H. -C. Humans perceive flicker artifacts at 500 Hz. Scientific Reports. 5, 7861(2015).
- Amiri, P., Kearney, R. E. Ankle intrinsic stiffness changes with postural sway. Journal of Biomechanics. 85, 50-58 (2019).
- van der Kooij, H., van Asseldonk, E., van der Helm, F. C. Comparison of different methods to identify and quantify balance control. Journal of Neuroscience Methods. 145 (1-2), 175-203 (2005).
- Amiri, P., MacLean, L. J., Kearney, R. E. Measurement of shank angle during stance using laser range finders. International Conference of the IEEE Engineering in Medicine and Biology. , Orlando, FL. (2016).
- The SENIAM project. , Available from: http://www.seniam.org/ (2019).
- Jalaleddini, K., Tehrani, E. S., Kearney, R. E. A Subspace Approach to the Structural Decomposition and Identification of Ankle Joint Dynamic Stiffness. IEEE Transactions on Biomedical Engineering. 64 (6), 1357-1368 (2017).
- Amiri, P., Kearney, R. E. A Closed-loop Method to Identify EMG-Ankle Torque Dynamic Relation in Human Balance Control. Conference Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society. , Berlin, Germany. (2019).
- Sobhani Tehrani, E., Jalaleddini, K., Kearney, R. E. Ankle Joint Intrinsic Dynamics is More Complex than a Mass-Spring-Damper Model. IEEE Transactions on Neural Systems and Rehabilitation Engineering. 25 (9), 1568-1580 (2017).
- NASA. Anthropometry and biomechanics. , Available from: http://msis.jsc.nasa.gov/sections/section03.htm (1995).
- Peterka, R. J. Sensorimotor integration in human postural control. Journal of Neurophysiology. 88 (3), 1097-1118 (2002).
- Amiri, P., Kearney, R. E. Ankle intrinsic stiffness is modulated by postural sway. Conference Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society. , Seogwipo, South Korea. (2017).
- Jeka, J. J., Allison, L. K., Kiemel, T. The dynamics of visual reweighting in healthy and fall-prone older adults. Journal of Motor Behavior. 42 (4), 197-208 (2010).
- Jilk, D. J., Safavynia, S. A., Ting, L. H. Contribution of vision to postural behaviors during continuous support-surface translations. Experimental Brain Research. 232 (1), 169-180 (2014).
- Winter, D. A., Patla, A. E., Prince, F., Ishac, M., Gielo-Perczak, K. Stiffness control of balance in quiet standing. Journal of Neurophysiology. 80 (3), 1211-1221 (1998).
- Pasma, J. H., Boonstra, T. A., van Kordelaar, J., Spyropoulou, V. V., Schouten, A. C. A Sensitivity Analysis of an Inverted Pendulum Balance Control Model. Frontiers in Computational Neuroscience. 11, 99(2017).
- Pasma, J. H., et al. Changes in sensory reweighting of proprioceptive information during standing balance with age and disease. Journal of Neurophysiology. 114 (6), 3220-3233 (2015).
- Pasma, J. H., et al. Impaired standing balance: The clinical need for closing the loop. Neuroscience. , 157-165 (2014).
- Engelhart, D., et al. Impaired Standing Balance in Elderly: A New Engineering Method Helps to Unravel Causes and Effects. Journal of the American Medical Directors Association. 15 (3), (2014).
- Pasma, J. H., Boonstra, T. A., Campfens, S. F., Schouten, A. C., Van der Kooij, H. Sensory reweighting of proprioceptive information of the left and right leg during human balance control. Journal of Neurophysiology. 108 (4), 1138-1148 (2012).
- Goodworth, A. D., Peterka, R. J. Sensorimotor integration for multisegmental frontal plane balance control in humans. Journal of Neurophysiology. 107 (1), 12-28 (2012).
- Kiemel, T., Zhang, Y., Jeka, J. J. Identification of neural feedback for upright stance in humans: stabilization rather than sway minimization. Journal of Neuroscience. 31 (42), 15144-15153 (2011).
- van der Kooij, H., van Asseldonk, E. H. F., Geelen, J., van Vugt, J. P. P., Bloem, B. R. Detecting asymmetries in balance control with system identification: first experimental results from Parkinson patients. Journal of Neural Transmission. 114 (10), 1333(2007).
- Fujisawa, N., et al. Human standing posture control system depending on adopted strategies. Medical and Biological Engineering and Computing. 43 (1), 107-114 (2005).
- Johansson, R., Magnusson, M., Fransson, P. A., Karlberg, M. Multi-stimulus multi-response posturography. Mathematical Biosciences. 174 (1), 41-59 (2001).
- Jeka, J., Oie, K., Schöner, G., Dijkstra, T., Henson, E. Position and Velocity Coupling of Postural Sway to Somatosensory Drive. Journal of Neurophysiology. 79 (4), 1661-1674 (1998).
- Peterka, R. J., Benolken, M. S. Role of somatosensory and vestibular cues in attenuating visually induced human postural sway. Experimental Brain Research. 105 (1), 101-110 (1995).
- Maki, B. E., Fernie, G. R. A system identification approach to balance testing. Progress in Brain Research. 76, 297-306 (1988).
- Johansson, R., Magnusson, M., Akesson, M. Identification of human postural dynamics. IEEE Transactions on Biomedical Engineering. 35 (10), 858-869 (1988).
- Maki, B. E., Holliday, P. J., Fernie, G. R. A Posture Control Model and Balance Test for the Prediction of Relative Postural Stability. IEEE Transactions on Biomedical Engineering. BME-34. 10 (10), 797-810 (1987).
- Werness, S. A., Anderson, D. J. Parametric analysis of dynamic postural responses. Biological Cybernetics. 51 (3), 155-168 (1984).
- Hwang, S., Agada, P., Kiemel, T., Jeka, J. J. Identification of the Unstable Human Postural Control System. Frontiers in Systems Neuroscience. 10, 22(2016).
- Ishida, A., Imai, S., Fukuoka, Y. Analysis of the posture control system under fixed and sway-referenced support conditions. IEEE Transactions on Biomedical Engineering. 44 (5), 331-336 (1997).
- Ishida, A., Miyazaki, S. Maximum likelihood identification of a posture control system. IEEE Transactions on Biomedical Engineering. 34 (1), 1-5 (1987).
- Ljung, L. System Identification: Theory for the User. , Prentice-Hall, Inc. Upper Saddle River, NJ. (1986).
- Forssell, U., Ljung, L. Closed-loop identification revisited. Automatica. 35 (7), 1215-1241 (1999).
- Horak, F. B., Nashner, L. M. Central programming of postural movements: adaptation to altered support-surface configurations. Journal of Neurophysiology. 55 (6), 1369-1381 (1986).
Access restricted. Please log in or start a trial to view this content.
Reimpressões e Permissões
Solicitar permissão para reutilizar o texto ou figuras deste artigo JoVE
Solicitar PermissãoThis article has been published
Video Coming Soon
Copyright © 2025 MyJoVE Corporation. Todos os direitos reservados