Entwurf und Anwendung eines Fehlererkennungsverfahrens auf Basis adaptiver Filter und Drehzahlschätzung für einen elektro-hydrostatischen Aktuator

Zusammenfassung

In dieser Arbeit werden ein adaptiver Filter, der auf einem normalisierten NLMS-Algorithmus (Least Mean Square) basiert, und eine Methode zur Schätzung der Drehzahl vorgestellt, um die elektrischen und hydraulischen Fehler des elektrohydrostatischen Aktuators (EHA) zu erkennen. Die Wirksamkeit und Machbarkeit der genannten Methoden wird durch Simulationen und Experimente überprüft.

Zusammenfassung

Der elektrohydrostatische Aktuator (EHA) ist aufgrund seiner hohen Leistungsdichte und seines geringen Wartungsaufwands ein vielversprechender Aktuator, der in Flugsteuerungssystemen für mehr elektrische Flugzeuge (MEA) eingesetzt wird. Da die Zuverlässigkeit des Systems mit zunehmender Komplexität abnimmt, wird die Fehlererkennung immer wichtiger. In dieser Arbeit wurde ein adaptiver Filter entwickelt, der auf einem normalisierten NLMS-Algorithmus (Least Mean Square) basiert, der den Widerstand der Motorwicklungen online identifizieren kann, um elektrische Fehler in der EHA zu erkennen. Zusätzlich wurde auf der Grundlage des analytischen Zusammenhangs zwischen Drehzahl und Verschiebung eine Methode zur Schätzung der Drehzahl entwickelt. Durch den Vergleich der tatsächlichen Drehzahl mit der geschätzten Drehzahl konnten hydraulische Fehler erkannt werden. Um die Wirksamkeit der oben genannten Methode zu überprüfen, wurde Software für die Modellierung und Simulationen eingesetzt, die Fehlerinjektion und -erkennung umfassten. Auf dieser Basis wurde eine Versuchsplattform aufgebaut und anschließend einer Reihe von Validierungsexperimenten unterzogen. Die Ergebnisse deuten darauf hin, dass die Fehlererkennungsmethode das Potenzial hat, elektrische und hydraulische Fehler in einem EHA zu erkennen.

Einleitung

Der elektrohydrostatische Aktuator (EHA) ist eine Schlüsselkomponente für die Flugsteuerung in elektrisch angetriebenen Flugzeugen (MEA). Der typische Aufbau einer EHA ist in Abbildung 1 dargestellt. Seine kompakte Bauweise garantiert eine hohe Leistungsdichte, einen geringen Wartungsaufwand sowie eine höhere Fehlertoleranz und Sicherheit im Vergleich zum herkömmlichen hydraulischen Servoaktuator (HSA)¹. Die derzeitige Zuverlässigkeit des EHA kann jedoch nicht den praktischen Anforderungen von mehr Elektroflugzeugen^{gerecht werden 2}. Aus diesem Grund wurde die Redundanztechnologie in das Design des EHA eingeführt. Um die Effektivität der Redundanztechnologie zu maximieren, sollte der Betriebszustand des Systems durch ein Fehlererkennungsverfahren³ überwacht werden. Je nach Fehlerort können die Fehlermodi des EHA in Servoreglerfehler und PCU-Fehler (Power Control Unit) unterteilt werden. PCU-Fehler können weiter unterteilt werden in Sensorfehler, elektromechanische Einheitsfehler und Hydraulikaggregatfehler. Der Fehlermechanismus des Servoreglers hat wenig Beziehung zum EHA-Körper, und die Fehlerwahrscheinlichkeit des Sensors ist viel geringer als die der Ausrüstungskomponente⁴. Daher konzentrieren wir uns in dieser Arbeit auf die Fehler der elektromechanischen Einheit und der hydraulischen Einheit.

Zu den Fehlern der elektromechanischen Einheit gehören Fehler des Motorantriebsmoduls und Fehler des bürstenlosen Gleichstrommotors (BLDCM). Im Allgemeinen ist die Wahrscheinlichkeit eines Fehlers der Leistungsantriebselektronik (PDE) (z. B. ein Kurzschlussfehler, ein Leerlauffehler) relativ hoch. Tritt ein Kurzschlussfehler auf, steigt der PDE-Strom in kurzer Zeit stark an, was schwerwiegende Folgen wie eine Motorabschaltung oder Schäden an den elektrischen Komponenten nach sich zieht. Obwohl der Motor seinen Betriebszustand nach einem Leerlauffehler beibehalten kann, sind Überstrom und Überspannung für die anderen elektrischen Komponenten immer noch unvermeidlich, und folglich können sekundäre Fehler auftreten⁵. Was die BLDCMs betrifft, so sind die Motorwicklungen am anfälligsten für Fehler durch einen Kurzschluss oder einen offenen Stromkreis⁶. Die PDE in der elektromechanischen Einheit ist mit den entsprechenden Motorwicklungen in Reihe geschaltet. Das für die Motorwicklungen ausgelegte Fehlererkennungsverfahren ist auch bei Fehlern in der PDE effektiv. Daher sollten elektromechanische Gerätefehler, sowohl im Motor als auch in der PDE, online erkannt werden.

Zu den Fehlern des Hydraulikaggregats gehören Fehler in der Kolbenpumpe mit fester Verdrängung, dem integrierten Ventilblock und dem Betätigungszylinder⁷. Die Kolbenpumpe der EHA besteht aus Kolben, Taumelscheiben und Ventilplatten; Schäden an der Dichtung und Verschleiß der Ventilplatte sind die Hauptformen des Fehlers⁸. Diese beiden Fehlermodi erhöhen die Leckage der Pumpe. Abnormale Änderungen des Ausgangsstroms und des Drucks folgen und führen schließlich zu einer Verringerung der Drehzahl des Stellzylinders und einer Verringerung der Servoleistung des Systems. Zu den Fehlermodi des integrierten Ventilblocks gehören ein Druckbehälterfehler, ein Rückschlagventilfehler, ein Überdruckventilfehler und ein Ventilfehler bei der Moduswahl. Der Druckbehälter nimmt in der Regel ein selbstverstärkendes Design mit hoher Zuverlässigkeit an. Wenn jedoch ein Fehler auftritt, führt ein unzureichender Ladedruck zu Kavitation der Pumpe, was zu einem abnormalen Ausgangsfluss führt. Federermüdung, Komponentenverschleiß und Verformung sind häufige Fehlermodi in den Rückschlagventilen und Überdruckventilen. Ein Rückschlagventilfehler stellt sich als umgekehrte Leckage dar, die direkt zu einem abnormalen Durchfluss führt. Ein Defekt des Überdruckventils führt zu einer ungültigen Schutzfunktion, was zu einem abnormalen Druck führt. Die häufigsten Fehler des Moduswahlventils sind der Ausfall der Rückstellfeder und gebrochene Drahtspulen. Ersteres bewirkt eine stromeinlaufende Umschaltung des Arbeitszustands, was zu einer abnormalen Bewegung des Betätigungszylinders führt. Ein Defekt des Betätigungszylinders führt zu einer Abnahme der Präzision der Positionsregelung und der dynamischen Leistung. Zusammenfassend lässt sich sagen, dass Fehler an den Hydraulikaggregaten zu abnormalem Durchfluss und Druck führen⁹. Da der Durchfluss und die Motordrehzahl in einem EHA-System annähernd proportional sind, kann die Drehzahl online überwacht werden, um abnormalen Durchfluss und Druck aufgrund plötzlicher Fehler zu erkennen.

Entsprechende Fehlererkennungsverfahren, die auf die zuvor erwähnten elektromechanischen Aggregatsfehler und Hydraulikaggregatfehler abzielen, müssen ausgelegt werden. Die Verfahren zur Fehlererkennung in einem elektromechanischen System umfassen hauptsächlich die Zustandsschätzung und die Parameteridentifikation¹⁰. Ein Zustandsbeobachter wird auf der Grundlage eines mathematischen Modells des Systems aufgebaut, das eine Zustandsschätzung vornimmt und Fehler durch Analyse der vom Beobachter erzeugten Restsequenz bestimmt. Alcorta et al. schlugen einen einfachen und neuartigen nichtlinearen Beobachter mit zwei Korrekturtermen für die Erkennung von Schwingungsfehlern in Verkehrsflugzeugen vor, der sehr effektiv ist¹¹. Diese Art von Methode muss jedoch das Robustheitsproblem des Beobachters lösen. Mit anderen Worten, es muss die Änderungen in der Restsequenz unterdrücken, die durch Nicht-Fehlerinformationen wie Modellfehler oder externe Störungen verursacht werden. Darüber hinaus erfordert diese Methode oft sehr genaue Modellinformationen, die in praktischen technischen Anwendungen normalerweise schwer zu erfassen sind.

Die Parameteridentifikationsmethode verwendet bestimmte Algorithmen, um die wichtigen Parameter im System zu identifizieren. Tritt eine Störung auf, ändert sich auch der entsprechende Parameterwert. Daher können Fehler erkannt werden, indem eine Änderung der Parameter erkannt wird. Die Parameteridentifikationsmethode erfordert keine Berechnung der Restsequenz, so dass die Auswirkungen von Störungen auf die Detektionsgenauigkeit vermieden werden können. Der adaptive Filter ist aufgrund seiner einfachen Implementierung und stabilen Leistung bei der Parameteridentifikation weit verbreitet gewesen, was bedeutet, dass er ein günstiges und praktikables Verfahren zur elektromechanischen Fehlererkennung¹² ist. Zhu et al. schlugen eine neue Multi-Modell-Methode zur adaptiven Schätzung von Fehlern vor, die auf kernadaptiven Filtern basiert und die Schätzung des realen Flugzustandswertes und die Fehlererkennung des Aktuators online mit guter Leistung realisiert¹³.

In Anlehnung an die bisherige Forschung wurden entsprechende Fehlererkennungsverfahren entwickelt. Der Widerstand der Wicklungen ändert sich schlagartig bei elektrischen Fehlern, wie z.B. Leerlauf- oder Kurzschlussfehlern. Daher wurde ein adaptiver Filter entwickelt, der auf einem NLMS-Algorithmus basiert, um den Widerstand der Wicklungen zu identifizieren, der feststellen kann, ob ein elektrischer Fehler aufgetreten ist. Die Kombination eines adaptiven Filters mit einem NLMS-Algorithmus zur Minimierung der Änderung des Parametervektors führt zu einem besseren und schnelleren Konvergenzeffekt¹⁴. Für Fehler im Hydraulikaggregat wurde ein Algorithmus zur Schätzung der Drehzahl vorgeschlagen, der auf der eindeutigen analytischen Beziehung zwischen der Drehzahl der Pumpe und der Position des Betätigungszylinders basiert. EHA-Hydraulikfehler wurden online erkannt, indem die geschätzte Drehzahl mit der tatsächlichen Drehzahl in Echtzeit verglichen wurde.

In dieser Arbeit wurde eine Testmethode verwendet, die Simulationen und Experimente kombiniert. Zunächst wurde ein mathematisches Modell der EHA erstellt und eine Simulation für die vorgeschlagene Fehlererkennungsmethode durchgeführt. Die Simulation umfasste die Verifizierung der Detektionsmethoden unter Nicht-Fehler- und Fehlerinjektionsbedingungen. Anschließend wurde die Fehlererkennungsmethode im realen Servoregler realisiert. Abschließend wurden die Ergebnisse der Simulationen und Experimente analysiert und verglichen, um die Wirksamkeit der Fehlererkennungsmethode zu bewerten.

Protokoll

1. Etablierung des EHA-Simulationsmodells

1. Öffnen Sie die Simulationssoftware auf einem PC.
2. Bauen Sie das Simulationsmodell für die EHA (Abbildung 2) gemäß den mathematischen Gleichungen des EHA-Modells¹⁵ auf und führen Sie eine PI mit drei Schleifen als Regler durch. Fassen Sie das Hydraulikmodul (Abbildung 2C), das elektrische Modul (Abbildung 2B) und die Steuerung (Abbildung 2B, D) in drei Untermodellen auf.
   ANMERKUNG: Die mathematischen Gleichungen des EHA-Modells lauten in Gleichung (1) wie folgt: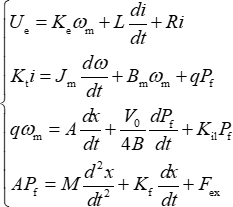
   (1)
   In dieser Gleichung ist U e die Spannung des Ankers, K _e ist der elektromotorische Gegenkraftkoeffizient des Motors, ω_m ist die Drehzahl des Motors, L ist die äquivalente Induktivität des Ankers, i ist der Strom der Wicklung, R ist der Widerstand der Wicklung, K_t ist der Drehmomentkoeffizient des Motors, J m ist das Trägheitsmoment des Rotors, B_m ist der Reibungskoeffizient des Motors, q ist die Verdrängung der Pumpe, P_f ist die Druckdifferenz zwischen den beiden Kammern im Hydraulikzylinder, A ist die effektive Fläche des Kolbens, x ist die Position der Kolbenstange, V₀ ist das effektive Hohlraumvolumen des Hydraulikzylinders, B ist der Volumenmodul des Hydrauliköls, K _il ist der gesamte interne Leckagekoeffizient des Systems, M ist die Masse des Kolbens und der Last, K_f ist der viskose Dämpfungskoeffizient des Hydraulikzylinders und F_ex ist die externe Belastungskraft.
3. Programmieren Sie den adaptiven Filter basierend auf einem NLMS-Algorithmus in einer M-Datei, die zur Laufzeit aufgerufen werden kann.
   HINWEIS: Die Ableitung des adaptiven Filters auf Basis des NLMS-Algorithmus ist hier dargestellt. Die elektromechanischen Fehler können durch die Identifizierung des Wicklungswiderstands beurteilt werden, und die diskretisierte Motorgleichung lautet wie folgt: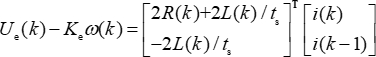
   (2)
   In dieser Formel ist t_s ist die Abtastzeit und R(k) und L(k) sind die Parameter, die identifiziert werden müssen. Gl (2)kann wie folgt geschrieben werden: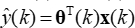
   (3)
   In dieser Formel ist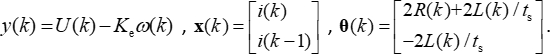
   Durch Addition von zwei Items für den Parametervektor θ(k), die Probenahmezeit, t_s, kann eliminiert werden, um den Widerstand zu erhalten, R(k). Wenn eine der dreiphasigen Wicklungen ausfällt, R(k) vom Normalwert abweicht.
   Ein adaptiver Filter kann konstruiert werden aus: Gl (3), und der Schätzfehler des Filters ist wie folgt: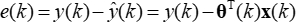
   (4)
   In dieser Formel ist e(k) ist ein fluktuierendes Zufallssignal. Wann e(k) klein genug ist, ist der geschätzte Wert des Filters ŷ(k). Schließlich, wenn es gegen die reale Ausgabe konvergieren kann, y(k), des Systems, dann ist der Parametervektor θ(k) konvergiert zu den realen Systemparametern.
   Der LMS-Algorithmus (Least Mean Square) verwendet den minimalen mittleren quadratischen Fehler als Kriterium, um die optimale Vorhersage und Filterung zu realisieren. Führen Sie eine automatische iterative Anpassung durch, um θ(k) konvergieren gegen den wahren Wert des Systems. Der Ausdruck der Kostenfunktion lautet wie folgt: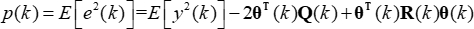
   (5)
   In dieser Formel ist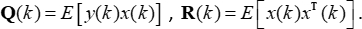
   Q(k) ist der Kreuzkorrelationsvektor von y(k) und x(k). R(k) ist die Autokorrelationsmatrix des Eingabevektors.
   Nach der Methode des steilsten Abstiegs ist die Wiederholungsformel für θ(k) nähert sich der optimalen Lösung wie folgt: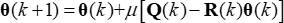
   (6)
   In dieser Formel ist µ ist die adaptive variable Schrittweite. Im eigentlichen iterativen Prozess werden die Werte des aktuellen Probenahmepunktes zur Schätzung verwendet Q(k) und R(k), die wie folgt ausgedrückt werden kann: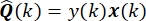 und .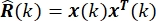
   Dann kann der LMS-Algorithmus wie folgt vereinfacht werden: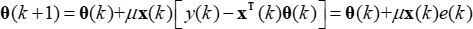
   (7)
   Der LMS-Algorithmus kann θ(k) nähern sich allmählich den realen Systemparametern an.
   In praktischen Anwendungen wird der NLMS-Algorithmus in der Regel verwendet, um die langsame Konvergenzgeschwindigkeit des LMS-Algorithmus zu überwinden. Die Einschränkung des NLMS-Algorithmus lautet wie folgt: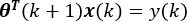
   (8)
   Bei Verwendung der Lagrange-Multiplikatormethode zur Lösung des eingeschränkten Optimierungsproblems lautet die Kostenfunktion wie folgt: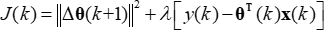
   
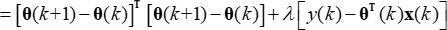   (9)
   In dieser Formel istλ ist der Lagrange-Koeffizient. Um den Mindestwert von J(k), finden Sie die partielle Ableitung von J(k) bis θ(k) und setzen Sie den Wert auf 0. Berechnen Sie die Lösung wie folgt: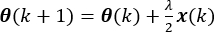
   (10)
   Stellen Gl (10) in Gl (8), und erhalten Sie dann die Lösung von λ folgendermaßen: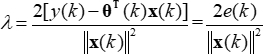
   (11)
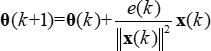   (12)
   Um die inkrementelle Änderung des Parametervektors zu steuern, wird ein Schrittfaktor, β, wird in diese Formel eingeführt, und der Ausdruck lautet wie folgt: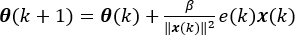
   (13)
   Um die Schwierigkeit der numerischen Berechnung aufgrund des kleinen Eingangsvektors zu vermeiden, ist gleichzeitig eine relativ kleine positive Konstante, γ, wird eingeführt. Li et al. bewiesen, dass, wenn 0 < β < 2 and 0 < γ < 1, the NLMS algorithm can achieve better convergence effects¹⁶. Der letzte Ausdruck lautet wie folgt: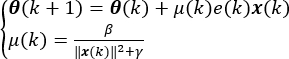
   (14)
4. Programmieren Sie den Algorithmus zur Schätzung der Drehzahl in einer M-Datei, die zur Laufzeit aufgerufen werden kann.
   HINWEIS: Die Ableitung des Algorithmus zur Schätzung der Drehzahl wird hier gezeigt. Die Strömungsgleichung des Aktors kann wie folgt geschrieben werden: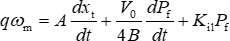
   (15)
   Wenn das Hydraulikaggregat in einem normalen Zustand arbeitet, kann der Gesamtdurchflussverlust Q_f, der durch Ölkompression und Leckage verursacht wird, ungefähr wie folgt ausgedrückt werden: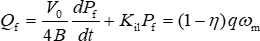
   (16)
   In dieser Formel ist η der volumetrische Wirkungsgrad des EHA.
   Somit kann die näherungsweise analytische Beziehung zwischen der Geschwindigkeit ω_m und der Verschiebung x wie folgt ermittelt werden: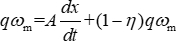
   (17)
   Die Fehlergleichung für die diskretisierte Rotationsgeschwindigkeitsschätzung lautet wie folgt: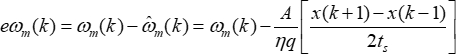
   
   In dieser Formel ist eω_m(k) der geschätzte Drehzahlfehler und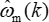 die geschätzte Drehzahl. Änderungen in eω_m(k) spiegeln den Betriebszustand des Hydraulikaggregats wider. Wenn eω_m(k) plötzlich vom Normalwert abweicht, bedeutet dies, dass der Zustand des Hydraulikaggregats abnormal ist, was zur Online-Erkennung von Hydraulikfehlern verwendet werden kann.
5. Bauen Sie das Fault-Injection-Modul auf und stellen Sie Fault-Injection-Schalter bereit (Abbildung 2E, F), die entscheiden können, ob ein Fehler eingespeist werden soll.
6. Stellen Sie die Parameter des Simulationsmodells gemäß Tabelle 1 ein, indem Sie auf die jeweilige Komponente in jedem Teilmodell doppelklicken.
7. Programmieren Sie die Zeichensoftware, die nach Abschluss einer Gruppe von Experimenten Simulationskurven zeichnen kann.

2. Simulation der Fehlererkennungsmethoden

1. Geben Sie einen Positionsbefehl aus, bei dem es sich um eine Sinuskurve mit einer Amplitude von 0,01 m und einer Frequenz von 1 Hz handelt.
2. Rufen Sie das Menü MODELLIERUNG auf und klicken Sie auf die Schaltfläche Modelleinstellungen . Legen Sie die Parameter der Simulationsoperation fest: eine Startzeit von 0 s, eine Stoppzeit von 6 s, den Schritt Typ als Variable und den Solver als automatisch.
3. Doppelklicken Sie auf die Schalter für die Fehlerinjektion , um das Modell so einzustellen, dass es in einem fehlerfreien Zustand funktioniert.
4. Klicken Sie auf die Schaltfläche Ausführen , um die Simulation auszuführen und die Ergebnisse der fehlerfreien Bedingung zu erhalten.
5. Führen Sie die Zeichensoftware aus, um die Kurve der Kolbenstangenverschiebung zu zeichnen.
6. Doppelklicken Sie auf den elektromechanischen Fehlerschalter einfügen , um einen elektromechanischen Fehler nach 3 s einzuspeisen, wodurch der Widerstand auf 1.000 Ω eingestellt wird, um einen Leerlauffehler der Motorwicklungen zu simulieren.
7. Wiederholen Sie die Schritte 2.4 und 2.5, um die Ergebnisse für den elektromechanischen Fehlerzustand zu erhalten. Führen Sie die Zeichensoftware aus, um die Kurven der Kolbenstangenverschiebung und des ermittelten Widerstands zu zeichnen.
8. Drehen Sie den hydraulischen Fehlerschalter , um einen hydraulischen Fehler nach 3 s einzuspritzen, wodurch der Leckagewert auf 2,5 × 10⁻⁹ (m³/s)/Pa erhöht wird, um einen Fehler des Hydraulikaggregats zu simulieren.
9. Wiederholen Sie die Schritte 2.3 und 2.4, um die Ergebnisse für den hydraulischen Fehlerzustand zu erhalten. Führen Sie die Zeichensoftware aus, um die Kurven der Ergebnisse der Kolbenstangenverschiebung und der Schätzung der Drehzahl zu zeichnen.

3. Aufbau der Versuchsplattform (Abbildung 3)

1. Bringen Sie PC, EHA und Servoregler in Position. Der EHA ist in Abbildung 4 und der Servoregler in Abbildung 5 dargestellt.
2. Verdrahten Sie die elektrischen Teile.
   1. Verbinden Sie die EHA-Sensoren über mehrere Luftfahrtstecker mit den Sensoranschlüssen für den Servoregler.
   2. Verbinden Sie den EHA-Motorantriebsanschluss über den Luftfahrtstecker mit dem Wechselrichteranschluss für den Servoregler.
   3. Verbinden Sie den Servoregler über den Luftfahrtstecker mit der Steuerleistung und der Antriebsleistung.
      VORSICHT: Schalten Sie die Spannung aus Sicherheitsgründen vorübergehend aus.
3. Stellen Sie die Kommunikation zwischen dem Servoregler und dem PC her.
   1. Öffnen Sie die Hostsoftwareschnittstelle (Abbildung 6) auf dem PC.
   2. Verbinden Sie den PC und den Servoregler über ein serielles 422-zu-USB-Kabel, um die Kommunikation einzurichten.
   3. Versorgen Sie den Servoregler mit Steuerstrom. Die Steuerspannung beträgt 24 V DC.
   4. Wählen Sie die entsprechende serielle Schnittstelle aus dem Dropdown-Fenster VISA-Ressourcenname in der Software aus.
      HINWEIS: Wenn die Kommunikation nicht erfolgreich hergestellt werden kann, überprüfen Sie das Kabel oder starten Sie die Software neu, bis die RS422-Kommunikation hergestellt ist.
   5. Klicken Sie auf die Schaltfläche Ausführen , um die Software zu starten.
   6. Beobachten Sie den Empfangsbereich und die entsprechenden Kurven der Software, um festzustellen, ob die Datenempfangsfunktion normal ist. Klicken Sie auf die Taste Magnetventil 1 , um zu beobachten, ob das Magnetventil ein Einzugsgeräusch hat, und um festzustellen, ob die Datenübertragungsfunktion normal ist.

4. Experiment für die Fehlererkennungsmethode

1. Versorgen Sie den Servoregler mit Antriebsstrom und stellen Sie die Spannung auf 50 V DC ein.
   HINWEIS: Ein 50-V-DC-Unterspannungsbetrieb sorgt für sicheres Arbeiten, da das System lastfrei ist.
2. Klicken Sie in der Software auf die Schaltfläche EHA-Schalter , um den EHA in einen Betriebszustand zu versetzen. Klicken Sie auf die Schaltfläche Datenprotokoll , um die Datenprotokollierung zu starten. Zu den aufgezeichneten Daten gehören die Ist-Position, die Soll-Position, die Ist-Geschwindigkeit, die Soll-Geschwindigkeit, der Busstrom, die Spannung usw.
3. Führen Sie einen Pre-Run für die EHA durch. Geben Sie Positionsbefehle in der Software, die einen Schritt von +0,005 m und -0,005 m beinhalten. Beobachten Sie, ob der EHA normal betätigt wird.
   VORSICHT: Wenn das EHA nicht normal funktioniert, überprüfen Sie den Fehler sofort, bevor Sie dieses Experiment fortsetzen.
4. Geben Sie einen Positionsbefehl auf der Software, bei dem es sich um eine Sinuskurve mit einer Amplitude von 0,01 m und einer Frequenz von 1 Hz handelt.
5. Beobachten Sie, ob der ermittelte Widerstand und die geschätzte Drehzahl mit den Werten unter fehlerfreien Betriebsbedingungen übereinstimmen.
6. Setzen Sie den Positionsbefehl auf den ursprünglichen Zustand zurück, wenn das Ergebnis korrekt ist. Klicken Sie auf die Schaltfläche EHA-Schalter , um den EHA zu stoppen und die Antriebsstromversorgung zu unterbrechen, die Host-Computersoftware zu stoppen und die Kommunikation zwischen dem Servoregler und dem PC zu unterbrechen.
7. Exportieren Sie die experimentellen Daten, analysieren Sie die Daten und zeichnen Sie Kurven der experimentellen Ergebnisse mit einer Zeichensoftware.
8. Analysieren Sie die experimentellen Ergebnisse und vergleichen Sie sie mit den Simulationsergebnissen, um Schlussfolgerungen abzuleiten.

Ergebnisse

In der Simulation ist die Ist-Position und die Soll-Positionskurve der EHA-Kolbenstange im fehlerfreien Zustand in Bild 7 dargestellt. Entsprechend der Kurve funktionierte das System normal und mit guten dynamischen Eigenschaften. Die Ist- und Soll-Positionskurve der EHA-Kolbenstange im elektromechanischen Fehlereinspritzzustand ist in Abbildung 8 dargestellt. Entsprechend der Kurve konnte das System das Ziel nicht genau verfolgen. Die Ergebnisse des Resistenzid...

Diskussion

Bei der Durchführung dieser experimentellen Schritte war es wichtig, die Echtzeitfähigkeit des Algorithmus sicherzustellen, um genaue Berechnungsergebnisse zu erhalten. Das weiße Rauschen in der Signalerfassung wurde verwendet, um die Eigenschaften des tatsächlichen Sensors zu simulieren und die Simulation näher an die Realität zu bringen. In den Simulationen und Experimenten wurden Gleitmittelfilter angewendet, um die Fluktuation des identifizierten Widerstands und der geschätzten Drehzahl zu reduzieren, wodurch ...

Materialien

Name	Company	Catalog Number	Comments
LabVIEW	NI	NI LabVIEW 2018
Matlab/SIMULINK	MathWorks.Inc	R2020a
Personal Computer	Lenovo	Y7000 2020H
24V Switching Power Supply	ECNKO	S-250-24
Programmable Current Source	Greens Pai	GDP-50-30