Fuente: Faisal Alamgir, School of Materials Science and Engineering, Georgia Institute of Technology, Atlanta, GA

La difracción de rayos X (RDX) es una técnica utilizada en la ciencia de materiales para determinar la estructura atómica y molecular de un material. Esto se hace irradiando una muestra del material con rayos X incidentes y luego midiendo las intensidades y ángulos de dispersión de los rayos X que están dispersos por el material. La intensidad de los rayos X dispersos se trazan en función del ángulo de dispersión, y la estructura del material se determina a partir del análisis de la ubicación, en ángulo y las intensidades de los picos de intensidad dispersa. Más allá de ser capaz de medir las posiciones medias de los átomos en el cristal, se puede determinar información sobre cómo la estructura real se desvía de la ideal, resultante, por ejemplo, de estrés interno o de defectos.

La difracción de los rayos X, que es fundamental para el método XRD, es un subconjunto de los fenómenos generales de dispersión de rayos X. El XRD, que generalmente se utiliza para significar la difracción de rayos X de gran angular (WAXD), se encuentra bajo varios métodos que utilizan las ondas de rayos X dispersas elásticamente. Otras técnicas de rayos X basadas en dispersión elástica incluyen dispersión de rayos X de ángulo pequeño (SAXS, por sus dados) donde los rayos X son incidentes en la muestra en el pequeño rango angular de 0.1-10⁰ típicamente). SAXS mide correlaciones estructurales de la escala de varios nanómetros o más grandes (como superestructuras de cristal), y reflectividad de rayos X que mide el grosor, la rugosidad y la densidad de las películas delgadas. WAXD cubre un rango angular superior a 10⁰.

Relación entre las posiciones pico difraczadas y la estructura cristalina:

Cuando las ondas de luz de longitud de onda suficientemente pequeña sufren incidentes sobre una celosía de cristal, se difuminan desde los puntos de celosía. En ciertos ángulos de incidencia, las ondas paralelas difractadas interfieren constructivamente y crean picos detectables de intensidad. W.H. Bragg identificó la relación ilustrada en la Figura 1 y derivó una ecuación correspondiente:

n á 2d_hkl sin á [1]

Aquí está la longitud de onda de los rayos X utilizados, d_hkl es el espaciado entre un conjunto particular de planos con (hkl) índices Miller*, y es el ángulo de incidencia en el que se mide un pico de difracción. Finalmente, n es un entero que representa el 'orden armónico' de la difracción. Por ejemplo, en el n-1, tenemos el primer armónico, lo que significa que la trayectoria de los rayos X difractada a través del cristal (equivalente a 2d_hkl sin ) es exactamente de1o,mientras que en el n-2, la trayectoria difractada es de2o. Por lo general, podemos asumir n-1 y, en general, n-1 para el valor de sin^-1(2o/d_h'k'l'),donde h'k'l' son los índices Miller de los planos que muestran el primer pico (en el valor más bajo de 2o) en un experimento de difracción. Los índices Miller son un conjunto de tres enteros que constituyen un sistema de notación para identificar direcciones y planos dentro de cristales. Para las direcciones, los índices [h k l] Miller representan la diferencia normalizada en las coordenadas x, y y z respectivas (en un sistema de coordenadas cartesianas) de dos puntos a lo largo de la dirección. Para los planos, los índices Miller (h k l) de un plano son simplemente los valores h k l de la dirección perpendicular al plano.

En un experimento XRD típico en modo de reflexión, la fuente de rayos X se fija en su posición y la muestra se gira con respecto al haz de rayos X sobre el . Un detector capta el haz difractado y tiene que mantenerse al día con la rotación de la muestra girando al doble de velocidad (es decir, para un ángulo de muestra determinado de - , el ángulo del detector es de 2o). La geometría del experimento se muestra esquemáticamente en la Figura 1.

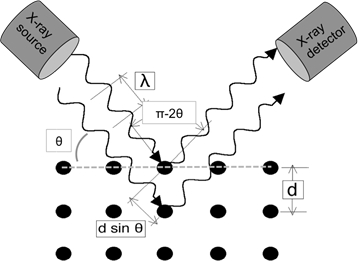
Figura 1: Ilustración de la Ley de Bragg.

Cuando se observa un pico de intensidad, la ecuación 1 se cumple necesariamente. En consecuencia, podemos calcular los espaciados d en función de los ángulos en los que se observan estos picos. Mediante el cálculo de los espaciados d de varios picos, la clase de cristal y la muestra de material de parámetros de estructura cristalina se pueden identificar utilizando una base de datos como el Manual de búsqueda de Hanawalt o bibliotecas de bases de datos disponibles con el software XRD que se está utilizando.

Suponiendo que la muestra que se está investigando no es un solo cristal. Si la muestra fuera un único cristal con un plano particular (h*k*l*) paralelo a la superficie de la muestra, tendría que girarse hasta que se cumpla la condición Bragg para el (h*k*l*) para ver un pico en intensidad difractada (para n-1) con picos armónicos potencialmente más altos (h*k*l*) (por ejemplo, para n-2) también detectables en ángulos más altos. En todos los demás ángulos no habría picos en una sola muestra de cristal. En su lugar, supongamos que la muestra es policristalina o que es un polvo, con un número estadísticamente significativo de granos cristalinos o partículas de polvo iluminadas por el haz de rayos X incidente. Bajo esta suposición, la muestra consiste en granos orientados aleatoriamente, con una probabilidad estadística similar para que todos los planos de celosía posibles difuminen.

Las relaciones entre el d_hkl y los parámetros de celda de la unidad se muestran a continuación en las ecuaciones 2-7 para las 7 clases de cristal, cúbica, tetragonal, hexagonal, romofídal, ortorrómbico, monoclínica y triclínica. Los parámetros de lacelda de la unidad consisten en longitudes de(a,b,c) y los ángulos entre los bordes de las celdas de la unidad para las 7 clases de cristal (la figura 1x muestra el ejemplo de una de las clases de cristal: la estructura tetragonal donde a-b-c, y el valor de 90⁰). Utilizando múltiples posiciones de pico difractadas (es decir, varios valores d_hkl distintos), los valores de los parámetros de celda de unidad se pueden resolver de forma única.

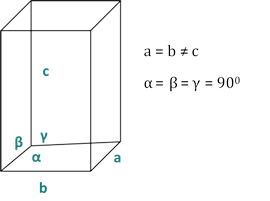
Figura 2: La estructura tetragonal como una de las siete clases de cristal.

Cúbico (a - b á c; á á á s a 90⁰):

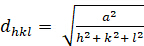[2]

Tetragonal (a á b a c; á á á a 90⁰):

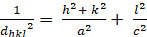[3]

Hexagonal (a - b á c; á á s 90⁰; á 120⁰):

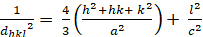[4]

Ortorrómbico (a a a b a c; á á á a 90⁰):

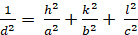[5]

Rhombohedral (a á b a c; á á á s a 90⁰):

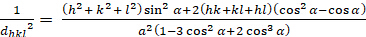[6]

Monoclínica (a - b á c; á á s 90⁰á á):

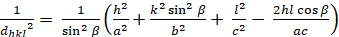[7]

Triclínico (a - b - c; á á á s a 90⁰):

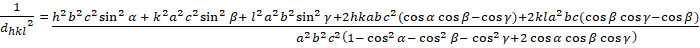      [8]

Relación entre las intensidades máximas difractadas y la estructura cristalina:

A continuación examinamos los factores que contribuyen a la intensidad en un patrón XRD. Los factores se pueden desglosar como 1) la contribución a la dispersión que resulta directamente de los aspectos estructurales únicos del material (los tipos y ubicaciones específicos de los átomos de dispersión en la estructura) y 2) aquellos que no son específicos del material. En el primero, hay dos factores: el "factor de absorción" y el "factor de estructura". El factor de absorción depende principalmente de la capacidad del material para absorber rayos X en su camino de entrada y salida. Este factor no tiene una dependencia de la posición, siempre que las muestras no sean delgadas (la muestra debe ser > 3 veces más gruesa que la longitud de atenuación de los rayos X). En otras palabras, la contribución del factor de absorción a la intensidad de los diferentes picos es constante. El «factor de estructura» afecta directamente a la intensidad de picos específicos como resultado directo de la estructura. Los factores restantes, la "multiplicidad", que representa todos los planos que pertenecen a la misma familia porque están relacionados simétricamente, y el factor 'Lorentz-Polarization', que proviene de la geometría del experimento XRD, también afectan al factor 'Lorentz-Polarization', que proviene de la geometría del experimento XRD, también afectan a la intensidad relativa de los picos, pero no son específicos de un material y se pueden contabilizar fácilmente con expresiones analíticas (es decir, el software de análisis XRD puede eliminarlos con funciones analíticas).

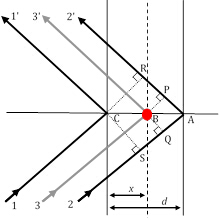
Figura 3: Tres trayectorias de rayos de difracción, de las cuales los rayos 11' y 22' satisfacen la condición Bragg, mientras que el rayo 33' resulta de dispersión por un átomo (círculo rojo) en una posición arbitraria.

Como el único factor que lleva la contribución estructural única de un material a las intensidades relativas de los picos XRD, el factor de estructura es muy importante y requiere una mirada más cercana. En la Figura 2, supongamos que la condición de difracción Bragg de 1^aorden (recuerde, que esto corresponde a n-1) se cumple entre el rayo_11' y el rayo_22' que están dispersos en dos planos atómicos en la dirección h00 (utilizando la notación de índices Miller descrita anteriormente) separados por una distancia d. Bajo esta condición, la diferencia en la longitud del trayecto entre el rayo_11' y el rayo_22' es á_(22'-11') - SA + AR . El desplazamiento de fase entre los rayos difractados 1 y 2 es, por lo tanto, de_{22'-11' (22'-11')}/o) 2o (suponiendo una simetría cúbica y, por lo tanto, d a/h en la dirección h00].

Con unos pocos pasos en geometría analítica, se puede demostrar que el desplazamiento de fase,_(33'-11'),con el rayo 3 difractado por un plano arbitrario de átomos que están espaciados una distancia arbitraria x, viene dado por:_(33'-11') a 2ohu, donde u-x/a (a es el parámetro de celda de la unidad en la dirección (h00).) Tomando las otras dos direcciones ortogonales, (0k0) y (00l), y v-y/a y w-z/a como coordenadas fraccionarias en las direcciones y y z, la expresión para el desplazamiento de fase se extiende a 2o(hu+kv+lw). Ahora, la onda de rayos X dispersada por el átomo j-ésimo en una celda de unidad tendrá una amplitud 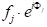de dispersión de f_j y una fase de á_j, de tal manera que la función que lo describe es . El factor de estructura que buscamos, por lo tanto, es la suma de todas las funciones de dispersión debido a todos los átomos únicos en una célula de unidad. Este factor de estructura, F, se da como:

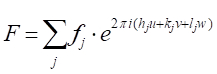[9]

y el factor de intensidad aportado por el factor de estructura es I - F².

Basado en las posiciones (u,v,w) de los átomos en planos particulares (h,k,l), existe la posibilidad de interferencia entre las ondas dispersas que es constructiva, destructiva o entre ellas, y esta interferencia afecta directamente a la amplitud de los picos XRD representando los planos (hkl).

Ahora, una gráfica de intensidad, Yo, versus 2o es lo que se mide en un experimento XRD. La determinación del tipo de cristal y de los parámetros de celda de unidad asociados(a, b, c, , ,) se puede llegar analíticamente observando la presencia/ausencia sistemática de picos, utilizando las ecuaciones 2-9, comparando valores con bases de datos, utilizando la deducción y un proceso de eliminación. Hoy en día, este es el proceso es bastante automatizado por una variedad de software vinculado a bases de datos de estructura cristalina.

El siguiente procedimiento se aplica a un instrumento XRD específico y su software asociado, y puede haber algunas variaciones cuando se utilizan otros instrumentos.

1. Examinaremos una muestra de polvo de Ni en un instrumento Panalytical Alpha-1 XRD.
2. En primer lugar, elija la máscara para fijar el tamaño de la viga de acuerdo con el diámetro de la muestra. La viga no debe tener una huella mayor que la muestra con el valor más pequeño (normalmente 7⁰-10⁰). Para una muestra de anchura, el tamaño de la viga debe ser < sin.
3. Cargue la muestra en la etapa del spinner de muestra y bloquee la muestra en su posición. El spinner de muestra ayuda a aleatorizar espacialmente la exposición de la muestra a la fuente de rayos X.
4. Elija el rango de ángulo para su escaneo XRD. Por ejemplo, 15-90 grados es un rango típico.
5. Elija un tamaño de paso, es decir, el incremento en 2o,y el tiempo de integración (contando). Generalmente un tamaño de paso de 0,05 grados y una integración de 4 segundos es el valor predeterminado para un escaneo de gran angular.
6. Una vez que todas las posiciones de pico se determinan a través de este escaneo inicial, los escaneos posteriores pueden centrarse en un rango de exploración más estrecho alrededor de picos específicos usando un tamaño de paso más pequeño en ángulo si se desean datos de resolución más alta de esos picos.

En la Figura 4 vemos los picos XRD para la muestra de polvo De. Tenga en cuenta que los picos que se observan (por ejemplo, {111}, {200}) son para aquellos que tienen todas las combinaciones pares o todas las combinaciones impares de h, ky l. Ni es cúbica centrada en la cara (FCC), y en todas las estructuras de la FCC, los picos correspondientes a los planos dehkldonde h, ky l son mezclas de enteros pares e impares, están ausentes debido a la interferencia destructiva de los rayos X dispersos. Faltan picos correspondientes a planos, como {210} y {211}. Este fenómeno se denomina reglas sistemáticas de presencia y ausencia, y proporcionan una herramienta analítica para evaluar la estructura cristalina de la muestra.

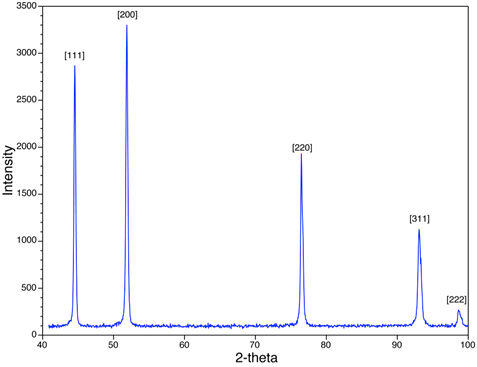
Figura 4:Se muestra un escaneo XRD de Ni con una estructura cúbica centrada en la cara.

Esta es una demostración de un experimento XRD estándar. El material examinado en este experimento fue en forma de polvo, pero XRD funciona igual de bien con una pieza sólida de material, siempre y cuando la muestra tenga una superficie plana que se puede establecer paralela al plano de la etapa de la muestra.

XRD es un método bastante ubicuo para determinar la presencia (o ausencia) del orden cristalográfico en los materiales. Más allá de la aplicación estándar de determinar la estructura cristalina, XRD se utiliza a menudo para obtener una variedad de otra información estructural como:

1. Si la estructura de un material es o no amorfo (caracterizado por una joroba amplia en la intensidad de difracción y la falta de picos cristalográficos discernibles),
2. Si la muestra es un material compuesto que consta de múltiples fases cristalográficas y, si es así, determinar la fracción de cada fase,
3. Determinar si un material es un compuesto amorfo/cristalino
4. Determinar el tamaño de grano/partícula del material,
5. Determinar el grado de textura (orientación preferida de los granos) en el material.