Análisis de boquillas: variaciones en el número de Mach y la presión a lo largo de una boquilla convergente y una convergente-divergente

Fuente: Shreyas Narsipur, Ingeniería Mecánica y Aeroespacial, Universidad Estatal de Carolina del Norte, Raleigh, Carolina del Norte

Una boquilla es un dispositivo que se utiliza comúnmente para acelerar o desacelerar el flujo en virtud de su sección transversal variable. Las boquillas son ampliamente utilizadas en sistemas de propulsión aeroespacial. En los cohetes, el propulsor que se expulsa de la cámara se acelera a través de una boquilla para crear una fuerza de reacción que impulsa el sistema. En los motores a reacción, una boquilla se utiliza para transformar la energía de una fuente de alta presión en energía cinética del escape para producir empuje. El modelo isentrópico a lo largo de la boquilla es suficiente para un análisis de primer orden ya que el flujo en una boquilla es muy rápido (y por lo tanto adiabático a una primera aproximación) con muy pocas pérdidas de fricción (porque el flujo es casi unidimensional con una presión favorable degradado, excepto si las ondas de choque se forman y las boquillas son relativamente cortas).

En este experimento, dos tipos de boquillas se montan en un equipo de prueba de boquillas, y se crea un flujo de presión utilizando una fuente de aire comprimido. Las boquillas se ejecutan para diferentes configuraciones de contrapresión para analizar el flujo interno en las boquillas en condiciones de flujo variables, identificar los diversos regímenes de flujo y comparar los datos con las predicciones teóricas.

Una boquilla comienza en el punto donde el diámetro de la cámara comienza a disminuir. Hay dos tipos principales de boquillas: la boquilla convergente y la boquilla convergente. Una de las relaciones isentrópicas que rigen entreel número Mach (M), el área de laboquilla (A) y lavelocidad (u) se representa mediante lasiguiente ecuación:

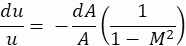(1)

donde u es la velocidad, A es el área de la boquilla, y M es el número Mach. Basado en la Ecuación 2,

1. En M - 0, el flujo es estático, es decir, la condición de no flujo existe
2. A 0 < M < 1, a medida que disminuye el área, se observa un aumento proporcional en la velocidad del flujo
3. En M- 1, cualquier aumento en el área producirá un aumento proporcional de la velocidad

Las boquillas convergentes, como se muestra en la Figura 1,son tubos con un área que disminuye desde la entrada de la boquilla hasta la salida (o garganta) de la boquilla. A medida que el área de la boquilla disminuye, la velocidad de flujo aumenta, con la velocidad máxima de flujo que ocurre en la garganta de la boquilla. A medida que aumenta la velocidad de flujo de entrada, la velocidad de flujo en la garganta de la boquilla sigue aumentando hasta que alcanza Mach 1. En este punto, el flujo en la garganta se ahoga, lo que significa que cualquier aumento adicional de la velocidad de flujo de entrada no aumentará la velocidad de flujo en la garganta. Es por esta razón que las boquillas convergentes se utilizan para acelerar los fluidos solo en el régimen de flujo subsónico y se pueden encontrar comúnmente en todos los chorros comerciales (excepto en el Concord) ya que viajan a velocidades subsónicas.

Figura 1. Esquema de una boquilla convergente. Haga clic aquí para ver una versión más grande de esta figura.

Para vehículos como cohetes y aviones militares, que deben viajar a y por encima de la velocidad del sonido, se utiliza una boquilla convergente, como se ilustra en la Figura 2. En una boquilla convergente, la sección convergente va seguida de una sección de boquilla divergente y está diseñada de tal manera que el flujo se atragante en la garganta de la sección convergente, fijando así el caudal de masa en el sistema. El flujo se expande entonces isentropicalmente para alcanzar números Mach supersónicos en la sección divergente. Las velocidades de flujo supersónicas establecidas en la sección divergente son una función de las relaciones de área de la boquilla después de la garganta. Basado en el diseño de la boquilla convergente, la velocidad de flujo después de la garganta de la boquilla puede: (i) disminuir a velocidades subsónicas, (ii) convertirse en supersónico, causar un choque normal, y luego disminuir a velocidades subsónicas en la salida de la boquilla, o (iii) siguen siendo supersónicos a lo largo de la sección divergente. La cantidad de empuje producida por la boquilla depende de la velocidad y la presión de salida y del caudal de masa a través de la boquilla.

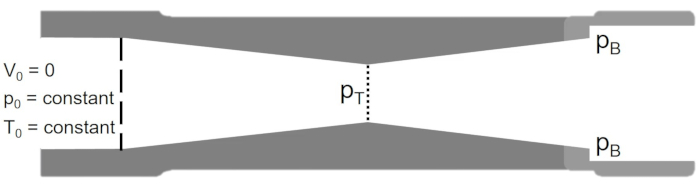
Figura 2. Esquema de una boquilla convergente. Haga clic aquí para ver una versión más grande de esta figura.

La contrapresión (p_B) es el factor de accionamiento que determina la condición de flujo en la boquilla. Cuando la presión de estancamiento, p_O a p_B, no hay flujo a través de la boquilla. A medida que se reduce la p_B, el número Mach en la garganta (p_T) aumenta hasta que el flujo se asfixia(M_T a 1). La condición en la que se produce el flujo asfixiado se puede calcular utilizando la relación isentrópica:

(2)

donde es la relación de calor específica del fluido. Sustituyendo el valor de 1,4 (relación de calor específica para el aire seco) en la Ecuación 2, obtenemos una relación de contrapresión de:

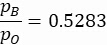(3)

La ecuación 3 define el límite entre los regímenes de flujo no estrangulado y asfixiado. Cuando se ahoga el flujo, el número Mach ya no aumenta y se tapa en M a 1.

En el caso de una boquilla convergente, la salida de la boquilla corresponde a la garganta de la boquilla (como se ve en la Figura 1); por lo tanto, el número Mach justo en la salida no excede 1, es decir, el flujo nunca va supersónico. Una vez que el flujo sale de la boquilla, se somete a una expansión, debido al aumento repentino en el área que podría conducir a velocidades de flujo supersónicos (no controlados).

Según la Figura 3,las siguientes son las condiciones de flujo que se pueden observar en una boquilla convergente:

1. No hay condición de flujo, donde la contrapresión es igual a la presión total.
2. Flujo subsónico, donde el flujo se acelera a medida que disminuye el área, y la presión disminuye.
3. Flujo subsónico, donde hay una aceleración significativamente mayor y la presión disminuye.
4. Flujo asfixiado, donde cualquier caída de presión no acelera el flujo.
5. Flujo asfixiado, donde el flujo se expande después de la salida de la boquilla (considerado no isentrópico).

Figura 3. Condiciones de flujo y regímenes en una boquilla convergente (predicciones teóricas). Haga clic aquí para ver una versión más grande de esta figura.

El parámetro de flujo de masa(MFP)es una variable que determina la velocidad a la que la masa fluye a través de la boquilla y se da por la ecuación:

(4)

Aquí, 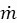está el caudal de masa a través de la boquilla, T_O es la temperatura de estancamiento, y A_T es el área de la garganta, que, en el caso de la boquilla convergente, es igual a la zona en la salida de la boquilla, A_E . Como se observa en la Figura 3,hasta que el flujo asfixiado, la impresora multifunción continúa aumentando. Una vez que se ahoga el flujo, el caudal de masa es fijo, y el MFP sigue siendo una constante para disminuir las relaciones de contrapresión.

Con el fin de lograr flujos supersónicos controlados en una boquilla, es necesario introducir una sección divergente después de la garganta de una boquilla convergente, como se ilustra en la Figura 2. Una vez que el flujo se ahoga en la garganta de una boquilla convergente (basada en la Ecuación 3), pueden ocurrir tres condiciones de flujo posibles: flujo isentrópico subsónico (el flujo se desacelera después de la condición asfixiada), flujo no isentrópico supersónico (donde el flujo se acelera sucaraicamente, forma una onda de choque - una región delgada de moléculas fusionadas que se forma normal a un cierto punto en la boquilla y causa un cambio repentino en las condiciones de flujo, generalmente conocido como un choque normal - y desacelera subsonópicamente después de la choque) o flujo isentrópico supersónico (donde el flujo se acelera supersonicamente después de la condición asfixiada). La Figura 4 muestra los siguientes siete perfiles en la gráfica de relación de posición frente a presión. Tenga en cuenta que la primera línea discontinua vertical a la izquierda de la_{P/p O} frente a la distancia a lo largo de la gráfica de la boquilla es la ubicación de la garganta, la segunda línea discontinua vertical es la ubicación de la salida de la boquilla y la línea discontinua horizontal marca la condición de estrangulado.

1. Flujo subsónico que nunca llega a la condición de asfixia.
2. Flujo subsónico que alcanza la condición asfixiada pero no alcanza velocidades supersónicas (considerado isentrópico).
3. Flujo subsónico que alcanza la condición asfixiada, con el flujo supersónico resultante formando un choque normal, que luego experimenta desaceleración subsónica. Aquí, el choque normal causa una caída repentina en la velocidad y un aumento en la contrapresión, como lo indica el aumento repentino de p/p_O.
4. Flujo subsónico que alcanza la condición de estrangulamiento, con el flujo supersónico resultante formando un choque normal después de la boquilla (considerado isentrópico en la boquilla).
5. Flujo sobre-expandido – la presión en la salida de la boquilla es menor que la presión ambiental, haciendo que el chorro que sale de la boquilla sea altamente inestable con enormes variaciones en la presión y la velocidad a medida que viaja aguas abajo.
6. El flujo después de la condición asfixiada es supersónico a través de la boquilla, y no se forma ningún choque.
7. Flujo subexpandido– la presión en la salida de la boquilla es mayor que la presión ambiental y resulta en efectos similares a los flujos sobreexpandidos.

Figura 4. Condiciones y regímenes de flujo en una boquilla convergente-divergente (predicciones teóricas). Haga clic aquí para ver una versión más grande de esta figura.

En esta demostración, se utilizó un equipo de prueba de boquillas, que consistía en una fuente de aire comprimido que canaliza el aire de alta presión a través de las boquillas que se están probando, como se muestra en la Figura 5. La presión de flujo oscila entre 0 y 120 psi y se controla mediante una válvula mecánica. Mientras que las presiones se miden utilizando un sensor externo, los caudales de masa en la boquilla se miden por un par de rotametros colocados justo antes del escape de la plataforma de prueba de la boquilla.

Figura 5. Equipo de prueba de boquillas. Haga clic aquí para ver una versión más grande de esta figura.

1. Medición de la presión axial en boquillas convergentes y divergentes convergentes

1. Monte la boquilla convergente en el centro del equipo de prueba de la boquilla, como se muestra en la figura 5. La sección 2D para la boquilla convergente con etiquetas para los grifos de presión se muestra en la Figura 6.

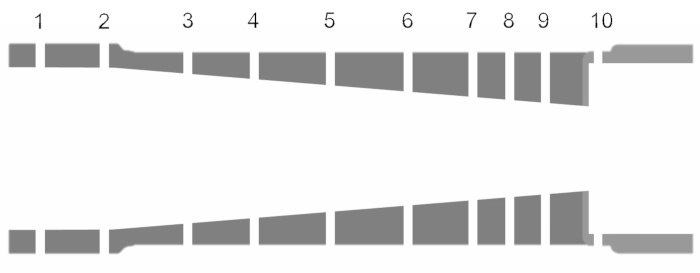
Figura 6. Geometría de la boquilla convergente. Haga clic aquí para ver una versión más grande de esta figura.

2. Conecte los 10 puertos de presión estática y el puerto de presión de estancamiento al sistema de medición de presión utilizando tubos de PVC flexibles de alta presión.
3. Conecte el sistema de medición de presión a la interfaz gráfica del software para la lectura de datos de presión en tiempo real.
4. Tome la lectura de la condición cero/sin flujo.
5. Abra la válvula de control de flujo mecánico para iniciar el flujo de aire.
6. Gire la válvula para ajustar el caudal para obtener una relación de contrapresión (p_B/p_O) de 0,9. Tenga en cuenta que la contrapresión para las boquillas convergentes y de divergentes convergentes corresponde a la lectura de datos de presión desde el puerto 10.
7. Registre los datos correspondientes al Cuadro 1.
8. Disminuya la relación de contrapresión en pasos de 0,1 hasta que p_B/p_O a 0,1 repita el paso 7 para cada ajuste. Además, repita el paso 7 para un p_B/p_O a 0.5283 para capturar los datos de flujo en la condición teórica de flujo estrangulado.
9. Sustituya la boquilla convergente por la boquilla convergente y repita los pasos 1.2 - 1.8. La sección 2D para la boquilla convergente con etiquetas para los grifos de presión se muestra en la Figura 7.
10. Una vez finalizadas las pruebas, desconecte todos los sistemas y desmonte la plataforma de prueba de la boquilla.

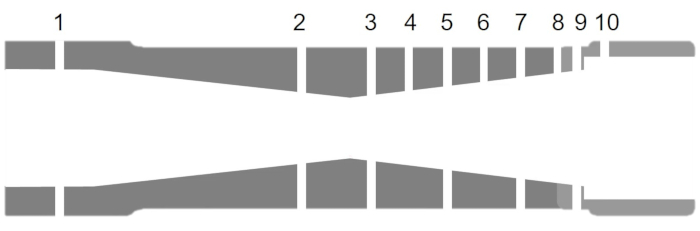
Figura 7. Geometría de la boquilla convergente. Haga clic aquí para ver una versión más grande de esta figura.

Tabla 1. Datos recogidos para el experimento de la boquilla.

Toque el número	Posición axial del grifo (pulg.)	Relación de área de la boquilla (A/Ai)	Pestático (psi)	Po (psi)	Masa Caudal (slugs/s)	Patm (psi)	To (F)
Figura 6/7	Tabla 2	Tabla 2	Presión del medidor	Calibre Presión	Rotámetro	Presión del medidor	Sensor de temperatura

Cuadro 2. Datos de geometría de la boquilla.

Toque el número	Boquilla convergente		Boquilla convergente-divergente
	Posición axial del grifo (pulg.)	Relación de área de la boquilla (A/Ai)	Posición axial del grifo (pulg.)	Relación de área de la boquilla (A/Ai)
1	0	60.14	0	60.14
2	1	51.379	4.5	6.093
3	2	35.914	6.5	1
4	3	23.218	6.9075	1.053
5	4	13.275	7.3795	1.222
6	5	6.094	7.8515	1.403
7	5.5	3.54	8.3235	1.595
8	6	1.672	8.7955	1.802
9	6.5	1	9.2675	2.02
10	7	60.041	9.5	60.041

En el análisis se utilizaron las siguientes constantes: calor específico del aire seco, 1,4; área de la boquilla de referencia, A_i a 0,0491 en², y presión atmosférica estándar, P_atm a 14,1 psi. Las figuras 8 y 9 muestran la variación en la relación de presión y el número Mach a lo largo de la longitud de la boquilla (normalizada en función de la longitud total de la boquilla) para varios ajustes de contrapresión para las boquillas convergentes y de divergentes, respectivamente. El parámetro de flujo de masa frente a la relación de contrapresión también se traza y estudia para ambas boquillas.

A partir de la Figura 8,observamos que a medida que disminuye la relación p_B/p_O (hasta 0.5283), el flujo en cada sección de la boquilla es subsónico y aumenta con el área decreciente. En y por debajo de la p_B/p_O a 0,5283, el número Mach en la garganta (distancia normalizada de la boquilla de 0,93) no supera uno. Esto demuestra claramente que el flujo se atraganta en la garganta. Más allá de la salida de la garganta/boquilla, hay una expansión incontrolada del flujo, lo que lleva a números Mach supersónicos. Las tendencias generales de la distribución p/p_O coinciden con las tendencias teóricas de la Figura 3. Las tendencias en MFP siguen los resultados teóricos hasta p_B/p_O a 0,6, pero comienzan a disminuir en lugar de la meseta para valores más bajos de relaciones de contrapresión. Dado que el flujo está asfixiado, la impresora multifunción debe ser constante. Sin embargo, en función de la ubicación del grifo que mide la presión de la garganta (toque 9, Figura 6), vemos que las mediciones se toman ligeramente antes de la verdadera garganta de la boquilla que a su vez conduce a una medición incorrecta de la impresora multifunción.

Para la boquilla convergente(Figura 9), se observa un flujo subsónico hasta p/p_O en la garganta (distancia de la boquilla normalizada á 0,68) es igual a 0,5283 (condición de flujo estrangulado). La reducción adicional de p_B/p_O muestra tres patrones distintos:
a. Patrón 1 - El flujo alcanza la condición de estrangulamiento en la garganta y se desacelera subsónicamente en la sección divergente (0,8 < p_B/p_O < 0,7).
b. Patrón 2 - El flujo acelera supersonicamente más allá de la garganta, forma un choque en la sección divergente y desacelera (en algunos casos a velocidades subsónicas) para 0.7 < p_B/p_O < 0.3.
c. Patrón 3 - El flujo continúa acelerándose supersonicamente durante la totalidad de la sección divergente para los valores p_B/pO inferiores a 0,3.

La mFP aumenta con la disminución de las relaciones de contrapresión, picos en p_B/p_O a 0,5, y comienza a disminuir en lugar de permanecer constante como se predijo por la teoría.

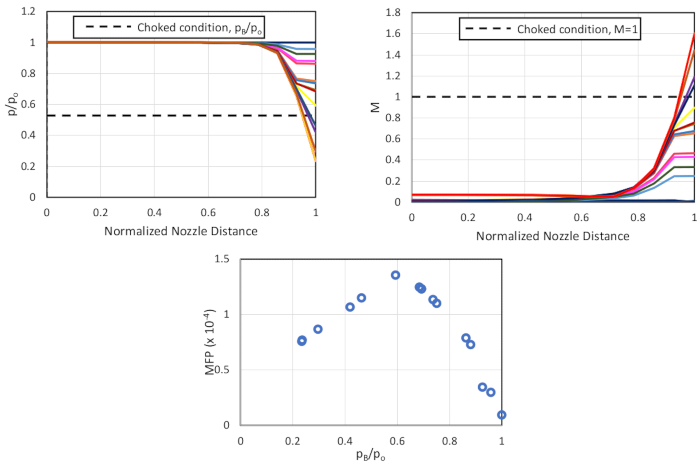
Figura 8. Resultados de la variación de la boquilla convergente (desde arriba a la derecha, en el sentido de las agujas del reloj) en la relación de presión a través de la boquilla; variación en el número Mach a través de la boquilla; y la variación en el parámetro de arado de masa con relación de contrapresión. Haga clic aquí para ver una versión más grande de esta figura.

Las boquillas se utilizan comúnmente en los sistemas de propulsión de aeronaves y cohetes, ya que ofrecen un método simple y eficaz para acelerar el flujo en distancias restringidas. Con el fin de diseñar boquillas para adaptarse a una aplicación determinada, una comprensión del comportamiento del flujo y los factores que afectan a dicho comportamiento para una gama de condiciones de flujo es esencial para diseñar sistemas de propulsión eficientes. En esta demostración, las boquillas convergentes y convergentes -dos de los tipos de boquillas más comunes utilizados en aplicaciones aeroespaciales- se probaron utilizando un equipo de prueba de boquillas. Las variaciones de presión y número Mach en las dos boquillas se estudiaron para una amplia gama de condiciones de flujo.

Los resultados de las pruebas de la boquilla convergente mostraron que el límite máximo hasta el cual se puede acelerar el flujo es m a 1, momento en el que el flujo en la garganta de la boquilla se ahoga. Una vez que el flujo se ahoga, cualquier aumento en la velocidad de flujo de entrada no aumentó la velocidad de flujo en la garganta / salida a velocidades supersónicas. El análisis de la boquilla convergente proporciona información sobre cómo se pueden lograr velocidades de flujo supersónico sin perder de vista una vez que el flujo se atragante en la garganta. También observamos tres tipos de flujos que se pueden obtener después de la garganta asfixiada dependiendo de la relación de contrapresión del flujo. Una comparación de las tendencias de presión obtenidas tanto para las boquillas de tipo convergentes como para las convergentes con los resultados teóricos fue excelente. Sin embargo, los resultados experimentales mostraron que el parámetro de flujo de masa disminuyó para valores más bajos de relación de contrapresión en lugar de meseta una vez que se logró el valor máximo, como lo predijo la teoría.

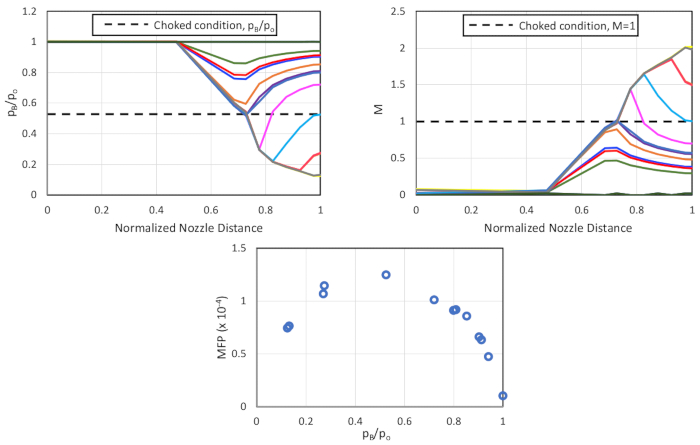
Figura 9. Resultados de la variación de la boquilla convergente (de arriba a la derecha, en el sentido de las agujas del reloj) en la relación de presión a través de la boquilla; variación en el número Mach a través de la boquilla; y la variación en el parámetro de arado de masa con relación de contrapresión. Haga clic aquí para ver una versión más grande de esta figura.