Patient-specific Modeling of the Heart: Estimation of Ventricular Fiber Orientations

Summary

A methodology to estimate ventricular fiber orientations from in vivo images of patient heart geometries for personalized modeling is described. Validation of the methodology performed using normal and failing canine hearts demonstrate that that there are no significant differences between estimated and acquired fiber orientations at a clinically observable level.

Abstract

Patient-specific simulations of heart (dys)function aimed at personalizing cardiac therapy are hampered by the absence of in vivo imaging technology for clinically acquiring myocardial fiber orientations. The objective of this project was to develop a methodology to estimate cardiac fiber orientations from in vivo images of patient heart geometries. An accurate representation of ventricular geometry and fiber orientations was reconstructed, respectively, from high-resolution ex vivo structural magnetic resonance (MR) and diffusion tensor (DT) MR images of a normal human heart, referred to as the atlas. Ventricular geometry of a patient heart was extracted, via semiautomatic segmentation, from an in vivo computed tomography (CT) image. Using image transformation algorithms, the atlas ventricular geometry was deformed to match that of the patient. Finally, the deformation field was applied to the atlas fiber orientations to obtain an estimate of patient fiber orientations. The accuracy of the fiber estimates was assessed using six normal and three failing canine hearts. The mean absolute difference between inclination angles of acquired and estimated fiber orientations was 15.4 °. Computational simulations of ventricular activation maps and pseudo-ECGs in sinus rhythm and ventricular tachycardia indicated that there are no significant differences between estimated and acquired fiber orientations at a clinically observable level.The new insights obtained from the project will pave the way for the development of patient-specific models of the heart that can aid physicians in personalized diagnosis and decisions regarding electrophysiological interventions.

Introduction

The computational approach is becoming central to the advancement of the understanding of the function of the heart in health and disease. State-of-the-art whole-heart models of electrophysiology and electromechanics are currently being used to study a wide range of phenomena, such as normal ventricular propagation, arrhythmia, defibrillation, electromechanical coupling, and cardiac resynchronization¹. However, for the computational approach to be directly applicable in the clinical environment, it is imperative that the models be patient-specific, i.e. the models must be based on the specific architecture and electrophysiological or electromechanical properties of the patient's diseased heart. Simulation with such models will aid physicians to arrive at highly personalized decisions for electrophysiological interventions as well as prophylaxis, thereby dramatically improving cardiac health care^2-4 .

Creation of realistic cardiac models requires the acquisition of the geometry and fiber structure of a patient heart. Fiber orientations determine directions of electrical propagation and strain distributions in the heart, and therefore acquiring them is essential to cardiac modeling^{5, 6}.With recent advances in medical imaging, it is now feasible to obtain the geometry of a patient heart, includingstructural remodeling such as infarction, in vivo with high resolution using magnetic resonance imaging (MRI) and computed tomography (CT) technologies. However, there is no practical method for acquiring fiber structure of a patient heart in vivo. Diffusion tensor (DT) MRI^{7, 8}, the only technique to acquire fiber orientations of the intact heart, is not widely available in vivo due to certain limitations ⁹. A brief description of the previous efforts to translate DTMRI to the clinical setting can be found elsewhere ². Though methodologies such as rule-based assignment of fiber orientations offer alternatives to DTMRI, these methodologies have certain serious limitations ^{2, 10}. Thus difficulties in acquiring cardiac fiber structure in vivo presently impede the application of electrophysiological and electromechanical cardiac simulations in clinical setting. The objective of this research was to directly address this need.

We hypothesized that ventricular fiber orientations of a heart can be accurately predicted given the geometry of the heart and an atlas, where the atlas is a heart whose geometry and fiber orientations are available. Accordingly, we used state of the art techniques to develop a methodology for estimation of cardiac fiber orientations in vivo, and tested the hypothesis in normal and failing canine ventricles². The central idea of our fiber estimation methodology is to exploit similarities in fiber orientations, relative to geometry, between different hearts in order to approximate the fiber structure of a (target) heart for which only the geometry information is available. At the heart of our estimation methodology is the registration of the atlas geometry with the target geometry using large deformation diffeomorphic metric mapping (LDDMM) ¹¹, and the morphing of atlas fiber orientations using preservation of principal components (PPD) ^{2, 12}.The diffeomorphicproperty of LDDMM guarantees that the atlas does not "foldover" itself during deformation, thereby preserving the integrityof anatomical structures. Figure 1 illustrates the processing pipeline of our methodology. The protocol text section §1 describes the various components of the pipeline by demonstrating how the estimation can be performed for an example patient. The numbers inside some of the blocks in Figure 1 refer to the corresponding subsections under section §1 of the protocol text.

We evaluated the performance of the proposed methodology by quantifying the estimation error, and measuring the effect of this error onsimulations of cardiac electrophysiology, by computationally simulating local electrical activation maps as well as pseudo-electrocardiograms (pseudo-ECGs). Due to the unavailability of human hearts, the performance evaluation was conducted using canine hearts available from previous studies ^13-15 . The estimation error was calculated by means of inclination angles ¹⁶, followingthe tradition of histology, where angular measurements are performedon tissue sections that are cut parallel to the epicardialsurface. Since the anglebetween the fiber direction and epicardial tangent plane is generallysmall ^{17, 18}, the information loss in describing a fiberdirection entirely using its inclination angle is insignificant. For the computational simulations, image-based models were built as reported previously ^{19, 20}, and cardiac tissue in the models was represented based on established mathematical techniques and experimental data ^21-25 . Sinus rhythm was simulated by replicating activation originating from the Purkinje network²⁶, and ventricular tachycardia, by an S1-S2 pacing protocol ²⁷. Pseudo-ECGs were computed ²⁸ and compared using the mean absolute deviation (MAD) metric ²⁹.

Protocol

1. Fiber Orientations Estimation

1. Acquire structural MRI and DTMRI images of a normal adult human heart in diastole, at a resolution of 1 mm³. Using ImageJ, extract the ventricular myocardium from the atlas structural image by fitting, for each short-axis slice, closed splines through a set of landmark points placed along the epicardial and endocardial boundaries in the slice (Figure 2A & Figure 2B). Perform the placement of landmark points manually for every 10^th slice in the image. Obtain the landmark points for the remaining slices by linearly interpolating the manually identified points, using MATLAB.Reconstruct the fiber orientations of the atlas heart by computing the primary eigenvectors of the DTs in the DTMRI image (Figure 2C).
2. Acquire an image of the geometry of the patient heart in diastole using in vivo cardiac CT or MRI. Reconstruct the patient heart geometry from the image similarly to the way the atlas was built (Figure 3A & Figure 3B). The patient image should be re-sampled prior to reconstruction such that the in-plane resolution is 1 mm². Similarly, the number of slices for which landmarks are manually picked, and the interval of out-of-plane interpolation must be adjusted so that the segmented patient heart image has a slice thickness of 1 mm.
3. Deform the atlas ventricular image to match the patient geometry image in two steps. In the first step, perform an affine transformation based on a set of thirteen landmarks points: the left ventricular (LV) apex, the two right ventricular (RV) insertion points at the base, the two RV insertion points midway between base and apex, and four sets of two points that evenly divide RV and LV epicardial contours at base, and midway between base and apex (Figure 4A & Figure 4B). In the second step, deform the affine-transformed atlas ventricles further to match the patient geometry, using large deformation diffeomorphic metric mapping (LDDMM) (Figure 4C).
4. Morph the DTMRI image of the atlas by re-positioning of image voxels and re-orientating the DTs according to the transformation matrix of the affine matching and the deformation field of the LDDMM transformation. Perform the re-orientation of the DTs using the preservation of principal directions (PPD) method.
5. Obtain the estimate of the patient fiber orientations from the morphed atlas DTMRI image by computing the primary eigenvector of the DTs (Figure 5).

2. Measurement of Estimation Error

1. Acquire ex vivo structural MR and DTMR images of six normal and three failing canine hearts, at a resolution of 312.5×312.5×800 μm³. Here, heart failure should be generated in the canines via radiofrequency ablation of the left bundle-branch followed by 3 weeks of tachypacing at 210 min^-1.
2. Segment the ventricles from the canine hearts similarly to the human atlas heart, as described in §1.1. Denote ventricles segmented from normal canine hearts as hearts 1 through 6, and those segmented from failing canine hearts as hearts 7 through 9 (Figure 6).
3. Obtain five different estimates of ventricular fiber orientations of heart 1 by using each of hearts 2 to 6 as an atlas (Figure 7).
4. Estimate fiber orientations for each of the failing ventricles using heart 1 as the atlas (Figure 8).
5. Foreach data point in each set of estimated fiber orientations, compute the estimation error as|θ_c-θ_a| , where θ_c and θ_a are the inclination angles of estimated and acquired fiber orientations at that point, respectively.
6. For each data point in each set of estimated fiber orientations, compute the acute angle betweenestimated and acquired fiber directions in three-dimensions (3D) by means of thevector dot product.

3. Measurement of the Effects of Estimation Error on Simulations

1. From heart 1, construct six models, one with the DTMRI-acquired fiber orientations of heart 1 (referred to as model 1), and five with the five estimated fiber orientations datasets (models 2 to 6).For each of the three failing heart geometries, construct two ventricular models, one with the DTMRI-acquired fiber orientations and the other with the estimated fiber orientations. Here the spatial resolution of the models, computed in terms of the average edge length of the meshes, should be about 600 μm. Denote the heart failure models with DTMRI-acquired fibers as models 7 to 9, and those with estimated fibers as models 10 to 12.In the models, use monodomain representation to describe the cardiac tissue, with governing equations:

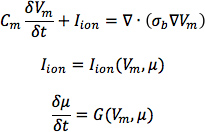
where σ_bis the bulk conductivity tensor which is calculated from the bidomain conductivity tensors as described by Potse et al³⁰; V_m is the transmembrane potential; C_m is the membrane specific capacitance; and I_ion is the density of the transmembrane current, which in turn depends on V_m and a set of state variables μ describing the dynamics of ionic fluxes across the membrane.For C_m , use a value of 1 μ F/cm². For σ_i in normal canine heart models, use longitudinal and transverse conductivity values of 0.34 S/m and 0.06 S/m, respectively. Represent l_lon by the Greenstein-Winslow ionic models of the canine ventricular myocyte. Decrease the electrical conductivities in canine heart failure ventricular models by 30% (Figure 9).

2. Using the software package CARP (CardioSolv, LLC), simulate sinus rhythm with all models. Induce reentrant ventricular tachycardia (VT) in the six failing models using an S1-S2 pacing protocol. Choose the timing between S1 and S2 to obtain sustained VT activity for 2 sec after S2 delivery. If VT is not induced for any S1-S2 timing, decrease the conductivities by up to 70% until VT was induced (Figure 10).
3. For each simulation, calculate pseudo-ECGs by taking the difference of extracellular potentials between two points in an isotropic bath surrounding the hearts. Place the two points near the base of the heart separated by 18 cm, such that the line connecting them is perpendicular to the base-apex plane of the septum as illustrated in Figure 10. For each simulation with estimated fiber orientations, compute the MAD metric as

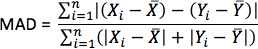
where X is the ECG waveform of the simulation with estimated fiber orientations, Y is the ECG waveform of thecorresponding simulation with acquired fiber orientations, X is the mean value of X,Y is the mean value of Y, and n is the length of X and Y.

Results

Figure 11, A-C displays streamlined visualizations of estimated as well as DTMRI-derived fiber orientations in normal and failing hearts. Qualitative examination shows that estimated fiber orientations align well with DTMRI-derived ones. Panel D illustrates, overlaid on the geometry of heart 1, the distribution of error in normal hearts' inclination angles, averaged across all five estimates. Panel E shows the mean distribution of error in failing hearts' inclination angles, overlaid on the geomet...

Discussion

This research demonstrates quantitatively that, in the absence of DTMRI, myocardial fiber orientations of normal and failing ventricles can be estimated from in-vivo images of their geometries for use in simulations of cardiac electrophysiology. The proposed methodology is demonstrated with in vivo CT data, but it is equally applicable to in vivo MR images of ventricular geometry, addressing the lack of ability to directly acquire patient fiber orientations. It is thus an important step ...

Materials

Name	Company	Catalog Number	Comments
LDDMM	Johns Hopkins University		http://cis.jhu.edu/software/lddmm-volume/index.php
MATLAB	Mathworks, Inc.	R2011b	http://www.mathworks.com/products/matlab/
ImageJ	National Institutes of Health		http://rsbweb.nih.gov/ij/
Tarantula	CAE Software Solutions		http://www.meshing.at/Spiderhome/Tarantula.html
CARP	CardioSolv		http://cardiosolv.com/
Canine images	Johns Hopkins University		http://www.ccbm.jhu.edu/research/DTMRIDS.php