JoVE 비디오를 활용하시려면 도서관을 통한 기관 구독이 필요합니다. 전체 비디오를 보시려면 로그인하거나 무료 트라이얼을 시작하세요.
Method Article
샘플링 모아레 프린지에서의 마이크로 / 나노 스케일 변형률 측정
요약
마이크로 / 나노 스케일에서 고정밀 변형률 분포 측정을위한 2 픽셀 및 다중 픽셀 샘플링 방법을 특징으로하는 샘플링 모아레 기법이 여기에 제시됩니다.
초록
이 연구는 전장 마이크로 / 나노 스케일 변형 측정을위한 샘플링 모아레 기법의 측정 절차와 원리를 설명합니다. 개발 된 기법은 두 가지 방식으로 수행 될 수 있습니다 : 재구성 된 곱셈 모아레 법 또는 공간 위상 변이 샘플링 모아레 법 사용. 표본 그리드 피치가 약 2 픽셀 인 경우, 2- 픽셀 샘플링 모아레 무늬가 생성되어 변형 측정을위한 곱셈 모아레 패턴을 재구성합니다. 변위 및 변형 감도는 동일한 넓은 시야에서 기존 스캐닝 모아레 방법보다 두 배 높습니다. 표본 그리드 피치가 3 픽셀 이상이거나 또는 그보다 크면 다중 픽셀 샘플링 모아레 무늬가 생성되고 공간 위상 변이 기술이 전체 필드 변형 측정을 위해 결합됩니다. 변형률 측정 정확도가 크게 향상되고 자동 배치 측정을 쉽게 수행 할 수 있습니다.두 가지 방법 모두 기존의 모아레 기법과 같이 표본 또는 주사선을 회전시키지 않고 단일 샷 그리드 이미지에서 2 차원 (2D) 변형률 분포를 측정 할 수 있습니다. 예를 들어 두 탄소 섬유 강화 플라스틱 시험편의 전단 변형률을 포함한 2D 변위 및 변형률 분포를 3 점 굽힘 시험에서 측정했습니다. 제안 된 기술은 다양한 재료의 기계적 성질, 균열 발생 및 잔류 응력의 비파괴적인 정량 평가에 중요한 역할을 할 것으로 기대된다.
서문
마이크로 / 나노 스케일 변형 측정은 기계적 특성, 불안정한 거동, 잔류 응력 및 첨단 소재의 균열 발생을 평가하는 데 필수적입니다. 광학 기술은 비접촉, 전계 및 비파괴이므로 지난 수십 년 동안 변형 측정을 위해 다양한 광학 방법이 개발되었습니다. 최근, 마이크로 / 나노 스케일 변형 측정 기술은 주로 모아레 법 1 , 2 , 3 , 4 , 기하 위상 분석 (GPA) 5 , 6 , 푸리에 변환 (FT), 디지털 이미지 상관 (DIC) 전자 스펙 클 패턴 간섭계 (ESPI). 이 기술들 중에서 GPA와 FT는 다중 주파수가 존재하기 때문에 복잡한 변형 측정에 적합하지 않습니다. DIC 방법은 sim입니다.변형 캐리어가 랜덤 스페 클 (random speckle)이기 때문에 소음에 대한 무력감. 마지막으로 ESPI는 진동에 매우 민감합니다.
마이크로 / 나노 스케일의 모아레 법 중에서 가장 일반적으로 사용되는 방법은 전자 스캐닝 모아레 7 , 8 , 9 , 레이저 스캐닝 모아레 10 , 11 및 원자 힘 현미경 (AFM) 모아레 12 와 같은 현미경 스캐닝 모아레 법입니다 , 디지털 / 겹침 모아레 13 , 14 , 15 방법 및 곱셈 / 분수 모아레 방법 16 , 17 과 같은 현미경 기반의 모아레 방법이 있습니다. 스캔 모아레 방법은 넓은 시야, 높은 해상도lution, 무작위 소음에 둔감합니다. 그러나 기존의 스캔 모아레 방법은 샘플 스테이지 또는 스캔 방향을 90 ° 회전시키고 두 방향으로 모아레 무늬를 생성하기 위해 두 번 스캔해야하기 때문에 2D 변형 측정에 불편합니다 18 . 회전 및 이중 스캐닝 프로세스는 회전 오차를 유발하고 오랜 시간이 걸리며 2D 변형의 측정 정확도, 특히 전단 응력에 심각하게 영향을 미칩니다. 시간 위상 시프트 기술 19 , 20 은 변형 측정 정확도를 향상시킬 수 있지만 동적 테스트에 부적합한 시간 및 특수 위상 시프트 장치가 필요합니다.
샘플링 모아레 법 (21 , 22) 은 변위 측정에서 높은 정확도를 가지며, 현재 자동차 p나귀. 샘플링 모아레 법을 마이크로 / 나노 스케일 2D 스트레인 측정으로 확장하기 위해 2 픽셀 샘플링 모아레 무늬로부터 재구성 된 멀티 플라이어 모아레 법이 새로 개발되었으며이 측정법은 측정 값이 두 배로 민감하며 스캔 모아레 법이 유지된다. 또한 공간 위상 편이 샘플링 모아레 법은 다중 픽셀 샘플링 모아레 무늬로부터 개발되어 고정밀 변형률 측정이 가능합니다. 이 프로토콜은 상세한 변형률 측정 절차를 소개하며 연구원 및 엔지니어가 변형 측정 방법을 배우고 재료 및 제품의 제조 프로세스를 개선하는 데 도움이 될 것으로 기대됩니다.
프로토콜
1. 시편의 미세 나노 눈금 확인
- 시편의 가공
- 현미경 ( 예 : 1x5x30mm3)에서 사용되는 특정 로딩 장치에 필요한 크기로 표본을 자르고 관찰 할 표면을 관심 영역보다 1.5x 크게 만듭니다.
- 자동 폴리싱 기계 ( 예 : SiC 호 320 번을 3 분간, # 800을 150 rpm으로 1 분간 사용)에 거친 미세한 모래지를 사용하여 관측 할 표본 표면을 관찰합니다 ( 예 : 1 x 30mm 2 ). 30 N). 각 연마 단계 후에 물을 사용하여 시험편을 청소하십시오.
- 동일한 시험편 표면을 자동 연마기 ( 예 : 5 분 동안 DP- 스프레이 P 15 μm, 8 분 동안 P 1 μm, 150 rpm에서 10 분 동안 P 0.25 μm 사용)에 대해 거친 연마제 및 미세 연마제를 사용하여 연속 연마합니다. 30 N). 각 연마 후 물로 표본을 닦으십시오.g 단계.
- 샘플에주기적인 패턴이 없다면 Micro / Nano-scale Grid의 제작
참고 : 자연스러운주기 패턴이 시편 표면의 마이크로 / 나노 스케일에 존재하는 경우이 단계를 생략 할 수 있습니다. 자외선 (UV) 또는 가열 나노 임프린트 리소그래피 (NIL) 26 , 전자 빔 리소그래피 (EBL) 2 및 집속 이온 빔 (FIB) 밀링 6 에서 그리드 제조 방법을 선택하십시오.
참고 : 예를 들어 UV NIL을 사용하여 그리드 제조 프로세스를 소개합니다.- 피펫을 사용하여 시료 표면에 UV 레지스트 2 mL를 떨어 뜨립니다.
- 스핀 코터를 사용하여 1,500 rpm에서 60 초 동안 시편 표면의 레지스트를 코팅합니다.
- 0.2 MPa의 압력에서 나노 임프린트 금형을 레지스트 층에 눌러 라. 30 초 동안 375 nm 파장의 UV에 레지스트를 노출 시키십시오.
- 나노 임프린트 금형을 시편 표면과 분리하십시오.
- 현미경을 이용한 시편 격자의 관찰
- 이온 코터를 사용하여 그리드 표면에 3-10 nm 두께의 백금 또는 금층을 코팅합니다 ( 예 : 3 Pa에서 30 초 동안 스퍼터링 전류 30 mA로 코팅).
- 표본을 레이저 스캐닝 현미경 (LSM) 23에 놓습니다.
참고 : 투과 전자 현미경 (TEM) 5 , 원자력 현미경 (AFM) 12 또는 주사 전자 현미경 (SEM) 7 과 같은 다른 현미경도 사용할 수 있습니다. - 현미경의 이미지 레코딩 소프트웨어에서 "Capture"및 "File | Export | Image File"을 클릭하여 현미경을 사용하여 포커스를 조정하고 하나의 격자 이미지를 저장합니다.
- 격자 이미지로부터 표본의 격자 피치 (nm 또는 μm) 계산
- 10 gr 이상의 평균값 계산ID는 주사 또는 렌즈 왜곡의 잠재적 인 영향을 피하기 위해 그리드 이미지의 중앙 영역에 투구됩니다.
참고 : 표본의 그리드는 실온에서 며칠 동안 저장할 수 있습니다.
- 10 gr 이상의 평균값 계산ID는 주사 또는 렌즈 왜곡의 잠재적 인 영향을 피하기 위해 그리드 이미지의 중앙 영역에 투구됩니다.
2. 적재 시험에서 격자 이미지 획득
- 현미경으로 하중 시험 준비
- 현미경으로 인장, 압축, 가열 또는 전기 적재 장치와 같은 로딩 장치에 시편을 고정시킵니다.
참고 : 그리드 피치가 20 nm보다 작 으면 TEM 또는 AFM을 사용해야합니다. 그리드 피치가 20nm 내지 10㎛이면, SEM이 사용될 수있다. 그리드 피치가 400 nm보다 크면 LSM을 사용할 수 있습니다. - 특정 요구 사항에 따라 하중 속도 ( 예 : 0.01 mm / s)와 하중 또는 변위 증분 단계 ( 예 : 0.5 N / 단계 또는 0.024 mm / 단계)를 설정하십시오. 하중과 변위를 모두 0으로 미리 설정하십시오.
- 그리드 서핑 만들기관측 평면에 에이스. 현미경의 샘플 스테이지를 움직이거나 회전시켜 낮은 배율에서 관심 영역을 선택하십시오.
- 이미지의 격자 피치를 1.8 x 1 픽셀 크기보다 크게하여 적절한 배율을 선택하십시오.
참고 : 일반적으로 이미지의 격자 피치를 2 픽셀 이상으로 만드는 것이 좋습니다. 하나의 격자 피치가 더 많은 픽셀에 해당할수록, 변형 측정의 정확도가 높아지지만 측정 시야가 더 작아집니다.
- 현미경으로 인장, 압축, 가열 또는 전기 적재 장치와 같은 로딩 장치에 시편을 고정시킵니다.
- 로딩 테스트에서 그리드 이미지 모음
- 현미경의 이미지 레코딩 소프트웨어에서 "Capture"및 "File | Export | Image File"을 클릭하여로드하기 전에 관심 영역의 그리드 이미지를 저장하십시오.
- 로드 장치의 운영 소프트웨어를 사용하여 첫 번째로드 단계 ( 예 : 0.5 N 또는 0.024 mm)를 실행하여 현미경에 시편을로드하기 시작합니다.
- 기록현미경의 이미지 기록 소프트웨어에서 "Capture"및 "File | Export | Image File"을 클릭하여 첫 번째로드 단계 ( 예 : 0.5 N 또는 0.024 mm) 후 관심 영역의 그리드 이미지를 정렬하십시오. 현미경의 배율과 작동 거리가 변하지 않도록하십시오.
- 적재 장치를 사용하여 각 적재 단계를 수행하여 시험편을 계속 적재하십시오. 시편이 깨지거나 일정 값에 도달 할 때까지 ( 예 : 1 N, 1.5 N, 2.0 N, ..., 10 N, 19 간격으로로드하고 0.5 간격으로 19 개 격자 이미지를 기록 할 때까지) N, 또는 0.048mm, 0.072mm, 0.096mm, ..., 0.48mm, 0.024mm 간격). 현미경의 배율과 작동 거리가 변하지 않았는지 확인하십시오.
참고 : 그리드 이미지는 임의의 시간 동안 저장할 수 있습니다.
3. Def 전후 모아레 무늬 샘플링 생성정사
- 격자 이미지의 격자 피치 (픽셀) 추정
- 이미지 처리 소프트웨어 ( 예 : Microsoft 그림판)에서 인접한 두 격자 점의 중심 사이의 거리를 측정하여로드하기 전에 격자 이미지의 격자 피치 (단위 : 픽셀)를 계산합니다.
- 최대 부하에서 그리드 이미지의 그리드 피치를 추정합니다.
- 샘플링 피치 (픽셀)의 결정
- 변형 전후의 그리드 피치가 1.8 ~ 2.5 픽셀 일 때 3.2.2 단계로 이동합니다. 변형 전후의 그리드 피치가 2.4 ~ 3.6 픽셀 인 경우 3.2.3 단계로 건너 뜁니다. 변형 전후의 그리드 피치가 3.2 픽셀보다 큰 경우 3.2.4 단계로 건너 뜁니다.
- 샘플링 피치를 T = 2 픽셀로 설정하십시오. 3.3 단계로 건너 뜁니다.
- 샘플링 피치를 T = 3 픽셀로 설정하십시오. 3.3 단계로 건너 뜁니다.
- 샘플링 피치 T 를 양수로 설정하십시오.풍부한 시뮬레이션 결과로 결정된, 변형 전후의 그리드 피치의 0.75 배와 1.25 배의 정수.
참고 : 3.2.1 및 3.2.4 단계의 요구 사항을 충족하는 2 개의 양의 정수가있는 경우 큰 정수를 샘플링 피치로 선택하는 것이 좋습니다. 요구 사항을 충족시키는 3 개 이상의 양의 정수가있는 경우 샘플링 피치보다 약간 큰 중간 정수를 선택하는 것이 좋습니다.
- 변형 전 샘플링 모아레 줄무늬 생성
- 변형되기 전에 그리드 이미지를 엽니 다. x 방향을 우측으로, y 방향을 수직 방향으로하고, 좌표 (0, 0)를 좌상 구석으로하고, x 방향의 화상 폭 W 및 y 방향의 상 높이 H 를 산출한다 .
참고 : y 방향은 다음과 같이 정의 할 수도 있습니다.수직 상향으로. - 3.3.3 단계로 이동하여 모아레 무늬를 y 방향으로 생성합니다. x 방향으로 모아레 무늬를 생성하려면 3.3.7 단계로 건너 뜁니다.
- 저역 통과 필터 (LPF)를 사용하여 그리드 이미지를 격자 이미지로 처리합니다. 예를 들어 FT 알고리즘을 사용하여 주 방향이 x 인 격자를 억제합니다. 주 방향은 격자 선에 수직 인 방향으로 정의됩니다. 필터 크기를 그리드 피치에 가깝게 설정하십시오.
- y = k 픽셀 ( k = 0) ( 그림 1 )에서 샘플링 피치 T ( T ≥2)의 간격을 사용하여 여러 가로선의 회색 값만 추출하여 그리드 이미지를 엷게 만듭니다. y = k 픽셀, y = k + T 픽셀, ..., y = k + iT 픽셀의 샘플링 라인에서의 값, 여기서 i 는 a양의 정수). 마지막 샘플링 라인 k + iT 의 좌표를 이미지 높이 H 보다 작게 만듭니다.
- 수평 샘플링 라인으로 이미지의 전계 강도 보간 (선형 또는 B 스플라인)을 수행하여 y 방향으로 샘플링 모아레 패턴을 생성합니다.
- 1 픽셀의 증분 단계에서 k 를 변경하여 3.3.4 및 3.3.5 T -1 번 단계를 반복하여 y 방향으로 다른 T -1 샘플링 모아레 패턴을 생성합니다 ( 예 : 시닝의 시작점을 y = k로 이동). k = 1, ..., T -1)을 생성한다.
- 단계 3.3.3에서 x 를 y 로 변경하고, 이미지 높이 H 를 이미지 너비 W 로 변경하여 3.3.3-3.3.6 단계와 동일한 절차를 사용하여 x 방향으로 T- 스텝 공간 위상 이동 샘플링 모아레 패턴을 생성합니다 단계 3.3에서 y 를 x 로 변경합니다.4-3.3.6.
참고 : x 방향의 샘플링 피치는 y 방향의 샘플링 피치와 다를 수 있습니다.
- 변형되기 전에 그리드 이미지를 엽니 다. x 방향을 우측으로, y 방향을 수직 방향으로하고, 좌표 (0, 0)를 좌상 구석으로하고, x 방향의 화상 폭 W 및 y 방향의 상 높이 H 를 산출한다 .
- 변형 후 샘플링 모아레 줄무늬의 생성
- 다른로드에서 모든 그리드 이미지를 엽니 다. 격자 이미지의 수가 N 이라고 가정합니다.
- 3.3.3-3.3.6 단계를 반복하여 Y 방향으로 T- 스텝 공간 위상 이동 모아레 무늬의 N 그룹을 생성합니다.
- 3.3.7 N 단계를 반복하여 x 방향으로 T- 스텝 공간 위상 이동 모아레 무늬의 N 그룹을 생성합니다.
4. 하중 시험시 시편의 변형 측정
- 변형 전후의 모아레 무늬의 강도 측정
- t에서 변형되기 전에 T- step 모아레 무늬의 강도를 추출합니다.3.3.5 및 3.3.6 단계에서 y 방향; 단계 3.3.7에서 x 방향의 므와 르 강도를 결정한다. 다음 방정식 23을 사용하여 j ( j = x , y ) 방향으로 변형하기 전의 T- 스텝 (T≥2) 모아레 강도를 기술하십시오.
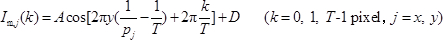 (1)
(1)
여기서 p j 는 j ( j = x , y ) 방향에서 변형되기 전의 그리드 피치, A 는 변조 된 진폭, D 는 배경 및 고주파 강도를 포함합니다. - 단계 3.4.2에서 y 방향 변형 후 T- 스텝 모아레 무늬의 강도를 추출하고 3.4.3 단계에서 x 방향의 모아레 강도를 결정합니다. 변형 후 T- step (T≥2) 모아레 강도를 기술하십시오.J ( k ), pj, A 및 D 를 I 'm, j ( k ), p '로 변경함으로써 상기 식 (식 1)과 동일한 방정식을 사용하여 j ( j = x , y ) j , A ', D '와 같이 나타낼 수있다.
참고 : 샘플링 피치가 3 픽셀 이상인 경우이 단계를 무시하고 4.3 단계로 건너 뜁니다.
- t에서 변형되기 전에 T- step 모아레 무늬의 강도를 추출합니다.3.3.5 및 3.3.6 단계에서 y 방향; 단계 3.3.7에서 x 방향의 므와 르 강도를 결정한다. 다음 방정식 23을 사용하여 j ( j = x , y ) 방향으로 변형하기 전의 T- 스텝 (T≥2) 모아레 강도를 기술하십시오.
- 다음의 식 23을 사용하여 변형 이전에 2 단계 샘플링 모아레 강도 ( 그림 1a ) 간의 곱셈 간섭으로부터 곱셈 모아레 무늬를 재구성합니다
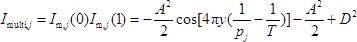 (2)
(2)
여기서 나는 멀티, j 는 강도 o를 의미한다.f : 변형 전의 j ( j = x , y ) 방향으로 재구성 된 곱셈 모아레 줄무늬. - 프린지 센터링 기술을 사용하여 변형하기 전에 재구성 된 다중화 모아레 줄무늬를 처리합니다 24 . 연속 된 정수와 반 정수 fj = [1, 1.5, 2, 2.5, ...]를 재구성 된 곱셈 모아레의 중심선에서 프린지 순서에 할당하십시오.
참고 : 곱셈 모아레 무늬가 너무 조밀하면 두 단계 샘플링 모아레의 프린지 순서가 먼저 결정될 수 있습니다 ( 즉, f j ( 0) = [1, 0, 2, 0, 3, 0, ...] 및 fj (1) = [0, 1.5, 0, 2.5, 0, 3.5, ...]). 곱셈 모아레 줄무늬의 프린지 순서는 fj = fj (0) + fj (1) = [1, 1.5, 2, 2.5, 3, 3.5, ...]가 될 것이다. 강체 변위는 변형률 결과에 영향을 미치지 않습니다. - 다음 식 23을 사용하여 샘플링 피치에 대한 변형 이전의 시험편의 상대 변형률을 측정합니다
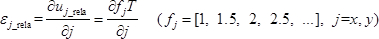 (삼)
(삼) 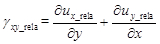 (4)
(4)
여기서 u j _rela 와 ε j _rela 는 각각 j ( j = x , y ) 방향에서의 변형 전의 시편의 상대 변위와 상대 변형률을 나타내고, γ xy _rela는 변형 전의 상대 전단 변형률을 나타낸다. - I multi, j , I m, j (0), I m, j를 변화시켜 N 회 동안 x 및 y 방향으로 변형시킨 후 시험편의 상대 변형을 결정하기 위해 4.2.1-4.2.3 단계를 반복 한다. I ' multi, j , I ' , j ' , j ' , j ' y '), ε'j_rela , 및 γ ' xy_rela 를 각각 사용하여, 각각 m, j (0), I 'm, j (1), p'j , A ', D ' 여기서 위 첨자 단일 인용 부호는 변형 이후를 의미합니다.
- j ( j = x , y ) 방향의 실제 수직 변형량 ε j 를 결정합니다.이 방향은 격자 피치와 전단 변형률 γ xy 의 상대 변화입니다.e 변형 전후의 상대 변형률에 의한 하중에 의한 시험편의 그리드 각도 변화 20 .
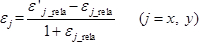 (5)
(5) 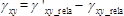 (6)
(6)
- 다음의 식 23을 사용하여 변형 이전에 2 단계 샘플링 모아레 강도 ( 그림 1a ) 간의 곱셈 간섭으로부터 곱셈 모아레 무늬를 재구성합니다
- 변형 측정 샘플링 피치가 T ≥ 3 픽셀 인 경우
- 공간 위상 이동 기술을 사용하여 k = 0 일 때 변형 이전에 j ( j = x , y ) 방향으로 샘플링 모아레 무늬의 위상을 계산합니다 ( 그림 1b ).
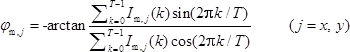 (7)
(7) - φ = m 을 대입하여 k = 0 일 때 변형 후 j ( j = x , y ) 방향으로 샘플링 모아레 무늬의 위상을 얻는다 . φ ' m, j 및 I 'm, j ( k )로 각각 식 (7)에서 I m, j 및 I m, j ( k ) N 개의 로드에 대해 N 번 반복합니다.
참고 : 4.3.1 및 4.3.2 단계의 위상 분포에 너무 많은 무작위 노이즈가있는 경우 sin / cos 필터 25 를 사용하여 위상을 평활화 할 수 있습니다. - 변형 전후의 j ( j = x , y ) 방향 ( 즉, Δ φ m, j = φ m, j - φ m, j )에서의 샘플링 모아레 무늬의 위상차를 결정한다.
- 변위의 분포 u j , 정상 변형 ε j 를 j ( j = x , y ) 방향과 하중에 의한 시편의 전단 변형률 γ xy 를 구한다. 다음 방정식 6 , 21을 사용하십시오.
 (8)
(8) 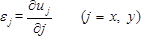 (9)
(9) 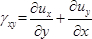 (10)
(10)
참고 : 변형률 분포에 너무 많은 노이즈가있는 경우 필터 크기가 2 그리드 피치보다 작은 평균 평활화 필터를 사용할 수 있습니다.
- 공간 위상 이동 기술을 사용하여 k = 0 일 때 변형 이전에 j ( j = x , y ) 방향으로 샘플링 모아레 무늬의 위상을 계산합니다 ( 그림 1b ).
- 결과 저장소
- .tif 또는 .bmp 파일과 같은 이미지 형식 및 .txt 또는 .csv와 같은 텍스트의 모아레 무늬, 위상 (샘플링 피치가 T ≥3 픽셀 일 때), 변위 및 변형을 저장합니다. 파일.
결과
2 개의 탄소 섬유 강화 플라스틱 (CFRP) 시편 (# 1 및 # 2)의 2D 변위 및 변형률 분포는 모아레 형성 원리 23 및 측정 프로세스 ( 그림 1 )에 따라 측정되었습니다. CFRP 시험편은 직경이 10-11 μm 인 K13D 탄소 섬유와 에폭시 수지로 만들어졌다. CFRP # 1의 변형은 2 단계 샘플링 모아레 무늬에서 재구성 된 곱셈 모아레 법을 사용하여 결정되었고, ...
토론
설명 된 기술에서 표본에 주기적 패턴이없는 경우 도전 과제 중 하나는 도전 과제 인 마이크로 / 나노 스케일 그리드 또는 격자 (그리드로 약칭 ) 입니다. 그리드 피치는 변형 측정에 중요한 매개 변수이기 때문에 변형 전에 일정해야합니다. 재료가 금속, 금속 합금 또는 세라믹 인 경우, UV 또는 가열 나노 임프린트 리소그래피 (NIL) ( 27) , 전자빔 리소그래피 (EBL) ...
공개
저자는 공개 할 것이 없습니다.
감사의 말
이 작업은 JSPS KAKENHI, 교부금 번호 JP16K17988 및 JP16K05996 및 내각부가 운영하는 구조적 재료 (SIP-IMASM)에 대한 혁신적인 측정 및 분석의 D66 부서 간 전략적 혁신 진흥 프로그램에 의해 지원되었습니다. 저자는 또한 Drs에게 감사하고 있습니다. NIMS의 Kishimoto Satoshi와 Naito Kimiyoshi의 CFRP 자료.
자료
| Name | Company | Catalog Number | Comments |
| Automatic Polishing Machine | Marumoto Struers K.K. | LaboPol-30, Labor Force-100 | |
| Carbon Fiber Reinforced Plastic | Mitsubishi Plastics, Inc. | HYEJ16M95DHX1 | |
| Computer | DELL Japan | VOSTRO | Can be replaced with another computer with C++ programming language |
| Image Recording Software | Lasertec Corporation | LMEYE7 | Installed in a laser scanning microscope |
| Ion Coater | Japan Electron Optics Laboratory Ltd. | JEC3000F | |
| Laser Scanning Microscope | Lasertec Corporation | OPTELICS HYBRID | |
| Nanoimprint Device | Japan Laser Corporation | EUN-4200 | Can be replaced with a electron beam lithography device or a focused ion beam milling device |
| Nanoimprint Mold | SCIVAX Corporation | 3.0μm pitch | Customized |
| Nanoimprint Resist | Toyo Gosei Co., Ltd | PAK01 | |
| Polishing Solution | Marumoto Struers K.K. | DP-Spray P 15μm, 1μm, 0.25μm | Use from coarse to fine |
| Pipet | AS ONE Corporation | 10mL | |
| Sand Paper | Marumoto Struers K.K. | SiC Foil #320, #800 | Use from coarse to fine |
| Spin Coater | MIKASA Corporation | MS-A100 |
참고문헌
- Weller, R., Shepard, B. Displacement measurement by mechanical interferometry. Proc. Soc. Exp. Stress Anal. 6 (1), 35-38 (1948).
- Kishimoto, S., Egashira, M., Shinya, N. Microcreep deformation measurements by a moiré method using electron beam lithography and electron beam scan. Opt. Eng. 32 (3), 522-526 (1993).
- Ifju, P., Han, B. Recent applications of moiré interferometry. Exp. Mech. 50 (8), 1129-1147 (2010).
- Zhang, H., Wu, C., Liu, Z., Xie, H. A curved surface micro-moiré method and its application in evaluating curved surface residual stress. Meas. Sci. Technol. 25 (9), 095002 (2014).
- Zhang, H., Liu, Z., Wen, H., Xie, H., Liu, C. Subset geometric phase analysis method for deformation evaluation of HRTEM images. Ultramicroscopy. 171, 34-42 (2016).
- Wang, Q., Kishimoto, S., Xie, H., Liu, Z., Lou, X. In situ high temperature creep deformation of micro-structure with metal film wire on flexible membrane using geometric phase analysis. Microelectron. Reliab. 53 (4), 652-657 (2013).
- Wang, Q., Kishimoto, S. Simultaneous analysis of residual stress and stress intensity factor in a resist after UV-nanoimprint lithography based on electron moiré fringes. J. Micromech. Microeng. 22 (10), 105021 (2012).
- Kishimoto, S., Wang, Q., Xie, H., Zhao, Y. Study of the surface structure of butterfly wings using the scanning electron microscopic moiré method. Appl. Opt. 46 (28), 7026-7034 (2007).
- Li, C., Liu, Z., Xie, H., Wu, D. Novel 3D SEM Moiré method for micro height measurement. Opt. Express. 21 (13), 15734-15746 (2013).
- Xie, H., Wang, Q., Kishimoto, S., Dai, F. Characterization of planar periodic structure using inverse laser scanning confocal microscopy moiré method and its application in the structure of butterfly wing. J. Appl. Phys. 101 (10), 103511 (2007).
- Tang, M., Xie, H., Wang, Q., Zhu, J. Phase-shifting laser scanning confocal microscopy moiré method and its applications. Meas. Sci. Technol. 21 (5), 055110 (2010).
- Xie, H., Kishimoto, S., Asundi, A., Boay, C. G., Shinya, N., Yu, J., Ngoi, B. K. In-plane deformation measurement using the atomic force microscope moiré method. Nanotechnology. 11 (1), 24 (2000).
- Xie, H., Liu, Z., Fang, D., Dai, F., Gao, H., Zhao, Y. A study on the digital nano-moiré method and its phase shifting technique. Meas. Sci. Technol. 15 (9), 1716 (2004).
- Wang, Q., Kishimoto, S., Yamauchi, Y. Three-directional structural characterization of hexagonal packed nanoparticles by hexagonal digital moiré method. Opt. Lett. 37 (4), 548-550 (2012).
- Liu, Z., Lou, X., Gao, J. Deformation analysis of MEMS structures by modified digital moiré methods. Opt. Lasers Eng. 48 (11), 1067-1075 (2010).
- Li, Y., Xie, H., Chen, P., Zhang, Q. Theoretical analysis of moiré fringe multiplication under a scanning electron microscope. Meas. Sci. Technol. 22 (2), 025301 (2010).
- Patorski, K., Wielgus, M., Ekielski, M., Kaźmierczak, P. AFM nanomoiré technique with phase multiplication. Meas. Sci. Technol. 24 (3), 035402 (2013).
- Wang, Q., Ri, S., Takashita, Y., Ogihara, S., Yoshida, S. Chapter 33: Full-field measurements of principal strains and orientations using moiré fringes. Advancement of Optical Methods in Experimental Mechanics. 3, 251-259 (2017).
- Wang, Z., Han, B. Advanced iterative algorithm for phase extraction of randomly phase-shifted interferograms. Opt. Lett. 29 (14), 1671-1673 (2004).
- Wang, Q., Xie, H., Hu, Z., Zhang, J., Sun, J., Liu, G. Residual thermo-creep deformation of copper interconnects by phase-shifting SEM moiré method. Appl. Mech. Mater. 83, 185-190 (2011).
- Ri, S., Fujigaki, M., Morimoto, Y. Sampling moiré method for accurate small deformation distribution measurement. Exp. Mech. 50 (4), 501-508 (2010).
- Ri, S., Muramatsu, T. Theoretical error analysis of the sampling moiré method and phase compensation methodology for single-shot phase analysis. Appl. Opt. 51 (16), 3214-3223 (2012).
- Wang, Q., Ri, S., Tsuda, H. Digital sampling Moiré as a substitute for microscope scanning Moiré for high-sensitivity and full-field deformation measurement at micron/nano scales. Appl. Opt. 55 (25), 6858-6865 (2016).
- Dai, F., Wang, Z. Automatic fringe patterns analysis using digital processing tehniques: I fringe center method. Acta Photonica Sinica. 28, 700-706 (1999).
- Gutmann, B., Weber, H. Phase-shifter calibration and error detection in phase-shifting applications: a new method. Appl. Opt. 37 (32), 7624-7631 (1998).
- Wang, Q., Kishimoto, S., Tanaka, Y., Kagawa, Y. Micro/submicro grating fabrication on metals for deformation measurement based on ultraviolet nanoimprint lithography. Opt. Lasers Eng. 51 (7), 944-948 (2013).
- Min-Jin, T., Hui-Min, X., Yan-Jie, L., Xiao-Jun, L., Dan, W. A new grating fabrication technique on metal films using UV-nanoimprint lithography. Chin. Phys. Lett. 29 (9), 098101 (2012).
재인쇄 및 허가
JoVE'article의 텍스트 или 그림을 다시 사용하시려면 허가 살펴보기
허가 살펴보기더 많은 기사 탐색
This article has been published
Video Coming Soon
Copyright © 2025 MyJoVE Corporation. 판권 소유