Simulazione basata sulla struttura e campionamento dei movimenti proteici del fattore di trascrizione lungo il DNA dallo stepping su scala atomica alla diffusione a grana grossa

Riepilogo

L'obiettivo di questo protocollo è quello di rivelare le dinamiche strutturali della diffusione unidimensionale delle proteine lungo il DNA, utilizzando una proteina di dominio WRKY del fattore di trascrizione vegetale come sistema esemplare. Per fare questo, sono state implementate simulazioni di dinamica molecolare sia atomistiche che a grana grossa insieme a vasti campionamenti computazionali.

Abstract

Lo scorrimento unidimensionale (1-D) della proteina del fattore di trascrizione (TF) lungo il DNA è essenziale per facilitare la diffusione del TF per individuare il sito del DNA bersaglio per la regolazione genetica. Rilevare la risoluzione della coppia di basi (bp) del TF che scivola o calpesta il DNA è ancora sperimentalmente impegnativo. Recentemente abbiamo eseguito simulazioni di dinamica molecolare all-atom (MD) catturando il passo spontaneo di 1 bp di una piccola proteina TF del dominio WRKY lungo il DNA. Sulla base del percorso di stepping WRKY da 10 μs ottenuto da tali simulazioni, il protocollo mostra qui come condurre campionamenti conformazionali più estesi dei sistemi TF-DNA, costruendo il modello di stato di Markov (MSM) per lo stepping proteico 1-bp, con vari numeri di micro e macro-stati testati per la costruzione MSM. Al fine di esaminare la ricerca diffusionale 1-D processiva della proteina TF insieme al DNA con basi strutturali, il protocollo mostra inoltre come condurre simulazioni MD a grana grossa (CG) per campionare la dinamica su scala a lungo termine del sistema. Tali modelli e simulazioni CG sono particolarmente utili per rivelare gli impatti elettrostatici proteina-DNA sui movimenti diffusionali processivi della proteina TF superiori a decine di microsecondi, rispetto ai movimenti di stepping proteico da sub-microsecondi a microsecondi rivelati dalle simulazioni di tutti gli atomi.

Introduzione

I fattori di trascrizione (TF) cercano il DNA bersaglio per legare e regolare la trascrizione genica e le attività correlate¹. Oltre alla diffusione tridimensionale (3D), la diffusione facilitata del TF è stata suggerita come essenziale per la ricerca del DNA target, in cui le proteine possono anche scivolare o saltare lungo il DNA unidimensionale (1D), o saltare con trasferimento intersegmentale sul DNA 2,3,4,5,6,7.

In un recente studio, abbiamo condotto decine di microsecondi (μs) simulazioni di dinamica molecolare di equilibrio all-atomo (MD) su una pianta TF - la proteina del dominio WRKY sul DNA⁸. È stato catturato un passo completo di 1 bp di WRKY sul DNA poly-A entro microsecondi. Sono stati osservati i movimenti della proteina lungo il solco del DNA e le dinamiche di rottura-reforming dei legami idrogeno (HBs). Mentre una tale traiettoria rappresenta un percorso campionato, un panorama generale di stepping proteico è ancora carente. Qui, mostriamo come espandere i campionamenti computazionali attorno al percorso di stepping proteico inizialmente catturato con il modello di stato di Markov costruito (MSM), che è stato ampiamente implementato per simulare una varietà di sistemi biomolecolari che comportano sostanziali cambiamenti conformazionali e separazione su scala temporale 9,10,11,12,13,14,15,16, 17,18,19. Lo scopo è quello di rivelare l'insieme conformazionale e gli stati meta-stabili della diffusione della proteina TF lungo il DNA per un passo ciclico.

Mentre la simulazione MD di cui sopra rivela la risoluzione atomica dei movimenti proteici per 1 bp sul DNA, la dinamica strutturale della diffusione processiva a lungo termine del TF lungo il DNA alla stessa alta risoluzione è difficilmente accessibile. Condurre simulazioni MD a grana grossa (CG) a livello di residuo è tuttavia tecnicamente accessibile. La scala temporale di simulazione CG può essere efficacemente estesa a decine o centinaia di volte più lunga delle simulazioni atomiche 20,21,22,23,24,25,26,27,28,29. Qui, mostriamo le simulazioni CG condotte implementando il software CafeMol sviluppato da Takada lab³⁰.

Nel protocollo attuale, presentiamo le simulazioni atomiche della proteina del dominio WRKY lungo il DNA poly-A e la costruzione MSM prima, che si concentrano sul campionamento dei movimenti di stepping proteico per solo 1 bp lungo il DNA. Quindi presentiamo la modellazione CG e le simulazioni dello stesso sistema proteina-DNA, che estendono il campionamento computazionale alla diffusione processiva della proteina su decine di bps lungo il DNA.

Qui, utilizziamo il software GROMACS^31,32,33 per condurre simulazioni MD e MSMbuilder³⁴ per costruire MSM per snapshot conformazionali campionati, nonché per utilizzare VMD³⁵ per visualizzare le biomolecole. Il protocollo richiede che l'utente sia in grado di installare e implementare il software di cui sopra. L'installazione e l'implementazione del software CafeMol³⁰ è quindi necessaria per condurre le simulazioni CG MD. Ulteriori analisi delle traiettorie e la visualizzazione sono condotte anche in VMD.

Protocollo

1. Costruzione del modello di stato di Markov (MSM) da simulazioni MD atomiche

1. Percorso spontaneo di stepping proteico e raccolta iniziale delle strutture
   1. Utilizzare^{una traiettoria} MD all-atom 8 da 10 μs ottenuta in precedenza per estrarre 10000 fotogrammi in modo uniforme da un percorso di stepping "in avanti" da 1 bp (cioè un fotogramma per ogni nanosecondo). Il numero totale di fotogrammi deve essere sufficientemente grande da includere tutte le conformazioni rappresentative.
   2. Preparare il percorso di transizione con 10000 fotogrammi in VMD facendo clic su File > Salva coordinate, digitare proteina o nucleico nella casella atomi selezionati e scegliere i fotogrammi nella casella Fotogrammi, fare clic su Salva per ottenere i fotogrammi necessari.
      NOTA: Una traiettoria di simulazione MD all-atom da 10 μs precedentemente ottenuta (chiamata "traiettoria di passo in avanti" qui) per WRKY stepping 1-bp di distanza su un DNA poly-A^omogeneo 34 bp 8 è stata utilizzata come percorso iniziale per lanciare ulteriori campionamenti conformazionali. Si noti che nella maggior parte delle pratiche, tuttavia, viene costruito un percorso iniziale, eseguendo simulazioni MD guidate o mirate, o implementando metodi generali di generazione del percorso, ecc.36,37,38,39.
   3. Allineare l'asse lungo del DNA di riferimento (dalla struttura cristallina) all'asse x e impostare il centro di massa iniziale (COM) del DNA completo a 34 bp all'origine dello spazio delle coordinate per la comodità di ulteriori analisi dei dati. A tale scopo, fare clic su Estensioni > console Tk in VMD e digitare nella finestra di comando della console Tk:
      origine rotate.tcl
      Lo script tcl è disponibile nel file supplementare 3.
   4. Quindi calcola la distanza media quadrata della radice (RMSD) della spina dorsale proteica allineando il DNA centrale di 10 bp (A da 14 a 23 e T da 14' a 23') a quello della struttura^{cristallina 40}, e l'RMSD rappresenta misure geometriche dei sistemi (vedi Figura 1A). A tale scopo, fare clic su VMD > Extensions > Analysis > strumento traiettoria RMSD e digitare nucleico e residuo da 14 a 23 e da 46 a 55 nella casella di selezione dell'atomo, fare clic su Allinea e quindi su casella RMSD per calcolare i valori RMSD.
   5. Calcola il grado di rotazione della proteina attorno al DNA Θ(t) sul piano y-z in MATLAB digitando il comando
      rad2deg(atan(z/y))
      con il posizionamento angolare iniziale definito come Θ(0)=0, come condotto in precedenza⁸.
   6. Digita il seguente comando in MATLAB⁴¹ per utilizzare i metodi K-means 42,43,44 e classifica le 10000 strutture in 25 cluster digitando:
      [idx, C]=kmeans( X, 25)
      qui X è una matrice 2D di RMSD e angolo di rotazione di WRKY sul DNA. Raccogli le strutture di questi 25 centri cluster per ulteriori simulazioni MD.
      NOTA: Poiché la proteina RMSD campionata rispetto al DNA copre un intervallo di circa 25 Å, scegliamo 25 cluster per avere un cluster per angstrom.
2. Condurre il 1^° round di simulazioni MD e le impostazioni di simulazione
   1. Costruire sistemi atomistici per le 25 strutture utilizzando il software GROMACS 5.1.2³² sotto parmbsc1 campo di forza⁴⁵ e utilizzando il file buildsystem.sh dal file supplementare 2 in shell.
   2. Condurre simulazioni MD 60-ns per questi 25 sistemi sotto insieme NPT con un passo temporale di 2 fs digitando il seguente comando in shell:
      gmx_mpi grompp -f md.mdp -c npt.gro -p topol.top -o md.tpr
      gmx_mpi mdrun -deffnm md
3. Clustering del 1^San traiettorie MD arrotondate
   1. Rimuovere i primi 10 ns di ogni traiettoria di simulazione digitando in shell:
      gmx_mpi trjcat -f md.xtc -b 10000 -e 600000 -o newtraj.xtc
      e raccogliere conformazioni dalle traiettorie 25 × 50 ns per il clustering per preparare le strutture di input per i successivi campionamenti più estesi (simulazioni MD^{di 2 °} round).
      NOTA: Per ridurre l'impatto dal percorso iniziale e consentire l'equilibrio locale, sono stati rimossi 10-ns del periodo iniziale di simulazioni.
   2. Scegli coppie di distanza tra proteine e DNA come parametri di input per l'analisi dei componenti indipendenti dal tempo (tICA)46,47,48 proiezione. Utilizzare il comando make_ndx in GROMACS per eseguire questa operazione:
      gmx_mpi make_ndx -f input.pdb -o index.ndx
      NOTA: Qui sono stati selezionati gli atomi di proteina CA e gli atomi pesanti (NH1, NH2, OH, NZ, NE2, ND2) del residuo Y119, K122, K125, R131, Y133, Q146, K144, R135, W116, R117, Y134, K118, Q121 che possono formare legami idrogeno (HBs) con il nucleotide del DNA, che si accoppiano con gli atomi O1P O2P e N6 del nucleotide del DNA (A14-20, T19-23). Gli amminoacidi selezionati possono formare HB stabili o ponti di sale con il DNA.
   3. Copiare l'indice atomo selezionato sopra dal file index.ndx in un nuovo file di testo (index.dat). Ottieni le informazioni sulla coppia tra questi atomi dallo script python dal file supplementare 1 generate_atom_indices.py e digitare:
      python2.6 indice generate_atom_indices.py.dat > AtomIndices.txt
      Questo genera le 415 coppie di distanza tra proteina e DNA.
   4. Calcolare le 415 coppie di distanza da ogni traiettoria digitando il seguente comando nella finestra di comando di MSMbuilder:
      msmb AtomPairsFeaturizer -out pair_features --pair_indices AtomIndices.txt --top references.pdb --trjs "trajectories/*.xtc" --transformed pair_features --stride 5
   5. Condurre tICA per ridurre la dimensione dei dati sui primi 2 componenti indipendenti dal tempo (tIC) o vettori digitando:
      msmb tICA -i .. /tica_rc_a/tmp/ -o tica_results --n_components 2 --lag_time 10 --gamma 0.05 -t tica_results.h5
      NOTA: tICA è un metodo di riduzione dimensionale che calcola l'autovalore della matrice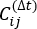 di correlazione ritardata nel tempo per determinare i gradi di libertà rilassanti più lenti del sistema di simulazione mediante l'equazione: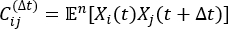
      
      dove X_i(t) è il valore dell'i-esima coordinata di reazione al tempo t, e X_j(t+Δt) è il valore della coordinata di reazione j-esima al tempo t+Δt.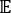 è il valore di aspettativa del prodotto delle traiettorie di simulazione complessive X _i(t) e X_j(t + Δt). Le direzioni lungo i gradi di libertà rilassanti più lenti corrispondono ai più grandi autovalori della matrice 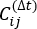di correlazione ritardata nel tempo di cui sopra . Qui, 2 tIC sembrano essere un insieme minimo per differenziare tre macrostati sulla nostra costruzione MSM (affrontato più avanti). Si può anche calcolare il punteggio⁴⁹ del quoziente di Rayleigh a matrice generalizzata (GMRQ), ad esempio, per esplorare un insieme ottimale di componenti da utilizzare.
   6. Utilizzare il comando in MSMbuilder per raggruppare i set di dati proiettati in 100 cluster con il metodo K-center^43,44 (vedere la Figura 1B):
      msmb KCenters -i ./tica_results.h5 -o kcenters_output -t kcenters_output --n_clusters 100.
      Selezionare la struttura centrale di ciascun cluster come struttura iniziale per il 2^° round di simulazioni MD. Mantenere le informazioni di simulazione delle 100 strutture simulate, comprese posizioni, temperature, pressioni, ecc., Ad eccezione delle velocità.
      NOTA: Dopo il primo round di 25 simulazioni, la memoria del percorso iniziale è stata ridotta, quindi generiamo più cluster, ad esempio 100 cluster, nel secondo round, per espandere sostanzialmente i campionamenti conformazionali.
4. Condurre il 2^° round ampie simulazioni MD
   1. Condurre simulazioni MD 60-ns partendo da queste 100 strutture iniziali dopo aver imposto velocità iniziali casuali su tutti gli atomi. Aggiungi le velocità iniziali casuali attivando la generazione della velocità nel file mdp, ad esempio modificando il file md.mdp gen_vel = no in gen_vel = yes.
   2. Rimuovere i primi 10 ns di ogni simulazione come descritto nel passaggio 1.3.1, raccogliere 2.500.000 istantanee dalle traiettorie 100 × 50 ns in modo uniforme per costruire l'MSM.
      NOTA: Si noti che nella successiva costruzione dei macrostati, è stato trovato un piccolo numero di stati fuori percorso con una popolazione particolarmente bassa (~ 0,2%, sul fondo del piano X-Θ). Questi stati fuori percorso sono classificati come un macrostato quando il numero totale di macrostati è impostato su 3 su 6 (Figura 2B). Poiché un macrostato di popolazione così basso comprende solo 3 traiettorie, che sono state rimosse alla fine, i risultati mostrati in questo protocollo sono stati ottenuti infatti da 97 × 50 traiettorie ns, con un totale di 2.425.000 fotogrammi o istantanee.
5. Clustering delle traiettorie MD del 2^° round
   1. Condurre tICA per le traiettorie del 2^° round come fatto in precedenza. Digitare IN MSMbuilder:
      msmb tICA -i .. /tica_rc_a/tmp/ -o tica_results --n_components 2 --lag_time 10 --gamma 0.05 -t tica_results.h5
   2. Calcolare la scala temporale implicita per convalidare i parametri per il tempo di ritardo di correlazione Δt e i numeri dei microstati (vedere figura 1C),
      
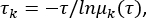
      dove τ rappresenta il tempo di ritardo utilizzato per costruire la matrice di probabilità di transizione (TPM); μ_k(τ) rappresenta l'autovalore kth del TPM in un tempo di ritardo di τ. Usa lo script python dal file supplementare 1 per questo python BuildMSMsAsVaryLagTime.py -d .. / -f .. /trajlist_num -i 50 -m 1000 -t 10 -n 20 -s 500.
   3. Variare il tempo di ritardo τ e il numero di microstati modificando i parametri utilizzati sopra:
      python BuildMSMsAsVaryLagTime.py -d .. / -f .. /trajlist_num -i 50 -m 1000 -t 5 10 20 30 40 -n 20 -s 20 200 400 500 800 2000
      NOTA: Il sistema è considerato markoviano quando le curve implicite della scala temporale iniziano a stabilizzarsi con la separazione della scala temporale. Quindi, scegli il Dt come tempo di ritardo di correlazione e il τ il tempo di ritardo in cui la scala temporale implicita inizia a livellarsi per costruire MSM.
   4. Di conseguenza, scegli un numero relativamente grande (ma non troppo grande) di stati, N = 500, e un tempo di ritardo di correlazione relativamente breve Δt = 10 ns. Il tempo di ritardo è risultato essere τ = 10 ns per costruire MSM.
   5. Classificare le conformazioni in 500 cluster (vedere la Figura 1D) utilizzando il comando:
      msmb KCenters -i ./tica_results.h5 -o kcenters_output -t kcenters_output --n_clusters 500
6. Costruzione MSM
   1. Raggruppa i 500 microstati in 3-6 macrostati per scoprire il numero di macrostati che si adattano meglio secondo l'algoritmo PCCA +⁵⁰ in MSMbuilder, utilizzando lo script python nel file supplementare 1 python msm_lumping_usingPCCAplus.py. Identificare una rete cinetica ridotta di modelli per i cambiamenti conformazionali più essenziali delle biomolecole, costruendo un piccolo numero di macrostati, cioè raggruppando cineticamente centinaia di microstati come descritto sotto^17,51.
   2. Mappare le conformazioni ad alta dimensione all'X (movimento proteico lungo l'asse lungo del DNA) e all'angolo di rotazione della proteina lungo il DNA per ciascun macrostato come descritto nei passaggi 1.1.3 e 1.1.4 (ad esempio, nessuno stato con popolazione troppo bassa < l'1%; vedi Figura 2C). Quindi trovare i 3 macrostati che meglio rappresentano il sistema (Figura 1E) . Vedere la Figura 2D per le istantanee del movimento delle proteine lungo il DNA e l'angolo di rotazione delle proteine attorno al DNA.
      NOTA: Nel lavoro precedente che ha generato il percorso di avanzamento della proteina spontanea da 10 μs, abbiamo inoltre condotto simulazioni MD di equilibrio 5 x 4 μs per espandere moderatamente i campionamenti. La Corte ha mostrato la mappatura del percorso in avanti originale (vedere la Figura 2A a sinistra) e ulteriori traiettorie di campionamento di 4 μs sul percorso in avanti condotte in precedenza (vedere figura 2A a destra)⁸. Viene mostrata la mappatura delle traiettorie originali di 100 × 50 ns (vedi Figura 2B a sinistra)⁸ e le traiettorie 97 × 50 ns utilizzate in questo lavoro (vedi Figura 2B a destra).
7. Calcolo dei tempi medi di primo passaggio (MFPT)
   1. Esegui cinque traiettorie Monte Carlo (MC) da 10 ms basate sul TPM del MSM a microstato 500 con il tempo di ritardo di 10 ns impostato come passo temporale di MC. Calcola MFPT⁵² tra ogni coppia di macrostati (Figura 3) dallo script python nel file supplementare 1 python python mfpt_msm3.py.
   2. Calcola l'errore medio e standard del MFPT usando il file bash nel file supplementare 2, digita:
      sh mfpt_analysis.bash

2. Condurre simulazioni a grana grossa (CG) per campionare dinamiche di lunga durata

1. Esegui una simulazione CG utilizzando il software CafeMol 3.0³⁰. Vedere le impostazioni di simulazione CG specificate nel file di configurazione di input con estensione .inp, incluse le strutture di input, i parametri di simulazione, i file di output, ecc. Digitare il seguente comando sul terminale per eseguire la simulazione CG:
   cafemol XXX.inp
2. Specificare i seguenti blocchi nel file di input, con ogni blocco che inizia con l'etichetta < and ending with >>>>.
   1. Impostare il blocco dei nomi file (obbligatorio) per specificare le directory di lavoro e il percorso dell'archivio dei file di input/output. Digitare quanto segue per il blocco dei nomi file per queste simulazioni:
      <<<< nomi di file
      path = XXXXX (percorso di lavoro)
      filename = wrky (i nomi dei file di output)
      OUTPUT psf pdb movie dcd rst
      path_pdb = XXXXX (percorso della struttura nativa di input)
      path_ini = XXXXX (percorso iniziale della struttura di input)
      path_natinfo = XXXXX (percorso file di informazioni nativo)
      path_para = XXXXX (percorso dei file dei parametri)
      >>>>
      NOTA: Poiché il go-model⁵³ viene utilizzato nella modellazione CG, cioè la proteina sarà distorta verso la conformazione nativa, quindi è necessario impostare la struttura modellata come conformazione nativa. Qui, la struttura cristallina di input è stata impostata come conformazione nativa.
   2. Impostare il blocco di controllo del processo (obbligatorio) per definire la modalità di esecuzione delle simulazioni. Digitare il comando seguente:
      <<<< job_cntl
      i_run_mode = 2 (= 2 la simulazione della temperatura costante)
      i_simulate_type = 1 (=1 dinamica di Langevin)
      i_initial_state = 2 (=2 significa che la configurazione iniziale è la configurazione nativa)
      >>>>
      Selezionare le simulazioni dinamiche di Langevin a temperatura costante.
   3. Impostare l'unità e il blocco di stato (obbligatorio) per definire le informazioni per le strutture di input. Digitare il comando seguente:
      <<<< unit_and_state
      i_seq_read_style = 1 (=1 significa sequenze di lettura da file PDB)
      i_go_native_read_style = 1 (=1 significa che la struttura nativa proviene da file PDB)
      1 proteina proteica.pdb (unità&stato molecular_type native_structure)
      DNA a 2-3 DNA.pdb (unità e stato molecular_type native_structure)
      >>>>
      NOTA: sono necessari i file iniziali della struttura di input (proteina.pdb e DNA.pdb qui). Le strutture sono scritte in formato pdb. Qui sono necessari due file pdb: uno è il file di struttura proteica contenente le coordinate atomiche pesanti di WRKY (unità 1), e l'altro sono le coordinate del DNA a doppio filamento (ds) da 200 bp (unità 2-3). La proteina viene inizialmente posizionata a 15 Å di distanza dal DNA.
   4. Impostare il blocco funzione di energia (obbligatorio) definito nel blocco energy_function. Digitare il comando seguente:
      <<<< energy_function
      LOCALE(1) L_GO
      LOCALE(2-3) L_DNA2
      NLOCAL(1/1) GO EXV ELE
      NLOCAL(2-3/2-3) ELE DNA
      NLOCAL(1/2-3) EXV ELE
      i_use_atom_protein = 0
      i_use_atom_dna = 0
      i_para_from_ninfo = 1
      i_triple_angle_term = 2
      >>>>
      NOTA: Nelle simulazioni CG, la proteina è a grana grossa dal go-modello⁵³ con ogni amminoacido rappresentato da una particella CG posta nella sua posizione Cα. La conformazione proteica sarà quindi orientata verso la struttura nativa, o struttura cristallina qui, sotto il potenziale Go (Figura 4A a sinistra). Il DNA è descritto dal modello 3SPN.2⁵⁴, in cui ogni nucleotide è rappresentato da 3 particelle CG S, P, N, che corrispondono rispettivamente a zucchero, fosfato e base azotata (Figura 4A a destra). Le interazioni elettrostatiche e vdW sono considerate tra diverse catene. Le interazioni elettrostatiche tra proteina e DNA nella simulazione CG sono approssimate dal potenziale di Debye-Hückel⁵⁵. L'energia repulsiva vdW assume la stessa forma del modello Go.
   5. Impostare il blocco md_information (obbligatorio) per definire le informazioni di simulazione. Digitare il comando seguente:
      <<<< md_information
      n_step_sim = 1
      n_tstep(1) = 500000000
      tstep_size = 0,1
      n_step_save = 1000
      n_step_neighbor = 100
      i_com_zeroing = 0
      i_no_trans_rot = 0
      tempk = 300,0
      n_seed = -1
      >>>>
      Il n_tstep è la fase di simulazione. Imposta il tstep_size come lunghezza temporale di ogni passaggio MD, ogni passaggio temporale CG Cafemol è di circa 200 fs³⁰, quindi ogni passaggio MD qui è 200 × 0,1 fs in linea di principio. Aggiorna l'elenco dei vicini ogni 100 passaggi MD (n_step_neighbor = 100). Impostare la temperatura di simulazione a 300 K. Controllare la temperatura utilizzando l'algoritmo Verlet di tipo velocità per aggiornare la struttura delle proteine con il termostato Berendsen⁵⁶.
      NOTA: il n_step_sim è il numero di bacino del potenziale basato sul modello Go o il numero minimo locale della curva di energia. Un potenziale multibacino consente la conformazione proteica distorta a diverse conformazioni in modo che la conformazione proteica possa cambiare da un minimo locale all'altro. Qui viene utilizzato solo il modello Go a bacino singolo, il che significa solo una conformazione distorta (struttura cristallina) per le proteine nelle simulazioni. Nel frattempo, poiché non esiste un'interazione di legame idrogeno proteina-DNA, ecc. modellata nel contesto CG, i moti molecolari possono essere campionati ancora più velocemente, cioè > 10 volte rispetto alle simulazioni atomiche.
   6. Impostare il blocco elettrostatico (richiesto solo quando si utilizza l'interazione elettrostatica) poiché l'interazione elettrostatica è considerata tra diverse catene, quindi utilizzare questo blocco per definire i parametri per l'interazione elettrostatica digitando:
      <<<< elettrostatico
      cutoff_ele = 10,0
      ionic_strength = 0,15
      >>>>
      Impostare la lunghezza di Debye nell'interazione elettrostatica su 10 Å, corrispondente alla condizione della soluzione. Impostare la forza ionica a 0,15 M, come alle condizioni fisiologiche.

Risultati

Scorrimento accoppiato a rotazione o stepping di 1 bp di WRKY dalla costruzione MSM
Tutte le conformazioni proteiche sul DNA sono mappate al movimento longitudinale X e all'angolo di rotazione della proteina COM lungo il DNA (vedi Figura 3A). L'accoppiamento lineare di questi due gradi indica uno stepping accoppiato alla rotazione della proteina del dominio WRKY sul DNA. Le conformazioni possono essere ulteriormente raggruppate in 3 macrostati (S1, S2 e S3) nel MSM. Il pa...

Discussione

Questo lavoro affronta come condurre simulazioni computazionali basate sulla struttura e campionamenti per rivelare un fattore di trascrizione o una proteina TF che si muove lungo il DNA, non solo al dettaglio atomico del passo, ma anche nella diffusione processiva, che è essenziale per la diffusione facilitata del TF nella ricerca del bersaglio del DNA. Per fare ciò, è stato costruito per la prima volta il modello di stato di Markov o MSM di una piccola proteina di dominio TF WRKY che cammina per 1-bp lungo il DNA po...

Materiali

Name	Company	Catalog Number	Comments
CafeMol	Kyoto University		coarse-grained (CG) simulations
GROMACS	University of Groningen Royal Institute of Technology Uppsala University		molecular dynamics simulations software
Matlab	MathWorks		Numerical calculation software
MSMbuilder	Stanford University		build MSM
VMD	UNIVERSITY OF ILLINOIS AT URBANA-CHAMPAIGN		molecular visualization program