7.9 : Das quantenmechanische Modell eines Atoms
Shortly after de Broglie published his ideas that the electron in a hydrogen atom could be better thought of as being a circular standing wave instead of a particle moving in quantized circular orbits, Erwin Schrödinger extended de Broglie’s work by deriving what is now known as the Schrödinger equation. When Schrödinger applied his equation to hydrogen-like atoms, he was able to reproduce Bohr’s expression for the energy and, thus, the Rydberg formula governing hydrogen spectra. Schrödinger described electrons as three-dimensional stationary waves, or wavefunctions, represented by the Greek letter psi, ψ.
A few years later, Max Born proposed an interpretation of the wavefunction ψ that is still accepted today: Electrons are still particles, and so the waves represented by ψ are not physical waves but, instead, are complex probability amplitudes. The square of the magnitude of a wavefunction ∣ψ∣2 describes the probability of the quantum particle being present near a certain location in space. This means that wavefunctions can be used to determine the distribution of the electron’s density with respect to the nucleus in an atom. In the most general form, the Schrödinger equation can be written as:
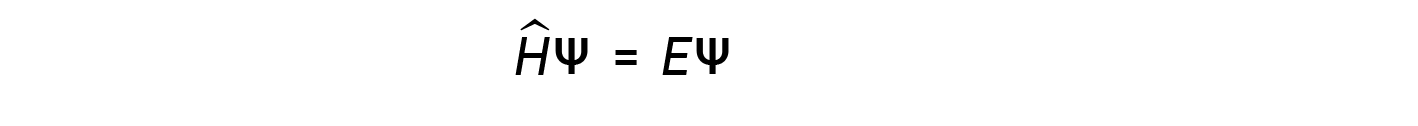
where, Ĥ is the Hamiltonian operator, a set of mathematical operations representing the total energy (potential plus kinetic) of the quantum particle (such as an electron in an atom), ψ is the wavefunction of this particle that can be used to find the special distribution of the probability of finding the particle, and E is the actual value of the total energy of the particle.
Schrödinger’s work, as well as that of Heisenberg and many other scientists following in their footsteps, is generally referred to as quantum mechanics.
The quantum mechanical model describes an orbital as a three-dimensional space around the nucleus within an atom, where the probability of finding an electron is the highest.
This text is adapted from Openstax, Chemistry 2e, Section 6.3: Development of Quantum Theory.
Aus Kapitel 7:

Now Playing
7.9 : Das quantenmechanische Modell eines Atoms
Elektronische Struktur von Atomen
41.7K Ansichten

7.1 : Das Licht als Welle
Elektronische Struktur von Atomen
48.1K Ansichten

7.2 : Das elektromagnetische Spektrum
Elektronische Struktur von Atomen
52.3K Ansichten

7.3 : Interferenz und Beugung
Elektronische Struktur von Atomen
30.5K Ansichten

7.4 : Photoelektrischer Effekt
Elektronische Struktur von Atomen
29.1K Ansichten

7.5 : Das Bohrsche Atommodell
Elektronische Struktur von Atomen
49.8K Ansichten

7.6 : Emissionsspektren
Elektronische Struktur von Atomen
49.4K Ansichten

7.7 : Die Materiewelle nach de Broglie
Elektronische Struktur von Atomen
25.2K Ansichten

7.8 : Das Heisenbergsche Unschärferelation
Elektronische Struktur von Atomen
22.9K Ansichten

7.10 : Quantenzahlen
Elektronische Struktur von Atomen
34.1K Ansichten

7.11 : Atomorbitale
Elektronische Struktur von Atomen
32.9K Ansichten

7.12 : Das Paulische Ausschließungsprinzip
Elektronische Struktur von Atomen
33.8K Ansichten

7.13 : Die Energien von Atomorbitalen
Elektronische Struktur von Atomen
23.6K Ansichten

7.14 : Das Aufbauprinzip und die Hundschen Regeln
Elektronische Struktur von Atomen
43.7K Ansichten

7.15 : Elektronenkonfiguration von Multielektronenatomen
Elektronische Struktur von Atomen
37.8K Ansichten
Copyright © 2025 MyJoVE Corporation. Alle Rechte vorbehalten