7.9 : O Modelo Mecânico-Quântico de um Átomo
Pouco depois de de Broglie ter publicado as suas ideias de que o eletrão em um átomo de hidrogénio poderia ser melhor pensado como sendo uma onda circular estacionária em vez de uma partícula que se move em órbitas circulares quantizadas, Erwin Schrödinger estendeu o trabalho de de Broglie ao derivar o que é agora conhecido como a equação de Schrödinger. Quando Schrödinger aplicou a sua equação a átomos hidrogenóides, ele foi capaz de reproduzir a expressão de Bohr para a energia e, assim, a fórmula de Rydberg que rege os espectros do hidrogénio. Schrödinger descreveu os eletrões como ondas estacionárias tridimensionais, ou funções de onda, representadas pela letra Grega psi, ψ.
Alguns anos depois, Max Born propôs uma interpretação da função de onda ψ que ainda é aceite hoje: Os eletrões são partículas estacionárias, pelo que as ondas representadas por ψ não são ondas físicas mas, em vez disso, são amplitudes de probabilidade complexas. O quadrado da magnitude de uma função de onda ∣ψ∣2 descreve a probabilidade de a partícula quântica estar presente perto de uma determinada localização no espaço. Isto significa que as funções de onda podem ser utilizadas para determinar a distribuição da densidade dos eletrões em relação ao núcleo em um átomo. Na forma mais geral, a equação de Schrödinger pode ser escrita como:
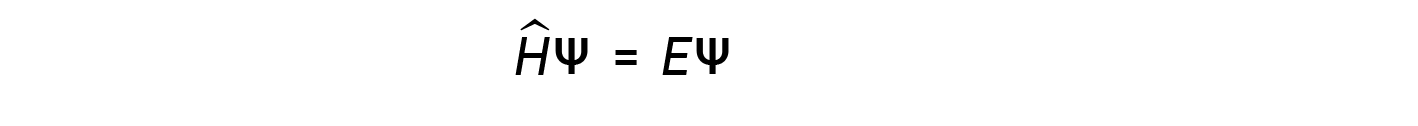
onde, Ĥ é o operador Hamiltoniano, um conjunto de operações matemáticas que representam a energia total (potencial mais cinética) da partícula quântica (como um eletrão em um átomo), ψ é a função de onda desta partícula que pode ser usada para encontrar a distribuição especial da probabilidade de encontrar a partícula, e E é o valor real da energia total da partícula.
O trabalho de Schrödinger, bem como o de Heisenberg e de muitos outros cientistas que seguiram os seus passos, é geralmente referido como mecânica quântica.
O modelo mecânico-quântico descreve uma orbital como um espaço tridimensional em torno do núcleo dentro de um átomo, onde a probabilidade de encontrar um eletrão é a mais alta.
Este texto é adaptado de Openstax, Chemistry 2e, Section 6.3: Development of Quantum Theory.
Do Capítulo 7:

Now Playing
7.9 : O Modelo Mecânico-Quântico de um Átomo
Estrutura Eletrônica dos Átomos
41.7K Visualizações

7.1 : A Natureza Ondulatória da Luz
Estrutura Eletrônica dos Átomos
48.1K Visualizações

7.2 : O Espectro Eletromagnético
Estrutura Eletrônica dos Átomos
52.3K Visualizações

7.3 : Interferência e Difração
Estrutura Eletrônica dos Átomos
30.6K Visualizações

7.4 : Efeito Fotoelétrico
Estrutura Eletrônica dos Átomos
29.1K Visualizações

7.5 : O Modelo de Bohr
Estrutura Eletrônica dos Átomos
49.9K Visualizações

7.6 : Espectros de Emissão
Estrutura Eletrônica dos Átomos
49.5K Visualizações

7.7 : O Comprimento de Onda de De Broglie
Estrutura Eletrônica dos Átomos
25.2K Visualizações

7.8 : O Princípio da Incerteza
Estrutura Eletrônica dos Átomos
22.9K Visualizações

7.10 : Números Quânticos
Estrutura Eletrônica dos Átomos
34.1K Visualizações

7.11 : Orbitais Atômicos
Estrutura Eletrônica dos Átomos
32.9K Visualizações

7.12 : O Princípio da Exclusão de Pauli
Estrutura Eletrônica dos Átomos
33.8K Visualizações

7.13 : As Energias das Orbitais Atômicos
Estrutura Eletrônica dos Átomos
23.6K Visualizações

7.14 : O Princípio de Aufbau e a Regra de Hund
Estrutura Eletrônica dos Átomos
43.8K Visualizações

7.15 : Configuração Eletrônica de Átomos com Múltiplos Elétrons
Estrutura Eletrônica dos Átomos
37.8K Visualizações
Copyright © 2025 MyJoVE Corporation. Todos os direitos reservados