計装AFMインデンテーションによる定量硬度測定

要約

This experimental protocol describes how atomic force microscopy can be used to measure hardness at the true nanometer scale and to detect single atomistic plasticity events.

要約

In this work, a combination of amplitude-modulated non-contact atomic force microscopy and atomic force spectroscopy is applied for instrumented hardness measurements on an Au(111) surface with atomistic resolution of single plasticity events. A careful experimental procedure is described that includes the force sensor selection, its calibration, the calibration of the cantilever deflection detection system, and the minimization of instrumental drift for accurate and reproducible force-distance measurements. Also, a method for the data analysis is presented that allows the extraction of force-penetration curves from recorded force-distance curves. A typical curve displays a clear elastic deformation regime up to the first plasticity event, or pop-in, with a length in the range of one to two Burger's vectors. Later plasticity events exhibit the same magnitude. The work of plasticity is further extracted from the measurements. Finally, the hardness is determined in combination with the indentation curve using non-contact atomic force microscopy images of the remaining indents.

概要

For the last 150 years, hardness values have been used to characterize the mechanical behavior of materials and to predict their performance under various loading conditions. The hardness of a material describes the resistance of its surface to the penetration of a harder indenter. For metallic materials, the hardness relates to resistance to plastic flow.

Although the implementation of hardness testing has proven to be relatively easy, the yielded results have long been rather empirical, making them unable to describe the intrinsic properties of the investigated material. The empirical nature of hardness testing results has been a consequence of the use of various indenter geometries, each of which has a different established hardness scale. However, all empirical hardness scales, such as the Brinell hardness (HB) test for spherical indenters and the Vickers (HV) and Knoop (HK) hardness tests for different types of four-sided pyramids, have one thing in common: the hardness number is determined from the ratio of the applied load to the developed area of the remaining indent. In an attempt to relate the hardness of metals to their fundamental mechanical properties, the hardness measured with a spherical indenter has been defined as the ratio of the applied load to the projected area of the remaining indent. This hardness value, also known as the Meyer's hardness (H), is equal to the mean contact pressure and directly relates to the yield strength of non-work-hardening metals¹.

Hardness testing has long been limited to the macro-scale, in which case the sizes of indents have been measured by optical means. The development of instrumented indentation, where force-displacement curves are recorded, has been recognized as a valuable alternative for determining the hardness of a material, although the size of the remaining indent may be too small to be accurately imaged. In this case, the projected area of the indent is calculated from the tip displacement according to a so-called indenter-area function². Due to this development, the analysis of the curvature of force-displacement curves and of the occurrence of distinct plasticity events in the shape of pop-ins is now widely used to study the mechanisms of plastic deformation at the micrometer scale, such as by means of nanoindentation³.

It is well accepted that the carriers of plastic deformation in metals, i.e., dislocations, operate at the nanometer scale. To understand their modes of operation at the atomic level, new experimental techniques with atomic resolution are needed. Initial investigations of atomistic plasticity events at the interfaces between nanometer-sized single asperities and single crystalline Au surfaces of different orientations have been carried out by interfacial force microscopy (IFM)^{4, 5}. Atomic force microscopy (AFM) indentation has been applied to observe the nucleation and gliding of single dislocations in KBr(100) single crystals⁶, Cu(100)⁷, and Au(111)^{8, 9}. There, atomistic plasticity events were observed in the shape of pop-ins, with lengths in the range of 1 Å. AFM indentation has also been used to measure the nano-hardness and -elasticity of gold nano-island grown on mica¹⁰. In this work, the nano-hardness was found to be smaller than the bulk value and was observed to depend linearly on the indentation area. Also, a detailed measurement protocol has been proposed to determine the hardness of hard surfaces, such as fused quartz and silicon, by AFM indentation with a diamond-tipped sapphire cantilever¹¹. In particular, this method takes into account the non-linearity of the photo-sensitive deflection detectors for large cantilever deflection¹². More recently, AFM indentation and non-contact AFM imaging have been combined to quantitatively determine the hardness and the fundamental mechanisms of plastic deformation of a Pt(111) single crystalline surface and Pt-based metallic glass¹³. For Pt(111), plastic deformation mechanisms at the nanometer scale were found to be consistent with the discrete mechanisms established for larger scales. Further, the nanometer-scale plastic deformation of the metallic glass was found to be not discrete, but rather continuous and highly localized around the indenting tip. These results revealed a lower size limit for metallic glasses, below which shear transformation mechanisms are not activated by indentation. AFM indentation has also been used to determine the hardness values of biological samples (such as collagen fibrils)¹⁴, polymers¹⁵, and colloidal crystals¹⁶.

In the present work, a careful experimental procedure is described that includes the force sensor selection, its calibration, the calibration of the cantilever deflection detection system, and the minimization of instrumental drift for accurate and reproducible force-distance measurements. Also, a method for the data analysis is presented that allows the extraction of force-penetration curves from recorded force-distance curves. Further representative results are shown and discussed in the light of recent findings in the field of plastic deformation of small volumes.

For this experiment, an atomic force microscope (AFM) was used. The cornerstone of an AFM is its micro-fabricated force sensor (usually a cantilever beam), with a sharp tip at the end whose radius is in the range of several nanometers. In the particular configuration of the instrument used for this experiment, the cantilever is mounted onto a piezo-electric z-scanner, while the sample to be investigated is mounted onto a piezo-electric x/y-scanner. During AFM imaging, the force sensor tip is scanned over a sample to register interaction forces with the sample surface that result in a deflection of the cantilever according to Hooke's law. The static or dynamic deflection of the cantilever can be measured with an optical beam deflection detector, consisting of a laser diode, a set of mirrors, and a photodiode that converts the cantilever deflection into a voltage. During imaging, the signal at the photodiode is controlled by a feedback loop so as to keep the interaction forces at the sample surface; this results in adjustments of the z-scanner position, which are recorded and displayed as a topography image.

Prerequisites for the experiment described below are that the piezo-electric scanners of the atomic force microscope are well-calibrated and that the instrument stays in the laboratory at a constant temperature and humidity level. The reader should be aware that, depending on the atomic force microscope model, some of the experimental procedure steps may have to be modified. In particular, all measurements are performed after setting the scanners' ranges to "small"; this function allows for the reduction of the x/y-scanner range to 5 x 5 µm² and the z-scanner range to 4 µm, which ensures a resolution at small scales. This function is not available on all commercial AFM and is not mentioned in the remainder of the text.

For data analysis, the use of the free SPM data analysis software Gwyddion¹⁷ and the Matlab software package¹⁸ are recommended.

This protocol gives a description of the experimental procedure to be followed in order to perform instrumented hardness measurements by AFM. Since the handling of different commercial AFMs may differ from one model to the other, the reader should refer to the manual provided by the AFM manufacturer for detailed setting procedures and software information. In the following text, in order to reproduce the described experiment, it is assumed that the reader is familiar with the handling of the particular AFM used here.

プロトコル

1.インストゥルメンタルセットアップとキャリブレーション

1. インストゥルメンタルセットアップ
   1. _0,1≥180 kHzの、品質係数Q≥300、および曲げ剛性k≥40 N / mのfは最初のフリー共振周波数にタイプDT-NCLRまたはCDT-NCLRの硬いダイヤモンド被覆カンチレバーを使用してください。
   2. AFMの製造元から提供されているクランプホルダーに選択されたカンチレバーをマウントします。その長軸がAFMの高速走査方向に対して垂直になるようにカンチレバーを配置するために特別な注意を払ってください。また、二成分エポキシ接着剤を使用して、AFMの製造元から提供されているカンチレバーホルダーにカンチレバーを接着。
   3. AFMヘッド上にカンチレバーホルダーをマウントし、AFMカンチレバーに集中するAFMシステムで通常利用可能な光学顕微鏡を使用しています。カンチレバーの長軸が高速走査方向に垂直であることを再確認してください。ない場合は、バックに行きますセクション1.1.2。
   4. それは、カンチレバーの最後に反映されるように、レーザービームの位置を合わせます。フォトダイオードの電圧の和を監視し、和信号を最大化するために微調整を行っています。典型的な和信号の値が2 [V]の範囲であります
   5. 縦と横方向の変位に対応する電圧がほぼゼロであるフォトダイオードの中心に反射されたレーザスポットを持参するように、ミラーの水平方向と垂直方向の傾斜角度を調整します。
2. 較正
   1. カンチレバーの_0,1 fの最初のフリーの曲げ共振を決定するために、周波数掃引を実行します。
   2. ¹⁹に従って計算カンチレバーkの曲げ剛性を決定します
      （1）
      Eはヤング率でありcantilの幅wは、Lは 、カンチレバーの長さでありますこれまで、およびtは厚さです。この目的のために、よりよい精度のために、光学顕微鏡または走査型電子顕微鏡によるカンチレバーの長さと幅を測定します。によると_、0,1 fはその最初のフリーの曲げ共振周波数からカンチレバーの厚さを計算します
      （2）
      ここで、ρは質量密度です。
   3. AFMの設定メニューで実験に使用される特定のカンチレバー型用のフォトダイオードの感度のデフォルト値を選択します。 アプローチ]ボタンをクリックすることで、荷重Fで基準サンプルと接触さカンチレバー先端を持参_のn = 10 nNの。
   4. AFMソフトウェアの力分光法メニューを開き、50 nmおよび0.3ミクロン/秒のzスキャナ後退/拡張にz軸スキャナの相対的な後退と拡張子を設定します。そう、力 - 距離曲線の記録はなります離れた試料表面から50 nmまでのzスキャナの後退の最初で構成し、同じ距離のアプローチや陥没の一連の。
   5. 試料の変形の影響を回避するために、そのようなナノ結晶ダイヤモンドやサファイアなどの滑らかで非準拠表面上1.2.4で提案セットパラメータと力距離曲線を記録します。これを行うには、AFMソフトウェアの力分光法メニューの取得]ボタンをクリックします。
   6. AFMソフトウェアのキャリブレーションメニューで、線形関数と力 - 距離曲線の反発部分を取り付けます。フィッティングラインの逆勾配は、フォトダイオードの感度Sに相当します。 実行キャリブレーション]ボタンをクリックすることで、AFMソフトウェアのキャリブレーションメニューで、機器・ソフトウェアのデフォルト値に決定された値を代入します。

2.試料の調製

注：THIで測定されたサンプルsの実験は、物理蒸着法によって雲母上に成長させた厚さ100nm、原子的に平滑な金（111）薄膜で構成されています。

1. 両面カーボンテープを用いて、機器の製造元から提供されている磁気サンプルホルダーにサンプルをマウントします。カーボンテープをリラックスさせるように、測定中の試料のドリフトを回避するために、測定の前に1日のサンプルをマウントします。また、通常は数分以内に乾燥銀ペイント、とホルダーにサンプルをマウントします。
2. X / Yスキャナ上に磁気試料ホルダーをマウントします。

3.測定手順

1. オフ共鳴し、これらの値が自動的にこの特定のカンチレバーのための機器・ソフトウェアによって設定されていることをA = 20 nmのノートでの振動振幅（この実験では、F = 190.67 kHz単位で）わずかに発振周波数を設定します。 _{セットポイント} = 5 nmで手動で発振セットポイントを設定します。
2. ドローAFMのステップモータを使用して、試料表面に向かってカンチレバー。力センサは、試料表面と衝突しないことを確認してください。粗アプローチの間に焦点が合ってカンチレバーを維持し、試料表面が完全な焦点になる前に粗大なアプローチを停止します。
3. 自動的にアプローチ]ボタンをクリックすることで力センサに近づきます。振動の振幅が設定値に達すると、先端は試料表面のトポグラフィーを走査する準備ができています。
4. 5×5から1×1μm²に至るまでの領域上の地形の一連の画像を記録する（利用可能な場合は、X / Y-スキャナを傾けることによって地形信号の傾きを調整します）。同じ領域の連続した画像は、ドリフトの兆候を示さないこと、およびzスキャナの位置はほぼ一定に保たれていることを確認します。そうでない場合は、システムが安定するまで、撮影を続けます。
5. システムが安定しており、滑らかな1×1μm²領域が発見されると、Fを引っ込めますORCEは後退ボタンをクリックすることで、試料表面から数マイクロメートルのセンサー。
6. 楽器メニューの力分光法モードを選択し、10nmの力セットポイントで、予め選択された1×1μm²エリアの中央に力センサを移動させます。それが一定になるまでのzスキャナの位置を監視します。
7. 中央予め選択された1×1μm²エリアの中心に対応する点の2×2のグリッドを選択します。 500 nmの2次隣接する点間の距離を設定します。
8. 300ナノメートル/秒の速度で0から150 nmまで変化させると、同じ距離を同じ速度で後退さ相対スキャナ距離を設定します。試料表面に関してカンチレバーの傾斜角を考えると、φは、傾斜角²⁰である垂直スキャナ拡張Z、中に日焼けφ×Zで横スキャナを移動させることでチルト補正を適用します。
   注：いくつかのinstにrumentsは、彼らの力分光法やインデントモードでは、カンチレバーの傾きを占めます。これは、この研究で使用したAFMの場合です。
9. AFMのインデントデータの取得を開始するために、機器のソフトウェアで開始ボタンを押してください。
10. AFMの押込測定が完了した後、数マイクロメートル離れて試料表面からの力センサを後退させます。
11. 機器のソフトウェアメニューの非接触AFMモードイメージングを選択し、セクション3.1および3.2に記載されている手順を繰り返します。
12. インデントの正確な位置を特定するために、3.3節と同様の1×1μm²表面積にわたってスキャンを実行します。 500×500nm²表面領域上にさらに表面スキャンは、より詳細に画像に残っているインデントを行うことができます。

4.データ解析

1. 画像処理
   1. 高速スキャンディレクトリ内の行を揃えるように記録された地形の画像を処理中央値の差に基づいてection。 Gwyddionの組み込み関数を使用してください。
2. Gwyddionのインデント解析機能を使用して、投影面積にインデントの_Pを計算_します。
3. Gwyddionの先端解析機能を用いてインデントのトポグラフィー画像からAFMチップの形状を推定します。そして、先端形状の画像を平均化し、平均先端形状の半開角αを測定します。
4. 力-距離曲線は、先端の変位を計算する^δ13に従ってにより力-変位曲線に変換します
   （3）
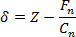
   ここで、Zは、相対的なスキャナの位置です。
5. さて、先端の変位対力をプロットします。結果の曲線は、通常、原子論的可塑性のイベントに対応するいくつかの100午後の範囲の長さ、で、いわゆるポップインが表示されます。 thesというの最初を使用電子ポップインは_エル ^4δ弾性限界で先端の変位を決定します。
6. ヘルツ機能²¹と力-変位曲線の弾性部分を取り付けます。
   （4）
   Rは、先端半径であり、E ^'*はで与え、弾力性の減少係数であります 、M _S、Tはそれぞれ、サンプルの先端の押し込み弾性率であると。この場合には、適合パラメータであります 。
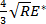7. フィット関数および実験曲線²¹の間の面積の差から塑性Wの_可塑性の仕事を計算するように塑性政権にフィット機能を拡張します。
8. ^、1に係る試料の硬度を算出する²
   （5）
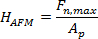
   そして
   （6）
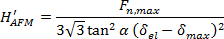
   F _{nは、maxは}最大荷重がある場合_、pは 4.2節で計算されたインデントの投影面積は、αは、4.3節で計算された先端の半開角であり、δ _エルは、最初の可塑性における先端変位でありますイベントは_、δmaxは最大の先端変位（4.4節を参照）です。

結果

この研究では、カンチレバーkの曲げ剛性は、幾何学的なビーム理論¹⁹に従って算出しました。この作業で使用される特定のダイヤモンド被覆カンチレバーのために、我々はK = 55.69 N / mのを見つけました。我々はダイヤモンドコーティングを無視していることに注意してください。ダイヤモンドコーティングの厚さは、カンチレバーの厚さよりも?...

ディスカッション

この方法は、ダイヤモンドコーティングされたAFMチップのAu（111）薄膜の表面上に一連のくぼみを行うために提示されています。非接触AFM画像及びAFMのインデントは、同一の力センサを用いて行きました。非接触イメージングのための要件は_0,1≥180キロヘルツとAFMのインデントに高い品質係数Q≥300 fが高い第一の自由共振周波数であり、適用される垂直方向の力は...

資料

Name	Company	Catalog Number	Comments
AFM XE-100	Park Instruments	discontinued	Atomic force microscope
CDT-NCLR	NanoSensors	CDT-NCLR	Conductive diamond coated non-contact lever
100 nm thick Au(111) thin film on Mica	Phasis	20020011	atomically smooth gold thin film