直交重ね合わせレオロジーの校正手順

要約

ニュートン流体を使用した市販の直交重ね合わせレオロジー手法の詳細な校正プロトコルを提示し、エンドエフェクト補正係数の決定方法と実験誤差を減らすためのベストプラクティスの推奨事項を示します。

要約

直交重ね合わせ(OSP)レオロジーは、一次せん断流に直交する小振幅振動せん断変形を重ね合わせる高度なレオロジー手法です。この手法は、非線形流れ条件下での複雑な流体の構造ダイナミクスの測定を可能にし、広範囲の複雑な流体の性能の理解と予測に重要です。OSPレオロジー技術は、主にこの技術の力を強調したカスタムビルドのデバイスを通じて、1960年代から長い開発の歴史があります。OSP技術は現在、レオロジーコミュニティに市販されています。OSP形状の複雑な設計と理想的でない流れ場を考えると、ユーザーは測定誤差の大きさと原因を理解する必要があります。この研究では、ニュートン流体を使用したキャリブレーション手順を示し、測定誤差を減らすためのベストプラクティスの推奨事項を示します。具体的には、最終効果因子の決定方法、サンプル充填手順、および適切な測定範囲(せん断速度、周波数など)の特定に関する詳細情報が提供されます。

概要

複雑な流体のレオロジー特性を理解することは、信頼性が高く再現性のある製品の開発と製造のために多くの産業にとって不可欠です¹。これらの「複雑な流体」には、パーソナルケア製品、食品、化粧品、家庭用品など、私たちの日常生活に広く存在する懸濁液、ポリマー液体、および泡が含まれます。レオロジー特性または流動特性(粘度など)は、最終用途と加工性の性能指標を確立する上で重要な量ですが、流動特性は複雑な流体内に存在する微細構造と相互に関連しています。複雑な流体が単純な液体と区別される顕著な特徴の1つは、複数の長さスケールにまたがる多様な微細構造を持っていることです²。これらの微細構造は、さまざまな流動条件の影響を受けやすく、その結果、巨視的特性が変化します。流れと変形に応答する複雑な流体の非線形粘弾性挙動を介してこの構造-特性ループを解き放つことは、実験レオロジストにとって依然として困難な作業です。

直交重ね合わせ(OSP)レオ^ロジー3 は、この測定の課題に対処するための堅牢な手法です。この手法では、小振幅の振動せん断流を一方向の一次定常せん断流に直交して重ね合わせることで、課せられた一次せん断流の下で粘弾性緩和スペクトルを同時に測定することができます。具体的には、線形粘弾性⁴の理論を用いて小さな振動せん断摂動を解析することができ、非線形流れ条件は一次定常せん断流によって達成される。2つの流れ場は直交しており、したがって結合されていないため、摂動スペクトルは、一次非線形流れ⁵の下での微細構造の変化に直接関係する可能性があります。この高度な測定技術は、複雑な流体の構造-特性-処理の関係を解明し、それらの定式化、処理、およびアプリケーションを最適化する機会を提供します。

現代のOSPレオロジーの実装は、突然のひらめきの結果ではありませんでした。むしろ、それはカスタムデバイスの何十年にもわたる開発に基づいています。最初のカスタムメイドのOSP装置は、シモンズ⁶によって1966年にさかのぼり、その後^7,8,9,10に多くの努力が払われました。これらの初期のカスタムビルドデバイスには、アライメントの問題、ポンピングフロー効果(直交振動を提供するためのボブの軸方向の動きによる)、機器の感度の制限など、多くの欠点があります。1997年、Vermantら³は、市販の独立したモータートランスデューサレオメーターのフォースリバランストランスデューサ(FRT)を変更し、以前のデバイスよりも広い粘度範囲の流体のOSP測定を可能にしました。この変更により、垂直力リバランストランスデューサは応力制御レオメーターとして機能し、軸力の測定に加えて軸方向の振動を課すことができます。最近、OSP測定に必要な形状は、Vermantによる方法論の後、市販の別のモータートランスデューサレオメーター用にリリースされました。

市販のOSPレオロジーの出現以来、この技術をさまざまな複雑な流体の調査に適用することに関心が高まっています。例としては、コロイド懸濁液11、12、コロイドゲル13、14およびガラス¹⁵、^16、17が挙げられる。市販の機器の入手可能性はOSP研究を促進しますが、複雑なOSP形状は、他の日常的なレオロジー技術よりも測定のより深い理解を必要とします。OSPフローセルは、二重壁同心円柱(またはクエット)ジオメトリに基づいています。上部が開き、下部が開いた設計により、環状のギャップとリザーバの間を流体が行き来することができます。メーカーによる形状設計の最適化にもかかわらず、OSP操作を行うと、流体は不均一な流れ場、幾何学的端効果、および残留ポンプ流を経験し、これらすべてがかなりの実験誤差を引き起こす可能性があります。我々の以前の研究¹⁸は、この技術のためのニュートン流体を用いた重要な最終効果補正手順を報告した。正しい粘度結果を得るには、一次方向と直交方向の両方に適切な最終効果係数を適用する必要があります。このプロトコルでは、OSPレオロジー技術の詳細な校正方法を提示し、測定誤差を低減するためのベストプラクティスの推奨事項を提供することを目的としています。OSP形状のセットアップ、サンプルのローディング、およびOSPテストの設定に関するこのホワイトペーパーで説明されている手順は、ニュートン流体以外の測定に簡単に採用および変換できます。流体分類(ニュートンまたは非ニュートン)のOSP測定の前に、ここで説明する校正手順を利用して、アプリケーションの最終効果補正係数を決定することをお勧めします。エンドファクターのキャリブレーション手順は以前に報告されていないことに注意してください。本稿で提供されるプロトコルでは、レオメーターユーザーが見落としがちな「生」データと「測定」データの理解に関する技術リソースについて、一般的な正確なレオロジー測定を実行する方法に関するステップバイステップガイドとヒントについても説明します。

プロトコル

1. レオメーターのセットアップ

注意: このセクションのプロトコルでは、セットアップの準備、適切な形状の設置、試験材料のロード、実験手順の設定、形状の指定、およびテストの開始など、レオロジー実験を実行するための基本的な手順について説明します(別のモータートランスデューサーレオメーターまたはモータートランスデューサーレオメーターの組み合わせの場合)。OSP 操作に関する具体的な手順と注意事項が提供されています。探触子の温度勾配を最小限に抑えるために、操作の前に少なくとも30分間レオメーターに電力を供給することをお勧めします。機器の制御とデータ収集のためにこのプロトコルで使用されるレオメーターソフトウェアは、 材料表に記載されています。レオメーターの仕様については 、表1 を参照してください。

1. レオメーターを設定する前に、レオメーターソフトウェアで 直交重ね合わせ 機能を有効にします。温度測定用のテストステーションと環境制御装置に下部プラチナ測温抵抗体(PRT)を設置します。
   注意: 持ち上げますtage取り付けプロセスの最大の高さまで(図1a)。環境制御装置を取り付ける前に、適切なPRTを取り付けてください。設置中は、環境制御装置でPRTを叩かないように注意してください。付属のスパナレンチを使用して、テストステーションの環境制御装置を固定します。
2. 二重壁同心円柱ジオメトリを取り付けます。
   1. 内側と外側のシリンダー(図1b)を適切に組み立てて、二重壁カップの構成を完了します。
      注意: カップを組み立てる前に、内筒のOリングの状態(亀裂、腫れ、その他の損傷がない)を確認し、必要に応じて交換してください。
   2. カップを環境制御装置に挿入し、ジオメトリを適切に位置合わせします。
   3. 下部ジオメトリ(カップ)を下に押して、トルクドライバー(0.56 N m固定)を使用してつまみネジを締めながら、バネ仕掛けのPRTを圧縮します。
      注意: 下部ジオメトリが正しく取り付けられているかどうかを確認するには、モーター電源を無効にし、指を使用してジオメトリを回転させます。下部ジオメトリが環境制御装置で自由に回転する場合は、適切にインストールされ、次の手順に進みます。自由に回転しない場合は、前の手順と逆の順序でテストステーションからコンポーネントを取り外してから、下部ジオメトリを再インストールします。温度信号が下部PRTから受信されていることを確認します。レオメーターは、デフォルトで温度センサーを自動的に認識する必要があります。そうでない場合は、レオメーターソフトウェアの温度制御オプションで、温度制御センサーソースとして下部のPRTを選択します。
   4. 上部ジオメトリ(ボブ)をトランスデューサーシャフトに取り付けます。レオメーターソフトウェアからトランスデューサーコントロールパネルの風袋引きトランスデューサーボタンをクリックするか、機器のタッチスクリーンの[計器]タブで[風袋引きトルクと風袋垂直]を使用して、法線力と垂直トルクを風袋引きします。レオメーターのセットアップ全体像を図1cに示します。
   5. レオメーターソフトウェアまたは機器のタッチスクリーンからギャップコントロールパネルの ゼロフィクスチャ ボタンをクリックして、上部と下部の形状間のギャップをゼロにします。必要に応じて、形状の質量キャリブレーションを実行します。
      注: 製造元が提供するジオメトリのドキュメントを参照して、工具質量の上限値が利用可能かどうかを確認してください。そうでない場合は、このステップの最後にジオメトリ質量キャリブレーションを実行します。画面の指示に従って、上部ツールの質量キャリブレーションを実行します。完了したら、正しい新しいフィクスチャ質量が受け入れられることを確認します。

2.試験材料のロード

1. ステージを持ち上げて、テスト材料をカップにロードするのに十分なワークスペースを提供します。
2. ピペットまたはヘラを使用して、試験材料をカップに入れます。流体への空気の巻き込みを最小限に抑えるために、試験材料を慎重に取り扱ってください。
   注意: 低粘度の試験材料(5 Pa s未満など)をロードする場合は、調整可能な容量ピペットを使用します(図2a)。ジオメトリを埋める最小体積は、レオメーターソフトウェアの[実験]パネルの下にある[ジオメトリ情報]にあります。現在入手可能なOSP形状に必要なおおよその容量、すなわち0.5mmおよび1.0mmの環状ギャップ幅は、それぞれ32mLおよび36mLである。より高い粘度の試験材料(5 Pa sを超えるなど)をロードする場合は、スパチュラまたは容積式ピペットを使用します(図2b)。高粘度液体の正確な体積制御は難しいため、高粘度液体を装填する場合、流体体積に基づく微調整は推奨されません。いずれにせよ、このステップでは、オーバーフィルではなく、わずかにアンダーフィルすることが期待されます。次の手順に従って、材料の正確な負荷を確保します。
3. ボブをカップに下げてジオメトリギャップ設定点まで下げ、持ち上げて、ロードされたジオメトリの液面を確認します。目標は、ボブ上部開口部の下端よりわずかに(約2 mm)上にある流体接触線を達成することです。
   注:このプロセスは、形状の環状ギャップ幅が小さく、必要なサンプル量が比較的多いため、目的の流体レベルに到達するまでに長い待ち時間が必要になる場合があります。待ち時間は主に試験材料の粘度に依存します。たとえば、高粘度の液体は、シリンダー間の隙間に流れ込み、ボブ表面を完全に濡らすのに時間がかかります。
4. 上部ジオメトリを流体に慎重に下げて、ジオメトリギャップ設定ポイント8mmに到達します。このプロセスは、 図 2c のステップ 1 として示されています。ボブがギャップが8mmに設定されている位置(iii)に保たれるまで数分待ちます。
   注意: ボブの端面が流体に接触したら、ボブの下向きの速度を下げます。高粘度の液体または降伏応力流体の場合は、垂直力の読み取り値を注意深く監視して、このプロセス中に探触子が過負荷にならないようにします。
5. 装置の低速旋回速度を使用して、濡れた流体接触線を目視検査できる位置までボブを垂直に持ち上げます(図3)。接触線は、ギャップ設定点でのジオメトリ内の流体レベルを示します。ボブの線がボブの上端(ボブの上部開口部の下縁)より下にある場合は、流体の高さがシリンダーの内側の高さよりも低いことを示しており、ジオメトリに追加のテスト材料を追加する必要があります。
6. ボブを前のローディング位置に慎重に持ち上げて、十分な作業スペースを確保し( 図2cのステップ2)、必要に応じて追加の量のテスト材料をカップにロードします。キャビテーションを避けるために、ボブをゆっくりと上下に動かします。追加の気泡が発生しないように、テスト材料を慎重に追加します。
7. 上部のジオメトリを流体に下げ、最終的なジオメトリ ギャップに再度設定します。図1aに示すように、ボブの接液接触線が上部ボブ開口部の下縁から約2 mm上になるまで、手順1と2(図3c)を繰り返します。また、ボブの上部開口部の下縁が適切に濡れていることを確認します(図3b)。ボブをジオメトリギャップ設定点に移動し、試験材料をリラックスさせます。
   注意: 待機時間は、標準材料の粘度によって異なります。たとえば、1 Pa sの液体の場合、15分の待機時間で十分です。一方、100 Pa sの液体の場合、はるかに長い待ち時間(4時間)が必要です。このプロセスは、 図 2c のステップ 3 として示されています。完全なサンプルロード手順を 図2に示します。高粘度の流体は長時間を必要とし、ロードが困難です。待ち時間を短縮するには、温度を数度上げると、粘性のある校正液の流れが促進される場合があります。

3.粘度校正測定の実行

メモ: このホワイトペーパーで提供されるキャリブレーションプロトコルは、OSP技術に適用される最終効果要因に固有です。これには、トルクおよび垂直力のキャリブレーション、位相角チェック、PDMSチェックなどを含む定期的なキャリブレーションまたは検証チェックは含まれません。個々のレオメーターメーカーが推奨しているもの。これらの手順は、本論文のキャリブレーションプロトコルの前に実行する必要があります。読者は、定期的な校正またはチェックを実行する手順については、レオメーターメーカーのユーザーマニュアルを参照する必要があります。このプロトコルで使用されるシリコーン粘度基準は、 材料表に記載されています。

1. ジオメトリを指定する
   注意: 実験を設定する前に、レオメーターソフトウェアで正しい形状が選択されていることを確認してください。初めて使用する場合は、以下の手順に従って、レオメーターソフトウェアで新しい直交二重壁同心円柱形状を作成します。
   1. 新しい直交二重壁同心円柱ジオメトリを追加します。
   2. 表 2 に示すように、ジオメトリの寸法を入力します。
      注意: 数字とそれに対応する記号は、ボブとカップに刻まれています。ここで使用されている実験ジオメトリの動作ギャップは8mmですが、メーカーが指定する必要があります。したがって、内筒の高さは(浸漬高さ+ 8 mm)に等しくなります。
2. ジオメトリ定数を指定します。ジオメトリ慣性とジオメトリ質量のフィールドに適切な値を入力します。最終効果係数と直交最終効果係数の両方に1.00と入力します。
   注意: メーカーが指定した0.5mmおよび1.0mmギャップOSPジオメトリの形状慣性は、それぞれ15.5μN m^s 2および10.3μN m s²です。上部ジオメトリ質量の正しい値が入力されていることを確認します。この値は、製造元が提供するジオメトリのドキュメントに記載されています。または、ジオメトリキャリブレーションタブ(プロトコルステップ1.2.5)でジオメトリ質量キャリブレーションを実行し、正しい新しいフィクスチャ質量が適用されていることを確認します。デフォルトの最終効果係数(CL)は1.065で、直交最終効果係数(CL₎は1.04です。両方のフィールドを 1.00 に変更します。応力定数は、寸法と最終効果係数から自動的に計算されます。ひずみ定数は、ジオメトリ寸法によってのみ決定されます(式は前の作業¹⁸で提供されています)。寸法の定義を表 2 に説明し、図 4 に示します。(一次)応力定数 K τ と直交(線形)応力定数 K_το の式は次のとおりです。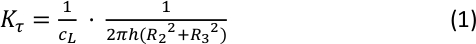
   
   

4.定常せん断速度掃引試験

注意: 粘度校正測定は、_CLまたは_CLOを校正するために、一次方向または直交方向のいずれかで独立して実行されます。一次方向については、せん断速度掃引試験を実行して安定したせん断粘度を測定します。直交方向については、直交周波数掃引試験を行うことにより動的複素粘度を測定します。

1. サンプルを25°Cで15分間調整して、試験材料が熱平衡に達するようにします。
   注意: 校正測定は、標準液の認定粘度が報告される温度、つまり25°Cで行われます。 リーダーは、ニュートン標準液体に適した異なるテスト温度を使用できます。平衡化時間または浸漬時間、すなわち15分は、環境制御装置、形状、およびサンプルが熱平衡に達することを確実にするために推奨される。
2. レオメーターソフトウェアの実験手順でフロースイープテストを選択します。環境制御下で試験温度を25°Cに設定します。
3. せん断速度の範囲を 0.01 s−1 から 100.0 s⁻¹ の範囲で指定し、10 年ごとに 10 ポイントで対数的にデータを記録します。自動定常状態決定を有効にします。
   注意: ここで使用されるせん断速度範囲は、機器のトルク感度制限(表1)と測定液に基づいています。例えば、より高い粘度の液体(例えば、300Pa s)の場合、10−^4s−1〜1s⁻¹のより低いせん断速度範囲が使用され得、逆もまた同様である。
4. レオメーターソフトウェアから実験を開始します。

5. 直交周波数掃引試験

1. レオメーターソフトウェアのトランスデューサーコントロールパネルから垂直力トランスデューサーをFRTモードに設定します。
   注意: 垂直力トランスデューサのデフォルトのトランスデューサ設定は、この別のモータートランスデューサレオメーターのスプリングモードです。OSP動作では、垂直力変換器は応力制御または複合モータトランスデューサレオメータとして動作し、軸力を同時に測定しながら軸方向変形を適用します。OSPテストを実行するには、通常の力変換器をFRTモードで設定する必要があります。
2. サンプルを25°Cで15分間調整して、熱平衡を確保します。
3. レオメーターソフトウェアの実験手順で直交周波数掃引テストを選択します。試験温度を25°Cに設定します。
4. 目的の垂直ひずみを指定し、回転方向のせん断速度に 0.0 s⁻¹ と入力します。
   注:最大垂直ひずみ(軸ひずみ振幅)は、OSP形状のギャップ幅に依存し、レオメーターの最大直交振動変位、つまり50μmによって制限されます(表1)。
5. 角周波数範囲を10年あたり10ポイントで0.1〜40rad/sの範囲で対数的に指定します。
   注意: ここで使用される角周波数範囲は、機器の軸方向周波数感度制限(表1)およびギャップ負荷条件¹⁸の考慮に基づいて、OSP動作の推奨範囲です。詳細については、「 ディスカッション」 セクションを参照してください。
6. レオメーターソフトウェアから実験を開始します。

6. 分析の実行

1. 主要な最終効果因子の決定
   1. 定常せん断速度掃引結果(プロトコル手順4.4)を.csvや.txtなどのオープンファイル形式にエクスポートします。
   2. スプレッドシートソフトウェアで適切なせん断速度範囲で報告された粘度の平均値を計算します。
      注意: 平均粘度の計算には、製造で指定された制限を超える対応するトルク値を持つ粘度データのみが使用されます。平均粘度値は、未補正の一次粘度として定義されます。
   3. 平均粘度値を使用して主要な最終効果係数を見つけます。
      注意: このセクションは、主要な最終効果係数とレオメーターソフトウェアからの直接粘度出力との関係の導出を示すためにここで提供されています。実験データからの終端因子の計算例は、代表的な結果セクションに示されています。一次定常せん断粘度は、せん断速度に対するせん断応力τの比であり、トルクMの生信号と回転速度Ωから形状定数(_KτおよびK_γ)を介して計算されます。式は次のように与えられます。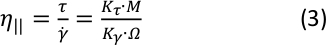
      
      ここで、_Kτは一次応力定数(式1)、K_γは幾何学的寸法にのみ依存する一次ひずみ定数です。したがって、式1を式3に代入すると、計算された一次粘度、またはレオメーターソフトウェアからの出力粘度値は、一次最終効果係数_CLに反比例することが示されます(式3の他のすべての変数は幾何学的定数または生の測定信号のいずれかであることに注意してください)。
      
      式3は、測定された粘度が生データ、すなわちトルクおよび速度から、使用される異なる形状(例えば、円錐プレート、平行平板、同心円柱など)に依存する応力およびひずみ定数を介して計算される任意の回転レオメトリーの一般的な式であることに注意してください。

7. 直交最終効果因子の決定

1. 直交周波数掃引結果(プロトコル手順5.6)を.csvや.txtなどのオープンファイル形式にエクスポートします。
2. 表計算ソフトウェアで、適切な角周波数範囲で報告されたOSP複素粘度の平均値を計算します。
   注意: 平均粘度の計算には、メーカーが指定した制限を超える対応する振動力値を持つ粘度データのみが使用されます。平均粘度値は、未補正直交複素粘度として定義される。
3. 平均複素粘度値を使用して直交最終効果係数を求めます。
   注:このセクションは、直交終末効果係数とレオメーターソフトウェアからの直交複素粘度出力の関係の導出を示すためにここで提供されています。実験データからの直交終端因子の計算例は、代表的な結果セクションに示されています。直交複素粘度は、直交複素せん断弾性率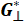を直交振動周波数ωで割ったものに等しく、振動力F、振動変位θ、周波数ω(3つとも生の信号)、および幾何定数(_Kτοおよび_Kγο)を介して次の式で表すことができます。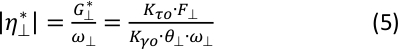
   
   ここで、K _το は直交応力定数 (式 2)、K_γο は直交ひずみ定数であり、これは幾何学的寸法にのみ関係しています。したがって、式2を式5に代入すると、計算された直交複素粘度、またはレオメーターソフトウェアから出力されたOSP複素粘度値は、直交終末効果係数_CLoに正比例することが示されます(式5の他のすべての変数は幾何定数または生の測定信号のいずれかであることに注意してください)。
   
   式5は、測定された複素粘度が生データ(力、変位、周波数)から、使用される形状(コーンプレート、平行プレート、同心円柱など)に依存する応力およびひずみ定数を介して計算される直線運動測定の一般的な式であることに注意してください。

8. OSP測定による粘度検証チェック

注意: この手順では、キャリブレーション実験から得られたキャリブレーションされたエンドエフェクトファクターを使用して、補正が有効かどうかを確認します。

1. ジオメトリ定数の下に端点効果係数と直交端効果係数のキャリブレーション値を入力し、最初はこれらの値を 1.00 に設定していました。応力定数は自動的に更新され、値は 表3のようになります。
2. 直交周波数掃引テストの手順に従って、同じ実験手順を設定します。せん断速度として 1.0 s⁻¹ と入力します。
3. 実験を開始します。

結果

12.2 Pa sのシリコーン粘度標準での粘度校正測定の代表的な結果を図5と図6に示します。キャリブレーション実行では、一次最終効果係数と直交最終効果係数の両方が1.00に設定されていることに注意してください。図5は、二重y軸プロット上のせん断速度の関数としての定常せん断粘度とトルクを示しています。シリコーン液?...

ディスカッション

このプロトコルでは、二重壁同心円柱形状を備えた市販の直交重ね合わせレオロジー技術のために、ニュートン流体を使用して粘度校正測定を実行するための詳細な実験手順を提示します。キャリブレーション係数、すなわち一次最終効果係数CLと直交最終効果係数CL_は、定常せん断速度掃引および直交周波数掃引試験を実施することによって独立?...

資料

Name	Company	Catalog Number	Comments
Advanced Peltier System	TA Instruments	402500.901	Enviromental control device
ARES-G2 Rheometer	TA Instruments	401000.501	Rheometer
Brookfield Silicone Fluid, 12500cP	AMTEK Brookfield	12500 cps	Viscosity standard liquid
OSP Slotted Bob, 33 mm	TA Instruments	402796.902	Bob, upper geometry
OSP Slotted Double Gap Cup, 34 mm	TA Instruments	402782.901	Double wall cup, lower geometry
Pipette (1 – 10 mL)	Eppendorf	3120000089	To load test materials
Pipette (100 – 1,000 µL)	Eppendorf	3123000063	To load test materials
Pipette Tips (0.5 – 10 mL)	Eppendorf	022492098	To load test materials
Pipette Tips (50 – 1,000 µL)	Eppendorf	022491555	To load test materials
Spatula	VWR	82027-532	To load test materials
TRIOS	TA Instruments	v4.3.1.39215	Rheometer software