Determination of the Photoisomerization Quantum Yield of a Hydrazone Photoswitch

Podsumowanie

Photoisomerization quantum yield is a fundamental photophysical property that should be accurately determined in the investigation of newly developed photoswitches. Here, we describe a set of procedures to measure the photoisomerization quantum yield of a photochromic hydrazone as a model bistable photoswitch.

Streszczenie

Photoswitching organic molecules that undergo light-driven structural transformations are key components to construct adaptive molecular systems, and they are utilized in a wide variety of applications. In most studies employing photoswitches, several important photophysical properties such as maximum wavelengths of absorption and emission, molar attenuation coefficient, fluorescence lifetime, and photoisomerization quantum yield are carefully determined to investigate their electronic states and transition processes. However, measurement of the photoisomerization quantum yield, the efficiency of photoisomerization with respect to the absorbed photons, in a typical laboratory setting is often complicated and prone to error because it requires the implementation of rigorous spectroscopic measurements and calculations based on an appropriate integration method. This article introduces a set of procedures to measure the photoisomerization quantum yield of a bistable photoswitch using a photochromic hydrazone. We anticipate that this article will be a useful guide for the investigation of bistable photoswitches that are being increasingly developed.

Wprowadzenie

Photochromic organic molecules have attracted considerable attention in a wide range of scientific disciplines as light is a unique stimulus that can drive a system away from its thermodynamic equilibrium non-invasively¹. Irradiation of light with appropriate energies allows structural modulation of photoswitches with high spatiotemporal precision^2,3,4. Thanks to these advantages, various types of photoswitches based on configurational isomerization of the double bonds (e.g., stilbenes, azobenzenes, imines, fumaramides, thioindigos) and ring opening/closure (e.g., spiropyrans, dithienylethenes, fulgides, donor-acceptor Stenhouse adducts) have been developed and utilized as the core components of adaptive materials at various length scales. Representative applications of photoswitches involve photochromic materials, drug delivery, switchable receptors and channels, information or energy storage, and molecular machines^{5,6,7,8,9,10,11,12}. In most studies presenting newly designed photoswitches, their photophysical properties such as λ_max of absorption and emission, molar attenuation coefficient (ε), fluorescence lifetime, and photoisomerization quantum yield are characterized thoroughly. The investigation of such properties provides key information on the electronic states and transitions that are crucial for understanding the optical properties and isomerization mechanism.

However, accurate measurement of photoisomerization quantum yield-the number of photoisomerization events that occurred divided by the number of photons at the irradiation wavelength absorbed by the reactant-is often complicated in a typical laboratory setting due to several reasons. Determination of the photoisomerization quantum yield is generally achieved by monitoring the advancement of reaction and measuring the number of absorbed photons during irradiation. The primary concern is that the amount of photon absorption per unit time changes progressively because the total absorption by the solution changes over time as the photochemical reaction proceeds. Therefore, the number of consumed reactants per unit time depends on the time section in which it is measured during the irradiation. Thus, one is obliged to estimate the photoisomerization quantum yield that is defined differentially.

A more troublesome problem arises when both the reactant and photoproduct absorb light at the irradiation wavelength. In this case, the photochemical isomerization occurs in both directions (i.e., a photoreversible reaction). The two independent quantum yields for the forward and backward reactions cannot be obtained directly from the observed reaction rate. Inaccurate light intensity is also a common cause of error. For example, the aging of the bulb gradually changes its intensity; irradiance of the Xenon arc lamp at 400 nm decreases by 30% after 1000 h of operation¹⁴. The spreading of non-collimated light makes the actual incident irradiance significantly smaller than the nominal power of the source. Thus, it is crucial to accurately quantify the effective photon flux. Of note, thermal relaxation of the metastable form at room temperature should be sufficiently small to be ignored.

This paper introduces a set of procedures to determine the photoisomerization quantum yield of a bistable photoswitch. A number of hydrazone photoswitches developed by the group of Aprahamian, the pioneering research team in the field, have been in the spotlight thanks to their selective photoisomerization and remarkable stability of their metastable isomers^15,16,17. Their hydrazone photoswitches comprise two aromatic rings joined by a hydrazone group, and the C=N bond undergoes selective E/Z isomerization upon irradiation at appropriate wavelengths (Figure 1). They have been successfully incorporated as the motile components of dynamic molecular systems^18,19,20,21. In this work, we prepared a new hydrazone derivative bearing amide groups and investigated its photoswitching properties for the determination of the photoisomerization quantum yield.

Protokół

1. ¹H NMR spectrum acquisition at photostationary state (PSS)

1. In a natural quartz NMR tube containing 4.2 mg (0.01 mmol) of hydrazone switch 1, add 1.0 mL of deuterated dimethyl sulfoxide (DMSO-d₆). Transfer half of the solution to another NMR tube.
2. Place one of the NMR tubes 1 cm in front of a Xenon arc lamp equipped with a 436 nm bandpass filter. Start irradiation to the NMR sample and record a ¹H NMR spectrum every day until there is no change in the spectra as switch 1 reaches PSS. After reaching PSS, keep the NMR tube in the dark at room temperature and record the ¹H NMR spectrum after 12 h to monitor the progress of thermal relaxation.
   NOTE: Switch 1 does not show any appreciable change in the ¹H NMR spectrum at room temperature due to its bistable nature.
3. For the other NMR tube, repeat step 1.2 with a 340 nm bandpass filter to obtain a ¹H NMR spectrum at the PSS under 340 nm irradiation.
4. Open fid files of the NMR spectra at the PSSs with NMR processing software. Integrate a distinctive set of peaks (H1: C2 proton of quinoline, H2: proton in para-position to the hydrazone group, H3: CH₃ of ethyl ester) of the distinct isomers and calculate the isomeric ratio (Figure 2).
   NOTE: Compositions ([1-Z]:[1-E] ratio) under 436 nm and 340 nm irradiation are 8:92 and 82:18, respectively.

2. UV-Vis absorption spectroscopy at PSS

1. In a glass vial containing 12.6 mg (0.03 mmol) of 1, add 2 mL of spectroscopy grade DMSO. Take 100 µL of the solution and dilute with 1400 µL of DMSO to make 1 mM solution of 1. Transfer 20 µL of 1 mM solution of 1 to a quartz cuvette with 1.0 cm optical path length and dilute with 1980 µL of DMSO to make a 10 µM solution of 1. Seal the cuvette with a PTFE stopper and keep the sample in the dark.
2. Prepare another quartz cuvette containing 2 mL of DMSO as a blank sample. Measure the UV-Vis spectrum of the blank sample for baseline correction.
3. Place the sample from step 2.1 1 cm in front of a Xenon arc lamp equipped with a 436 nm bandpass filter. Start irradiation to the sample and measure the UV-Vis spectrum every 2 h until there is no change in the spectra as 1 reaches PSS (Figure 3).
   NOTE: The time taken to reach PSS for the UV-Vis spectroscopy sample is much shorter than for the NMR sample with a higher concentration.
4. Repeat step 2.3 with a 340 nm bandpass filter to obtain the UV-Vis spectrum at the PSS under 340 nm irradiation.
5. Deduce absorbance spectra of the pure 1-Z and 1-E using Eq (1) and Eq (2) (Figure 4).
   (1)
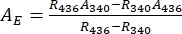   (2)
   Where R₄₃₆ = the ratio of 1-Z at the PSS under 436 nm irradiation; R₃₄₀ = the ratio of 1-Z at the PSS under 340 nm irradiation; A₄₃₆ = the absorbance of 1 in DMSO at the PSS under 436 nm irradiation; A₃₄₀ = the absorbance of 1 in DMSO at the PSS under 340 nm irradiation.
6. Calculate the molar attenuation coefficients of pure 1-Z and 1-E at all wavelengths by dividing the observed absorbance by the sample concentration (10 µM) and the optical path length (1 cm).

3. Kinetic studies on thermal relaxation

1. Heat the silicon oil filled in a heating bath circulator to the desired temperature (131 °C) and check if the temperature of the bath is stabilized. Submerge two NMR samples from step 1.2 in the heating bath.
   NOTE: The temperature and duration of heating are adjusted depending on the relaxation rate.
2. After 1 h of heating, transfer the NMR tubes quickly to a dry ice bath to pause the thermal relaxation caused by latent heat (Figure 5).
   NOTE: Inaccurate heating temperature or time may lead to serious error in the estimation of the rate constant.
3. Thaw the NMR samples obtained from step 3.2 at room temperature and ensure DMSO is defrosted. Record the ¹H NMR spectra of the samples.
4. Repeat steps 3.1-3.3 until there is no change in the ¹H NMR spectra as 1 reaches thermodynamic equilibrium.
5. Repeat steps 3.1-3.4 at different temperatures (134, 137, 140, and 143 °C).
6. Open fid files of the NMR spectra obtained in the course of heating at 131 °C. Calculate the averaged isomeric ratios as described in step 1.4. Calculate the concentration of 1-E (metastable isomer) based on the total sample concentration (10 mM) and the isomeric ratio.
7. Plot the averaged concentration of 1-E (C_E) as a function of the heating time. Perform an exponential fit to the data to obtain the rate constant of thermal relaxation using Eq (3)^15,22 (Figure 6).
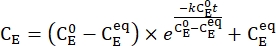   (3)
   Where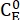 (M) = the concentration of 1-E at the initial state; 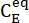(M) = the concentration of 1-E at the thermodynamic equilibrium at a specific temperature; k (s^-1) = the rate constant of thermal relaxation at a specific temperature; t (s) = the heating time.
8. Repeat steps 3.6 to 3.7 using the data obtained at different temperatures.
9. Plot ln(k) versus and perform a linear fit according to the Arrhenius equation (Eq (4)) to extrapolate the rate constant at room temperature (Figure 7).
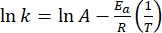   (4)
   Where A = the pre-exponential factor; E_a (J·mol^-1) = the activation energy for thermal relaxation; R = the ideal gas constant (8.3145 J·mol^-1K^-1); T (K) = the absolute temperature.
10. Calculate the thermal half-life of 1-E at room temperature using Eq 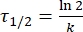(5).
    (5)
    Where τ_1/2 (s) = the thermal half-life of 1-E at room temperature; k (s^-1) = the rate constant of thermal relaxation at room temperature obtained from step 3.9.
11. If the rate constant of thermal relaxation is estimated only at a single temperature, calculate the rate constant at room temperature using the following rearranged Eyring equation (Eq (6))^18,23.
    (6)
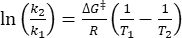    (7)
    Where (J·mol^-1) = the Gibbs energy of activation for thermal relaxation; k₁ (s^-1) = the rate constant of thermal relaxation estimated at the elevated temperature; k₂ (s^-1) = the rate constant of thermal relaxation at room temperature (298.15 K); T₁ (K) = the absolute temperature at which k₁ is obtained; (K) = room temperature (298.15 K).

4. Ferrioxalate actinometry

NOTE: All procedures for ferrioxalate actinometry must be performed in the dark or >600 nm light to prevent the influence of ambient light.

1. In a 20 mL glass vial containing 29.48 mg (0.06 mmol) of potassium ferrioxalate trihydrate, add 8 mL of deionized water. Add 1 mL of 0.5 M aqueous H₂SO₄ to the ferrioxalate solution and dilute to 10 mL with deionized water to prepare a 0.006 M ferrioxalate in 0.05 M aqueous H₂SO₄ solution.
2. In another 20 mL glass vial containing 10 mg of 1,10-phenanthroline and 1.356 g of anhydrous sodium acetate, add 10 mL of 0.5 M aqueous H₂SO₄ to make a buffered 0.1% (w/v) phenanthroline solution.
3. Transfer 2 mL of the 0.006 M ferrioxalate solution from step 4.1 to a quartz cuvette with 1.0 cm optical path length. Seal the cuvette with a PTFE stopper and keep the sample in the dark.
4. Prepare another quartz cuvette containing 2 mL of 0.05 M aqueous H₂SO₄ as a blank sample. Measure the UV-Vis absorbance of the blank sample for baseline correction.
5. Measure the UV-Vis absorbance of the 0.006 M ferrioxalate solution. Determine the fraction of light absorbed using the absorbances of the 0.006 M ferrioxalate solution at 340 and 436 nm and Eq (8) (Figure 8).
   (8)
   Where f = the fraction of light absorbed by 0.006 M ferrioxalate solution; A_λ = the absorbance of 0.006 M ferrioxalate solution at wavelength λ.
6. Prepare two quartz cuvettes with 1.0 cm optical path length and add 2 mL of the 0.006 M ferrioxalate solution.
7. Place one of the samples from step 4.6 1 cm in front of the Xenon arc lamp equipped with a 436 nm bandpass filter. Keep the other sample in the dark. Start irradiation to the sample for 90 s. After irradiation, add 0.35 mL of the buffered 0.1% phenanthroline solution and a magnetic bar to both cuvettes followed by stirring for 1 h in the dark to form a [Fe(phen)₃]²⁺ complex.
   NOTE: Ferrioxalate is photochemically reduced to Fe²⁺, followed by the nearly quantitative formation of tris-1,10-phenanthroline iron (II) complex.
8. Measure the UV-Vis absorption spectrum of the non-irradiated sample from step 4.6 for baseline correction.
9. Measure the UV-Vis absorption spectrum of the irradiated sample from step 4.7.
10. Repeat steps 4.6-4.9 with a 340 nm bandpass filter (Figure 9).
    NOTE: Once the ferrioxalate sample is exposed to light, the sample cannot be reused.
11. Calculate the molar photon flux arriving at the cuvette using Eq 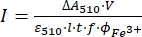(9).
    (9)
    Where I (mol·s^-1) = the molar photon flux arriving at the cuvette; ΔA₅₁₀ = the difference in absorbance at 510 nm between the non-irradiated and irradiated samples; V = the total volume of solution (2.35 mL); ε₅₁₀ = the molar attenuation coefficient of [Fe(phen)₃]²⁺ complex (11100 M^-1cm^-1)²⁴; I = the optical path length of quartz cuvette (1.0 cm); t = irradiation time (90 s); f = the absorbed fraction of light obtained from step 4.5; Φ_Fe³⁺ = the quantum yield of the photoreduction of Fe³⁺ to Fe²⁺ (1.22 for 340 nm, 1.11 for 436 nm)²⁵.

5. Determination of the photoisomerization quantum yield

1. Prepare a quartz cuvette with 1.0 cm optical path length containing 2 mL of DMSO as the blank sample. Measure the UV-Vis absorbance of the blank sample for baseline correction.
2. Prepare a quartz cuvette with 1.0 cm optical path length containing 2 mL of 10 µM solution of 1 in DMSO obtained from step 2.4 (Z-enriched). Seal the cuvettes with a PTFE stopper.
3. Place the sample from step 5.2 1 cm in front of the Xenon arc lamp equipped with a 436 nm bandpass filter. Start irradiation at 436 nm to the sample and measure UV-Vis absorption spectrum with different intervals until there is no change in the spectra as 1 reaches PSS (Figure 10).
   NOTE: The irradiation setup must be exactly the same as that used for the molar photon flux measurement. The irradiation interval should be adjusted based on the rate of photoisomerization. Generally, 15-20 data points before reaching PSS are suitable.
4. Prepare a quartz cuvette with 1.0 cm optical path length containing 2 mL of 10 µM solution of 1 in DMSO obtained from step 2.3 (E-enriched). Seal the cuvettes with a PTFE stopper.
5. Replace the 436 nm bandpass filter with the 340 nm bandpass filter and repeat step 5.3 for the sample obtained from step 5.4.
6. Calculate the photokinetic factor F(t) using the observed absorbances from step 5.3 and Eq (10)²⁶.
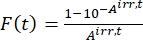   (10)
   Where A^irr,t = the absorbance at the irradiation wavelength at time t.
7. Calculate the pseudo quantum yield Q using the photokinetic factor values obtained from step 5.6 and Eq (11)²⁷.
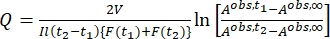   (11)
   Where Q (M^-1cm^-1) = the pseudo quantum yield defined as ;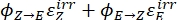 ; V(L) = the volume of sample; I (mol·s^-1) = the molar photon flux arriving at the cuvette; l (cm) = the optical path length; t₁, t₂ (s) = the two consecutive time points of irradiation; F(t₁), F(t₂) = the photokinetic factors at time t₁ and t₂, respectively; A^obs,t₁, A^obs,t₂, A^obs,∞ = the absorbances at specific wavelength at time , t₁, and t₂ at PSS, respectively.
   NOTE: Using absorbances at λ_max of 1-Z is recommended for accuracy.
8. Calculate the averaged value of the pseudo quantum yield using the first ten data points.
9. Calculate the unidirectional quantum yields for Z-to-E and E-to-Z photoisomerizations using Eq (12) and Eq (13).
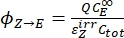   (12)
   (13)
   Where Φ_Z→E, Φ_E→Z = the unidirectional quantum yields for Z-to-E and E-to-Z photoisomerization processes, respectively; , 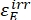(M^-1cm^-1) = the molar attenuation coefficients of 1-Z and 1-E at the irradiation wavelength; 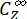, 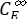(M) = the concentrations of 1-Z and 1-E at PSS, respectively; C_tot (M) = the total concentration of 1.
10. Repeat steps 5.6-5.9 using the data obtained from step 5.5 for calculation of the unidirectional photoisomerization quantum yields under irradiation at 340 nm.

Wyniki

Upon irradiation of 1 in an NMR tube with 436 nm light (Z:E = 54:46 in the initial state), the proportion of 1-E increases due to the dominant Z-to-E isomerization of the hydrazone C=N bond (Figure 1). The isomeric ratio can be readily obtained from the relative signal intensities of distinct isomers in the ¹H NMR spectrum (Figure 2). After 5 days of irradiation at 436 nm, the sampl...

Dyskusje

Various strategies to tune the spectral and switching properties of photoswitches have been developed, and the register of photoswitches is rapidly expanding²⁸. It is thus crucial to correctly determine their photophysical properties, and we anticipate the methods summarized in this article will be a helpful guide to experimenters. Provided that the thermal relaxation rate is very slow at room temperature, measurement of PSS compositions at different irradiation wavelengths, molar attenuation coef...

Materiały

Name	Company	Catalog Number	Comments
1,10-phenanthroline	Sigma-Aldrich	131377-2.5G
340 nm bandpass filter, 25 mm diameter, 10 nm FWHM	Edmund Optics	#65-129
436 nm bandpass filter, 25 mm diameter, 10 nm FWHM	Edmund Optics	#65-138
Anhydrous sodium acetate	Alfa aesar	A13184.30
Dimethyl sulfoxide	Samchun	D1138	HPLC grade
Dimethyl sulfoxide-d6	Sigma-Aldrich	151874-25g
Gemini 2000; 300 MHz NMR spectrometer	Varian
H2SO4	Duksan	235
Heating bath	JeioTech	CW-05G
MestReNova 14.1.1	Mestrelab Research S.L., https://mestrelab.com/
Natural quartz NMR tube	Norell	S-5-200-QTZ-7
Potassium ferrioxalate trihydrate	Alfa aesar	31124.06
Quartz absorption cell	Hellma	HE.110.QS10
UV-VIS spectrophotometer	Scinco	S-3100
Xenon arc lamp	Thorlabs	SLS205	Fiber adapter was removed