Bestimmung der Photoisomerisierungsquantenausbeute eines Hydrazon-Photoschalters

Zusammenfassung

Die Photoisomerisierungsquantenausbeute ist eine grundlegende photophysikalische Eigenschaft, die bei der Untersuchung neu entwickelter Photoschalter genau bestimmt werden sollte. Hier beschreiben wir eine Reihe von Verfahren zur Messung der Photoisomerisierungsquantenausbeute eines photochromen Hydrazons als bistabilen Modell-Photoschalter.

Zusammenfassung

Photoschaltende organische Moleküle, die lichtgetriebene Strukturtransformationen durchlaufen, sind Schlüsselkomponenten für die Konstruktion adaptiver molekularer Systeme und werden in einer Vielzahl von Anwendungen eingesetzt. In den meisten Studien mit Photoschaltern werden mehrere wichtige photophysikalische Eigenschaften wie maximale Wellenlängen der Absorption und Emission, molare Dämpfungskoeffizient, Fluoreszenzlebensdauer und Photoisomerisierungsquantenausbeute sorgfältig bestimmt, um ihre elektronischen Zustände und Übergangsprozesse zu untersuchen. Die Messung der Photoisomerisierungsquantenausbeute, der Effizienz der Photoisomerisierung in Bezug auf die absorbierten Photonen, in einer typischen Laborumgebung ist jedoch oft kompliziert und fehleranfällig, da sie die Durchführung strenger spektroskopischer Messungen und Berechnungen auf der Grundlage einer geeigneten Integrationsmethode erfordert. Dieser Artikel stellt eine Reihe von Verfahren zur Messung der Photoisomerisierungsquantenausbeute eines bistabilen Photoschalters mit einem photochromen Hydrazon vor. Wir gehen davon aus, dass dieser Artikel ein nützlicher Leitfaden für die Untersuchung von bistabilen Fotoschaltern sein wird, die zunehmend entwickelt werden.

Einleitung

Photochrome organische Moleküle haben in einer Vielzahl von wissenschaftlichen Disziplinen beträchtliche Aufmerksamkeit erregt, da Licht ein einzigartiger Reiz ist, der ein System nicht-invasiv aus seinem thermodynamischen Gleichgewicht treiben kann¹. Die Bestrahlung von Licht mit geeigneten Energien ermöglicht die strukturelle Modulation von Photoschaltern mit hoher raumzeitlicher Präzision ^2,3,4. Dank dieser Vorteile wurden verschiedene Arten von Photoschaltern, die auf der Konfigurationsisomerisierung der Doppelbindungen (z. B. Stilbene, Azobenzene, Imine, Fumaramide, Thioindigos) und Ringöffnung/-verschluss (z. B. Spiropyrane, Dithienylethene, Fulgide, Donor-Akzeptor-Stenhouse-Addukte) basieren und als Kernkomponenten adaptiver Materialien auf verschiedenen Längenskalen verwendet wurden. Repräsentative Anwendungen von Photoschaltern umfassen photochrome Materialien, Wirkstoffabgabe, schaltbare Rezeptoren und Kanäle, Informations- oder Energiespeicher und molekulare Maschinen 5,6,7,8,9,10,11,12. In den meisten Studien, die neu entwickelte Photoschalter präsentieren, werden ihre photophysikalischen Eigenschaften wie λ_max der Absorption und Emission, molarer Dämpfungskoeffizient (ε), Fluoreszenzlebensdauer und Photoisomerisierungsquantenausbeute gründlich charakterisiert. Die Untersuchung solcher Eigenschaften liefert Schlüsselinformationen über die elektronischen Zustände und Übergänge, die für das Verständnis der optischen Eigenschaften und des Isomerisierungsmechanismus entscheidend sind.

Die genaue Messung der Photoisomerisierungsquantenausbeute - die Anzahl der Photoisomerisierungsereignisse, die durch die Anzahl der Photonen bei der vom Reaktanten absorbierten Bestrahlungswellenlänge dividiert wurden - ist jedoch in einer typischen Laborumgebung aus mehreren Gründen oft kompliziert. Die Bestimmung der Photoisomerisierungsquantenausbeute wird im Allgemeinen durch die Überwachung des Fortschreitens der Reaktion und die Messung der Anzahl der absorbierten Photonen während der Bestrahlung erreicht. Die Hauptsorge ist, dass sich die Menge der Photonenabsorption pro Zeiteinheit progressiv ändert, da sich die Gesamtabsorption durch die Lösung im Laufe der Zeit ändert, während die photochemische Reaktion fortschreitet. Daher hängt die Anzahl der verbrauchten Reaktanden pro Zeiteinheit von dem Zeitabschnitt ab, in dem sie während der Bestrahlung gemessen wird. Somit ist man verpflichtet, die unterschiedlich definierte Photoisomerisierungsquantenausbeute abzuschätzen.

Ein problematischeres Problem entsteht, wenn sowohl der Reaktant als auch das Photoprodukt Licht bei der Bestrahlungswellenlänge absorbieren. In diesem Fall erfolgt die photochemische Isomerisierung in beide Richtungen (d.h. eine photoreversible Reaktion). Die beiden unabhängigen Quantenausbeuten für die Vorwärts- und Rückwärtsreaktion können nicht direkt aus der beobachteten Reaktionsgeschwindigkeit gewonnen werden. Ungenaue Lichtintensität ist auch eine häufige Fehlerursache. Zum Beispiel ändert die Alterung der Glühbirne allmählich ihre Intensität; Die Bestrahlungsstärke der Xenon-Bogenlampe bei 400 nm nimmt nach 1000 h Betrieb¹⁴ um 30% ab. Die Streuung von nicht kollimiertem Licht macht die tatsächlich einfallende Bestrahlungsstärke deutlich kleiner als die Nennleistung der Quelle. Daher ist es entscheidend, den effektiven Photonenfluss genau zu quantifizieren. Bemerkenswert ist, dass die thermische Relaxation der metastabilen Form bei Raumtemperatur so gering sein sollte, dass sie ignoriert werden kann.

Dieses Papier stellt eine Reihe von Verfahren zur Bestimmung der Photoisomerisierungsquantenausbeute eines bistabilen Photoschalters vor. Eine Reihe von Hydrazon-Photoschaltern, die von der Gruppe von Aprahamian, dem bahnbrechenden Forschungsteam auf diesem Gebiet, entwickelt wurden, standen dank ihrer selektiven Photoisomerisierung und bemerkenswerten Stabilität ihrer metastabilen Isomere^15,16,17 im Rampenlicht. Ihre Hydrazon-Photoschalter bestehen aus zwei aromatischen Ringen, die durch eine Hydrazongruppe verbunden sind, und die C=N-Bindung durchläuft bei Bestrahlung bei geeigneten Wellenlängen eine selektive E/Z-Isomerisierung (Abbildung 1). Sie wurden erfolgreich als bewegliche Komponenten dynamischer molekularer Systeme 18,19,20,21 integriert. In dieser Arbeit haben wir ein neues Hydrazonderivat mit Amidgruppen vorbereitet und seine photoschaltenden Eigenschaften für die Bestimmung der Photoisomerisierungsquantenausbeute untersucht.

Protokoll

1. ¹H NMR-Spektrumerfassung im photostationären Zustand (PSS)

1. In einem natürlichen Quarz-NMR-Röhrchen, das 4,2 mg (0,01 mmol) Hydrazonschalter 1 enthält, fügen Sie 1,0 ml deuteriertes Dimethylsulfoxid (DMSO-d ₆₎ hinzu. Übertragen Sie die Hälfte der Lösung in eine andere NMR-Röhre.
2. Platzieren Sie eine der NMR-Röhren 1 cm vor einer Xenon-Bogenlampe, die mit einem 436-nm-Bandpassfilter ausgestattet ist. Beginnen Sie mit der Bestrahlung der NMR-Probe und zeichnen Sie jeden Tag ein 1-H-NMR-Spektrum auf, bis sich die Spektren nicht ändern, wenn Schalter ¹PSS erreicht. Nachdem Sie PSS erreicht haben, halten Sie die NMR-Röhre bei Raumtemperatur im Dunkeln und zeichnen Sie das 1 H NMR-Spektrum nach ¹²h auf, um den Fortschritt der thermischen Entspannung zu überwachen.
   HINWEIS: Schalter 1 zeigt aufgrund seiner bistabilen Natur keine nennenswerte Veränderung des 1 H NMR-Spektrums bei Raumtemperatur.
3. Für die andere NMR-Röhre wiederholen Sie Schritt 1.2 mit einem 340-nm-Bandpassfilter, um ein 1-H-NMR-Spektrum am PSS unter 340-nm-Bestrahlung zu erhalten.
4. Öffnen Sie fid-Dateien der NMR-Spektren an den PSS mit NMR-Verarbeitungssoftware. Integrieren Sie einen unverwechselbaren Satz von Peaks (H1: C2-Proton von Chinolin, H2: Proton in Para-Position zur Hydrazongruppe, H3: CH₃ von Ethylester) der verschiedenen Isomere und berechnen Sie das isomere Verhältnis (Abbildung 2).
   HINWEIS: Zusammensetzungen ([1-Z]:[1-E] Verhältnis) unter 436 nm und 340 nm Bestrahlung sind 8:92 bzw. 82:18.

2. UV-Vis-Absorptionsspektroskopie am PSS

1. In einer Durchstechflasche aus Glas mit 12,6 mg (0,03 mmol) 1 werden 2 ml DMSO in Spektroskopiequalität zugegeben. Nehmen Sie 100 μL der Lösung und verdünnen Sie sie mit 1400 μL DMSO, um 1 mM Lösung von 1 zu erhalten. 20 μL 1 mM Lösung von 1 auf eine Quarzküvette mit 1,0 cm optischer Weglänge übertragen und mit 1980 μL DMSO verdünnen, um eine 10 μM-Lösung von 1 zu erhalten. Verschließen Sie die Küvette mit einem PTFE-Stopper und bewahren Sie die Probe im Dunkeln auf.
2. Bereiten Sie eine weitere Quarzküvette mit 2 ml DMSO als leere Probe vor. Messen Sie das UV-Vis-Spektrum der leeren Probe für die Baseline-Korrektur.
3. Legen Sie die Probe aus Schritt 2.1 1 cm vor eine Xenon-Bogenlampe, die mit einem 436-nm-Bandpassfilter ausgestattet ist. Beginnen Sie mit der Bestrahlung der Probe und messen Sie das UV-Vis-Spektrum alle 2 Stunden, bis sich die Spektren nicht ändern, wenn 1 PSS erreicht (Abbildung 3).
   HINWEIS: Die Zeit, die benötigt wird, um PSS für die UV-Vis-Spektroskopie-Probe zu erreichen, ist viel kürzer als für die NMR-Probe mit einer höheren Konzentration.
4. Wiederholen Sie Schritt 2.3 mit einem 340 nm Bandpassfilter, um das UV-Vis-Spektrum am PSS unter 340 nm Bestrahlung zu erhalten.
5. Ableiten von Absorptionsspektren der reinen 1-Z und 1-E unter Verwendung von Eq (1) und Eq (2) (Abbildung 4).
   (1)
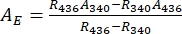   (2)
   wobei R 436 = das Verhältnis von 1-Z am PSS unter ₄₃₆ nm Bestrahlung; R₃₄₀ = das Verhältnis von 1-Z am PSS unter 340 nm Bestrahlung; A 436 = die Absorption von 1 in DMSO am PSS unter ₄₃₆ nm Bestrahlung; A₃₄₀ = die Absorption von 1 in DMSO am PSS unter 340 nm Bestrahlung.
6. Berechnen Sie die molaren Dämpfungskoeffizienten von reinem 1-Z und 1-E bei allen Wellenlängen, indem Sie die beobachtete Absorption durch die Probenkonzentration (10 μM) und die optische Weglänge (1 cm) dividieren.

3. Kinetische Untersuchungen zur thermischen Relaxation

1. Erhitzen Sie das in einem Heizbadthermostat gefüllte Silikonöl auf die gewünschte Temperatur (131 °C) und prüfen Sie, ob die Temperatur des Bades stabilisiert ist. Tauchen Sie zwei NMR-Proben aus Schritt 1.2 in das Heizbad.
   HINWEIS: Die Temperatur und die Dauer der Erwärmung werden in Abhängigkeit von der Entspannungsrate angepasst.
2. Nach 1 Stunde Erwärmung die NMR-Röhrchen schnell in ein Trockeneisbad geben, um die durch latente Wärme verursachte thermische Entspannung anzuhalten (Abbildung 5).
   HINWEIS: Eine ungenaue Heiztemperatur oder -zeit kann zu schwerwiegenden Fehlern bei der Schätzung der Ratenkonstante führen.
3. Tauen Sie die aus Schritt 3.2 gewonnenen NMR-Proben bei Raumtemperatur auf und stellen Sie sicher, dass DMSO aufgetaut ist. Zeichnen Sie die ¹H NMR-Spektren der Proben auf.
4. Wiederholen Sie die Schritte 3.1-3.3, bis sich die 1-H-NMR-Spektren nicht mehr ändern, da ¹das thermodynamische Gleichgewicht erreicht.
5. Wiederholen Sie die Schritte 3.1-3.4 bei unterschiedlichen Temperaturen (134, 137, 140 und 143 °C).
6. Öffnen Sie fid-Dateien der NMR-Spektren, die beim Erhitzen bei 131 °C erhalten wurden. Berechnen Sie die gemittelten isomeren Verhältnisse wie in Schritt 1.4 beschrieben. Berechnen Sie die Konzentration von 1-E (metastabiles Isomer) basierend auf der Gesamtprobenkonzentration (10 mM) und dem isomeren Verhältnis.
7. Zeichnen Sie die gemittelte Konzentration von 1-E (C_E) als Funktion der Heizzeit auf. Führen Sie eine exponentielle Anpassung an die Daten durch, um die Ratenkonstante der thermischen Relaxation mit Eq (3)^15,22 zu erhalten (Abbildung 6^).
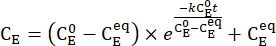   (3)
   wobei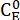 (M) = die Konzentration von 1-E im Ausgangszustand; (M) = die Konzentration von 1-E im thermodynamischen Gleichgewicht bei einer bestimmten Temperatur; 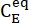k (^s-1) = die Geschwindigkeitskonstante der thermischen Relaxation bei einer bestimmten Temperatur; t (s) = die Aufheizzeit.
8. Wiederholen Sie die Schritte 3.6 bis 3.7 unter Verwendung der Daten, die bei unterschiedlichen Temperaturen erhalten wurden.
9. Zeichnen Sie ln(k) versus und führen Sie eine lineare Anpassung gemäß der Arrhenius-Gleichung (Eq (4)) durch, um die Ratenkonstante bei Raumtemperatur zu extrapolieren (Abbildung 7).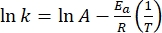
   (4)
   wobei A = der präexponentielle Faktor ist; E_a (J·^mol-1) = die Aktivierungsenergie für thermische Relaxation; R = die ideale Gaskonstante (8,3145 J·mol-1 ^K-1); T (K) = die absolute Temperatur.
10. Berechnen Sie die thermische Halbwertszeit von 1-E bei Raumtemperatur mit Eq 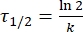(5).
    (5)
    wobei τ 1_/2 (s) = die thermische Halbwertszeit von 1-E bei Raumtemperatur; K (^S-1) = die aus Schritt 3.9 erhaltene Geschwindigkeitskonstante der thermischen Entspannung bei Raumtemperatur.
11. Wenn die Geschwindigkeitskonstante der thermischen Relaxation nur bei einer einzigen Temperatur geschätzt wird, berechnen Sie die Geschwindigkeitskonstante bei Raumtemperatur unter Verwendung der folgenden neu angeordneten Eyring-Gleichung (Eq (6))^18,23.
    (6)
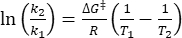    (7)
    wobei (J·mol-1) = die ^{Gibbs-Aktivierungsenergie} zur thermischen Relaxation; K 1 (^S-1) = die Geschwindigkeitskonstante der thermischen Relaxation, die bei der erhöhten Temperatur geschätzt wird; K ₂ (^s-1) = die Geschwindigkeitskonstante der thermischen Entspannung bei Raumtemperatur (298,15 K); T1 (K) = die absolute Temperatur, bei der k₁ erhalten wird; (K) = Raumtemperatur (298,15 K).

4. Ferrioxalat-Aktinometrie

HINWEIS: Alle Verfahren zur Ferrioxalat-Actinometrie müssen bei Dunkelheit oder >600 nm Licht durchgeführt werden, um den Einfluss von Umgebungslicht zu verhindern.

1. In einer Durchstechflasche aus 20 ml Glas, die 29,48 mg (0,06 mmol) Kaliumferrioxalattrihydrat enthält, werden 8 ml entionisiertes Wasser zugegeben. 1 ml 0,5 M wässriges_H2SO4 in die Ferrioxalatlösung geben und mit entionisiertem Wasser auf 10 ml verdünnen, um ein 0,006 M Ferrioxalat in 0,05 m wässriger_{H2SO4-Lösung herzustellen.}
2. In einer weiteren Durchstechflasche mit 20 ml Glas mit 10 mg 1,10-Phenanthrolin und 1,356 g wasserfreiem Natriumacetat 10 ml wässriges_{H2SO4 hinzufügen zu einer} gepufferten 0,1%igen(w/v) Phenanthrollösung.
3. 2 ml der 0,006 M Ferrioxalatlösung aus Schritt 4.1 in eine Quarzküvette mit 1,0 cm optischer Weglänge überführen. Verschließen Sie die Küvette mit einem PTFE-Stopper und bewahren Sie die Probe im Dunkeln auf.
4. Eine weitere Quarzküvette mit 2 ml 0,05 m wässrigem_H2SO4 alsBlindprobe wird hergestellt. Messen Sie die UV-Vis-Absorption der leeren Probe für die Baseline-Korrektur.
5. Messen Sie die UV-Vis-Absorption der 0,006 M Ferrioxalatlösung. Bestimmen Sie den Anteil des absorbierten Lichts unter Verwendung der Absorptionen der 0,006 M Ferrioxalatlösung bei 340 und 436 nm und Eq (8) (Abbildung 8).
   (8)
   wobei f = der Anteil des Lichts, der von 0,006 M Ferrioxalatlösung absorbiert wird; A λ = die Absorption von 0,006 M Ferrioxalatlösung bei Wellenlänge _λ.
6. Bereiten Sie zwei Quarzküvetten mit 1,0 cm optischer Weglänge vor und fügen Sie 2 ml der 0,006 M Ferrioxalatlösung hinzu.
7. Legen Sie eine der Proben aus Schritt 4.6 1 cm vor die Xenon-Bogenlampe, die mit einem 436-nm-Bandpassfilter ausgestattet ist. Halten Sie die andere Probe im Dunkeln. Beginnen Sie die Bestrahlung der Probe für 90 s. Nach der Bestrahlung 0,35 ml der gepufferten 0,1%igen Phenanthrollösung und einen Magnetstab in beide Küvetten geben, gefolgt von 1 h Rühren im Dunkeln, um einen [Fe(phen)₃^]2+-Komplex zu bilden.
   HINWEIS: Ferrioxalat ist photochemisch auf Fe²⁺ reduziert, gefolgt von der fast quantitativen Bildung von Tris-1,10-phenanthrolinem Eisen (II) -Komplex.
8. Messen Sie das UV-Vis-Absorptionsspektrum der nicht bestrahlten Probe aus Schritt 4.6 zur Baseline-Korrektur.
9. Messen Sie das UV-Vis-Absorptionsspektrum der bestrahlten Probe aus Schritt 4.7.
10. Wiederholen Sie die Schritte 4.6-4.9 mit einem 340-nm-Bandpassfilter (Abbildung 9).
    HINWEIS: Sobald die Ferrioxalatprobe Licht ausgesetzt ist, kann die Probe nicht wiederverwendet werden.
11. Berechnen Sie den molaren Photonenfluss, der an der Küvette ankommt, mit Eq 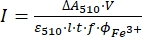(9).
    (9)
    wobei I (mol·^s-1) = der molare Photonenfluss, der an der Küvette ankommt; ΔA 510 = die Absorptionsdifferenz bei ₅₁₀ nm zwischen den nicht bestrahlten und den bestrahlten Proben; V = das Gesamtvolumen der Lösung (2,35 ml); ε₅₁₀ = der molare Dämpfungskoeffizient von [Fe(phen)3]2+ Komplex (11100 M-1 ^cm-1)₂₄; I = die optische Weglänge der Quarzküvette (1,0 cm); t = Bestrahlungszeit (90 s); f = der absorbierte Lichtanteil aus Schritt 4.5; Φ Fe3+ = die Quantenausbeute der Photoreduktion von^Fe3+ auf _Fe2⁺ (1,22 für 340 nm, 1,11 für 436 nm)²⁵.

5. Bestimmung der Photoisomerisierungsquantenausbeute

1. Bereiten Sie eine Quarzküvette mit 1,0 cm optischer Weglänge vor, die 2 ml DMSO als leere Probe enthält. Messen Sie die UV-Vis-Absorption der leeren Probe für die Baseline-Korrektur.
2. Es wird eine Quarzküvette mit einer optischen Weglänge von 1,0 cm hergestellt, die 2 ml 10 μM-Lösung von 1 in DMSO enthält, die aus Schritt 2.4 (Z-angereichert) erhalten wurde. Verschließen Sie die Küvetten mit einem PTFE-Stopper.
3. Legen Sie die Probe aus Schritt 5.2 1 cm vor die Xenon-Bogenlampe, die mit einem 436-nm-Bandpassfilter ausgestattet ist. Beginnen Sie mit der Bestrahlung bei 436 nm zur Probe und messen Sie das UV-Vis-Absorptionsspektrum mit unterschiedlichen Intervallen, bis sich die Spektren nicht ändern , wenn 1 PSS erreicht (Abbildung 10).
   HINWEIS: Der Bestrahlungsaufbau muss genau der gleiche sein, der für die Messung des molaren Photonenflusses verwendet wird. Das Bestrahlungsintervall sollte basierend auf der Photoisomerisierungsrate angepasst werden. Im Allgemeinen sind 15-20 Datenpunkte vor dem Erreichen von PSS geeignet.
4. Es wird eine Quarzküvette mit einer optischen Weglänge von 1,0 cm hergestellt, die 2 ml 10 μM Lösung von 1 in DMSO enthält, die aus Schritt 2.3 (E-angereichert) erhalten wurde. Verschließen Sie die Küvetten mit einem PTFE-Stopper.
5. Ersetzen Sie den 436-nm-Bandpassfilter durch den 340-nm-Bandpassfilter, und wiederholen Sie Schritt 5.3 für die aus Schritt 5.4 erhaltene Probe.
6. Berechnen Sie den photokinetischen Faktor F(t) unter Verwendung der beobachteten Absorptionen aus Schritt 5.3 und Eq (10)²⁶.
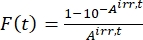   (10)
   Dabei ist ^{A irr,t} = die Absorption bei der Bestrahlungswellenlänge zum Zeitpunkt t.
7. Berechnen Sie die Pseudoquantenausbeute Q unter Verwendung der photokinetischen Faktorwerte, die aus Schritt 5.6 und Eq (11) ²⁷ erhalten wurden.
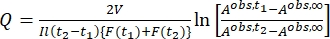   (11)
   Dabei ist Q (M-1 ^cm-1) = die Pseudoquantenausbeute, definiert als ;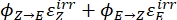 ; V(L) = das Volumen der Probe; I (mol·^s-1) = der molare Photonenfluss, der an der Küvette ankommt; l (cm) = die optische Weglänge; t ₁, t₂₍s) = die beiden aufeinanderfolgenden Zeitpunkte der Bestrahlung; F(t 1), F(t 2) = die photokinetischen Faktoren zum Zeitpunkt t ₁ bzw. t_2; A obs,t 1, A obs,t 2, A ^obs,∞ = die Absorptionen bei einer bestimmten Wellenlänge zum Zeitpunkt , t ₁ bzw. t₂ bei PSS.
   HINWEIS: Die Verwendung von Absorptionsraten bei λ_max von 1-Z wird aus Gründen der Genauigkeit empfohlen.
8. Berechnen Sie den gemittelten Wert der Pseudoquantenausbeute anhand der ersten zehn Datenpunkte.
9. Berechnen Sie die unidirektionalen Quantenausbeuten für Z-zu-E- und E-zu-Z-Photoisomerisierungen unter Verwendung von Eq (12) und Eq (13).
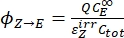   (12)
   (13)
   wobei Φ Z→E, Φ E→Z = die unidirektionalen Quantenausbeuten für Z-zu-E- bzw. _{E-zu-Z-Photoisomerisierungsprozesse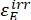}; , (M-1 cm-1) = die molaren Dämpfungskoeffizienten von 1-Z und 1-E bei der Bestrahlungswellenlänge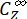; , 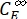(M) = die Konzentrationen von 1-Z bzw. ^1-Ebei PSS; C_tot (M) = die Gesamtkonzentration von 1.
10. Wiederholen Sie die Schritte 5.6-5.9 unter Verwendung der aus Schritt 5.5 erhaltenen Daten zur Berechnung der unidirektionalen Photoisomerisierungsquantenausbeuten unter Bestrahlung bei 340 nm.

Ergebnisse

Bei Bestrahlung von 1 in einer NMR-Röhre mit 436 nm Licht (Z:E = 54:46 im Ausgangszustand) steigt der Anteil von 1-E aufgrund der dominanten Z-zu-E-Isomerisierung der Hydrazon-C=N-Bindung an (Abbildung 1). Das isomere Verhältnis kann leicht aus den relativen Signalintensitäten verschiedener Isomere im ^{1-H-NMR-Spektrum}erhalten werden (Abbildung 2). Nach 5 Tagen Bestrahlung bei 436...

Diskussion

Verschiedene Strategien zur Abstimmung der Spektral- und Schalteigenschaften von Photoschaltern wurden entwickelt, und das Register der Photoschalter erweitert sich schnell²⁸. Es ist daher entscheidend, ihre photophysikalischen Eigenschaften korrekt zu bestimmen, und wir gehen davon aus, dass die in diesem Artikel zusammengefassten Methoden ein hilfreicher Leitfaden für Experimentatoren sein werden. Unter der Voraussetzung, dass die thermische Relaxationsrate bei Raumtemperatur sehr langsam ist, ...

Materialien

Name	Company	Catalog Number	Comments
1,10-phenanthroline	Sigma-Aldrich	131377-2.5G
340 nm bandpass filter, 25 mm diameter, 10 nm FWHM	Edmund Optics	#65-129
436 nm bandpass filter, 25 mm diameter, 10 nm FWHM	Edmund Optics	#65-138
Anhydrous sodium acetate	Alfa aesar	A13184.30
Dimethyl sulfoxide	Samchun	D1138	HPLC grade
Dimethyl sulfoxide-d6	Sigma-Aldrich	151874-25g
Gemini 2000; 300 MHz NMR spectrometer	Varian
H2SO4	Duksan	235
Heating bath	JeioTech	CW-05G
MestReNova 14.1.1	Mestrelab Research S.L., https://mestrelab.com/
Natural quartz NMR tube	Norell	S-5-200-QTZ-7
Potassium ferrioxalate trihydrate	Alfa aesar	31124.06
Quartz absorption cell	Hellma	HE.110.QS10
UV-VIS spectrophotometer	Scinco	S-3100
Xenon arc lamp	Thorlabs	SLS205	Fiber adapter was removed