Détermination du rendement quantique de photoisomérisation d’un photocommutateur Hydrazone

Résumé

Le rendement quantique de photoisomérisation est une propriété photophysique fondamentale qui doit être déterminée avec précision dans l’étude des photocommutateurs nouvellement développés. Ici, nous décrivons un ensemble de procédures pour mesurer le rendement quantique de photoisomérisation d’une hydrazone photochromique en tant que modèle de photocommutateur bistable.

Résumé

Les molécules organiques photocommutantes qui subissent des transformations structurelles entraînées par la lumière sont des composants clés pour construire des systèmes moléculaires adaptatifs, et elles sont utilisées dans une grande variété d’applications. Dans la plupart des études utilisant des photocommutateurs, plusieurs propriétés photophysiques importantes telles que les longueurs d’onde maximales d’absorption et d’émission, le coefficient d’atténuation molaire, la durée de vie de la fluorescence et le rendement quantique de la photoisomérisation sont soigneusement déterminées pour étudier leurs états électroniques et leurs processus de transition. Cependant, la mesure du rendement quantique de la photoisomérisation, l’efficacité de la photoisomérisation par rapport aux photons absorbés, dans un environnement de laboratoire typique est souvent compliquée et sujette à l’erreur car elle nécessite la mise en œuvre de mesures spectroscopiques rigoureuses et de calculs basés sur une méthode d’intégration appropriée. Cet article présente un ensemble de procédures pour mesurer le rendement quantique de photoisomérisation d’un photocommutateur bistable à l’aide d’une hydrazone photochromique. Nous prévoyons que cet article sera un guide utile pour l’étude des photocommutateurs bistables qui sont de plus en plus développés.

Introduction

Les molécules organiques photochromiques ont attiré une attention considérable dans un large éventail de disciplines scientifiques, car la lumière est un stimulus unique qui peut éloigner un système de son équilibre thermodynamique de manière non invasive¹. L’irradiation de la lumière avec des énergies appropriées permet une modulation structurelle des photocommutateurs avec une précision spatio-temporelle élevée ^2,3,4. Grâce à ces avantages, divers types de photocommutateurs basés sur l’isomérisation configurationnelle des doubles liaisons (par exemple, stilbènes, azobenzènes, imines, fumaramides, thioindigos) et l’ouverture/fermeture de l’anneau (par exemple, spiropyranes, dithienylethenes, fulgides, adduits Stenhouse donneur-accepteur) ont été développés et utilisés comme composants de base de matériaux adaptatifs à différentes échelles de longueur. Les applications représentatives des photocommutateurs impliquent les matériaux photochromiques, l’administration de médicaments, les récepteurs et canaux commutables, le stockage d’informations ou d’énergie et les machines moléculaires ^{5,6,7,8,9,10,11,12}. Dans la plupart des études présentant des photocommutateurs nouvellement conçus, leurs propriétés photophysiques telles que λ_max d’absorption et d’émission, le coefficient d’atténuation molaire (ε), la durée de vie de la fluorescence et le rendement quantique de photoisomérisation sont caractérisées de manière approfondie. L’étude de ces propriétés fournit des informations clés sur les états et les transitions électroniques qui sont cruciales pour comprendre les propriétés optiques et le mécanisme d’isomérisation.

Cependant, la mesure précise du rendement quantique de photoisomérisation - le nombre d’événements de photoisomérisation qui se sont produits divisé par le nombre de photons à la longueur d’onde d’irradiation absorbée par le réactif - est souvent compliquée dans un environnement de laboratoire typique pour plusieurs raisons. La détermination du rendement quantique de photoisomérisation est généralement obtenue en surveillant l’avancement de la réaction et en mesurant le nombre de photons absorbés pendant l’irradiation. La principale préoccupation est que la quantité d’absorption de photons par unité de temps change progressivement parce que l’absorption totale par la solution change au fil du temps au fur et à mesure que la réaction photochimique se poursuit. Par conséquent, le nombre de réactifs consommés par unité de temps dépend de la section de temps dans laquelle il est mesuré pendant l’irradiation. Ainsi, on est obligé d’estimer le rendement quantique de photoisomérisation qui est défini différentiellement.

Un problème plus gênant survient lorsque le réactif et le photoproduit absorbent la lumière à la longueur d’onde d’irradiation. Dans ce cas, l’isomérisation photochimique se produit dans les deux sens (c.-à-d. une réaction photoréversible). Les deux rendements quantiques indépendants pour les réactions avant et arrière ne peuvent pas être obtenus directement à partir de la vitesse de réaction observée. Une intensité lumineuse inexacte est également une cause fréquente d’erreur. Par exemple, le vieillissement de l’ampoule change progressivement d’intensité; l’irradiance de la lampe à arc au xénon à 400 nm diminue de 30% après 1000 h de fonctionnement¹⁴. La propagation de la lumière non collimée rend l’irradiance incidente réelle nettement inférieure à la puissance nominale de la source. Ainsi, il est crucial de quantifier avec précision le flux de photons effectif. Il convient de noter que la relaxation thermique de la forme métastable à température ambiante doit être suffisamment faible pour être ignorée.

Cet article présente un ensemble de procédures pour déterminer le rendement quantique de photoisomérisation d’un photocommutateur bistable. Un certain nombre de photocommutateurs d’hydrazone développés par le groupe d’Aprahamian, l’équipe de recherche pionnière dans le domaine, ont été à l’honneur grâce à leur photoisomérisation sélective et à la stabilité remarquable de leurs isomères métastables 15,16,17. Leurs photocommutateurs d’hydrazone comprennent deux cycles aromatiques reliés par un groupe d’hydrazone, et la liaison C = N subit une isomérisation sélective E / Z lors de l’irradiation à des longueurs d’onde appropriées (Figure 1). Ils ont été incorporés avec succès en tant que composants mobiles de systèmes moléculaires dynamiques 18,19,20,21. Dans ce travail, nous avons préparé un nouveau dérivé d’hydrazone portant des groupes amides et étudié ses propriétés de photocommutation pour la détermination du rendement quantique de photoisomérisation.

Protocole

1. ^{Acquisition du}spectre RMN 1 H à l’état photostationnaire (PSS)

1. Dans un tube RMN à quartz naturel contenant 4,2 mg (0,01 mmol) d’hydrazone switch 1, ajouter 1,0 mL de diméthylsulfoxyde deutéré (DMSO-d ₆). Transférer la moitié de la solution dans un autre tube RMN.
2. Placez l’un des tubes RMN de 1 cm devant une lampe à arc au xénon équipée d’un filtre passe-bande de 436 nm. Commencez l’irradiation sur l’échantillon RMN et enregistrez un spectre RMN ^{de 1}H chaque jour jusqu’à ce qu’il n’y ait pas de changement dans les spectres lorsque le commutateur 1 atteint le PSS. Après avoir atteint le PSS, maintenez le tube RMN dans l’obscurité à température ambiante et enregistrez le spectre RMN ¹H après 12 h pour surveiller la progression de la relaxation thermique.
   REMARQUE: Le commutateur 1 ne montre aucun changement appréciable dans le spectre RMN ¹H à température ambiante en raison de sa nature bistable.
3. Pour l’autre tube RMN, répétez l’étape 1.2 avec un filtre passe-bande de 340 nm pour obtenir un spectre RMN ^{de 1}H au PSS sous irradiation de 340 nm.
4. Ouvrez les fichiers fid des spectres RMN sur les PSS avec le logiciel de traitement RMN. Intégrer un ensemble distinctif de pics (H1: proton C2 de quinoléine, H2: proton en para-position au groupe hydrazone, H3:_CH3 de l’ester éthylique) des isomères distincts et calculer le rapport isomérique (Figure 2).
   REMARQUE: Les compositions (rapport [1-Z]:[1-E]) sous irradiation de 436 nm et 340 nm sont respectivement de 8:92 et 82:18.

2. Spectroscopie d’absorption UV-Vis au PSS

1. Dans un flacon en verre contenant 12,6 mg (0,03 mmol) de 1, ajouter 2 mL de DMSO de qualité spectroscopique. Prendre 100 μL de la solution et diluer avec 1400 μL de DMSO pour obtenir 1 mM de solution de 1. Transférer 20 μL de solution de 1 mM de 1 dans une cuvette de quartz d’une longueur de chemin optique de 1,0 cm et diluer avec 1980 μL de DMSO pour obtenir une solution de 10 μM de 1. Scellez la cuvette avec un bouchon en PTFE et gardez l’échantillon dans l’obscurité.
2. Préparer une autre cuvette de quartz contenant 2 mL de DMSO sous forme d’échantillon vierge. Mesurez le spectre UV-Vis de l’échantillon vierge pour la correction de base.
3. Placez l’échantillon de l’étape 2,1 à 1 cm devant une lampe à arc au xénon équipée d’un filtre passe-bande de 436 nm. Commencez l’irradiation de l’échantillon et mesurez le spectre UV-Vis toutes les 2 h jusqu’à ce qu’il n’y ait pas de changement dans les spectres lorsque 1 atteint le PSS (Figure 3).
   REMARQUE: Le temps nécessaire pour atteindre le PSS pour l’échantillon de spectroscopie UV-Vis est beaucoup plus court que pour l’échantillon RMN avec une concentration plus élevée.
4. Répétez l’étape 2.3 avec un filtre passe-bande de 340 nm pour obtenir le spectre UV-Vis au PSS sous irradiation de 340 nm.
5. Déduire les spectres d’absorbance des 1-Z et 1-E purs en utilisant Eq (1) et Eq (2) (Figure 4).
   (1)
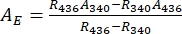   (2)
   Où R₄₃₆ = le rapport de 1-Z au PSS sous irradiation de 436 nm; R₃₄₀ = rapport de 1-Z au PSS sous irradiation de 340 nm; A₄₃₆ = l’absorbance de 1 dans le DMSO au PSS sous irradiation de 436 nm; A₃₄₀ = l’absorbance de 1 dans le DMSO au PSS sous irradiation de 340 nm.
6. Calculer les coefficients d’atténuation molaire de 1-Z et 1-E purs à toutes les longueurs d’onde en divisant l’absorbance observée par la concentration de l’échantillon (10 μM) et la longueur du chemin optique (1 cm).

3. Études cinétiques sur la relaxation thermique

1. Chauffer l’huile de silicium remplie dans un circulateur de bain chauffant à la température souhaitée (131 °C) et vérifier si la température du bain est stabilisée. Immergez deux échantillons RMN de l’étape 1.2 dans le bain chauffant.
   REMARQUE: La température et la durée du chauffage sont ajustées en fonction du taux de relaxation.
2. Après 1 h de chauffage, transférer rapidement les tubes RMN dans un bain de glace carbonique pour mettre en pause la relaxation thermique causée par la chaleur latente (Figure 5).
   REMARQUE: Une température ou un temps de chauffage inexact peut entraîner une erreur grave dans l’estimation de la constante de vitesse.
3. Décongeler les échantillons RMN obtenus à partir de l’étape 3.2 à température ambiante et s’assurer que le DMSO est décongelé. Enregistrez les spectres RMN ¹H des échantillons.
4. Répétez les étapes 3.1 à 3.3 jusqu’à ce qu’il n’y ait pas de changement dans les spectres RMN ¹H lorsque 1 atteint l’équilibre thermodynamique.
5. Répétez les étapes 3.1 à 3.4 à différentes températures (134, 137, 140 et 143 °C).
6. Ouvrir des fichiers fid des spectres RMN obtenus au cours du chauffage à 131 °C. Calculer les rapports isomériques moyens comme décrit à l’étape 1.4. Calculer la concentration de 1-E (isomère métastable) en fonction de la concentration totale de l’échantillon (10 mM) et du rapport isomérique.
7. Tracer la concentration moyenne de 1-E (C_E) en fonction du temps de chauffage. Effectuez un ajustement exponentiel aux données pour obtenir la constante de vitesse de relaxation thermique à l’aide de Eq (3)^15,22 (Figure 6).
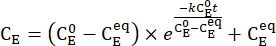   (3)
   Où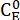 (M) = la concentration de 1-E à l’état initial; 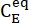(M) = la concentration de 1-E à l’équilibre thermodynamique à une température spécifique; k (^s-1) = la constante de vitesse de relaxation thermique à une température spécifique; t(s) = le temps de chauffage.
8. Répétez les étapes 3.6 à 3.7 en utilisant les données obtenues à différentes températures.
9. Tracer ln(k) versus et effectuer un ajustement linéaire selon l’équation d’Arrhenius (Eq (4)) pour extrapoler la constante de vitesse à température ambiante (Figure 7).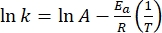
   (4)
   Où A = le facteur pré-exponentiel; E_a (J·^mol-1) = l’énergie d’activation pour la relaxation thermique; R = la constante de gaz idéale (8,3145 J·^{mol-1 K-1}); T (K) = la température absolue.
10. Calculer la demi-vie thermique de 1-E à température ambiante en utilisant Eq 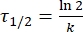(5).
    (5)
    Où τ_1/2 (s) = la demi-vie thermique du 1-E à température ambiante; k (^s-1) = la constante de vitesse de relaxation thermique à température ambiante obtenue à partir de l’étape 3.9.
11. Si la constante de vitesse de relaxation thermique n’est estimée qu’à une seule température, calculez la constante de vitesse à température ambiante à l’aide de l’équation d’Eyring réarrangée suivante (Eq (6))^18,23.
    (6)
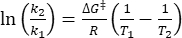    (7)
    Où (J·^mol-1) = l’énergie de Gibbs d’activation pour la relaxation thermique ; k₁ (^s-1) = la constante de vitesse de relaxation thermique estimée à la température élevée; k₂ (^s-1) = la constante de vitesse de relaxation thermique à température ambiante (298,15 K); T₁ (K) = température absolue à laquelle k₁ est obtenu; (K) = température ambiante (298,15 K).

4. Actinométrie de ferrioxalate

REMARQUE: Toutes les procédures d’actinométrie de ferrioxalate doivent être effectuées dans l’obscurité ou >600 nm pour éviter l’influence de la lumière ambiante.

1. Dans un flacon en verre de 20 mL contenant 29,48 mg (0,06 mmol) de ferrioxalate de potassium trihydraté, ajouter 8 mL d’eau désionisée. Ajouter 1 mL de H2_SO4 aqueux de 0,5 M à la solution de ferrioxalate et diluer à 10 mL avec de l’eau désionisée pour préparer un ferrioxalate de 0,006 M dans une solution aqueuse_H2SO₄ de 0,05 M.
2. Dans un autre flacon en verre de 20 mL contenant 10 mg de 1,10-phénanthroline et 1,356 g d’acétate de sodium anhydre, ajouter 10 mL_{de H2}SO₄ aqueux à 0,5 M pour obtenir une solution tamponnée de phénanthroline à 0,1 % (p/v).
3. Transférer 2 mL de la solution de ferrioxalate de 0,006 M de l’étape 4.1 vers une cuvette de quartz d’une longueur de chemin optique de 1,0 cm. Scellez la cuvette avec un bouchon en PTFE et gardez l’échantillon dans l’obscurité.
4. Préparer une autre cuvette de quartz contenant 2 mL de H2_SO4aqueux de 0,05_{M sous forme} d’échantillon à blanc. Mesurer l’absorbance UV-Vis de l’échantillon vierge pour la correction de base.
5. Mesurer l’absorbance UV-Vis de la solution de ferrioxalate de 0,006 M. Déterminer la fraction de lumière absorbée à l’aide des absorbances de la solution de ferrioxalate de 0,006 M à 340 et 436 nm et Eq (8) (Figure 8).
   (8)
   Où f = la fraction de lumière absorbée par 0,006 M de solution de ferrioxalate; A_λ = l’absorbance d’une solution de ferrioxalate de 0,006 M à la longueur d’onde λ.
6. Préparer deux cuvettes de quartz d’une longueur de trajet optique de 1,0 cm et ajouter 2 mL de la solution de ferrioxalate de 0,006 M.
7. Placez l’un des échantillons de l’étape 4,6 1 cm devant la lampe à arc au xénon équipée d’un filtre passe-bande de 436 nm. Gardez l’autre échantillon dans l’obscurité. Commencez l’irradiation de l’échantillon pendant 90 s. Après irradiation, ajouter 0,35 mL de la solution de phénanthroline tamponnée à 0,1 % et une barre magnétique aux deux cuvettes, puis remuer pendant 1 h dans l’obscurité pour former un complexe [Fe(phen)₃]²⁺ .
   REMARQUE: Le ferrioxalate est réduit photochimiquement à Fe²⁺, suivi de la formation presque quantitative du complexe tris-1,10-phénanthroline fer (II).
8. Mesurer le spectre d’absorption UV-Vis de l’échantillon non irradié à partir de l’étape 4.6 pour la correction initiale.
9. Mesurer le spectre d’absorption UV-Vis de l’échantillon irradié à partir de l’étape 4.7.
10. Répétez les étapes 4.6 à 4.9 avec un filtre passe-bande de 340 nm (Figure 9).
    REMARQUE: Une fois que l’échantillon de ferrioxalate est exposé à la lumière, l’échantillon ne peut pas être réutilisé.
11. Calculer le flux de photons molaires arrivant à la cuvette en utilisant Eq 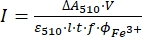(9).
    (9)
    Où I (mol·^s-1) = le flux de photons molaires arrivant à la cuvette ; ΔA₅₁₀ = la différence d’absorbance à 510 nm entre les échantillons non irradiés et irradiés; V = volume total de la solution (2,35 mL); ε₅₁₀ = coefficient d’atténuation molaire du complexe [Fe(phen)₃]²⁺ (11100 ^{M-1 cm-1})²⁴; I = la longueur du trajet optique de la cuvette de quartz (1,0 cm); t = temps d’irradiation (90 s); f = la fraction absorbée de la lumière obtenue à partir de l’étape 4.5; Φ_Fe³⁺ = le rendement quantique de la photoréduction de Fe³⁺ à Fe²⁺ (1,22 pour 340 nm, 1,11 pour 436 nm)²⁵.

5. Détermination du rendement quantique de photoisomérisation

1. Préparer une cuvette de quartz avec une longueur de chemin optique de 1,0 cm contenant 2 mL de DMSO comme échantillon vierge. Mesurer l’absorbance UV-Vis de l’échantillon vierge pour la correction de base.
2. Préparer une cuvette de quartz avec une longueur de chemin optique de 1,0 cm contenant 2 mL de solution de 10 μM de 1 dans du DMSO obtenue à partir de l’étape 2.4 (enrichie en Z). Scellez les cuvettes avec un bouchon en PTFE.
3. Placez l’échantillon de l’étape 5,2 à 1 cm devant la lampe à arc au xénon équipée d’un filtre passe-bande de 436 nm. Commencez l’irradiation à 436 nm vers l’échantillon et mesurez le spectre d’absorption UV-Vis avec différents intervalles jusqu’à ce qu’il n’y ait pas de changement dans les spectres lorsque 1 atteint le PSS (Figure 10).
   REMARQUE: La configuration de l’irradiation doit être exactement la même que celle utilisée pour la mesure du flux de photons molaires. L’intervalle d’irradiation doit être ajusté en fonction du taux de photoisomérisation. Généralement, 15 à 20 points de données avant d’atteindre le PSS conviennent.
4. Préparer une cuvette de quartz d’une longueur de trajet optique de 1,0 cm contenant 2 mL de solution de 10 μM de 1 dans du DMSO obtenue à partir de l’étape 2.3 (enrichie en E). Scellez les cuvettes avec un bouchon en PTFE.
5. Remplacez le filtre passe-bande de 436 nm par le filtre passe-bande de 340 nm et répétez l’étape 5.3 pour l’échantillon obtenu à partir de l’étape 5.4.
6. Calculer le facteur photocinétique F(t) en utilisant les absorbances observées à partir des étapes 5.3 et Eq (10)²⁶.
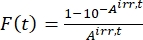   (10)
   Où A^irr,t = l’absorbance à la longueur d’onde d’irradiation au temps t.
7. Calculer le pseudo rendement quantique Q en utilisant les valeurs du facteur photocinétique obtenues à partir des étapes 5.6 et Eq (11)²⁷.
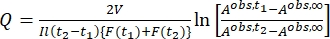   (11)
   Où Q (^{M-1 cm-1}) = le pseudo rendement quantique défini comme ;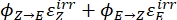 ; V(L) = le volume de l’échantillon; I (mol·^s-1) = le flux de photons molaires arrivant à la cuvette; l (cm) = la longueur du chemin optique; t₁, t₂ (s) = les deux points temporels consécutifs de l’irradiation; F(t₁), F(t₂) = les facteurs photocinétiques aux temps t₁ et t₂, respectivement; A^obs,t₁, A^obs,t₂, A^obs,∞ = les absorbances à longueur d’onde spécifique au temps, t₁ et t₂ à PSS, respectivement.
   REMARQUE: L’utilisation d’absorbances à λ_max de 1-Z est recommandée pour plus de précision.
8. Calculez la valeur moyenne du rendement pseudo quantique à l’aide des dix premiers points de données.
9. Calculer les rendements quantiques unidirectionnels pour les photoisomérisations Z-to-E et E-to-Z en utilisant Eq (12) et Eq (13).
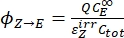   (12)
   (13)
   Où Φ_Z→E, Φ_E→Z = les rendements quantiques unidirectionnels pour les processus de photoisomérisation Z-to-E et E-to-Z, respectivement; , 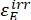(^{M-1 cm-1}) = les coefficients d’atténuation molaire de 1-Z et 1-E à la longueur d’onde d’irradiation; 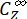, 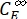(M) = les concentrations de 1-Z et 1-E à PSS, respectivement; C_tot (M) = la concentration totale de 1.
10. Répétez les étapes 5.6 à 5.9 en utilisant les données obtenues à partir de l’étape 5.5 pour le calcul des rendements quantiques de photoisomérisation unidirectionnelle sous irradiation à 340 nm.

Résultats

Lors de l’irradiation de 1 dans un tube RMN avec une lumière de 436 nm (Z:E = 54:46 à l’état initial), la proportion de 1-E augmente en raison de l’isomérisation dominante Z-to-E de la liaison hydrazone C=N (Figure 1). Le rapport isomérique peut être facilement obtenu à partir des intensités de signal relatives d’isomères distincts dans le spectre RMN ¹H (figure 2)....

Discussion

Diverses stratégies pour régler les propriétés spectrales et de commutation des photocommutateurs ont été développées, et le registre des photocommutateurs s’étend rapidement²⁸. Il est donc crucial de déterminer correctement leurs propriétés photophysiques, et nous prévoyons que les méthodes résumées dans cet article seront un guide utile pour les expérimentateurs. A condition que le taux de relaxation thermique soit très lent à température ambiante, la mesure des composition...

matériels

Name	Company	Catalog Number	Comments
1,10-phenanthroline	Sigma-Aldrich	131377-2.5G
340 nm bandpass filter, 25 mm diameter, 10 nm FWHM	Edmund Optics	#65-129
436 nm bandpass filter, 25 mm diameter, 10 nm FWHM	Edmund Optics	#65-138
Anhydrous sodium acetate	Alfa aesar	A13184.30
Dimethyl sulfoxide	Samchun	D1138	HPLC grade
Dimethyl sulfoxide-d6	Sigma-Aldrich	151874-25g
Gemini 2000; 300 MHz NMR spectrometer	Varian
H2SO4	Duksan	235
Heating bath	JeioTech	CW-05G
MestReNova 14.1.1	Mestrelab Research S.L., https://mestrelab.com/
Natural quartz NMR tube	Norell	S-5-200-QTZ-7
Potassium ferrioxalate trihydrate	Alfa aesar	31124.06
Quartz absorption cell	Hellma	HE.110.QS10
UV-VIS spectrophotometer	Scinco	S-3100
Xenon arc lamp	Thorlabs	SLS205	Fiber adapter was removed