Determinazione della resa quantistica di fotoisomerazione di un interruttore foto Hydrazone

Riepilogo

La resa quantistica della fotoisomerizzazione è una proprietà fotofisica fondamentale che dovrebbe essere determinata con precisione nello studio dei fotointerruttori di nuova concezione. Qui, descriviamo una serie di procedure per misurare la resa quantistica di fotoisomerazione di un idratone fotocromatico come un fotointerruttore bistabile modello.

Abstract

Le molecole organiche fotointercabilizzate che subiscono trasformazioni strutturali guidate dalla luce sono componenti chiave per costruire sistemi molecolari adattivi e sono utilizzate in un'ampia varietà di applicazioni. Nella maggior parte degli studi che impiegano fotointerruttori, diverse importanti proprietà fotofisiche come le lunghezze d'onda massime di assorbimento ed emissione, il coefficiente di attenuazione molare, la durata della fluorescenza e la resa quantistica della fotoisomerizzazione sono attentamente determinate per studiare i loro stati elettronici e processi di transizione. Tuttavia, la misurazione della resa quantistica di fotoisomerizzazione, l'efficienza della fotoisomerizzazione rispetto ai fotoni assorbiti, in un tipico ambiente di laboratorio è spesso complicata e soggetta a errori perché richiede l'implementazione di rigorose misure spettroscopiche e calcoli basati su un metodo di integrazione appropriato. Questo articolo introduce una serie di procedure per misurare la resa quantistica di fotoisomerazione di un fotointerruttore bistabile utilizzando un idrazzone fotocromatico. Prevediamo che questo articolo sarà una guida utile per l'indagine dei fotointerruttori babili che sono sempre più in fase di sviluppo.

Introduzione

Le molecole organiche fotocromatiche hanno attirato una notevole attenzione in una vasta gamma di discipline scientifiche poiché la luce è uno stimolo unico che può allontanare un sistema dal suo equilibrio termodinamico in modo non invasivo¹. L'irradiazione della luce con energie appropriate consente la modulazione strutturale di fotointerruttori con elevata precisione ^{spaziotemporale 2,3,4}. Grazie a questi vantaggi, sono stati sviluppati e utilizzati vari tipi di fotointerruttori basati sull'isomerizzazione configurazionale dei doppi legami (ad esempio, stilbene, azobenzeni, imine, fumaramidi, tioindigos) e sull'apertura/chiusura dell'anello (ad esempio, spiropirani, ditienilteni, fulgidi, addotti Stenhouse donatore-accettore). Le applicazioni rappresentative dei fotointerruttori coinvolgono materiali fotocromatici, somministrazione di farmaci, recettori e canali commutabili, informazioni o accumulo di energia e macchine molecolari ^{5,6,7,8,9,10,11,12}. Nella maggior parte degli studi che presentano fotointerruttori di nuova progettazione, le loro proprietà fotofisiche come λ_max di assorbimento ed emissione, coefficiente di attenuazione molare (ε), durata di fluorescenza e resa quantistica di fotoisomerizzazione sono caratterizzate in modo approfondito. L'indagine di tali proprietà fornisce informazioni chiave sugli stati elettronici e le transizioni che sono cruciali per comprendere le proprietà ottiche e il meccanismo di isomerizzazione.

Tuttavia, la misurazione accurata della resa quantistica di fotoisomerizzazione - il numero di eventi di fotoisomerizzazione che si sono verificati diviso per il numero di fotoni alla lunghezza d'onda di irradiazione assorbita dal reagente - è spesso complicata in un tipico ambiente di laboratorio a causa di diversi motivi. La determinazione della resa quantistica di fotoisomerizzazione è generalmente ottenuta monitorando l'avanzamento della reazione e misurando il numero di fotoni assorbiti durante l'irradiazione. La preoccupazione principale è che la quantità di assorbimento di fotoni per unità di tempo cambia progressivamente perché l'assorbimento totale da parte della soluzione cambia nel tempo man mano che la reazione fotochimica procede. Pertanto, il numero di reagenti consumati per unità di tempo dipende dalla sezione temporale in cui viene misurato durante l'irradiazione. Pertanto, si è obbligati a stimare la resa quantistica di fotoisomerizzazione che è definita in modo differenziale.

Un problema più fastidioso sorge quando sia il reagente che il fotoprodotto assorbono la luce alla lunghezza d'onda dell'irradiazione. In questo caso, l'isomerizzazione fotochimica avviene in entrambe le direzioni (cioè una reazione fotoreversibile). I due rendimenti quantistici indipendenti per le reazioni avanti e indietro non possono essere ottenuti direttamente dalla velocità di reazione osservata. Anche l'intensità della luce imprecisa è una causa comune di errore. Ad esempio, l'invecchiamento del bulbo cambia gradualmente la sua intensità; l'irraggiamento della lampada ad arco allo xeno a 400 nm diminuisce del 30% dopo 1000 ore di funzionamento¹⁴. La diffusione della luce non collimata rende l'irraggiamento incidente effettivo significativamente inferiore alla potenza nominale della sorgente. Pertanto, è fondamentale quantificare con precisione il flusso di fotoni efficace. Da notare, il rilassamento termico della forma metastabile a temperatura ambiente dovrebbe essere sufficientemente piccolo da essere ignorato.

Questo documento introduce una serie di procedure per determinare la resa quantistica di fotoisomerazione di un fotointerruttore bistabile. Un certo numero di fotointerruttori di idrazone sviluppati dal gruppo di Aprahamian, il team di ricerca pioniere nel campo, sono stati sotto i riflettori grazie alla loro fotoisomeria selettiva e alla notevole stabilità dei loro isomeri metastabili 15,16,17. I loro fotointerruttori dell'idrazone comprendono due anelli aromatici uniti da un gruppo di idrazone e il legame C = N subisce un'isomerizzazione selettiva E / Z dopo irradiazione a lunghezze d'onda appropriate (Figura 1). Sono stati incorporati con successo come componenti mobili di sistemi molecolari dinamici 18,19,20,21. In questo lavoro, abbiamo preparato un nuovo derivato dell'idrazone che porta gruppi ammidici e ne abbiamo studiato le proprietà di fotointerruttoria per la determinazione della resa quantistica della fotoisomerizzazione.

Protocollo

1. Acquisizione dello spettro NMR ¹H allo stato fotostazionario (PSS)

1. In un tubo NMR di quarzo naturale contenente 4,2 mg (0,01 mmol) di interruttore idrazico 1, aggiungere 1,0 ml di dimetilsolfossido deuterato (DMSO-d ₆). Trasferire metà della soluzione in un altro tubo NMR.
2. Posizionare uno dei tubi NMR di 1 cm davanti a una lampada ad arco allo xeno dotata di un filtro passa-banda da 436 nm. Avviare l'irradiazione al campione NMR e registrare uno spettro NMR ¹H ogni giorno fino a quando non vi è alcun cambiamento negli spettri quando l'interruttore 1 raggiunge PSS. Dopo aver raggiunto PSS, mantenere il tubo NMR al buio a temperatura ambiente e registrare lo spettro NMR ¹H dopo 12 ore per monitorare l'avanzamento del rilassamento termico.
   NOTA: l'interruttore 1 non mostra alcun cambiamento apprezzabile nello spettro NMR ¹H a temperatura ambiente a causa della sua natura bistabile.
3. Per l'altro tubo NMR, ripetere il passaggio 1.2 con un filtro passa-banda da 340 nm per ottenere uno spettro NMR ¹H all'irradiazione PSS sotto 340 nm.
4. Apri i file fid degli spettri NMR presso i PSS con il software di elaborazione NMR. Integrare un insieme distintivo di picchi (H1: C2 protone di chinolina, H2: protone in para-posizione al gruppo idrazico, H3: CH₃ di estere etilico) degli isomeri distinti e calcolare il rapporto isomerico (Figura 2).
   NOTA: Le composizioni (rapporto [1-Z]:[1-E]) sotto l'irradiazione di 436 nm e 340 nm sono rispettivamente 8:92 e 82:18.

2. Spettroscopia di assorbimento UV-Vis al PSS

1. In un flaconcino di vetro contenente 12,6 mg (0,03 mmol) di 1, aggiungere 2 mL di DMSO di grado spettroscopico. Prendere 100 μL della soluzione e diluire con 1400 μL di DMSO per ottenere 1 mM di soluzione da 1. Trasferire 20 μL di 1 mM di soluzione di 1 in una cuvetta di quarzo con lunghezza del percorso ottico di 1,0 cm e diluire con 1980 μL di DMSO per ottenere una soluzione da 10 μM di 1. Sigillare la cuvetta con un tappo in PTFE e tenere il campione al buio.
2. Preparare un'altra cuvetta di quarzo contenente 2 ml di DMSO come campione in bianco. Misurare lo spettro UV-Vis del campione in bianco per la correzione al basale.
3. Posizionare il campione dal passo 2,1 1 cm davanti a una lampada ad arco allo xeno dotata di un filtro passa-banda da 436 nm. Avviare l'irradiazione al campione e misurare lo spettro UV-Vis ogni 2 ore fino a quando non vi è alcun cambiamento negli spettri quando 1 raggiunge PSS (Figura 3).
   NOTA: Il tempo impiegato per raggiungere la PSS per il campione di spettroscopia UV-Vis è molto più breve rispetto al campione NMR con una concentrazione più elevata.
4. Ripetere il passaggio 2.3 con un filtro passa-banda da 340 nm per ottenere lo spettro UV-Vis al PSS sotto l'irradiazione a 340 nm.
5. Dedurre gli spettri di assorbanza dei puri 1-Z e 1-E usando Eq (1) ed Eq (2) (Figura 4).
   (1)
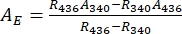   (2)
   dove R₄₃₆ = il rapporto di 1-Z al PSS sotto l'irradiazione di 436 nm; R₃₄₀ = il rapporto di 1-Z al PSS sotto l'irradiazione di 340 nm; A₄₃₆ = l'assorbanza di 1 in DMSO al PSS sotto irradiazione a 436 nm; A₃₄₀ = l'assorbanza di 1 in DMSO al PSS sotto irradiazione a 340 nm.
6. Calcolare i coefficienti di attenuazione molare di 1-Z e 1-E puri a tutte le lunghezze d'onda dividendo l'assorbanza osservata per la concentrazione del campione (10 μM) e la lunghezza del percorso ottico (1 cm).

3. Studi cinetici sul rilassamento termico

1. Riscaldare l'olio di silicio riempito in un circolatore a bagno riscaldante alla temperatura desiderata (131 °C) e verificare se la temperatura del bagno è stabilizzata. Immergere due campioni NMR dal punto 1.2 nel bagno di riscaldamento.
   NOTA: La temperatura e la durata del riscaldamento vengono regolate in base alla velocità di rilassamento.
2. Dopo 1 ora di riscaldamento, trasferire rapidamente i tubi NMR in un bagno di ghiaccio secco per mettere in pausa il rilassamento termico causato dal calore latente (Figura 5).
   NOTA: temperatura o tempo di riscaldamento imprecisi possono portare a gravi errori nella stima della costante di velocità.
3. Scongelare i campioni NMR ottenuti dal passaggio 3.2 a temperatura ambiente e assicurarsi che il DMSO sia scongelato. Registrare gli spettri NMR ¹H dei campioni.
4. Ripetere i passaggi 3.1-3.3 fino a quando non vi è alcun cambiamento negli spettri NMR ¹H quando 1 raggiunge l'equilibrio termodinamico.
5. Ripetere i passaggi da 3,1 a 3,4 a temperature diverse (134, 137, 140 e 143 °C).
6. File fid aperti degli spettri NMR ottenuti nel corso del riscaldamento a 131 °C. Calcolare i rapporti isomerici medi come descritto nel passaggio 1.4. Calcolare la concentrazione di 1-E (isomero metastabile) in base alla concentrazione totale del campione (10 mM) e al rapporto isomerico.
7. Traccia la concentrazione media di 1-E (C_E) in funzione del tempo di riscaldamento. Eseguire un adattamento esponenziale ai dati per ottenere la costante di velocità del rilassamento termico utilizzando Eq (3)^15,22 (Figura 6).
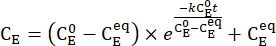   (3)
   Dove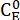 (M) = la concentrazione di 1-E allo stato iniziale; 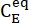(M) = la concentrazione di 1-E all'equilibrio termodinamico ad una temperatura specifica; k (^s-1) = la costante di velocità del rilassamento termico a una temperatura specifica; t (s) = il tempo di riscaldamento.
8. Ripetere i passaggi da 3,6 a 3,7 utilizzando i dati ottenuti a temperature diverse.
9. Tracciare ln(k) versus ed eseguire un adattamento lineare secondo l'equazione di Arrhenius (Eq (4)) per estrapolare la costante di velocità a temperatura ambiente (Figura 7).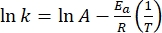
   (4)
   Dove A = il fattore pre-esponenziale; E_a (J·^mol-1) = l'energia di attivazione per il rilassamento termico; R = la costante ideale del gas (8.3145 J·^{mol-1 K-1}); T (K) = la temperatura assoluta.
10. Calcolare l'emivita termica di 1-E a temperatura ambiente utilizzando Eq 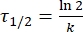(5).
    (5)
    Dove τ_1/2 (s) = l'emivita termica di 1-E a temperatura ambiente; k (^s-1) = la velocità costante di rilassamento termico a temperatura ambiente ottenuta dal passo 3.9.
11. Se la costante di velocità del rilassamento termico è stimata solo a una singola temperatura, calcolare la costante di velocità a temperatura ambiente utilizzando la seguente equazione di Eyring riorganizzata (Eq (6))^18,23.
    (6)
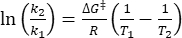    (7)
    Dove (J·^mol-1) = l'energia di Gibbs di attivazione per il rilassamento termico; k₁ (^s-1) = la costante di velocità di rilassamento termico stimata alla temperatura elevata; k₂ (^s-1) = la velocità costante di rilassamento termico a temperatura ambiente (298,15 K); T₁ (K) = la temperatura assoluta alla quale si ottiene k₁ ; (K) = temperatura ambiente (298,15 K).

4. Attinometria ferriossalato

NOTA: Tutte le procedure per l'actinometria ferriossalato devono essere eseguite al buio o >600 nm per prevenire l'influenza della luce ambientale.

1. In un flaconcino di vetro da 20 mL contenente 29,48 mg (0,06 mmol) di ferriossalato di potassio triidrato, aggiungere 8 mL di acqua deionizzata. Aggiungere 1 mL di H₂SO₄ acquoso 0,5 M alla soluzione ferriossalata e diluire a 10 mL con acqua deionizzata per preparare un ferriossalato da 0,006 M in soluzione acquosa H₂SO_{4 da} 0,05 M.
2. In un altro flaconcino di vetro da 20 mL contenente 10 mg di 1,10-fenantrolina e 1,356 g di acetato di sodio anidro, aggiungere 10 mL di H 2 SO 4 acquoso_da0,5 M per ottenere una soluzione tamponata di fenantrolina allo 0,1% (p/v).
3. Trasferire 2 mL della soluzione di ferriossalato da 0,006 M dal passo 4.1 a una cuvetta di quarzo con lunghezza del percorso ottico di 1,0 cm. Sigillare la cuvetta con un tappo in PTFE e tenere il campione al buio.
4. Preparare un'altra cuvetta di quarzo contenente 2 mL di 0,05 M acquoso H₂SO₄ come campione in bianco. Misurare l'assorbanza UV-Vis del campione in bianco per la correzione al basale.
5. Misurare l'assorbanza UV-Vis della soluzione di ferriossalato 0,006 M. Determinare la frazione di luce assorbita utilizzando le assorbanze della soluzione di ferriossalato da 0,006 M a 340 e 436 nm e Eq (8) (Figura 8).
   (8)
   Dove f = la frazione di luce assorbita da 0,006 M di soluzione di ferriossalato; A_λ = l'assorbanza della soluzione di ferriossalato 0,006 M alla lunghezza d'onda λ.
6. Preparare due cuvette di quarzo con lunghezza del percorso ottico di 1,0 cm e aggiungere 2 mL della soluzione di ferriossalato da 0,006 M.
7. Posizionare uno dei campioni dal passo 4,6 1 cm davanti alla lampada ad arco allo xeno dotata di un filtro passabanda da 436 nm. Tenere l'altro campione al buio. Avviare l'irradiazione al campione per 90 s. Dopo l'irradiazione, aggiungere 0,35 mL della soluzione tamponata allo 0,1% di fenantrolina e una barra magnetica a entrambe le cuvette, quindi mescolare per 1 ora al buio per formare un complesso [Fe(phen)₃]²⁺ .
   NOTA: Il ferriossalato è fotochimicamente ridotto a Fe²⁺, seguito dalla formazione quasi quantitativa del complesso di ferro tris-1,10-fenantrolina (II).
8. Misurare lo spettro di assorbimento UV-Vis del campione non irradiato dal passaggio 4.6 per la correzione al basale.
9. Misurare lo spettro di assorbimento UV-Vis del campione irradiato dal punto 4.7.
10. Ripetere i passaggi 4.6-4.9 con un filtro passa-banda da 340 nm (Figura 9).
    NOTA: Una volta che il campione di ferriossalato è esposto alla luce, il campione non può essere riutilizzato.
11. Calcolare il flusso di fotoni molari che arriva alla cuvetta usando Eq 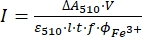(9).
    (9)
    Dove I (mol·^s-1) = il flusso di fotoni molari che arriva alla cuvetta; ΔA₅₁₀ = la differenza di assorbanza a 510 nm tra i campioni non irradiati e irradiati; V = il volume totale della soluzione (2,35 ml); ε₅₁₀ = il coefficiente di attenuazione molare del complesso [Fe(phen)₃]²⁺ (11100 ^{M-1 cm-1})²⁴; I = la lunghezza del percorso ottico della cuvetta di quarzo (1,0 cm); t = tempo di irradiazione (90 s); f = la frazione assorbita di luce ottenuta dal punto 4.5; Φ_Fe³⁺ = la resa quantistica della fotoriduzione di Fe³⁺ a Fe²⁺ (1,22 per 340 nm, 1,11 per 436 nm)²⁵.

5. Determinazione della resa quantistica di fotoisomerizzazione

1. Preparare una cuvetta di quarzo con una lunghezza del percorso ottico di 1,0 cm contenente 2 ml di DMSO come campione in bianco. Misurare l'assorbanza UV-Vis del campione in bianco per la correzione al basale.
2. Preparare una cuvetta di quarzo con percorso ottico di 1,0 cm di lunghezza contenente 2 mL di soluzione da 10 μM di 1 in DMSO ottenuta dal punto 2.4 (arricchito con Z). Sigillare le cuvette con un tappo in PTFE.
3. Posizionare il campione dal passo 5,2 1 cm davanti alla lampada ad arco allo xeno dotata di un filtro passa-banda da 436 nm. Avviare l'irradiazione a 436 nm al campione e misurare lo spettro di assorbimento UV-Vis con intervalli diversi fino a quando non vi è alcun cambiamento negli spettri quando 1 raggiunge PSS (Figura 10).
   NOTA: la configurazione dell'irradiazione deve essere esattamente la stessa utilizzata per la misurazione del flusso di fotoni molari. L'intervallo di irradiazione deve essere regolato in base alla velocità di fotoisomerizzazione. Generalmente, sono adatti 15-20 punti dati prima di raggiungere PSS.
4. Preparare una cuvetta di quarzo con percorso ottico di 1,0 cm di lunghezza contenente 2 mL di soluzione da 10 μM di 1 in DMSO ottenuta dal punto 2.3 (arricchito con E). Sigillare le cuvette con un tappo in PTFE.
5. Sostituire il filtro passa-banda da 436 nm con il filtro passa-banda da 340 nm e ripetere il passaggio 5.3 per il campione ottenuto dal passaggio 5.4.
6. Calcola il fattore fotocinetico F(t) usando le assorbanze osservate dal passo 5.3 e Eq (10)²⁶.
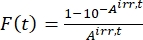   (10)
   Dove A^irr,t = l'assorbanza alla lunghezza d'onda dell'irradiazione al tempo t.
7. Calcola la resa pseudo quantistica Q usando i valori del fattore fotocinetico ottenuti dal passo 5.6 e Eq (11)²⁷.
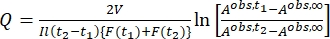   (11)
   Dove Q (^{M-1 cm-1}) = la pseudo resa quantistica definita come ;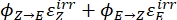 ; V(L) = il volume del campione; I (mol·^s-1) = il flusso di fotoni molari che arriva alla cuvetta; l (cm) = la lunghezza del percorso ottico; t₁, t₂ (s) = i due punti temporali consecutivi di irradiazione; F(t₁), F(t₂) = i fattori fotocinetici al tempo t₁ e t₂, rispettivamente; A^obs,t₁, A^obs,t₂, A^obs,∞ = le assorbanze a lunghezza d'onda specifica al tempo, t₁ e t₂ a PSS, rispettivamente.
   NOTA: l'uso di assorbanze a λ_max di 1-Z è raccomandato per la precisione.
8. Calcola il valore medio della resa pseudo quantistica utilizzando i primi dieci punti dati.
9. Calcola i rendimenti quantistici unidirezionali per le fotoisomerizzazioni Z-to-E ed E-to-Z usando Eq (12) ed Eq (13).
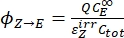   (12)
   (13)
   Dove Φ_Z→E, Φ_E→Z = i rendimenti quantistici unidirezionali per i processi di fotoisomerizzazione Z-to-E ed E-to-Z, rispettivamente; , 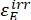(^{M-1 cm-1}) = i coefficienti di attenuazione molare di 1-Z e 1-E alla lunghezza d'onda dell'irradiazione; 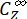, 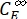(M) = le concentrazioni di 1-Z e 1-E a PSS, rispettivamente; C_tot (M) = la concentrazione totale di 1.
10. Ripetere i passaggi 5.6-5.9 utilizzando i dati ottenuti dal passaggio 5.5 per il calcolo dei rendimenti quantistici di fotoisomerizzazione unidirezionale sotto irradiazione a 340 nm.

Risultati

Dopo irradiazione di 1 in un tubo NMR con luce 436 nm (Z:E = 54:46 nello stato iniziale), la proporzione di 1-E aumenta a causa dell'isomerizzazione dominante Z-to-E del legame idrazone C=N (Figura 1). Il rapporto isomerico può essere facilmente ottenuto dalle intensità relative del segnale di isomeri distinti nello spettro NMR ¹H (Figura 2). Dopo 5 giorni di irradiazione a 436 nm...

Discussione

Sono state sviluppate varie strategie per sintonizzare le proprietà spettrali e di commutazione dei fotointerruttori e il registro dei fotointerruttori è in rapida espansione²⁸. È quindi fondamentale determinare correttamente le loro proprietà fotofisiche e prevediamo che i metodi riassunti in questo articolo saranno una guida utile per gli sperimentatori. A condizione che la velocità di rilassamento termico sia molto lenta a temperatura ambiente, la misurazione delle composizioni PSS a diver...

Materiali

Name	Company	Catalog Number	Comments
1,10-phenanthroline	Sigma-Aldrich	131377-2.5G
340 nm bandpass filter, 25 mm diameter, 10 nm FWHM	Edmund Optics	#65-129
436 nm bandpass filter, 25 mm diameter, 10 nm FWHM	Edmund Optics	#65-138
Anhydrous sodium acetate	Alfa aesar	A13184.30
Dimethyl sulfoxide	Samchun	D1138	HPLC grade
Dimethyl sulfoxide-d6	Sigma-Aldrich	151874-25g
Gemini 2000; 300 MHz NMR spectrometer	Varian
H2SO4	Duksan	235
Heating bath	JeioTech	CW-05G
MestReNova 14.1.1	Mestrelab Research S.L., https://mestrelab.com/
Natural quartz NMR tube	Norell	S-5-200-QTZ-7
Potassium ferrioxalate trihydrate	Alfa aesar	31124.06
Quartz absorption cell	Hellma	HE.110.QS10
UV-VIS spectrophotometer	Scinco	S-3100
Xenon arc lamp	Thorlabs	SLS205	Fiber adapter was removed