Method Article
Picometer-Precision Atomic Position Tracking through Electron Microscopy
In This Article
Summary
This work presents a workflow for atomic position tracking in atomic resolution transmission electron microscopy imaging. This workflow is performed using an open-source Matlab app (EASY-STEM).
Abstract
The modern aberration-corrected scanning transmission electron microscopes (AC-STEM) have successfully achieved direct visualization of atomic columns with sub-angstrom resolution. With this significant progress, advanced image quantification and analysis are still at the early stages. In this work, we present the complete pathway for the metrology of atomic resolution scanning transmission electron microscopy (STEM) images. This includes (1) tips for acquiring high-quality STEM images; (2) denoising and drift-correction for enhancing measurement accuracy; (3) obtaining initial atomic positions; (4) indexing the atoms based on unit cell vectors; (5) quantifying the atom column positions with either 2D-Gaussian single peak fitting or (6) multi-peak fitting routines for slightly overlapping atomic columns; (7) quantification of lattice distortion/strain within the crystal structures or at the defects/interfaces where the lattice periodicity is disrupted; and (8) some common methods to visualize and present the analysis.
Furthermore, a simple self-developed free MATLAB app (EASY-STEM) with a graphical user interface (GUI) will be presented. The GUI can assist in the analysis of STEM images without the need for writing dedicated analysis code or software. The advanced data analysis methods presented here can be applied for the local quantification of defect relaxations, local structural distortions, local phase transformations, and non-centrosymmetry in a wide range of materials.
Introduction
The development of spherical aberration correction in the modern scanning transmission electron microscope (STEM) has enabled microscopists to probe crystals with sub-angstrom sized electron beams1,2. This has allowed imaging of individual atomic columns in a wide variety of crystals with interpretable atomic resolution images for both heavy and light elements3,4. Recent developments in pixelated direct electron detectors and data analysis algorithms have enabled phase reconstruction imaging techniques, such as ptychography, with further improvements in spatial resolution to around 30 pm5,6,7. Additionally, the recent progress in STEM tomography has even enabled three-dimensional atomic resolution reconstruction of the single nano-particle8. The electron microscope has thus become an extraordinarily powerful tool for quantifying structural properties in materials with both high precision and site-specificity.
With the ultra-high resolution STEM images as the data input, direct measurements of structural distortions were performed to extract physical information from crystals at the atomic scale9,10. For example, the defect coupling between a Mo dopant in the WS2 monolayer and a single S vacancy was directly visualized by measuring the atomic positions and then calculating projected bond lengths11. Furthermore, the measurement on crystal interfaces, such as the coalesced grain boundaries in monolayer WS2, can exhibit the local atomic arrangement12. The interfacial analysis performed on the ferroelectric domain walls in LiNbO3 revealed the domain wall to be a combination of Ising and Neel states13. Another example is the visualization of the polar vortex structures achieved in the SrTiO3-PbTiO3 superlattices, achieved through calculation of the titanium atomic column displacements with respect to the strontium and lead column positions14. Finally, the advances in computer vision algorithms, such as image denoising with non-local principle component analysis15, Richardson and Lucy deconvolution16, drift-correction with non-linear registration17, and pattern recognition with deep learning, have significantly strengthened the accuracy of the measurement to sub-picometer precision18. One such example is the alignment and image registration of multiple fast-scan cryogenic-STEM images to enhance the signal-to-noise ratio. Subsequently, the Fourier-masking technique was applied to analyze the charge density waves in crystals by directly visualizing the periodic lattice distortion19. Even though the incredible aberration-corrected STEM instrumentation is increasingly accessible to researchers around the globe, the advanced data analysis procedures and methods remain uncommon and an enormous barrier for one without experience in data analysis.
In the present work, we showcase the complete pathway for the metrology of atomic resolution STEM images. This process includes firstly acquiring the STEM images with an aberration-corrected microscope followed by performing post-acquisition denoising/drift-correction for enhanced measurement accuracy. We will then further discuss the existing methods to clearly resolve and accurately quantify the atom column positions with either 2D-Gaussian single peak fitting or multi-peak fitting routines for slightly overlapping atomic columns20,21. Lastly, this tutorial will discuss methods for the quantification of lattice distortion/strain within the crystal structures or at the defects/interfaces where the lattice periodicity is disrupted. We will also introduce a simple self-developed free MATLAB app (EASY-STEM) with a graphical user interface (GUI) that can help with the analysis of STEM images without the need for writing dedicated analysis code or software. The advanced data analysis methods presented here can be applied for the local quantification of defect relaxations, local structural distortions, local phase transformations, and non-centrosymmetry in a wide range of materials.
Protocol
NOTE: The flow chart in Figure 1 shows the general procedure of the atomic position quantification.
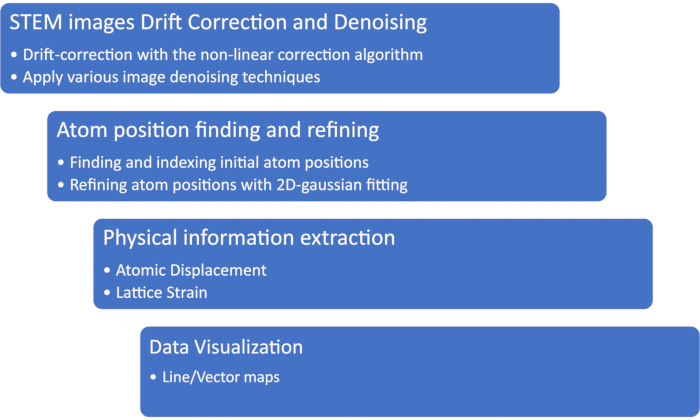
Figure 1: The workflow of the atomic position quantification and structural measurement. Please click here to view a larger version of this figure.
1. STEM image drift-correction and denoising
- Acquire high-quality annular dark-field (ADF)/annular bright-field (ABF) STEM images.
NOTE: The quality of the input data is key to ensuring the accuracy of data analysis, so we start the protocol with a few tips for acquiring good image data.- Ensure a high-quality TEM sample. The sample quality is extremely crucial. Use thin and clean TEM samples with no beam damage for imaging. Avoid touching the sample during handling and loading as this can cause sample contamination.
- Clean the sample before insertion (if possible). Clean the sample by using plasma cleaner, baking in a vacuum, or irradiating the region of interest in the sample at low magnifications by spreading the electron beam after sample insertion into the microscope ('beam shower'). Avoid damaged or contaminated areas when imaging.
- Align the microscope and tune the aberration correctors to minimize the lens aberrations as much as possible. Test the resolution by acquiring a few STEM images on a standard sample to confirm that the spatial resolution can resolve the specific crystal structures and further fine-tune the aberrations in the image.
- Tilt the sample until the optical axis is aligned with the specific zone axis of the crystal. For certain crystals, make observations from a required zone axis. For instance, align the viewing axis with the planes of the domain walls in ferroelectric crystals for the measurement.
- Optimize the electron dose while limiting electron beam damage and the sample drift during imaging. If the sample is stable under the electron beam and does not show drift or damage during the acquisition, it may be possible to try a higher electron dose or acquire multiple images of the same region to boost the signal-to-noise ratio. The goal here is to have a higher signal-to-noise ratio without beam damage or image artifacts.
- Acquire STEM images with different scanning directions to correct for potential drift during acquisition. First, acquire an image and then take the second one from the same region immediately after rotating the scan direction by 90°.
- Take images using the same imaging condition except for the scan directions. The purpose of this step is to feed the rotated images to the drift correction algorithm developed recently17.
NOTE: One can also input more than two images with more varying scanning directions (with arbitrary angles) into the algorithm. However, successive scanning of the same region may lead to lattice damage or drift in that area. Additionally, it is recommended that the scan direction and the low index lattice planes not maintain parallel or perpendicular directions with each other and instead maintain oblique angles. If the scan direction coincides with certain horizontal or vertical features (lattice planes, interfaces, etc.), the drift along the direction of the strong vertically/laterally varying features may cause artifacts during image registration.
- Take images using the same imaging condition except for the scan directions. The purpose of this step is to feed the rotated images to the drift correction algorithm developed recently17.
- Perform drift-correction with a non-linear correction algorithm.
NOTE: The non-linear drift correction algorithm was proposed and constructed by C. Ophus et al.17, and the open-source Matlab code can be found in the paper. Two or more images with different scanning directions are fed into the correction algorithm, and the algorithm will output the drift corrected STEM images. The downloaded code package includes a detailed yet simple procedure for the implementation. A more detailed algorithm and description of the process can be found in the original paper. - Apply various image denoising techniques.
NOTE: After the drift correction, perform image denoising to enhance the accuracy of future analysis. Some of the common denoising techniques are listed here. Furthermore, we introduce a free interactive Matlab app named EASY-STEM with a graphical user interface to help with the analysis. The interface is shown in Figure 2, with all the steps labeled on the corresponding buttons.
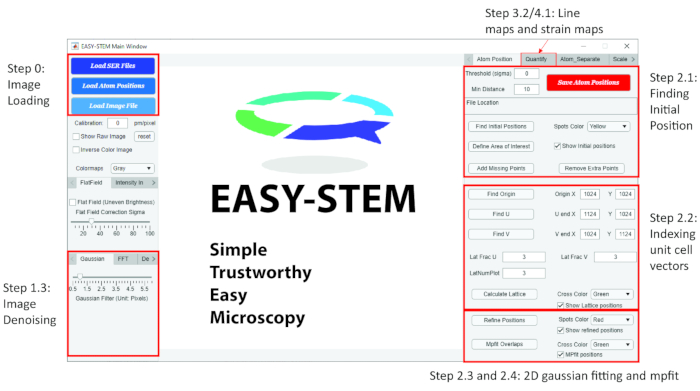
Figure 2: The graphical user interface (GUI) of the Matlab app EASY-STEM. All steps described in the protocol section are labeled accordingly. Please click here to view a larger version of this figure.
- Apply the Gaussian filtering. In the EASY-STEM app, find a tab called Gaussian on the bottom left. Use the slider to select how many nearby pixels to average. Move the slider to apply the Gaussian filter to the image.
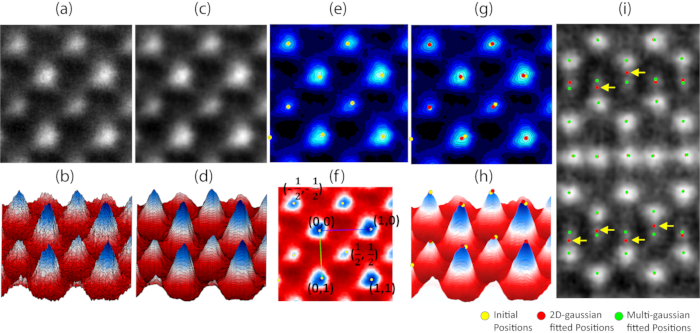
Figure 3: Example results of atomic position tracking. (i) An example of the position refining with the mp-fit algorithm. The results of regular 2D-Gaussian fitting and mpfit algorithm are shown with red and green circles respectively. The yellow arrows highlight the failure of regular 2D-Gaussian fitting due to the intensity from neighboring atoms. (a) The drift-corrected ADF-STEM image showing a typical unit cell of the ABO3 Perovskite. (b) The 3D plot of the intensity in (a). (c) The same image denoised with a Gaussian filter. (d) The 3D plot of the intensity in (c). (e) The contour plot of the intensity in (c) with the initial atomic positions (yellow circles) overlaid. (f) An example of the unit cell vector indexing system showing the index of the atomic positions in the image. (g) The contour plot of the intensity in (c) with the initial atomic positions (yellow circles) and refined atomic positions (red circles) overlaid, and (h) the 3D plot of the intensity with initial and refined atomic positions shown with yellow and red circles. Please click here to view a larger version of this figure.
NOTE: This technique uses a filter that averages the intensity of the nearby pixels in the images. The effect of the Gaussian filtering is presented in Figure 3a-d.
- Apply Fourier filtering. In the EASY-STEM app, find a tab called FFT on the bottom left. There is a slider to restrict the spatial frequency to reduce high-frequency noise. Move the slider to apply the Fourier filter to the image.
NOTE: This technique limits the spatial frequency of the image to remove the high-frequency noise in the image. - Apply the Richardson-Lucy deconvolution. In the EASY-STEM app, find a tab called Deconvolution on the bottom left, where there are two input boxes for the iterations of blind deconvolution and Richardson-Lucy deconvolution, respectively. Change the value and apply this denoising algorithm by clicking the button.
NOTE: This technique is a deconvolution algorithm for effectively removing the noise in the image by calculating the point spread function.
2. Finding and refining the atom position
- Find the initial atomic positions.
NOTE: After the post-acquisition image processing, the initial atomic positions can be simply extracted as the local intensity maximum or minimum for the ADF or ABF STEM images respectively. A minimum distance between the neighboring atomic columns needs to be defined to remove the extra positions.- Define the minimum distance (in pixels) by changing the value in the input box that determines the distance between the neighboring peaks.
- Click the Find Initial Positions button in the EASY-STEM app. The result is shown in Figure 3e.
NOTE: Frequently, extra positions or missing positions are observed with a simple local max/min finding algorithm. Thus, a manual correction mode is created in the EASY-STEM app to further refine the atomic positions (Add Missing/Remove Extra Points buttons). This feature enables the addition and removal of the initial positions by using the mouse cursor.
- Index the initial atomic positions with a unit-cell vector-based system.
- Define an origin point in the image. In the EASY-STEM app, click on the Find Origin button. After clicking the button, drag the pointer to one of the initial atomic positions to define it as the origin.
- Define the 2D unit cell u and v vectors and the unit cell fractions.
- Click the Find U/V button and drag the pointer to the end of the unit cells.
- Define the lattice fraction value by changing the value in the Lat Frac U and Lat Frac V input boxes.
NOTE: This value determines the lattice fraction value along the unit cell vector. For example, in the ABO3 perovskite unit cell, the unit cell can be divided equally into two halves along the two perpendicular unit cell vector directions. Consequently, there are two fractions along each unit cell vector direction, so the unit cell fraction values are 2 and 2 for u and v directions, respectively. The example result of the indexing and the corresponding u and v unit cell vectors are demonstrated in Figure 3f. For example, in Figure 3f, we will index the atoms on the corners as (0, 0), (1, 0), (0, 1), (1, 1); and we will index the atom in the center as (1/2, 1/2). This indexing system helps with information extraction in the following steps. - Click on the Calculate Lattice button to index all the atoms.
- Click on the Refine Positions button in the EASY-STEM app to refine atomic positions with 2D-Gaussian fitting.
NOTE: After obtaining the initial atomic positions and indexing the atoms in the image, a 2D-Gaussian fitting around each atomic column needs to be applied to achieve the sub-pixel level precision in the analysis. With this algorithm, it is possible to first crop an area in the image around each initial atomic position in the image and then fit a 2D-Gaussian peak in the cropped image. We then use the centers of the fitted 2D-Gaussian peaks as the refined atomic positions. This algorithm fits the 2D-Gaussian function to each atomic column in the image and the center of the fitted peak will be plotted after fitting. The result of the 2D-Gaussian fitting is shown in Figure 3g,h. - (Optional) Click the mpfit Overlaps button in EASY-STEM to refine atomic positions with 2D-Gaussian multi-peak fitting (mp-fit).
NOTE: Refine the atomic positions using the mp-fit algorithm when the intensities from adjacent atomic columns are overlapping with each other. The mp-fit algorithm and its effectiveness are discussed in detail by D. Mukherjee et al.21. The EASY-STEM app has incorporated this algorithm and can be used to separate neighboring atoms with overlapping intensities. The result of mp-fit is shown in Figure 3i. - Save the results by clicking the Save Atomic positions button.
NOTE: The app will prompt the user for location saving and file name. All saved results are included in the variable called "atom_pos".
3. Physical information extraction
- Measure the atomic displacements based on the unit cell vector indexing and atomic positions.
- Define a unit cell center.
NOTE: For example, for an ABO3 perovskite unit cell looking from its [100] axis, the unit cell centers can be defined as the average position of the four A-site atoms. In the first unit cell, those A-site atoms have been previously indexed as (0, 0), (1, 0), (0, 1), (1, 1). - Find the position of the displaced atoms.
NOTE: In the case of the ABO3 perovskite unit cell, the displaced atom is the B-site atom, which was previously labeled as (1/2, 1/2). - Iteratively find the position of the reference unit cell centers and displacement atoms for all the complete unit cells in the image.
NOTE: Unit cells may be incomplete near the edge of the TEM image. The atomic positions in those unit cells are discarded. - Measure the displacement vector by entering the following command:
d = pos(B) - mean(pos(A))
- Define a unit cell center.
- Quantify the lattice strain.
- Extract the unit cell vectors from each unit cell based on the atomic positions.
NOTE: Extract vector matrix "C", which is a 2x2 matrix consisting of u-vector and v-vector for each unit cell in x and y directions. - Define a reference vector, "C0".
NOTE: C0 can be defined as the average unit cell vectors from the part of the image (recommended) or the theoretically calculated unit cell vector value. - Calculate the 2x2 transformation matrix "T" using the following equation:
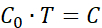 or
or 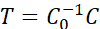 (1)
(1) - Calculate the distortion matrix "D":
D = T - I (2)
where the "I" is the identity matrix. - Decompose the distortion "D" to symmetric strain matrix "ε" and anti-symmetric rotation matrix "ω":
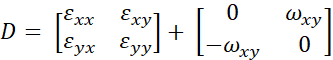 (3)
(3)
NOTE: Strain matrix "ε" and rotation matrix "ω" can be extracted by using the equations:
ε =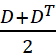 (4) And ω =
(4) And ω = 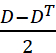 (5).
(5). - Iteratively calculate strains for all unit cells.
- In the EASY-STEM app, click on the Calculate Strain based on the atomic positions button under the Quantify tab on the top-left of the interface.
NOTE: The users can customize the displayed range of the strain map by changing the value within the Strain Upper/Lower limit input box.
- Extract the unit cell vectors from each unit cell based on the atomic positions.
4. Data Visualization
- Create colored line maps.
NOTE: Colored line mapping of the atomic bonds is a straightforward way to present the distance between nearby atoms. In Matlab, the command to draw a line between two points is: Line([x1 x2],[y1 y2],'Color',[r g b]). The inputs [x1 x2]and [y1 y2] are the coordinate values of the first and the second position. The distance variation can be presented with varying colors in the line map, which is defined by the [r g b] value. The [r g b] values stand for the red, green, and blue color values, each ranging from 0 to 1. Then iteratively connect all nearby atoms with colored lines.- Generate colored line maps in the EASY-STEM app.
NOTE: In the EASY-STEM app, line maps can be generated by a simple button clicking, which is under the Quantity tab on the top right of the interface.- Adjust the value (in pm) in the Mean Distance input box and Measurement Range input box in EASY-STEM. These two values define the average distance of the projected atom distance and the distance range of the measurement.
- In the EASY-STEM app, click on the Calculate Bond Length Based on Near Neighbor button.
NOTE: The line maps will be generated automatically. The users can adjust the colormap, line style, and line width for better visualization.
- Generate colored line maps in the EASY-STEM app.
- Create vector maps.
NOTE: Vector maps can present atomic displacements in an area of the crystal. Since the displacement analysis is unique to individual systems, we have not integrated the code into the EASY-STEM app, but instead, here, we will introduce the Matlab commands for such analysis based on the standard ABO3 perovskite unit cells.- Calculate the reference position for displacement measurement.
NOTE: In the example of ABO3 perovskite, we have indexed the atoms on the corners (A-site) as (0, 0), (1, 0), (0, 1), (1, 1), and the atom in the center (B-site) as (1/2, 1/2). To compute the displacement with respect to the unit cell center, we first calculate the reference position as the averaged position of the corner (A-site) atoms. The Matlab command for this calculation is:
ref_center=(positionA1+positionA2+positionA3+
PostionA4)/4 - Calculate the displacement by entering the command:
[displace_x displace_y] = PositionB - ref_center - Implement the vector map:
quiver(x,y,displace_x,displace_y)
NOTE: The input x and y are the positions of the displaced atom. The variables displace_x and displace_y are the displacement magnitudes in x and y directions. The vector maps can be uniformly colored (e.g., yellow, white, red…) or shaded based on the displacement magnitude.
- Calculate the reference position for displacement measurement.
- Create false-colored maps.
- Generate the false-colored maps by upsampling to estimate the measured value (displacement, strain, etc.) for each pixel in the image:
ImageSize = Size(Image);
[xi,yi] = meshgrid(1:1:ImageSize(1),1:1:ImageSize(2));
Upsampled_Data = griddata(x,y,YourData,xi,yi,'v4');
NOTE: The "griddata" function upsamples the data at position (x,y) to estimate the value for each pixel in the entire image. The inputs xi and yi are the grid coordinates, and the 'v4' is the bicubic upsampling method. - Plot the upsampled data using user-defined color scale.
- Generate the false-colored maps by upsampling to estimate the measured value (displacement, strain, etc.) for each pixel in the image:
Results
Figure 3 shows the example results of atomic position tracking by following steps 1 and 2 in the protocol. A raw ADF-STEM image of a unit cell of the ABO3 perovskite is shown in Figure 3a, and its intensity profile is plotted in 3-D in Figure 3b. Figure 3c shows the result after Gaussian filtering is applied to the STEM image in Figure 3a, and the intensity profile is plotted in Figure 3d. The initial positions are determined by finding the local maxima in the image and the positions are indicated by yellow circles in Figure 3e. The atomic positions are indexed based on the unit cell vector and shown in Figure 3f. After the initial position is found and indexed, 2D-Gaussian fitting is applied to further refine the measurement. In Figure 3g and Figure 3h, the fitted positions are indicated as red circles, the measurement precision is improved as the refined positions are closer to the center compared to the initial positions (yellow circles). Lastly, the advantage of applying the mpfit algorithm on the overlapping intensities is showcased in an ADF-STEM image of BaMnSb2 crystal (Figure 3i). The regular 2D-Gaussian fitting (red circles) fails severely on the Mn columns as highlighted by yellow arrows, while the mpfit algorithm can determine the positions much more accurately (green circles).

Figure 4: HAADF-STEM image of the Ca3Ru2O7 (CRO). (a) The magnified image of the ADF-STEM image of the Ca3Ru2O7 (CRO) crystal with the crystal structure schematic superimposed. The relative displacement of the Ca atom in the perovskite layer is highlighted with the yellow arrow. (b) Drift-corrected and denoised ADF-STEM image of CRO and (c) with overlaying refined atomic positions (red dots). (d) An example of using an indexing system to identify the upper (red), center (blue) and lower (yellow) Ca atoms in the perovskite layer. Please click here to view a larger version of this figure.
The HAADF-STEM image of the Ca3Ru2O7 (CRO) is shown in Figure 4a and Figure 4b (with the overlaid crystal structure). CRO is a Ruddlesden-Popper phase perovskite crystal with the polar space group A21am. ADF-STEM imaging shows the contrast from the heavier elements well (Ca and Ru), but the O atoms are not visualized as lighter atoms do not scatter the beam strong enough to become visible with HAADF detectors. The non-centrosymmetry of the crystal structure is caused by the tilting of O octahedra and can be visualized in ADF-STEM images by analyzing the displacement of the Ca atom in the center of the double perovskite layer. By following the steps listed in the Protocol section, all atomic positions in this image can be located by finding the centers of the fitted 2D-Gaussian peaks, as shown in Figure 4c. Furthermore, using the indexing system, in step 3.2, each type of atom in the unit cell can be identified and used for further processing. For example, the Ca atoms at the upper, center, and lower side of the perovskite double layer can be easily identified and their positions are presented with circles filled with different colors, as shown in Figure 4d.
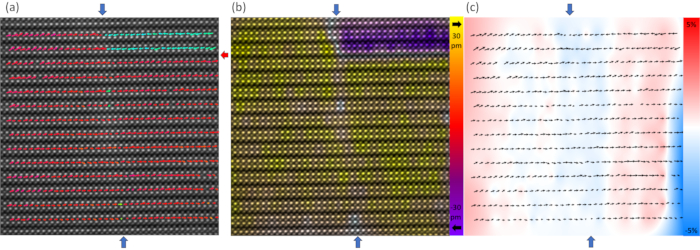
Figure 5: Physical information. (a) An example of the implementation of the vector map showing the polarization obtained from the center Ca displacement pattern. The arrows are colored based on the orientation (red to the right, blue to the left). The vertical 90° head-to-head and head-to-tail domain walls are indicated with blue arrows and a horizontal 180° domain wall is indicated with a red arrow. (b) An example of the implementation of the false-colored map showing the polarization. The color indicates the magnitude in left (yellow) and right (purple) directions. Reduced magnitude results in faded color. (c) An example of implementation of the false-colored map showing the εxx strain in the image. The color indicates the value of tensile (red) and compressive (blue) strain. Please click here to view a larger version of this figure.
After positioning and indexing the atoms in the STEM images, the physical information can be extracted and visualized via various types of plots, as shown in Figure 5. The vector map that shows the polarization direction is shown in Figure 5a. The arrows point towards the projected polarization direction, and by coloring the arrows based on their orientation, a vertical head-to-head 90° domain wall (labeled with blue arrows), and a horizontal 180° domain wall (labeled with red arrows) are shown at the top of the image. By constructing the false-colored map as shown in Figure 5b, a decreasing polar displacement magnitude can be observed via the fading color in the center, and thus the head-to-tail domain wall can be visualized. By combining the vector map and false-color map, the T-junction formed by three domain walls is shown in the ADF-STEM image. Additionally, with the dimension of each unit cell in the image measured, an εxx strain map can be constructed, as shown in Figure 5c.
Discussion
When working on the post-acquisition processing, some caution needs to be taken as well. To start with, during the image drift-correction, the algorithm assumes that the 0° image has the horizontal fast scanning direction, so double-check the direction before the calculation. If the scanning direction is not correctly set, the drift-correction algorithm will fail and may even introduce artifacts in the output17. Then during the imaging denoising, certain methods may introduce an artifact; for example, the Fourier filtering may create atom column contrast at the vacancy sites or remove fine features in the images, if the spatial resolution is not limited properly. As a result, it is vitally important to verify if the denoised images closely resemble the original raw input images.
Next, when determining the initial atomic positions based on local maximum/minimum, try to adjust the restriction minimum distance between peaks to avoid creating redundant positions between atomic columns. These redundant positions are artifacts generated due to the algorithm mistakenly recognizing the local maxima/minima in the image as atomic columns. Additionally, one can adjust the threshold value to find most of the positions if there are large contrast differences between various atomic species in the image (e.g., in ADF-STEM images of WS2). After obtaining most of the initial atomic positions in the image, try to manually add missing ones or remove extra ones with best effort. Moreover, the method for the indexing of the atoms is the most effective when there are not large interruptions in the periodicities within the image. When there are interruptions such as grain boundaries or phase boundaries presented in the image, the indexing may fail. The solution to this problem is to define the areas of interest in the image (by clicking the Define Area of Interest button in EASY-STEM app), and then indexing and refining the positions within each area separately. Afterward, one can easily combine datasets of different areas in the same image into one set of data and work on the analysis.
Finally, after applying 2D-Gaussian peak fittings, scatter the refined positions points onto the input image to verify the fitting results to see if the refined positions deviate from the atomic columns. The accuracy provided by the single Gaussian fitting algorithm is sufficient in most of the STEM experiments; however, if the position deviates due to the intensity from a neighboring atom, use the multi-peak fitting (mpfit) algorithm instead to isolate the intensity from adjacent atomic columns21. Otherwise, if the position deviates due to the image quality issue or the low intensity from the specific atom columns, it is suggested to discard the fitted position at that location.
There are several existing and specialized algorithms for the atomic position measurement, for example, the oxygen octahedra picker software22, Atomap python package23, and StatSTEM Matlab package24. However, these algorithms have some limitations in certain aspects. For instance, the oxygen octahedra picker requires the input of STEM images to contain only clearly resolved atomic columns and thus failed to address the issue in the images with atomic columns overlapping intensities21. On the other hand, although Atomap can calculate the positions of "dumbbell-like" atomic columns, the process is not very straightforward. Additionally, the StatSTEM is a great algorithm for quantifying the overlapping intensities, but its iterative model-based fitting process is computationally expensive21. In contrast, our approach, introduced in this work along with the Matlab app EASY-STEM, which is integrated with the advanced mpfit algorithm, can address the problem of the overlapping intensity and is less computationally expensive than StatSTEM, while offering competitive measurement precision. Furthermore, the analysis from Atomap and the oxygen octahedra picker software packages are designed and specialized for analyzing the data from ABO3 perovskite crystals, while the indexing system shown in this work is much more flexible about different materials systems. With the method in this work, users can fully design and customize the data analysis for their unique material systems based on the output results that contain both refined atomic positions and the unit cell vector indexing.
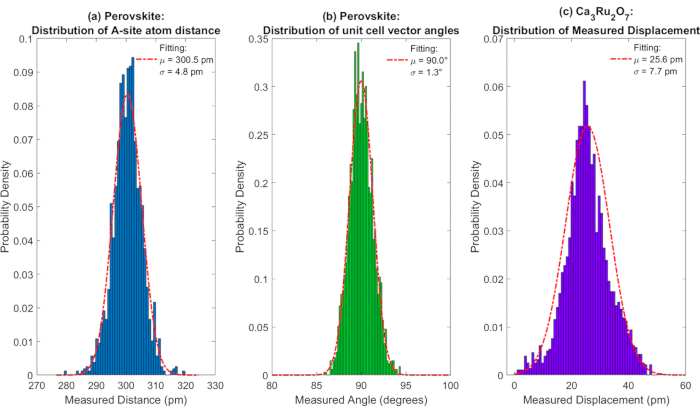
Figure 6: Statistical quantification of the atomic position finding. (a) The distribution of the perovskite A-site to A-site distance presented in a histogram. The normal distribution fitting is plotted and overlaid as the red dashed line showing the mean of 300.5 pm and the standard deviation of 4.8 pm. (b) The statistical quantification of the perovskite unit cell vector angle measurement is presented as a histogram. The normal distribution fitting is plotted and overlaid as the red dashed line showing the mean of 90.0° and the standard deviation of 1.3°. (c) The statistical quantification of the polar displacement measurement in Ca3Ru2O7 (CRO) is presented as histogram. The normal distribution fitting is plotted and overlaid as the red dashed line showing the mean of 25.6 pm and the standard deviation of 7.7 pm. Please click here to view a larger version of this figure.
The method introduced here provides picometer-level precision and simplicity for implementation. To demonstrate the measurement precision, the statistical quantification of the atomic position finding is presented in Figure 6. The measurements of cubic ABO3 perovskite A-site distance distribution and unit cell vector angle distribution are plotted using histogram in Figure 6a and Figure 6b, respectively. By fitting the normal distribution curve to the distributions, the A-site distance distribution shows a mean of 300.5 pm and standard deviation of 4.8 pm and unit cell vector angle distribution shows a mean of 90.0° and standard deviation of 1.3°. The statistical quantification indicates the method proposed here enables picometer-level precision and can greatly alleviate the distortion due to drift during imaging. This result suggests that this measurement is trustworthy when the physical information to be measured is greater or equal to roughly 10 pm. For example, in the case of aforementioned CRO crystals, the measurement of the magnitude of the polar displacement is presented in Figure 6c. The measurement shows a mean of 25.6 pm, a standard deviation of 7.7 pm, and it shows that the polar displacement measurement in CRO STEM images is solid. Additionally, more caution needs to be taken in case of experimental limitations such as low signal-to-noise ratio when imaging beam-sensitive samples. In those cases, the measured atomic positions need to be closely examined against the raw images to ensure the validity of the measurement. Consequently, the analysis method introduced here has limitations to the measurement precision when compared to more recent and advanced algorithms. Our method is insufficient when the precision is required at the sub-picometer level, so a more advanced analysis routine is necessary if the feature to be extracted in the image is below a certain threshold. For example, the non-rigid registration algorithm has shown sub-picometer precision measurement on silicon and it enables accurate measurement of bond length variation on a single Pt nanoparticle25. Most recently, the deep learning algorithm was employed to identify various types of point defects in 2-D transition metal dichalcogenides monolayers from a huge amount of STEM image data. Later, the measurement was conducted on the averaged image of different types of defects and this method also demonstrated sub-picometer level precision on the distortion around those defects18. Consequently, as a future plan for increasing the analysis capacity, we are in the progress of developing and implementing more advanced algorithms such as deep learning. We will also try to integrate them into the future data analysis tool updates.
Disclosures
The authors have nothing to disclose.
Acknowledgements
L.M. and N.A.'s work supported by the Penn State Center for Nanoscale Sciences, an NSF MRSEC under the grant number DMR-2011839 (2020 - 2026). D.M. was supported by ORNL's Laboratory Directed Research and Development (LDRD) Program, which is managed by UT-Battelle, LLC, for the U.S. Department of Energy (DOE). A.C. and N.A. acknowledge the Air Force Office of Scientific Research (AFOSR) program FA9550-18-1-0277 as well as GAME MURI, 10059059-PENN for support.
Materials
| Name | Company | Catalog Number | Comments |
| EASY-STEM | Nasim Alem Group, Pennsylvania State University | Matlab app for STEM image processing; Download link: https://github.com/miaoleixin1994/EASY-STEM.git | |
| JoVE article example script | Nasim Alem Group, Pennsylvania State University | Example Script for sorting atoms in unit cells | |
| Matlab Optimization Tool Box | MathWorks | Optimization add-on packge in Matlab | |
| Matlab | MathWorks | Numerical calculation software | |
| Matlab: Image Processing Tool Box | MathWorks | Image processing add-on packge in Matlab |
References
- Batson, P. E., Dellby, N., Krivanek, O. L. Sub-aångstrom resolution using aberration corrected electron optics. Nature. , (2002).
- Haider, M., et al. Electron microscopy image enhanced. Nature. , (1998).
- Muller, D. A., Nakagawa, N., Ohtomo, A., Grazul, J. L., Hwang, H. Y. Atomic-scale imaging of nanoengineered oxygen vacancy profiles in SrTiO3. Nature. , (2004).
- Findlay, S. D., et al. Robust atomic resolution imaging of light elements using scanning transmission electron microscopy. Applied Physics Letters. , (2009).
- Tate, M. W., et al. High Dynamic Range Pixel Array Detector for Scanning Transmission Electron Microscopy. Microscopy and Microanalysis. , (2016).
- Rodenburg, J. M., McCallum, B. C., Nellist, P. D. Experimental tests on double-resolution coherent imaging via STEM. Ultramicroscopy. 48, 304-314 (1993).
- Jiang, Y., et al. Electron ptychography of 2D materials to deep sub-ångström resolution. Nature. 559, 343-349 (2018).
- Yang, Y., et al. Deciphering chemical order/disorder and material properties at the single-atom level. Nature. , (2017).
- Bals, S., Van Aert, S., Van Tendeloo, G., Ávila-Brande, D. Statistical estimation of atomic positions from exit wave reconstruction with a precision in the picometer range. Physics Review Letters. , (2006).
- Kim, Y. M., He, J., Biegalski, M., et al. Probing oxygen vacancy concentration and homogeneity in solid-oxide fuel-cell cathode materials on the subunit-cell level. Nature Mater. 11, (2012).
- Azizi, A., et al. Defect Coupling and Sub-Angstrom Structural Distortions in W1-xMoxS2 Monolayers. Nano Letters. , (2017).
- Reifsnyder Hickey, D., et al. Illuminating Invisible Grain Boundaries in Coalesced Single-Orientation WS2 Monolayer Films. arXiv. , (2020).
- Mukherjee, D., et al. Atomic-scale measurement of polar entropy. Physics Review B. 100, 1-21 (2019).
- Yadav, A. K., et al. Observation of polar vortices in oxide superlattices. Nature. , (2016).
- Yankovich, A. B., et al. Non-rigid registration and non-local principle component analysis to improve electron microscopy spectrum images. Nanotechnology. , (2016).
- Ishizuka, K., Abe, E. Improvement of Spatial Resolution of STEM-HAADF Image by Maximum-Entropy and Richardson-Lucy Deconvolution. EMC. , (2004).
- Ophus, C., Ciston, J., Nelson, C. T. Correcting nonlinear drift distortion of scanning probe and scanning transmission electron microscopies from image pairs with orthogonal scan directions. Ultramicroscopy. , (2016).
- Lee, C. H., et al. Deep learning enabled strain mapping of single-atom defects in two-dimensional transition metal dichalcogenides with sub-picometer precision. Nano Letters. , (2020).
- Savitzky, B. H., et al. Bending and breaking of stripes in a charge ordered manganite. Nature Communications. 8, 1-6 (2017).
- Stone, G., et al. Atomic scale imaging of competing polar states in a Ruddlesden-Popper layered oxide. Natature Communications. 7, 1-9 (2016).
- Mukherjee, D., Miao, L., Stone, G., Alem, N. mpfit: a robust method for fitting atomic resolution images with multiple Gaussian peaks. Advanced Structural and Chemical Imaging. , (2020).
- Wang, Y., Salzberger, U., Sigle, W., Eren Suyolcu, Y., van Aken, P. A. Oxygen octahedra picker: A software tool to extract quantitative information from STEM images. Ultramicroscopy. 168, 46-52 (2016).
- Nord, M., Vullum, P. E., MacLaren, I., Tybell, T., Holmestad, R. Atomap: a new software tool for the automated analysis of atomic resolution images using two-dimensional Gaussian fitting. Advanced Structral and Chemical Imaging. 3, 9(2017).
- De Backer, A., vanden Bos, K. H. W., Vanden Broek, W., Sijbers, J., Van Aert, S. StatSTEM: An efficient approach for accurate and precise model-based quantification of atomic resolution electron microscopy images. Ultramicroscopy. 171, 104-116 (2016).
- Yankovich, A. B., et al. Picometre-precision analysis of scanning transmission electron microscopy images of platinum nanocatalysts. Nature Communications. , (2014).
Reprints and Permissions
Request permission to reuse the text or figures of this JoVE article
Request PermissionExplore More Articles
This article has been published
Video Coming Soon
Copyright © 2025 MyJoVE Corporation. All rights reserved