Determinación del rendimiento cuántico de fotoisomerización de un interruptor de fotos de hidrazona

Resumen

El rendimiento cuántico de fotoisomerización es una propiedad fotofísica fundamental que debe determinarse con precisión en la investigación de los fotointerruptores recientemente desarrollados. Aquí, describimos un conjunto de procedimientos para medir el rendimiento cuántico de fotoisomerización de una hidrazona fotocromática como un modelo de fotointerruptor biestable.

Resumen

Las moléculas orgánicas fotoconmutantes que se someten a transformaciones estructurales impulsadas por la luz son componentes clave para construir sistemas moleculares adaptativos, y se utilizan en una amplia variedad de aplicaciones. En la mayoría de los estudios que emplean fotointerruptores, varias propiedades fotofísicas importantes, como las longitudes de onda máximas de absorción y emisión, el coeficiente de atenuación molar, la vida útil de la fluorescencia y el rendimiento cuántico de fotoisomerización, se determinan cuidadosamente para investigar sus estados electrónicos y procesos de transición. Sin embargo, la medición del rendimiento cuántico de fotoisomerización, la eficiencia de la fotoisomerización con respecto a los fotones absorbidos, en un entorno de laboratorio típico es a menudo complicada y propensa a errores porque requiere la implementación de mediciones y cálculos espectroscópicos rigurosos basados en un método de integración apropiado. Este artículo presenta un conjunto de procedimientos para medir el rendimiento cuántico de fotoisomerización de un fotointerruptor biestable utilizando una hidrazona fotocromática. Anticipamos que este artículo será una guía útil para la investigación de los fotointerruptores biestables que se están desarrollando cada vez más.

Introducción

Las moléculas orgánicas fotocrómicas han atraído una atención considerable en una amplia gama de disciplinas científicas, ya que la luz es un estímulo único que puede alejar a un sistema de su equilibrio termodinámico de forma no invasiva¹. La irradiación de luz con energías apropiadas permite la modulación estructural de fotointerruptores con alta precisión espaciotemporal ^2,3,4. Gracias a estas ventajas, se han desarrollado y utilizado varios tipos de fotointerruptores basados en la isomerización configuracional de los dobles enlaces (por ejemplo, estilbenos, azobencenos, iminas, fumaramidas, tioindigos) y apertura/cierre de anillos (por ejemplo, espiropiropirotranos, ditieniletenos, fulgidas, aductos stenhouse donante-aceptor) como componentes centrales de materiales adaptativos a varias escalas de longitud. Las aplicaciones representativas de los fotointerruptores incluyen materiales fotocrómicos, administración de fármacos, receptores y canales conmutables, almacenamiento de información o energía y máquinas moleculares ^{5,6,7,8,9,10,11,12}. En la mayoría de los estudios que presentan fotointerruptores de nuevo diseño, sus propiedades fotofísicas, como λ_max de absorción y emisión, el coeficiente de atenuación molar (ε), la vida útil de la fluorescencia y el rendimiento cuántico de fotoisomerización se caracterizan a fondo. La investigación de tales propiedades proporciona información clave sobre los estados electrónicos y las transiciones que son cruciales para comprender las propiedades ópticas y el mecanismo de isomerización.

Sin embargo, la medición precisa del rendimiento cuántico de fotoisomerización, el número de eventos de fotoisomerización que ocurrieron dividido por el número de fotones en la longitud de onda de irradiación absorbida por el reactivo, a menudo se complica en un entorno de laboratorio típico debido a varias razones. La determinación del rendimiento cuántico de fotoisomerización generalmente se logra monitoreando el avance de la reacción y midiendo el número de fotones absorbidos durante la irradiación. La principal preocupación es que la cantidad de absorción de fotones por unidad de tiempo cambia progresivamente porque la absorción total por la solución cambia con el tiempo a medida que avanza la reacción fotoquímica. Por lo tanto, el número de reactivos consumidos por unidad de tiempo depende de la sección de tiempo en la que se mide durante la irradiación. Por lo tanto, uno está obligado a estimar el rendimiento cuántico de fotoisomerización que se define diferencialmente.

Un problema más problemático surge cuando tanto el reactivo como el fotoproducto absorben la luz en la longitud de onda de irradiación. En este caso, la isomerización fotoquímica ocurre en ambas direcciones (es decir, una reacción fotorevernsibilizable). Los dos rendimientos cuánticos independientes para las reacciones hacia adelante y hacia atrás no se pueden obtener directamente de la velocidad de reacción observada. La intensidad de luz inexacta también es una causa común de error. Por ejemplo, el envejecimiento del bulbo cambia gradualmente su intensidad; la irradiancia de la lámpara de arco de xenón a 400 nm disminuye en un 30% después de 1000 h de^{operación 14}. La propagación de la luz no colimada hace que la irradiancia incidente real sea significativamente menor que la potencia nominal de la fuente. Por lo tanto, es crucial cuantificar con precisión el flujo efectivo de fotones. Cabe destacar que la relajación térmica de la forma metaestable a temperatura ambiente debe ser lo suficientemente pequeña como para ser ignorada.

Este artículo presenta un conjunto de procedimientos para determinar el rendimiento cuántico de fotoisomerización de un fotointerruptor biestable. Varios fotointerruptores de hidrazona desarrollados por el grupo de Aprahamian, el equipo de investigación pionero en el campo, han estado en el punto de mira gracias a su fotoisomerización selectiva y la notable estabilidad de sus isómeros metaestables 15,16,17. Sus fotointerruptores de hidrazona comprenden dos anillos aromáticos unidos por un grupo de hidrazona, y el enlace C = N sufre isomerización selectiva E / Z tras la irradiación en longitudes de onda apropiadas (Figura 1). Se han incorporado con éxito como componentes móviles de sistemas moleculares dinámicos 18,19,20,21. En este trabajo, preparamos un nuevo derivado de hidrazona que contiene grupos amida e investigamos sus propiedades de fotointerferencia para la determinación del rendimiento cuántico de fotoisomerización.

Protocolo

1. Adquisición del espectro de RMN ^{de 1}H en estado fotoestacionario (PSS)

1. En un tubo de RMN de cuarzo natural que contenga 4,2 mg (0,01 mmol) de interruptor de hidrazona 1, agregue 1,0 ml de dimetilsulfóxido deuterado (DMSO-d ₆). Transfiera la mitad de la solución a otro tubo de RMN.
2. Coloque uno de los tubos de RMN 1 cm delante de una lámpara de arco de xenón equipada con un filtro de paso de banda de 436 nm. Comience la irradiación a la muestra de RMN y registre un espectro de RMN ^{de 1}H todos los días hasta que no haya cambios en los espectros a medida que el interruptor 1 llegue a PSS. Después de llegar a PSS, mantenga el tubo de RMN en la oscuridad a temperatura ambiente y registre el espectro de RMN ^{de 1}H después de 12 h para monitorear el progreso de la relajación térmica.
   NOTA: El interruptor 1 no muestra ningún cambio apreciable en el espectro de RMN ^{de 1}H a temperatura ambiente debido a su naturaleza biestable.
3. Para el otro tubo de RMN, repita el paso 1.2 con un filtro de paso de banda de 340 nm para obtener un espectro de RMN ^{de 1}H en el PSS bajo irradiación de 340 nm.
4. Abra los archivos fid de los espectros de RMN en los PSS con el software de procesamiento de RMN. Integrar un conjunto distintivo de picos (H1: C2 protón de quinolina, H2: protón en posición para el grupo hidrazona, H3: CH₃ de éster etílico) de los distintos isómeros y calcular la relación isomérica (Figura 2).
   NOTA: Las composiciones ([1-Z]:[1-E] relación) bajo irradiación de 436 nm y 340 nm son 8:92 y 82:18, respectivamente.

2. Espectroscopia de absorción UV-Vis en PSS

1. En un vial de vidrio que contenga 12,6 mg (0,03 mmol) de 1, agregue 2 ml de DMSO de grado espectroscopia. Tomar 100 μL de la solución y diluir con 1400 μL de DMSO para hacer 1 mM de solución de 1. Transfiera 20 μL de 1 mM de solución de 1 a una cubeta de cuarzo con una longitud de trayectoria óptica de 1,0 cm y diluya con 1980 μL de DMSO para hacer una solución de 10 μM de 1. Selle la cubeta con un tapón de PTFE y mantenga la muestra en la oscuridad.
2. Prepare otra cubeta de cuarzo que contenga 2 ml de DMSO como muestra en blanco. Mida el espectro UV-Vis de la muestra en blanco para la corrección basal.
3. Coloque la muestra del paso 2,1 1 cm delante de una lámpara de arco de xenón equipada con un filtro de paso de banda de 436 nm. Comience la irradiación a la muestra y mida el espectro UV-Vis cada 2 h hasta que no haya cambios en los espectros a medida que 1 alcanza PSS (Figura 3).
   NOTA: El tiempo necesario para alcanzar PSS para la muestra de espectroscopia UV-Vis es mucho más corto que para la muestra de RMN con una concentración más alta.
4. Repita el paso 2.3 con un filtro de paso de banda de 340 nm para obtener el espectro UV-Vis en el PSS bajo irradiación de 340 nm.
5. Deducir espectros de absorbancia de los 1-Z y 1-E puros utilizando Eq (1) y Eq (2) (Figura 4).
   (1)
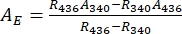   (2)
   Donde R₄₃₆ = la relación de 1-Z en el PSS bajo irradiación de 436 nm; R₃₄₀ = la relación de 1-Z en el PSS bajo irradiación de 340 nm; A₄₃₆ = la absorbancia de 1 en DMSO en el PSS bajo irradiación de 436 nm; A₃₄₀ = la absorbancia de 1 en DMSO en el PSS bajo irradiación de 340 nm.
6. Calcule los coeficientes de atenuación molar de 1-Z y 1-E puros en todas las longitudes de onda dividiendo la absorbancia observada por la concentración de la muestra (10 μM) y la longitud de la trayectoria óptica (1 cm).

3. Estudios cinéticos sobre relajación térmica

1. Calentar el aceite de silicio lleno en un circulador de baño de calefacción a la temperatura deseada (131 °C) y comprobar si la temperatura del baño está estabilizada. Sumerja dos muestras de RMN del paso 1.2 en el baño de calentamiento.
   NOTA: La temperatura y la duración de la calefacción se ajustan en función de la tasa de relajación.
2. Después de 1 h de calentamiento, transfiera los tubos de RMN rápidamente a un baño de hielo seco para pausar la relajación térmica causada por el calor latente (Figura 5).
   NOTA: La temperatura o el tiempo de calentamiento inexactos pueden conducir a un error grave en la estimación de la constante de velocidad.
3. Descongele las muestras de RMN obtenidas del paso 3.2 a temperatura ambiente y asegúrese de que el DMSO se descongele. Registre los espectros de RMN de ¹H de las muestras.
4. Repita los pasos 3.1-3.3 hasta que no haya cambios en los espectros de RMN ^{de 1}H a medida que 1 alcanza el equilibrio termodinámico.
5. Repita los pasos 3.1-3.4 a diferentes temperaturas (134, 137, 140 y 143 °C).
6. Abrir archivos fid de los espectros de RMN obtenidos en el curso del calentamiento a 131 °C. Calcule las relaciones isoméricas promediadas como se describe en el paso 1.4. Calcular la concentración de 1-E (isómero metaestable) en función de la concentración total de la muestra (10 mM) y la relación isomérica.
7. Grafique la concentración promediada de 1-E (C_E) en función del tiempo de calentamiento. Realizar un ajuste exponencial a los datos para obtener la tasa constante de relajación térmica utilizando Eq (3)^15,22 (Figura 6).
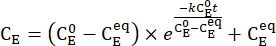   (3)
   Donde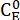 (M) = la concentración de 1-E en el estado inicial; 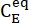(M) = la concentración de 1-E en el equilibrio termodinámico a una temperatura específica; k (^s-1) = la constante de velocidad de relajación térmica a una temperatura específica; t (s) = el tiempo de calentamiento.
8. Repita los pasos 3.6 a 3.7 utilizando los datos obtenidos a diferentes temperaturas.
9. Trazar ln(k) versus y realizar un ajuste lineal según la ecuación de Arrhenius (Eq (4)) para extrapolar la constante de velocidad a temperatura ambiente (Figura 7).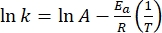
   (4)
   Donde A = el factor preexponencial; E_a (J·^mol-1) = la energía de activación para la relajación térmica; R = la constante de gas ideal (8.3145 J·^{mol-1 K-1}); T (K) = la temperatura absoluta.
10. Calcule la vida media térmica de 1-E a temperatura ambiente utilizando Eq 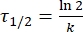(5).
    (5)
    Donde τ_1/2 (s) = la vida media térmica de 1-E a temperatura ambiente; k (^s-1) = la constante de velocidad de relajación térmica a temperatura ambiente obtenida a partir del paso 3.9.
11. Si la constante de velocidad de relajación térmica se estima solo a una sola temperatura, calcule la constante de tasa a temperatura ambiente utilizando la siguiente ecuación de Eyring reorganizada (Eq (6))^18,23.
    (6)
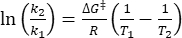    (7)
    Donde (J·^mol-1) = la energía de Gibbs de activación para la relajación térmica; k₁ (^s-1) = la constante de relajación térmica estimada a la temperatura elevada; k₂ (^s-1) = la constante de velocidad de relajación térmica a temperatura ambiente (298,15 K); T₁ (K) = la temperatura absoluta a la que se obtiene k₁ ; (K) = temperatura ambiente (298,15 K).

4. Actinometría de ferrioxalato

NOTA: Todos los procedimientos para la actinometría de ferrioxalato deben realizarse en la luz oscura o >600 nm para evitar la influencia de la luz ambiental.

1. En un vial de vidrio de 20 ml que contenga 29,48 mg (0,06 mmol) de trihidrato de ferrioxalato de potasio, agregue 8 ml de agua desionizada. Añadir 1 mL de H 2 SO₄ acuoso_de0,5 M a la solución de ferrioxalato y diluir a 10 mL con agua desionizada para preparar un ferrioxalato de 0,006 M en solución acuosa de H₂SO_{4 de} 0,05 M.
2. En otro vial de vidrio de 20 ml que contenga 10 mg de 1,10-fenantrolina y 1,356 g de acetato de sodio anhidro, agregue 10 ml de H 2 SO₄ acuoso_de0,5 M para hacer una solución tamponada de fenantrolina al 0,1% (p/v).
3. Transfiera 2 ml de la solución de ferrioxalato de 0,006 M del paso 4,1 a una cubeta de cuarzo con una longitud de trayectoria óptica de 1,0 cm. Selle la cubeta con un tapón de PTFE y mantenga la muestra en la oscuridad.
4. Preparar otra cubeta de cuarzo que contenga 2 mL de 0,05 M acuosos H₂SO₄ como muestra en blanco. Mida la absorbancia UV-Vis de la muestra en blanco para la corrección basal.
5. Mida la absorbancia UV-Vis de la solución de ferrioxalato de 0,006 M. Determinar la fracción de luz absorbida utilizando las absorbancias de la solución de ferrioxalato de 0,006 M a 340 y 436 nm y Eq (8) (Figura 8).
   (8)
   Donde f = la fracción de luz absorbida por 0,006 M de solución de ferrioxalato; A_λ = la absorbancia de la solución de ferrioxalato de 0,006 M en longitud de onda λ.
6. Prepare dos cubetas de cuarzo con una longitud de trayectoria óptica de 1,0 cm y agregue 2 ml de la solución de ferrioxalato de 0,006 M.
7. Coloque una de las muestras del paso 4,6 1 cm delante de la lámpara de arco de xenón equipada con un filtro de paso de banda de 436 nm. Mantenga la otra muestra en la oscuridad. Iniciar la irradiación a la muestra durante 90 s. Después de la irradiación, agregue 0,35 ml de la solución tamponada de fenantrolina al 0,1% y una barra magnética a ambas cubetas, seguido de agitar durante 1 h en la oscuridad para formar un complejo [Fe(phen)₃]²⁺ .
   NOTA: El ferrioxalato se reduce fotoquímicamente a Fe²⁺, seguido de la formación casi cuantitativa del complejo de hierro (II) tris-1,10-fenantrolina.
8. Mida el espectro de absorción UV-Vis de la muestra no irradiada del paso 4.6 para la corrección basal.
9. Mida el espectro de absorción UV-Vis de la muestra irradiada a partir del paso 4.7.
10. Repita los pasos 4.6-4.9 con un filtro de paso de banda de 340 nm (Figura 9).
    NOTA: Una vez que la muestra de ferrioxalato se expone a la luz, la muestra no se puede reutilizar.
11. Calcule el flujo de fotones molares que llega a la cubeta utilizando Eq 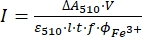(9).
    (9)
    Donde I (mol·^s-1) = el flujo de fotones molares que llega a la cubeta; ΔA₅₁₀ = la diferencia de absorbancia a 510 nm entre las muestras no irradiadas e irradiadas; V = el volumen total de la solución (2,35 ml); ε₅₁₀ = el coeficiente de atenuación molar del complejo [Fe(phen)₃]²⁺ (11100 ^{M-1 cm-1})²⁴; I = la longitud de la trayectoria óptica de la cubeta de cuarzo (1,0 cm); t = tiempo de irradiación (90 s); f = la fracción absorbida de luz obtenida a partir del paso 4.5; Φ_Fe³⁺ = el rendimiento cuántico de la fotorreducción de Fe³⁺ a Fe²⁺ (1,22 para 340 nm, 1,11 para 436 nm)²⁵.

5. Determinación del rendimiento cuántico de fotoisomerización

1. Prepare una cubeta de cuarzo con una longitud de trayectoria óptica de 1,0 cm que contenga 2 ml de DMSO como muestra en blanco. Mida la absorbancia UV-Vis de la muestra en blanco para la corrección basal.
2. Preparar una cubeta de cuarzo con una longitud de trayectoria óptica de 1,0 cm que contenga 2 mL de solución de 10 μM de 1 en DMSO obtenida a partir del paso 2.4 (enriquecido con Z). Selle las cubetas con un tapón de PTFE.
3. Coloque la muestra del paso 5,2 1 cm delante de la lámpara de arco de xenón equipada con un filtro de paso de banda de 436 nm. Iniciar la irradiación a 436 nm a la muestra y medir el espectro de absorción UV-Vis con diferentes intervalos hasta que no haya ningún cambio en los espectros a medida que 1 alcanza PSS (Figura 10).
   NOTA: La configuración de irradiación debe ser exactamente la misma que la utilizada para la medición del flujo de fotones molares. El intervalo de irradiación debe ajustarse en función de la tasa de fotoisomerización. En general, 15-20 puntos de datos antes de llegar a PSS son adecuados.
4. Preparar una cubeta de cuarzo con una longitud de trayectoria óptica de 1,0 cm que contenga 2 ml de solución de 10 μM de 1 en DMSO obtenida a partir del paso 2.3 (enriquecido con E). Selle las cubetas con un tapón de PTFE.
5. Reemplace el filtro de paso de banda de 436 nm por el filtro de paso de banda de 340 nm y repita el paso 5.3 para la muestra obtenida del paso 5.4.
6. Calcular el factor fotocinético F(t) utilizando las absorbancias observadas a partir del paso 5.3 y Eq (10)²⁶.
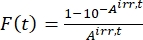   (10)
   Donde A^irr,t = la absorbancia en la longitud de onda de irradiación en el tiempo t.
7. Calcular el rendimiento pseudocuántico Q utilizando los valores del factor fotocinético obtenidos del paso 5.6 y Eq (11)²⁷.
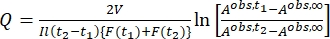   (11)
   Donde Q (^{M-1 cm-1}) = el rendimiento pseudo cuántico definido como ;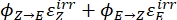 ; V(L) = el volumen de la muestra; I (mol·^s-1) = el flujo de fotones molares que llega a la cubeta; l (cm) = la longitud de la trayectoria óptica; t₁, t₂ (s) = los dos puntos de tiempo consecutivos de irradiación; F(t₁), F(t₂) = los factores fotocinéticos en el tiempo t₁ y t₂, respectivamente; A^obs,t₁, A^obs,t₂, A^obs,∞ = las absorbancias en longitud de onda específica en el tiempo , t₁ y t₂ en PSS, respectivamente.
   NOTA: Se recomienda el uso de absorbancias a λ_máximo de 1-Z para mayor precisión.
8. Calcule el valor promediado del rendimiento pseudo cuántico utilizando los primeros diez puntos de datos.
9. Calcule los rendimientos cuánticos unidireccionales para las fotoisomerizaciones de Z a E y E a Z utilizando Eq (12) y Eq (13).
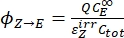   (12)
   (13)
   Donde Φ_Z→E, Φ_E→Z = los rendimientos cuánticos unidireccionales para los procesos de fotoisomerización Z-to-E y E-to-Z, respectivamente; , 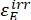(^{M-1 cm-1}) = los coeficientes de atenuación molar de 1-Z y 1-E en la longitud de onda de irradiación; 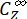, 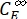(M) = las concentraciones de 1-Z y 1-E en PSS, respectivamente; C_tot (M) = la concentración total de 1.
10. Repita los pasos 5.6-5.9 utilizando los datos obtenidos del paso 5.5 para el cálculo de los rendimientos cuánticos de fotoisomerización unidireccional bajo irradiación a 340 nm.

Resultados

Tras la irradiación de 1 en un tubo de RMN con luz de 436 nm (Z:E = 54:46 en el estado inicial), la proporción de 1-E aumenta debido a la isomerización dominante de Z a E del enlace hidrazona C=N (Figura 1). La relación isomérica se puede obtener fácilmente a partir de las intensidades de señal relativas de distintos isómeros en el espectro de RMN ^{de 1}H (Figura 2). Después ...

Discusión

Se han desarrollado varias estrategias para ajustar las propiedades espectrales y de conmutación de los fotointerruptores, y el registro de fotointerruptores se está expandiendo rápidamente²⁸. Por lo tanto, es crucial determinar correctamente sus propiedades fotofísicas, y anticipamos que los métodos resumidos en este artículo serán una guía útil para los experimentadores. Siempre que la tasa de relajación térmica sea muy lenta a temperatura ambiente, la medición de las composiciones d...

Materiales

Name	Company	Catalog Number	Comments
1,10-phenanthroline	Sigma-Aldrich	131377-2.5G
340 nm bandpass filter, 25 mm diameter, 10 nm FWHM	Edmund Optics	#65-129
436 nm bandpass filter, 25 mm diameter, 10 nm FWHM	Edmund Optics	#65-138
Anhydrous sodium acetate	Alfa aesar	A13184.30
Dimethyl sulfoxide	Samchun	D1138	HPLC grade
Dimethyl sulfoxide-d6	Sigma-Aldrich	151874-25g
Gemini 2000; 300 MHz NMR spectrometer	Varian
H2SO4	Duksan	235
Heating bath	JeioTech	CW-05G
MestReNova 14.1.1	Mestrelab Research S.L., https://mestrelab.com/
Natural quartz NMR tube	Norell	S-5-200-QTZ-7
Potassium ferrioxalate trihydrate	Alfa aesar	31124.06
Quartz absorption cell	Hellma	HE.110.QS10
UV-VIS spectrophotometer	Scinco	S-3100
Xenon arc lamp	Thorlabs	SLS205	Fiber adapter was removed