14.4 : Gravity between Spherical Bodies
Newton's law of gravitation describes the gravitational force between any two point masses. However, for extended spherical objects like the Earth, the Moon, and other planets, the law holds with an assumption that masses of spherical objects are concentrated at their respective centers.
This assumption can be proved easily by showing that the expression for gravitational potential energy between a hollow sphere of mass (M) and a point mass (m) is the same as it would be for a pair of extended spherical solid objects.
Consider a tiny ring of width Rdϕ and mass dM on the surface of a spherical hollow sphere at a distance s from the point mass as shown in Figure 1(a).
The gravitational potential energy between the ring and the point mass (m) is expressed as:
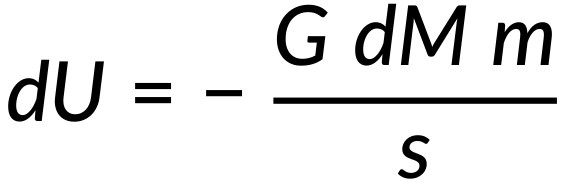
The ratio of the ring's mass to the entire shell's mass is equal to the ratio of the ring's area to the shell's area. Therefore, on simplification, the ring's mass can be expressed as:
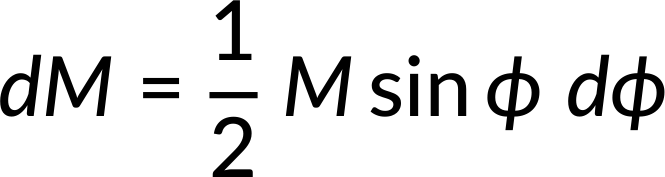
Now, the square of distance (s) can be expressed as the sum of squares of the triangle's other two sides, as seen in Figure 1(b).
Simplifying further and taking differentials on either side,
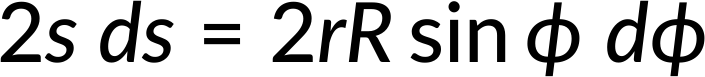
Considering the entire shell, s can vary between r − R and r + R, as seen in Figure 1(c).
Therefore, substituting dM and s in the potential energy equation and integrating within the limits of r − R to r + R, the relation obtained is the potential energy between point masses m and M at a distance r.
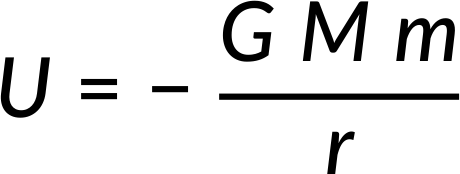
Therefore, the assumption is proven.
Since force is a derivative of potential energy, the assumption holds for gravitational forces between two spherically solid objects like the Earth and the Moon. Therefore, Newton's law of gravitation can be used to determine the gravitational force between the Earth and the Moon, and the Earth and the Sun.
Bölümden 14:

Now Playing
14.4 : Gravity between Spherical Bodies
Kütle Çekimi
8.3K Görüntüleme Sayısı

14.1 : Yerçekimi
Kütle Çekimi
6.3K Görüntüleme Sayısı

14.2 : Newton'un Yerçekimi Yasası
Kütle Çekimi
12.5K Görüntüleme Sayısı

14.3 : Küresel simetrik kütleler arasındaki yerçekimi
Kütle Çekimi
854 Görüntüleme Sayısı

14.5 : Azaltılmış Kütle Koordinatları: İzole İki Cisim Problemi
Kütle Çekimi
1.2K Görüntüleme Sayısı

14.6 : Dünyadaki Yerçekimi Nedeniyle İvme
Kütle Çekimi
10.6K Görüntüleme Sayısı

14.7 : Diğer Gezegenlerde Yerçekimi Nedeniyle İvme
Kütle Çekimi
4.1K Görüntüleme Sayısı

14.8 : Görünür Ağırlık ve Dünya'nın Dönüşü
Kütle Çekimi
3.5K Görüntüleme Sayısı

14.9 : Dünya Yüzeyine Yakın Yerçekimi Nedeniyle İvmedeki Değişim
Kütle Çekimi
2.4K Görüntüleme Sayısı

14.10 : Yerçekiminden Kaynaklanan Potansiyel Enerji
Kütle Çekimi
5.4K Görüntüleme Sayısı

14.11 : Süperpozisyon İlkesi ve Yerçekimi Alanı
Kütle Çekimi
1.3K Görüntüleme Sayısı

14.12 : Kurtulma hızı
Kütle Çekimi
5.6K Görüntüleme Sayısı

14.13 : Uydular için Dairesel Yörüngeler ve Kritik Hız
Kütle Çekimi
2.9K Görüntüleme Sayısı

14.14 : Dairesel yörüngedeki bir uydunun enerjisi
Kütle Çekimi
2.2K Görüntüleme Sayısı

14.15 : Kepler'in Gezegensel Hareketin Birinci Yasası
Kütle Çekimi
3.9K Görüntüleme Sayısı
See More
JoVE Hakkında
Telif Hakkı © 2020 MyJove Corporation. Tüm hakları saklıdır