14.4 : Gravity between Spherical Bodies
Newton's law of gravitation describes the gravitational force between any two point masses. However, for extended spherical objects like the Earth, the Moon, and other planets, the law holds with an assumption that masses of spherical objects are concentrated at their respective centers.
This assumption can be proved easily by showing that the expression for gravitational potential energy between a hollow sphere of mass (M) and a point mass (m) is the same as it would be for a pair of extended spherical solid objects.
Consider a tiny ring of width Rdϕ and mass dM on the surface of a spherical hollow sphere at a distance s from the point mass as shown in Figure 1(a).
The gravitational potential energy between the ring and the point mass (m) is expressed as:
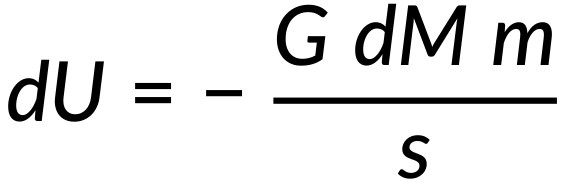
The ratio of the ring's mass to the entire shell's mass is equal to the ratio of the ring's area to the shell's area. Therefore, on simplification, the ring's mass can be expressed as:
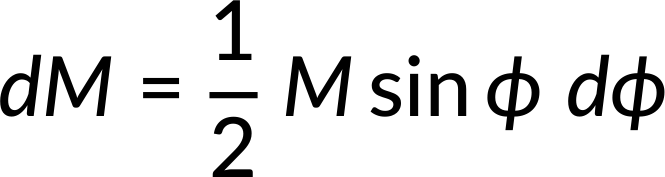
Now, the square of distance (s) can be expressed as the sum of squares of the triangle's other two sides, as seen in Figure 1(b).
Simplifying further and taking differentials on either side,
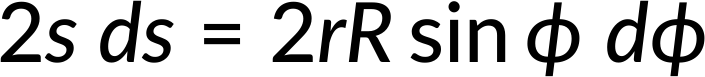
Considering the entire shell, s can vary between r − R and r + R, as seen in Figure 1(c).
Therefore, substituting dM and s in the potential energy equation and integrating within the limits of r − R to r + R, the relation obtained is the potential energy between point masses m and M at a distance r.
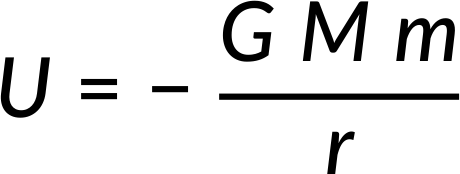
Therefore, the assumption is proven.
Since force is a derivative of potential energy, the assumption holds for gravitational forces between two spherically solid objects like the Earth and the Moon. Therefore, Newton's law of gravitation can be used to determine the gravitational force between the Earth and the Moon, and the Earth and the Sun.
Dal capitolo 14:

Now Playing
14.4 : Gravity between Spherical Bodies
Gravitation
8.3K Visualizzazioni

14.1 : Gravitazione
Gravitation
6.2K Visualizzazioni

14.2 : Legge di Gravitazione di Newton
Gravitation
12.4K Visualizzazioni

14.3 : Gravitazione tra masse sfericamente simmetriche
Gravitation
850 Visualizzazioni

14.5 : Coordinate di massa ridotte: problema isolato a due corpi
Gravitation
1.2K Visualizzazioni

14.6 : Accelerazione dovuta alla gravità sulla Terra
Gravitation
10.6K Visualizzazioni

14.7 : Accelerazione dovuta alla gravità su altri pianeti
Gravitation
4.1K Visualizzazioni

14.8 : Peso apparente e rotazione terrestre
Gravitation
3.5K Visualizzazioni

14.9 : Variazione dell'accelerazione dovuta alla gravità vicino alla superficie terrestre
Gravitation
2.4K Visualizzazioni

14.10 : Energia potenziale dovuta alla gravitazione
Gravitation
5.4K Visualizzazioni

14.11 : Il principio di sovrapposizione e il campo gravitazionale
Gravitation
1.3K Visualizzazioni

14.12 : Velocità di fuga
Gravitation
5.6K Visualizzazioni

14.13 : Orbite circolari e velocità critica per i satelliti
Gravitation
2.9K Visualizzazioni

14.14 : Energia di un satellite in orbita circolare
Gravitation
2.2K Visualizzazioni

14.15 : La prima legge del moto planetario di Keplero
Gravitation
3.9K Visualizzazioni
See More