A subscription to JoVE is required to view this content. Sign in or start your free trial.
Research Article
طريقة التحكم شبه النشطة العشوائية للهيكل على أساس المخمدات المغناطيسية مع مراعاة التأخير الزمني
In This Article
Summary
تم اقتراح طريقة التحكم شبه النشط العشوائي الأمثل مع تعويض التأخير الزمني (SOSC-PSO) في هذه الورقة ، والتي تم تصميمها للحفاظ على موثوقية الهياكل التي يتم التحكم فيها بواسطة مخمدات MR.
Abstract
يواجه استخدام المخمدات المغناطيسية (MR) في أنظمة التحكم شبه النشطة تحديا رئيسيا: التأخير الزمني الناجم عن عمليات التغذية الراجعة ، مما يقلل من موثوقية هياكل الهندسة المدنية تحت الإثارة العشوائية. تقترح هذه الورقة طريقة التحكم شبه النشط العشوائي الأمثل مع تعويض التأخير الزمني (SOSC-PSO) ، والاستفادة من نظرية التحكم الأمثل العشوائي الفيزيائي (PSO) لمعالجة هذه المشكلة والحفاظ على الموثوقية الهيكلية. تستمد الطريقة المقترحة قوة التحكم شبه النشطة كدالة لكل من الحالات الحالية والسابقة ، مما يعوض التأخيرات الزمنية في عملية التحكم. لتحسين فعالية التحكم ، يتم ضبط المعلمات الرئيسية بناء على معيار موثوقية النظام. تظهر تحليلات التحقق من الصحة على هياكل أحادية الدرجة من الحرية ومتعددة درجات الحرية تحت الإثارة الزلزالية العشوائية أن التأخير الزمني يضعف بشكل كبير أداء مخمدات MR. ومع ذلك ، فإن طريقة SOSC-PSO مع تعويض تأخير الوقت تعمل بشكل كبير على تحسين فعالية التحكم ، ومع المعلمات المحسنة ، فإنها تعزز موثوقية نظام التحكم الهيكلي بما يتجاوز الطرق دون تحسين المعلمات.
Introduction
لا يزال تحسين أداء الهياكل الهندسية في مواجهة الأحداث الكارثية ، مثل الزلازل والرياح الشديدة ، مصدر قلق أساسي داخل مجتمع الهندسة المدنية. ثبت أن التحكم الهيكلي ، وهو تقنية فعالة لتقليل الاهتزازات ، يعزز سلامة ووظائف هذه الهياكل1،2،3. على مدى العقود القليلة الماضية ، تم تطوير العديد من الأساليب والتقنيات المتقدمة لهذا الغرض. يمكن تصنيف هذه الطرق على نطاق واسع إلى أربع فئات بناء على نوع الطاقة المستخدمة لقيادة أجهزة التحكم: أنظمة التحكم النشطة وشبه النشطة والسلبية والهجينة4،5،6،7.
في التحكم النشط ، يتم تطبيق قوة التحكم المطلوبة مباشرة من خلال أجهزة التحكم ، مما يتطلب كمية كبيرة من الطاقة8،9،10. من ناحية أخرى ، يتضمن التحكم شبه النشط ضبط خصائص أجهزة التحكم (مثل التخميد أو الصلابة) بناء على إشارات التحكم ، مما يتطلب طاقة أقل بكثير مقارنة بالأنظمةالنشطة 11. على النقيض من ذلك ، يعتمد التحكم السلبي على تبديد الطاقة دون أي مدخلات طاقة خارجية في النظام12،13،14. تجمع الأنظمة الهجينة بين ميزات استراتيجيات التحكم النشط / شبه النشط والسلبي لتحقيق أداء أكثر فعالية15. من بين هذه الأساليب ، تعتبر التحكم شبه النشط واعدة بشكل خاص بسبب توازن استهلاكه المنخفض للطاقة والكفاءة العالية16 ، 17 ، 18. يعتبر المثبط المغناطيسي (MR) ، بخصائصه الديناميكية الفائقة ، أحد أكثر أجهزة التحكم شبه النشطة فعالية19،20،21،22.
ومع ذلك ، ينشأ تحد في أنظمة التحكم شبه النشطة التي تستخدم مخمدات MR ، حيث يؤدي منطق التغذية الراجعة حتما إلى تأخيرات زمنيا. عادة ما تكون هذه التأخيرات ناتجة عن عدة عوامل23،24،25 ، بما في ذلك: (1) الحصول على بيانات المستشعر ومعالجتها ، (2) حساب قوة التحكم المطلوبة بواسطة وحدة التحكم26 ، (3) نقل الإشارة من خلال محولات الطاقة إلى مخمدات MR27 ، و (4) توليد القوة الفعلية بواسطة مخمدات MR نفسها28. يمكن أن تؤدي مثل هذه التأخيرات الزمنية إلى تناقضات بين قوة التحكم المنتجة والقوة التي يتوقعها الهيكل ، مما يضر بشكل كبير بفعالية التحكم29. لسوء الحظ ، فإن معظم خوارزميات التحكم الحالية لمخمدات MR لا تأخذ في الحسبان هذه التأخير.
بالإضافة إلى ذلك ، نظرا للعشوائية المتأصلة في الأحداث الكارثية ، يجب أن تكون أي خوارزمية تحكم شبه نشطة فعالة قادرة على الحفاظ على الأداء في ظل الإثارة العشوائية. تم استكشاف طريقة التحكم الغوسية التربيعية الخطية (LQG) ، وهي تقنية تحسين عشوائية كلاسيكية ، للتخفيف من الاهتزازات في الهياكل المجهزة بمخمدات MR. على سبيل المثال ، Dyke et al. اقترح استراتيجية تحكم مثالية مقطوعة LQG لتحسين الاستجابة الزلزالية للهياكل المزودة بمخمدات MR ، باستخدام ردود فعل التسارع30. Ying et al. قدم استراتيجية تحكم عشوائية مثالية شبه نشطة غير مقطوعة للهياكل غير الخطية مع مخمدات MR ، تتضمن متوسط عشوائي وتقنيات البرمجةالديناميكية 31. طبقت دراسات أخرى التحكم في LQG القائم على النموذج لتعزيز الأداء الزلزالي للمباني المعزولةبالقاعدة 19 وحللت فعاليته في تخفيف الاهتزاز في أبراج توربينات الرياح32. ومع ذلك ، فإن طرق LQG الكلاسيكية ، التي تفترض ضوضاء غاوسية بيضاء ، ليست مناسبة تماما لنمذجة الطبيعة غير الثابتة وغير الغوسية للإثارة في العالم الحقيقي مثل الزلازل أو الرياح القوية. لمعالجة هذا الأمر ، تم تطوير مفهوم التحكم الأمثل العشوائي القائم على الأساس المادي (PSO)33 ، 34 ، والذي يتغلب على قيود طرق LQG التقليدية ويوفر إطارا أكثر دقة للتعامل مع الإثارة العشوائيةالمتنوعة 35. أظهرت الدراسات أن التحكم الأمثل العشوائي شبه النشط القائم على PSO يحسن بشكل كبير تخفيف الاهتزاز لكل من الهياكل الخطية وغير الخطية المعرضة لقوى زلزاليةعشوائية 36.
وبالتالي ، هناك حاجة ملحة لطريقة تحكم شبه نشطة قوية تعوض التأخيرات الزمنية ، مما يعزز موثوقية الهياكل التي تتحكم فيها مخمدات MR25،37. علاوة على ذلك ، لضمان أداء التحكم الأمثل في ظل الإثارة العشوائية ، من الضروري تحسين المعلمات الحرجة لطريقة التحكم المقترحة باستخدام نهج قائم على الموثوقية. لذلك ، تم اقتراح طريقة التحكم شبه النشط العشوائي الأمثل مع تعويض التأخير الزمني (SOSC-PSO) في هذه الورقة لتحسين موثوقية الهياكل ذات مخمدات MR.
Protocol
1. طريقة التحكم شبه النشطة العشوائية المثلى
نظرا لأن تأثير التحكم في مخمد MR يتأثر بشكل كبير بالتأخير الزمني الحتمي ، فقد تم تطوير طريقة تحكم شبه نشطة مع خوارزمية تعويض تأخير الوقت لزيادة أداء الهيكل المتحكم فيه. إلى جانب ذلك ، فإن العشوائية المتأصلة في الإثارة الخارجية تسبب عدم اليقين الواضح في الاستجابات الديناميكية. تم إدخال التحكم في PSO لتحسين المعلمات الهامة للطريقة المقترحة لضمان موثوقية نظام التحكم في الهيكل.
1.1 خوارزمية التعويض للتحكم شبه النشط
دون فقدان العمومية ، ضع في اعتبارك هيكل n-Degree-Freedoms (n-DOF) الذي تسيطر عليه مخمدات MR مع تأخير زمني ، والتي يتم إعطاء معادلة الحركة المعرضة للإثارة العشوائية من خلال:
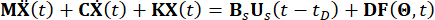 (1)
(1)
حيث  تمثل مصفوفات الكتلة n x n والتخميد والصلابة للهيكل ، على التوالي ؛ n يمثل عدد درجات حرية الهيكل الخاضع للرقابة. يتم تمثيل متجهات الإزاحة والسرعة والتسارع للهيكل ب
تمثل مصفوفات الكتلة n x n والتخميد والصلابة للهيكل ، على التوالي ؛ n يمثل عدد درجات حرية الهيكل الخاضع للرقابة. يتم تمثيل متجهات الإزاحة والسرعة والتسارع للهيكل ب 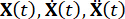 ، على التوالي. تمثل النقطة الصغيرة والنقطتان فوق الرموز مشتقات المرة الأولى والثانية. يمثل Us (t - tD) المتجه r الأبعاد لقوة التحكم المتأخرة زمنيا لمخمدات MR ، ويمثل r عدد المخمدات ؛ ر يمثل الوقت. يشير tD إلى التأخير الزمني ، الذي يفترض أنه موحد عبر جميع المخمدات في هذه الدراسة ، حيث
، على التوالي. تمثل النقطة الصغيرة والنقطتان فوق الرموز مشتقات المرة الأولى والثانية. يمثل Us (t - tD) المتجه r الأبعاد لقوة التحكم المتأخرة زمنيا لمخمدات MR ، ويمثل r عدد المخمدات ؛ ر يمثل الوقت. يشير tD إلى التأخير الزمني ، الذي يفترض أنه موحد عبر جميع المخمدات في هذه الدراسة ، حيث 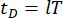 ، مع الرقم
، مع الرقم 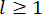 المتكامل هنا ، ويشير
المتكامل هنا ، ويشير 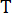 إلى فترة أخذ العينات.
إلى فترة أخذ العينات. 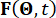 يمثل المتجه ذو الأبعاد p للإثارة العشوائية ، ويمثل
يمثل المتجه ذو الأبعاد p للإثارة العشوائية ، ويمثل  متجه المعلمة العشوائية التي تميز العشوائية المرتبطة بالإثارة الخارجية. يعتمد بعد
متجه المعلمة العشوائية التي تميز العشوائية المرتبطة بالإثارة الخارجية. يعتمد بعد  على النموذج المستخدم في الإثارة الخارجية ولكنه لا يرتبط بالدرجات الميكانيكية للحرية للهيكل. Bs و D هما مصفوفتان n x r و n x p تحدد مواقع المخمدات والإثارة الخارجية ، على التوالي. في تمثيل مساحة الحالة ، المعادلة (1) مكتوبة على النحو التالي:
على النموذج المستخدم في الإثارة الخارجية ولكنه لا يرتبط بالدرجات الميكانيكية للحرية للهيكل. Bs و D هما مصفوفتان n x r و n x p تحدد مواقع المخمدات والإثارة الخارجية ، على التوالي. في تمثيل مساحة الحالة ، المعادلة (1) مكتوبة على النحو التالي:
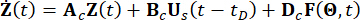 (2)
(2)
حيث 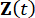 يمثل متجه الحالة 2n الأبعاد ؛
يمثل متجه الحالة 2n الأبعاد ؛ 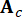 يمثل مصفوفة نظام 2n x 2n ؛
يمثل مصفوفة نظام 2n x 2n ؛ 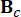 يمثل مصفوفة موقع 2n x r لمخمدات MR ؛
يمثل مصفوفة موقع 2n x r لمخمدات MR ؛ 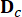 يمثل مصفوفة موقع 2n × p للإثارة الخارجية. يتم التعبير عن هذه المعلمات على النحو التالي:
يمثل مصفوفة موقع 2n × p للإثارة الخارجية. يتم التعبير عن هذه المعلمات على النحو التالي:
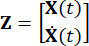 ،
، 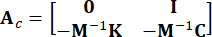 ،
،  ، (
، (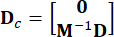 3)
3)
حيث 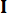 يشير إلى مصفوفة هوية بنفس ترتيب
يشير إلى مصفوفة هوية بنفس ترتيب 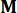 . ولتسهيل الحساب، يمكن التعبير عن معادلة فضاء الحالة المستمرة المعادلة (2) في شكل منفصل على النحو التالي:
. ولتسهيل الحساب، يمكن التعبير عن معادلة فضاء الحالة المستمرة المعادلة (2) في شكل منفصل على النحو التالي:
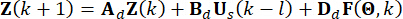 (4)
(4)
حيث يتم تبسيط النقطة 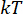 الزمنية ك
الزمنية ك 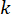 . و
. و  ،
، 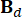 ،
، 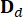 تشير إلى مصفوفات 2n x 2n و 2n x r و 2n x p ، والتي يتم التعبير عنها على النحو التالي:
تشير إلى مصفوفات 2n x 2n و 2n x r و 2n x p ، والتي يتم التعبير عنها على النحو التالي:
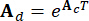 ،
،  (
(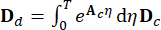 5)
5)
حيث 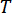 يشير إلى فترة أخذ العينات.
يشير إلى فترة أخذ العينات.
لتحقيق فعالية مماثلة للتحكم النشط ، يقترح طريقة تحكم بسيطة وفعالة تستند إلى خوارزمية Hrovat 38 للتحكم القائم على مخمد MR مع تأخير زمني:
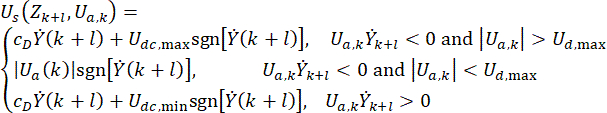 (6)
(6)
حيث  يمثل إشارة قوة التحكم شبه النشطة في النقطة الزمنية \
يمثل إشارة قوة التحكم شبه النشطة في النقطة الزمنية \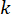 لمخمد MR ؛
لمخمد MR ؛ 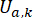 يمثل قوة التحكم النشطة المرجعية مع تعويض التأخر الزمني ؛
يمثل قوة التحكم النشطة المرجعية مع تعويض التأخر الزمني ؛  يمثل قوة التخميد القصوى لمخمد MR ، وهو قابل للتغيير ؛
يمثل قوة التخميد القصوى لمخمد MR ، وهو قابل للتغيير ؛ 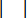 يمثل رمز عملية القيمة المطلقة ؛
يمثل رمز عملية القيمة المطلقة ؛ 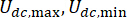 تمثل الحد الأقصى والحد الأدنى من القوى الكولومبية لمخمد MR ؛
تمثل الحد الأقصى والحد الأدنى من القوى الكولومبية لمخمد MR ؛  يمثل معامل التخميد اللزج ؛
يمثل معامل التخميد اللزج ؛ 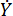 يمثل مدخلات السرعة في مخمد MR ، وهي سرعة حركة المكبس بالنسبة لأسطوانة المثبط. في المعادلة (6)،
يمثل مدخلات السرعة في مخمد MR ، وهي سرعة حركة المكبس بالنسبة لأسطوانة المثبط. في المعادلة (6)،  تمثل المعلمات المصممة لمخمد MR.
تمثل المعلمات المصممة لمخمد MR.
المعادلة (6) يبين حساب قوة التحكم شبه النشطة لمخمد MR مع تأخير زمني. من الملاحظ أن قوة  التحكم شبه النشطة ، في الخطوة
التحكم شبه النشطة ، في الخطوة  الزمنية في المعادلة (4) ، يتم حسابها بناء على قوة
الزمنية في المعادلة (4) ، يتم حسابها بناء على قوة  التحكم النشطة في الخطوة
التحكم النشطة في الخطوة  الزمنية ومتغير
الزمنية ومتغير 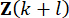 الحالة في الخطوة
الحالة في الخطوة  الزمنية منذ
الزمنية منذ 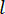 تأخير الخطوات الزمنية. للحصول على قوة
تأخير الخطوات الزمنية. للحصول على قوة  التحكم النشطة ، يتم إنشاء وظيفة التكلفة التقليدية من قبل
التحكم النشطة ، يتم إنشاء وظيفة التكلفة التقليدية من قبل
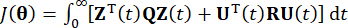 (7)
(7)
حيث  يمثل مصفوفة الترجيح شبه المحددة الموجبة المتماثلة 2n × 2n لحالة النظام ؛
يمثل مصفوفة الترجيح شبه المحددة الموجبة المتماثلة 2n × 2n لحالة النظام ؛  يمثل مصفوفة الترجيح المحددة الموجبة المتماثلة r x r لقوة التحكم. يلاحظ أن الإثارة الخارجية لا تذكر. في الواقع ، بناء على المعادلة (7) ، يمكن لنظام التحكم في الهيكل تحقيق تأثير التحكم الأمثل مهما كان نوع الإثارة الخارجية. كصيغة منفصلة ، يتم التعبير عن المعادلة (7) على أنها39:
يمثل مصفوفة الترجيح المحددة الموجبة المتماثلة r x r لقوة التحكم. يلاحظ أن الإثارة الخارجية لا تذكر. في الواقع ، بناء على المعادلة (7) ، يمكن لنظام التحكم في الهيكل تحقيق تأثير التحكم الأمثل مهما كان نوع الإثارة الخارجية. كصيغة منفصلة ، يتم التعبير عن المعادلة (7) على أنها39:
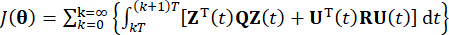 (8)
(8)
يؤدي تقليل دالة  التكلفة إلى مشكلة القيمة القصوى الشرطية ، ويتم حساب قوة
التكلفة إلى مشكلة القيمة القصوى الشرطية ، ويتم حساب قوة  التحكم النشطةبمقدار 25:
التحكم النشطةبمقدار 25:
 (9)
(9)
حيث 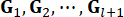 تشير إلى مكاسب التحكم لمتغير
تشير إلى مكاسب التحكم لمتغير 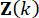 الحالة في الخطوة
الحالة في الخطوة  الزمنية وقوة
الزمنية وقوة 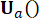 التحكم النشطة في الخطوة
التحكم النشطة في الخطوة 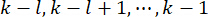 الزمنية ، والتي يتم تحديدها بواسطة مصفوفات
الزمنية ، والتي يتم تحديدها بواسطة مصفوفات 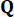 الترجيح و
الترجيح و 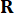 37. منذ التأخير الزمني الحتمي ، يتم عمل قوة
37. منذ التأخير الزمني الحتمي ، يتم عمل قوة 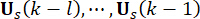 التحكم التي تم الحصول عليها على الهيكل في نقاط
التحكم التي تم الحصول عليها على الهيكل في نقاط 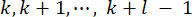 زمنية . لذلك ، فإن قوة التحكم النشطة في المعادلة (9) يتم حسابها من خلال:
زمنية . لذلك ، فإن قوة التحكم النشطة في المعادلة (9) يتم حسابها من خلال:
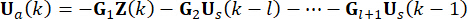 (10)
(10)
من أجل وضوح المفهوم ، يتم التعبير عن قوة التحكم شبه النشطة في المعادلة (10) على النحو التالي بناء على المعادلة (6):
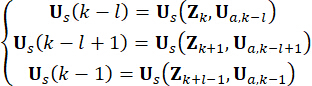 (11)
(11)
حيث  يشير إلى قوة التحكم النشطة في نقطة
يشير إلى قوة التحكم النشطة في نقطة  زمنية. الاستعاضة عن المعادلة (11) بالمعادلة (10) ،
زمنية. الاستعاضة عن المعادلة (11) بالمعادلة (10) ،
 (12)
(12)
ملاحظة: جميع قيم الحالة  من النقطة
من النقطة  الزمنية إلى
الزمنية إلى 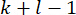 مطلوبة لحساب
مطلوبة لحساب  . لذلك ، يتم تقديم طريقة التنبؤ بالحالة التالية40.
. لذلك ، يتم تقديم طريقة التنبؤ بالحالة التالية40.
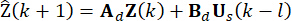 (13)
(13)
حيث  يشير إلى المتغير المتوقع. من خلال تكرار المعادلة (13) ، يتم حساب الحالة
يشير إلى المتغير المتوقع. من خلال تكرار المعادلة (13) ، يتم حساب الحالة  في
في  . يتم التعبير عن قوة التحكم النشطة Ua (k) على النحو التالي:
. يتم التعبير عن قوة التحكم النشطة Ua (k) على النحو التالي:
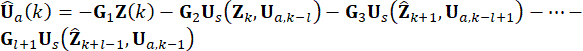 (14)
(14)
يمكن الحصول على قوة التحكم شبه النشطة من خلال الجمع بين Eqs. (6) و (12) و (13).
1.2 تحليل الموثوقية لنظام التحكم في الهيكل
وفقا لمبدأ الحفاظ على الاحتمالات ، فإن النظام 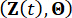 المعزز والبنية
المعزز والبنية 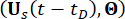 مع مخمدات MR محفوظة من حيث الاحتمالات ، ويتم التحكم فيهما بواسطة معادلات تطور كثافة الاحتمالات المعممة التالية (GDEEs)38:
مع مخمدات MR محفوظة من حيث الاحتمالات ، ويتم التحكم فيهما بواسطة معادلات تطور كثافة الاحتمالات المعممة التالية (GDEEs)38:
 (15)
(15)
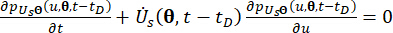 (16)
(16)
حيث  ،
،  تشير إلى المكونات المقابلة لحالة النظام وقوة التحكم شبه النشطة مع تأخير زمني ، على التوالي ؛
تشير إلى المكونات المقابلة لحالة النظام وقوة التحكم شبه النشطة مع تأخير زمني ، على التوالي ؛ 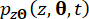 وتشير
وتشير  إلى وظائف كثافة الاحتمال المشترك لأنظمة
إلى وظائف كثافة الاحتمال المشترك لأنظمة 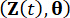 العينة المعززة و
العينة المعززة و 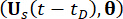 ، على التوالي ؛
، على التوالي ؛ 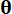 تشير إلى العينة داخل مساحة العينة ؛
تشير إلى العينة داخل مساحة العينة ؛ 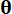
 و
و  ) تشير إلى المشتقات الجزئية الزمنية من الدرجة الأولى لحالة النظام ومكونات قوة التحكم شبه النشطة ، على التوالي. وظائف
) تشير إلى المشتقات الجزئية الزمنية من الدرجة الأولى لحالة النظام ومكونات قوة التحكم شبه النشطة ، على التوالي. وظائف 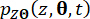 كثافة الاحتمال المشترك ويمكن
كثافة الاحتمال المشترك ويمكن  تحقيقها عن طريق حل المعادلات. (15) و (16) مع الشروط الأولية التالية:
تحقيقها عن طريق حل المعادلات. (15) و (16) مع الشروط الأولية التالية:
 (17)
(17)
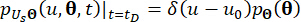 (18)
(18)
حيث 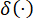 يشير إلى دالة دلتا ديراك.
يشير إلى دالة دلتا ديراك. 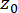 وتشير
وتشير 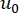 إلى القيم الأولية الحتمية ل
إلى القيم الأولية الحتمية ل  و
و 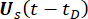 ، على التوالي ؛
، على التوالي ؛ 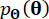 تشير إلى دالة كثافة الاحتمال للعينة
تشير إلى دالة كثافة الاحتمال للعينة 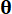 .
.
وظائف  كثافة الاحتمال اللحظي ويمكن
كثافة الاحتمال اللحظي ويمكن 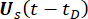 الحصول عليها من خلال التكامل أحادي البعد لمجال
الحصول عليها من خلال التكامل أحادي البعد لمجال 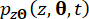 مساحة العينة وعبره
مساحة العينة وعبره  :
:
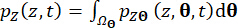 (19)
(19)
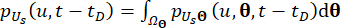 (20)
(20)
حيث 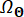 يشير إلى مجال
يشير إلى مجال  توزيع .
توزيع .
بناء على المعادلات. (19) و (20) ، يلاحظ أن المعلومات الاحتمالية الكاملة للكميات الفيزيائية المعنية يتم اشتقاقها بسهولة ، إذا تم تحديد علاقاتها المرتبطة بمعلمات الخوارزمية. يمكن حساب موثوقية الكميات الفيزيائية المعنية من خلال وظيفة الأداء ذات الصلة التالية:
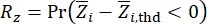 (21)
(21)
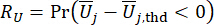 (22)
(22)
حيث 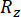 وتشير
وتشير 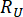 إلى الموثوقية المحسوبة لكمية الحالة المعنية وقوة التحكم شبه النشطة ، على التوالي ؛
إلى الموثوقية المحسوبة لكمية الحالة المعنية وقوة التحكم شبه النشطة ، على التوالي ؛  تشير إلى متجه القيمة القصوى المكافئ للكمية الفيزيائية المعنية للهيكل الخاضع للرقابة ؛
تشير إلى متجه القيمة القصوى المكافئ للكمية الفيزيائية المعنية للهيكل الخاضع للرقابة ؛ 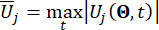 يشير إلى متجه القيمة القصوى المكافئ لقوة التحكم j-th ؛ تشير القبعة '-' على الرموز إلى متجه القيمة القصوى المكافئ41 ؛
يشير إلى متجه القيمة القصوى المكافئ لقوة التحكم j-th ؛ تشير القبعة '-' على الرموز إلى متجه القيمة القصوى المكافئ41 ؛  يشير إلى الكمية المادية المعنية من k-th DOF للهيكل الخاضع للرقابة.
يشير إلى الكمية المادية المعنية من k-th DOF للهيكل الخاضع للرقابة. 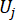 يشير إلى قوة التحكم J-TH ؛
يشير إلى قوة التحكم J-TH ؛ 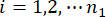 ،
، 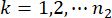 ،
،  ،
،
 ، وتشير
، وتشير  إلى عدد الكميات الفيزيائية المعنية و DOF للهيكل ومخمدات MR المثبتة في الهيكل ، على التوالي.
إلى عدد الكميات الفيزيائية المعنية و DOF للهيكل ومخمدات MR المثبتة في الهيكل ، على التوالي. 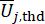
 وتشير إلى عتبات
وتشير إلى عتبات  و
و  ؛
؛  تشير إلى احتمال الحدث العشوائي.
تشير إلى احتمال الحدث العشوائي.
1.3 تحسين المعلمات
نسبة اتساع  وتؤثر
وتؤثر  بشكل كبير على فعالية التحكم38 في طريقة التحكم في التغذية الراجعة. لذلك ، لتحقيق أفضل فعالية للتحكم ،
بشكل كبير على فعالية التحكم38 في طريقة التحكم في التغذية الراجعة. لذلك ، لتحقيق أفضل فعالية للتحكم ، وتحتاج
وتحتاج  إلى تحسينها. إلى جانب ذلك ، كطريقة تحكم قائمة على مخمد MR ، تتأثر فعالية التحكم أيضا بمعلمات الجهاز ،
إلى تحسينها. إلى جانب ذلك ، كطريقة تحكم قائمة على مخمد MR ، تتأثر فعالية التحكم أيضا بمعلمات الجهاز ،  في المعادلة (6). ولتحقيق الموثوقية المثلى لنظام التحكم في الهيكل، يقترح المعيار القائم على الموثوقية في المكافئ (25).
في المعادلة (6). ولتحقيق الموثوقية المثلى لنظام التحكم في الهيكل، يقترح المعيار القائم على الموثوقية في المكافئ (25).
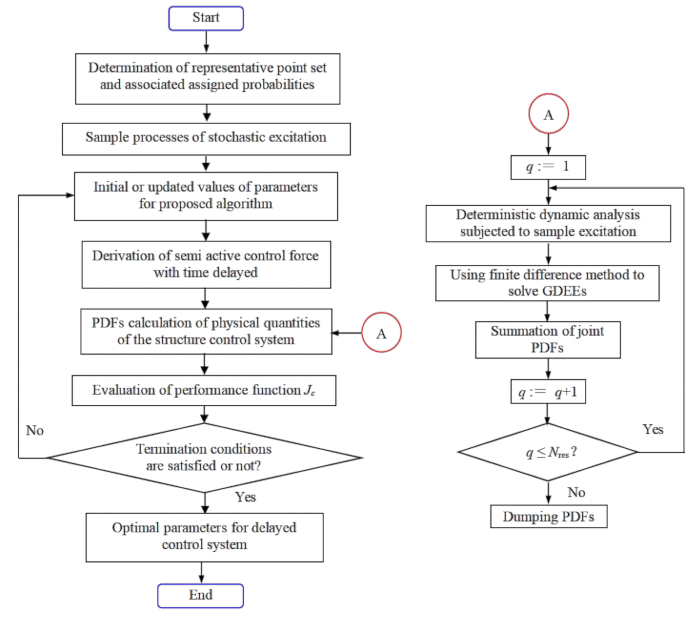
الشكل 1: مخطط انسيابي لتحسين المعلمة للتحكم الأمثل في الهيكل شبه النشط العشوائي مع تعويض التأخير الزمني. الاختصارات: GDEE = المعادلة التفاضلية المعممة للحدث ؛ PDF = دالة كثافة الاحتمال. الرجاء النقر هنا لعرض نسخة أكبر من هذا الرقم.
باختصار ، هناك حاجة إلى مرحلتين لتنفيذ التحكم الأمثل في الهيكل شبه النشط العشوائي بناء على مخمدات MR مع تعويض تأخير الوقت:
1.3.1 التقليل إلى أدنى حد من دالة  التكلفة المبينة في المعادلة (7) ، يتم تحقيق منطق التغذية المرتدة للحالة بمعنى العينات ، أي المعادلة 12)
التكلفة المبينة في المعادلة (7) ، يتم تحقيق منطق التغذية المرتدة للحالة بمعنى العينات ، أي المعادلة 12)
1.3.2 تقليل وظيفة  الأداء القائمة على الموثوقية ، يتم تحقيق المعلمات المثلى بمعنى الإحصائيات. يعرض الشكل 1 المخطط الانسيابي لتحسين معلمات وحدة التحكم في الخطوة 1.3.2.
الأداء القائمة على الموثوقية ، يتم تحقيق المعلمات المثلى بمعنى الإحصائيات. يعرض الشكل 1 المخطط الانسيابي لتحسين معلمات وحدة التحكم في الخطوة 1.3.2.
الخطوات التالية في الخطوة 1.3.2 ، والتي تتضمن طبقتين من الحلقات ، هي كما يلي:
1.3.2.1 يسمح تقسيم المساحة المخصصة للاحتمالات للإثارة العشوائية ، والتي تتميز بمتجه  المعلمة العشوائية ، بتحديد مجموعة من النقاط
المعلمة العشوائية ، بتحديد مجموعة من النقاط 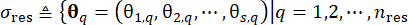 التمثيلية جنبا إلى جنب مع الاحتمالات المعينة المرتبطة بهاPq. يتيح هذا النهج التوليد الفعال لعمليات العينة للإثارة العشوائية ، والتي يشار إليها ب
التمثيلية جنبا إلى جنب مع الاحتمالات المعينة المرتبطة بهاPq. يتيح هذا النهج التوليد الفعال لعمليات العينة للإثارة العشوائية ، والتي يشار إليها ب 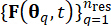 ، للحصول عليها بسهولة.
، للحصول عليها بسهولة.
1.3.2.2 من أجل تحسين معلمات نظام التحكم في الهيكل شبه النشط ، قم بتهيئة أو تحديث قيم أوزان  دالة التكلفة و
دالة التكلفة و  . ثم يتم حساب قوة التحكم في التغذية الراجعة للحالة المرتبطة بالتأخير الزمني ، انظر المعادلة (12).
. ثم يتم حساب قوة التحكم في التغذية الراجعة للحالة المرتبطة بالتأخير الزمني ، انظر المعادلة (12).
1.3.2.3 الحصول على وظائف كثافة الاحتمالات (PDFs) للاستجابات الهيكلية وقوة التحكم عن طريق حل GDEEs الموضحة في Eqs. (17) – (20):
يتم الانتهاء من التحسين دون اتصال بالإنترنت ولكن ليس عبر الإنترنت. في تطبيق الطريقة المقترحة في أنظمة التحكم في الهيكل الحقيقي ، فإن الأمثل  وقد
وقد  تم تحقيقه ، والتحسين ليس ضروريا في العملية الحقيقية القابلة للتطبيق.
تم تحقيقه ، والتحسين ليس ضروريا في العملية الحقيقية القابلة للتطبيق.
التحليل الديناميكي الحتمي لنظام التحكم في الهيكل شبه النشط الخاضع لإثارة العينة ، والذي يتم من خلاله حساب الكميات 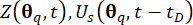 الفيزيائية المعنية ومشتقاتها
الفيزيائية المعنية ومشتقاتها .
.
من خلال استخدام طريقة الفرق المحدودة ، مثل مخطط Lax-Wendroff المعدل مع خصائص تناقص التباين الكلي (TVD) ، يمكن حل المعادلات التفاضلية المعممة (GDEEs) ، ويمكن اشتقاق الحلول العددية لوظائف 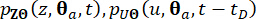 كثافة الاحتمال المشترك.
كثافة الاحتمال المشترك.
بتكرار الخطوتين المذكورتين أعلاه من التحليل الديناميكي الحتمي وطريقة الفرق المحدود ، وتشغيل جميع النقاط 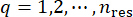 التمثيلية ، يمكن الحصول على وظائف كثافة الاحتمالات عن طريق الجمع:
التمثيلية ، يمكن الحصول على وظائف كثافة الاحتمالات عن طريق الجمع:
 (23)
(23)
 (24)
(24)
حيث  يمثل قياس مساحة المجال الفرعي المرتبط بنقطة
يمثل قياس مساحة المجال الفرعي المرتبط بنقطة 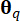 العينة . تعرف الطريقة المستخدمة لحل المعادلة التفاضلية المعممة للحدث (GDEE) باسم طريقة تطور كثافة الاحتمالات (PDEM) 42.
العينة . تعرف الطريقة المستخدمة لحل المعادلة التفاضلية المعممة للحدث (GDEE) باسم طريقة تطور كثافة الاحتمالات (PDEM) 42.
1.3.2.4 تستخدم ملفات PDF الخاصة بالكميات المادية ذات الصلة لتقييم موثوقيتها ، ثم يتم إدراجها في وظيفة  الأداء للمعيار الاحتمالي.
الأداء للمعيار الاحتمالي.
5.2.3.1 تقييم ما إذا كانت معايير الإنهاء لعملية تحسين المعلمات قد تم استيفائها. إذا لم يتم استيفاء الشروط، ارجع إلى الخطوة 1.3.2.2؛ إذا كان الأمر كذلك ، فيمكن تحديد المعلمات المثلى لنظام التحكم المتأخر زمنيا. في هذا العمل ، يتم استخدام صندوق أدوات الخوارزمية الجينية (GA) في MATLAB لتحسين المعلمات ، مما يسهل تحديثات المعلمات ويحدد شروط الإنهاء. من خلال الخوارزمية الجينية ، يمكن تحقيق القيم المثلى في غضون عشر تكرارات ، ويكون التقارب مستقرا بدون مشاكل الحد الأدنى المحلي. على الرغم من أن التكلفة الحسابية ل GA أكبر من تحسين سرب الجسيمات أو الطرق القائمة على التدرج ، إلا أن GA جيد في التعامل مع المشكلات المعقدة وغير القابلة للتمايز ، مثل تلك الموجودة في هذه المخطوطة. لذلك ، يتم تطبيق GA. وبما أن خاصية التقارب السريع ، فإن التكلفة الحسابية ل GA مقبولة.
1.3.2.6 لتحقيق التحكم الأمثل في الموثوقية ، تصاغ وظيفة  الأداء التالية. تصغير
الأداء التالية. تصغير  لتحديد القيم المثلى للمعلمات
لتحديد القيم المثلى للمعلمات  و
و  :
:
 } (25)
} (25)
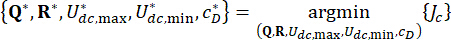 (26)
(26)
كما ذكرنا سابقا ، فإن مصفوفات الترجيح لوحدة التحكم متماثلة ، حيث تتوافق العناصر الموجودة في المصفوفة  مع الأوزان المخصصة للإزاحة والسرعة وتفاعلها ، بينما تمثل العناصر الموجودة في المصفوفة
مع الأوزان المخصصة للإزاحة والسرعة وتفاعلها ، بينما تمثل العناصر الموجودة في المصفوفة  الأوزان المتعلقة بقوة التحكم. بناء على نتائج الدراسات السابقة38 ، لوحظ أن اختلاف تشكيلات أوزان
الأوزان المتعلقة بقوة التحكم. بناء على نتائج الدراسات السابقة38 ، لوحظ أن اختلاف تشكيلات أوزان  وظيفة التكلفة وله
وظيفة التكلفة وله  تأثير ضئيل على فعالية الرقابة. وبناء على ذلك، تم اعتماد تكوين مبسط في هذه الدراسة، على النحو المبين أدناه:
تأثير ضئيل على فعالية الرقابة. وبناء على ذلك، تم اعتماد تكوين مبسط في هذه الدراسة، على النحو المبين أدناه:
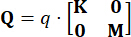 ،
، 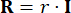 (27)
(27)
حيث 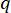 يشير إلى معامل مصفوفة ترجيح الحالة المراد تعريفها ؛
يشير إلى معامل مصفوفة ترجيح الحالة المراد تعريفها ؛ 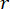 يشير إلى معامل مصفوفة ترجيح التحكم المراد تعريفها ؛
يشير إلى معامل مصفوفة ترجيح التحكم المراد تعريفها ؛ 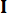 يشير إلى مصفوفة الهوية. يتأثر تأثير التحكم بنسبة
يشير إلى مصفوفة الهوية. يتأثر تأثير التحكم بنسبة 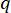 إلى
إلى 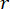 القيم نفسها ولكن ليس منها. إلى جانب ذلك ،
القيم نفسها ولكن ليس منها. إلى جانب ذلك ، 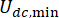 في المعادلة (6) يشير إلى الحد الأدنى من القوة الكولومبية لمخمد MR ، مما يعني أنه
في المعادلة (6) يشير إلى الحد الأدنى من القوة الكولومبية لمخمد MR ، مما يعني أنه  مع وجود المدخلات الحالية في المخمد هي صفرا. بعد ذلك ، المعادلة (26) يمكن التعبير عنها بشكل أكبر على النحو التالي: T
مع وجود المدخلات الحالية في المخمد هي صفرا. بعد ذلك ، المعادلة (26) يمكن التعبير عنها بشكل أكبر على النحو التالي: T
 (28)
(28)
أين 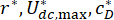 هي المعاملات المثلى للقلق. لجعلها معقولة في الهندسة ، تعتمد النطاقات المثلى لها على الطاقة الإنتاجية لمصانع المثبط MR.
هي المعاملات المثلى للقلق. لجعلها معقولة في الهندسة ، تعتمد النطاقات المثلى لها على الطاقة الإنتاجية لمصانع المثبط MR.
من الواضح أن المعلمات المثلى التي تم الحصول عليها بواسطة المعادلة (28) تحافظ على فعالية التحكم المثلى لخوارزمية التحكم شبه النشطة المقترحة مع تأخير زمني ، مما يمكن نظام التحكم في الهيكل من تحقيق الموثوقية المثلى المتوازنة المعرضة للإثارة العشوائية.
2. دراسة حالة
لتحليل فعالية طريقة التحكم شبه النشطة المقترحة مع تعويض التأخير الزمني لمخمد MR ، تعرض هيكل إطار القص المستوي أحادي الطابق المتصل بمخمد MR للحركة الأرضية الزلزالية العشوائية الأفقية ، كما هو موضح في الشكل 2. معلمات نظام الهيكل شبه النشط هي كما يلي: كتلة 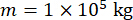 الهيكل ، التردد
الهيكل ، التردد  الدائري الطبيعي ، نسبة
الدائري الطبيعي ، نسبة 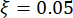 التخميد. وفقا للتجربة السابقة ومقاييس المثبط الموجودة في السوق ، فإن قيم عتبة الإزاحة الهيكلية والسرعة والتسارع وقوة التحكم هي 10 مم و 100 مم / ثانية و 1,500 مم / ثانية2 و 150 كيلو نيوتن على التوالي. لتمثيل حركة الأرض الزلزالية العشوائية ، تم استخدام نموذج الحركة الأرضية العشوائية ذات الدوافع الجسدية43:
التخميد. وفقا للتجربة السابقة ومقاييس المثبط الموجودة في السوق ، فإن قيم عتبة الإزاحة الهيكلية والسرعة والتسارع وقوة التحكم هي 10 مم و 100 مم / ثانية و 1,500 مم / ثانية2 و 150 كيلو نيوتن على التوالي. لتمثيل حركة الأرض الزلزالية العشوائية ، تم استخدام نموذج الحركة الأرضية العشوائية ذات الدوافع الجسدية43:
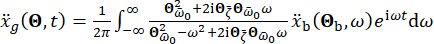 (29)
(29)
حيث 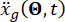 يمثل الحركة الأرضية في المجال الزمني في الموقع الهندسي ، ويشير
يمثل الحركة الأرضية في المجال الزمني في الموقع الهندسي ، ويشير 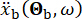 إلى حركة الأرض في مجال التردد عند حجر الأساس. يميز المتجه
إلى حركة الأرض في مجال التردد عند حجر الأساس. يميز المتجه  الطبيعة العشوائية للحركة الأرضية على سطح الموقع الهندسي. المعلمات
الطبيعة العشوائية للحركة الأرضية على سطح الموقع الهندسي. المعلمات 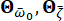 عبارة عن متغيرات عشوائية تصف خصائص تربة الموقع ، بما في ذلك التردد
عبارة عن متغيرات عشوائية تصف خصائص تربة الموقع ، بما في ذلك التردد  السائد والتخميد
السائد والتخميد  المكافئ. يمثل المتجه
المكافئ. يمثل المتجه 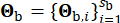 الطبيعة العشوائية للحركة الأرضية عند حجر الأساس ، والتي تتأثر بخصائص المصدر ومسار الانتشار ، مع
الطبيعة العشوائية للحركة الأرضية عند حجر الأساس ، والتي تتأثر بخصائص المصدر ومسار الانتشار ، مع 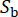 الإشارة إلى عدد المتغيرات العشوائية المتضمنة في هذه المرحلة.
الإشارة إلى عدد المتغيرات العشوائية المتضمنة في هذه المرحلة.  يشير إلى التردد الدائري ، و i هي الوحدة الخيالية.
يشير إلى التردد الدائري ، و i هي الوحدة الخيالية.
يعد التردد  السائد ونسبة
السائد ونسبة  التخميد المكافئة للموقع الهندسي من المعلمات الرئيسية التي تميز الخصائص الديناميكية لتربة الموقع. يمكن تحديد التوزيع الاحتمالي والمعلمات الإحصائية لهذه الكميات بناء على سجلات التسارع الزلزالي التي تم جمعها من فئة معينة من المواقع الهندسية. لأغراض توضيحية ، تم النظر في فئة موقع بنطاق سرعة موجة القص [150 ، 250] م / ث ، وتم ضبط فترة التصميم المميزة للحركة الأرضية على 0.45 ثانية.
التخميد المكافئة للموقع الهندسي من المعلمات الرئيسية التي تميز الخصائص الديناميكية لتربة الموقع. يمكن تحديد التوزيع الاحتمالي والمعلمات الإحصائية لهذه الكميات بناء على سجلات التسارع الزلزالي التي تم جمعها من فئة معينة من المواقع الهندسية. لأغراض توضيحية ، تم النظر في فئة موقع بنطاق سرعة موجة القص [150 ، 250] م / ث ، وتم ضبط فترة التصميم المميزة للحركة الأرضية على 0.45 ثانية.
تم التعامل مع المعلمات 
 الحرجة كمتغيرات عشوائية مستقلة بشكل متبادل ، وكلاهما يتبع توزيعا لوغاريتميا طبيعيا لتحديد المعلمة. وكانت المعلمات الإحصائية على النحو التالي: كانت الوسائل
الحرجة كمتغيرات عشوائية مستقلة بشكل متبادل ، وكلاهما يتبع توزيعا لوغاريتميا طبيعيا لتحديد المعلمة. وكانت المعلمات الإحصائية على النحو التالي: كانت الوسائل  12
12  راد / ثانية و 0.1 على التوالي. معاملات التباين
راد / ثانية و 0.1 على التوالي. معاملات التباين  وبلغت
وبلغت  0.42 و 0.35 على التوالي. تم نمذجة الحركة الأرضية عند حجر الأساس على أنها عملية ضوضاء بيضاء غاوسية بسعة فورييه تبلغ 0.20 م / ث2 ، وهو ما يتوافق مع ذروة تسارع أرضي تبلغ 0.11 جم. تمت الإشارة إلى زاوية الطور المستخدمة لتوليد حركة الأساس الصخري على أنها
0.42 و 0.35 على التوالي. تم نمذجة الحركة الأرضية عند حجر الأساس على أنها عملية ضوضاء بيضاء غاوسية بسعة فورييه تبلغ 0.20 م / ث2 ، وهو ما يتوافق مع ذروة تسارع أرضي تبلغ 0.11 جم. تمت الإشارة إلى زاوية الطور المستخدمة لتوليد حركة الأساس الصخري على أنها 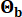 . لذلك ، Sb = 1 و
. لذلك ، Sb = 1 و 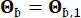 . يمكن اعتبار هذا النهج بمثابة نمذجة للحركات الأرضية العشوائية الشرطية مع احتمال تجاوز معين44. يستخدم افتراض التوزيع اللوغاريتمي الطبيعي على نطاق واسع في نمذجة الحركة الأرضية نظرا لقدرته على التقاط الطبيعة المنحرفة لمعلمات الحركة الأرضية المرصودة.
. يمكن اعتبار هذا النهج بمثابة نمذجة للحركات الأرضية العشوائية الشرطية مع احتمال تجاوز معين44. يستخدم افتراض التوزيع اللوغاريتمي الطبيعي على نطاق واسع في نمذجة الحركة الأرضية نظرا لقدرته على التقاط الطبيعة المنحرفة لمعلمات الحركة الأرضية المرصودة.
لتقييم حساسية هذا الافتراض ، تم إجراء التحليلات الإضافية باستخدام التوزيعات الاحتمالية البديلة ، بما في ذلك التوزيعات الطبيعية وجاما في أبحاث أخرى45،46. تشير النتائج إلى أنه في حين أن الاتجاهات العامة لا تزال متسقة ، فإن التوزيع اللوغاريتمي الطبيعي يوفر أفضل ملاءمة للبيانات المرصودة ، لا سيما لالتقاط سلوك الذيل لمقاييس شدة الحركة الأرضية
بموجب طريقة المجالات المماسية47 ، تم اختيار مجموعة من 221 نقطة تمثيلية مع الاحتمالات المعينة المرتبطة بها وتم تجميع التسارعات الأرضية التمثيلية. كان تردد أخذ العينات 50 هرتز ، وكانت مدة الحركات الأرضية 20.48 ثانية. ولتعيين شدة غير ثابتة لمحاكاة الحركة الأرضية، استخدمت دالة تشكيل منتظمة وكانت صياغتها على النحو التالي:
 (30)
(30)
حيث  تأخذ 2 و 16 ثانية ، على التوالي.
تأخذ 2 و 16 ثانية ، على التوالي.
يظهر المتوسط والانحراف المعياري للحركة الأرضية الزلزالية العشوائية ، والتاريخ الزمني للحركة الأرضية الزلزالية التمثيلية في الشكل 3. كان اتساع المتوسط (0.06 م / ث2) ~ 8٪ من اتساع الانحراف المعياري (0.8 م / ث2) ، مما يشير إلى أن نموذج الحركة الأرضية العشوائية بدوافع جسدية أظهر خاصية المتوسط الصفر. وفي الوقت نفسه ، أظهرت حركة الأرض الزلزالية سلوكيات غير ثابتة ملحوظة في كل من المجالات الزمنية والترددية.
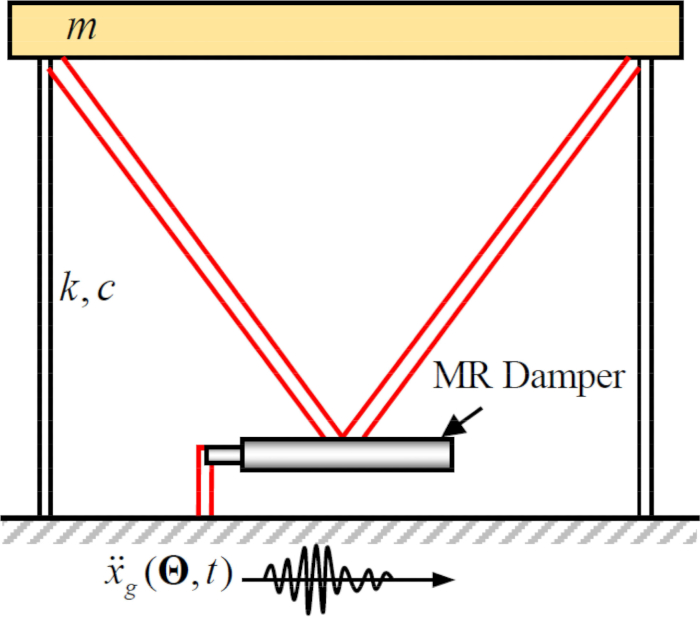
الشكل 2: رسم تخطيطي لإطار قص من طابق واحد مع مخمد مغناطيسي. 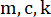 تشير إلى كتلة الهيكل ونسبة التخميد والصلابة ؛
تشير إلى كتلة الهيكل ونسبة التخميد والصلابة ؛ 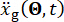 يدل على الإثارة الزلزالية العشوائية. الرجاء النقر هنا لعرض نسخة أكبر من هذا الرقم.
يدل على الإثارة الزلزالية العشوائية. الرجاء النقر هنا لعرض نسخة أكبر من هذا الرقم.
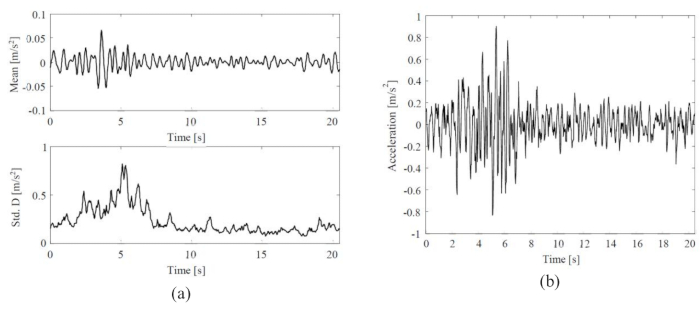
الشكل 3: إحصائيات وعينات تمثيلية لحركات أرضية زلزالية مختارة. (أ) متوسط الحركة الأرضية الزلزالية العشوائية والانحراف المعياري؛ (ب) التاريخ الزمني للحركة الأرضية الزلزالية التمثيلية. الرجاء النقر هنا لعرض نسخة أكبر من هذا الرقم.
2.1 تأثير تحليل التأخير الزمني
لتحليل تأثير التأخير الزمني على فعالية التحكم شبه النشط لمخمد MR ، يوضح الشكل 4 الإزاحة والسرعة والتسارع RMS (استجابة الجذر متوسط المربع) للهيكل المتحكم فيه. كانت نسبة مصفوفة الترجيح ومعلمات 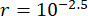 المثبط ،
المثبط ، 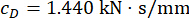 و
و 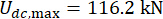 ، وهي النتائج المثلى دون تأخير زمني38. كانت استجابات الهيكل الخاضع للرقابة مع تأخير زمني أكبر من الهيكل الخاضع للرقابة دون تأخير زمني ، ويمثل تأثير التأخير الزمني على تأثير التحكم الدورية جنبا إلى جنب مع زيادة التأخير الزمني. نظرا لأن طريقة التحكم شبه النشطة مع مخمد MR هي نوع من طريقة التغذية الراجعة ، فقد اعتبرت دورية التأثير مرتبطة بالفترة الطبيعية للهيكل المتحكم فيه (T = 0.56 ثانية).
، وهي النتائج المثلى دون تأخير زمني38. كانت استجابات الهيكل الخاضع للرقابة مع تأخير زمني أكبر من الهيكل الخاضع للرقابة دون تأخير زمني ، ويمثل تأثير التأخير الزمني على تأثير التحكم الدورية جنبا إلى جنب مع زيادة التأخير الزمني. نظرا لأن طريقة التحكم شبه النشطة مع مخمد MR هي نوع من طريقة التغذية الراجعة ، فقد اعتبرت دورية التأثير مرتبطة بالفترة الطبيعية للهيكل المتحكم فيه (T = 0.56 ثانية).
بالمقارنة مع استجابات الهيكل غير المنضبط ، والتي كان الحد الأقصى لإزاحة MRS وسرعتها وتسارعها 24.6 مم و 270.0 مم / ثانية و 3111.3 مم / ثانية2 ، حقق الهيكل الذي يتم التحكم فيه بواسطة مخمد MR تأثيرا ملحوظا. على عكس عدم استقرار الهيكل النشط المتحكم فيه مع التأخيرالزمني 25 ، لا تزال طريقة التحكم شبه النشطة القائمة على مخمد MR تحصل على بعض التأثير حتى مع التأخير الزمني.
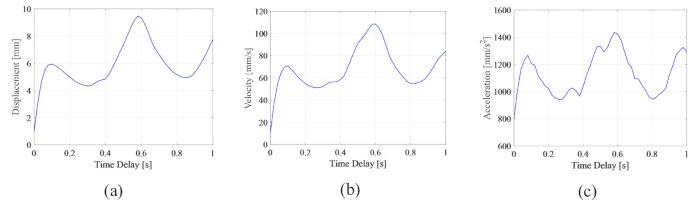
الشكل 4: الحد الأقصى لمربعات متوسط الجذر لاستجابات الهيكل المتحكم فيه بمرور الوقت. (أ) التشرد؛ (ب) السرعة؛ (ج) التسارع. الرجاء النقر هنا لعرض نسخة أكبر من هذا الرقم.
لتحليل تأثير التأخير الزمني على موثوقية هيكل يتم التحكم فيه بشكل شبه نشط ، يوضح الشكل 5 موثوقية الإزاحة والسرعة والتسارع مع زيادة التأخير الزمني. كانت موثوقية استجابات الهيكل الخاضع للرقابة مع أي تأخير زمني أقل من القيم دون تأخير زمني ، مما يعني أن موثوقية الهيكل الخاضع للرقابة قد انخفضت بسبب التأخير الزمني. وفي الوقت نفسه ، على غرار الحد الأقصى RMS ، أظهر تأثير التحكم في الموثوقية دورية مع زيادة التأخير الزمني. علاوة على ذلك ، كانت موثوقية الهيكل الخاضع للرقابة ، مع أو بدون تأخير زمني ، أعلى من قيم الهياكل غير الخاضعة للرقابة مع موثوقية الإزاحة والسرعة والتسارع 0.0954 و 0.1058 و 0.1111.
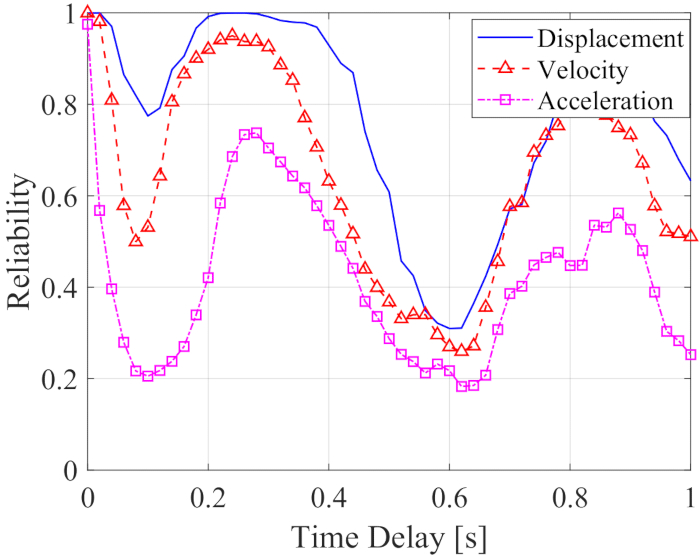
الشكل 5: موثوقية الاستجابات للهيكل المتحكم فيه مع زيادة التأخير الزمني. الرجاء النقر هنا لعرض نسخة أكبر من هذا الرقم.
باختصار ، تم التخفيف من استجابات الهيكل بواسطة طريقة التحكم شبه النشطة. ومع ذلك، انخفضت فعالية التحكم، بغض النظر عن RMS أو موثوقيتها، لطريقة التحكم شبه النشطة بسبب التأخير الزمني. لذلك ، من الضروري التعويض عن التأخير الزمني.
2-1-1 تحليل طريقة التعويض عن التأخر الزمني
لتحليل فعالية طريقة تعويض التأخير الزمني المقترحة ، تمت مقارنة تواريخ RMS الزمنية للإزاحة والسرعة والتسارع غير المنضبط (Unc) ، والنظام المتأخر زمنيا مع التحكم في عدم التعويض (TDN-SAC-PSO) ، والنظام المتأخر زمنيا مع التحكم في التعويض (TDC-SAC-PSO) في الشكل 6 ، حيث كان التأخير الزمني 0.1 ثانية. معلمات مصفوفة الترجيح وطريقة التحكم شبه النشطة هي نفسها كما في الخطوة 2.1.
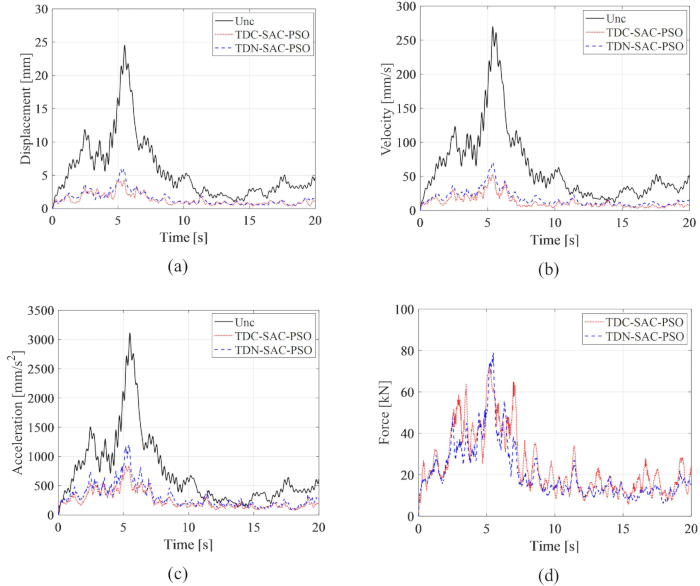
الشكل 6: مقارنة تاريخ الوقت الجذر ومتوسط المربع للهياكل التي يتم التحكم فيها بطرق مختلفة. (أ) التشرد؛ (ب) السرعة؛ (ج) التسارع؛ (د) قوة المراقبة. الاختصارات: Unc = غير خاضع للرقابة. TDC-SAC-PSO = نظام تأخر الوقت مع التحكم في التعويض ؛ TDN -SAC-PSO = نظام متأخر بالوقت مع التحكم في عدم التعويض. الرجاء النقر هنا لعرض نسخة أكبر من هذا الرقم.
قللت كلتا طريقتي التحكم بشكل كبير من استجابات الهيكل مقارنة بالهيكل غير المنضبط ، مما يكشف عن مزايا طريقة التحكم القائمة على مخمد MR. بالمقارنة مع الهيكل غير المنضبط ، يتم تقليل الحد الأقصى RMS للإزاحة والسرعة والتسارع بنسبة 75.79٪ و 73.75٪ و 61.22٪ باستخدام طريقة TDN-SAC-PSO. علاوة على ذلك ، مع تعويض التأخير الزمني ، تنخفض استجابات الهيكل الخاضع للرقابة بنسبة 82.59٪ و 80.40٪ و 73.04٪ باستخدام طريقة TDC-SAC-PSO. انخفض الحد الأقصى RMS لقوة التحكم باستخدام طريقة TDC-SAC-PSO بنسبة 8.43٪ مقارنة بطريقة TDN-SAC-PSO ، على الرغم من أن استجابات الاهتزاز للطريقة الأولى كانت أقل من الأخيرة. يشير التحليل أعلاه إلى أن تأثير التأخر الزمني على طريقة التحكم القائمة على المثبط بالرنين المغناطيسي قد انخفض بشكل فعال من خلال طريقة التعويض ، والتي تبين ضرورة تعويض التأخر الزمني لطريقة التحكم شبه النشطة للمخمد بالرنين المغناطيسي.
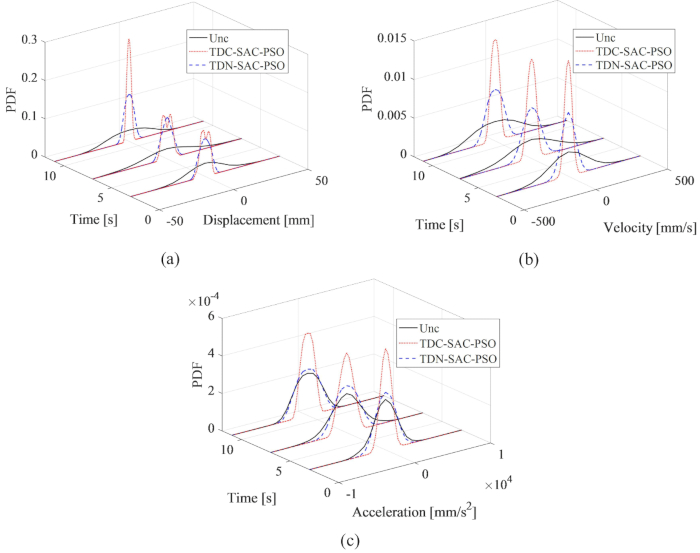
الشكل 7: مقارنة PDF في الأوقات النموذجية لاستجابات الهيكل. (أ) التشرد؛ (ب) السرعة؛ (ج) التسارع. الاختصارات: PDF = دالة كثافة الاحتمال. unc = غير خاضع للرقابة. TDC-SAC-PSO = نظام تأخر الوقت مع التحكم في التعويض ؛ TDN -SAC-PSO = نظام متأخر بالوقت مع التحكم في عدم التعويض. الرجاء النقر هنا لعرض نسخة أكبر من هذا الرقم.
للكشف بشكل شامل عن تأثير طريقة التعويض المقترحة على عدم اليقين في استجابات الهيكل المتحكم فيه ، تظهر مقارنات دالة كثافة الاحتمالية (PDF) للإزاحة والسرعة والتسارع في الأوقات النموذجية ، 3 و 7 و 11 ثانية ، في الشكل 7. كانت ملفات PDF الخاصة بطريقة TDN-SAC-PSO أضيق من تلك الخاصة بالبنية غير الخاضعة للرقابة ، مما يعني أن عدم اليقين في استجابات الهيكل قد انخفض من خلال طريقة التحكم شبه النشطة حتى مع التأخير الزمني. وعندما تم التعويض عن التأخير الزمني، تم تضييق نطاق ملفات PDF الخاصة بالردود. لذلك ، فإن طريقة التعويض المقترحة ضرورية لتحسين تأثير التحكم شبه النشط.
| طريقة التحكم | التشريد | السرعه | تسريع | قوة التحكم | الحد الأدنى للقيمة |
| جامعة الأمم المتحدة | 0.0954 | 0.1058 | 0.1111 | -- | 0.1111 |
| TDC - SAC - PSO | 0.9565 | 0.8107 | 0.7654 | 0.9845 | 0.7654 |
| TDN-SAC-PSO | 0.7747 | 0.531 | 0.2054 | 0.884 | 0.2054 |
الجدول 1: استجابات الاهتزاز وموثوقية قوة التحكم للهياكل التي يتم التحكم فيها بطرق مختلفة. الاختصارات: Unc = غير خاضع للرقابة. TDC-SAC-PSO = نظام تأخر الوقت مع التحكم في التعويض ؛ TDN -SAC-PSO = نظام متأخر بالوقت مع التحكم في عدم التعويض.
يتم عرض استجابات الاهتزاز وموثوقية قوة التحكم للهياكل التي يتم التحكم فيها بطريقة TDC-SAC-PSO- و TDN-SAC-PSO غير المنضبطة في الجدول 1. مع التحكم في طريقة TDN-SAC-PSO ، زادت موثوقية الهيكل بشكل كبير مقارنة بالهيكل غير المتحكم فيه ، والذي يتحقق من فعالية طريقة التحكم القائمة على مخمد MR ، حتى مع مرور الوقت. ومع ذلك ، مع تعويض التأخير الزمني ، زادت الموثوقية بشكل كبير مقارنة بعدم التعويض ، خاصة بالنسبة للتسارع. ومن الجدير بالذكر أيضا أن موثوقية الاستجابات المختلفة وقوة التحكم أظهرت اختلافات كبيرة بالنسبة لطريقة TDC-SAC-PSO. يشير هذا إلى أن القيم المثلى للمعلمات الحرجة للتحكم دون تأخير زمني ليست مثالية للتحكم مع تأخير زمني. لتحقيق تأثير التحكم الأمثل لاستجابات الاهتزاز وقوة التحكم مع تأثير تأخير الوقت ، يجب تحسين المعلمات بشكل أكبر. بناء على التحليل أعلاه ، تم استنتاج أن طريقة التحكم شبه النشطة مع مخمد MR يمكن أن تقلل بشكل فعال من استجابات الاهتزاز للهيكل ، بينما تحتاج المعلمات إلى التحسين بسبب تأثير التأخير الزمني.
2.2 تحسين المعلمة
لتحقيق القيم المثلى للمعلمات ، تم تطبيق طريقة التحسين المتكاملة القائمة على معيار الموثوقية38. تم إجراء تحسين المعلمات الحرجة باستخدام 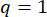 ،
، 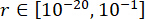 ،
،  ،
، 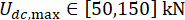 ، والأوقات القابلة للضبط لقوة المثبط MR s = 8. تم استخدام مجموعة أدوات GA داخل MATLAB لتنفيذ التحسين.
، والأوقات القابلة للضبط لقوة المثبط MR s = 8. تم استخدام مجموعة أدوات GA داخل MATLAB لتنفيذ التحسين.
نتائج التحسين للمعلمات هي  ،
، 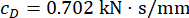 ، وللتأخير
، وللتأخير 
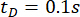 الزمني. يوضح الشكل 8 تواريخ وقت RMS للإزاحة والسرعة والتسارع وقوة التحكم للهياكل غير المنضبطة (Unc) و TDC-SAC-PSO وطريقة SOSC-PSO. تشير طريقة SOSC-PSO إلى طريقة التحكم شبه النشطة مع تعويض التأخر الزمني وقيم المعلمات الحرجة المحسنة.
الزمني. يوضح الشكل 8 تواريخ وقت RMS للإزاحة والسرعة والتسارع وقوة التحكم للهياكل غير المنضبطة (Unc) و TDC-SAC-PSO وطريقة SOSC-PSO. تشير طريقة SOSC-PSO إلى طريقة التحكم شبه النشطة مع تعويض التأخر الزمني وقيم المعلمات الحرجة المحسنة.
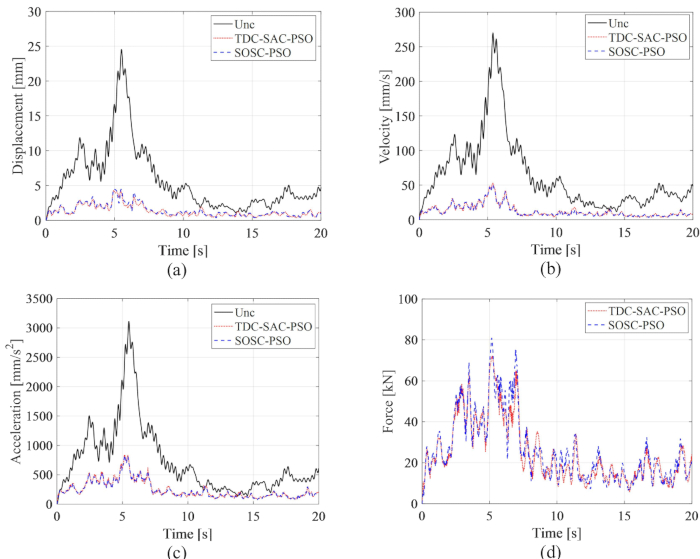
الشكل 8: تواريخ وقت RMS للإزاحة والسرعة والتسارع وقوة التحكم للهياكل غير المنضبطة وطريقة TDC-SAC-PSO والهياكل التي يتم التحكم فيها بواسطة طريقة SOSC-PSO. (أ) التشرد؛ (ب) السرعة؛ (ج) التسارع؛ (د) قوة المراقبة. الاختصارات: Unc = غير خاضع للرقابة. TDC-SAC-PSO = نظام تأخر الوقت مع التحكم في التعويض ؛ SOSC-PSO = طريقة التحكم شبه النشطة العشوائية المثلى مع تعويض التأخير الزمني. الرجاء النقر هنا لعرض نسخة أكبر من هذا الرقم.
من الشكل 8 ، يتضح أن تأثيرات التحكم لطرق TDC-SAC-PSO و SOSC-PSO أظهرت اختلافا طفيفا. كان الحد الأقصى RMS لسرعة الإزاحة والتسارع للطريقة الأولى 81.60٪ ، 81.21٪ ، 73.62٪ من الهيكل غير المنضبط و 82.59٪ ، 80.40٪ ، 73.04٪ للطريقة الأخيرة. لتحليل شامل للخصائص الاحتمالية للاستجابات لكلتا طريقتي التحكم ، يوضح الشكل 9 ملفات PDF للإزاحة والسرعة والتسارع للهياكل غير المنضبطة ، وطريقة TDC-SAC-PSO وطريقة SOSC-PSO. كان لكلتا طريقتي التحكم نفس ملفات PDF تقريبا للإزاحة والسرعة في الأوقات النموذجية. كانت ملفات PDF للتسريع لطريقة SOSC-PSO أضيق من تلك الخاصة بطريقة TDC-SAC-PSO ، مما يعني أن عدم اليقين في التسارع حقق تأثير تحكم أفضل بالطريقة السابقة.
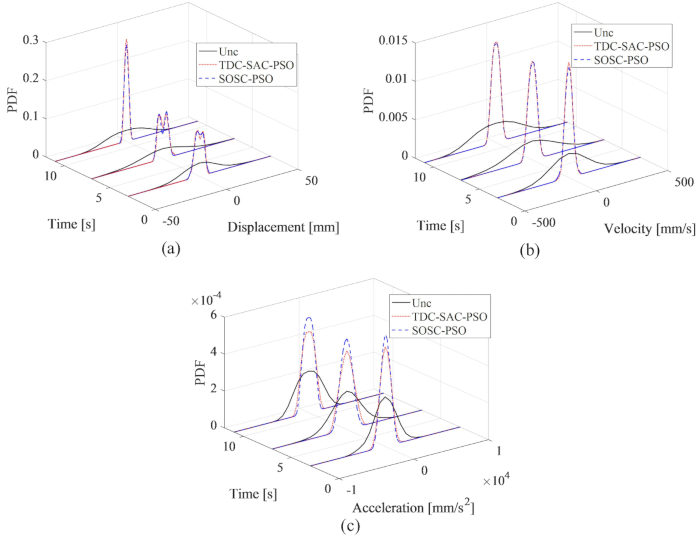
الشكل 9: مقارنة ملفات PDF للإزاحة والسرعة والتسارع لمختلف الهياكل الخاضعة للرقابة. (أ) التشرد؛ (ب) السرعة؛ (ج) التسارع. الاختصارات: ملفات PDF = وظائف كثافة الاحتمالات. unc = غير خاضع للرقابة. TDC-SAC-PSO = نظام تأخر الوقت مع التحكم في التعويض ؛ SOSC-PSO = طريقة التحكم شبه النشطة العشوائية المثلى مع تعويض التأخير الزمني. الرجاء النقر هنا لعرض نسخة أكبر من هذا الرقم.
يتم عرض موثوقية الإزاحة والسرعة والتسارع وقوة التحكم للهياكل غير المنضبطة والتي يتم التحكم فيها بواسطة طريقة TDC-SAC-PSO- و SOSC-PSO في الجدول 2. حققت كلتا طريقتي التحكم زيادة كبيرة في الموثوقية مقارنة بالهيكل غير الخاضع للرقابة. أظهرت موثوقية الإزاحة فرقا طفيفا بين طريقتي TDC-SAC-PSO و SOSC-PSO. في حين أن موثوقية التسارع ، وهي أدنى موثوقية للهيكل المتحكم فيه ، حققت زيادة ملحوظة. وهذا يعني أن طريقة SOSC-PSO تحقق تأثير التحكم الأمثل في التوازن.
| طريقة التحكم | التشريد | السرعه | تسريع | قوة التحكم | الحد الأدنى للقيمة |
| جامعة الأمم المتحدة | 0.0954 | 0.1058 | 0.1111 | -- | 0.1111 |
| TDC - SAC - PSO | 0.9565 | 0.8107 | 0.7654 | 0.9845 | 0.7654 |
| SOSC-PSO | 0.953 | 0.8704 | 0.8934 | 0.9586 | 0.8934 |
الجدول 2: موثوقية الهياكل التي يتم التحكم فيها بطرق مختلفة. الاختصارات: Unc = غير خاضع للرقابة. TDC-SAC-PSO = نظام تأخر الوقت مع التحكم في التعويض ؛ SOSC-PSO = طريقة التحكم شبه النشطة العشوائية المثلى مع تعويض التأخير الزمني.
تم تحليل فعالية طريقة SOSC-PSO المقترحة مع التأخير 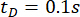 الزمني. لمزيد من التحقق من الطريقة المقترحة للتأخيرات الزمنية المختلفة ، يبين الجدول 3 قيم المعلمات المثلى والموثوقية المقابلة لمدى
الزمني. لمزيد من التحقق من الطريقة المقترحة للتأخيرات الزمنية المختلفة ، يبين الجدول 3 قيم المعلمات المثلى والموثوقية المقابلة لمدى 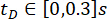 التأخر الزمني .
التأخر الزمني .
| رد (ق) | إل جي (ص *) | جد (كيلو نيوتن / مم) | UDC ، ماكس (كيلو نيوتن) | التشريد | السرعه | تسريع | قوة التحكم |
| 0 | -2.524 | 1.44 | 116.163 | 0.9997 | 0.9998 | 0.9752 | 1 |
| 0.02 | -4.413 | 0.414 | 144.066 | 0.9989 | 0.9988 | 0.872 | 0.9011 |
| 0.04 | -4.416 | 0.25 | 141.759 | 0.9998 | 0.9846 | 0.8881 | 0.9135 |
| 0.06 | -3.226 | 0.203 | 145.613 | 0.993 | 0.9318 | 0.8756 | 0.9556 |
| 0.08 | -5.207 | 0.345 | 133.692 | 0.9646 | 0.8998 | 0.8998 | 0.953 |
| 0.1 | -4.669 | 0.702 | 130.739 | 0.9531 | 0.8704 | 0.8934 | 0.9586 |
| 0.12 | -4.895 | 0.833 | 69.72 | 0.9526 | 0.863 | 0.888 | 0.9686 |
| 0.14 | -4.231 | 0.921 | 75.221 | 0.9531 | 0.8681 | 0.8697 | 0.9671 |
| 0.16 | -5.594 | 0.662 | 138.922 | 0.9529 | 0.8461 | 0.8262 | 0.931 |
| 0.18 | -4.262 | 0.882 | 76.335 | 0.9516 | 0.7873 | 0.7614 | 0.9618 |
| 0.2 | -3.926 | 0.783 | 67.951 | 0.904 | 0.7277 | 0.7116 | 0.9653 |
| 0.22 | -5.965 | 1.071 | 52.554 | 0.8377 | 0.6411 | 0.6205 | 0.965 |
| 0.24 | -4.481 | 1.216 | 128.148 | 0.7567 | 0.474 | 0.474 | 0.9687 |
| 0.26 | -3.53 | 0.672 | 53.706 | 0.53 | 0.4096 | 0.4158 | 0.9921 |
| 0.28 | -4.433 | 0.638 | 64.225 | 0.3547 | 0.3745 | 0.3464 | 0.9928 |
| 0.3 | -3.536 | 0.459 | 57.705 | 0.2735 | 0.316 | 0.2736 | 0.9929 |
| جامعة الأمم المتحدة | -- | -- | -- | 0.0954 | 0.1058 | 0.1111 | -- |
الجدول 3: قيم المعلمات المثلى وقيم الموثوقية المقابلة للتأخيرات الزمنية المختلفة. 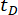 يدل على تأخير الوقت.
يدل على تأخير الوقت.  تشير إلى القيمة اللوغاريتمية المثلى ل r ، r تشير إلى معامل مصفوفة ترجيح التحكم ؛
تشير إلى القيمة اللوغاريتمية المثلى ل r ، r تشير إلى معامل مصفوفة ترجيح التحكم ؛ 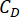 يشير إلى معامل التخميد اللزج لمخمد MR ؛
يشير إلى معامل التخميد اللزج لمخمد MR ؛ 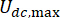 تشير إلى الحد الأقصى والحد الأدنى للقوى الكولومبية لمخمد MR.
تشير إلى الحد الأقصى والحد الأدنى للقوى الكولومبية لمخمد MR.
يمكن ملاحظة أن موثوقية الإزاحة والسرعة والتسارع قد تحسنت مقارنة بالهيكل غير المنضبط ، حتى في وجود تأخير زمني ، مما يدل على متانة الطريقة المقترحة تجاه مثل هذه التأخير. ومع ذلك، انخفضت موثوقية الاستجابات الهيكلية مع طريقة التحكم المقترحة مع زيادة التأخر الزمني، مما يشير إلى أنه في حين يمكن التخفيف من أثر التأخر الزمني على فعالية الرقابة، فإنه لا يمكن القضاء عليه تماما. والجدير بالذكر أن موثوقية قوة التحكم ظلت أعلى من 90٪ خلال التأخيرات الزمنية المختلفة.
3. مثال عددي
للتحقق من طريقة SOSC-PSO المقترحة في هيكل MDOF ، تم تحليل هيكل من ستة طوابق مع مخمدات MR مثبتة في الطابقين الأول والثالث ، كما هو موضح في الشكل 10. تم تطبيق العينات الزلزالية الناتجة عن النموذج الزلزالي العشوائي في القسم 2 ، وكانت عتبات الموثوقية للإزاحة والسرعة والتسارع وقوة التحكم 20 مم و 200 مم / ثانية و 3,000 مم / ث2 و 200 كيلو نيوتن. المعادلات. (27) تم استخدامها كمصفوفة ترجيح مع 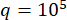 . تم استخدام صندوق أدوات GA الخاص ب MATLAB لتحسين
. تم استخدام صندوق أدوات GA الخاص ب MATLAB لتحسين 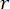 ،
، و
و  ، مع النطاقات
، مع النطاقات 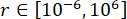 المثلى ،
المثلى ،  و
و 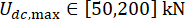 .
.
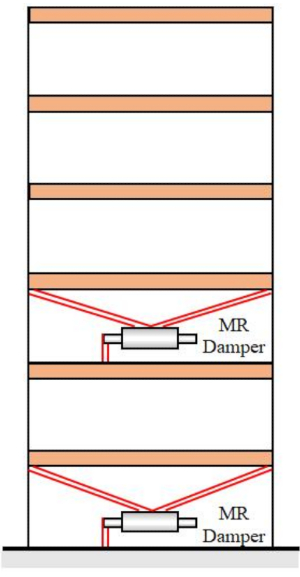
الشكل 10: هيكل من ستة طوابق مع مخمدات MR. الاختصار: MR = مغناطيسي. الرجاء النقر هنا لعرض نسخة أكبر من هذا الرقم.
3.1 تأثير تحليل التأخير الزمني
لتحليل تأثير التأخير الزمني على فعالية التحكم في مخمد MR في هيكل MDOF ، يوضح الشكل 11 الحد الأقصى RMS للإزاحة (الإزاحة بين الطوابق) ، والسرعة (السرعة بين الطوابق) ، والتسارع (تسارع المجموعة) جنبا إلى جنب مع التأخير الزمني لطريقة TDC-SAC-PSO. كانت 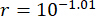 المعلمات ،
المعلمات ، ولمخمد
ولمخمد  MR في الطابق الأول ؛
MR في الطابق الأول ؛  وللمثبط
وللمثبط  MR في الطابق الثالث ، وهي النتائج المثلى دون تأخير زمني. أظهر الحد الأقصى RMS لاستجابات الهيكل الخاضع للرقابة تذبذبات الفترة جنبا إلى جنب مع التأخير الزمني. كان الحد الأقصى RMS للإزاحة والسرعة في الطابق الأول ، وهو أقصى تسارع في الطابق السادس. إلى جانب ذلك ، كان كل الحد الأقصى ل MRS للاستجابات مع أي تأخير زمني أكبر من القيم بدون تأخير زمني ، مما يعني أن التأخير الزمني يقلل من تأثير التحكم في مثبط MR.
MR في الطابق الثالث ، وهي النتائج المثلى دون تأخير زمني. أظهر الحد الأقصى RMS لاستجابات الهيكل الخاضع للرقابة تذبذبات الفترة جنبا إلى جنب مع التأخير الزمني. كان الحد الأقصى RMS للإزاحة والسرعة في الطابق الأول ، وهو أقصى تسارع في الطابق السادس. إلى جانب ذلك ، كان كل الحد الأقصى ل MRS للاستجابات مع أي تأخير زمني أكبر من القيم بدون تأخير زمني ، مما يعني أن التأخير الزمني يقلل من تأثير التحكم في مثبط MR.
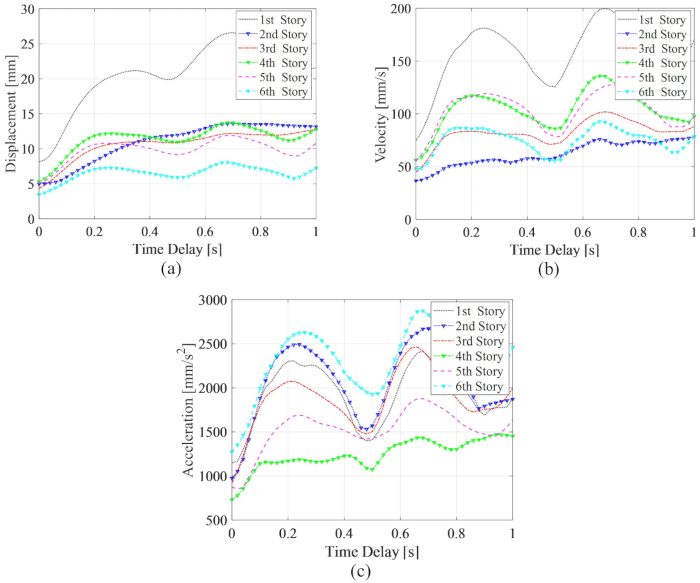
الشكل 11: الحد الأقصى RMS للردود جنبا إلى جنب مع التأخير الزمني للهيكل الخاضع للرقابة بطريقة TDC-SAC-PSO. (أ) التشرد؛ (ب) السرعة؛ (ج) التسارع. الاختصارات: RMS = جذر متوسط مربع. TDC-SAC-PSO = نظام تأخر الوقت مع التحكم في التعويض. الرجاء النقر هنا لعرض نسخة أكبر من هذا الرقم.
تظهر موثوقية الإزاحة والسرعة والتسارع جنبا إلى جنب مع التأخير الزمني في الشكل 12. تظهر موثوقية السرعة والتسارع تذبذب الفترة جنبا إلى جنب مع التأخير الزمني ، بينما انخفضت موثوقية الإزاحة بشكل كبير مع التأخير الزمني. كانت جميع قيم الموثوقية في أي تأخير زمني أقل من تلك التي لم يتم تأخيرها زمنيا. لذلك ، فإن طريقة تعويض التأخير الزمني ضرورية لتقليل تأثير التأخير الزمني على موثوقية الهيكل الذي يتم التحكم فيه بواسطة مخمد MR.
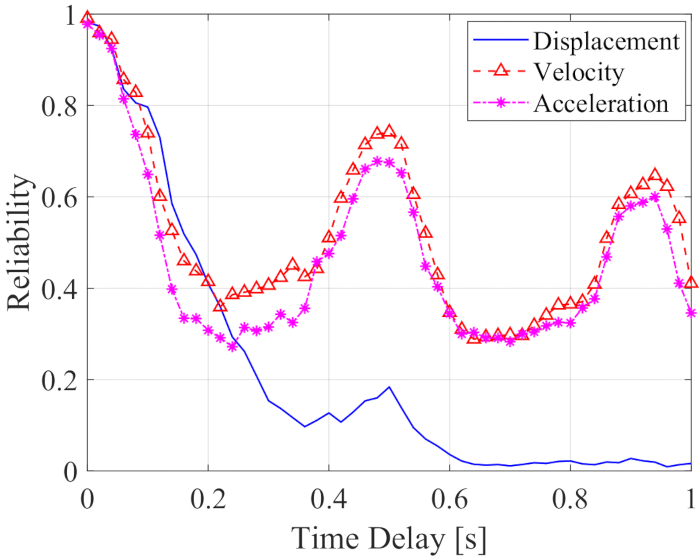
الشكل 12: موثوقية استجابات الهيكل الخاضع للرقابة جنبا إلى جنب مع التأخير الزمني. الرجاء النقر هنا لعرض نسخة أكبر من هذا الرقم.
3.2 تأثير التحكم في تعويض التأخر الزمني
بناء على طريقة TDC-SAC-PSO المقترحة ، تم تحليل هيكل 6-DOF مع مخمدات MR. يوضح الشكل 13 تواريخ وقت RMS للإزاحة والتسارع في الطابقين الأول والثالث للهياكل غير المنضبطة (Unc) و TDC-SAC-PSO التي يتم التحكم فيها بطريقة TDN-SAC-PSO. كان التأخير 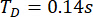 الزمني ، ونسبة
الزمني ، ونسبة 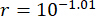 مصفوفة الترجيح ؛ كانت معلمات
مصفوفة الترجيح ؛ كانت معلمات  المثبط MR ،
المثبط MR ،  للطابق الأول ؛
للطابق الأول ؛  وللطابق
وللطابق  الثالث.
الثالث.

الشكل 13: تواريخ وقت RMS للإزاحة والتسارع في الطابقين الأول والثالث للهياكل التي يتم التحكم فيها بطرق مختلفة. (أ) النزوح في الطابق الأول؛ (ب) النزوح في الطابق الثالث؛ (ج) التسارع في الطابق الأول؛ (د) التسارع في الطابق الثالث. الاختصارات: RMS = جذر متوسط مربع. unc = غير خاضع للرقابة. TDC-SAC-PSO = نظام تأخر الوقت مع التحكم في التعويض ؛ TDN -SAC-PSO = نظام متأخر بالوقت مع التحكم في عدم التعويض. الرجاء النقر هنا لعرض نسخة أكبر من هذا الرقم.
تم تخفيض الحد الأقصى RMS للإزاحة في الطابقين الأول والثالث بنسبة 35.42٪ و 30.44٪ بطريقة TDN-SAC-PSO ، حيث لم يتم تعويض التأخير الزمني. بينما مع التعويض ، تم تخفيض الحد الأقصى RMS للإزاحة في الطابقين الأول والثالث بنسبة 49.33٪ و 53.39٪ على التوالي. بدون تعويض ، ارتفع الحد الأقصى للتسارع في الطابقين الأول والثالث بنسبة 16.22٪ و 2.88٪ ولكنه انخفض بنسبة 25.77٪ و 36.00٪ على التوالي ، مع التعويض. لذلك ، فإن تعويض التأخير الزمني في طريقة التحكم في المثبط بالرنين المغناطيسي ضروري لتقليل استجابات الهيكل ، خاصة بالنسبة للتسارع.
الشكل 14: ملفات PDF للإزاحة والتسارع في الطابقين الأول والثالث لطرق التحكم المختلفة. (أ) النزوح في الطابق الأول؛ (ب) النزوح في الطابق الثالث؛ (ج) التسارع في الطابق الأول؛ (د) التسارع في الطابق الثالث. الاختصارات: ملفات PDF = وظائف كثافة الاحتمالات. unc = غير خاضع للرقابة. TDC-SAC-PSO = نظام تأخر الوقت مع التحكم في التعويض ؛ TDN -SAC-PSO = نظام متأخر بالوقت مع التحكم في عدم التعويض. الرجاء النقر هنا لعرض نسخة أكبر من هذا الرقم.
يتم عرض ملفات PDF الخاصة بالإزاحة والتسارع في الطابقين الأول والثالث في الشكل 14 ، مما يكشف عن تأثيرات التحكم المختلفة لطرق TDC-SAC-PSO و TDN-SAC-PSO مقارنة بالهيكل غير الخاضع للرقابة. بدون تعويض ، كانت ملفات PDF الخاصة بالنزوح في الطابقين الأول والثالث لا تزال أضيق من تلك الموجودة في الهيكل غير الخاضع للرقابة. علاوة على ذلك ، مع تعويض التأخير الزمني ، أصبحت ملفات PDF الخاصة بالإزاحة أضيق من تلك الخاصة بالهيكل الذي يتم التحكم فيه بواسطة طريقة TDN-SAC-PSO. على عكس الإزاحة ، بدون تعويض ، كانت ملفات PDF الخاصة بالتسارع في الطابق الأول لطريقة TDN-SAC-PSO أوسع من تلك الخاصة بالهيكل غير الخاضع للرقابة. ومع ذلك ، مع التعويض ، كانت ملفات PDF الخاصة بالتسارع في كل من الطابقين الأول والثالث أضيق من تلك الموجودة في الهيكل غير الخاضع للرقابة. وبالتالي ، يتم التحقق من ضرورة تعويض التأخر الزمني لزيادة يقين استجابات الهيكل ، خاصة بالنسبة للتسارع.
| طريقة التحكم | التشريد | السرعه | تسريع | قوة التحكمفي الطابق 1 | قوة التحكمفي الطابق 3 |
| جامعة الأمم المتحدة | 0.0114 | 0.5822 | 0.6372 | -- | -- |
| TDN-SAC-PSO | 0.5851 | 0.5258 | 0.398 | 1 | 1 |
| TDC - SAC - PSO | 0.806 | 0.8674 | 0.8037 | 1 | 1 |
الجدول 4: موثوقية الهياكل التي يتم التحكم فيها بطرق مختلفة. الاختصارات: Unc = غير خاضع للرقابة. TDC-SAC-PSO = نظام تأخر الوقت مع التحكم في التعويض ؛ TDN -SAC-PSO = نظام متأخر بالوقت مع التحكم في عدم التعويض.
يتم عرض قيم موثوقية الإزاحة والسرعة والتسارع وقوة التحكم مع أنظمة الهيكل التي تتحكم فيها الطرق المختلفة في الجدول 4. تم حساب قيم موثوقية استجابات الهيكل باستخدام طريقة القيمة القصوى المكافئة25. من خلال التحكم في طريقة TDN-SAC-PSO ، زادت موثوقية الإزاحة مقارنة بالهيكل غير المنضبط ، بينما انخفضت موثوقية السرعة والتسارع. مع تعويض التأخير الزمني في طريقة TDC-SAC-PSO ، زادت موثوقية الإزاحة والسرعة والتسارع بشكل كبير. وإلى جانب ذلك، يتم الحفاظ على قيم موثوقية قوة التحكم لكل من الطريقتين TDN-SAC-PSO وTDN-SAC-PSO بما فيه الكفاية. وبالتالي ، فإن طريقة التحكم في تعويض التأخير الزمني المقترحة تحقق تأثير تحكم موات للهيكل الذي يتم التحكم فيه بواسطة مخمد MR.
3.3 تحسين المعلمة
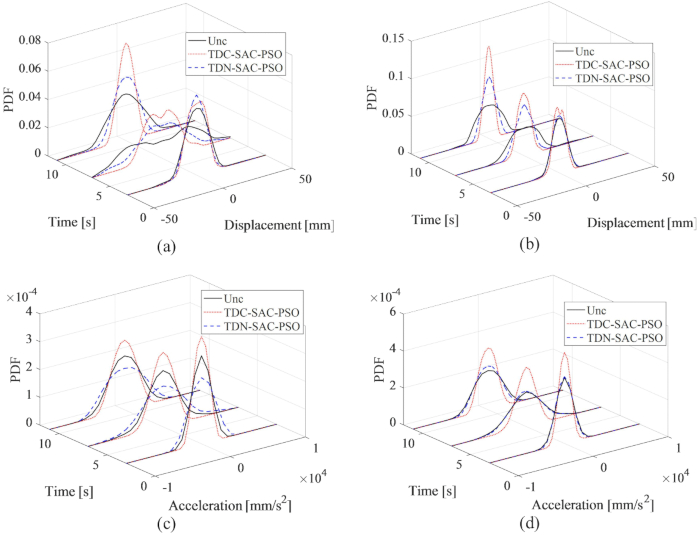
لتحقيق تأثير التحكم الأمثل ، تم تحسين معلمات طريقة التحكم المقترحة بناء على معيار الموثوقية. مع التأخير 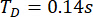 الزمني ، كانت
الزمني ، كانت  النتيجة المثلى ؛
النتيجة المثلى ؛ 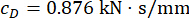 ، وبالنسبة
، وبالنسبة 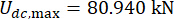 لمخمد MR في الطابق الأول ؛
لمخمد MR في الطابق الأول ؛ 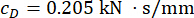 وبالنسبة
وبالنسبة  لمخمد MR الثالث.
لمخمد MR الثالث.
يتم عرض التاريخ الزمني RMS للإزاحة والتسارع في الطابقين الأول والثالث في الشكل 15 حيث تتم مقارنة تأثيرات التحكم لطرق TDC-SAC-PSO و SOSC-PSO والهيكل غير المنضبط. مع التحكم في المثبط بالرنين المغناطيسي ، مع أو بدون تعويض تأخير زمني ، انخفض RMS للإزاحة والتسارع بشكل كبير. باستخدام طريقة SOSC-PSO ، انخفض الحد الأقصى للإزاحة في الطابقين الأول والثالث بنسبة 65.15٪ و 63.16٪ بالنسبة للهيكل غير الخاضع للرقابة ، على التوالي. بالمقارنة مع طريقة TDC-SAC-PSO ، انخفضت الاستجابة للإزاحة بشكل أكبر. يتم تقليل الحد الأقصى للتسارع في الطابقين الأول والثالث بنسبة 23.39٪ و 35.60٪ لطريقة SOSC-PSO. كان هناك اختلاف طفيف في تأثير التحكم في التسارع لطريقتي SOSC-PSO و TDC-SAC-PSO، مما يشير إلى أن تأثير التحكم في تعويض التأخر الزمني كان مختلفا بالنسبة للإزاحة والتسارع.
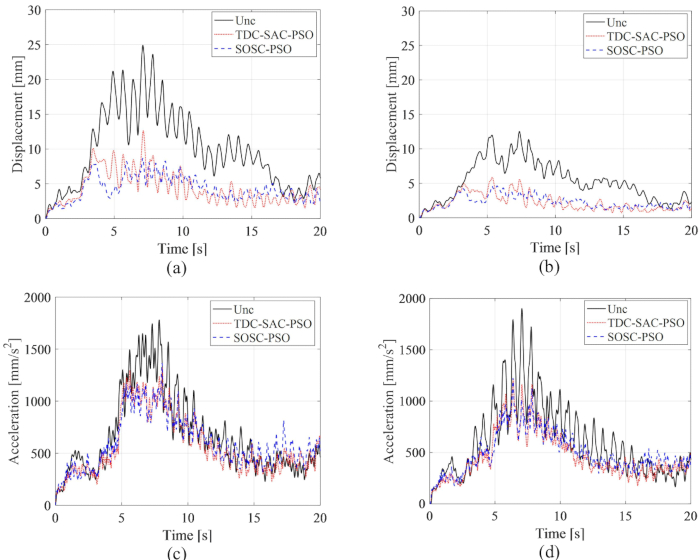
الشكل 15: تاريخ وقت RMS للإزاحة والتسارع في الطابقين الأول والثالث لطرق التحكم المختلفة. (أ) النزوح في الطابق الأول؛ (ب) النزوح في الطابق الثالث؛ (ج) التسارع في الطابق الأول؛ (د) التسارع في الطابق الثالث. الاختصارات: RMS = جذر متوسط مربع. unc = غير خاضع للرقابة. TDC-SAC-PSO = نظام تأخر الوقت مع التحكم في التعويض ؛ SOSC-PSO = طريقة التحكم شبه النشطة العشوائية المثلى مع تعويض التأخير الزمني. الرجاء النقر هنا لعرض نسخة أكبر من هذا الرقم.
يتم عرض ملفات PDF الخاصة بالإزاحة والتسارع في الطابقين الأول والثالث في الشكل 16. تم تضييق ملفات PDF الخاصة بالإزاحة والتسارع بواسطة طرق TDC-SAC-PSO و SOSC-PSO مقارنة بالبنية غير الخاضعة للرقابة. إلى جانب ذلك ، تم تضييق ملفات PDF الخاصة بالإزاحة والتسارع لطريقة SOSC-PSO مقارنة بتلك الخاصة بالهيكل المتحكم فيه بطريقة TDC-SAC-PSO. لذلك ، مع تحسين المعلمات ، حققت طريقة التحكم في تعويض التأخير الزمني المقترحة تأثير تحكم أفضل من عدم التحسين.
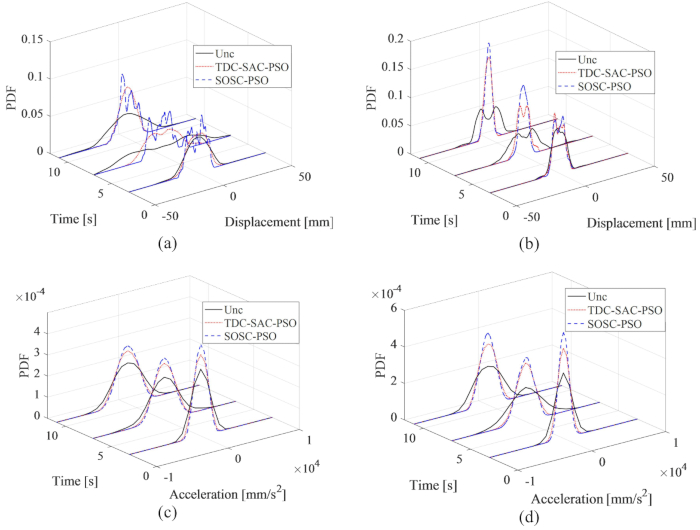
الشكل 16: ملفات PDF للإزاحة والتسارع في الطابقين الأول والثالث لطرق التحكم المختلفة. (أ) النزوح في الطابق الأول؛ (ب) النزوح في الطابق الثالث؛ (ج) التسارع في الطابق الأول؛ (د) التسارع في الطابق الثالث. الاختصارات: ملفات PDF = وظائف كثافة الاحتمالات. unc = غير خاضع للرقابة. TDC-SAC-PSO = نظام تأخر الوقت مع التحكم في التعويض ؛ SOSC-PSO = طريقة التحكم شبه النشطة العشوائية المثلى مع تعويض التأخير الزمني الرجاء النقر هنا لعرض نسخة أكبر من هذا الشكل.
يتم عرض قيم موثوقية الإزاحة والسرعة والتسارع وقوة التحكم في الجدول 5. كانت قيم الموثوقية لطريقة SOSC-PSO أعلى من تلك الخاصة بطريقة TDC-SAC-PSO. وفي الوقت نفسه ، لا تزال قوة التحكم تحتفظ بالموثوقية الكافية. وبالتالي ، فإن تحسين المعلمات ضروري لتحقيق أفضل تأثير تحكم لطريقة التحكم القائمة على مخمد MR.
| طريقة التحكم | التشريد | السرعه | تسريع | قوة التحكمفي الطابق 1 | قوة التحكمفي الطابق 3 |
| جامعة الأمم المتحدة | 0.0114 | 0.5822 | 0.6372 | -- | -- |
| TDC - SAC - PSO | 0.806 | 0.8674 | 0.8037 | 1 | 1 |
| SOSC-PSO | 0.9544 | 0.9314 | 0.8788 | 1 | 1 |
الجدول 5: موثوقية الهياكل التي يتم التحكم فيها بطرق مختلفة. الاختصارات: Unc = غير خاضع للرقابة. TDC-SAC-PSO = نظام تأخر الوقت مع التحكم في التعويض ؛ SOSC-PSO = طريقة التحكم شبه النشطة العشوائية المثلى مع تعويض التأخير الزمني.
النتائج
بهدف تأثير التأخير الزمني على فعالية التحكم في الطريقة القائمة على المثبط بالرنين المغناطيسي ، تم اقتراح طريقة تحكم شبه نشطة مع تعويض تأخير الوقت في هذه الورقة. في الطريقة المقترحة ، يتم تحسين المعلمات الحرجة بناء على معيار الموثوقية. من خلال مقارنة فعالية المكافحة ، يت...
Discussion
مع إدخال نظرية التحكم الأمثل العشوائي الفيزيائي (PSO) ، تم اقتراح طريقة التحكم شبه النشط العشوائي الأمثل مع تعويض التأخير الزمني (SOSC-PSO) في هذه الورقة ، والتي تم تصميمها للحفاظ على موثوقية الهياكل التي يتم التحكم فيها بواسطة مخمدات MR. للتعويض عن التأخير الزمني في الطريقة ال...
Disclosures
ليس لدى جميع المؤلفين تضارب في المصالح للإعلان عنه.
Acknowledgements
يعرب المؤلفون عن امتنانه للدعم المقدم من مؤسسة العلوم الطبيعية في مقاطعة خبي (المنحة رقم E2023210007).
Materials
| Name | Company | Catalog Number | Comments |
| MATLAB | MathWorks | 2016 | Using for the calculation of the proposed method |
References
- Yao, J. T. P. Concept of structural control. J Struct Div. 98 (7), 1567-1574 (1972).
- Liu, J., Silva, C. E., Dyke, S. J., Wu, Y., Liu, H. Using real-time hybrid simulation for active mass damper experimentation and validation. Mech Mach Theory. 191, 105474 (2024).
- Pan, H., Li, C., Cao, L. Bidirectional pendulum-type tuned tendem mass dampers-inerters for integrated control of alongwind and crosswind responses in super-tall buildings. J Build Eng. 100, 111676 (2025).
- Housner, G. W. et al. Structural control: past, present, and future. J Eng Mech. 123 (9), 897-971 (1997).
- Rahman, M., Ong, Z. C., Chong, W. T., Julai, S. Smart Semi-active PID-ACO control strategy for tower vibration reduction in Wind Turbines with MR damper. Earthq Eng Eng Vib. 18 (4), 887-902 (2019).
- Morales-Beltran, M., Paul, J. Active and semi-active strategies to control building structures under large earthquake motion. J Earthquake Eng. 19 (7), 1086-1111 (2015).
- Shu, Z., You, R., Xie, Y. Viscoelastic dampers for vibration control of building structures: A state-of-art review. J Earthq Eng. 28 (12), 3558-3585 (2024).
- Soong, T. T. Active structural control: Theory and practice. Longman Scientific & Technical. New York (1990).
- Wan, H. P., Ma, Q., Dong, G. S., Luo, Y., Ni, Y. Q. Data-driven model reduction approach for active vibration control of cable-strut structures. Eng Struct. 302, 117434 (2024).
- Cao, L., Li, X., Huang, Y., Li, C., Pan, H. High robust eddy current tuned tandem mass dampers-inerters for structures under the ground acceleration. Soil Dyn Earthq Eng. 188, 109040 (2025).
- Chha, H., Peng, Y. Adaptive semiactive control of structure with magnetorheological dampers using wavelet packet transform. Adv Struct Eng. 27 (9), 1509-1527 (2024).
- Zeng, X., Peng, Y., Chen, J. Serviceability-based damping optimization of randomly wind-excited high-rise buildings. Struct Des Tall Spec. 26 (11), e1371 (2017).
- Li, C., Chang, K., Cao, L., Huang, Y. Performance of a nonlinear hybrid base isolation system under the ground motions. Soil Dyn Earthq Eng. 143, 106589 (2021).
- Cao, L., Li, C. A high performance hybrid passive base-isolated system. Struct Control Health Monitoring. 29 (3), e2887 (2022).
- Zareie, S., Issa, A. S., Seethaler, R., Zabihollah, A., Ahmad, R. A novel SMA-magnetorheological hybrid bracing system for seismic control. Eng Struct. 244, 112709 (2021).
- Chu, S. Y., Soong, T. T., Reinhorn, A. M. Active, hybrid and semi-active structural control. John Wiley & Sons, New York (2005).
- Danielian, S. A., Jabbari, F., Zareian, F. Effects and distribution of semi-active resettable springs on the seismic response of asymmetric structures. Earthq Eng Struct D. 52 (10). 2966-2982 (2023).
- Shuang, Z., Wenliuhan, H. S., Liu, Y. H., Inoue, N., Zhai, Z. P. Seismic response control for bridge piers with semi-active MR damper based on displacement feedback. J Earthq Eng. 28 (3). 849-865 (2024).
- Wang, Y., Dyke, S. Modal-based LQG for smart base isolation system design in seismic response control. Struct Control Health Monitoring. 20 (5), 753-768 (2013).
- Desai, R. M. et al. Performance evaluation of a single sensor control scheme using a twin-tube MR damper based semi-active suspension. J Vib Eng Technol. 9, 1193-1210 (2021).
- Abdi, M. S., Nekooei, M. Jafari, M. A. Seismic control of multi-degrees-of-freedom structures by vertical mass isolation method using MR dampers. Earthq Eng Eng Vib. 23 (2), 503-510 (2024).
- Bhowmik, K., Debnath, N. Semi-active vibration control of soft-storey building with magnetorheological damper under seismic excitation. J Vib Eng Technol. 12 (4), 6943-6961 (2024).
- Yang, J. N., Akbarpour, A., Askar, G. Effect of time delay on control of seismic-excited buildings. J Struct Eng. 116 (10), 2801-2814 (1990).
- Temimi, H., Ben-Romdhane, M., El-Borgi, S., Cha, Y. Time-delay effects on controlled seismically excited linear and nonlinear structures. Int J Struct Stab Dyn. 16 (7), 1550031 (2016).
- Peng, J., Wang, L., Zhao, Y., Lenci, S. Time-delay dynamics of the MR damper-cable system with one-to-one internal resonances. Nonlinear Dynamics. 105 (2), 1343-1356 (2021).
- Cha, Y. J., Agrawal, A. K., Dyke, S. J. Time delay effects on large-scale MR damper based semi-active control strategies. Smart Mater Struct. 22 (1), 015011 (2013).
- Yu, Y. et al. Experimental study of wireless structural vibration control considering different time delays. Smart Mater Struct. 24, 045005 (2015).
- Ahmadizadeh, M., Mosqueda, G., Reinhorn, A. M. Compensation of actuator delay and dynamics for real-time hybrid structural simulation. Earthq Eng Struct Dyn. 37 (1), 21-42 (2008).
- Bathaei, A., Zahrai, S. M. Compensating time delay in semi-active control of a SDOF structure with MR damper using predictive control. Struc Eng Mech. 82 (4), 445-458 (2022).
- Dyke, S. J., Spencer, Jr, B. F., Sain, M. K., Carlson, J. D. Modeling and control of magnetorheological dampers for seismic response reduction. Smart Mater Struct. 5 (5), 565-575 (1996).
- Ying, Z. G., Ni, Y. Q., Ko, J. M. A semi-active stochastic optimal control strategy for nonlinear structural systems with MR dampers. Smart Struct Syst. 5 (1), 69-79 (2009).
- Rosol, M., Martynowicz, P. Implementation of the LQG controller for a wind turbine tower-nacelle model with a MR tuned vibration absorber. J Theor App Mech-Pol. 54 (4), 1109-1123 (2016).
- Lyu, M. Z., Feng, D. C., Chen, J. B., Li, J. A decoupled approach for determination of the joint probability density function of a high-dimensional nonlinear stochastic dynamical system via the probability density evolution method. Comput Method Appl M. 418 (A), 116443 (2024).
- Chha, H., Peng, Y. Multiscale stochastic optimal control of hysteretic structures based on wavelet transform and probability density evolution method. Eng Computation. 41 (4), 865-896 (2024).
- Li, J., Peng, Y. B., Chen, J. B. A physical approach to structural stochastic optimal controls. Probabilist Eng Mech. 25 (1), 127-141 (2010).
- Peng, Y. B., Yang, J. G., Li, J. Seismic risk-based stochastic optimal control of structures using magnetorheological dampers. Nat Hazards Rev. 18 (1), B4016001 (2017).
- Dong, X. M., Yu, M., Li, Z., Liao, C., Chen, W. Neural network compensation of semi-active Control for magneto-rheological suspension with time delay uncertainty. Smart Mater Struct. 18 (1), 015014 (2008).
- Peng, Y. B., Zhang, Z. Optimal MR damper-based semiactive control scheme for strengthening seismic capacity and structural reliability. J Eng Mech. 146 (6), 04020045 (2020).
- Luo, M. X., Gao, M. Cai, G. Delayed full-state feedback control of airfoil flutter using sliding mode control method. J Fluid Struct. 61, 262-273 (2016).
- Xu, J., Chung, K. W., Chan, C. L. An efficient method for studying weak resonant double Hopf bifurcation in nonlinear systems with delayed feedbacks. Siam J Appl Dyn Syst. 6 (1), 29-60 (2007).
- Yang, J. S., Jensen, H., Chen, J. B. Structural optimization under dynamic reliability constraints utilizing probability density evolution method and metamodels in augmented input space. Struct Multidiscip Optimization. 65, 107 (2022).
- Li, J., Chen, J. B. Stochastic dynamics of structures. John Wiley & Sons, Singapore (2009).
- Peng, Y. B., Li, J. Stochastic optimal control of structures. Springer (2019).
- Dowrick, C. Beyond depression: A new approach to understanding and management. Oxford University Press (2009).
- Wang, D., Li, J. Physical random function model of ground motions for engineering purposes. Sci China Technol Sci. 54 (1), 175-182 (2011).
- Wang, D., Li, J. A random physical model of seismic ground motion field on local engineering site. Sci China Technol Sci. 55 (7), 2057-2065 (2012).
- Chen, J. B., Li, J. Strategy for selecting representative points via tangent spheres in the probability density evolution method. Int J Numer Meth Eng. 74 (13), 1988-2014 (2008).
Reprints and Permissions
Request permission to reuse the text or figures of this JoVE article
Request PermissionExplore More Articles
This article has been published
Video Coming Soon
Copyright © 2025 MyJoVE Corporation. All rights reserved