Se requiere una suscripción a JoVE para ver este contenido. Inicie sesión o comience su prueba gratuita.
Research Article
Método de control semiactivo estocástico de la estructura basado en amortiguadores magnetorreológicos teniendo en cuenta el retardo temporal
En este artículo
Resumen
En este trabajo se propone un método de control semiactivo óptimo estocástico con compensación de retardo de tiempo (SOSC-PSO), que está diseñado para mantener la confiabilidad de las estructuras controladas por amortiguadores MR.
Resumen
El uso de amortiguadores magnetorreológicos (MR) en sistemas de control semiactivos se enfrenta a un desafío clave: el retardo de tiempo causado por los procesos de retroalimentación, lo que reduce la confiabilidad de las estructuras de ingeniería civil bajo excitaciones estocásticas. Este artículo propone un método de control semiactivo óptimo estocástico con compensación de retardo de tiempo (SOSC-PSO), aprovechando la teoría de control óptimo estocástico físico (PSO) para abordar este problema y mantener la confiabilidad estructural. El método propuesto deriva la fuerza de control semiactiva en función de los estados actuales y anteriores, compensando los retrasos de tiempo en el proceso de control. Para optimizar la eficacia del control, los parámetros clave se ajustan en función de un criterio de fiabilidad del sistema. Los análisis de validación en estructuras de un solo grado de libertad y múltiples grados de libertad bajo excitaciones sísmicas estocásticas muestran que los retrasos de tiempo perjudican significativamente el rendimiento de los amortiguadores de RM. Sin embargo, el método SOSC-PSO con compensación de retardo de tiempo mejora significativamente la efectividad del control y, con parámetros optimizados, mejora la confiabilidad del sistema de control estructural más allá de los métodos sin optimización de parámetros.
Introducción
Mejorar el rendimiento de las estructuras de ingeniería frente a eventos catastróficos, como terremotos y vientos extremos, sigue siendo una preocupación primordial dentro de la comunidad de ingeniería civil. Se ha demostrado que el control estructural, una técnica eficaz para reducir las vibraciones, mejora tanto la seguridad como la funcionalidad de dichas estructuras 1,2,3. En las últimas décadas, se han desarrollado varios métodos y tecnologías avanzados para este propósito. Estos métodos se pueden clasificar en cuatro categorías según el tipo de energía utilizada para accionar los dispositivos de control: sistemas de control activos, semiactivos, pasivos e híbridos 4,5,6,7.
En el control activo, la fuerza de control requerida se aplica directamente a través de los dispositivos de control, lo que requiere una cantidad significativa de energía 8,9,10. El control semiactivo, por otro lado, implica ajustar las propiedades de los dispositivos de control (como la amortiguación o la rigidez) en función de las señales de control, requiriendo mucha menos energía en comparación con los sistemas activos11. El control pasivo, por el contrario, se basa en la disipación de energía sin ninguna entrada de energía externa en el sistema 12,13,14. Los sistemas híbridos combinan las características de las estrategias de control activo/semiactivo y pasivo para lograr un rendimiento más eficaz15. Entre estos enfoques, el control semiactivo se considera particularmente prometedor debido a su equilibrio entre el bajo consumo de energía y la alta eficiencia 16,17,18. El amortiguador magnetorreológico (MR), con sus características superiores de amortiguación dinámica, se considera uno de los dispositivos de control semiactivo más eficaces 19,20,21,22.
Sin embargo, surge un desafío en los sistemas de control semiactivos que utilizan amortiguadores MR, ya que la lógica de retroalimentación inevitablemente introduce retrasos de tiempo. Estos retrasos suelen estar causados por varios factores 23,24,25, entre ellos: (i) la adquisición y el procesamiento de los datos de los sensores, (ii) el cálculo de la fuerza de control requerida por el controlador26, (iii) la transmisión de señales a través de transductores a los amortiguadores MR27, y (iv) la generación de fuerza real por los propios amortiguadores MR28. Tales retrasos pueden conducir a discrepancias entre la fuerza de control producida y la fuerza esperada por la estructura, comprometiendo significativamente la efectividad del control29. Desafortunadamente, la mayoría de los algoritmos de control existentes para los amortiguadores MR no tienen en cuenta estos retrasos.
Además, debido a la aleatoriedad inherente de los eventos catastróficos, cualquier algoritmo de control semiactivo eficaz debe ser capaz de mantener el rendimiento bajo excitaciones estocásticas. El método de control gaussiano cuadrático lineal (LQG), una técnica clásica de optimización estocástica, se ha explorado para mitigar las vibraciones en estructuras equipadas con amortiguadores de resonancia magnética. Por ejemplo, Dyke et al. propusieron una estrategia de control óptima recortada LQG para mejorar la respuesta sísmica de estructuras equipadas con amortiguadores MR, utilizando retroalimentación de aceleración30. Ying et al. introdujeron una estrategia de control óptimo del estocástico semiactivo no recortado para estructuras no lineales con amortiguadores de RM, incorporando técnicas de promediación estocástica y programación dinámica31. Otros estudios han aplicado el control LQG basado en modales para mejorar el rendimiento sísmico de edificios aislados en base19 y han analizado su efectividad para la mitigación de vibraciones en torres de turbinas eólicas32. Sin embargo, los métodos clásicos de LQG, que asumen ruido gaussiano blanco, no son adecuados para modelar la naturaleza no estacionaria y no gaussiana de excitaciones del mundo real como terremotos o vientos fuertes. Para abordar esto, se ha desarrollado el concepto de control estocástico óptimo (PSO) basado en la física33,34, que supera las limitaciones de los métodos tradicionales de LQG y ofrece un marco más preciso para el manejo de diversas excitaciones estocásticas35. Los estudios han demostrado que el control óptimo del estocástico semiactivo basado en PSO mejora significativamente la mitigación de la vibración para estructuras lineales y no lineales sometidas a fuerzas sísmicas estocásticas36.
Por lo tanto, existe una necesidad urgente de un método de control semiactivo robusto que compense los retrasos de tiempo, mejorando la confiabilidad de las estructuras controladas por amortiguadores MR25,37. Además, para garantizar un rendimiento de control óptimo bajo excitaciones estocásticas, es esencial optimizar los parámetros críticos del método de control propuesto utilizando un enfoque basado en la fiabilidad. Por lo tanto, en este trabajo se propone un método de control semiactivo óptimo estocástico con compensación de retardo de tiempo (SOSC-PSO) para mejorar la confiabilidad de las estructuras con amortiguadores MR.
Protocolo
1. Método de control semiactivo óptimo estocástico
Dado que el efecto de control de un amortiguador MR está significativamente influenciado por el inevitable retardo de tiempo, se desarrolla un método de control semiactivo con un algoritmo de compensación de retardo de tiempo para aumentar el rendimiento de la estructura controlada. Además, la aleatoriedad inherente a las excitaciones externas causa las incertidumbres obvias de las respuestas dinámicas. El control PSO se introduce para optimizar los parámetros críticos del método propuesto para garantizar la confiabilidad del sistema de control de estructuras.
1.1 Algoritmo de compensación del control semiactivo
Sin pérdida de generalidad, considere una estructura de n grados de libertades (n-DOF) controlada por amortiguadores MR con retardo de tiempo, de la cual la ecuación de movimiento sometida a excitaciones estocásticas viene dada por:
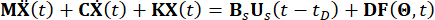 (1)
(1)
Donde  representan las matrices de masa, amortiguamiento y rigidez de la estructura, respectivamente; n representa el número de grados de libertad de la estructura controlada. Los vectores de desplazamiento, velocidad y aceleración de la estructura están representados por
representan las matrices de masa, amortiguamiento y rigidez de la estructura, respectivamente; n representa el número de grados de libertad de la estructura controlada. Los vectores de desplazamiento, velocidad y aceleración de la estructura están representados por 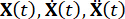 , respectivamente. Los puntos pequeños uno y dos encima de los símbolos representan las derivadas de primera y segunda vez. Us (t - tD) representa el vector r-dimensional de la fuerza de control retardada en el tiempo de los amortiguadores MR, y r representa el número de amortiguadores; t representa el tiempo; tD denota un retardo de tiempo, que se supone que es uniforme en todos los amortiguadores en este estudio, donde
, respectivamente. Los puntos pequeños uno y dos encima de los símbolos representan las derivadas de primera y segunda vez. Us (t - tD) representa el vector r-dimensional de la fuerza de control retardada en el tiempo de los amortiguadores MR, y r representa el número de amortiguadores; t representa el tiempo; tD denota un retardo de tiempo, que se supone que es uniforme en todos los amortiguadores en este estudio, donde 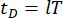 , con aquí el número
, con aquí el número 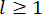 entero , y
entero , y 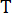 denota el período de muestreo.
denota el período de muestreo. 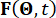 representa el vector p-dimensional de las excitaciones estocásticas, y
representa el vector p-dimensional de las excitaciones estocásticas, y  representa el vector de parámetros estocásticos que caracteriza la aleatoriedad asociada con las excitaciones externas. La dimensión de
representa el vector de parámetros estocásticos que caracteriza la aleatoriedad asociada con las excitaciones externas. La dimensión de  depende del modelo utilizado para las excitaciones externas, pero no está relacionada con los grados de libertad mecánicos de la estructura. Bs y D son matrices n x r y n x p que especifican las ubicaciones de los amortiguadores y las excitaciones externas, respectivamente. En la representación del espacio de estados, la Ec. (1) se escribe como:
depende del modelo utilizado para las excitaciones externas, pero no está relacionada con los grados de libertad mecánicos de la estructura. Bs y D son matrices n x r y n x p que especifican las ubicaciones de los amortiguadores y las excitaciones externas, respectivamente. En la representación del espacio de estados, la Ec. (1) se escribe como:
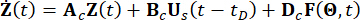 (2)
(2)
Donde 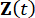 representa el vector de estado de 2n dimensiones;
representa el vector de estado de 2n dimensiones; 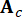 representa la matriz del sistema de 2n x 2n;
representa la matriz del sistema de 2n x 2n; 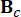 representa la matriz de ubicación de 2n x r de los amortiguadores de resonancia magnética;
representa la matriz de ubicación de 2n x r de los amortiguadores de resonancia magnética; 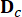 Representa la matriz de ubicación 2n x p de excitaciones externas. Estos parámetros se expresan como:
Representa la matriz de ubicación 2n x p de excitaciones externas. Estos parámetros se expresan como:
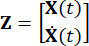 , ,
, , 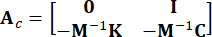 ,
,  (
(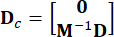 3)
3)
Donde 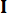 denota una matriz de identidad con el mismo orden de
denota una matriz de identidad con el mismo orden de 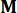 . Para facilitar el cálculo, la ecuación del espacio de estados continuos Ec. (2) se puede expresar en forma discreta como:
. Para facilitar el cálculo, la ecuación del espacio de estados continuos Ec. (2) se puede expresar en forma discreta como:
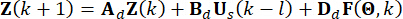 (4)
(4)
Donde el punto 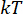 de tiempo se simplifica como
de tiempo se simplifica como 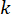 . Y
. Y  ,
, 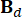 ,
, 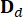 denotan matrices 2n x 2n, 2n x r y 2n x p, que se expresan como:
denotan matrices 2n x 2n, 2n x r y 2n x p, que se expresan como:
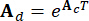 , ,
, , 
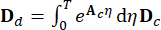 (5)
(5)
Donde 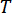 denota el período de muestreo.
denota el período de muestreo.
Para lograr una eficacia similar a la del control activo, se propone un método de control sencillo y eficiente basado en el algoritmo de Hrovat38 para el control basado en amortiguadores de RM con retardo de tiempo:
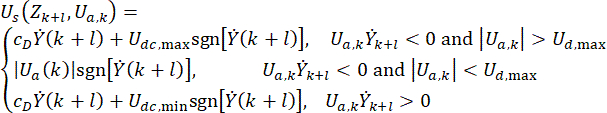 (6)
(6)
donde  representa la señal de fuerza de control semiactiva en el punto de tiempo\
representa la señal de fuerza de control semiactiva en el punto de tiempo\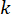 para el amortiguador MR;
para el amortiguador MR; 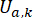 representa la fuerza de control activo de referencia con compensación de retardo de tiempo;
representa la fuerza de control activo de referencia con compensación de retardo de tiempo;  representa la fuerza de amortiguación máxima del amortiguador MR, que es modificable;
representa la fuerza de amortiguación máxima del amortiguador MR, que es modificable; 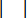 representa el símbolo de operación de valor absoluto;
representa el símbolo de operación de valor absoluto; 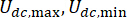 representan las fuerzas coulombicas máximas y mínimas del amortiguador MR;
representan las fuerzas coulombicas máximas y mínimas del amortiguador MR;  representa el coeficiente de amortiguación viscosa;
representa el coeficiente de amortiguación viscosa; 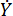 representa la entrada de velocidad en el amortiguador MR, que es la velocidad de movimiento del pistón en relación con el cilindro del amortiguador. En la Ec. (6),
representa la entrada de velocidad en el amortiguador MR, que es la velocidad de movimiento del pistón en relación con el cilindro del amortiguador. En la Ec. (6),  representan los parámetros diseñados del amortiguador MR.
representan los parámetros diseñados del amortiguador MR.
La Ec. (6) muestra el cálculo de la fuerza de control semiactiva del amortiguador MR con retardo de tiempo. Se observa que la fuerza  de control semiactiva, en el paso
de control semiactiva, en el paso  de tiempo en la Ec. (4), se calcula en función de la fuerza
de tiempo en la Ec. (4), se calcula en función de la fuerza  de control activa en el paso
de control activa en el paso  de tiempo y la variable
de tiempo y la variable 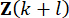 de estado en el paso
de estado en el paso  de tiempo desde el retardo de los pasos de
de tiempo desde el retardo de los pasos de 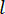 tiempo. Para obtener la fuerza
tiempo. Para obtener la fuerza  de control activo, la función de costo convencional se establece mediante
de control activo, la función de costo convencional se establece mediante
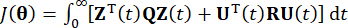 (7)
(7)
Donde  representa la matriz de ponderación semidefinida positiva simétrica 2n x 2n del estado del sistema;
representa la matriz de ponderación semidefinida positiva simétrica 2n x 2n del estado del sistema;  representa la matriz de ponderación definida positiva simétrica r x r de la fuerza de control. Se ve que la excitación externa es insignificante. De hecho, según la Ec. (7), el sistema de control de la estructura puede lograr el efecto de control óptimo sea cual sea el tipo de excitación externa. Como forma discreta, la Ec. (7) se expresa como39:
representa la matriz de ponderación definida positiva simétrica r x r de la fuerza de control. Se ve que la excitación externa es insignificante. De hecho, según la Ec. (7), el sistema de control de la estructura puede lograr el efecto de control óptimo sea cual sea el tipo de excitación externa. Como forma discreta, la Ec. (7) se expresa como39:
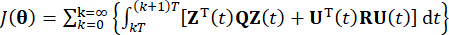 (8)
(8)
La minimización de la función  de costo conduce a un problema de valor extremo condicional, y la fuerza
de costo conduce a un problema de valor extremo condicional, y la fuerza  de control activa se calcula por25:
de control activa se calcula por25:
 (9)
(9)
Donde 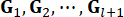 denotan las ganancias de control para la variable
denotan las ganancias de control para la variable 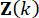 de estado en el período
de estado en el período  de tiempo y la fuerza
de tiempo y la fuerza 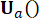 de control activa en el período
de control activa en el período 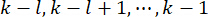 de tiempo , que se determina mediante las matrices de
de tiempo , que se determina mediante las matrices de 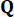 ponderación y
ponderación y 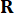 37. Desde el inevitable retardo de tiempo, la fuerza
37. Desde el inevitable retardo de tiempo, la fuerza 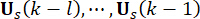 de control obtenida se actúa sobre la estructura en puntos de
de control obtenida se actúa sobre la estructura en puntos de 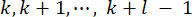 tiempo. Por lo tanto, la fuerza de control activa en la Ec. (9) se calcula mediante:
tiempo. Por lo tanto, la fuerza de control activa en la Ec. (9) se calcula mediante:
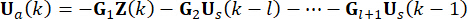 (10)
(10)
Para la claridad de la concepción, la fuerza de control semiactiva en la Ec. (10) se expresa de la siguiente manera en función de la Ec. (6):
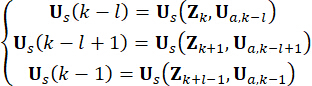 (11)
(11)
Donde  denota la fuerza de control activa en el punto
denota la fuerza de control activa en el punto  de tiempo . Sustituyendo la Ec. (11) por la Ec. (10),
de tiempo . Sustituyendo la Ec. (11) por la Ec. (10),
 (12)
(12)
NOTA: Todos los valores de estado  desde el punto
desde el punto  de tiempo hasta
de tiempo hasta 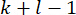 son necesarios para calcular
son necesarios para calcular  . Por lo tanto, se introduce el siguiente método de predicción de estado40.
. Por lo tanto, se introduce el siguiente método de predicción de estado40.
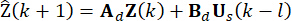 (13)
(13)
Donde  denota la variable predicha. Por la iteración de la Ec. (13), se calcula el estado
denota la variable predicha. Por la iteración de la Ec. (13), se calcula el estado  en
en  . La fuerza de control activo Ua(k) se expresa como:
. La fuerza de control activo Ua(k) se expresa como:
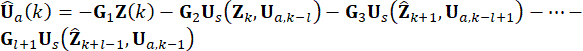 (14)
(14)
La fuerza de control semiactiva se puede obtener combinando Eqs. (6), (12) y (13).
1.2 Análisis de fiabilidad del sistema de control de estructuras
De acuerdo con el principio de preservación de la probabilidad, el sistema 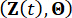 aumentado y
aumentado y 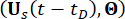 la estructura con amortiguadores de RM se conservan en función de la probabilidad, y se rigen por las siguientes ecuaciones generalizadas de evolución de la densidad de probabilidad (GDEE)38:
la estructura con amortiguadores de RM se conservan en función de la probabilidad, y se rigen por las siguientes ecuaciones generalizadas de evolución de la densidad de probabilidad (GDEE)38:
 (15)
(15)
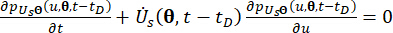 (16)
(16)
Donde  ,
,  denotan los componentes correspondientes del estado del sistema y la fuerza de control semiactiva con retardo de tiempo, respectivamente;
denotan los componentes correspondientes del estado del sistema y la fuerza de control semiactiva con retardo de tiempo, respectivamente; 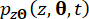 y
y  denotan las funciones de densidad de probabilidad conjunta de los sistemas
denotan las funciones de densidad de probabilidad conjunta de los sistemas 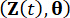 de muestreo aumentados y
de muestreo aumentados y 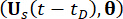 , respectivamente;
, respectivamente; 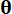 denotan la muestra dentro del espacio de muestra de
denotan la muestra dentro del espacio de muestra de 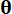 ;
;  y
y  ) denotan las derivadas parciales de tiempo de primer orden de los componentes de estado del sistema y de fuerza de control semiactiva, respectivamente. La densidad de probabilidad conjunta funciona
) denotan las derivadas parciales de tiempo de primer orden de los componentes de estado del sistema y de fuerza de control semiactiva, respectivamente. La densidad de probabilidad conjunta funciona 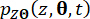 y
y  se puede lograr resolviendo las Ecs. (15) y (16) con las siguientes condiciones iniciales:
se puede lograr resolviendo las Ecs. (15) y (16) con las siguientes condiciones iniciales:
 (17)
(17)
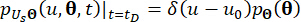 (18)
(18)
Donde 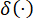 denota la función delta de Dirac;
denota la función delta de Dirac; 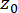 y
y 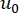 denotan los valores iniciales deterministas de
denotan los valores iniciales deterministas de  y
y 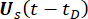 , respectivamente;
, respectivamente; 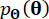 denotan la función de densidad de probabilidad de la muestra
denotan la función de densidad de probabilidad de la muestra 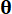 .
.
Las funciones de densidad de probabilidad instantánea de  y
y 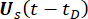 se pueden obtener mediante la integración unidimensional de
se pueden obtener mediante la integración unidimensional de 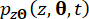 y
y  sobre el dominio del espacio muestral:
sobre el dominio del espacio muestral:
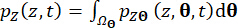 (19)
(19)
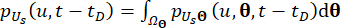 (20)
(20)
Donde 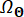 denota el dominio de distribución de
denota el dominio de distribución de  .
.
Basado en las Ecs. (19) y (20), se ve que la información probabilística completa de las magnitudes físicas en cuestión se deriva fácilmente, si se definen sus relaciones asociadas con los parámetros del algoritmo. La fiabilidad de las magnitudes físicas en cuestión puede calcularse mediante la siguiente función de rendimiento pertinente:
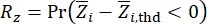 (21)
(21)
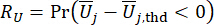 (22)
(22)
Donde 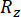 y
y 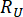 denotan la fiabilidad calculada de la cantidad de estado en cuestión y de la fuerza de control semiactiva, respectivamente;
denotan la fiabilidad calculada de la cantidad de estado en cuestión y de la fuerza de control semiactiva, respectivamente;  denota el vector de valor extremo equivalente de la i-ésima cantidad física de que se trate de la estructura controlada;
denota el vector de valor extremo equivalente de la i-ésima cantidad física de que se trate de la estructura controlada; 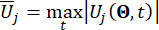 denota el vector de valor extremo equivalente de la j-ésima fuerza de control; el sombrero '-' en los símbolos indica el vector de valor extremo equivalente41
denota el vector de valor extremo equivalente de la j-ésima fuerza de control; el sombrero '-' en los símbolos indica el vector de valor extremo equivalente41 ; denota la i-ésima cantidad física de la k-ésima DOF de la estructura controlada;
; denota la i-ésima cantidad física de la k-ésima DOF de la estructura controlada; 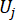 denota la j-ésima fuerza de control;
denota la j-ésima fuerza de control; 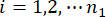 ,
, 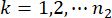 ,
,  ,
, ,
,  y
y  denotan el número de magnitudes físicas afectadas y la profundidad de campo de la estructura y los amortiguadores MR instalados en la estructura, respectivamente.
denotan el número de magnitudes físicas afectadas y la profundidad de campo de la estructura y los amortiguadores MR instalados en la estructura, respectivamente.  y
y 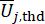 denota los umbrales de
denota los umbrales de  y
y  ;
;  denota la probabilidad del evento aleatorio.
denota la probabilidad del evento aleatorio.
1.3 Optimización de parámetros
La relación de las amplitudes de y  altamente influye en la efectividad del
altamente influye en la efectividad del  control38 en la modalidad de control de retroalimentación. Por lo tanto, para lograr la mejor efectividad de control,
control38 en la modalidad de control de retroalimentación. Por lo tanto, para lograr la mejor efectividad de control, y
y  deben optimizarse. Además, como método de control basado en amortiguadores MR, la efectividad del control también se ve afectada por los parámetros del dispositivo,
deben optimizarse. Además, como método de control basado en amortiguadores MR, la efectividad del control también se ve afectada por los parámetros del dispositivo,  en la Ec. (6). Para lograr la confiabilidad óptima del sistema de control de estructuras, el criterio basado en la confiabilidad se propone en la Ec. (25).
en la Ec. (6). Para lograr la confiabilidad óptima del sistema de control de estructuras, el criterio basado en la confiabilidad se propone en la Ec. (25).
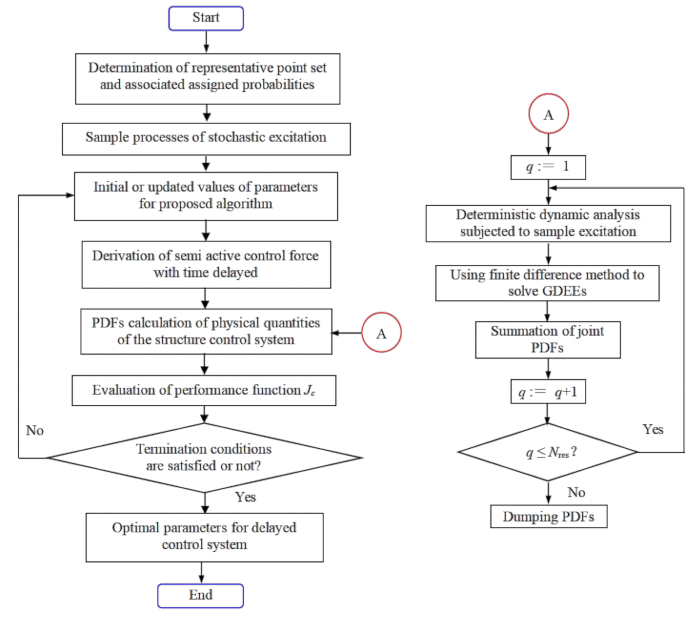
Figura 1: Diagrama de flujo de optimización de parámetros para el control de estructura semiactiva óptima estocástica con compensación de retardo de tiempo. Abreviaturas: GDEE = Ecuación Diferencial Generalizada del Evento ; PDF = Función de densidad de probabilidad. Haga clic aquí para ver una versión más grande de esta figura.
En resumen, se requieren dos etapas para llevar a cabo el control estocástico óptimo de la estructura semiactiva basado en amortiguadores MR con compensación de retardo de tiempo:
1.3.1 Minimizando la función  de costo mostrada en la Ec. (7), se logra la lógica de retroalimentación de estado en el sentido de muestras, es decir, Ec. 12)
de costo mostrada en la Ec. (7), se logra la lógica de retroalimentación de estado en el sentido de muestras, es decir, Ec. 12)
1.3.2 Minimizando la función  de rendimiento basada en la confiabilidad, se logran los parámetros óptimos en el sentido de las estadísticas. La Figura 1 presenta el diagrama de flujo de optimización de los parámetros del controlador en el paso 1.3.2.
de rendimiento basada en la confiabilidad, se logran los parámetros óptimos en el sentido de las estadísticas. La Figura 1 presenta el diagrama de flujo de optimización de los parámetros del controlador en el paso 1.3.2.
Los siguientes pasos en el paso 1.3.2, que involucran dos capas de bucles, son los siguientes:
1.3.2.1 La partición del espacio de probabilidades asignadas de las excitaciones estocásticas, que se caracteriza por el vector  de parámetros estocásticos, permite la identificación de un conjunto de puntos
de parámetros estocásticos, permite la identificación de un conjunto de puntos 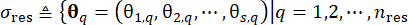 representativos junto con sus probabilidades asignadas asociadasPq. Este enfoque permite la generación eficiente de procesos de muestra para que la excitación estocástica, denotada como
representativos junto con sus probabilidades asignadas asociadasPq. Este enfoque permite la generación eficiente de procesos de muestra para que la excitación estocástica, denotada como 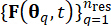 , se obtenga fácilmente.
, se obtenga fácilmente.
1.3.2.2 Para la optimización de parámetros del sistema de control de estructura semiactiva, inicialice o actualice los valores de las ponderaciones  de costo-función y
de costo-función y  . A continuación, se calcula la fuerza de control de retroalimentación de estado asociada con retardo de tiempo, véase la Ec. (12).
. A continuación, se calcula la fuerza de control de retroalimentación de estado asociada con retardo de tiempo, véase la Ec. (12).
1.3.2.3 Obtención de las funciones de densidad de probabilidad (FDP) de las respuestas estructurales y la fuerza de control resolviendo las GDEEs mostradas en las Ecs. (17)–(20):
La optimización se realiza sin conexión, pero no en línea. En la aplicación del método propuesto en sistemas de control de estructuras reales, se han logrado los óptimos  y
y  la optimización no es necesaria en el proceso real aplicable.
la optimización no es necesaria en el proceso real aplicable.
Análisis dinámico determinístico del sistema de control de estructura semiactiva sometido a excitación de muestra, mediante el cual se calculan las 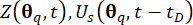 cantidades físicas en cuestión y sus derivadas
cantidades físicas en cuestión y sus derivadas  .
.
Mediante el empleo de un método de diferencia finita, como el esquema de Lax-Wendroff modificado con propiedades de variación total decreciente (TVD), se pueden resolver las ecuaciones diferenciales generalizadas (GDEE) y se pueden derivar soluciones numéricas para las funciones 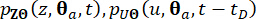 de densidad de probabilidad conjunta.
de densidad de probabilidad conjunta.
Repitiendo los dos pasos anteriores del análisis dinámico determinista y el método de diferencias finitas, y recorriendo todos los puntos representativos 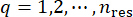 , las funciones de densidad de probabilidad se pueden obtener por sumatoria:
, las funciones de densidad de probabilidad se pueden obtener por sumatoria:
 (23)
(23)
 (24)
(24)
Donde  representa la medida de área del subdominio asociado con el punto
representa la medida de área del subdominio asociado con el punto 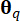 de muestreo. El método utilizado para resolver la Ecuación Diferencial Generalizada del Evento (GDEE) se conoce como el método de evolución de la densidad de probabilidad (PDEM)42.
de muestreo. El método utilizado para resolver la Ecuación Diferencial Generalizada del Evento (GDEE) se conoce como el método de evolución de la densidad de probabilidad (PDEM)42.
1.3.2.4 Para evaluar su fiabilidad se utilizan las PDF de las magnitudes físicas pertinentes, que luego se incorporan a la función  de rendimiento del criterio probabilístico.
de rendimiento del criterio probabilístico.
1.3.2.5 Evaluar si se han cumplido los criterios de terminación para el proceso de optimización de parámetros. Si no se cumplen las condiciones, vuelva al paso 1.3.2.2; Si es así, se pueden determinar los parámetros óptimos para el sistema de control retardado en el tiempo. En este trabajo, se utiliza la caja de herramientas del algoritmo genético (GA) en MATLAB para la optimización de parámetros, lo que facilita la actualización de parámetros y define las condiciones de terminación. Mediante un algoritmo genético, los valores óptimos se pueden lograr dentro de diez iteraciones, y la convergencia es estable sin problemas de mínimos locales. Aunque el costo computacional del AG es mayor que la optimización del enjambre de partículas o los métodos basados en gradientes, el AG es bueno para tratar problemas complejos e indiferenciables, como el de este manuscrito. Por lo tanto, se aplica el GA. Y dado que la propiedad de convergencia rápida, el costo computacional de GA es aceptable.
1.3.2.6 Para lograr un control óptimo de la fiabilidad, se formula la siguiente función  de rendimiento. Minimice
de rendimiento. Minimice  para determinar los valores óptimos de los parámetros
para determinar los valores óptimos de los parámetros  y
y  :
:
 } (25)
} (25)
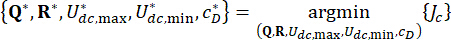 (26)
(26)
Como se mencionó anteriormente, las matrices de ponderación del controlador son simétricas, donde los elementos de la matriz  corresponden a los pesos asignados al desplazamiento, la velocidad y su interacción, mientras que los elementos de la matriz
corresponden a los pesos asignados al desplazamiento, la velocidad y su interacción, mientras que los elementos de la matriz  representan los pesos relacionados con la fuerza de control. Con base en los hallazgos de estudios previos
representan los pesos relacionados con la fuerza de control. Con base en los hallazgos de estudios previos  38, se ha observado que la variación de las configuraciones de los pesos costo-función tiene
38, se ha observado que la variación de las configuraciones de los pesos costo-función tiene  un impacto mínimo en la efectividad del control. En consecuencia, en este estudio se adopta una configuración simplificada, como se describe a continuación:
un impacto mínimo en la efectividad del control. En consecuencia, en este estudio se adopta una configuración simplificada, como se describe a continuación:
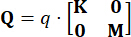 ,
, 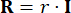 (27)
(27)
Donde 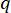 denota el coeficiente de la matriz de ponderación de estado que se va a definir;
denota el coeficiente de la matriz de ponderación de estado que se va a definir; 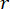 denota el coeficiente de la matriz de ponderación de control que se va a definir;
denota el coeficiente de la matriz de ponderación de control que se va a definir; 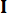 denota la matriz de identidad. El efecto de control está influenciado por la relación de
denota la matriz de identidad. El efecto de control está influenciado por la relación de 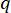 a,
a, 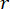 pero no por los valores en sí. Además,
pero no por los valores en sí. Además, 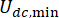 en la Ec. (6) denota la fuerza coulombica mínima del amortiguador MR, lo que significa que
en la Ec. (6) denota la fuerza coulombica mínima del amortiguador MR, lo que significa que  con la entrada de corriente en el amortiguador siendo cero. Entonces, la Ec. (26) se puede expresar aún más como:T
con la entrada de corriente en el amortiguador siendo cero. Entonces, la Ec. (26) se puede expresar aún más como:T
 (28)
(28)
¿Dónde 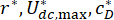 están los coeficientes óptimos de interés? Para hacerlos razonables en ingeniería, los rangos óptimos de ellos se basan en la capacidad de producción de las fábricas de amortiguadores MR.
están los coeficientes óptimos de interés? Para hacerlos razonables en ingeniería, los rangos óptimos de ellos se basan en la capacidad de producción de las fábricas de amortiguadores MR.
Obviamente, los parámetros óptimos obtenidos por la Ec. (28) mantienen la efectividad de control óptima del algoritmo de control semiactivo propuesto con retardo de tiempo, lo que permite que el sistema de control de la estructura logre la confiabilidad óptima equilibrada sometida a excitaciones estocásticas.
2. Estudio de caso
Para analizar la efectividad del método de control semiactivo propuesto con compensación de retardo de tiempo para un amortiguador de RM, una estructura plana de marco de corte de un solo piso unida a un amortiguador de RM se sometió al movimiento sísmico del suelo estocástico horizontal, como se muestra en la Figura 2. Los parámetros del sistema de estructura controlado semiactivamente son los siguientes: masa 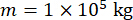 de la estructura, frecuencia
de la estructura, frecuencia  circular natural, relación
circular natural, relación 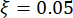 de amortiguación. De acuerdo con la experiencia pasada y las escalas de amortiguadores existentes en el mercado, los valores umbral de desplazamiento estructural, velocidad, aceleración y fuerza de control son 10 mm, 100 mm/s, 1.500 mm/s2 y 150 kN, respectivamente. Para representar el movimiento sísmico estocástico del suelo, se empleó el modelo de movimiento estocástico del suelo motivado físicamente43:
de amortiguación. De acuerdo con la experiencia pasada y las escalas de amortiguadores existentes en el mercado, los valores umbral de desplazamiento estructural, velocidad, aceleración y fuerza de control son 10 mm, 100 mm/s, 1.500 mm/s2 y 150 kN, respectivamente. Para representar el movimiento sísmico estocástico del suelo, se empleó el modelo de movimiento estocástico del suelo motivado físicamente43:
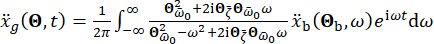 (29)
(29)
Donde 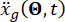 representa el movimiento del suelo en el dominio del tiempo en el sitio de ingeniería y
representa el movimiento del suelo en el dominio del tiempo en el sitio de ingeniería y 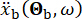 denota el movimiento del suelo en el dominio de la frecuencia en el lecho rocoso. El vector
denota el movimiento del suelo en el dominio de la frecuencia en el lecho rocoso. El vector  caracteriza la naturaleza estocástica del movimiento del suelo en la superficie del sitio de ingeniería. Los parámetros
caracteriza la naturaleza estocástica del movimiento del suelo en la superficie del sitio de ingeniería. Los parámetros 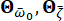 son variables estocásticas que describen las características del suelo del sitio, incluyendo la frecuencia
son variables estocásticas que describen las características del suelo del sitio, incluyendo la frecuencia  predominante y el amortiguamiento
predominante y el amortiguamiento  equivalente. El vector
equivalente. El vector 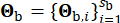 representa la naturaleza estocástica del movimiento del suelo en el lecho rocoso, que está influenciada por las propiedades de la fuente y la trayectoria de propagación, indicando
representa la naturaleza estocástica del movimiento del suelo en el lecho rocoso, que está influenciada por las propiedades de la fuente y la trayectoria de propagación, indicando 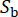 el número de variables estocásticas involucradas en esta etapa.
el número de variables estocásticas involucradas en esta etapa.  se refiere a la frecuencia circular, e i es la unidad imaginaria.
se refiere a la frecuencia circular, e i es la unidad imaginaria.
La frecuencia  predominante y la relación
predominante y la relación  de amortiguamiento equivalente del sitio de ingeniería son parámetros clave que caracterizan las propiedades dinámicas del suelo del sitio. La distribución probabilística y los parámetros estadísticos de estas cantidades se pueden determinar en función de los registros de aceleración sísmica recopilados de una clase específica de sitios de ingeniería. Con fines ilustrativos, se consideró una clase de sitio con un rango de velocidad de onda de corte de [150, 250] m/s, y el período característico de diseño del movimiento del suelo se estableció en 0,45 s.
de amortiguamiento equivalente del sitio de ingeniería son parámetros clave que caracterizan las propiedades dinámicas del suelo del sitio. La distribución probabilística y los parámetros estadísticos de estas cantidades se pueden determinar en función de los registros de aceleración sísmica recopilados de una clase específica de sitios de ingeniería. Con fines ilustrativos, se consideró una clase de sitio con un rango de velocidad de onda de corte de [150, 250] m/s, y el período característico de diseño del movimiento del suelo se estableció en 0,45 s.
Los parámetros  críticos,
críticos,  se trataron como variables estocásticas mutuamente independientes, ambas siguiendo una distribución log-normal para la identificación de parámetros. Los parámetros estadísticos fueron los siguientes: las medias de
se trataron como variables estocásticas mutuamente independientes, ambas siguiendo una distribución log-normal para la identificación de parámetros. Los parámetros estadísticos fueron los siguientes: las medias de  ,
,  fueron 12 rad/s y 0,1, respectivamente. Los coeficientes de variación de
fueron 12 rad/s y 0,1, respectivamente. Los coeficientes de variación de  y
y  fueron de 0,42 y 0,35, respectivamente. El movimiento del suelo en el lecho rocoso se modeló como un proceso de ruido blanco gaussiano con una amplitud de Fourier de 0,20 m/s2, correspondiente a una aceleración máxima del suelo de 0,11 g. El ángulo de fase utilizado para generar el movimiento del lecho rocoso se denotó como
fueron de 0,42 y 0,35, respectivamente. El movimiento del suelo en el lecho rocoso se modeló como un proceso de ruido blanco gaussiano con una amplitud de Fourier de 0,20 m/s2, correspondiente a una aceleración máxima del suelo de 0,11 g. El ángulo de fase utilizado para generar el movimiento del lecho rocoso se denotó como 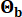 . Por lo tanto, Sb = 1 y
. Por lo tanto, Sb = 1 y 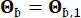 . Este enfoque puede considerarse como el modelado de movimientos estocásticos condicionales del suelo con una probabilidad de superación dada44. La suposición de distribución logarítmica normal se utiliza ampliamente en el modelado del movimiento del suelo debido a su capacidad para capturar la naturaleza sesgada de los parámetros de movimiento del suelo observados.
. Este enfoque puede considerarse como el modelado de movimientos estocásticos condicionales del suelo con una probabilidad de superación dada44. La suposición de distribución logarítmica normal se utiliza ampliamente en el modelado del movimiento del suelo debido a su capacidad para capturar la naturaleza sesgada de los parámetros de movimiento del suelo observados.
Para evaluar la sensibilidad de esta suposición, en otras investigaciones se han realizado análisis adicionales utilizando distribuciones probabilísticas alternativas, incluyendo las distribuciones normal y gamma45,46. Los resultados indican que, si bien las tendencias generales siguen siendo consistentes, la distribución logarítmica normal proporciona el mejor ajuste a los datos observados, particularmente para capturar el comportamiento de la cola de las medidas de intensidad del movimiento del suelo
En virtud del método de las esferas tangentes47, se seleccionó una colección de 221 puntos representativos con probabilidades asignadas asociadas y se sintetizaron aceleraciones de terreno representativas. La frecuencia de muestreo fue de 50 Hz y la duración de los movimientos del suelo fue de 20,48 s. Para asignar una intensidad no estacionaria al movimiento del suelo simulado, se utilizó una función de modulación uniforme y su formulación fue la siguiente42:
 (30)
(30)
Donde  tomar 2 y 16 s, respectivamente.
tomar 2 y 16 s, respectivamente.
En la Figura 3 se muestran la media y la desviación estándar del movimiento sísmico estocástico del suelo, así como una historia temporal del movimiento sísmico representativo del suelo. La amplitud de la media (0,06 m/s2) fue ~8% de la amplitud de la desviación estándar (0,8 m/s2), lo que indica que el modelo de movimiento estocástico del suelo motivado físicamente exhibía la propiedad de media cero. Mientras tanto, el movimiento sísmico del suelo exhibió notables comportamientos no estacionarios tanto en el dominio temporal como en el de frecuencia.
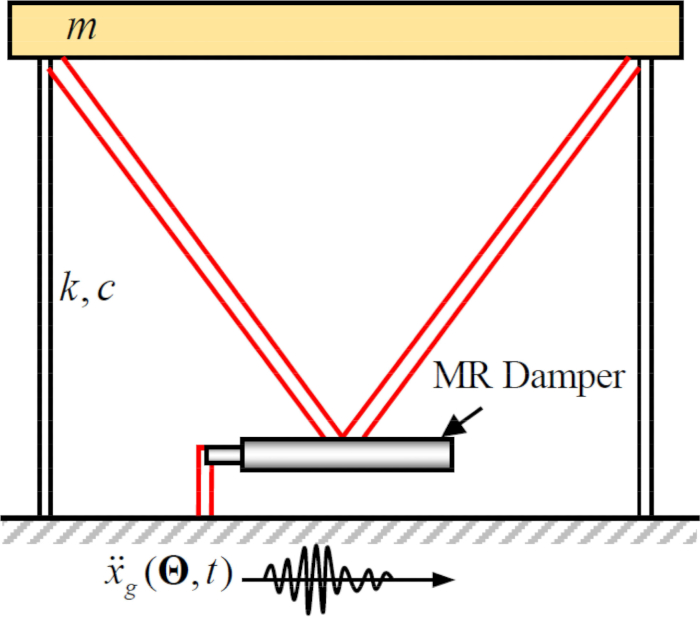
Figura 2: Croquis de un marco de corte de un solo piso con un amortiguador magnetorreológico. 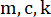 denotan la masa de la estructura, la relación de amortiguación y la rigidez;
denotan la masa de la estructura, la relación de amortiguación y la rigidez; 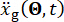 denota la excitación sísmica estocástica. Haga clic aquí para ver una versión más grande de esta figura.
denota la excitación sísmica estocástica. Haga clic aquí para ver una versión más grande de esta figura.
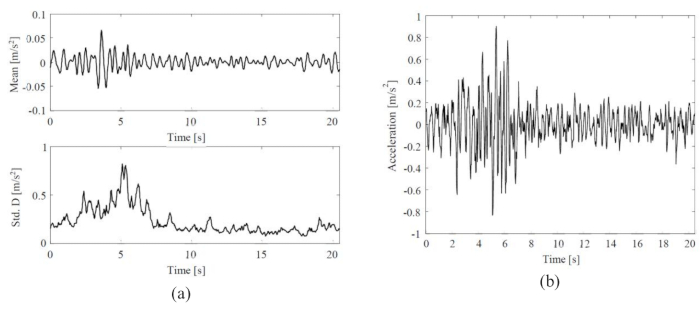
Figura 3: Estadísticas y muestras representativas de movimientos sísmicos del terreno seleccionados. (A) Media y desviación estándar del movimiento sísmico estocástico del suelo; (B) Historia temporal del movimiento sísmico representativo del terreno. Haga clic aquí para ver una versión más grande de esta figura.
2.1 Análisis de la influencia del retardo
Para analizar la influencia del retardo de tiempo en la efectividad del control semiactivo de un amortiguador MR, la Figura 4 muestra el desplazamiento, la velocidad y la aceleración RMS (respuesta cuadrática media) de la estructura controlada. La relación de la matriz de ponderación y los parámetros del amortiguador fueron 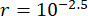 ,
, 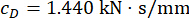 , y
, y 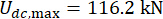 , que son los resultados optimizados sin retardode tiempo 38. Las respuestas de la estructura controlada con retardo de tiempo fueron mayores que las de la estructura controlada sin retardo de tiempo, y la influencia del retardo de tiempo en el efecto de control representó la periodicidad junto con el aumento del retardo de tiempo. Dado que el método de control semiactivo con un amortiguador de RM es un tipo de método de retroalimentación, se consideró que la periodicidad de la influencia estaba relacionada con el período natural de la estructura controlada (T = 0,56 s).
, que son los resultados optimizados sin retardode tiempo 38. Las respuestas de la estructura controlada con retardo de tiempo fueron mayores que las de la estructura controlada sin retardo de tiempo, y la influencia del retardo de tiempo en el efecto de control representó la periodicidad junto con el aumento del retardo de tiempo. Dado que el método de control semiactivo con un amortiguador de RM es un tipo de método de retroalimentación, se consideró que la periodicidad de la influencia estaba relacionada con el período natural de la estructura controlada (T = 0,56 s).
En comparación con las respuestas de la estructura no controlada, de las cuales el desplazamiento, la velocidad y la aceleración máximos de la MRS fueron de 24,6 mm, 270,0 mm/s y 3111,3 mm/s2, la estructura controlada por el amortiguador de la RM logró un efecto notable. A diferencia de la inestabilidad de la estructura controlada activa con retardo de tiempo25, el método de control semiactivo basado en amortiguadores MR aún obtuvo algún efecto incluso con retardo de tiempo.
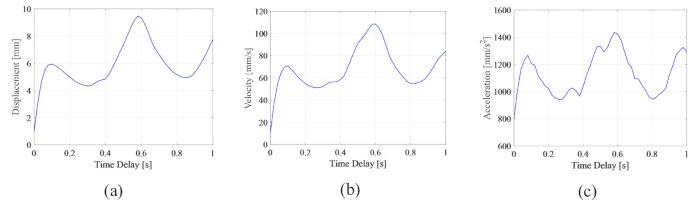
Figura 4: Los cuadrados medios máximos de las respuestas de la estructura controlada con el tiempo. A) Desplazamiento; b) Velocidad; c) Aceleración. Haga clic aquí para ver una versión más grande de esta figura.
Para analizar la influencia del retardo de tiempo en la confiabilidad de una estructura controlada semiactivamente, la Figura 5 muestra la confiabilidad del desplazamiento, la velocidad y la aceleración con el retardo de tiempo creciente. La fiabilidad de las respuestas de la estructura controlada con cualquier retardo de tiempo fue menor que los valores sin retardo de tiempo, lo que significa que la fiabilidad de la estructura controlada disminuyó con el retardo de tiempo. Mientras tanto, al igual que el RMS máximo, el efecto del control de confiabilidad mostró periodicidad con el aumento del retardo de tiempo. Además, la fiabilidad de la estructura controlada, con o sin retardo de tiempo, fue superior a los valores de las estructuras no controladas con fiabilidad de desplazamiento, velocidad y aceleración de 0,0954, 0,1058 y 0,1111.
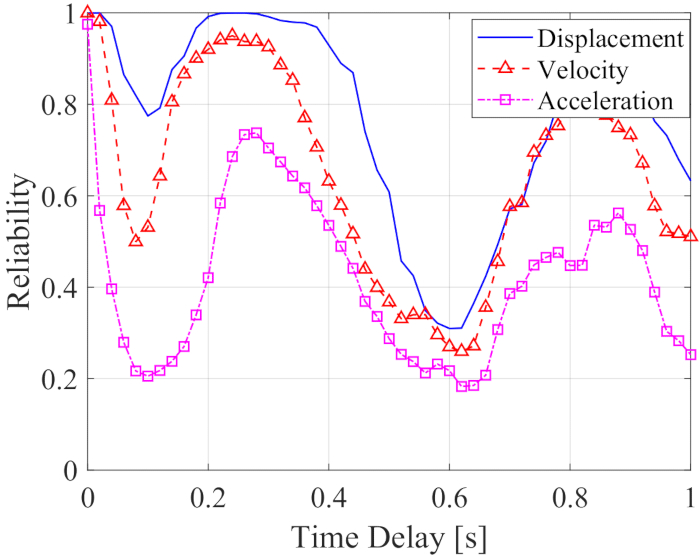
Figura 5: Fiabilidad de las respuestas de la estructura controlada con un retardo de tiempo creciente. Haga clic aquí para ver una versión más grande de esta figura.
En resumen, las respuestas de la estructura se mitigaron mediante el método de control semiactivo. Sin embargo, la efectividad del control, independientemente del RMS o la confiabilidad, del método de control semiactivo disminuyó por el retardo de tiempo. Por lo tanto, es necesario compensar el retraso de tiempo.
2.1.1 Análisis del método de compensación de retardo
Para analizar la efectividad del método de compensación de retardo de tiempo propuesto, se comparan los historiales de tiempo RMS de desplazamiento, velocidad y aceleración para el sistema no controlado (Unc), el sistema con retardo de tiempo con control sin compensación (TDN-SAC-PSO) y el sistema de retardo de tiempo con compensación controlada (TDC-SAC-PSO) en la Figura 6, donde el retardo de tiempo fue de 0,1 s. Los parámetros de la matriz de ponderación y el método de control semiactivo son los mismos que en el paso 2.1.
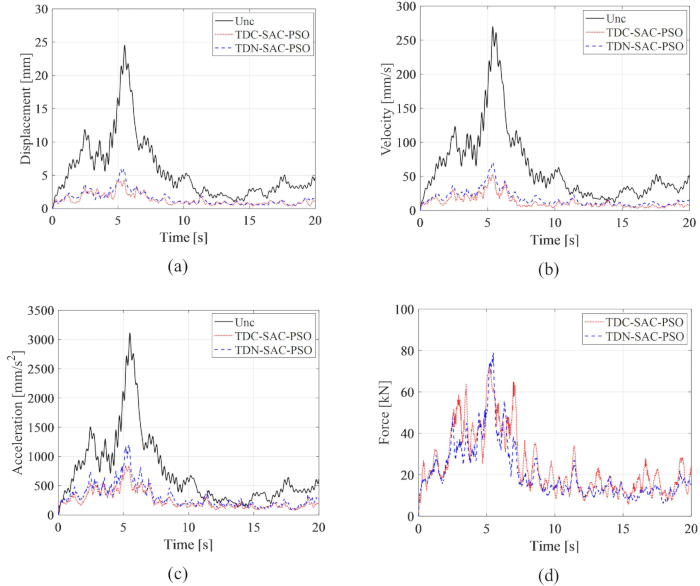
Figura 6: Comparación de la historia del tiempo de raíz cuadrada media de estructuras controladas por diferentes métodos. A) Desplazamiento; b) Velocidad; c) aceleración; (D) Fuerza de control. Abreviaturas: Unc = no controlado; TDC-SAC-PSO = sistema de retardo temporizado con compensación controlada; TDN -SAC-PSO = sistema temporizado con control sin compensación. Haga clic aquí para ver una versión más grande de esta figura.
Ambos métodos de control disminuyeron significativamente las respuestas de la estructura en comparación con la estructura no controlada, lo que revela las ventajas del método de control basado en amortiguadores MR. En comparación con la estructura no controlada, el RMS máximo de desplazamiento, velocidad y aceleración se reduce en un 75,79%, 73,75% y 61,22% con el método TDN-SAC-PSO. Además, con la compensación de retardo de tiempo, las respuestas de la estructura controlada disminuyen en un 82,59%, 80,40% y 73,04% con el método TDC-SAC-PSO. El RMS máximo de la fuerza de control con el método TDC-SAC-PSO disminuyó en un 8,43% en comparación con el método TDN-SAC-PSO, aunque las respuestas a las vibraciones del primer método fueron menores que las del segundo. El análisis anterior indica que la influencia del retardo de tiempo en el método de control basado en el amortiguador MR disminuyó efectivamente mediante el método de compensación, lo que muestra la necesidad de compensación de retardo de tiempo para el método de control semiactivo del amortiguador MR.
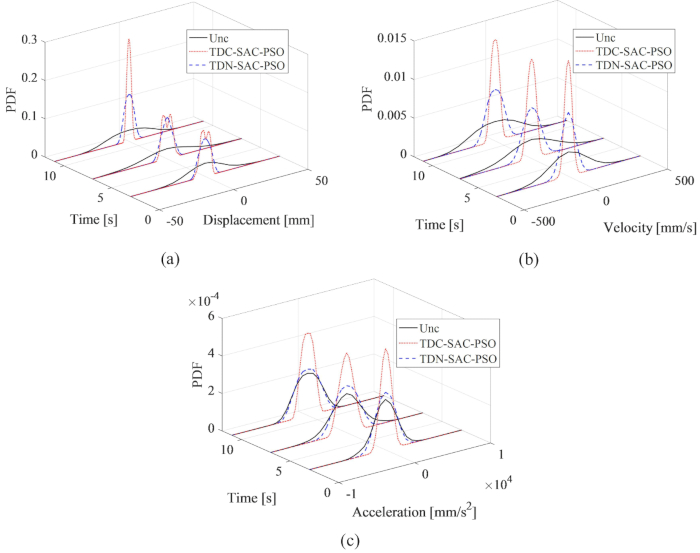
Figura 7: Comparación en PDF en momentos típicos de las respuestas de la estructura. A) Desplazamiento; b) Velocidad; c) Aceleración. Abreviaturas: PDF = función de densidad de probabilidad; Unc = incontrolado; TDC-SAC-PSO = sistema de retardo temporizado con compensación controlada; TDN -SAC-PSO = sistema temporizado con control sin compensación. Haga clic aquí para ver una versión más grande de esta figura.
Para revelar de manera integral el efecto del método de compensación propuesto sobre la incertidumbre de las respuestas de la estructura controlada, en la Figura 7 se muestran las comparaciones de la función de densidad de probabilidad (PDF) de desplazamiento, velocidad y aceleración en tiempos típicos, 3, 7 y 11s. Las PDF para el método TDN-SAC-PSO fueron más estrechas que las de la estructura no controlada, lo que significa que la incertidumbre de las respuestas de la estructura disminuyó con el método de control semi-activo incluso con retardo de tiempo. Cuando se compensó el retraso de tiempo, los PDF de las respuestas se redujeron aún más. Por lo tanto, el método de compensación propuesto es necesario para mejorar el efecto de control semiactivo.
| Método de control | Desplazamiento | Velocidad | Aceleración | Fuerza de control | Valor mínimo |
| Unc | 0.0954 | 0.1058 | 0.1111 | -- | 0.1111 |
| TDC-SAC-PSO | 0.9565 | 0.8107 | 0.7654 | 0.9845 | 0.7654 |
| TDN-SAC-PSO | 0.7747 | 0.531 | 0.2054 | 0.884 | 0.2054 |
Tabla 1: Respuestas a las vibraciones y fiabilidad de la fuerza de control de estructuras controladas por diferentes métodos. Abreviaturas: Unc = no controlado; TDC-SAC-PSO = sistema de retardo temporizado con compensación controlada; TDN -SAC-PSO = sistema temporizado con control sin compensación.
En la Tabla 1 se muestran las respuestas a la vibración y la fiabilidad de la fuerza de control de las estructuras controladas por el método No controlado, TDC-SAC-PSO-y TDN-SAC-PSO. Con el control del método TDN-SAC-PSO, la fiabilidad de la estructura aumentó drásticamente en comparación con la estructura no controlada, lo que valida la eficacia del método de control basado en amortiguadores MR, incluso con el tiempo. Sin embargo, con la compensación de retardo de tiempo, la fiabilidad aumentó significativamente en comparación con sin compensación, especialmente para la aceleración. También es destacable que la confiabilidad de las diferentes respuestas y la fuerza de control mostraron diferencias significativas para el método TDC-SAC-PSO. Esto indica que los valores óptimos de los parámetros críticos para el control sin retardo de tiempo no son óptimos para el control con retardo de tiempo. Para lograr el efecto de control óptimo de las respuestas de vibración y la fuerza de control con influencia de retardo de tiempo, los parámetros deben optimizarse aún más. Sobre la base del análisis anterior, se concluye que el método de control semiactivo con un amortiguador MR puede disminuir efectivamente las respuestas a la vibración de la estructura, mientras que los parámetros deben optimizarse debido a la influencia del retardo de tiempo.
2.2 Optimización de parámetros
Para alcanzar los valores óptimos de los parámetros, se aplicó el método de optimización integrada basado en el criterio de confiabilidad38. La optimización de los parámetros críticos se llevó a cabo con 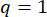 ,
, 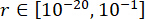 ,
,  ,
, 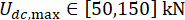 , y los tiempos sintonizables de las fuerzas del amortiguador MR s = 8. Para implementar la optimización se utilizó la caja de herramientas GA de MATLAB.
, y los tiempos sintonizables de las fuerzas del amortiguador MR s = 8. Para implementar la optimización se utilizó la caja de herramientas GA de MATLAB.
Los resultados de optimización de los parámetros son  ,
, 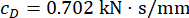 y
y  para el retardo
para el retardo 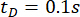 de tiempo . La Figura 8 muestra los historiales de tiempo RMS de desplazamiento, velocidad, aceleración y fuerza de control para las estructuras controladas por el método no controlado (Unc), TDC-SAC-PSO y SOSC-PSO. El método SOSC-PSO denota el método de control semiactivo con compensación de retardo de tiempo y valores de parámetros críticos optimizados.
de tiempo . La Figura 8 muestra los historiales de tiempo RMS de desplazamiento, velocidad, aceleración y fuerza de control para las estructuras controladas por el método no controlado (Unc), TDC-SAC-PSO y SOSC-PSO. El método SOSC-PSO denota el método de control semiactivo con compensación de retardo de tiempo y valores de parámetros críticos optimizados.
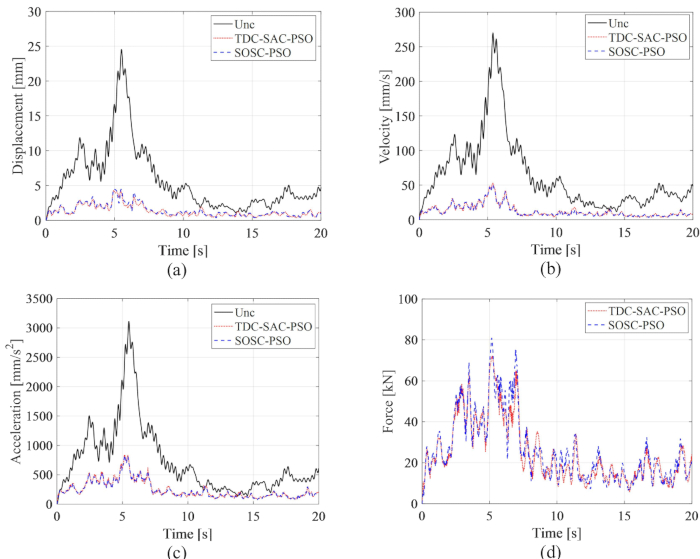
Figura 8: Historiales de tiempo RMS de desplazamiento, velocidad, aceleración y fuerza de control para estructuras controladas por el método no controlado y TDC-SAC-PSO y el método SOSC-PSO. A) Desplazamiento; b) Velocidad; c) aceleración; (D) Fuerza de control. Abreviaturas: Unc = no controlado; TDC-SAC-PSO = sistema de retardo temporizado con compensación controlada; SOSC-PSO = Método de control semiactivo óptimo estocástico con compensación de retardo de tiempo. Haga clic aquí para ver una versión más grande de esta figura.
En la Figura 8 se observa que los efectos de control de los métodos TDC-SAC-PSO y SOSC-PSO mostraron poca diferencia. El RMS máximo de la velocidad de desplazamiento y la aceleración para el primer método fue 81,60%, 81,21%, 73,62% de la estructura no controlada y 82,59%, 80,40%, 73,04% para el segundo método. Para analizar exhaustivamente las características de probabilidad de las respuestas para ambos métodos de control, la Figura 9 muestra los PDF de desplazamiento, velocidad y aceleración para las estructuras controladas por el método no controlado, TDC-SAC-PSO y SOSC-PSO. Ambos métodos de control tenían casi los mismos PDF de desplazamiento y velocidad en tiempos típicos. Las FDP de aceleración del método SOSC-PSO fueron más estrechas que las del método TDC-SAC-PSO, lo que significa que la incertidumbre de la aceleración logró un mejor efecto de control con el método anterior.
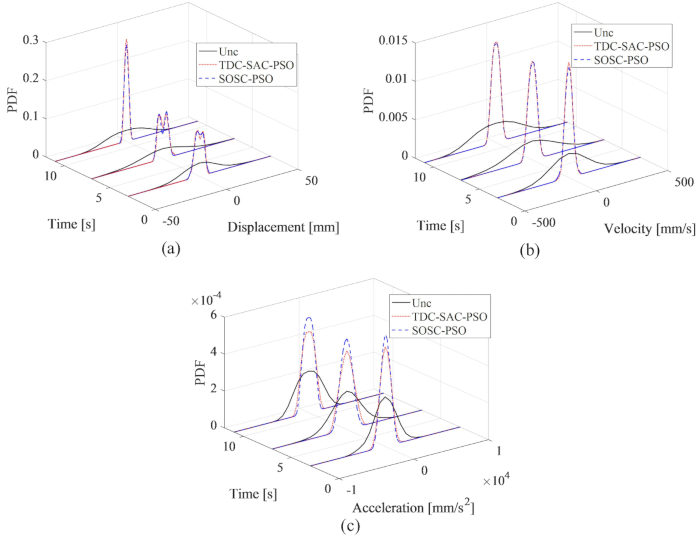
Figura 9: Comparación de PDFs de desplazamiento, velocidad y aceleración para diferentes estructuras controladas. A) Desplazamiento; b) Velocidad; c) Aceleración. Abreviaturas: PDFs = funciones de densidad de probabilidad; Unc = incontrolado; TDC-SAC-PSO = sistema de retardo temporizado con compensación controlada; SOSC-PSO = Método de control semiactivo óptimo estocástico con compensación de retardo de tiempo. Haga clic aquí para ver una versión más grande de esta figura.
En la Tabla 2 se muestra la confiabilidad del desplazamiento, la velocidad, la aceleración y la fuerza de control para las estructuras no controladas y controladas por el método TDC-SAC-PSO y SOSC-PSO. Ambos métodos de control lograron un aumento significativo en la confiabilidad en comparación con la estructura no controlada. La fiabilidad del desplazamiento mostró poca diferencia entre los métodos TDC-SAC-PSO y SOSC-PSO. Mientras que la fiabilidad de la aceleración, la menor fiabilidad de la estructura controlada, logró un aumento notable. Esto significa que el método SOSC-PSO logra el efecto de control óptimo del equilibrio.
| Método de control | Desplazamiento | Velocidad | Aceleración | Fuerza de control | Valor mínimo |
| Unc | 0.0954 | 0.1058 | 0.1111 | -- | 0.1111 |
| TDC-SAC-PSO | 0.9565 | 0.8107 | 0.7654 | 0.9845 | 0.7654 |
| SOSC-PSO | 0.953 | 0.8704 | 0.8934 | 0.9586 | 0.8934 |
Tabla 2: Fiabilidad para estructuras controladas por diferentes métodos. Abreviaturas: Unc = no controlado; TDC-SAC-PSO = sistema de retardo temporizado con compensación controlada; SOSC-PSO = Método de control semiactivo óptimo estocástico con compensación de retardo de tiempo.
Se analizó la efectividad del método SOSC-PSO propuesto con retardo 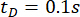 temporal. Para verificar aún más el método propuesto para diferentes retardos de tiempo, la Tabla 3 muestra los valores óptimos de los parámetros y la confiabilidad correspondiente para el rango
temporal. Para verificar aún más el método propuesto para diferentes retardos de tiempo, la Tabla 3 muestra los valores óptimos de los parámetros y la confiabilidad correspondiente para el rango 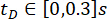 de retardo de tiempo.
de retardo de tiempo.
| tD(s) | lg(r*) | CD(kN·s/mm) | U dc,máx (kN) | Desplazamiento | Velocidad | Aceleración | Fuerza de control |
| 0 | -2.524 | 1.44 | 116.163 | 0.9997 | 0.9998 | 0.9752 | 1 |
| 0.02 | -4.413 | 0.414 | 144.066 | 0.9989 | 0.9988 | 0.872 | 0.9011 |
| 0.04 | -4.416 | 0.25 | 141.759 | 0.9998 | 0.9846 | 0.8881 | 0.9135 |
| 0.06 | -3.226 | 0.203 | 145.613 | 0.993 | 0.9318 | 0.8756 | 0.9556 |
| 0.08 | -5.207 | 0.345 | 133.692 | 0.9646 | 0.8998 | 0.8998 | 0.953 |
| 0.1 | -4.669 | 0.702 | 130.739 | 0.9531 | 0.8704 | 0.8934 | 0.9586 |
| 0.12 | -4.895 | 0.833 | 69.72 | 0.9526 | 0.863 | 0.888 | 0.9686 |
| 0.14 | -4.231 | 0.921 | 75.221 | 0.9531 | 0.8681 | 0.8697 | 0.9671 |
| 0.16 | -5.594 | 0.662 | 138.922 | 0.9529 | 0.8461 | 0.8262 | 0.931 |
| 0.18 | -4.262 | 0.882 | 76.335 | 0.9516 | 0.7873 | 0.7614 | 0.9618 |
| 0.2 | -3.926 | 0.783 | 67.951 | 0.904 | 0.7277 | 0.7116 | 0.9653 |
| 0.22 | -5.965 | 1.071 | 52.554 | 0.8377 | 0.6411 | 0.6205 | 0.965 |
| 0.24 | -4.481 | 1.216 | 128.148 | 0.7567 | 0.474 | 0.474 | 0.9687 |
| 0.26 | -3.53 | 0.672 | 53.706 | 0.53 | 0.4096 | 0.4158 | 0.9921 |
| 0.28 | -4.433 | 0.638 | 64.225 | 0.3547 | 0.3745 | 0.3464 | 0.9928 |
| 0.3 | -3.536 | 0.459 | 57.705 | 0.2735 | 0.316 | 0.2736 | 0.9929 |
| Unc | -- | -- | -- | 0.0954 | 0.1058 | 0.1111 | -- |
Tabla 3: Los valores óptimos de los parámetros y los correspondientes valores de fiabilidad para diferentes retardos de tiempo. 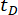 denota retardo de tiempo;
denota retardo de tiempo;  denotan el valor logarítmico óptimo de r,r denota el coeficiente de la matriz de ponderación de control;
denotan el valor logarítmico óptimo de r,r denota el coeficiente de la matriz de ponderación de control; 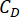 denota el coeficiente de amortiguación viscosa del amortiguador MR;
denota el coeficiente de amortiguación viscosa del amortiguador MR; 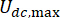 denotan las fuerzas Coulombicas máximas y mínimas del amortiguador MR.
denotan las fuerzas Coulombicas máximas y mínimas del amortiguador MR.
Se puede observar que la confiabilidad del desplazamiento, la velocidad y la aceleración mejoraron en comparación con la estructura no controlada, incluso en presencia de retardo de tiempo, lo que demuestra la robustez del método propuesto frente a dichos retardos. Sin embargo, la fiabilidad de las respuestas estructurales con el método de control propuesto disminuyó a medida que aumentaba el retardo de tiempo, lo que indica que, si bien el impacto del retardo de tiempo en la eficacia del control puede mitigarse, no puede eliminarse por completo. En particular, la fiabilidad de la fuerza de control se mantuvo por encima del 90% en diferentes retardos de tiempo.
3. Ejemplo numérico
Para verificar el método SOSC-PSO propuesto en la estructura MDOF, se analizó una estructura de seis pisos con dos amortiguadores MR instalados en el primer y tercer piso, como se muestra en la Figura 10. Se aplicaron las muestras sísmicas producidas por el modelo sísmico estocástico de la Sección 2, y los umbrales de confiabilidad de desplazamiento, velocidad, aceleración y fuerza de control fueron 20 mm, 200 mm/s, 3.000 mm/s2 y 200 kN. Ecs. (27) se utilizaron como matriz de ponderación con 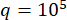 . Se utilizó la caja de herramientas GA de MATLAB para optimizar
. Se utilizó la caja de herramientas GA de MATLAB para optimizar 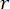 ,
, , y
, y  , con rangos óptimos
, con rangos óptimos 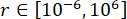 ,
,  , y
, y 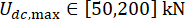 .
.
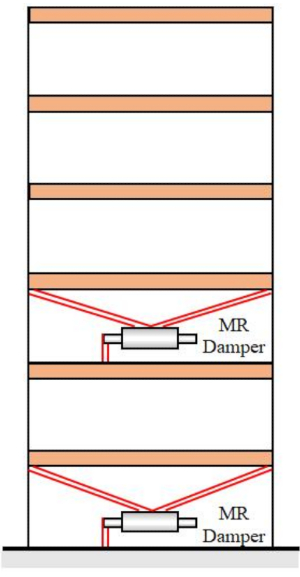
Figura 10: Estructura de seis pisos con dos amortiguadores MR. Abreviatura: MR = magnetorreológico. Haga clic aquí para ver una versión más grande de esta figura.
3.1 Análisis de la influencia del retardo temporal
Para analizar la influencia del retardo de tiempo en la efectividad del control del amortiguador de RM en la estructura MDOF, la Figura 11 muestra el RMS máximo de desplazamiento (desplazamiento entre pisos), velocidad (velocidad entre pisos) y aceleración (aceleración de pisos) junto con el retardo de tiempo para el método TDC-SAC-PSO. Los parámetros fueron 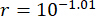 ,
, , y
, y  para el amortiguador MR en el 1er piso;
para el amortiguador MR en el 1er piso;  y
y  para el amortiguador MR en el 3er piso, que son los resultados optimizados sin retardo de tiempo. El RMS máximo de las respuestas de la estructura controlada mostró fluctuación de período junto con retraso de tiempo. El RMS máximo de desplazamiento y velocidad estaba en el 1er piso, la aceleración máxima en el 6to piso. Además, todas las TMS máximas de las respuestas con cualquier retardo de tiempo fueron mayores que los valores sin retardo de tiempo, lo que significa que el retardo de tiempo disminuye el efecto de control del amortiguador de RM.
para el amortiguador MR en el 3er piso, que son los resultados optimizados sin retardo de tiempo. El RMS máximo de las respuestas de la estructura controlada mostró fluctuación de período junto con retraso de tiempo. El RMS máximo de desplazamiento y velocidad estaba en el 1er piso, la aceleración máxima en el 6to piso. Además, todas las TMS máximas de las respuestas con cualquier retardo de tiempo fueron mayores que los valores sin retardo de tiempo, lo que significa que el retardo de tiempo disminuye el efecto de control del amortiguador de RM.
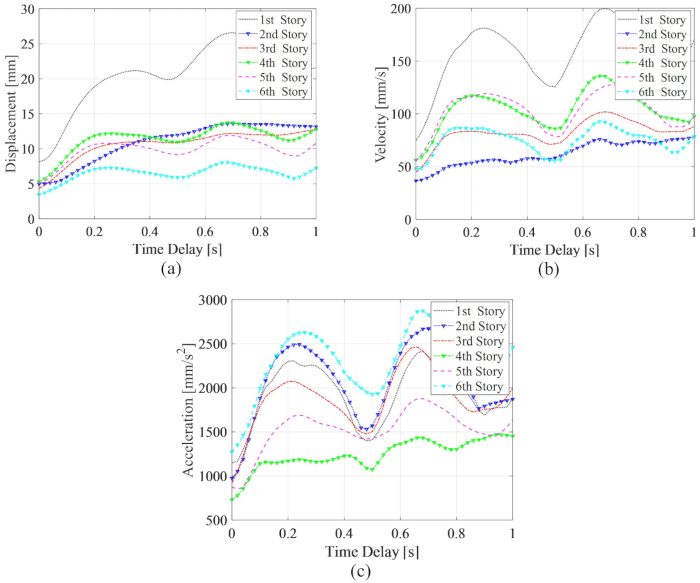
Figura 11: RMS máximo de las respuestas junto con el retardo de tiempo para la estructura controlada por el método TDC-SAC-PSO. A) Desplazamiento; b) Velocidad; c) Aceleración. Abreviaturas: RMS = raíz cuadrada media; TDC-SAC-PSO = sistema de retardo temporizado con compensación controlada. Haga clic aquí para ver una versión más grande de esta figura.
La fiabilidad del desplazamiento, la velocidad y la aceleración, junto con el retardo de tiempo, se muestra en la Figura 12. La confiabilidad de la velocidad y la aceleración muestran la fluctuación del período junto con el retraso del tiempo, mientras que la confiabilidad del desplazamiento disminuyó drásticamente junto con el retraso del tiempo; Todos los valores de fiabilidad con cualquier retardo fueron inferiores a los que no lo tenían. Por lo tanto, el método de compensación de retardo de tiempo es necesario para reducir la influencia del retardo de tiempo en la confiabilidad de la estructura controlada por amortiguador MR.
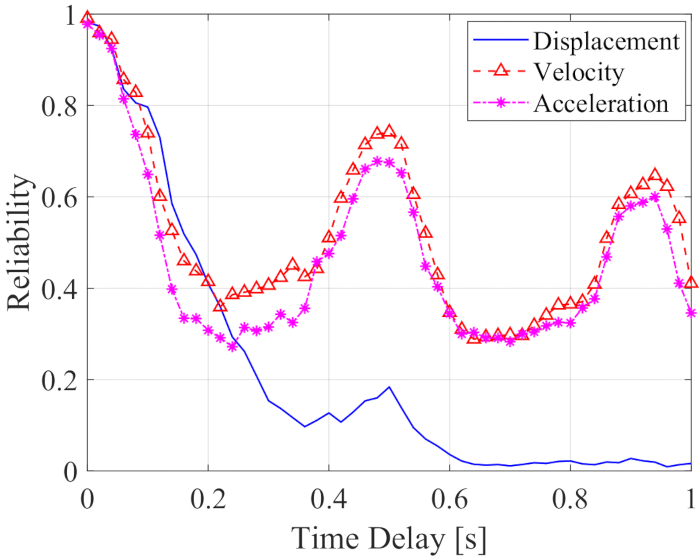
Figura 12: Fiabilidad de las respuestas controladas de la estructura junto con el retardo de tiempo. Haga clic aquí para ver una versión más grande de esta figura.
3.2 Efecto de control de la compensación de retardo de tiempo
Con base en el método TDC-SAC-PSO propuesto, se analizó la estructura de 6-DOF con dos amortiguadores de RM. La Figura 13 muestra los historiales de tiempo RMS de desplazamiento y aceleración en los pisos 1 y 3 para las estructuras no controladas (Unc), controladas por el método TDC-SAC-PSO y controladas por el método TDN-SAC-PSO. El retardo de tiempo fue 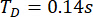 , y la relación
, y la relación 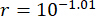 de la matriz de ponderación; los parámetros del amortiguador MR fueron
de la matriz de ponderación; los parámetros del amortiguador MR fueron  ,
,  para el 1er piso;
para el 1er piso;  y
y  para el 3er piso.
para el 3er piso.

Figura 13: Historias de tiempo RMS de desplazamiento y aceleración en el 1er y 3er piso para estructuras controladas por diferentes métodos. (A) Desplazamiento en el 1er piso; (B) Desplazamiento en el 3er piso; (C) Aceleración en el 1er piso; (D) Aceleración en el 3er piso. Abreviaturas: RMS = raíz cuadrada media; Unc = incontrolado; TDC-SAC-PSO = sistema de retardo temporizado con compensación controlada; TDN -SAC-PSO = sistema temporizado con control sin compensación. Haga clic aquí para ver una versión más grande de esta figura.
El RMS máximo de desplazamiento en los pisos 1º y 3º se redujo en un 35,42% y en un 30,44% por el método TDN-SAC-PSO, donde no se compensó el retardo temporal. Mientras que con compensación, el RMS máximo de desplazamiento en los pisos 1º y 3º se redujo 49,33% y 53,39%, respectivamente. Sin compensación, el RMS máximo de aceleración en los pisos 1º y 3º aumentó un 16,22% y un 2,88%, pero disminuyó un 25,77% y un 36,00%, respectivamente, con compensación. Por lo tanto, la compensación del retardo de tiempo en el método de control del amortiguador MR es necesaria para reducir las respuestas de la estructura, especialmente para la aceleración.
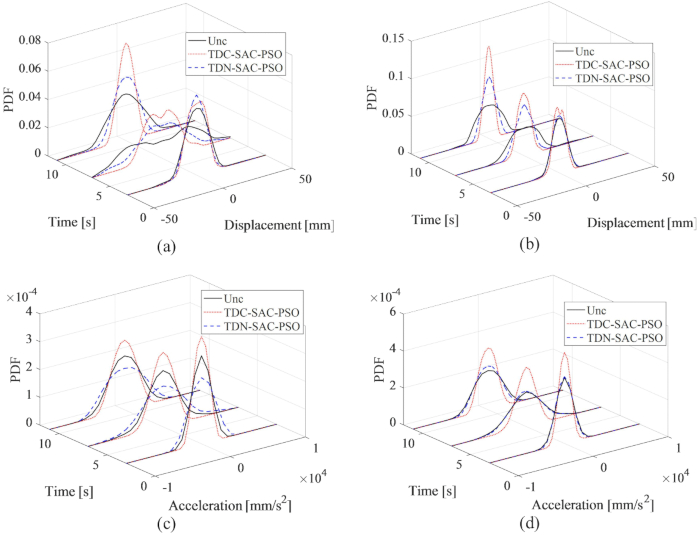
Figura 14: Imágenes de desplazamiento y aceleración en los pisos 1º y 3º para diferentes métodos de control. (A) Desplazamiento en el 1er piso; (B) Desplazamiento en el 3er piso; (C) Aceleración en el 1er piso; (D) Aceleración en el 3er piso. Abreviaturas: PDFs = funciones de densidad de probabilidad; Unc = incontrolado; TDC-SAC-PSO = sistema de retardo temporizado con compensación controlada; TDN -SAC-PSO = sistema temporizado con control sin compensación. Haga clic aquí para ver una versión más grande de esta figura.
En la Figura 14 se muestran los PDF de desplazamiento y aceleración en los pisos 1 y 3, que revelan los diferentes efectos de control de los métodos TDC-SAC-PSO y TDN-SAC-PSO en comparación con la estructura no controlada. Sin compensación, las columnas de desplazamiento en los pisos 1º y 3º seguían siendo más estrechas que las de la estructura incontrolada. Además, con la compensación del retardo de tiempo, las PDF de desplazamiento se hicieron más estrechas que las de la estructura controlada por el método TDN-SAC-PSO. A diferencia del desplazamiento, sin compensación, los PDF de aceleración en el 1er piso para el método TDN-SAC-PSO fueron más anchos que los de la estructura no controlada. Sin embargo, con compensación, los PDF de aceleración tanto en el piso 1 como en el 3 eran más estrechos que los de la estructura incontrolada. Por lo tanto, se verifica la necesidad de compensación de retardo de tiempo para aumentar la certeza de las respuestas de la estructura, especialmente para la aceleración.
| Método de control | Desplazamiento | Velocidad | Aceleración | Fuerza de control en la1ª planta | Fuerza de control en el3º piso |
| Unc | 0.0114 | 0.5822 | 0.6372 | -- | -- |
| TDN-SAC-PSO | 0.5851 | 0.5258 | 0.398 | 1 | 1 |
| TDC-SAC-PSO | 0.806 | 0.8674 | 0.8037 | 1 | 1 |
Tabla 4: Fiabilidad de las estructuras controladas por diferentes métodos. Abreviaturas: Unc = no controlado; TDC-SAC-PSO = sistema de retardo temporizado con compensación controlada; TDN -SAC-PSO = sistema temporizado con control sin compensación.
En la Tabla 4 se muestran los valores de confiabilidad de desplazamiento, velocidad, aceleración y fuerza de control con los sistemas de estructura controlados por los diferentes métodos. Los valores de confiabilidad de las respuestas de la estructura se calcularon utilizando el método de valores extremos equivalentes25. Mediante el control del método TDN-SAC-PSO, la confiabilidad del desplazamiento aumentó en comparación con la estructura no controlada, mientras que la confiabilidad de la velocidad y la aceleración disminuyó. Con la compensación de retardo de tiempo en el método TDC-SAC-PSO, la confiabilidad del desplazamiento, la velocidad y la aceleración aumentaron significativamente. Además, los valores de fiabilidad de la fuerza de control para los métodos TDN-SAC-PSO y TDN-SAC-PSO se mantienen suficientemente. Por lo tanto, el método de control de compensación de retardo de tiempo propuesto logra un efecto de control favorable para la estructura controlada por el amortiguador MR.
3.3 Optimización de parámetros
Para lograr el efecto de control óptimo, se optimizaron los parámetros del método de control propuesto en base al criterio de fiabilidad. Con el retardo 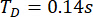 de tiempo, el resultado óptimo fue
de tiempo, el resultado óptimo fue  ;
; 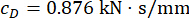 , y
, y 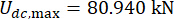 para el amortiguador MR del 1er piso;
para el amortiguador MR del 1er piso; 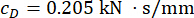 y
y  para el amortiguador MR del 3er.
para el amortiguador MR del 3er.
En la Figura 15 se muestran los historiales de tiempo RMS de desplazamiento y aceleración en los pisos 1 y 3, donde se comparan los efectos de control de los métodos TDC-SAC-PSO y SOSC-PSO y la estructura no controlada. Con el control del amortiguador MR, con o sin compensación de retardo de tiempo, el RMS de la cilindrada y la aceleración disminuyó significativamente. Con el método SOSC-PSO, el RMS máximo de desplazamiento en los pisos 1º y 3º disminuyó en un 65,15% y 63,16% en relación con la estructura no controlada, respectivamente. En comparación con el método TDC-SAC-PSO, la respuesta de desplazamiento se redujo aún más. El RMS máximo de aceleración en las plantas 1ª y 3ª se reduce en un 23,39% y en un 35,60% para el método SOSC-PSO. Hubo poca diferencia en el efecto de control de la aceleración para los métodos SOSC-PSO y TDC-SAC-PSO, lo que indica que el efecto de control de la compensación del retardo de tiempo fue diferente para el desplazamiento y la aceleración.
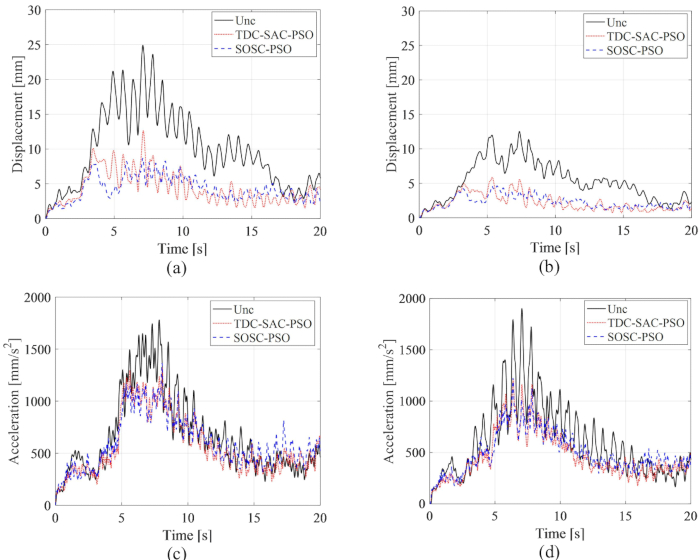
Figura 15: Historiales de tiempo RMS de desplazamiento y aceleración en los pisos 1 y 3 para diferentes métodos de control. (A) Desplazamiento en el 1er piso; (B) Desplazamiento en el 3er piso; (C) Aceleración en el 1er piso; (D) Aceleración en el 3er piso. Abreviaturas: RMS = raíz cuadrada media; Unc = incontrolado; TDC-SAC-PSO = sistema de retardo temporizado con compensación controlada; SOSC-PSO = Método de control semiactivo óptimo estocástico con compensación de retardo de tiempo. Haga clic aquí para ver una versión más grande de esta figura.
En la Figura 16 se presentan los PDF de desplazamiento y aceleración en los pisos 1º y 3º; los PDF de desplazamiento y aceleración se redujeron mediante los métodos TDC-SAC-PSO y SOSC-PSO en comparación con la estructura no controlada. Además, los PDF de desplazamiento y aceleración para el método SOSC-PSO se redujeron aún más en comparación con los de la estructura controlada por el método TDC-SAC-PSO. Por lo tanto, con la optimización de parámetros, el método de control de compensación de retardo de tiempo propuesto logró un mejor efecto de control que sin optimización.
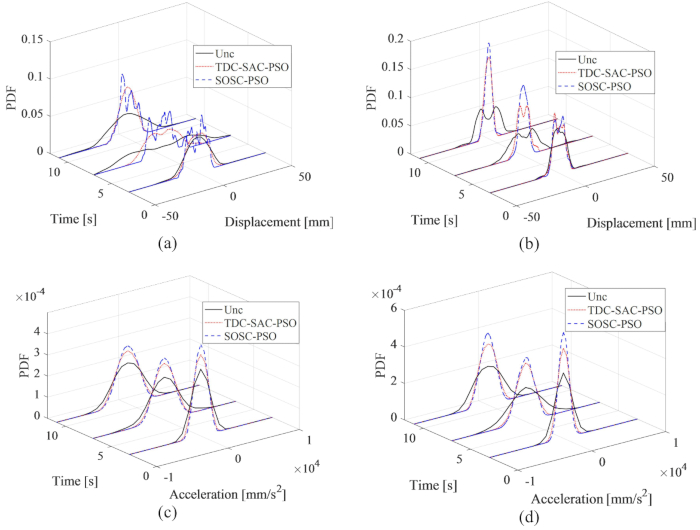
Figura 16: Imágenes de desplazamiento y aceleración en los pisos 1º y 3º para diferentes métodos de control. (A) Desplazamiento en el 1er piso; (B) Desplazamiento en el 3er piso; (C) Aceleración en el 1er piso; (D) Aceleración en el 3er piso. Abreviaturas: PDFs = funciones de densidad de probabilidad; Unc = incontrolado; TDC-SAC-PSO = sistema de retardo temporizado con compensación controlada; SOSC-PSO = Método de control semiactivo óptimo estocástico con compensación de retardo de tiempo Haga clic aquí para ver una versión más grande de esta figura.
Los valores de confiabilidad de desplazamiento, velocidad, aceleración y fuerza de control se muestran en la Tabla 5. Los valores de fiabilidad para el método SOSC-PSO fueron superiores a los del método TDC-SAC-PSO. Mientras tanto, la fuerza de control aún conservaba suficiente confiabilidad. Por lo tanto, la optimización de los parámetros es necesaria para lograr el mejor efecto de control para el método de control basado en amortiguadores MR.
| Método de control | Desplazamiento | Velocidad | Aceleración | Fuerza de control en la1ª planta | Fuerza de control en el3º piso |
| Unc | 0.0114 | 0.5822 | 0.6372 | -- | -- |
| TDC-SAC-PSO | 0.806 | 0.8674 | 0.8037 | 1 | 1 |
| SOSC-PSO | 0.9544 | 0.9314 | 0.8788 | 1 | 1 |
Tabla 5: Fiabilidad de las estructuras controladas por diferentes métodos. Abreviaturas: Unc = no controlado; TDC-SAC-PSO = sistema de retardo temporizado con compensación controlada; SOSC-PSO = Método de control semiactivo óptimo estocástico con compensación de retardo de tiempo.
Resultados
Con el objetivo de determinar la influencia del retardo de tiempo en la efectividad del control del método basado en amortiguadores de RM, en este artículo se propone un método de control semiactivo con compensación de retardo de tiempo. En el método propuesto, los parámetros críticos se optimizan en función del criterio de fiabilidad. Al comparar la efectividad del control, se abordan las siguientes conclusiones:
(1) El método de control semiactivo b...
Discusión
Con la introducción de la teoría de control óptimo estocástico físico (PSO), se propone en este documento un método de control semiactivo óptimo estocástico con compensación de retardo de tiempo (SOSC-PSO), que está diseñado para mantener la confiabilidad de las estructuras controladas por amortiguadores MR. Para compensar el retardo de tiempo en el método propuesto, la fuerza de control semiactiva se deriva como la función no solo de los estados presentes, sino también de ...
Divulgaciones
Todos los autores no tienen conflictos de intereses que declarar.
Agradecimientos
Los autores agradecen el apoyo de la Fundación de Ciencias Naturales de la Provincia de Hebei (Subvención Nº E2023210007).
Materiales
| Name | Company | Catalog Number | Comments |
| MATLAB | MathWorks | 2016 | Using for the calculation of the proposed method |
Referencias
- Yao, J. T. P. Concept of structural control. J Struct Div. 98 (7), 1567-1574 (1972).
- Liu, J., Silva, C. E., Dyke, S. J., Wu, Y., Liu, H. Using real-time hybrid simulation for active mass damper experimentation and validation. Mech Mach Theory. 191, 105474 (2024).
- Pan, H., Li, C., Cao, L. Bidirectional pendulum-type tuned tendem mass dampers-inerters for integrated control of alongwind and crosswind responses in super-tall buildings. J Build Eng. 100, 111676 (2025).
- Housner, G. W. et al. Structural control: past, present, and future. J Eng Mech. 123 (9), 897-971 (1997).
- Rahman, M., Ong, Z. C., Chong, W. T., Julai, S. Smart Semi-active PID-ACO control strategy for tower vibration reduction in Wind Turbines with MR damper. Earthq Eng Eng Vib. 18 (4), 887-902 (2019).
- Morales-Beltran, M., Paul, J. Active and semi-active strategies to control building structures under large earthquake motion. J Earthquake Eng. 19 (7), 1086-1111 (2015).
- Shu, Z., You, R., Xie, Y. Viscoelastic dampers for vibration control of building structures: A state-of-art review. J Earthq Eng. 28 (12), 3558-3585 (2024).
- Soong, T. T. Active structural control: Theory and practice. Longman Scientific & Technical. New York (1990).
- Wan, H. P., Ma, Q., Dong, G. S., Luo, Y., Ni, Y. Q. Data-driven model reduction approach for active vibration control of cable-strut structures. Eng Struct. 302, 117434 (2024).
- Cao, L., Li, X., Huang, Y., Li, C., Pan, H. High robust eddy current tuned tandem mass dampers-inerters for structures under the ground acceleration. Soil Dyn Earthq Eng. 188, 109040 (2025).
- Chha, H., Peng, Y. Adaptive semiactive control of structure with magnetorheological dampers using wavelet packet transform. Adv Struct Eng. 27 (9), 1509-1527 (2024).
- Zeng, X., Peng, Y., Chen, J. Serviceability-based damping optimization of randomly wind-excited high-rise buildings. Struct Des Tall Spec. 26 (11), e1371 (2017).
- Li, C., Chang, K., Cao, L., Huang, Y. Performance of a nonlinear hybrid base isolation system under the ground motions. Soil Dyn Earthq Eng. 143, 106589 (2021).
- Cao, L., Li, C. A high performance hybrid passive base-isolated system. Struct Control Health Monitoring. 29 (3), e2887 (2022).
- Zareie, S., Issa, A. S., Seethaler, R., Zabihollah, A., Ahmad, R. A novel SMA-magnetorheological hybrid bracing system for seismic control. Eng Struct. 244, 112709 (2021).
- Chu, S. Y., Soong, T. T., Reinhorn, A. M. Active, hybrid and semi-active structural control. John Wiley & Sons, New York (2005).
- Danielian, S. A., Jabbari, F., Zareian, F. Effects and distribution of semi-active resettable springs on the seismic response of asymmetric structures. Earthq Eng Struct D. 52 (10). 2966-2982 (2023).
- Shuang, Z., Wenliuhan, H. S., Liu, Y. H., Inoue, N., Zhai, Z. P. Seismic response control for bridge piers with semi-active MR damper based on displacement feedback. J Earthq Eng. 28 (3). 849-865 (2024).
- Wang, Y., Dyke, S. Modal-based LQG for smart base isolation system design in seismic response control. Struct Control Health Monitoring. 20 (5), 753-768 (2013).
- Desai, R. M. et al. Performance evaluation of a single sensor control scheme using a twin-tube MR damper based semi-active suspension. J Vib Eng Technol. 9, 1193-1210 (2021).
- Abdi, M. S., Nekooei, M. Jafari, M. A. Seismic control of multi-degrees-of-freedom structures by vertical mass isolation method using MR dampers. Earthq Eng Eng Vib. 23 (2), 503-510 (2024).
- Bhowmik, K., Debnath, N. Semi-active vibration control of soft-storey building with magnetorheological damper under seismic excitation. J Vib Eng Technol. 12 (4), 6943-6961 (2024).
- Yang, J. N., Akbarpour, A., Askar, G. Effect of time delay on control of seismic-excited buildings. J Struct Eng. 116 (10), 2801-2814 (1990).
- Temimi, H., Ben-Romdhane, M., El-Borgi, S., Cha, Y. Time-delay effects on controlled seismically excited linear and nonlinear structures. Int J Struct Stab Dyn. 16 (7), 1550031 (2016).
- Peng, J., Wang, L., Zhao, Y., Lenci, S. Time-delay dynamics of the MR damper-cable system with one-to-one internal resonances. Nonlinear Dynamics. 105 (2), 1343-1356 (2021).
- Cha, Y. J., Agrawal, A. K., Dyke, S. J. Time delay effects on large-scale MR damper based semi-active control strategies. Smart Mater Struct. 22 (1), 015011 (2013).
- Yu, Y. et al. Experimental study of wireless structural vibration control considering different time delays. Smart Mater Struct. 24, 045005 (2015).
- Ahmadizadeh, M., Mosqueda, G., Reinhorn, A. M. Compensation of actuator delay and dynamics for real-time hybrid structural simulation. Earthq Eng Struct Dyn. 37 (1), 21-42 (2008).
- Bathaei, A., Zahrai, S. M. Compensating time delay in semi-active control of a SDOF structure with MR damper using predictive control. Struc Eng Mech. 82 (4), 445-458 (2022).
- Dyke, S. J., Spencer, Jr, B. F., Sain, M. K., Carlson, J. D. Modeling and control of magnetorheological dampers for seismic response reduction. Smart Mater Struct. 5 (5), 565-575 (1996).
- Ying, Z. G., Ni, Y. Q., Ko, J. M. A semi-active stochastic optimal control strategy for nonlinear structural systems with MR dampers. Smart Struct Syst. 5 (1), 69-79 (2009).
- Rosol, M., Martynowicz, P. Implementation of the LQG controller for a wind turbine tower-nacelle model with a MR tuned vibration absorber. J Theor App Mech-Pol. 54 (4), 1109-1123 (2016).
- Lyu, M. Z., Feng, D. C., Chen, J. B., Li, J. A decoupled approach for determination of the joint probability density function of a high-dimensional nonlinear stochastic dynamical system via the probability density evolution method. Comput Method Appl M. 418 (A), 116443 (2024).
- Chha, H., Peng, Y. Multiscale stochastic optimal control of hysteretic structures based on wavelet transform and probability density evolution method. Eng Computation. 41 (4), 865-896 (2024).
- Li, J., Peng, Y. B., Chen, J. B. A physical approach to structural stochastic optimal controls. Probabilist Eng Mech. 25 (1), 127-141 (2010).
- Peng, Y. B., Yang, J. G., Li, J. Seismic risk-based stochastic optimal control of structures using magnetorheological dampers. Nat Hazards Rev. 18 (1), B4016001 (2017).
- Dong, X. M., Yu, M., Li, Z., Liao, C., Chen, W. Neural network compensation of semi-active Control for magneto-rheological suspension with time delay uncertainty. Smart Mater Struct. 18 (1), 015014 (2008).
- Peng, Y. B., Zhang, Z. Optimal MR damper-based semiactive control scheme for strengthening seismic capacity and structural reliability. J Eng Mech. 146 (6), 04020045 (2020).
- Luo, M. X., Gao, M. Cai, G. Delayed full-state feedback control of airfoil flutter using sliding mode control method. J Fluid Struct. 61, 262-273 (2016).
- Xu, J., Chung, K. W., Chan, C. L. An efficient method for studying weak resonant double Hopf bifurcation in nonlinear systems with delayed feedbacks. Siam J Appl Dyn Syst. 6 (1), 29-60 (2007).
- Yang, J. S., Jensen, H., Chen, J. B. Structural optimization under dynamic reliability constraints utilizing probability density evolution method and metamodels in augmented input space. Struct Multidiscip Optimization. 65, 107 (2022).
- Li, J., Chen, J. B. Stochastic dynamics of structures. John Wiley & Sons, Singapore (2009).
- Peng, Y. B., Li, J. Stochastic optimal control of structures. Springer (2019).
- Dowrick, C. Beyond depression: A new approach to understanding and management. Oxford University Press (2009).
- Wang, D., Li, J. Physical random function model of ground motions for engineering purposes. Sci China Technol Sci. 54 (1), 175-182 (2011).
- Wang, D., Li, J. A random physical model of seismic ground motion field on local engineering site. Sci China Technol Sci. 55 (7), 2057-2065 (2012).
- Chen, J. B., Li, J. Strategy for selecting representative points via tangent spheres in the probability density evolution method. Int J Numer Meth Eng. 74 (13), 1988-2014 (2008).
Reimpresiones y Permisos
Solicitar permiso para reutilizar el texto o las figuras de este JoVE artículos
Solicitar permisoThis article has been published
Video Coming Soon
ACERCA DE JoVE
Copyright © 2025 MyJoVE Corporation. Todos los derechos reservados