このコンテンツを視聴するには、JoVE 購読が必要です。 サインイン又は無料トライアルを申し込む。
Research Article
時間遅延を考慮した磁性流体ダンパーに基づく確率的セミアクティブ構造制御法
要約
この論文では、MRダンパーによって制御される構造物の信頼性を維持するように設計された、時間遅延補償付き確率最適セミアクティブ制御法(SOSC-PSO)を提案しています。
要約
セミアクティブ制御システムにおける磁性流体(MR)ダンパーの使用は、フィードバックプロセスによって引き起こされる時間遅延という重要な課題に直面しており、確率的加振下での土木構造物の信頼性を低下させます。本稿では、物理的確率最適制御理論(PSO)を活用して、この問題に対処し、構造信頼性を維持するために、時間遅延補償付き確率最適セミアクティブ制御法(SOSC-PSO)を提案します。提案手法は、セミアクティブ制御力を現在の状態と以前の状態の両方の関数として導き出し、制御プロセスの時間遅延を補償します。制御の有効性を最適化するために、主要なパラメータはシステムの信頼性基準に基づいて調整されます。確率的地震加振下での単一自由度および多自由度構造の検証解析では、時間遅延がMRダンパーの性能を著しく損なうことが示されています。しかし、時間遅延補償を施したSOSC-PSO法は、制御効果を大幅に向上させ、パラメータの最適化により、パラメータの最適化を行わない方法よりも構造制御システムの信頼性を高めることができます。
概要
地震や強風などの壊滅的な事態に直面した場合のエンジニアリング構造物の性能向上は、土木工学コミュニティ内で依然として主要な関心事です。振動を低減するための効果的な技術である構造制御は、そのような構造の安全性と機能性の両方を向上させることが証明されています1,2,3。過去数十年にわたり、この目的のためにさまざまな高度な方法と技術が開発されてきました。これらの方法は、制御装置を駆動するために使用されるエネルギーの種類に基づいて、アクティブ、セミアクティブ、パッシブ、およびハイブリッド制御システム4、5、6、7の4つのカテゴリに大きく分類することができる。
アクティブ制御では、必要な制御力が制御装置を通じて直接加えられるため、大量のエネルギー8,9,10が必要になる。一方、セミアクティブ制御は、制御信号に基づいて制御装置の特性(減衰や剛性など)を調整することを含み、アクティブシステム11と比較してはるかに少ないエネルギーを必要とする。対照的に、パッシブ制御は、システム12,13,14への外部エネルギー入力なしのエネルギー散逸に依存する。ハイブリッドシステムは、アクティブ/セミアクティブおよびパッシブ制御戦略の機能を組み合わせて、より効果的なパフォーマンスを実現します15。これらのアプローチの中で、セミアクティブ制御は、低エネルギー消費と高効率のバランスにより、特に有望であると考えられています16,17,18。磁性流体(MR)ダンパーは、その優れた動的減衰特性により、最も効果的なセミアクティブ制御装置の1つと見なされています19,20,21,22。
しかし、MRダンパーを使用するセミアクティブ制御システムでは、フィードバックロジックが必然的に時間遅延を引き起こすという課題が生じます。これらの遅延は、典型的には、いくつかの要因23、24、25、以下を含む:(i)センサデータの取得および処理、(ii)コントローラ26による必要な制御力の計算、(iii)トランスデューサを介したMRダンパ27への信号伝送、および(iv)MRダンパ自体による実際の力の生成28.このような時間遅延は、生成される制御力と構造によって予想される力との間に不一致を生じさせ、制御の有効性を著しく損なう可能性がある29。残念ながら、MRダンパーの既存の制御アルゴリズムのほとんどは、これらの遅延を考慮していません。
さらに、壊滅的なイベントに固有のランダム性により、効果的なセミアクティブ制御アルゴリズムは、確率的励起の下でパフォーマンスを維持できなければなりません。古典的な確率最適化手法である線形二次ガウス(LQG)制御法は、MRダンパーを装備した構造物の振動を軽減するために研究されています。例えば、Dykeらは、加速度フィードバック30を用いて、MRダンパーを装着した構造物の地震応答を改善するためのLQGクリップ最適制御戦略を提案した。Yingらは、確率平均化と動的計画法を組み込んだ、MRダンパーを備えた非線形構造のための非クリップセミアクティブ確率最適制御戦略を導入した31。他の研究では、モーダルベースのLQG制御を適用して、免震建物の耐震性能を向上させ19、風力タービンタワー32の振動緩和に対するその有効性を分析しました。ただし、ホワイト ガウス ノイズを前提とする従来の LQG 手法は、地震や強風などの実世界の励起の非定常性、非ガウス性をモデル化するのには適していません。これに対処するために、物理ベースの確率的最適(PSO)制御の概念が開発され33,34、従来のLQG手法の制限を克服し、多様な確率的励起35を処理するためのより正確なフレームワークを提供する。研究によると、PSOベースのセミアクティブ確率最適制御は、確率的地震力36を受ける線形構造と非線形構造の両方の振動緩和を大幅に改善することが示されています。
したがって、時間遅延を補償し、MRダンパー25,37によって制御される構造の信頼性を向上させる堅牢なセミアクティブ制御方法が緊急に必要とされている。さらに、確率的加振下での最適な制御性能を確保するためには、信頼性ベースのアプローチを使用して、提案された制御方法の重要なパラメータを最適化することが不可欠です。そこで、本論文では、MRダンパーを用いた構造物の信頼性を向上させるために、時間遅延補償を用いた確率最適セミアクティブ制御法(SOSC-PSO)を提案しています。
プロトコル
1. ストキャスティクス最適セミアクティブ制御法
MRダンパーの制御効果は避けられない時間遅延の影響を大きく受けるため、時間遅延補償アルゴリズムを用いたセミアクティブ制御方式を開発し、制御構造の性能を向上させています。さらに、外部励起に固有のランダム性は、動的応答の明らかな不確実性を引き起こします。PSO制御は、構造制御システムの信頼性を確保するための提案された方法の重要なパラメータを最適化するために導入されます。
1.1 セミアクティブ制御の補償アルゴリズム
一般性を損なうことなく、時間遅延のあるMRダンパーによって制御されるn自由度(n-DOF)構造を考えてみて、確率的励起を受ける運動方程式は次式で与えられます。
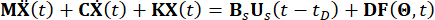 (1)
(1)
ここで、  は、それぞれ構造の n x n 質量、減衰、および剛性行列を表します。n は、制御された構造の自由度の数を表します。構造の変位ベクトル、速度ベクトル、および加速度ベクトルは、それぞれ
は、それぞれ構造の n x n 質量、減衰、および剛性行列を表します。n は、制御された構造の自由度の数を表します。構造の変位ベクトル、速度ベクトル、および加速度ベクトルは、それぞれ 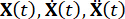 で表されます。シンボルの上にある小さな 1 つと 2 つのドットは、1 回目と 2 回目の導関数を表しています。 Us (t -t D) は MR ダンパーの時間遅延制御力の r 次元ベクトルを表し、r はダンパーの数を表します。t は時間を表します。tD は時間遅延を示し、このスタディではすべてのダンパーで均一であると仮定します。ここで (
で表されます。シンボルの上にある小さな 1 つと 2 つのドットは、1 回目と 2 回目の導関数を表しています。 Us (t -t D) は MR ダンパーの時間遅延制御力の r 次元ベクトルを表し、r はダンパーの数を表します。t は時間を表します。tD は時間遅延を示し、このスタディではすべてのダンパーで均一であると仮定します。ここで (  )、ここで積分数
)、ここで積分数  、
、 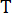 はサンプリング周期を示します。
はサンプリング周期を示します。 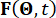 は確率的励起の p 次元ベクトルを表し、
は確率的励起の p 次元ベクトルを表し、  は外部励起に関連するランダム性を特徴付ける確率的パラメータ ベクトルを表します。
は外部励起に関連するランダム性を特徴付ける確率的パラメータ ベクトルを表します。  の寸法は、外部加振に使用されるモデルによって異なりますが、構造の機械的な自由度とは関係ありません。 Bs と D は n x r 行列と n x p 行列で、それぞれダンパーと外部加振の位置を指定します。状態空間表現では、式 (1) は次のように記述されます。
の寸法は、外部加振に使用されるモデルによって異なりますが、構造の機械的な自由度とは関係ありません。 Bs と D は n x r 行列と n x p 行列で、それぞれダンパーと外部加振の位置を指定します。状態空間表現では、式 (1) は次のように記述されます。
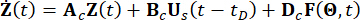 (2)
(2)
ここで、 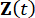 は 2n 次元の状態ベクトル、
は 2n 次元の状態ベクトル、 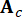 は 2n x 2n システム行列、
は 2n x 2n システム行列、 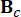 は MR ダンパーの 2n x r 位置行列を表します。
は MR ダンパーの 2n x r 位置行列を表します。 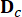 は、外部励起の 2n x p 位置行列を表します。これらのパラメータは、次のように表されます。
は、外部励起の 2n x p 位置行列を表します。これらのパラメータは、次のように表されます。
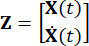 、
、 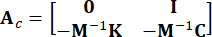 、
、  、
、 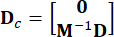 (3)
(3)
ここで、 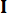 は、同じ
は、同じ 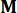 の順序の単位行列を示します。計算の便宜上、連続状態空間方程式式 (2) は離散形式で次のように表すことができます。
の順序の単位行列を示します。計算の便宜上、連続状態空間方程式式 (2) は離散形式で次のように表すことができます。
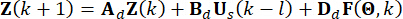 (4)
(4)
ここで、時点 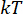 は次のように簡略化
は次のように簡略化 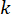 。また、
。また、  、
、 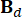 、
、 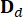 は 2n x 2n、2n x r、および 2n x p 行列を表し、次のように表されます。
は 2n x 2n、2n x r、および 2n x p 行列を表し、次のように表されます。
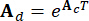 、
、  、
、 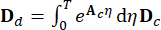 (5)
(5)
ここで、 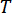 はサンプリング期間を示します。
はサンプリング期間を示します。
アクティブ制御と同様の有効性を達成するために、Hrovatアルゴリズム38に基づくシンプルで効率的な制御方法が、時間遅延のあるMRダンパーベースの制御に提案されています。
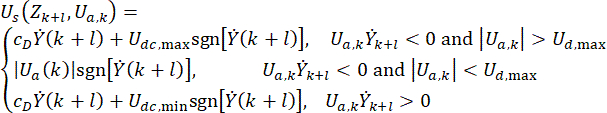 (6)
(6)
ここで、 MRダンパーの時間点でのセミアクティブ制御力信号
MRダンパーの時間点でのセミアクティブ制御力信号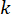 を表します。
を表します。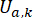 時間遅延補償付きの基準アクティブ制御力を表します。
時間遅延補償付きの基準アクティブ制御力を表します。 はMRダンパーの最大減衰力を表し、これは変更可能です
はMRダンパーの最大減衰力を表し、これは変更可能です 絶対値演算シンボルを表します。
絶対値演算シンボルを表します。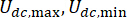 は、MRダンパーの最大クーロン力と最小クーロン力を表します
は、MRダンパーの最大クーロン力と最小クーロン力を表します 粘性減衰係数を表します。
粘性減衰係数を表します。 、MRダンパーに入力される速度を表し、ダンパーシリンダーに対するピストンの運動速度です。式(6)では、
、MRダンパーに入力される速度を表し、ダンパーシリンダーに対するピストンの運動速度です。式(6)では、 MRダンパーの設計パラメータを表しています。
MRダンパーの設計パラメータを表しています。
式(6)は、MRダンパーのセミアクティブ制御力の時間遅延による計算を示しています。式(4)の時間ステップ におけるセミアクティブ制御力
におけるセミアクティブ制御力 は、時間ステップ
は、時間ステップ でのアクティブ制御力
でのアクティブ制御力 と時間ステップ
と時間ステップ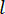
 における状態変数
における状態変数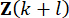 に基づいて計算されていることが分かります。アクティブ制御力
に基づいて計算されていることが分かります。アクティブ制御力 を得るために、従来のコスト関数は次のように確立されます。
を得るために、従来のコスト関数は次のように確立されます。
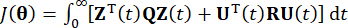 (7)
(7)
ここで、  はシステム状態の 2n x 2n 対称正定値重み付け行列を表し、
はシステム状態の 2n x 2n 対称正定値重み付け行列を表し、  は制御力の r x r 対称正定値重み行列を表します。外部励起は無視できることがわかります。実際、式(7)に基づくと、構造制御システムは、外部励起の種類に関係なく、最適な制御効果を達成できます。離散形式として、式 (7) は39 と表されます。
は制御力の r x r 対称正定値重み行列を表します。外部励起は無視できることがわかります。実際、式(7)に基づくと、構造制御システムは、外部励起の種類に関係なく、最適な制御効果を達成できます。離散形式として、式 (7) は39 と表されます。
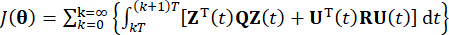 (8)
(8)
コスト関数  の最小化は条件付き極値問題につながり、アクティブ制御力
の最小化は条件付き極値問題につながり、アクティブ制御力  は25 で計算されます。
は25 で計算されます。
 (9)
(9)
ここで、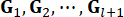 は、時間ステップ
は、時間ステップ  での状態変数 の
での状態変数 の 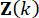 と時間ステップ
と時間ステップ 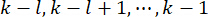 でのアクティブ制御力
でのアクティブ制御力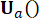 の制御ゲインを示し、重み付け行列 (
の制御ゲインを示し、重み付け行列 (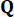 と
と 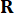 37) によって決定されます。時間遅延は避けられないため、得られた制御力
37) によって決定されます。時間遅延は避けられないため、得られた制御力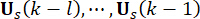 は
は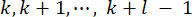 時点で構造物に作用する。したがって、式(9)の有効制御力は、次のように計算されます。
時点で構造物に作用する。したがって、式(9)の有効制御力は、次のように計算されます。
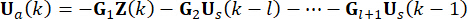 (10)
(10)
概念を明確にするために、式(10)のセミアクティブ制御力は、式(6)に基づいて次のように表されます。
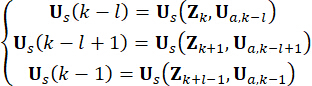 (11)
(11)
ここで、  は、
は、  時点におけるアクティブな制御力を示します。式(11)を式(10)に代入し、
時点におけるアクティブな制御力を示します。式(11)を式(10)に代入し、
 (12)
(12)
注:  の計算には、
の計算には、 から
から 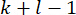 までのすべての状態
までのすべての状態 値が必要です。そこで、以下の状態予測方法40が導入される。
値が必要です。そこで、以下の状態予測方法40が導入される。
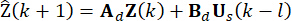 (13)
(13)
ここで、 は予測変数を示します。式 (13) の反復により、
は予測変数を示します。式 (13) の反復により、 での
での 状態が計算されます。アクティブ制御力Ua(k)は次のように表されます。
状態が計算されます。アクティブ制御力Ua(k)は次のように表されます。
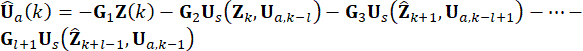 (14)
(14)
セミアクティブ制御力は、Eqsを組み合わせることで取得できます。(6)、(12)、(13)です。
1.2 構造物制御システムの信頼性解析
確率保存の原理によれば、MRダンパーによる構造の拡張システム 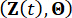 と構造の
と構造の 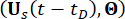 は確率保存され、それらは次の一般化確率密度進化方程式(GDEE)38によって支配されます。
は確率保存され、それらは次の一般化確率密度進化方程式(GDEE)38によって支配されます。
 (15)
(15)
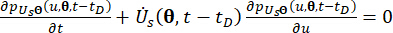 (16)
(16)
ここで、  は、
は、  それぞれシステム状態と時間遅延を伴うセミアクティブ制御力の対応する成分を示し、
それぞれシステム状態と時間遅延を伴うセミアクティブ制御力の対応する成分を示し、 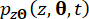 と
と  は、それぞれ拡張サンプルシステム
は、それぞれ拡張サンプルシステム 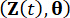 と
と 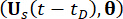 の同時確率密度関数を示し、
の同時確率密度関数を示し、 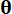 は
は 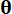 のサンプル空間内のサンプルを示し、
のサンプル空間内のサンプルを示し、  と
と  )は、それぞれシステム状態とセミアクティブ制御力コンポーネントの1次時間偏微分を示す。結合確率密度関数
)は、それぞれシステム状態とセミアクティブ制御力コンポーネントの1次時間偏微分を示す。結合確率密度関数 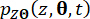 と
と  は、Eqs を解くことで実現できます。(15)および(16)を次の初期条件で設定します。
は、Eqs を解くことで実現できます。(15)および(16)を次の初期条件で設定します。
 (17)
(17)
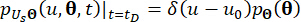 (18)
(18)
ここで、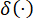 はディラックのデルタ関数を示します。
はディラックのデルタ関数を示します。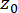
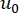 は、それぞれ
は、それぞれ  と
と 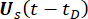 の決定論的初期値を示します。
の決定論的初期値を示します。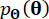 は、サンプル
は、サンプル 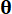 の確率密度関数を示します。
の確率密度関数を示します。
 と
と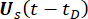 の瞬時確率密度関数は、サンプル空間の領域にわたる
の瞬時確率密度関数は、サンプル空間の領域にわたる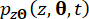 と
と の一次元積分によって取得できます。
の一次元積分によって取得できます。
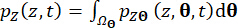 (19)
(19)
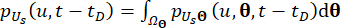 △ 20
△ 20
ここで、 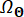 は
は  の分布領域を示します。
の分布領域を示します。
Eqsに基づきます。(19)および(20)では、アルゴリズムパラメータに関連付けられたそれらの関係が定義されている場合、関係する物理量の完全な確率的情報が容易に導出されることがわかる。関連する物理量の信頼性は、次の関連するパフォーマンス関数によって計算できます。
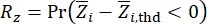 (21)
(21)
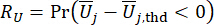 (22)
(22)
ここで、 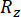 と
と 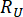 は、それぞれ、関係する状態量とセミアクティブ制御力の計算信頼性を示し、
は、それぞれ、関係する状態量とセミアクティブ制御力の計算信頼性を示し、  は、制御構造のi番目の関係物理量の等価極値ベクトルを示し、
は、制御構造のi番目の関係物理量の等価極値ベクトルを示し、 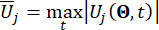 は、j番目の制御力の等価極値ベクトルを示し、記号のハット「-」は、等価極値ベクトル41を示す
は、j番目の制御力の等価極値ベクトルを示し、記号のハット「-」は、等価極値ベクトル41を示す  は、制御された構造のk番目の自由度のi番目の関係する物理量を示します
は、制御された構造のk番目の自由度のi番目の関係する物理量を示します 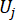 j番目の制御力を示します。
j番目の制御力を示します。 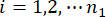 、
、 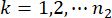 、
、  、
、 、
、  、
、  は、それぞれ、構造物と構造物に設置されたMRダンパーの関連する物理量とDOFの数を示します。
は、それぞれ、構造物と構造物に設置されたMRダンパーの関連する物理量とDOFの数を示します。  と
と 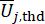 は、
は、  と
と  のしきい値を示し、
のしきい値を示し、  は、ランダムイベントの確率を示します。
は、ランダムイベントの確率を示します。
1.3 パラメータの最適化
 と
と の振幅の比は、フィードバック制御モダリティにおける制御有効性38に大きく影響する。したがって、最高の制御効果を達成するためには、
の振幅の比は、フィードバック制御モダリティにおける制御有効性38に大きく影響する。したがって、最高の制御効果を達成するためには、 と
と を最適化する必要があります。また、MRダンパーによる制御方式として、式(6)
を最適化する必要があります。また、MRダンパーによる制御方式として、式(6) 装置パラメータによっても制御効果が影響を受けます。構造制御システムの最適な信頼性を達成するために、信頼性に基づく基準が式(25)で提案されています。
装置パラメータによっても制御効果が影響を受けます。構造制御システムの最適な信頼性を達成するために、信頼性に基づく基準が式(25)で提案されています。
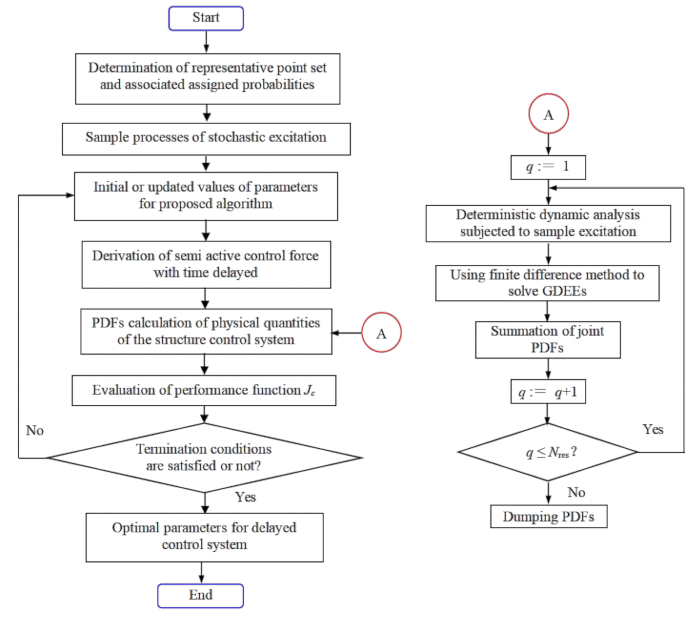
図1:時間遅延補償による確率的最適セミアクティブ構造制御のためのパラメータ最適化のフローチャート。 略語: GDEE = イベントの一般化微分方程式 ;PDF = 確率密度関数。 この図の拡大版を表示するには、ここをクリックしてください。
要約すると、時間遅延補償を備えたMRダンパーに基づく確率的最適セミアクティブ構造制御を実行するには、2つのステージが必要です。
1.3.1 式(7)に示されているコスト関数 最小化すると、サンプルの意味でのステートフィードバックロジック、つまり式12)が達成されます
最小化すると、サンプルの意味でのステートフィードバックロジック、つまり式12)が達成されます
1.3.2信頼性ベースのパフォーマンス関数  を最小限に抑えると、統計の意味で最適なパラメータが達成されます。図 1 は、ステップ 1.3.2 のコントローラーのパラメーターの最適化フローチャートを示しています。
を最小限に抑えると、統計の意味で最適なパラメータが達成されます。図 1 は、ステップ 1.3.2 のコントローラーのパラメーターの最適化フローチャートを示しています。
ステップ 1.3.2 の次の手順には、2 つのループ層が含まれます。このステップは次のとおりです。
1.3.2.1 確率的励起の確率割り当て空間を分割すると、確率的パラメータベクトル によって特徴付けられ、代表的な点のセットとそれらに関連する割り当てられた確率Pqとともに
によって特徴付けられ、代表的な点のセットとそれらに関連する割り当てられた確率Pqとともに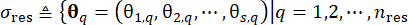 を特定できます。このアプローチにより、確率的励起(
を特定できます。このアプローチにより、確率的励起(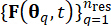 と呼ばれる)のサンプルプロセスを効率的に生成することが容易になります。
と呼ばれる)のサンプルプロセスを効率的に生成することが容易になります。
1.3.2.2 セミアクティブ構造制御システムのパラメータ最適化のために、コスト関数の重み  と
と  の値を初期化または更新します。次に、時間遅延に関連する状態フィードバック制御力(式(12)を参照)が計算されます。
の値を初期化または更新します。次に、時間遅延に関連する状態フィードバック制御力(式(12)を参照)が計算されます。
1.3.2.3 式で示されるGDEEを解くことにより、構造応答と制御力の確率密度関数(PDF)を取得します。(17)〜(20):
最適化はオフラインで完了しますが、オンラインでは完了しません。提案手法の実構造制御システムへの適用では、最適な  と
と  が得られており、実際の適用プロセスでは最適化は必要ない。
が得られており、実際の適用プロセスでは最適化は必要ない。
サンプル加振を受けるセミアクティブ構造制御システムの決定論的動的解析により、関連する物理量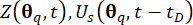 とその導関数
とその導関数 が計算されます。
が計算されます。
全変動減少(TVD)特性を持つ修正Lax-Wendroffスキームなどの有限差分法を採用することにより、一般化微分方程式(GDEE)を解くことができ、結合確率密度関数 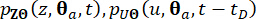 の数値解を導くことができます。
の数値解を導くことができます。
上記の2つのステップを決定論的動的解析と有限差分法で繰り返し、 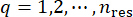 すべての代表的な点を実行すると、確率密度関数は合計によって取得できます。
すべての代表的な点を実行すると、確率密度関数は合計によって取得できます。
 (23)
(23)
 (24)
(24)
ここで、  は、サンプル ポイント
は、サンプル ポイント 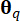 に関連付けられたサブドメインの面積メジャーを表します。一般化微分方程式(GDEE)を解くために使用される方法は、確率密度発展法(PDEM)42として知られている。
に関連付けられたサブドメインの面積メジャーを表します。一般化微分方程式(GDEE)を解くために使用される方法は、確率密度発展法(PDEM)42として知られている。
1.3.2.4 関連する物理量のPDFは、その信頼性を評価するために使用され、その後、確率的基準の性能関数  に組み込まれます。
に組み込まれます。
1.3.2.5 パラメータ最適化プロセスの終了基準が満たされているかどうかを評価します。条件が満たされない場合は、ステップ 1.3.2.2 に戻ります。そうであれば、時間遅延制御システムの最適なパラメータを決定できます。この作業では、MATLAB の遺伝的アルゴリズム (GA) ツールボックスをパラメーターの最適化に使用し、パラメーターの更新を容易にし、終了条件を定義します。遺伝的アルゴリズムにより、最適値は10回の反復で達成でき、収束は局所的な最小値の問題なしに安定しています。GAの計算コストは、粒子群最適化や勾配ベースの方法よりも大きくなりますが、GAは、この原稿で取り上げたような複雑で微分不可能な問題を扱うのに適しています。したがって、GA が適用されます。また、急速収束特性があるため、GAの計算コストは許容範囲内です。
1.3.2.6 最適な信頼性制御を実現するために、以下の性能関数 が定式化されます。パラメータ (
が定式化されます。パラメータ (
 ) の最適値を決定するための
) の最適値を決定するための を最小化します。
を最小化します。
 } (25)
} (25)
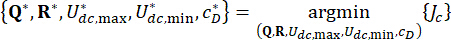 (26)
(26)
前述のように、コントローラーの重み付け行列は対称であり、マトリックス  の要素は変位、速度、およびそれらの相互作用に割り当てられた重みに対応し、マトリックス
の要素は変位、速度、およびそれらの相互作用に割り当てられた重みに対応し、マトリックス  の要素は制御力に関連する重みを表します。以前の研究38の結果に基づいて、コスト関数の重み
の要素は制御力に関連する重みを表します。以前の研究38の結果に基づいて、コスト関数の重み  および
および  の構成を変更しても、制御の有効性への影響は最小限であることが観察されている。したがって、この調査では、以下に概説するように、簡略化された構成が採用されています。
の構成を変更しても、制御の有効性への影響は最小限であることが観察されている。したがって、この調査では、以下に概説するように、簡略化された構成が採用されています。
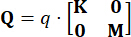 、
、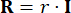 (27)
(27)
ここで、 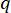 は定義する状態重み付け行列の係数、
は定義する状態重み付け行列の係数、 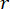 は定義する制御重み付け行列の係数、
は定義する制御重み付け行列の係数、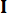 は単位行列を示します。制御効果は、
は単位行列を示します。制御効果は、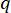 と
と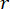 の比率の影響を受けますが、値自体には影響されません。また、式(6)の
の比率の影響を受けますが、値自体には影響されません。また、式(6)の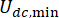 はMRダンパーの最小クーロン力を示しており、ダンパーの電流入力がゼロの場合の
はMRダンパーの最小クーロン力を示しており、ダンパーの電流入力がゼロの場合の を意味します。次に、式(26)はさらに次のように表すことができます。
を意味します。次に、式(26)はさらに次のように表すことができます。
 △ 28
△ 28
ここで、 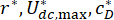 は最適な関心係数です。エンジニアリングで合理的にするために、それらの最適な範囲はMRダンパー工場の生産能力に基づいています。
は最適な関心係数です。エンジニアリングで合理的にするために、それらの最適な範囲はMRダンパー工場の生産能力に基づいています。
明らかに、式(28)によって得られた最適パラメータは、提案されたセミアクティブ制御アルゴリズムの時間遅延を伴う最適な制御効果を維持し、これにより、構造制御システムは確率的励起を受けるバランスの取れた最適な信頼性を達成することができます。
2. ケーススタディ
MRダンパーの時間遅延補償付きセミアクティブ制御法の提案の有効性を解析するために、MRダンパーに取り付けられた平面単層せん断フレーム構造に、図2に示すように水平確率的地震動を施しました。セミアクティブ制御構造システムのパラメータは、構造質量 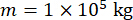 、固有円周波
、固有円周波  、減衰比
、減衰比 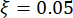 です。過去の経験と市場に出回っている既存のダンパースケールによると、構造変位、速度、加速度、および制御力のしきい値は、それぞれ10 mm、100 mm / s、1,500 mm / s2、および150 kNです。確率的地震動を表現するために、物理的に動機付けられた確率的地震動モデルが採用された43。
です。過去の経験と市場に出回っている既存のダンパースケールによると、構造変位、速度、加速度、および制御力のしきい値は、それぞれ10 mm、100 mm / s、1,500 mm / s2、および150 kNです。確率的地震動を表現するために、物理的に動機付けられた確率的地震動モデルが採用された43。
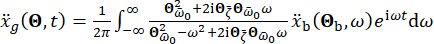 △ 29
△ 29
ここで、 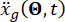 はエンジニアリング サイトの時間領域での地震動を表し、
はエンジニアリング サイトの時間領域での地震動を表し、 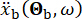 は岩盤の周波数領域での地震動を示します。ベクトル
は岩盤の周波数領域での地震動を示します。ベクトル  は、エンジニアリングサイトの表面での地震動の確率的性質を特徴付けます。
は、エンジニアリングサイトの表面での地震動の確率的性質を特徴付けます。 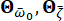 パラメーターは、主要な周波数
パラメーターは、主要な周波数  や同等の減衰
や同等の減衰  など、サイトの土壌の特性を記述する確率変数です。ベクトル
など、サイトの土壌の特性を記述する確率変数です。ベクトル 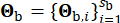 は、震源の特性と伝播経路の影響を受ける岩盤での地震動の確率的性質を表し、
は、震源の特性と伝播経路の影響を受ける岩盤での地震動の確率的性質を表し、 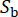 はこの段階に関与する確率変数の数を示します。
はこの段階に関与する確率変数の数を示します。  は円形周波数を指し、i は虚数単位です。
は円形周波数を指し、i は虚数単位です。
エンジニアリングサイトの支配的な周波数  と等価減衰比
と等価減衰比  は、サイトの土壌の動的特性を特徴付ける重要なパラメータです。これらの量の確率分布と統計パラメータは、特定のクラスのエンジニアリングサイトから収集された地震加速度記録に基づいて決定できます。説明のために、せん断波速度範囲が[150、250]m/sのサイトクラスが考慮され、地震動の設計特性周期が0.45秒に設定されました。
は、サイトの土壌の動的特性を特徴付ける重要なパラメータです。これらの量の確率分布と統計パラメータは、特定のクラスのエンジニアリングサイトから収集された地震加速度記録に基づいて決定できます。説明のために、せん断波速度範囲が[150、250]m/sのサイトクラスが考慮され、地震動の設計特性周期が0.45秒に設定されました。
 、
、 の臨界パラメータは、相互に独立した確率変数として扱われ、どちらもパラメータ識別のための対数正規分布に従っていました。統計パラメータは次の通りでした:
の臨界パラメータは、相互に独立した確率変数として扱われ、どちらもパラメータ識別のための対数正規分布に従っていました。統計パラメータは次の通りでした: の平均、
の平均、 はそれぞれ12 rad / sと0.1でした。
はそれぞれ12 rad / sと0.1でした。 と
と の変動係数はそれぞれ0.42と0.35でした。岩盤での地震動は、フーリエ振幅が0.20 m/s2で、ピーク地盤加速度が0.11 gに対応するガウスホワイトノイズプロセスとしてモデル化されました。岩盤運動を生成するために使用される位相角は、
の変動係数はそれぞれ0.42と0.35でした。岩盤での地震動は、フーリエ振幅が0.20 m/s2で、ピーク地盤加速度が0.11 gに対応するガウスホワイトノイズプロセスとしてモデル化されました。岩盤運動を生成するために使用される位相角は、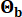 として表されました。したがって、Sb = 1および
として表されました。したがって、Sb = 1および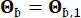 です。このアプローチは、与えられた超過確率44で条件付き確率的地震動をモデル化すると考えることができます。対数正規分布の仮定は、観測された地震動パラメータの歪んだ性質を捉えることができるため、地震動モデリングで広く使用されています。
です。このアプローチは、与えられた超過確率44で条件付き確率的地震動をモデル化すると考えることができます。対数正規分布の仮定は、観測された地震動パラメータの歪んだ性質を捉えることができるため、地震動モデリングで広く使用されています。
この仮定の感度を評価するために、正規分布とガンマ分布を含む代替の確率分布を使用した追加の分析が他の研究で行われてきた45,46。この知見は、全体的な傾向は一貫しているものの、対数正規分布が観測データに最も適合していること、特に地震動強度測定のテール挙動を捉える上で最適であることを示しています
接球法47により、関連する割り当てられた確率を持つ221の代表的な点の集合が選択され、代表的な地上加速度が合成された。サンプリング周波数は50Hzで、地震動の持続時間は20.48秒でした。シミュレートされた地動に非定常強度を割り当てるために、均一な変調関数が使用され、その定式化は次のとおりであった42。
 △ 30
△ 30
ここで  それぞれ2秒と16秒かかります。
それぞれ2秒と16秒かかります。
確率的地震動の平均と標準偏差、および代表的な地震動の時刻歴を図3に示します。平均の振幅(0.06 m/s2)は、標準偏差の振幅(0.8 m/s2)の~8%であり、物理的に動機付けられた確率的地震動モデルがゼロ平均の特性を示したことを示しています。一方、地震動は時間領域と周波数領域の両方で顕著な非定常挙動を示しました。
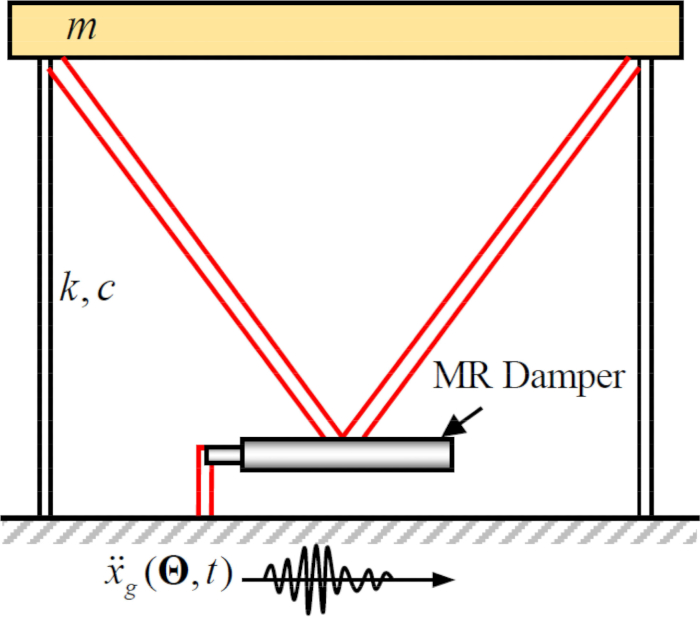
図2:磁性流体ダンパーを備えた1階建てせん断フレームのスケッチ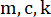 は、構造の質量、減衰比、剛性を示します。
は、構造の質量、減衰比、剛性を示します。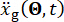 は確率的地震動を示します。この図の拡大版を表示するには、ここをクリックしてください。
は確率的地震動を示します。この図の拡大版を表示するには、ここをクリックしてください。
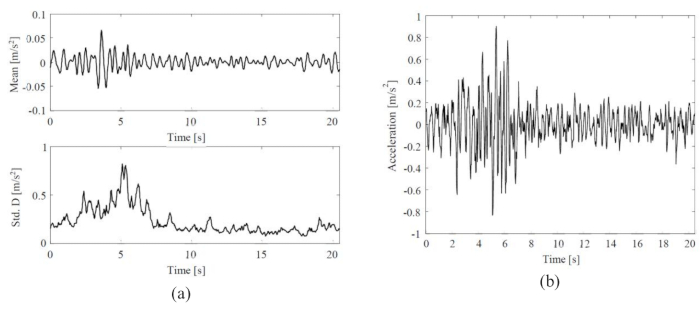
図3:選択した地震動の統計と代表的なサンプル。 (A)確率的地震動の平均と標準偏差。(B)代表的な地震動の時刻歴。 この図の拡大版を表示するには、ここをクリックしてください。
2.1 時間遅延の影響解析
MRダンパーのセミアクティブ制御の有効性に対する時間遅延の影響を解析するために、 図4 は制御された構造の変位、速度、加速度のRMS(二乗平均平方根応答)を示しています。重み付けマトリックス比およびダンパーパラメータは、 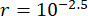 、
、 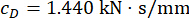 、および
、および 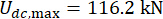 であり、これらは時間遅延38なしで最適化された結果である。時間遅延のある制御構造の応答は、時間遅延のない制御構造よりも大きく、制御効果に対する時間遅延の影響は、時間遅延の増加とともに周期性を表していました。MRダンパーを用いたセミアクティブ制御法はフィードバック法の一種であるため、影響の周期性は制御構造の固有周期(T=0.56秒)と関連していると考えられた。
であり、これらは時間遅延38なしで最適化された結果である。時間遅延のある制御構造の応答は、時間遅延のない制御構造よりも大きく、制御効果に対する時間遅延の影響は、時間遅延の増加とともに周期性を表していました。MRダンパーを用いたセミアクティブ制御法はフィードバック法の一種であるため、影響の周期性は制御構造の固有周期(T=0.56秒)と関連していると考えられた。
最大MRS変位、最大速度、加速度が24.6mm、270.0mm/s、3111.3mm/s2であった非制御構造の応答と比較して、MRダンパー制御構造は顕著な効果を発揮しました。MRダンパーベースのセミアクティブ制御方式は、時間遅延25によるアクティブ制御構造の不安定性とは異なり、時間遅延があっても一定の効果を得ていた。
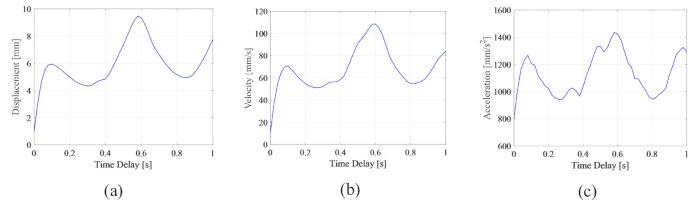
図4:制御された構造の応答の最大二乗平均平方根の経時変化。(A)変位;(b)速度;(C)加速。この図の拡大版を表示するには、ここをクリックしてください。
セミアクティブ制御構造の信頼性に対する時間遅延の影響を解析するために、 図5 は、時間遅延の増加に伴う変位、速度、および加速度の信頼性を示しています。任意の時間遅延がある場合の制御構造応答の信頼性は、時間遅延がない場合の値よりも低かったため、制御構造の信頼性は時間遅延によって低下したことを意味します。一方、最大RMSと同様に、信頼性制御効果は時間遅延の増加に伴って周期性を示しました。さらに、制御された構造の信頼性は、時間遅延の有無にかかわらず、変位、速度、および加速度の信頼性が0.0954、0.1058、および0.1111の制御されていない構造の値よりも高かった。
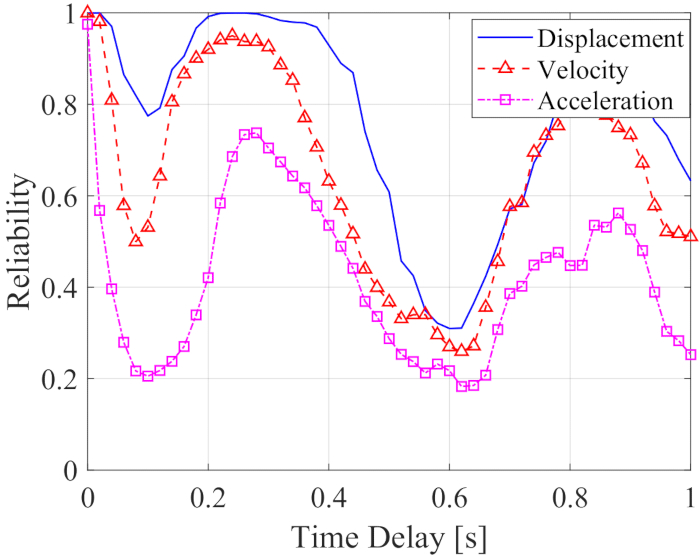
図5:時間遅延の増加に伴う制御構造の応答の信頼性。この図の拡大版を表示するには、ここをクリックしてください。
要約すると、構造の応答はセミアクティブ制御法によって緩和されました。しかし、RMSや信頼性に関わらず、セミアクティブ制御方式の制御効果は時間遅延により低下していた。そのため、時間遅れを補う必要があります。
2.1.1 時間遅延補償法の解析
提案された時間遅延補償法の有効性を分析するために、図 6で、非制御(Unc)、非補償制御の時間遅延システム(TDN-SAC-PSO)、および時間遅延制御された時間遅延システム(TDC-SAC-PSO)の変位、速度、および加速度のRMS時間履歴を比較します(時間遅延は0.1秒でした)。重み付け行列とセミアクティブ制御法のパラメータは、ステップ2.1と同じです。
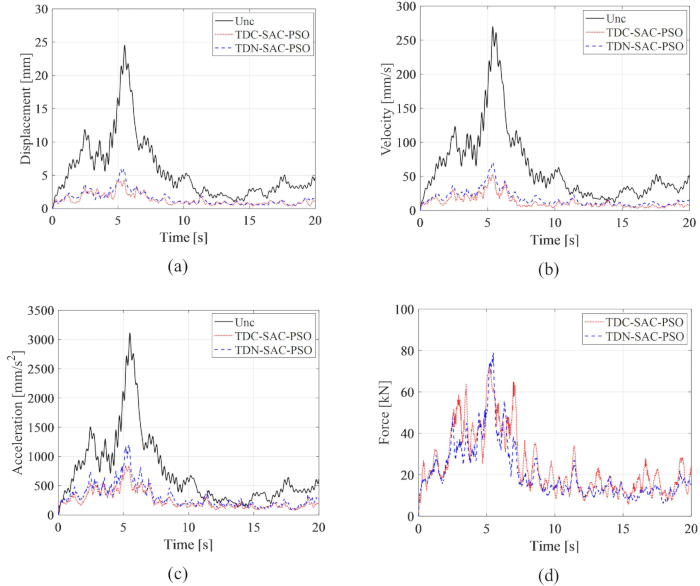
図6:異なる方法で制御された構造の二乗平均平方根の時刻歴比較。 (A)変位;(b)速度;(C)加速;(D)制御力。略語: Unc = 制御されていない;TDC-SAC-PSO = 補償が制御された時間遅延システム。TDN -SAC-PSO = 非補償制御の時間遅延システム。 この図の拡大版を表示するには、ここをクリックしてください。
いずれの制御方法も、非制御構造と比較して構造の応答性が大幅に低下し、MRダンパーベースの制御方法の利点が明らかになりました。制御されていない構造と比較して、TDN-SAC-PSO法では、変位、速度、加速度の最大RMSが75.79%、73.75%、61.22%減少します。さらに、時間遅延補償により、制御された構造の応答は、TDC-SAC-PSO方式で82.59%、80.40%、および73.04%減少します。TDC-SAC-PSO法の制御力の最大RMSは、TDN-SAC-PSO法と比較して8.43%減少しましたが、前者の方法の振動応答は後者よりも小さくなりました。以上の分析から、MRダンパーによる制御方式に対する時間遅延の影響は、補償方式によって効果的に低減されたことが示され、MRダンパーセミアクティブ制御方式における時間遅延補償の必要性が示された。
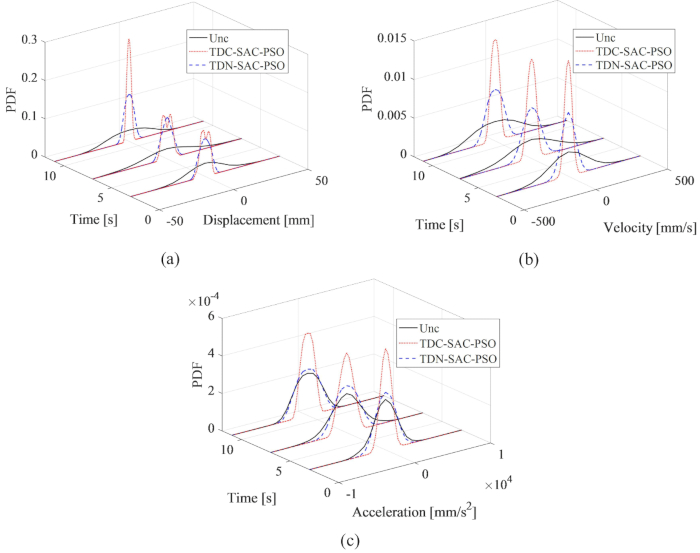
図7:構造応答の一般的な時間におけるPDFの比較。(A)変位;(b)速度;(C)加速。略語:PDF =確率密度関数;Unc = 制御されていない;TDC-SAC-PSO = 補償が制御された時間遅延システム。TDN -SAC-PSO = 非補償制御の時間遅延システム。 この図の拡大版を表示するには、ここをクリックしてください。
提案された補償法が制御構造の応答の不確かさに及ぼす影響を包括的に明らかにするために、典型的な時間(3、7、11)での変位、速度、加速度の確率密度関数(PDF)の比較を 図7に示します。TDN-SAC-PSO法のPDFは、Uncontrold構造のPDFよりも狭かったため、時間遅延があってもセミアクティブ制御法によって構造応答の不確かさが減少した。時間遅延を補正すると、回答のPDFはさらに絞り込まれました。したがって、提案された補償方法は、セミアクティブ制御効果を改善するために必要である。
| 制御方法 | 排水量 | 速度 | 加速度 | 制御力 | 最小値 |
| UNCの | 0.0954 | 0.1058 | 0.1111 | -- | 0.1111 |
| TDC-SAC-PSOの | 0.9565 | 0.8107 | 0.7654 | 0.9845 | 0.7654 |
| TDN-SAC-PSO | 0.7747 | 0.531 | 0.2054 | 0.884 | 0.2054 |
表1:異なる方法で制御された構造物の振動応答と制御力の信頼性。 略語: Unc = 制御されていない;TDC-SAC-PSO = 補償が制御された時間遅延システム。TDN -SAC-PSO = 非補償制御の時間遅延システム。
Uncontrolled、TDC-SAC-PSO-、およびTDN-SAC-PSO法制御構造の振動応答と制御力の信頼性を 表1に示します。TDN-SAC-PSO方式制御では、Uncontrold構造と比較して構造の信頼性が飛躍的に向上し、MRダンパーベースの制御方式の有効性が経時的にも検証されました。しかし、時間遅延補償により、特に加速について、補償なしと比較して信頼性が大幅に向上しました。また、TDC-SAC-PSO法では、異なる応答の信頼性と制御力に大きな違いが見られたことも注目に値します。これは、時間遅延のない制御のクリティカル パラメータの最適値が、時間遅延のある制御に最適ではないことを示しています。振動応答と時間遅延の影響による制御力の最適な制御効果を実現するには、パラメータをさらに最適化する必要があります。以上の解析から、MRダンパーを用いたセミアクティブ制御方式は、構造物の振動応答を効果的に低減できる一方、時間遅延の影響によりパラメータを最適化する必要があると結論付けられます。
2.2 パラメータの最適化
パラメータの最適値を達成するために、信頼性基準に基づく統合最適化法を適用した38。重要なパラメータの最適化は、  、
、 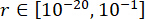 、
、  、
、 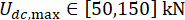 、およびMRダンパー力s = 8の調整可能な時間で実行されました。MATLAB 内の GA ツールボックスを使用して最適化を実装しました。
、およびMRダンパー力s = 8の調整可能な時間で実行されました。MATLAB 内の GA ツールボックスを使用して最適化を実装しました。
パラメーターの最適化結果は、時間遅延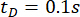 の
の 、
、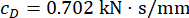 、および
、および です。図8は、Uncontrold(Unc)、TDC-SAC-PSO法、およびSOSC-PSO法で制御された構造の変位、速度、加速度、および制御力のRMS時刻歴を示しています。SOSC-PSO方式は、時間遅延補償と最適化されたクリティカルパラメータ値を備えたセミアクティブ制御方式を示します。
です。図8は、Uncontrold(Unc)、TDC-SAC-PSO法、およびSOSC-PSO法で制御された構造の変位、速度、加速度、および制御力のRMS時刻歴を示しています。SOSC-PSO方式は、時間遅延補償と最適化されたクリティカルパラメータ値を備えたセミアクティブ制御方式を示します。
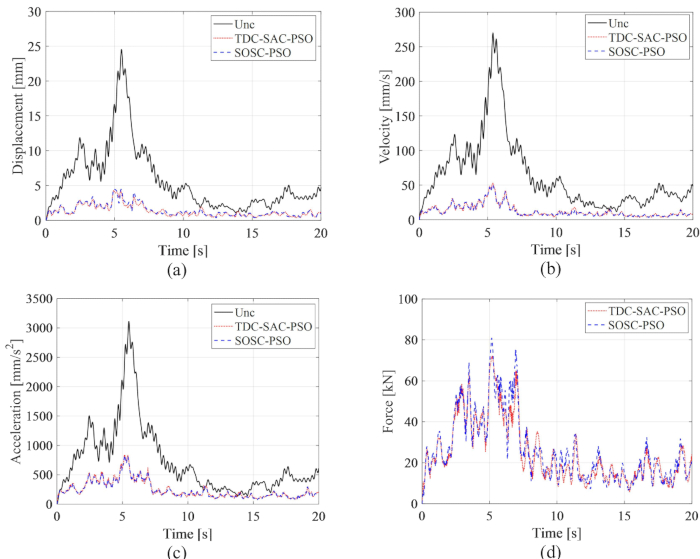
図8:UncontroldおよびTDC-SAC-PSO法およびSOSC-PSO法で制御された構造物の変位、速度、加速度、および制御力のRMS時間履歴。 (A)変位;(b)速度;(C)加速;(D)制御力。略語: Unc = 制御されていない;TDC-SAC-PSO = 補償が制御された時間遅延システム。SOSC-PSO = 時間遅延補償付きストキャスティクス最適セミアクティブ制御法。 この図の拡大版を表示するには、ここをクリックしてください。
図8から、TDC-SAC-PSO法とSOSC-PSO法の制御効果にはほとんど差が見られないことがわかります。変位速度と加速度の最大RMSは、前者の手法が非制御構造の81.60%、81.21%、73.62%、後者の手法が82.59%、80.40%、73.04%であった。図9に、両制御法の応答の確率特性を包括的に解析するために、非制御構造、TDC-SAC-PSO法およびSOSC-PSO法制御構造の変位、速度、加速度のPDFを示します。どちらの制御方法も、典型的な時間における変位と速度のPDFはほぼ同じでした。SOSC-PSO法の加速度PDFはTDC-SAC-PSO法よりも狭かったため、加速の不確かさは前者の方法の方が優れた制御効果を達成したことを意味します。
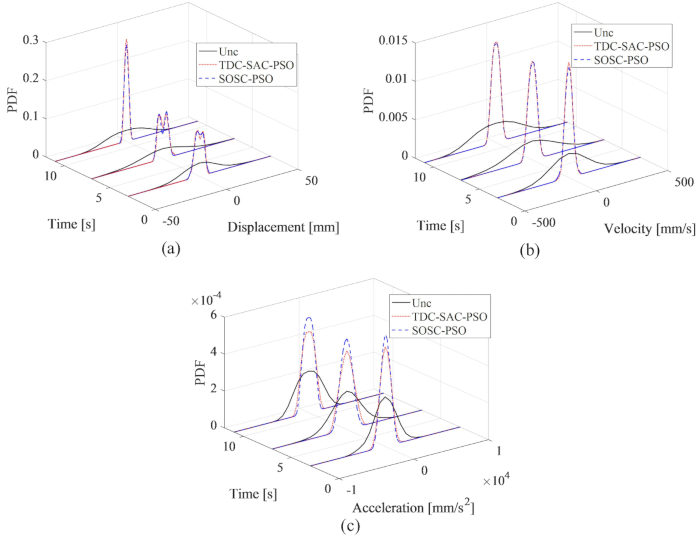
図9:異なる制御構造の変位、速度、加速度のPDF比較。 (A)変位;(b)速度;(C)加速。略語:PDF =確率密度関数;Unc = 制御されていない;TDC-SAC-PSO = 補償が制御された時間遅延システム。SOSC-PSO = 時間遅延補償付きストキャスティクス最適セミアクティブ制御法。 この図の拡大版を表示するには、ここをクリックしてください。
非制御構造とTDC-SAC-PSO-およびSOSC-PSO法で制御された構造の変位、速度、加速度、および制御力の信頼性を 表2に示します。どちらの制御方法も、非制御構造と比較して信頼性の大幅な向上を達成しました。変位信頼性は、TDC-SAC-PSO法とSOSC-PSO法でほとんど差が見られませんでした。一方、制御された構造の中で最も信頼性が低い加速信頼性は、顕著な向上を達成しました。これは、SOSC-PSO方式がバランス最適制御効果を達成することを意味します。
| 制御方法 | 排水量 | 速度 | 加速度 | 制御力 | 最小値 |
| UNCの | 0.0954 | 0.1058 | 0.1111 | -- | 0.1111 |
| TDC-SAC-PSOの | 0.9565 | 0.8107 | 0.7654 | 0.9845 | 0.7654 |
| SOSC-PSOの | 0.953 | 0.8704 | 0.8934 | 0.9586 | 0.8934 |
表2:さまざまな方法で制御される構造の信頼性。 略語: Unc = 制御されていない;TDC-SAC-PSO = 補償が制御された時間遅延システム。SOSC-PSO = 時間遅延補償付きストキャスティクス最適セミアクティブ制御法。
提案したSOSC-PSO法の時間遅延 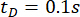 の有効性について検討した。さまざまな時間遅延について提案された方法をさらに検証するために、 表3 に、時間遅延範囲
の有効性について検討した。さまざまな時間遅延について提案された方法をさらに検証するために、 表3 に、時間遅延範囲 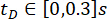 の最適なパラメータ値と対応する信頼性を示します。
の最適なパラメータ値と対応する信頼性を示します。
| tD(s) | LG(R*) | CD(kN・s/mm) | Udc、最大 (kN) | 排水量 | 速度 | 加速度 | 制御力 |
| 0 | -2.524 | 1.44 | 116.163 | 0.9997 | 0.9998 | 0.9752 | 1 |
| 0.02 | -4.413 | 0.414 | 144.066 | 0.9989 | 0.9988 | 0.872 | 0.9011 |
| 0.04 | -4.416 | 0.25 | 141.759 | 0.9998 | 0.9846 | 0.8881 | 0.9135 |
| 0.06 | -3.226 | 0.203 | 145.613 | 0.993 | 0.9318 | 0.8756 | 0.9556 |
| 0.08 | -5.207 | 0.345 | 133.692 | 0.9646 | 0.8998 | 0.8998 | 0.953 |
| 0.1 | -4.669 | 0.702 | 130.739 | 0.9531 | 0.8704 | 0.8934 | 0.9586 |
| 0.12 | -4.895 | 0.833 | 69.72 | 0.9526 | 0.863 | 0.888 | 0.9686 |
| 0.14 | -4.231 | 0.921 | 75.221 | 0.9531 | 0.8681 | 0.8697 | 0.9671 |
| 0.16 | -5.594 | 0.662 | 138.922 | 0.9529 | 0.8461 | 0.8262 | 0.931 |
| 0.18 | -4.262 | 0.882 | 76.335 | 0.9516 | 0.7873 | 0.7614 | 0.9618 |
| 0.2 | -3.926 | 0.783 | 67.951 | 0.904 | 0.7277 | 0.7116 | 0.9653 |
| 0.22 | -5.965 | 1.071 | 52.554 | 0.8377 | 0.6411 | 0.6205 | 0.965 |
| 0.24 | -4.481 | 1.216 | 128.148 | 0.7567 | 0.474 | 0.474 | 0.9687 |
| 0.26 | -3.53 | 0.672 | 53.706 | 0.53 | 0.4096 | 0.4158 | 0.9921 |
| 0.28 | -4.433 | 0.638 | 64.225 | 0.3547 | 0.3745 | 0.3464 | 0.9928 |
| 0.3 | -3.536 | 0.459 | 57.705 | 0.2735 | 0.316 | 0.2736 | 0.9929 |
| UNCの | -- | -- | -- | 0.0954 | 0.1058 | 0.1111 | -- |
表3:さまざまな時間遅延に対する最適なパラメータ値と対応する信頼性値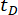 は時間遅延を示します。
は時間遅延を示します。 は r の最適な対数値を示し、r は制御重み付け行列の係数を示します。
は r の最適な対数値を示し、r は制御重み付け行列の係数を示します。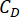 はMRダンパーの粘性減衰係数を示します
はMRダンパーの粘性減衰係数を示します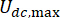 は、MRダンパーの最大クーロン力と最小クーロン力を示します。
は、MRダンパーの最大クーロン力と最小クーロン力を示します。
変位、速度、加速度の信頼性は、時間遅延が存在する場合でも、制御されていない構造と比較して向上していることが観察でき、提案手法の遅延に対するロバスト性を示しています。しかし、提案制御方式では、時間遅延が大きくなると構造応答の信頼性が低下しており、時間遅延による制御効果への影響は軽減できるものの、完全に排除することはできないことが示された。特に、制御力の信頼性は、さまざまな時間遅延にわたって90%を超え続けました。
3. 数値例
提案したSOSC-PSO法をMDOF構造で検証するため、 図10に示すように、1階と3階にMRダンパーを2基設置した6階建て構造を解析しました。セクション2の確率的地震モデルによって生成された地震サンプルを適用し、変位、速度、加速度、および制御力の信頼性しきい値は、20 mm、200 mm/s、3,000 mm/s2、および200 kNでした。式。(27)は、 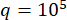 との重み付け行列として使用した。MATLAB の GA ツールボックスを使用して、
との重み付け行列として使用した。MATLAB の GA ツールボックスを使用して、 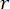 、
、 、
、  を最適化し、最適な範囲
を最適化し、最適な範囲 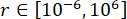 、
、  、
、 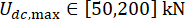 を実現しました。
を実現しました。
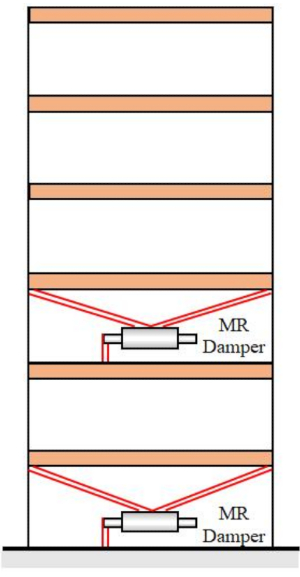
図10:MRダンパーが2つある6階構造。 略語:MR =磁性流体学。 この図の拡大版を表示するには、ここをクリックしてください。
3.1 時間遅延の影響分析
MDOF構造におけるMRダンパーの制御効果に対する時間遅延の影響を解析するために、 図11 にTDC-SAC-PSO法の変位(層間変位)、速度(層間速度)、加速度(層加速度)の最大RMSと時間遅延を示しています。パラメータは、1階のMRダンパーが  、
、 、
、  、3階のMRダンパーが
、3階のMRダンパーが  、
、  で、時間遅延なく最適化した結果です。制御された構造応答の最大RMSは、時間遅延とともに周期変動を示しました。変位と速度の最大RMSは1階にあり、最大加速度は6階でした。また、任意の時間遅延のある応答の最大MRSは、時間遅延なしの値よりもすべて大きく、時間遅延はMRダンパーの制御効果を低下させることを意味します。
で、時間遅延なく最適化した結果です。制御された構造応答の最大RMSは、時間遅延とともに周期変動を示しました。変位と速度の最大RMSは1階にあり、最大加速度は6階でした。また、任意の時間遅延のある応答の最大MRSは、時間遅延なしの値よりもすべて大きく、時間遅延はMRダンパーの制御効果を低下させることを意味します。
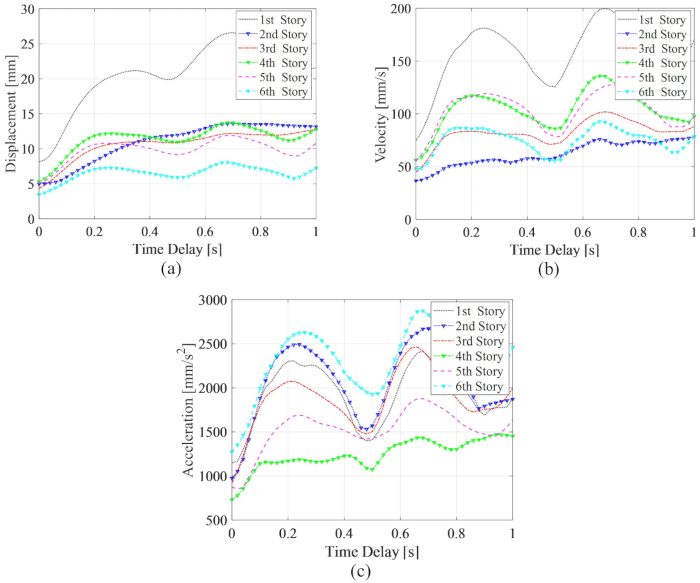
図11:TDC-SAC-PSOメソッド制御構造の応答の最大RMSと時間遅延。 (A)変位;(b)速度;(C)加速。略語: RMS = 二乗平均平方根;TDC-SAC-PSO = 補正が制御された時間遅延システム。 この図の拡大版を表示するには、ここをクリックしてください。
変位、速度、加速度の信頼性と時間遅延を 図12に示します。速度と加速度の信頼性は、時間遅延とともに周期変動を示しますが、変位の信頼性は時間遅延とともに劇的に減少します。任意の時間遅延におけるすべての信頼性値は、時間遅延がない場合よりも小さかった。そのため、MRダンパー制御構造の信頼性に対する時間遅延の影響を低減するためには、時間遅延補償法が必要である。
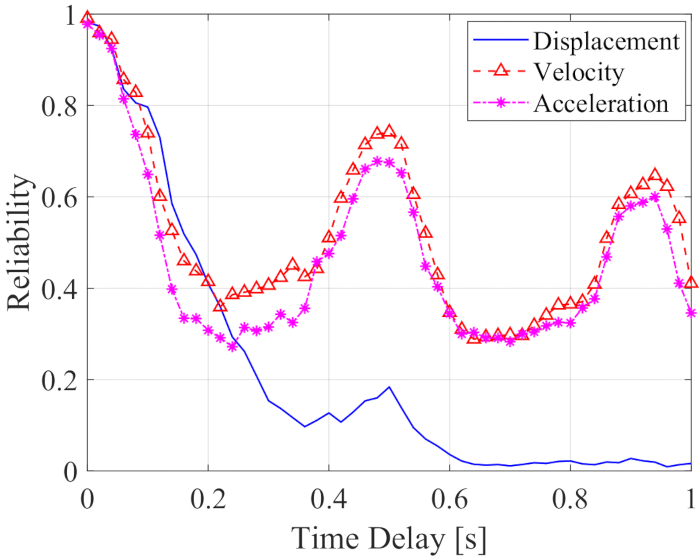
図12:制御された構造の応答と時間遅延の信頼性。この図の拡大版を表示するには、ここをクリックしてください。
3.2 時間遅延補償の制御効果
提案したTDC-SAC-PSO法に基づき、MRダンパーを2個備えた6自由度構造を解析しました。 図13 は、Uncontrold(Unc)、TDC-SAC-PSO方式制御構造、およびTDN-SAC-PSO方式制御構造の1階と3階の変位と加速度のRMS時刻歴を示しています。時間遅延は  、重み付けマトリックス比は
、重み付けマトリックス比は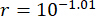 、MRダンパーパラメータは
、MRダンパーパラメータは  、1階は
、1階は  、3階は
、3階は  と
と  でした。
でした。

図13:異なる方法で制御された構造物の1階と3階での変位と加速度のRMS時間履歴。 (A)1階での変位。(B)3階での移動。(C)1階での加速。(D) 3階での加速。略語: RMS = 二乗平均平方根;Unc = 制御されていない;TDC-SAC-PSO = 補償が制御された時間遅延システム。TDN -SAC-PSO = 非補償制御の時間遅延システム。 この図の拡大版を表示するには、ここをクリックしてください。
1階と3階の最大変位RMSは、時間遅延が補正されていないTDN-SAC-PSO法により35.42%と30.44%減少しました。補償ありながら、1階と3階の最大RMS変位はそれぞれ49.33%と53.39%減少しました。補正なしの場合、1階と3階の最大加速度RMSは16.22%と2.88%増加しましたが、補償ありでそれぞれ25.77%と36.00%減少しました。そのため、MRダンパー制御法における時間遅れの補償は、構造物の応答、特に加速度の低減のために必要となります。
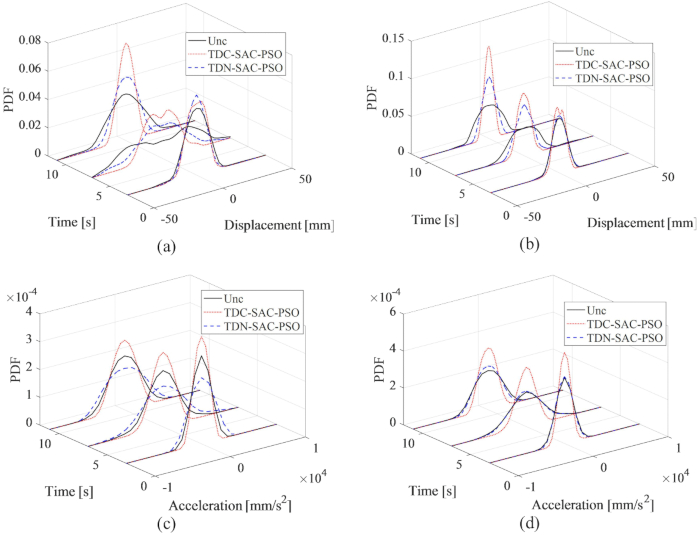
図14:1階と3階の変位と加速度のPDFで、制御方法別に (A)1階での変位。(B)3階での移動。(C)1階での加速。(D) 3階での加速。略語:PDF =確率密度関数;Unc = 制御されていない;TDC-SAC-PSO = 補償が制御された時間遅延システム。TDN -SAC-PSO = 非補償制御の時間遅延システム。 この図の拡大版を表示するには、ここをクリックしてください。
図14に1階と3階の変位と加速度のPDFを示し、TDC-SAC-PSO法とTDN-SAC-PSO法の制御効果と非制御構造の比較結果を明らかにしています。補償がない場合、1階と3階の変位のPDFは、制御されていない構造のPDFよりも依然として狭かった。また、時間遅延を補正することで、TDN-SAC-PSO法制御構造の変位PDFよりも変位のPDFが狭くなった。変位とは異なり、補償なしの場合、TDN-SAC-PSO法の1階での加速度のPDFは、制御されていない構造のPDFよりも広くなりました。しかし、補正により、1階と3階の両方での加速度のPDFは、制御されていない構造のPDFよりも狭くなっていました。したがって、特に加速度に対する構造応答の確実性を高めるためには、時間遅延補償の必要性が検証されます。
| 制御方法 | 排水量 | 速度 | 加速度 | 1階 での制御力 | 3階 での制御力 |
| UNCの | 0.0114 | 0.5822 | 0.6372 | -- | -- |
| TDN-SAC-PSO | 0.5851 | 0.5258 | 0.398 | 1 | 1 |
| TDC-SAC-PSOの | 0.806 | 0.8674 | 0.8037 | 1 | 1 |
表4:さまざまな方法で制御される構造の信頼性。 略語: Unc = 制御されていない;TDC-SAC-PSO = 補償が制御された時間遅延システム。TDN -SAC-PSO = 非補償制御の時間遅延システム。
変位、速度、加速度、および制御力の信頼性値を、さまざまな方法で制御される構造システムとともに表 4に示します。構造応答の信頼性値は、等価極値法25を使用して計算した。TDN-SAC-PSO法の制御により、制御されていない構造と比較して変位の信頼性は向上し、速度と加速度の信頼性は低下しました。TDC-SAC-PSO方式の時間遅延補償により、変位、速度、加速度の信頼性が大幅に向上しました。また、TDN-SAC-PSO方式とTDN-SAC-PSO方式の両法における制御力の信頼性値は十分に維持されています。このように、提案する時間遅れ補償制御方式は、MRダンパー制御構造に対して良好な制御効果を発揮する。
3.3 パラメータの最適化
最適な制御効果を得るために、提案した制御方法のパラメータは、信頼性基準に基づいて最適化されました。時間遅延 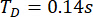 、1階MRダンパーは
、1階MRダンパーは  、
、 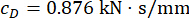 、
、 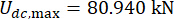 、3階MRダンパーは
、3階MRダンパーは 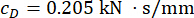 、
、  が最適な結果となりました。
が最適な結果となりました。
図15に、1階と3階の変位と加速度のRMS時刻歴を示し、TDC-SAC-PSO法とSOSC-PSO法の制御効果と非制御構造の比較を示します。MRダンパー制御では、時間遅延補正の有無にかかわらず、変位と加速度のRMSが大幅に減少しました。SOSC-PSO法では、1階と3階の最大変位RMSは、非制御構造と比較してそれぞれ65.15%と63.16%減少しました。TDC-SAC-PSO方式と比較して、変位応答はさらに減少しました。1階と3階の最大加速度RMSは、SOSC-PSO方式で23.39%、35.60%減少します。SOSC-PSO方式とTDC-SAC-PSO方式では加速度の制御効果にほとんど差がなく、変位と加速度で時間遅延補償の制御効果が異なることが示された。
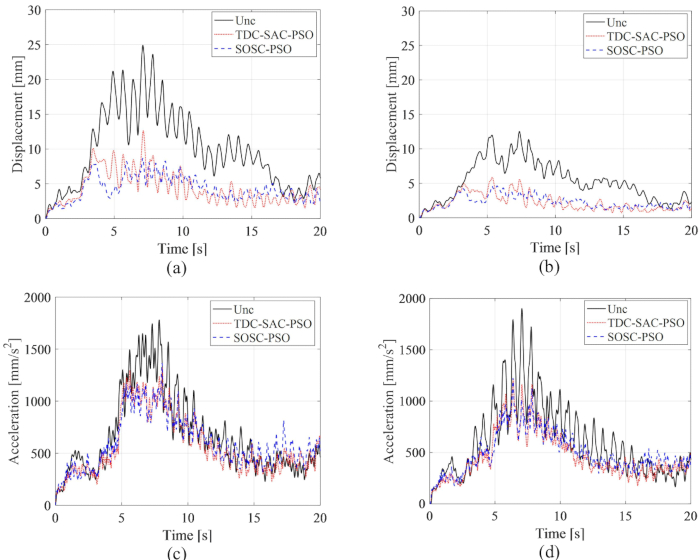
図15:さまざまな制御方法の1階と3階での変位と加速度のRMS時刻歴。 (A)1階での変位。(B)3階での移動。(C)1階での加速。(D) 3階での加速。略語: RMS = 二乗平均平方根;Unc = 制御されていない;TDC-SAC-PSO = 補償が制御された時間遅延システム。SOSC-PSO = 時間遅延補償付きストキャスティクス最適セミアクティブ制御法。 この図の拡大版を表示するには、ここをクリックしてください。
1階と3階の変位と加速度のPDFを 図16に示します。変位と加速度のPDFは、TDC-SAC-PSOおよびSOSC-PSO法によって、Uncontrold構造と比較して狭められました。また、SOSC-PSO法の変位と加速度のPDFは、TDC-SAC-PSO法で制御された構造のものと比較してさらに狭くなっていました。したがって、パラメータの最適化により、提案された時間遅延補償制御方法は、最適化を使用しない場合よりも優れた制御効果を達成しました。
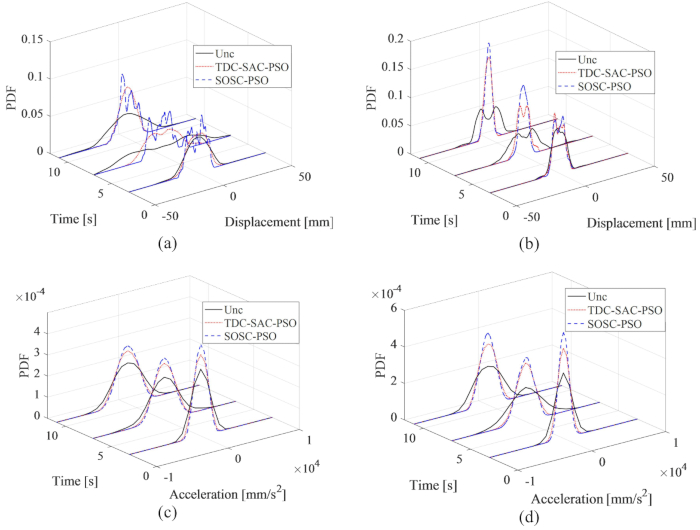
図16:1階と3階の変位と加速度のPDFで、制御方法ごとに比較したものです。 (A)1階での変位。(B)3階での移動。(C)1階での加速。(D) 3階での加速。略語:PDF =確率密度関数;Unc = 制御されていない;TDC-SAC-PSO = 補償が制御された時間遅延システム。SOSC-PSO = 時間遅延補償付き確率最適セミアクティブ制御法 この図の拡大版を表示するには、ここをクリックしてください。
変位、速度、加速度、および制御力の信頼性値を 表5に示します。SOSC-PSO法の信頼性値は、TDC-SAC-PSO法の信頼性値よりも高かった。一方、制御力は依然として十分な信頼性を保持していました。したがって、MRダンパーベースの制御方法の最良の制御効果を達成するためには、パラメータの最適化が必要です。
| 制御方法 | 排水量 | 速度 | 加速度 | 1階 での制御力 | 3階 での制御力 |
| UNCの | 0.0114 | 0.5822 | 0.6372 | -- | -- |
| TDC-SAC-PSOの | 0.806 | 0.8674 | 0.8037 | 1 | 1 |
| SOSC-PSOの | 0.9544 | 0.9314 | 0.8788 | 1 | 1 |
表5:さまざまな方法で制御される構造の信頼性。 略語: Unc = 制御されていない;TDC-SAC-PSO = 補償が制御された時間遅延システム。SOSC-PSO = 時間遅延補償付きストキャスティクス最適セミアクティブ制御法。
結果
本論文では、MRダンパーを用いた手法の制御効果に対する時間遅延の影響に着目し、時間遅延補償を用いたセミアクティブ制御手法を提案します。提案手法では、信頼性基準に基づいて臨界パラメータを最適化します。制御の有効性を比較することにより、次の結論が解決されます。
(1)MRダンパーによるセミアクティブ制御方式は、アクティブ制...
ディスカッション
本稿では、物理確率最適制御理論(PSO)の導入に伴い、MRダンパーによって制御される構造物の信頼性を維持するための時間遅延補償付き確率最適セミアクティブ制御法(SOSC-PSO)を提案しています。提案手法における時間遅れを補償するために、セミアクティブ制御力は、現在の状態だけでなく、離散状態空間における前の時間ステップの状態と制御力の関数としても導?...
開示事項
すべての著者は、宣言すべき利益相反はありません。
謝辞
著者らは、河北省自然科学基金会(助成金第E2023210007号)の支援に感謝します。
資料
| Name | Company | Catalog Number | Comments |
| MATLAB | MathWorks | 2016 | Using for the calculation of the proposed method |
参考文献
- Yao, J. T. P. Concept of structural control. J Struct Div. 98 (7), 1567-1574 (1972).
- Liu, J., Silva, C. E., Dyke, S. J., Wu, Y., Liu, H. Using real-time hybrid simulation for active mass damper experimentation and validation. Mech Mach Theory. 191, 105474 (2024).
- Pan, H., Li, C., Cao, L. Bidirectional pendulum-type tuned tendem mass dampers-inerters for integrated control of alongwind and crosswind responses in super-tall buildings. J Build Eng. 100, 111676 (2025).
- Housner, G. W. et al. Structural control: past, present, and future. J Eng Mech. 123 (9), 897-971 (1997).
- Rahman, M., Ong, Z. C., Chong, W. T., Julai, S. Smart Semi-active PID-ACO control strategy for tower vibration reduction in Wind Turbines with MR damper. Earthq Eng Eng Vib. 18 (4), 887-902 (2019).
- Morales-Beltran, M., Paul, J. Active and semi-active strategies to control building structures under large earthquake motion. J Earthquake Eng. 19 (7), 1086-1111 (2015).
- Shu, Z., You, R., Xie, Y. Viscoelastic dampers for vibration control of building structures: A state-of-art review. J Earthq Eng. 28 (12), 3558-3585 (2024).
- Soong, T. T. Active structural control: Theory and practice. Longman Scientific & Technical. New York (1990).
- Wan, H. P., Ma, Q., Dong, G. S., Luo, Y., Ni, Y. Q. Data-driven model reduction approach for active vibration control of cable-strut structures. Eng Struct. 302, 117434 (2024).
- Cao, L., Li, X., Huang, Y., Li, C., Pan, H. High robust eddy current tuned tandem mass dampers-inerters for structures under the ground acceleration. Soil Dyn Earthq Eng. 188, 109040 (2025).
- Chha, H., Peng, Y. Adaptive semiactive control of structure with magnetorheological dampers using wavelet packet transform. Adv Struct Eng. 27 (9), 1509-1527 (2024).
- Zeng, X., Peng, Y., Chen, J. Serviceability-based damping optimization of randomly wind-excited high-rise buildings. Struct Des Tall Spec. 26 (11), e1371 (2017).
- Li, C., Chang, K., Cao, L., Huang, Y. Performance of a nonlinear hybrid base isolation system under the ground motions. Soil Dyn Earthq Eng. 143, 106589 (2021).
- Cao, L., Li, C. A high performance hybrid passive base-isolated system. Struct Control Health Monitoring. 29 (3), e2887 (2022).
- Zareie, S., Issa, A. S., Seethaler, R., Zabihollah, A., Ahmad, R. A novel SMA-magnetorheological hybrid bracing system for seismic control. Eng Struct. 244, 112709 (2021).
- Chu, S. Y., Soong, T. T., Reinhorn, A. M. Active, hybrid and semi-active structural control. John Wiley & Sons, New York (2005).
- Danielian, S. A., Jabbari, F., Zareian, F. Effects and distribution of semi-active resettable springs on the seismic response of asymmetric structures. Earthq Eng Struct D. 52 (10). 2966-2982 (2023).
- Shuang, Z., Wenliuhan, H. S., Liu, Y. H., Inoue, N., Zhai, Z. P. Seismic response control for bridge piers with semi-active MR damper based on displacement feedback. J Earthq Eng. 28 (3). 849-865 (2024).
- Wang, Y., Dyke, S. Modal-based LQG for smart base isolation system design in seismic response control. Struct Control Health Monitoring. 20 (5), 753-768 (2013).
- Desai, R. M. et al. Performance evaluation of a single sensor control scheme using a twin-tube MR damper based semi-active suspension. J Vib Eng Technol. 9, 1193-1210 (2021).
- Abdi, M. S., Nekooei, M. Jafari, M. A. Seismic control of multi-degrees-of-freedom structures by vertical mass isolation method using MR dampers. Earthq Eng Eng Vib. 23 (2), 503-510 (2024).
- Bhowmik, K., Debnath, N. Semi-active vibration control of soft-storey building with magnetorheological damper under seismic excitation. J Vib Eng Technol. 12 (4), 6943-6961 (2024).
- Yang, J. N., Akbarpour, A., Askar, G. Effect of time delay on control of seismic-excited buildings. J Struct Eng. 116 (10), 2801-2814 (1990).
- Temimi, H., Ben-Romdhane, M., El-Borgi, S., Cha, Y. Time-delay effects on controlled seismically excited linear and nonlinear structures. Int J Struct Stab Dyn. 16 (7), 1550031 (2016).
- Peng, J., Wang, L., Zhao, Y., Lenci, S. Time-delay dynamics of the MR damper-cable system with one-to-one internal resonances. Nonlinear Dynamics. 105 (2), 1343-1356 (2021).
- Cha, Y. J., Agrawal, A. K., Dyke, S. J. Time delay effects on large-scale MR damper based semi-active control strategies. Smart Mater Struct. 22 (1), 015011 (2013).
- Yu, Y. et al. Experimental study of wireless structural vibration control considering different time delays. Smart Mater Struct. 24, 045005 (2015).
- Ahmadizadeh, M., Mosqueda, G., Reinhorn, A. M. Compensation of actuator delay and dynamics for real-time hybrid structural simulation. Earthq Eng Struct Dyn. 37 (1), 21-42 (2008).
- Bathaei, A., Zahrai, S. M. Compensating time delay in semi-active control of a SDOF structure with MR damper using predictive control. Struc Eng Mech. 82 (4), 445-458 (2022).
- Dyke, S. J., Spencer, Jr, B. F., Sain, M. K., Carlson, J. D. Modeling and control of magnetorheological dampers for seismic response reduction. Smart Mater Struct. 5 (5), 565-575 (1996).
- Ying, Z. G., Ni, Y. Q., Ko, J. M. A semi-active stochastic optimal control strategy for nonlinear structural systems with MR dampers. Smart Struct Syst. 5 (1), 69-79 (2009).
- Rosol, M., Martynowicz, P. Implementation of the LQG controller for a wind turbine tower-nacelle model with a MR tuned vibration absorber. J Theor App Mech-Pol. 54 (4), 1109-1123 (2016).
- Lyu, M. Z., Feng, D. C., Chen, J. B., Li, J. A decoupled approach for determination of the joint probability density function of a high-dimensional nonlinear stochastic dynamical system via the probability density evolution method. Comput Method Appl M. 418 (A), 116443 (2024).
- Chha, H., Peng, Y. Multiscale stochastic optimal control of hysteretic structures based on wavelet transform and probability density evolution method. Eng Computation. 41 (4), 865-896 (2024).
- Li, J., Peng, Y. B., Chen, J. B. A physical approach to structural stochastic optimal controls. Probabilist Eng Mech. 25 (1), 127-141 (2010).
- Peng, Y. B., Yang, J. G., Li, J. Seismic risk-based stochastic optimal control of structures using magnetorheological dampers. Nat Hazards Rev. 18 (1), B4016001 (2017).
- Dong, X. M., Yu, M., Li, Z., Liao, C., Chen, W. Neural network compensation of semi-active Control for magneto-rheological suspension with time delay uncertainty. Smart Mater Struct. 18 (1), 015014 (2008).
- Peng, Y. B., Zhang, Z. Optimal MR damper-based semiactive control scheme for strengthening seismic capacity and structural reliability. J Eng Mech. 146 (6), 04020045 (2020).
- Luo, M. X., Gao, M. Cai, G. Delayed full-state feedback control of airfoil flutter using sliding mode control method. J Fluid Struct. 61, 262-273 (2016).
- Xu, J., Chung, K. W., Chan, C. L. An efficient method for studying weak resonant double Hopf bifurcation in nonlinear systems with delayed feedbacks. Siam J Appl Dyn Syst. 6 (1), 29-60 (2007).
- Yang, J. S., Jensen, H., Chen, J. B. Structural optimization under dynamic reliability constraints utilizing probability density evolution method and metamodels in augmented input space. Struct Multidiscip Optimization. 65, 107 (2022).
- Li, J., Chen, J. B. Stochastic dynamics of structures. John Wiley & Sons, Singapore (2009).
- Peng, Y. B., Li, J. Stochastic optimal control of structures. Springer (2019).
- Dowrick, C. Beyond depression: A new approach to understanding and management. Oxford University Press (2009).
- Wang, D., Li, J. Physical random function model of ground motions for engineering purposes. Sci China Technol Sci. 54 (1), 175-182 (2011).
- Wang, D., Li, J. A random physical model of seismic ground motion field on local engineering site. Sci China Technol Sci. 55 (7), 2057-2065 (2012).
- Chen, J. B., Li, J. Strategy for selecting representative points via tangent spheres in the probability density evolution method. Int J Numer Meth Eng. 74 (13), 1988-2014 (2008).
転載および許可
このJoVE論文のテキスト又は図を再利用するための許可を申請します
許可を申請さらに記事を探す
This article has been published
Video Coming Soon
Copyright © 2023 MyJoVE Corporation. All rights reserved