Un abonnement à JoVE est nécessaire pour voir ce contenu. Connectez-vous ou commencez votre essai gratuit.
Research Article
Méthode de contrôle stochastique semi-actif de la structure basée sur des amortisseurs magnétorhéologiques tenant compte du retard
Dans cet article
Résumé
Une méthode de contrôle semi-actif optimal stochastique avec compensation de retard (SOSC-PSO) est proposée dans cet article, qui est conçue pour maintenir la fiabilité des structures contrôlées par des amortisseurs MR.
Résumé
L’utilisation d’amortisseurs magnétorhéologiques (MR) dans les systèmes de contrôle semi-actifs se heurte à un défi majeur : le retard causé par les processus de rétroaction, ce qui réduit la fiabilité des structures de génie civil sous excitations stochastiques. Cet article propose une méthode de contrôle semi-actif optimal stochastique avec compensation de retard (SOSC-PSO), en s’appuyant sur la théorie du contrôle optimal stochastique physique (PSO) pour résoudre ce problème et maintenir la fiabilité structurelle. La méthode proposée calcule la force de commande semi-active en fonction des états actuel et précédent, compensant les retards dans le processus de contrôle. Pour optimiser l’efficacité du contrôle, les paramètres clés sont ajustés en fonction d’un critère de fiabilité du système. Les analyses de validation sur des structures à un ou plusieurs degrés de liberté sous excitations sismiques stochastiques montrent que les retards temporels altèrent considérablement les performances des amortisseurs MR. Cependant, la méthode SOSC-PSO avec compensation de retard améliore considérablement l’efficacité du contrôle et, avec des paramètres optimisés, elle améliore la fiabilité du système de contrôle structurel au-delà des méthodes sans optimisation des paramètres.
Introduction
L’amélioration de la performance des ouvrages d’art face à des événements catastrophiques, tels que les tremblements de terre et les vents extrêmes, demeure une préoccupation majeure au sein de la communauté du génie civil. Il a été prouvé que le contrôle structurel, une technique efficace pour réduire les vibrations, améliore à la fois la sécurité et la fonctionnalité de ces structures 1,2,3. Au cours des dernières décennies, diverses méthodes et technologies de pointe ont été développées à cet effet. Ces méthodes peuvent être classées en quatre grandes catégories en fonction du type d’énergie utilisé pour faire fonctionner les dispositifs de contrôle : systèmes de contrôle actifs, semi-actifs, passifs et hybrides 4,5,6,7.
Dans le contrôle actif, la force de commande requise est appliquée directement à travers les dispositifs de contrôle, ce qui nécessite une quantité importante d’énergie 8,9,10. Le contrôle semi-actif, quant à lui, consiste à ajuster les propriétés des dispositifs de contrôle (telles que l’amortissement ou la rigidité) en fonction des signaux de commande, nécessitant beaucoup moins d’énergie par rapport aux systèmes actifs11. Le contrôle passif, en revanche, repose sur la dissipation d’énergie sans aucune entrée d’énergie externe dans le système 12,13,14. Les systèmes hybrides combinent les caractéristiques des stratégies de contrôle actif/semi-actif et passif pour obtenir des performances plus efficaces15. Parmi ces approches, le contrôle semi-actif est considéré comme particulièrement prometteur en raison de son équilibre entre faible consommation d’énergie et rendement élevé 16,17,18. L’amortisseur magnétorhéologique (MR), avec ses caractéristiques d’amortissement dynamique supérieures, est considéré comme l’un des dispositifs de contrôle semi-actif les plus efficaces 19,20,21,22.
Cependant, un défi se pose dans les systèmes de contrôle semi-actifs qui utilisent des amortisseurs MR, car la logique de rétroaction introduit inévitablement des retards. Ces retards sont généralement causés par plusieurs facteurs 23,24,25, notamment : (i) l’acquisition et le traitement des données du capteur, (ii) le calcul de la force de commande requise par le contrôleur26, (iii) la transmission du signal par les transducteurs aux amortisseurs MR27, et (iv) la génération réelle de force par les amortisseurs MR eux-mêmes 28. De tels retards peuvent entraîner des écarts entre la force de commande produite et la force attendue par la structure, compromettant ainsi considérablement l’efficacité du contrôle29. Malheureusement, la plupart des algorithmes de contrôle existants pour les amortisseurs MR ne tiennent pas compte de ces retards.
De plus, en raison du caractère aléatoire inhérent aux événements catastrophiques, tout algorithme de contrôle semi-actif efficace doit être capable de maintenir les performances sous des excitations stochastiques. La méthode de contrôle LQG (Linear Quadratic Gaussian), une technique classique d’optimisation stochastique, a été explorée pour atténuer les vibrations dans les structures équipées d’amortisseurs MR. Par exemple, Dyke et al. ont proposé une stratégie de contrôle optimal LQG pour améliorer la réponse sismique des structures équipées de registres MR, en utilisant la rétroaction d’accélération30. Ying et al. ont introduit une stratégie de contrôle stochastique optimale semi-active non écrêtée pour les structures non linéaires avec des amortisseurs MR, incorporant des techniques de calcul de la moyenne stochastique et de programmation dynamique31. D’autres études ont appliqué un contrôle LQG basé sur le modal pour améliorer la performance sismique des bâtiments isolés de la base19 et analysé son efficacité pour l’atténuation des vibrations dans les tours d’éoliennes32. Cependant, les méthodes classiques de LQG, qui supposent un bruit blanc gaussien, ne sont pas bien adaptées à la modélisation de la nature non stationnaire et non gaussienne des excitations du monde réel comme les tremblements de terre ou les vents forts. Pour résoudre ce problème, le concept de contrôle stochastique optimal (PSO) basé sur la physique a été développé33,34, qui surmonte les limites des méthodes LQG traditionnelles et offre un cadre plus précis pour gérer diverses excitations stochastiques35. Des études ont montré que le contrôle optimal stochastique semi-actif basé sur le PSO améliore considérablement l’atténuation des vibrations pour les structures linéaires et non linéaires soumises à des forces sismiques stochastiques36.
Ainsi, il est urgent de disposer d’une méthode de contrôle semi-active robuste qui compense les retards, améliorant ainsi la fiabilité des structures contrôlées par des registres MR25,37. De plus, pour assurer des performances de contrôle optimales sous excitations stochastiques, il est essentiel d’optimiser les paramètres critiques de la méthode de contrôle proposée à l’aide d’une approche basée sur la fiabilité. Par conséquent, une méthode de contrôle semi-actif optimal stochastique avec compensation de retard (SOSC-PSO) est proposée dans cet article pour améliorer la fiabilité des structures avec des amortisseurs MR.
Protocole
1. Méthode de contrôle semi-active optimale stochastique
Comme l’effet de contrôle d’un amortisseur MR est considérablement influencé par l’inévitable retard, une méthode de contrôle semi-active avec un algorithme de compensation de retard est développée pour augmenter les performances de la structure contrôlée. De plus, le caractère aléatoire inhérent aux excitations externes est à l’origine des incertitudes évidentes des réponses dynamiques. Le contrôle PSO est introduit pour optimiser les paramètres critiques de la méthode proposée afin d’assurer la fiabilité du système de contrôle de la structure.
1.1 Algorithme de compensation du contrôle semi-actif
Sans perte de généralité, considérons une structure à n degrés de liberté (n-DOF) contrôlée par des amortisseurs MR avec retard temporel, dont l’équation de mouvement soumise à des excitations stochastiques est donnée par :
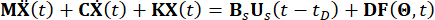 (1)
(1)
Où  représentent respectivement les matrices n x n de masse, d’amortissement et de rigidité de la structure ; n représente le nombre de degrés de liberté de la structure contrôlée. Les vecteurs déplacement, vitesse et accélération de la structure sont représentés respectivement par
représentent respectivement les matrices n x n de masse, d’amortissement et de rigidité de la structure ; n représente le nombre de degrés de liberté de la structure contrôlée. Les vecteurs déplacement, vitesse et accélération de la structure sont représentés respectivement par 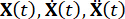 , . Le petit et les deux points au-dessus des symboles représentent les dérivées de première et de deuxième fois. Us (t - tD) représente le vecteur de dimension r de la force de commande retardée des amortisseurs MR, et r représente le nombre d’amortisseurs ; t représente le temps ; tD désigne un retard temporel, supposé uniforme pour tous les amortisseurs dans cette étude, où
, . Le petit et les deux points au-dessus des symboles représentent les dérivées de première et de deuxième fois. Us (t - tD) représente le vecteur de dimension r de la force de commande retardée des amortisseurs MR, et r représente le nombre d’amortisseurs ; t représente le temps ; tD désigne un retard temporel, supposé uniforme pour tous les amortisseurs dans cette étude, où 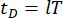 , avec ici le nombre
, avec ici le nombre 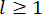 intégral , et
intégral , et 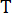 désignant la période d’échantillonnage.
désignant la période d’échantillonnage. 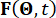 représente le vecteur de dimension p des excitations stochastiques, et
représente le vecteur de dimension p des excitations stochastiques, et  représente le vecteur de paramètre stochastique caractérisant le caractère aléatoire associé aux excitations externes. La dimension de
représente le vecteur de paramètre stochastique caractérisant le caractère aléatoire associé aux excitations externes. La dimension de  dépend du modèle utilisé pour les excitations externes mais n’est pas liée aux degrés mécaniques de liberté de la structure. Bs et D sont des matrices n x r et n x p qui spécifient l’emplacement des amortisseurs et des excitations externes, respectivement. Dans la représentation de l’espace d’état, l’équation (1) s’écrit comme suit :
dépend du modèle utilisé pour les excitations externes mais n’est pas liée aux degrés mécaniques de liberté de la structure. Bs et D sont des matrices n x r et n x p qui spécifient l’emplacement des amortisseurs et des excitations externes, respectivement. Dans la représentation de l’espace d’état, l’équation (1) s’écrit comme suit :
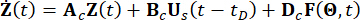 (2)
(2)
Où 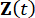 représente le vecteur d’état à 2n dimensions ;
représente le vecteur d’état à 2n dimensions ; 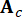 représente la matrice de système 2n x 2n ;
représente la matrice de système 2n x 2n ; 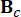 représente la matrice d’emplacement 2n x r des amortisseurs MR ;
représente la matrice d’emplacement 2n x r des amortisseurs MR ; 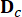 Représente la matrice de localisation 2n x p des excitations externes. Ces paramètres sont exprimés comme suit :
Représente la matrice de localisation 2n x p des excitations externes. Ces paramètres sont exprimés comme suit :
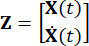 ,
, 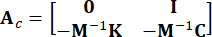 ,
,  ,
, 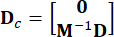 (3)
(3)
Où 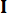 désigne une matrice identité du même ordre que
désigne une matrice identité du même ordre que 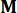 . Pour faciliter le calcul, l’équation de l’espace d’états continu Eq. (2) peut être exprimée sous forme discrète comme suit :
. Pour faciliter le calcul, l’équation de l’espace d’états continu Eq. (2) peut être exprimée sous forme discrète comme suit :
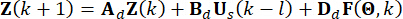 (4)
(4)
Où le point 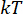 temporel est simplifié comme .
temporel est simplifié comme . 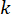 Et
Et  ,
, 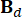 ,
, 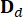 désignent les matrices 2n x 2n, 2n x r et 2n x p, qui s’expriment comme suit :
désignent les matrices 2n x 2n, 2n x r et 2n x p, qui s’expriment comme suit :
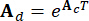 ,
,  ,
, 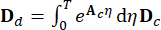 (5)
(5)
Où 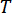 désigne la période d’échantillonnage.
désigne la période d’échantillonnage.
Pour obtenir une efficacité similaire à celle du contrôle actif, une méthode de contrôle simple et efficace basée sur l’algorithme de Hrovat38 est proposée pour le contrôle basé sur l’amortisseur MR avec temporisation :
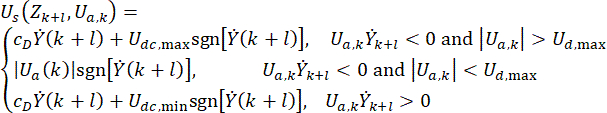 (6)
(6)
où  représente le signal de force de commande semi-actif au point temporel\
représente le signal de force de commande semi-actif au point temporel\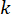 pour l’amortisseur MR ;
pour l’amortisseur MR ; 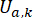 représente la force de commande active de référence avec compensation de temporisation ;
représente la force de commande active de référence avec compensation de temporisation ;  représente la force d’amortissement maximale de l’amortisseur MR, qui est modifiable ;
représente la force d’amortissement maximale de l’amortisseur MR, qui est modifiable ; 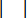 représente le symbole d’opération de valeur absolue ;
représente le symbole d’opération de valeur absolue ; 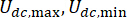 représentent les forces coulombiennes maximales et minimales de l’amortisseur
représentent les forces coulombiennes maximales et minimales de l’amortisseur  MR ;représente le coefficient d’amortissement visqueux ;
MR ;représente le coefficient d’amortissement visqueux ; 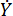 représente la vitesse d’entrée dans l’amortisseur MR, qui est la vitesse de mouvement du piston par rapport au cylindre de l’amortisseur. Dans l’équation (6),
représente la vitesse d’entrée dans l’amortisseur MR, qui est la vitesse de mouvement du piston par rapport au cylindre de l’amortisseur. Dans l’équation (6),  représenter les paramètres conçus de l’amortisseur MR.
représenter les paramètres conçus de l’amortisseur MR.
L’équation (6) montre le calcul de la force de commande semi-active de l’amortisseur MR avec retard. On voit que la force  de contrôle semi-active, au pas
de contrôle semi-active, au pas  de temps dans l’équation (4), est calculée sur la base de la force
de temps dans l’équation (4), est calculée sur la base de la force  de contrôle active au pas
de contrôle active au pas  de temps et de la variable
de temps et de la variable 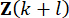 d’état au pas
d’état au pas  de temps depuis le retard des pas de
de temps depuis le retard des pas de 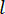 temps. Pour obtenir la force
temps. Pour obtenir la force  de contrôle active , la fonction de coût conventionnelle est établie par
de contrôle active , la fonction de coût conventionnelle est établie par
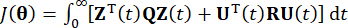 (7)
(7)
Où représente la matrice de pondération semi-définie positive symétrique 2n x 2n de l’état du système ;  représente
représente  la matrice de pondération définie positive symétrique r x r de la force de commande. On voit que l’excitation externe est négligeable. En fait, sur la base de l’équation (7), le système de contrôle de la structure peut obtenir l’effet de contrôle optimal quel que soit le type d’excitation externe. En tant que forme discrète, l’équation (7) s’exprime par39 :
la matrice de pondération définie positive symétrique r x r de la force de commande. On voit que l’excitation externe est négligeable. En fait, sur la base de l’équation (7), le système de contrôle de la structure peut obtenir l’effet de contrôle optimal quel que soit le type d’excitation externe. En tant que forme discrète, l’équation (7) s’exprime par39 :
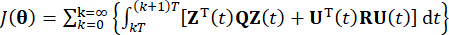 (8)
(8)
La minimisation de la fonction  de coût conduit à un problème conditionnel de valeurs extrêmes, et la force
de coût conduit à un problème conditionnel de valeurs extrêmes, et la force  de contrôle active est calculée par25 :
de contrôle active est calculée par25 :
 (9)
(9)
Où 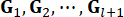 désigne les gains de contrôle pour la variable
désigne les gains de contrôle pour la variable 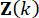 d’état au pas
d’état au pas  de temps et la force
de temps et la force 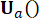 de contrôle active au pas
de contrôle active au pas 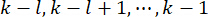 de temps , qui est déterminée par les matrices
de temps , qui est déterminée par les matrices 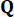 de pondération et
de pondération et 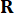 37. Depuis l’inévitable retard, la force
37. Depuis l’inévitable retard, la force 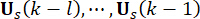 de contrôle obtenue est influencée sur la structure à des points
de contrôle obtenue est influencée sur la structure à des points 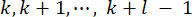 temporels. Par conséquent, la force de commande active dans l’équation (9) est calculée comme suit :
temporels. Par conséquent, la force de commande active dans l’équation (9) est calculée comme suit :
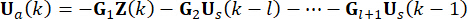 (10)
(10)
Pour la clarté de la conception, la force de contrôle semi-active dans l’équation (10) est exprimée comme suit sur la base de l’équation (6) :
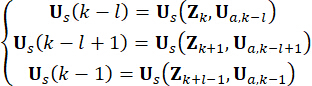 (11)
(11)
Où  désigne la force de contrôle active au point
désigne la force de contrôle active au point  temporel . en remplaçant l’équation (11) par l’équation (10),
temporel . en remplaçant l’équation (11) par l’équation (10),
 (12)
(12)
REMARQUE : Toutes les valeurs d’état  du point
du point  temporel à
temporel à 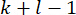 sont nécessaires pour le calcul
sont nécessaires pour le calcul  de . Par conséquent, la méthode de prédiction d’état suivante est introduite40.
de . Par conséquent, la méthode de prédiction d’état suivante est introduite40.
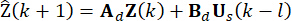 (13)
(13)
Où  désigne la variable prédite. Par l’itération de l’équation (13), l’état
désigne la variable prédite. Par l’itération de l’équation (13), l’état  en
en  est calculé. La force de commande active Ua(k) est exprimée comme suit :
est calculé. La force de commande active Ua(k) est exprimée comme suit :
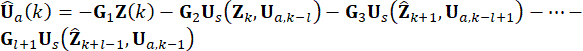 (14)
(14)
La force de contrôle semi-active peut être obtenue en combinant les équations. (6), (12) et (13).
1.2 Analyse de la fiabilité du système de contrôle de la structure
Selon le principe de préservation des probabilités, le système 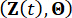 augmenté et
augmenté et 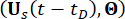 la structure avec des amortisseurs MR sont conservés en termes de probabilités, et ils sont régis par les équations généralisées d’évolution de la densité de probabilité (GDEE) suivantes38 :
la structure avec des amortisseurs MR sont conservés en termes de probabilités, et ils sont régis par les équations généralisées d’évolution de la densité de probabilité (GDEE) suivantes38 :
 (15)
(15)
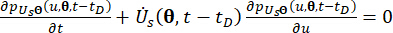 (16)
(16)
Où  ,
,  désignent les composantes correspondantes de l’état du système et de la force de commande semi-active avec retard, respectivement ;
désignent les composantes correspondantes de l’état du système et de la force de commande semi-active avec retard, respectivement ; 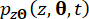 et
et  désignent les fonctions de densité de probabilité conjointe des systèmes
désignent les fonctions de densité de probabilité conjointe des systèmes 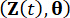 d’échantillonnage augmentés et
d’échantillonnage augmentés et 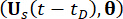 , respectivement ;
, respectivement ; 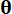 désigne l’échantillon dans l’espace d’échantillonnage de
désigne l’échantillon dans l’espace d’échantillonnage de 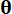 ;
;  et
et  ) désignent les dérivées partielles temporelles du premier ordre des composantes de l’état du système et de la force de commande semi-active, respectivement. La densité de probabilité conjointe fonctionne
) désignent les dérivées partielles temporelles du premier ordre des composantes de l’état du système et de la force de commande semi-active, respectivement. La densité de probabilité conjointe fonctionne 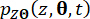 et
et  peut être obtenue en résolvant des équations. (15) et (16) aux conditions initiales suivantes :
peut être obtenue en résolvant des équations. (15) et (16) aux conditions initiales suivantes :
 (17)
(17)
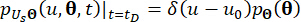 (18)
(18)
où 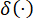 désigne la fonction delta de Dirac ;
désigne la fonction delta de Dirac ; 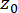 et
et 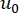 désignent respectivement les valeurs initiales déterministes de
désignent respectivement les valeurs initiales déterministes de  et
et 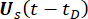 , ;
, ; 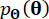 désigne la fonction de densité de probabilité de l’échantillon
désigne la fonction de densité de probabilité de l’échantillon 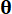 .
.
Les fonctions de densité de probabilité instantanée de  et
et 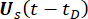 peuvent être obtenues par l’intégration unidimensionnelle de
peuvent être obtenues par l’intégration unidimensionnelle de 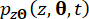 et
et  sur le domaine de l’espace d’échantillonnage :
sur le domaine de l’espace d’échantillonnage :
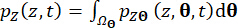 (19)
(19)
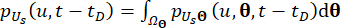 (20)
(20)
Où 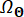 désigne le domaine de distribution de
désigne le domaine de distribution de  .
.
Basé sur les équations. (19) et (20), on constate que l’information probabiliste complète des grandeurs physiques concernées est facilement dérivée, si leurs relations associées aux paramètres de l’algorithme sont définies. La fiabilité des grandeurs physiques concernées peut être calculée à l’aide de la fonction de performance pertinente suivante :
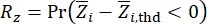 (21)
(21)
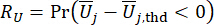 (22)
(22)
où 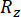 et désignent
et désignent 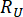 la fiabilité calculée de la grandeur d’état concernée et de la force de contrôle semi-active, respectivement ;
la fiabilité calculée de la grandeur d’état concernée et de la force de contrôle semi-active, respectivement ;  désigne le vecteur de valeur extrême équivalente de la ième grandeur physique concernée de la structure contrôlée ;
désigne le vecteur de valeur extrême équivalente de la ième grandeur physique concernée de la structure contrôlée ; 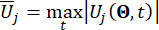 désigne le vecteur de valeur extrême équivalente de la j-ème force de contrôle ; le chapeau '-' sur les symboles indique le vecteur de valeur extrême équivalent41 ;
désigne le vecteur de valeur extrême équivalente de la j-ème force de contrôle ; le chapeau '-' sur les symboles indique le vecteur de valeur extrême équivalent41 ;  désigne la i-ième grandeur physique concernée de la k-ième DOF de la structure contrôlée ;
désigne la i-ième grandeur physique concernée de la k-ième DOF de la structure contrôlée ; 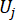 désigne la J-ème force de contrôle ;
désigne la J-ème force de contrôle ; 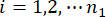 ,
, 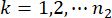 ,
,  ,
, ,
,  et
et  désignent le nombre de grandeurs physiques concernées et la profondeur de champ de la structure et les amortisseurs MR installés dans la structure, respectivement.
désignent le nombre de grandeurs physiques concernées et la profondeur de champ de la structure et les amortisseurs MR installés dans la structure, respectivement.  et
et 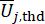 désignent les seuils de
désignent les seuils de  et
et  ;
;  désigne la probabilité de l’événement aléatoire.
désigne la probabilité de l’événement aléatoire.
1.3 Optimisation des paramètres
Le rapport des amplitudes de et  influence fortement l’efficacité du
influence fortement l’efficacité du  contrôle38 dans la modalité de contrôle par rétroaction. Par conséquent, pour obtenir la meilleure efficacité de contrôle,
contrôle38 dans la modalité de contrôle par rétroaction. Par conséquent, pour obtenir la meilleure efficacité de contrôle, et
et  doivent être optimisés. En outre, en tant que méthode de contrôle basée sur l’amortisseur MR, l’efficacité du contrôle est également influencée par les paramètres du dispositif,
doivent être optimisés. En outre, en tant que méthode de contrôle basée sur l’amortisseur MR, l’efficacité du contrôle est également influencée par les paramètres du dispositif,  dans l’équation (6). Pour obtenir la fiabilité optimale du système de contrôle de la structure, le critère basé sur la fiabilité est proposé à l’équation (25).
dans l’équation (6). Pour obtenir la fiabilité optimale du système de contrôle de la structure, le critère basé sur la fiabilité est proposé à l’équation (25).
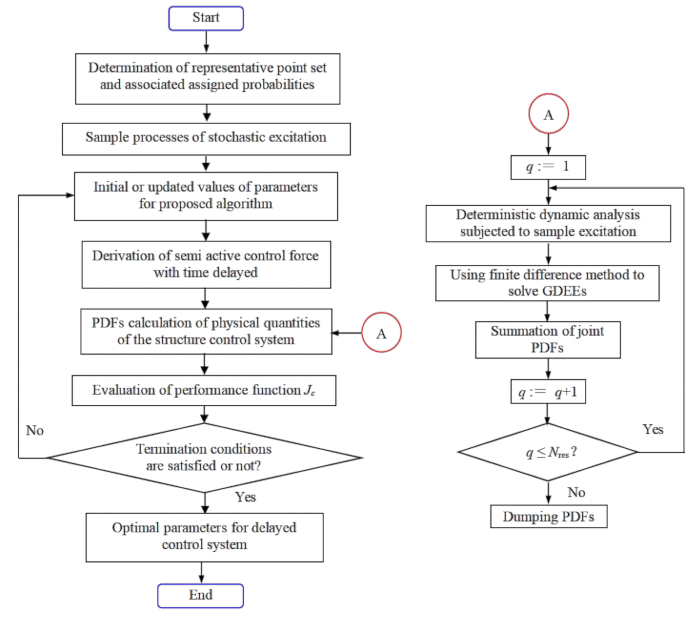
Figure 1 : Organigramme de l’optimisation des paramètres pour un contrôle stochastique optimal de la structure semi-active avec compensation de retard. Abréviations : GDEE = Équation différentielle généralisée de l’événement ; PDF = Fonction de densité de probabilité. Veuillez cliquer ici pour voir une version agrandie de cette figure.
En résumé, deux étapes sont nécessaires pour effectuer le contrôle stochastique optimal de la structure semi-active basé sur des amortisseurs MR avec compensation de retard :
1.3.1 En minimisant la fonction  de coût montrée dans l’équation (7), la logique de rétroaction d’état au sens d’échantillons est atteinte, c’est-à-dire l’équation 12)
de coût montrée dans l’équation (7), la logique de rétroaction d’état au sens d’échantillons est atteinte, c’est-à-dire l’équation 12)
1.3.2 En minimisant la fonction  de performance basée sur la fiabilité, les paramètres optimaux au sens des statistiques sont atteints. La figure 1 présente l’organigramme d’optimisation des paramètres du contrôleur à l’étape 1.3.2.
de performance basée sur la fiabilité, les paramètres optimaux au sens des statistiques sont atteints. La figure 1 présente l’organigramme d’optimisation des paramètres du contrôleur à l’étape 1.3.2.
Les étapes suivantes de l’étape 1.3.2, qui impliquent deux couches de boucles, sont les suivantes :
1.3.2.1 Le partitionnement de l’espace des excitations stochastiques attribué aux probabilités, qui est caractérisé par le vecteur  de paramètre stochastique , permet d’identifier un ensemble de points
de paramètre stochastique , permet d’identifier un ensemble de points 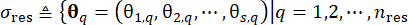 représentatifs ainsi que leurs probabilités associées Pq. Cette approche permet de générer efficacement des processus d’échantillonnage pour l’excitation stochastique, notée
représentatifs ainsi que leurs probabilités associées Pq. Cette approche permet de générer efficacement des processus d’échantillonnage pour l’excitation stochastique, notée 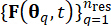 , à obtenir facilement.
, à obtenir facilement.
1.3.2.2 Pour l’optimisation des paramètres du système de contrôle de la structure semi-active, initialiser ou mettre à jour les valeurs des pondérations  coût-fonction et
coût-fonction et  . La force de contrôle de rétroaction d’état associée avec délai, voir l’équation (12), est ensuite calculée.
. La force de contrôle de rétroaction d’état associée avec délai, voir l’équation (12), est ensuite calculée.
1.3.2.3 Obtention des fonctions de densité de probabilité (PDF) des réponses structurelles et de la force de contrôle en résolvant les GDEE indiquées dans les équations. (17)–(20) :
L’optimisation se fait hors ligne, mais pas en ligne. Dans l’application de la méthode proposée dans les systèmes de contrôle de structure réels, l’optimal  et
et  ont été atteints, et l’optimisation n’est pas nécessaire dans le processus réel applicable.
ont été atteints, et l’optimisation n’est pas nécessaire dans le processus réel applicable.
Analyse dynamique déterministe du système de contrôle de structure semi-actif soumis à l’excitation de l’échantillon, par laquelle les grandeurs 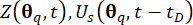 physiques concernées et leurs dérivées
physiques concernées et leurs dérivées  sont calculées.
sont calculées.
En utilisant une méthode de différences finies, telle que le schéma de Lax-Wendroff modifié avec les propriétés de diminution de la variation totale (TVD), les équations différentielles généralisées (GDEE) peuvent être résolues et des solutions numériques pour les fonctions 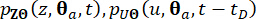 de densité de probabilité conjointe peuvent être dérivées.
de densité de probabilité conjointe peuvent être dérivées.
En répétant les deux étapes ci-dessus de l’analyse dynamique déterministe et de la méthode des différences finies, et en passant sur tous les points 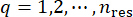 représentatifs, les fonctions de densité de probabilité peuvent être obtenues par sommation :
représentatifs, les fonctions de densité de probabilité peuvent être obtenues par sommation :
 (23)
(23)
 (24)
(24)
Où  représente la mesure de surface du sous-domaine associé au point
représente la mesure de surface du sous-domaine associé au point 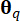 d’échantillonnage . La méthode utilisée pour résoudre l’équation différentielle généralisée de l’événement (GDEE) est connue sous le nom de méthode d’évolution de la densité de probabilité (PDEM)42.
d’échantillonnage . La méthode utilisée pour résoudre l’équation différentielle généralisée de l’événement (GDEE) est connue sous le nom de méthode d’évolution de la densité de probabilité (PDEM)42.
1.3.2.4 Les PDF des grandeurs physiques pertinentes sont utilisées pour évaluer leur fiabilité, qui sont ensuite intégrées dans la fonction  de performance du critère probabiliste.
de performance du critère probabiliste.
1.3.2.5 Évaluer si les critères de fin du processus d’optimisation des paramètres ont été respectés. Si les conditions ne sont pas remplies, retournez à l’étape 1.3.2.2 ; Si c’est le cas, les paramètres optimaux pour le système de commande temporisée peuvent être déterminés. Dans ce travail, la boîte à outils de l’algorithme génétique (GA) de MATLAB est utilisée pour l’optimisation des paramètres, ce qui facilite les mises à jour des paramètres et définit les conditions de terminaison. Grâce à un algorithme génétique, les valeurs optimales peuvent être atteintes en dix itérations, et la convergence est stable sans problèmes de minima locaux. Bien que le coût de calcul de l’AG soit plus important que celui de l’optimisation en essaim de particules ou des méthodes basées sur le gradient, l’AG est bon pour traiter des problèmes complexes et non différenciables, comme celui de ce manuscrit. Par conséquent, l’AG est appliquée. Et comme la propriété de convergence rapide, le coût de calcul de GA est acceptable.
1.3.2.6 Pour obtenir un contrôle optimal de la fiabilité, la fonction  de performance suivante est formulée. Réduire au minimum
de performance suivante est formulée. Réduire au minimum  pour déterminer les valeurs optimales des paramètres
pour déterminer les valeurs optimales des paramètres  et
et  :
:
 } (25)
} (25)
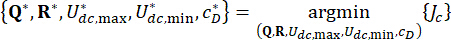 (26)
(26)
Comme mentionné précédemment, les matrices de pondération du contrôleur sont symétriques, où les éléments de la matrice  correspondent aux poids attribués au déplacement, à la vitesse et à leur interaction, tandis que les éléments de la matrice
correspondent aux poids attribués au déplacement, à la vitesse et à leur interaction, tandis que les éléments de la matrice  représentent les poids liés à la force de contrôle. D’après les résultats d’études antérieures38, il a été observé que la variation des configurations des pondérations
représentent les poids liés à la force de contrôle. D’après les résultats d’études antérieures38, il a été observé que la variation des configurations des pondérations  coût-fonction a
coût-fonction a  un impact minime sur l’efficacité du contrôle. Par conséquent, une configuration simplifiée est adoptée dans cette étude, comme indiqué ci-dessous :
un impact minime sur l’efficacité du contrôle. Par conséquent, une configuration simplifiée est adoptée dans cette étude, comme indiqué ci-dessous :
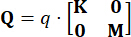 ,
, 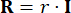 (27)
(27)
Où désigne le coefficient de la matrice de pondération d’état à définir ; 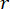 désigne
désigne 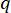 le coefficient de la matrice de pondération de contrôle à définir ;
le coefficient de la matrice de pondération de contrôle à définir ; 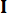 désigne la matrice d’identité. L’effet de contrôle est influencé par le rapport entre
désigne la matrice d’identité. L’effet de contrôle est influencé par le rapport entre 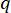 les valeurs et les
les valeurs et les 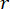 valeurs elles-mêmes. De plus,
valeurs elles-mêmes. De plus, 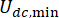 dans l’équation (6) désigne la force coulombienne minimale de l’amortisseur MR, ce qui signifie que l’entrée
dans l’équation (6) désigne la force coulombienne minimale de l’amortisseur MR, ce qui signifie que l’entrée  de courant dans l’amortisseur est nulle. Ensuite, l’équation (26) peut être exprimée comme suit : T
de courant dans l’amortisseur est nulle. Ensuite, l’équation (26) peut être exprimée comme suit : T
 (28)
(28)
Où 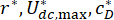 sont les coefficients optimaux préoccupants. Pour les rendre raisonnables en ingénierie, les gammes optimales d’entre eux sont basées sur la capacité de production des usines d’amortisseurs MR.
sont les coefficients optimaux préoccupants. Pour les rendre raisonnables en ingénierie, les gammes optimales d’entre eux sont basées sur la capacité de production des usines d’amortisseurs MR.
De toute évidence, les paramètres optimaux obtenus par l’équation (28) maintiennent l’efficacité de contrôle optimale de l’algorithme de contrôle semi-actif proposé avec retardement, ce qui permet au système de contrôle de la structure d’atteindre la fiabilité optimale équilibrée soumise à des excitations stochastiques.
2. Étude de cas
Afin d’analyser l’efficacité de la méthode de contrôle semi-active proposée avec compensation de retard pour un registre MR, une structure planaire à cadre de cisaillement d’un étage fixée à un registre MR a été soumise au mouvement sismique stochastique horizontal du sol, comme le montre la figure 2. Les paramètres du système de structure semi-activement contrôlé sont les suivants : masse 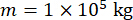 de la structure, fréquence
de la structure, fréquence  circulaire naturelle, rapport
circulaire naturelle, rapport 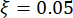 d’amortissement. Selon l’expérience passée et les balances d’amortisseurs existantes sur le marché, les valeurs seuils de déplacement structurel, de vitesse, d’accélération et de force de contrôle sont respectivement de 10 mm, 100 mm/s, 1 500 mm/s2 et 150 kN. Pour représenter le mouvement sismique stochastique du sol, le modèle stochastique du mouvement du sol à motivation physique a été utilisé43 :
d’amortissement. Selon l’expérience passée et les balances d’amortisseurs existantes sur le marché, les valeurs seuils de déplacement structurel, de vitesse, d’accélération et de force de contrôle sont respectivement de 10 mm, 100 mm/s, 1 500 mm/s2 et 150 kN. Pour représenter le mouvement sismique stochastique du sol, le modèle stochastique du mouvement du sol à motivation physique a été utilisé43 :
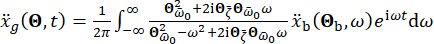 (29)
(29)
Où 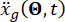 représente le mouvement du sol dans le domaine temporel sur le site d’ingénierie, et
représente le mouvement du sol dans le domaine temporel sur le site d’ingénierie, et 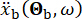 désigne le mouvement du sol dans le domaine fréquentiel au niveau du substrat rocheux. Le vecteur
désigne le mouvement du sol dans le domaine fréquentiel au niveau du substrat rocheux. Le vecteur  caractérise la nature stochastique du mouvement du sol à la surface du site d’ingénierie. Les paramètres
caractérise la nature stochastique du mouvement du sol à la surface du site d’ingénierie. Les paramètres 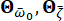 sont des variables stochastiques qui décrivent les caractéristiques du sol du site, y compris la fréquence
sont des variables stochastiques qui décrivent les caractéristiques du sol du site, y compris la fréquence  prédominante et l’amortissement équivalent.
prédominante et l’amortissement équivalent.  Le vecteur
Le vecteur 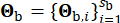 représente la nature stochastique du mouvement du sol au niveau du substrat rocheux, qui est influencée par les propriétés de la source et le chemin de propagation, avec
représente la nature stochastique du mouvement du sol au niveau du substrat rocheux, qui est influencée par les propriétés de la source et le chemin de propagation, avec 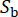 indication du nombre de variables stochastiques impliquées à ce stade.
indication du nombre de variables stochastiques impliquées à ce stade.  fait référence à la fréquence circulaire, et i est l’unité imaginaire.
fait référence à la fréquence circulaire, et i est l’unité imaginaire.
La fréquence  prédominante et le taux
prédominante et le taux  d’amortissement équivalent du site d’ingénierie sont des paramètres clés qui caractérisent les propriétés dynamiques du sol du site. La distribution probabiliste et les paramètres statistiques de ces grandeurs peuvent être déterminés à partir des enregistrements d’accélération sismique recueillis auprès d’une classe spécifique de sites d’ingénierie. À titre d’illustration, une classe de site avec une plage de vitesse d’onde transversale de [150, 250] m/s a été prise en compte, et la période caractéristique de conception du mouvement du sol a été fixée à 0,45 s.
d’amortissement équivalent du site d’ingénierie sont des paramètres clés qui caractérisent les propriétés dynamiques du sol du site. La distribution probabiliste et les paramètres statistiques de ces grandeurs peuvent être déterminés à partir des enregistrements d’accélération sismique recueillis auprès d’une classe spécifique de sites d’ingénierie. À titre d’illustration, une classe de site avec une plage de vitesse d’onde transversale de [150, 250] m/s a été prise en compte, et la période caractéristique de conception du mouvement du sol a été fixée à 0,45 s.
Les paramètres  critiques ont
critiques ont  été traités comme des variables stochastiques mutuellement indépendantes, toutes deux suivant une distribution log-normale pour l’identification des paramètres. Les paramètres statistiques étaient les suivants : les moyennes de
été traités comme des variables stochastiques mutuellement indépendantes, toutes deux suivant une distribution log-normale pour l’identification des paramètres. Les paramètres statistiques étaient les suivants : les moyennes de  ,
,  étaient respectivement de 12 rad/s et de 0,1. Les coefficients de variation de et
étaient respectivement de 12 rad/s et de 0,1. Les coefficients de variation de et  étaient respectivement
étaient respectivement  de 0,42 et 0,35. Le mouvement du sol au niveau du substratum rocheux a été modélisé comme un processus de bruit blanc gaussien avec une amplitude de Fourier de 0,20 m/s2, correspondant à une accélération maximale du sol de 0,11 g. L’angle de phase utilisé pour générer le mouvement du substratum rocheux a été noté
de 0,42 et 0,35. Le mouvement du sol au niveau du substratum rocheux a été modélisé comme un processus de bruit blanc gaussien avec une amplitude de Fourier de 0,20 m/s2, correspondant à une accélération maximale du sol de 0,11 g. L’angle de phase utilisé pour générer le mouvement du substratum rocheux a été noté 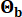 . Par conséquent, Sb = 1 et
. Par conséquent, Sb = 1 et 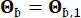 . Cette approche peut être considérée comme la modélisation de mouvements stochastiques conditionnels du sol avec une probabilité de dépassement donnéede 44. L’hypothèse de la distribution log-normale est largement utilisée dans la modélisation des mouvements du sol en raison de sa capacité à capturer la nature asymétrique des paramètres de mouvement du sol observés.
. Cette approche peut être considérée comme la modélisation de mouvements stochastiques conditionnels du sol avec une probabilité de dépassement donnéede 44. L’hypothèse de la distribution log-normale est largement utilisée dans la modélisation des mouvements du sol en raison de sa capacité à capturer la nature asymétrique des paramètres de mouvement du sol observés.
Pour évaluer la sensibilité de cette hypothèse, des analyses supplémentaires utilisant des distributions probabilistes alternatives, y compris les distributions normales et gamma, ont été effectuées dans d’autres recherches45,46. Les résultats indiquent que même si les tendances globales restent constantes, la distribution log-normale fournit le meilleur ajustement aux données observées, en particulier pour capturer le comportement de la queue des mesures d’intensité des mouvements du sol
En vertu de la méthode des sphères tangentes47, une collection de 221 points représentatifs avec des probabilités associées a été sélectionnée et des accélérations représentatives du sol ont été synthétisées. La fréquence d’échantillonnage était de 50 Hz et la durée des mouvements au sol était de 20,48 s. Pour attribuer une intensité non stationnaire au mouvement du sol simulé, une fonction de modulation uniforme a été utilisée et sa formulation a été la suivante42 :
 (30)
(30)
Où  prennent respectivement 2 et 16 s.
prennent respectivement 2 et 16 s.
La moyenne et l’écart-type du mouvement sismique stochastique du sol, ainsi qu’un historique temporel du mouvement sismique représentatif du sol sont illustrés à la figure 3. L’amplitude de la moyenne (0,06 m/s2) était de ~8 % de l’amplitude de l’écart-type (0,8 m/s2), ce qui indique que le modèle stochastique de mouvement du sol à motivation physique présentait la propriété de la moyenne nulle. Pendant ce temps, le mouvement sismique du sol a montré des comportements non stationnaires remarquables à la fois dans les domaines temporel et fréquentiel.
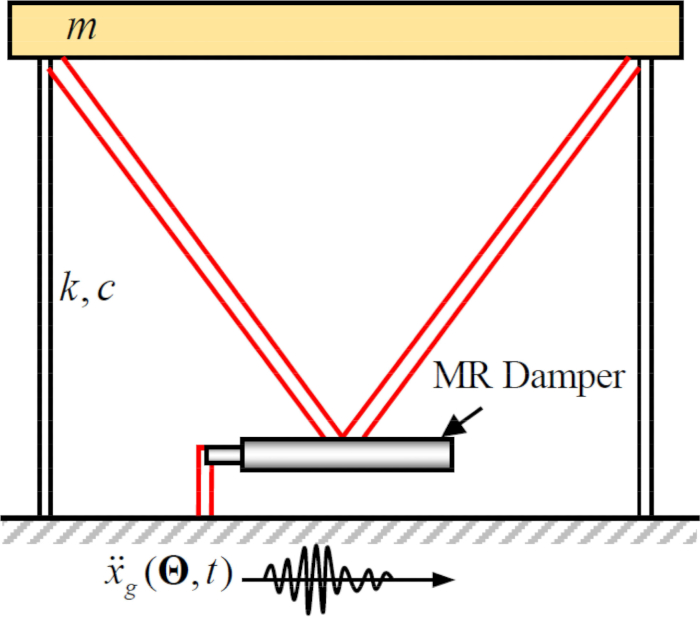
Figure 2 : Croquis d’un cadre de cisaillement à un étage avec un amortisseur magnétorhéologique. 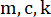 désignent la masse de la structure, le rapport d’amortissement et la rigidité ;
désignent la masse de la structure, le rapport d’amortissement et la rigidité ; 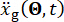 désigne l’excitation sismique stochastique. Veuillez cliquer ici pour voir une version agrandie de cette figure.
désigne l’excitation sismique stochastique. Veuillez cliquer ici pour voir une version agrandie de cette figure.
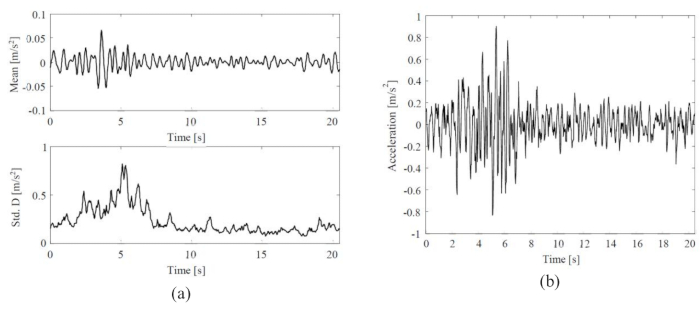
Figure 3 : Statistiques et échantillons représentatifs de mouvements sismiques du sol sélectionnés. (A) Moyenne et écart-type du mouvement sismique stochastique du sol ; (B) Historique temporel des mouvements sismiques représentatifs du sol. Veuillez cliquer ici pour voir une version agrandie de cette figure.
2.1 Analyse d’influence du temps de propagation
Pour analyser l’influence de la temporisation sur l’efficacité du contrôle semi-actif d’un amortisseur MR, la figure 4 montre le déplacement, la vitesse et l’accélération RMS (réponse quadratique moyenne) de la structure contrôlée. Le rapport de la matrice de pondération et les paramètres de l’amortisseur étaient 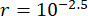 ,
, 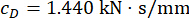 et
et 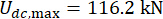 , qui sont les résultats optimisés sans retard38. Les réponses de la structure contrôlée avec retard temporel étaient plus importantes que celles de la structure contrôlée sans retard temporel, et l’influence du retard temporel sur l’effet de contrôle représentait la périodicité avec l’augmentation du retard temporel. Étant donné que la méthode de contrôle semi-actif avec un amortisseur MR est une sorte de méthode de rétroaction, la périodicité de l’influence a été considérée comme liée à la période naturelle de la structure contrôlée (T = 0,56 s).
, qui sont les résultats optimisés sans retard38. Les réponses de la structure contrôlée avec retard temporel étaient plus importantes que celles de la structure contrôlée sans retard temporel, et l’influence du retard temporel sur l’effet de contrôle représentait la périodicité avec l’augmentation du retard temporel. Étant donné que la méthode de contrôle semi-actif avec un amortisseur MR est une sorte de méthode de rétroaction, la périodicité de l’influence a été considérée comme liée à la période naturelle de la structure contrôlée (T = 0,56 s).
Par rapport aux réponses d’une structure non contrôlée, dont le déplacement, la vitesse et l’accélération maximums du MRS étaient de 24,6 mm, 270,0 mm/s et 3111,3 mm/s2, la structure contrôlée par amortisseur MR a obtenu un effet notable. Contrairement à l’instabilité de la structure contrôlée active avec une temporisationde 25, la méthode de commande semi-active basée sur l’amortisseur MR a tout de même obtenu un certain effet même avec une temporisation.
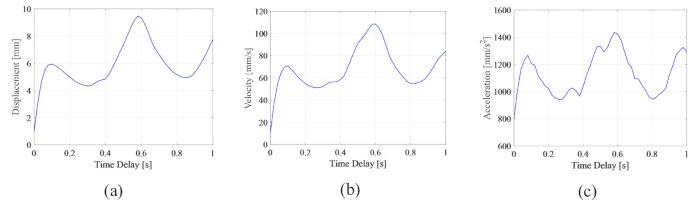
Figure 4 : La racine carrée moyenne maximale des réponses de la structure contrôlée avec le temps. a) Déplacement ; b) la vitesse ; c) Accélération. Veuillez cliquer ici pour voir une version agrandie de cette figure.
Pour analyser l’influence de la temporisation sur la fiabilité d’une structure semi-activement contrôlée, la figure 5 montre la fiabilité du déplacement, de la vitesse et de l’accélération avec l’augmentation de la temporalité. La fiabilité des réponses de la structure contrôlée avec n’importe quel retard était inférieure aux valeurs sans retard, ce qui signifie que la fiabilité de la structure contrôlée a été diminuée par le retard. Pendant ce temps, à l’instar de la valeur efficace maximale, l’effet du contrôle de la fiabilité a montré une périodicité avec un retard de temps croissant. De plus, la fiabilité de la structure contrôlée, avec ou sans retard, était supérieure aux valeurs des structures non contrôlées avec une fiabilité du déplacement, de la vitesse et de l’accélération de 0,0954, 0,1058 et 0,1111.
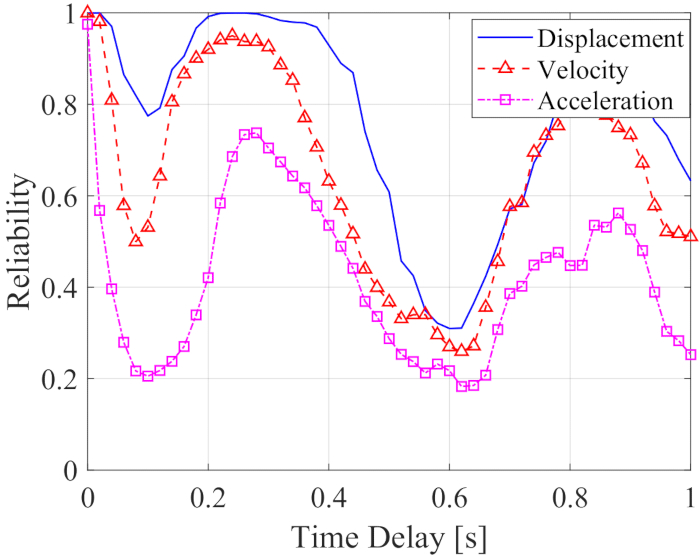
Figure 5 : Fiabilité des réponses de la structure contrôlée avec un délai croissant. Veuillez cliquer ici pour voir une version agrandie de cette figure.
En résumé, les réponses de la structure ont été atténuées par la méthode de contrôle semi-actif. Cependant, l’efficacité du contrôle, indépendamment de l’efficacité efficace ou de la fiabilité, de la méthode de contrôle semi-actif a été diminuée par le délai. Par conséquent, il est nécessaire de compenser le décalage temporel.
2.1.1 Analyse de la méthode de compensation du temps de retard
Pour l’analyse de l’efficacité de la méthode de compensation de retard proposée, les historiques temporels RMS de déplacement, de vitesse et d’accélération pour les systèmes non contrôlés (Unc), temporisés avec non contrôlés par compensation (TDN-SAC-PSO) et les systèmes retardés avec compensation contrôlée (TDC-SAC-PSO) sont comparés à la figure 6, où le retard était de 0,1 s. Les paramètres de la matrice de pondération et de la méthode de contrôle semi-actif sont les mêmes qu’à l’étape 2.1.
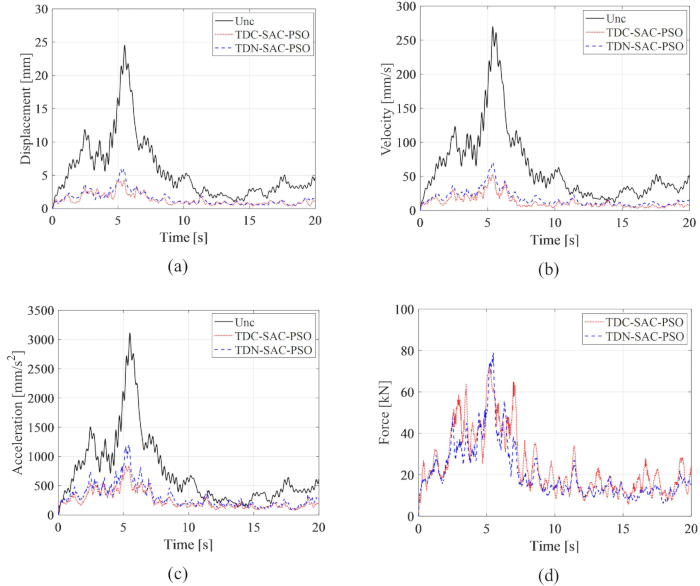
Figure 6 : Comparaison de l’historique temporel moyen des structures contrôlées par différentes méthodes. a) Déplacement ; b) la vitesse ; c) Accélération ; (D) Force sur les commandes. Abréviations : Unc = non contrôlé ; TDC-SAC-PSO = système temporisé avec compensation contrôlée ; TDN -SAC-PSO = système temporisé sans compensation. Veuillez cliquer ici pour voir une version agrandie de cette figure.
Les deux méthodes de contrôle ont considérablement diminué les réponses de la structure par rapport à la structure non contrôlée, révélant les avantages de la méthode de contrôle basée sur l’amortisseur MR. Par rapport à la structure non contrôlée, la valeur efficace maximale du déplacement, de la vitesse et de l’accélération est diminuée de 75,79 %, 73,75 % et 61,22 % avec la méthode TDN-SAC-PSO. De plus, avec la compensation de temporisation, les réponses de la structure contrôlée sont diminuées de 82,59 %, 80,40 % et 73,04 % avec la méthode TDC-SAC-PSO. La valeur efficace maximale de la force sur la commande avec la méthode TDC-SAC-PSO a diminué de 8,43 % par rapport à la méthode TDN-SAC-PSO, bien que les réponses vibratoires de la première méthode aient été inférieures à celles de la seconde. L’analyse ci-dessus indique que l’influence de la temporisation sur la méthode de contrôle basée sur l’amortisseur MR a été effectivement diminuée par la méthode de compensation, qui montre la nécessité de la compensation de retard pour la méthode de contrôle semi-active de l’amortisseur MR.
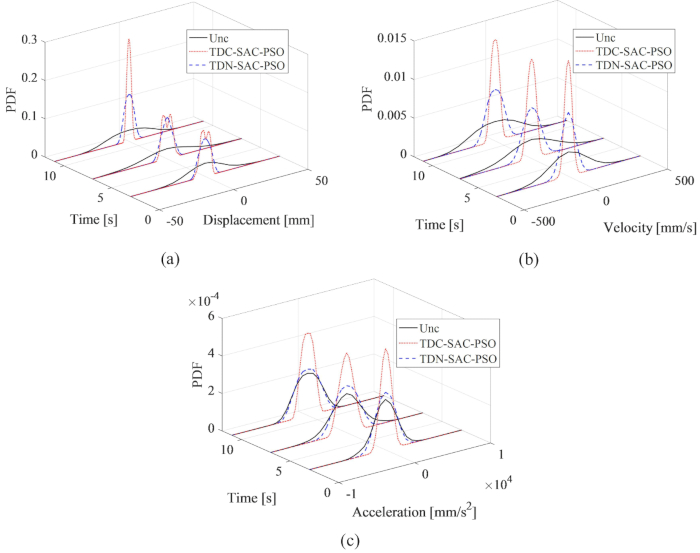
Figure 7 : Comparaison des PDF à des moments typiques des réponses de la structure. a) Déplacement ; b) la vitesse ; c) Accélération. Abréviations : PDF = fonction de densité de probabilité ; Unc = non contrôlé ; TDC-SAC-PSO = système temporisé avec compensation contrôlée ; TDN -SAC-PSO = système temporisé sans compensation. Veuillez cliquer ici pour voir une version agrandie de cette figure.
Pour révéler de manière exhaustive l’effet de la méthode de compensation proposée sur l’incertitude des réponses de la structure contrôlée, les comparaisons de la fonction de densité de probabilité (PDF) du déplacement, de la vitesse et de l’accélération à des temps typiques, 3, 7 et 11s, sont présentées à la figure 7. Les PDF de la méthode TDN-SAC-PSO étaient plus étroites que ceux de la structure non contrôlée, ce qui signifie que l’incertitude des réponses de la structure a été réduite par la méthode de contrôle semi-actif, même avec un délai de retard. Lorsque le retard a été compensé, les PDF des réponses ont été encore plus restreints. Par conséquent, la méthode de compensation proposée est nécessaire pour améliorer l’effet de contrôle semi-actif.
| Méthode de contrôle | Déplacement | Vitesse | Accélération | Force de contrôle | Valeur minimale |
| Unc | 0.0954 | 0.1058 | 0.1111 | -- | 0.1111 |
| TDC-SAC-PSO | 0.9565 | 0.8107 | 0.7654 | 0.9845 | 0.7654 |
| TDN-SAC-PSO | 0.7747 | 0.531 | 0.2054 | 0.884 | 0.2054 |
Tableau 1 : Réponses aux vibrations et fiabilité de la force de régulation des structures contrôlées par différentes méthodes. Abréviations : Unc = non contrôlé ; TDC-SAC-PSO = système temporisé avec compensation contrôlée ; TDN -SAC-PSO = système temporisé sans compensation.
Le tableau 1 montre les réponses aux vibrations et la fiabilité de la force de régulation des structures contrôlées par la méthode TDC-SAC-PSO et TDN-SAC-PSO sont illustrées. Avec le contrôle par la méthode TDN-SAC-PSO, la fiabilité de la structure a été considérablement augmentée par rapport à la structure non contrôlée, ce qui valide l’efficacité de la méthode de contrôle basée sur l’amortisseur MR, même avec le temps. Cependant, avec la compensation de retard, la fiabilité a été considérablement augmentée par rapport à l’absence de compensation, en particulier pour l’accélération. Il convient également de noter que la fiabilité des différentes réponses et la force de contrôle ont montré des différences significatives pour la méthode TDC-SAC-PSO. Cela indique que les valeurs optimales des paramètres critiques pour la commande sans temporisation ne sont pas optimales pour la commande avec temporisation. Pour obtenir l’effet de contrôle optimal des réponses aux vibrations et de la force de contrôle avec l’influence du retard, les paramètres doivent être optimisés davantage. Sur la base de l’analyse ci-dessus, il est conclu que la méthode de contrôle semi-actif avec un amortisseur MR peut réduire efficacement les réponses vibratoires de la structure, tandis que les paramètres doivent être optimisés en raison de l’influence de la temporisation.
2.2 Optimisation des paramètres
Pour obtenir les valeurs optimales des paramètres, la méthode d’optimisation intégrée basée sur le critère de fiabilité a été appliquée38. L’optimisation des paramètres critiques a été réalisée avec 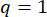 ,
, 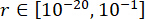 ,
,  ,
, 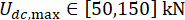 , et les temps réglables de la force d’amortissement MR s = 8. La boîte à outils GA de MATLAB a été utilisée pour mettre en œuvre l’optimisation.
, et les temps réglables de la force d’amortissement MR s = 8. La boîte à outils GA de MATLAB a été utilisée pour mettre en œuvre l’optimisation.
Les résultats d’optimisation des paramètres sont  ,
, 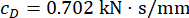 et
et  pour le retard
pour le retard 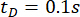 . La figure 8 montre les historiques temporels RMS du déplacement, de la vitesse, de l’accélération et de la force de commande pour les structures contrôlées par méthode Unc (Unc), TDC-SAC-PSO et SOSC-PSO. La méthode SOSC-PSO désigne la méthode de contrôle semi-active avec compensation de retard et valeurs de paramètres critiques optimisées.
. La figure 8 montre les historiques temporels RMS du déplacement, de la vitesse, de l’accélération et de la force de commande pour les structures contrôlées par méthode Unc (Unc), TDC-SAC-PSO et SOSC-PSO. La méthode SOSC-PSO désigne la méthode de contrôle semi-active avec compensation de retard et valeurs de paramètres critiques optimisées.
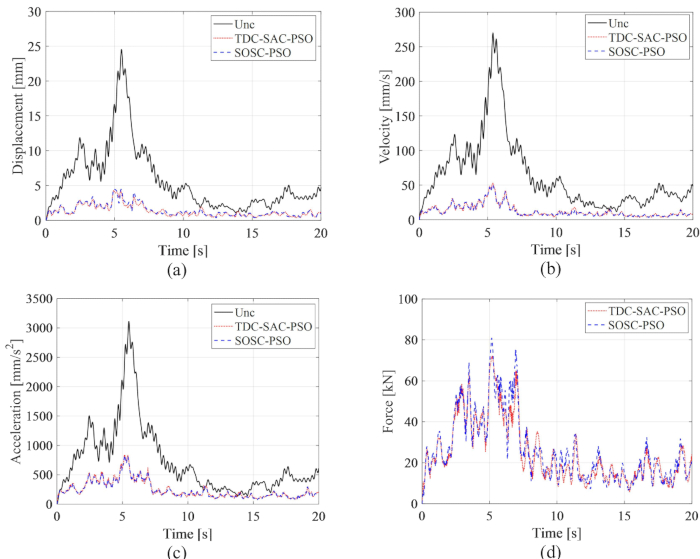
Figure 8 : Historiques temporels RMS du déplacement, de la vitesse, de l’accélération et de la force de contrôle pour les structures non contrôlées et contrôlées par méthode TDC-SAC-PSO et SOSC-PSO. a) Déplacement ; b) la vitesse ; c) Accélération ; (D) Force sur les commandes. Abréviations : Unc = non contrôlé ; TDC-SAC-PSO = système temporisé avec compensation contrôlée ; SOSC-PSO = Méthode de contrôle semi-active optimal stochastique avec compensation de retard. Veuillez cliquer ici pour voir une version agrandie de cette figure.
La figure 8 montre que les effets de contrôle des méthodes TDC-SAC-PSO et SOSC-PSO ont montré peu de différence. La valeur efficace maximale de la vitesse de déplacement et de l’accélération pour la première méthode était de 81,60 %, 81,21 %, 73,62 % pour la structure non contrôlée et de 82,59 %, 80,40 %, 73,04 % pour la seconde méthode. Afin d’analyser de manière exhaustive les caractéristiques de probabilité des réponses pour les deux méthodes de contrôle, la figure 9 montre les PDF de déplacement, de vitesse et d’accélération pour les structures contrôlées par méthode TDC-SAC-PSO non contrôlée, TDC-SAC-PSO et SOSC-PSO. Les deux méthodes de contrôle avaient presque les mêmes PDF de déplacement et de vitesse à des moments typiques. Les PDF d’accélération de la méthode SOSC-PSO étaient plus étroites que celles de la méthode TDC-SAC-PSO, ce qui signifie que l’incertitude de l’accélération a obtenu un meilleur effet de contrôle avec la méthode précédente.
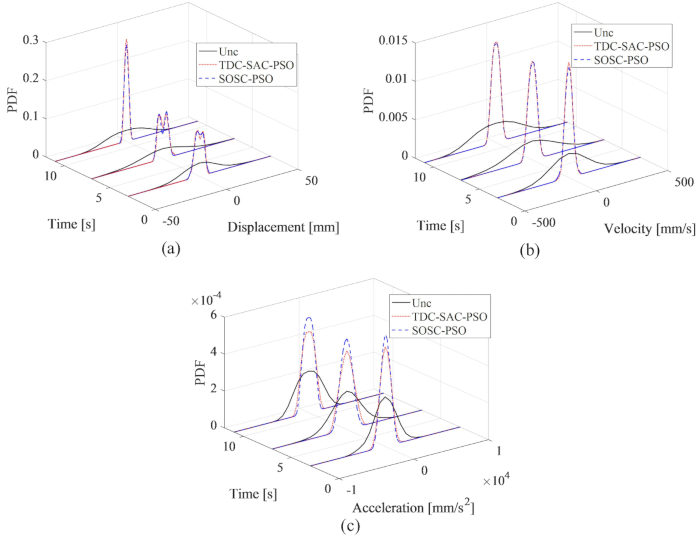
Figure 9 : Comparaison du déplacement, de la vitesse et de l’accélération pour différentes structures contrôlées. a) Déplacement ; b) la vitesse ; c) Accélération. Abréviations : PDF = fonctions de densité de probabilité ; Unc = non contrôlé ; TDC-SAC-PSO = système temporisé avec compensation contrôlée ; SOSC-PSO = Méthode de contrôle semi-active optimal stochastique avec compensation de retard. Veuillez cliquer ici pour voir une version agrandie de cette figure.
La fiabilité du déplacement, de la vitesse, de l’accélération et de la force de contrôle pour les structures non contrôlées et contrôlées par les méthodes TDC-SAC-PSO et SOSC-PSO est illustrée dans le tableau 2. Les deux méthodes de contrôle ont permis d’augmenter considérablement la fiabilité par rapport à la structure non contrôlée. La fiabilité du déplacement a montré peu de différence entre les méthodes TDC-SAC-PSO et SOSC-PSO. Alors que la fiabilité de l’accélération, la fiabilité la plus basse de la structure contrôlée, a réalisé une augmentation notable. Cela signifie que la méthode SOSC-PSO permet d’obtenir un effet de contrôle optimal de l’équilibre.
| Méthode de contrôle | Déplacement | Vitesse | Accélération | Force de commande | Valeur minimale |
| Unc | 0.0954 | 0.1058 | 0.1111 | -- | 0.1111 |
| TDC-SAC-PSO | 0.9565 | 0.8107 | 0.7654 | 0.9845 | 0.7654 |
| SOSC-PSO | 0.953 | 0.8704 | 0.8934 | 0.9586 | 0.8934 |
Tableau 2 : Fiabilité des structures contrôlées par différentes méthodes. Abréviations : Unc = non contrôlé ; TDC-SAC-PSO = système temporisé avec compensation contrôlée ; SOSC-PSO = Méthode de contrôle semi-active optimal stochastique avec compensation de retard.
L’efficacité de la méthode SOSC-PSO proposée avec temporisation 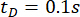 a été analysée. Pour vérifier davantage la méthode proposée pour les différents retards, le Tableau 3 montre les valeurs optimales des paramètres et la fiabilité correspondante pour la plage
a été analysée. Pour vérifier davantage la méthode proposée pour les différents retards, le Tableau 3 montre les valeurs optimales des paramètres et la fiabilité correspondante pour la plage 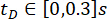 de temporisation.
de temporisation.
| tD(s) | LG(R*) | CD(kN·s/mm) | Udc,max (kN) | Déplacement | Vitesse | Accélération | Force de commande |
| 0 | -2.524 | 1.44 | 116.163 | 0.9997 | 0.9998 | 0.9752 | 1 |
| 0.02 | -4.413 | 0.414 | 144.066 | 0.9989 | 0.9988 | 0.872 | 0.9011 |
| 0.04 | -4.416 | 0.25 | 141.759 | 0.9998 | 0.9846 | 0.8881 | 0.9135 |
| 0.06 | -3.226 | 0.203 | 145.613 | 0.993 | 0.9318 | 0.8756 | 0.9556 |
| 0.08 | -5.207 | 0.345 | 133.692 | 0.9646 | 0.8998 | 0.8998 | 0.953 |
| 0.1 | -4.669 | 0.702 | 130.739 | 0.9531 | 0.8704 | 0.8934 | 0.9586 |
| 0.12 | -4.895 | 0.833 | 69.72 | 0.9526 | 0.863 | 0.888 | 0.9686 |
| 0.14 | -4.231 | 0.921 | 75.221 | 0.9531 | 0.8681 | 0.8697 | 0.9671 |
| 0.16 | -5.594 | 0.662 | 138.922 | 0.9529 | 0.8461 | 0.8262 | 0.931 |
| 0.18 | -4.262 | 0.882 | 76.335 | 0.9516 | 0.7873 | 0.7614 | 0.9618 |
| 0.2 | -3.926 | 0.783 | 67.951 | 0.904 | 0.7277 | 0.7116 | 0.9653 |
| 0.22 | -5.965 | 1.071 | 52.554 | 0.8377 | 0.6411 | 0.6205 | 0.965 |
| 0.24 | -4.481 | 1.216 | 128.148 | 0.7567 | 0.474 | 0.474 | 0.9687 |
| 0.26 | -3.53 | 0.672 | 53.706 | 0.53 | 0.4096 | 0.4158 | 0.9921 |
| 0.28 | -4.433 | 0.638 | 64.225 | 0.3547 | 0.3745 | 0.3464 | 0.9928 |
| 0.3 | -3.536 | 0.459 | 57.705 | 0.2735 | 0.316 | 0.2736 | 0.9929 |
| Unc | -- | -- | -- | 0.0954 | 0.1058 | 0.1111 | -- |
Tableau 3 : Les valeurs optimales des paramètres et les valeurs de fiabilité correspondantes pour différents retards. 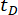 indique un retard dans le temps ;
indique un retard dans le temps ;  désigne la valeur logarithmique optimale de r,r désigne la matrice de pondération du coefficient de contrôle ;
désigne la valeur logarithmique optimale de r,r désigne la matrice de pondération du coefficient de contrôle ; 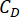 désigne le coefficient d’amortissement visqueux de l’amortisseur MR ;
désigne le coefficient d’amortissement visqueux de l’amortisseur MR ; 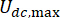 désignent les forces coulombiennes maximales et minimales de l’amortisseur MR.
désignent les forces coulombiennes maximales et minimales de l’amortisseur MR.
On peut observer que la fiabilité du déplacement, de la vitesse et de l’accélération a été améliorée par rapport à la structure non contrôlée, même en présence d’un décalage temporel, démontrant la robustesse de la méthode proposée vis-à-vis de tels retards. Cependant, la fiabilité des réponses structurelles avec la méthode de contrôle proposée diminuait à mesure que le délai augmentait, ce qui indique que même si l’impact du délai sur l’efficacité du contrôle peut être atténué, il ne peut pas être complètement éliminé. Notamment, la fiabilité de la force de commande est demeurée supérieure à 90 % sur différentes temporalités.
3. Exemple numérique
Pour vérifier la méthode SOSC-PSO proposée dans la structure du MDOF, une structure de six étages avec deux volets MR installés aux premier et troisième étages a été analysée, comme le montre la figure 10. Les échantillons sismiques produits par le modèle sismique stochastique de la section 2 ont été appliqués, et les seuils de fiabilité du déplacement, de la vitesse, de l’accélération et de la force de contrôle étaient de 20 mm, 200 mm/s, 3 000 mm/s2 et 200 kN. Équations. (27) ont été utilisés comme matrice de pondération avec 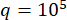 . La boîte à outils GA de MATLAB a été utilisée pour optimiser
. La boîte à outils GA de MATLAB a été utilisée pour optimiser 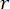 ,, et
,, et  , avec des plages optimales
, avec des plages optimales 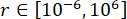 ,
,  , et
, et 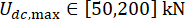
 .
.
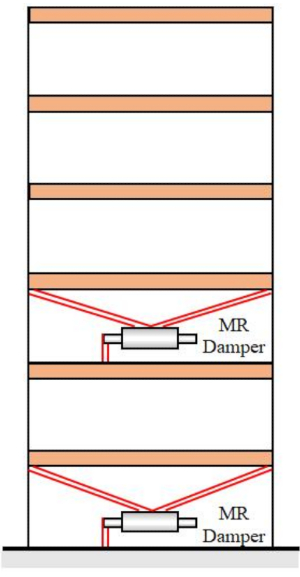
Figure 10 : Structure à six étages avec deux amortisseurs MR. Abréviation : MR = magnétorhéologique. Veuillez cliquer ici pour voir une version agrandie de cette figure.
3.1 Analyse d’influence du retard
Pour analyser l’influence de la temporisation sur l’efficacité du contrôle de l’amortisseur MR dans la structure MDOF, la figure 11 montre la valeur efficace maximale du déplacement (déplacement entre étages), de la vitesse (vitesse entre étages) et de l’accélération (accélération d’étage) ainsi que la temporisation pour la méthode TDC-SAC-PSO. Les paramètres étaient 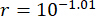 ,
, , et
, et  pour le volet MR au 1er étage,
pour le volet MR au 1er étage,  et
et  pour le volet MR au 3ème étage, qui sont les résultats optimisés sans délai. La valeur efficace maximale des réponses de la structure contrôlée présentait une fluctuation de période ainsi qu’un décalage temporel. La valeur efficace maximale du déplacement et de la vitesse était au 1er étage, l’accélération maximale au 6e étage. De plus, toutes les MRS maximales des réponses avec n’importe quel retard étaient supérieures aux valeurs sans retard, ce qui signifie que le retard diminue l’effet de contrôle de l’amortisseur MR.
pour le volet MR au 3ème étage, qui sont les résultats optimisés sans délai. La valeur efficace maximale des réponses de la structure contrôlée présentait une fluctuation de période ainsi qu’un décalage temporel. La valeur efficace maximale du déplacement et de la vitesse était au 1er étage, l’accélération maximale au 6e étage. De plus, toutes les MRS maximales des réponses avec n’importe quel retard étaient supérieures aux valeurs sans retard, ce qui signifie que le retard diminue l’effet de contrôle de l’amortisseur MR.
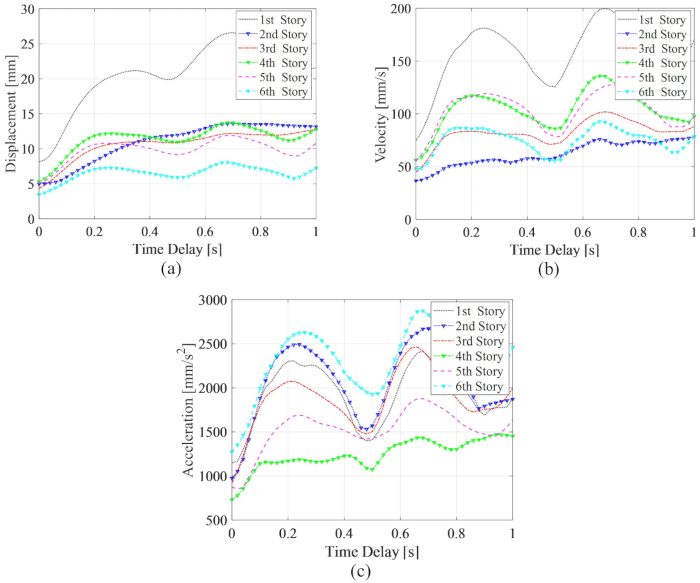
Figure 11 : Efficacité maximale des réponses avec délai pour la structure contrôlée par la méthode TDC-SAC-PSO. a) Déplacement ; b) la vitesse ; c) Accélération. Abréviations : RMS = racine-moyenne-carrée ; TDC-SAC-PSO = système temporisé avec compensation contrôlée. Veuillez cliquer ici pour voir une version agrandie de cette figure.
La fiabilité du déplacement, de la vitesse et de l’accélération ainsi que du retard temporel est illustrée à la figure 12. La fiabilité de la vitesse et de l’accélération montre une fluctuation de période avec le décalage temporel, tandis que la fiabilité du déplacement diminue considérablement avec le décalage temporel ; Toutes les valeurs de fiabilité à n’importe quel délai étaient inférieures à celles sans délai. Par conséquent, la méthode de compensation de la temporisation est nécessaire pour réduire l’influence de la temporisation sur la fiabilité de la structure commandée par l’amortisseur MR.
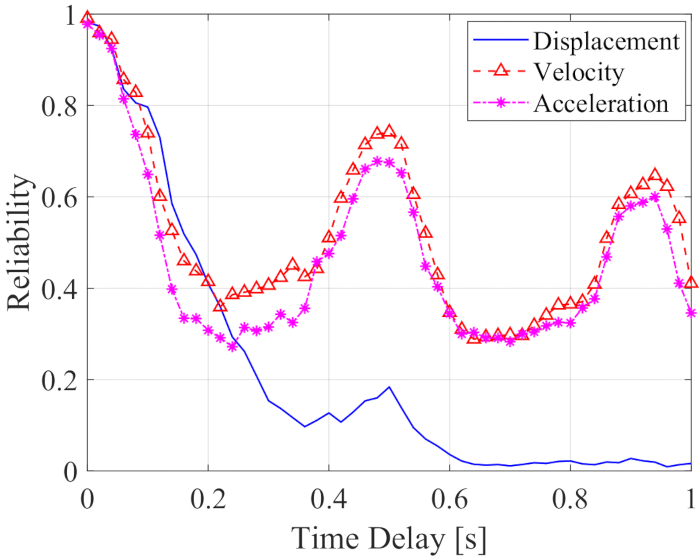
Figure 12 : Fiabilité des réponses de la structure contrôlée avec délai. Veuillez cliquer ici pour voir une version agrandie de cette figure.
3.2 Effet de contrôle de la compensation de retard
Sur la base de la méthode TDC-SAC-PSO proposée, la structure à 6 degrés de liberté avec deux amortisseurs MR a été analysée. La figure 13 montre l’historique temporel efficace du déplacement et de l’accélération aux 1er et 3e étages pour les structures non contrôlées (Unc), contrôlées par la méthode TDC-SAC-PSO et contrôlées par la méthode TDN-SAC-PSO. Le retard était 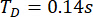 de , et le rapport
de , et le rapport 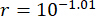 de la matrice de pondération ; les paramètres de l’amortisseur MR étaient
de la matrice de pondération ; les paramètres de l’amortisseur MR étaient  de ,
de ,  pour le 1er étage et
pour le 1er étage et 
 pour le 3ème étage.
pour le 3ème étage.

Figure 13 : Historiques temporels RMS du déplacement et de l’accélération aux 1er et 3e étages pour des structures contrôlées par différentes méthodes. (A) Déplacement au 1er étage ; (B) Déplacement au 3e étage ; (C) Accélération au 1er étage ; (D) Accélération au 3ème étage. Abréviations : RMS = racine-moyenne-carrée ; Unc = non contrôlé ; TDC-SAC-PSO = système temporisé avec compensation contrôlée ; TDN -SAC-PSO = système temporisé sans compensation. Veuillez cliquer ici pour voir une version agrandie de cette figure.
La valeur efficace maximale du déplacement aux 1er et 3e étages a été réduite de 35,42 % et de 30,44 % par la méthode TDN-SAC-PSO, où le retard n’a pas été compensé. Alors qu’avec compensation, les RMS maximum de déplacement aux 1er et 3e étages ont été réduits de 49,33 % et 53,39 %, respectivement. Sans compensation, la valeur efficace maximale de l’accélération aux 1er et 3e étages a augmenté de 16,22 % et 2,88 %, mais a diminué de 25,77 % et 36,00 %, respectivement, avec compensation. Par conséquent, la compensation du retard dans la méthode de contrôle de l’amortisseur MR est nécessaire pour réduire les réponses de la structure, en particulier pour l’accélération.
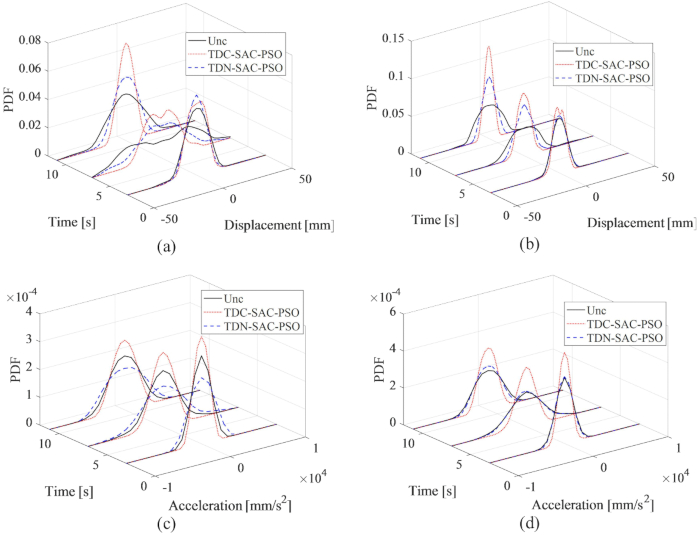
Figure 14 : PDF du déplacement et de l’accélération aux 1er et 3e étages pour différentes méthodes de contrôle. (A) Déplacement au 1er étage ; (B) Déplacement au 3e étage ; (C) Accélération au 1er étage ; (D) Accélération au 3ème étage. Abréviations : PDF = fonctions de densité de probabilité ; Unc = non contrôlé ; TDC-SAC-PSO = système temporisé avec compensation contrôlée ; TDN -SAC-PSO = système temporisé sans compensation. Veuillez cliquer ici pour voir une version agrandie de cette figure.
Les PDF de déplacement et d’accélération aux 1er et 3e étages sont illustrés à la figure 14, révélant les différents effets de contrôle des méthodes TDC-SAC-PSO et TDN-SAC-PSO par rapport à la structure non contrôlée. Sans compensation, les PDF de déplacement aux 1er et 3e étages étaient encore plus étroits que ceux de la structure non contrôlée. De plus, avec la compensation du retard, les PDF de déplacement sont devenus plus étroits que ceux de la structure contrôlée par la méthode TDN-SAC-PSO. Contrairement au déplacement, sans compensation, les PDF d’accélération au 1er étage pour la méthode TDN-SAC-PSO étaient plus larges que ceux de la structure non contrôlée. Cependant, avec la compensation, les PDF de l’accélération aux 1er et 3e étages étaient plus étroits que ceux de la structure non contrôlée. Ainsi, la nécessité de la compensation de retard est vérifiée pour augmenter la certitude des réponses de la structure, en particulier pour l’accélération.
| Méthode de contrôle | Déplacement | Vitesse | Accélération | Force de commande au1er étage | Force de contrôle au 3e étage |
| Unc | 0.0114 | 0.5822 | 0.6372 | -- | -- |
| TDN-SAC-PSO | 0.5851 | 0.5258 | 0.398 | 1 | 1 |
| TDC-SAC-PSO | 0.806 | 0.8674 | 0.8037 | 1 | 1 |
Tableau 4 : Fiabilité des structures contrôlées par différentes méthodes. Abréviations : Unc = non contrôlé ; TDC-SAC-PSO = système temporisé avec compensation contrôlée ; TDN -SAC-PSO = système temporisé sans compensation.
Les valeurs de fiabilité du déplacement, de la vitesse, de l’accélération et de la force de contrôle avec les systèmes de structure contrôlés par les différentes méthodes sont indiquées dans le tableau 4. Les valeurs de fiabilité des réponses de la structure ont été calculées à l’aide de la méthode des valeurs extrêmes équivalentes25. Par la méthode de contrôle TDN-SAC-PSO, la fiabilité du déplacement a augmenté par rapport à la structure non contrôlée, tandis que la fiabilité de la vitesse et de l’accélération a diminué. Avec la compensation de retard dans la méthode TDC-SAC-PSO, la fiabilité du déplacement, de la vitesse et de l’accélération a considérablement augmenté. En outre, les valeurs de fiabilité de la force de régulation pour les méthodes TDN-SAC-PSO et TDN-SAC-PSO sont suffisamment maintenues. Ainsi, la méthode de contrôle de compensation de retard proposée permet d’obtenir un effet de contrôle favorable pour la structure contrôlée par amortisseur MR.
3.3 Optimisation des paramètres
Pour obtenir un effet de contrôle optimal, les paramètres de la méthode de contrôle proposée ont été optimisés sur la base du critère de fiabilité. Avec le temporisation 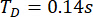 , le résultat optimal a été
, le résultat optimal a été  ;
; 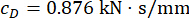 , et
, et 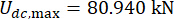 pour le volet MR du 1er étage ;
pour le volet MR du 1er étage ; 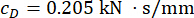 et
et  pour le volet MR du 3e.
pour le volet MR du 3e.
Les historiques temporels RMS du déplacement et de l’accélération aux 1er et 3e étages sont illustrés à la figure 15 , où les effets de contrôle des méthodes TDC-SAC-PSO et SOSC-PSO et de la structure non contrôlée sont comparés. Avec le contrôle de l’amortisseur MR, avec ou sans compensation de retard, la valeur efficace du déplacement et de l’accélération a considérablement diminué. Avec la méthode SOSC-PSO, la valeur efficace maximale du déplacement aux 1er et 3e étages a diminué de 65,15 % et 63,16 % par rapport à la structure non contrôlée, respectivement. Par rapport à la méthode TDC-SAC-PSO, la réponse de déplacement a été encore réduite. Les RMS maximaux d’accélération aux 1er et 3e étages sont diminués de 23,39 % et de 35,60 % pour la méthode SOSC-PSO. Il y avait peu de différence dans l’effet de contrôle de l’accélération pour les méthodes SOSC-PSO et TDC-SAC-PSO, ce qui indique que l’effet de contrôle de la compensation de retard était différent pour le déplacement et l’accélération.
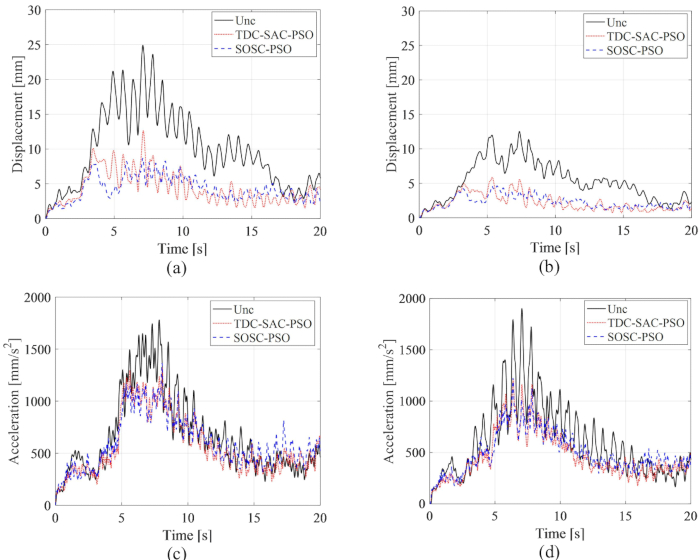
Figure 15 : Historique temporel efficace du déplacement et de l’accélération aux 1er et 3e étages pour différentes méthodes de contrôle. (A) Déplacement au 1er étage ; (B) Déplacement au 3e étage ; (C) Accélération au 1er étage ; (D) Accélération au 3ème étage. Abréviations : RMS = racine-moyenne-carrée ; Unc = non contrôlé ; TDC-SAC-PSO = système temporisé avec compensation contrôlée ; SOSC-PSO = Méthode de contrôle semi-active optimal stochastique avec compensation de retard. Veuillez cliquer ici pour voir une version agrandie de cette figure.
Les PDF du déplacement et de l’accélération aux 1er et 3e étages sont présentés à la figure 16 ; les PDF de déplacement et d’accélération ont été réduites par les méthodes TDC-SAC-PSO et SOSC-PSO par rapport à la structure non contrôlée. De plus, les PDF de déplacement et d’accélération de la méthode SOSC-PSO ont été encore plus réduits par rapport à ceux de la structure contrôlée par la méthode TDC-SAC-PSO. Par conséquent, avec l’optimisation des paramètres, la méthode de contrôle de compensation de retard proposée a obtenu un meilleur effet de contrôle que sans optimisation.
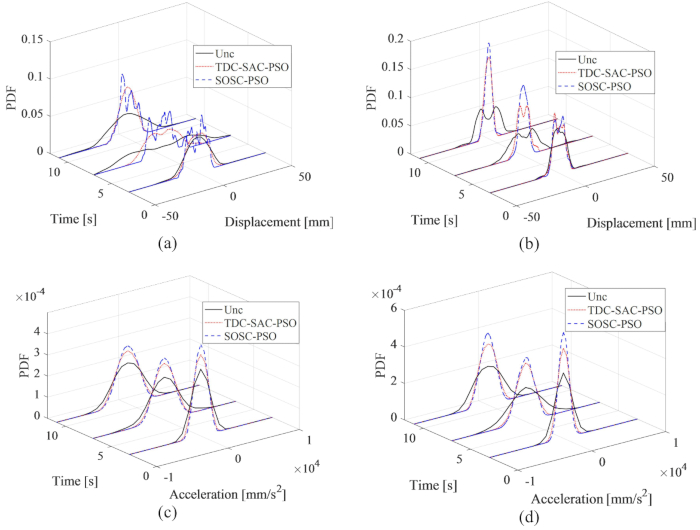
Figure 16 : PDF du déplacement et de l’accélération aux 1er et 3e étages pour différentes méthodes de contrôle. (A) Déplacement au 1er étage ; (B) Déplacement au 3e étage ; (C) Accélération au 1er étage ; (D) Accélération au 3ème étage. Abréviations : PDF = fonctions de densité de probabilité ; Unc = non contrôlé ; TDC-SAC-PSO = système temporisé avec compensation contrôlée ; SOSC-PSO = Stochastic Optimal Semi-active Control method with time delay compensation Veuillez cliquer ici pour voir une version agrandie de cette figure.
Les valeurs de fiabilité du déplacement, de la vitesse, de l’accélération et de la force sur les commandes sont indiquées dans le Tableau 5. Les valeurs de fiabilité de la méthode SOSC-PSO étaient plus élevées que celles de la méthode TDC-SAC-PSO. Pendant ce temps, la force de contrôle conservait encore une fiabilité suffisante. Ainsi, l’optimisation des paramètres est nécessaire pour obtenir le meilleur effet de contrôle pour la méthode de contrôle basée sur l’amortisseur MR.
| Méthode de contrôle | Déplacement | Vitesse | Accélération | Force de commande au1er étage | Force de contrôle au 3e étage |
| Unc | 0.0114 | 0.5822 | 0.6372 | -- | -- |
| TDC-SAC-PSO | 0.806 | 0.8674 | 0.8037 | 1 | 1 |
| SOSC-PSO | 0.9544 | 0.9314 | 0.8788 | 1 | 1 |
Tableau 5 : Fiabilité des structures contrôlées par différentes méthodes. Abréviations : Unc = non contrôlé ; TDC-SAC-PSO = système temporisé avec compensation contrôlée ; SOSC-PSO = Méthode de contrôle semi-active optimal stochastique avec compensation de retard.
Résultats
Dans le but d’évaluer l’influence de la temporisation sur l’efficacité du contrôle de la méthode basée sur l’amortisseur MR, une méthode de contrôle semi-active avec compensation de temporisation est proposée dans cet article. Dans la méthode proposée, les paramètres critiques sont optimisés en fonction du critère de fiabilité. En comparant l’efficacité du contrôle, les conclusions suivantes sont tirées :
(1) La méthode de contrôle...
Discussion
Avec l’introduction de la théorie du contrôle optimal stochastique physique (PSO), une méthode de contrôle semi-actif optimal stochastique avec compensation de retard (SOSC-PSO) est proposée dans cet article, qui est conçue pour maintenir la fiabilité des structures contrôlées par des amortisseurs MR. Pour compenser le retard dans la méthode proposée, la force de contrôle semi-active est dérivée en fonction non seulement des états actuels, mais aussi des états et des fo...
Déclarations de divulgation
Tous les auteurs n’ont aucun conflit d’intérêts à déclarer.
Remerciements
Les auteurs remercient chaleureusement la Fondation des sciences naturelles de la province du Hebei pour son soutien (subvention n° E2023210007).
matériels
| Name | Company | Catalog Number | Comments |
| MATLAB | MathWorks | 2016 | Using for the calculation of the proposed method |
Références
- Yao, J. T. P. Concept of structural control. J Struct Div. 98 (7), 1567-1574 (1972).
- Liu, J., Silva, C. E., Dyke, S. J., Wu, Y., Liu, H. Using real-time hybrid simulation for active mass damper experimentation and validation. Mech Mach Theory. 191, 105474 (2024).
- Pan, H., Li, C., Cao, L. Bidirectional pendulum-type tuned tendem mass dampers-inerters for integrated control of alongwind and crosswind responses in super-tall buildings. J Build Eng. 100, 111676 (2025).
- Housner, G. W. et al. Structural control: past, present, and future. J Eng Mech. 123 (9), 897-971 (1997).
- Rahman, M., Ong, Z. C., Chong, W. T., Julai, S. Smart Semi-active PID-ACO control strategy for tower vibration reduction in Wind Turbines with MR damper. Earthq Eng Eng Vib. 18 (4), 887-902 (2019).
- Morales-Beltran, M., Paul, J. Active and semi-active strategies to control building structures under large earthquake motion. J Earthquake Eng. 19 (7), 1086-1111 (2015).
- Shu, Z., You, R., Xie, Y. Viscoelastic dampers for vibration control of building structures: A state-of-art review. J Earthq Eng. 28 (12), 3558-3585 (2024).
- Soong, T. T. Active structural control: Theory and practice. Longman Scientific & Technical. New York (1990).
- Wan, H. P., Ma, Q., Dong, G. S., Luo, Y., Ni, Y. Q. Data-driven model reduction approach for active vibration control of cable-strut structures. Eng Struct. 302, 117434 (2024).
- Cao, L., Li, X., Huang, Y., Li, C., Pan, H. High robust eddy current tuned tandem mass dampers-inerters for structures under the ground acceleration. Soil Dyn Earthq Eng. 188, 109040 (2025).
- Chha, H., Peng, Y. Adaptive semiactive control of structure with magnetorheological dampers using wavelet packet transform. Adv Struct Eng. 27 (9), 1509-1527 (2024).
- Zeng, X., Peng, Y., Chen, J. Serviceability-based damping optimization of randomly wind-excited high-rise buildings. Struct Des Tall Spec. 26 (11), e1371 (2017).
- Li, C., Chang, K., Cao, L., Huang, Y. Performance of a nonlinear hybrid base isolation system under the ground motions. Soil Dyn Earthq Eng. 143, 106589 (2021).
- Cao, L., Li, C. A high performance hybrid passive base-isolated system. Struct Control Health Monitoring. 29 (3), e2887 (2022).
- Zareie, S., Issa, A. S., Seethaler, R., Zabihollah, A., Ahmad, R. A novel SMA-magnetorheological hybrid bracing system for seismic control. Eng Struct. 244, 112709 (2021).
- Chu, S. Y., Soong, T. T., Reinhorn, A. M. Active, hybrid and semi-active structural control. John Wiley & Sons, New York (2005).
- Danielian, S. A., Jabbari, F., Zareian, F. Effects and distribution of semi-active resettable springs on the seismic response of asymmetric structures. Earthq Eng Struct D. 52 (10). 2966-2982 (2023).
- Shuang, Z., Wenliuhan, H. S., Liu, Y. H., Inoue, N., Zhai, Z. P. Seismic response control for bridge piers with semi-active MR damper based on displacement feedback. J Earthq Eng. 28 (3). 849-865 (2024).
- Wang, Y., Dyke, S. Modal-based LQG for smart base isolation system design in seismic response control. Struct Control Health Monitoring. 20 (5), 753-768 (2013).
- Desai, R. M. et al. Performance evaluation of a single sensor control scheme using a twin-tube MR damper based semi-active suspension. J Vib Eng Technol. 9, 1193-1210 (2021).
- Abdi, M. S., Nekooei, M. Jafari, M. A. Seismic control of multi-degrees-of-freedom structures by vertical mass isolation method using MR dampers. Earthq Eng Eng Vib. 23 (2), 503-510 (2024).
- Bhowmik, K., Debnath, N. Semi-active vibration control of soft-storey building with magnetorheological damper under seismic excitation. J Vib Eng Technol. 12 (4), 6943-6961 (2024).
- Yang, J. N., Akbarpour, A., Askar, G. Effect of time delay on control of seismic-excited buildings. J Struct Eng. 116 (10), 2801-2814 (1990).
- Temimi, H., Ben-Romdhane, M., El-Borgi, S., Cha, Y. Time-delay effects on controlled seismically excited linear and nonlinear structures. Int J Struct Stab Dyn. 16 (7), 1550031 (2016).
- Peng, J., Wang, L., Zhao, Y., Lenci, S. Time-delay dynamics of the MR damper-cable system with one-to-one internal resonances. Nonlinear Dynamics. 105 (2), 1343-1356 (2021).
- Cha, Y. J., Agrawal, A. K., Dyke, S. J. Time delay effects on large-scale MR damper based semi-active control strategies. Smart Mater Struct. 22 (1), 015011 (2013).
- Yu, Y. et al. Experimental study of wireless structural vibration control considering different time delays. Smart Mater Struct. 24, 045005 (2015).
- Ahmadizadeh, M., Mosqueda, G., Reinhorn, A. M. Compensation of actuator delay and dynamics for real-time hybrid structural simulation. Earthq Eng Struct Dyn. 37 (1), 21-42 (2008).
- Bathaei, A., Zahrai, S. M. Compensating time delay in semi-active control of a SDOF structure with MR damper using predictive control. Struc Eng Mech. 82 (4), 445-458 (2022).
- Dyke, S. J., Spencer, Jr, B. F., Sain, M. K., Carlson, J. D. Modeling and control of magnetorheological dampers for seismic response reduction. Smart Mater Struct. 5 (5), 565-575 (1996).
- Ying, Z. G., Ni, Y. Q., Ko, J. M. A semi-active stochastic optimal control strategy for nonlinear structural systems with MR dampers. Smart Struct Syst. 5 (1), 69-79 (2009).
- Rosol, M., Martynowicz, P. Implementation of the LQG controller for a wind turbine tower-nacelle model with a MR tuned vibration absorber. J Theor App Mech-Pol. 54 (4), 1109-1123 (2016).
- Lyu, M. Z., Feng, D. C., Chen, J. B., Li, J. A decoupled approach for determination of the joint probability density function of a high-dimensional nonlinear stochastic dynamical system via the probability density evolution method. Comput Method Appl M. 418 (A), 116443 (2024).
- Chha, H., Peng, Y. Multiscale stochastic optimal control of hysteretic structures based on wavelet transform and probability density evolution method. Eng Computation. 41 (4), 865-896 (2024).
- Li, J., Peng, Y. B., Chen, J. B. A physical approach to structural stochastic optimal controls. Probabilist Eng Mech. 25 (1), 127-141 (2010).
- Peng, Y. B., Yang, J. G., Li, J. Seismic risk-based stochastic optimal control of structures using magnetorheological dampers. Nat Hazards Rev. 18 (1), B4016001 (2017).
- Dong, X. M., Yu, M., Li, Z., Liao, C., Chen, W. Neural network compensation of semi-active Control for magneto-rheological suspension with time delay uncertainty. Smart Mater Struct. 18 (1), 015014 (2008).
- Peng, Y. B., Zhang, Z. Optimal MR damper-based semiactive control scheme for strengthening seismic capacity and structural reliability. J Eng Mech. 146 (6), 04020045 (2020).
- Luo, M. X., Gao, M. Cai, G. Delayed full-state feedback control of airfoil flutter using sliding mode control method. J Fluid Struct. 61, 262-273 (2016).
- Xu, J., Chung, K. W., Chan, C. L. An efficient method for studying weak resonant double Hopf bifurcation in nonlinear systems with delayed feedbacks. Siam J Appl Dyn Syst. 6 (1), 29-60 (2007).
- Yang, J. S., Jensen, H., Chen, J. B. Structural optimization under dynamic reliability constraints utilizing probability density evolution method and metamodels in augmented input space. Struct Multidiscip Optimization. 65, 107 (2022).
- Li, J., Chen, J. B. Stochastic dynamics of structures. John Wiley & Sons, Singapore (2009).
- Peng, Y. B., Li, J. Stochastic optimal control of structures. Springer (2019).
- Dowrick, C. Beyond depression: A new approach to understanding and management. Oxford University Press (2009).
- Wang, D., Li, J. Physical random function model of ground motions for engineering purposes. Sci China Technol Sci. 54 (1), 175-182 (2011).
- Wang, D., Li, J. A random physical model of seismic ground motion field on local engineering site. Sci China Technol Sci. 55 (7), 2057-2065 (2012).
- Chen, J. B., Li, J. Strategy for selecting representative points via tangent spheres in the probability density evolution method. Int J Numer Meth Eng. 74 (13), 1988-2014 (2008).
Réimpressions et Autorisations
Demande d’autorisation pour utiliser le texte ou les figures de cet article JoVE
Demande d’autorisationThis article has been published
Video Coming Soon