Для просмотра этого контента требуется подписка на Jove Войдите в систему или начните бесплатную пробную версию.
Research Article
Стохастический полуактивный метод управления структурой на основе магнитореологических демпферов с учетом временного запаздывания
В этой статье
Резюме
В данной работе предложен метод стохастического оптимального полуактивного управления с компенсацией временной задержки (SOSC-PSO), который предназначен для поддержания надежности конструкций, управляемых MR-демпферами.
Аннотация
Применение магнитореологических (МР) демпферов в полуактивных системах управления сталкивается с ключевой проблемой: временное запаздывание, вызванное процессами обратной связи, что снижает надежность строительных конструкций при стохастических возбуждениях. В данной статье предлагается метод стохастического оптимального полуактивного управления с компенсацией временной задержки (SOSC-PSO), использующий теорию физического стохастического оптимального управления (PSO) для решения этой проблемы и поддержания структурной надежности. Предложенный метод выводит полуактивную силу управления как функцию как текущего, так и предыдущего состояния, компенсируя временные задержки в процессе управления. Для оптимизации эффективности управления ключевые параметры настраиваются на основе критерия надежности системы. Валидационные анализы одностепенных и многостепенных свободных конструкций при стохастических сейсмических возбуждениях показывают, что временные задержки значительно ухудшают характеристики MR-демпферов. Тем не менее, метод SOSC-PSO с компенсацией временной задержки значительно повышает эффективность управления, а при оптимизации параметров повышает надежность системы управления конструкцией по сравнению с методами без оптимизации параметров.
Введение
Повышение эксплуатационных характеристик инженерных конструкций перед лицом катастрофических событий, таких как землетрясения и экстремальные ветры, остается одной из основных задач в сообществе гражданского строительства. Было доказано, что структурный контроль, эффективный метод снижения вибраций, повышает как безопасность, так и функциональность таких конструкций 1,2,3. За последние несколько десятилетий для этой цели были разработаны различные передовые методы и технологии. Эти методы можно в целом разделить на четыре категории в зависимости от типа энергии, используемой для привода устройств управления: активные, полуактивные, пассивные и гибридные системы управления 4,5,6,7.
При активном управлении необходимое управляющее усилие прикладывается непосредственно через устройства управления, что требует значительного количества энергии 8,9,10. Полуактивное управление, с другой стороны, включает в себя регулировку свойств управляющих устройств (таких как демпфирование или жесткость) на основе управляющих сигналов, что требует гораздо меньше энергии по сравнению с активными системами11. Пассивное управление, напротив, основано на рассеивании энергии без какого-либо внешнего ввода энергии в систему 12,13,14. Гибридные системы сочетают в себе черты активной/полуактивной и пассивной стратегий управления для достижения более эффективных характеристик15. Среди этих подходов полуактивное управление считается особенно перспективным из-за его баланса между низким энергопотреблением и высоким КПД 16,17,18. Магнитореологический (MR) демпфер, обладающий превосходными динамическими демпфирующими характеристиками, считается одним из наиболее эффективных полуактивных устройств управления 19,20,21,22.
Однако в полуактивных системах управления, использующих MR-демпферы, возникает проблема, поскольку логика обратной связи неизбежно приводит к временным задержкам. Эти задержки обычно вызваны несколькими факторами 23,24,25, в том числе: (i) сбором и обработкой данных датчиков, (ii) расчетом требуемой управляющей силы контроллером26, (iii) передачей сигнала через преобразователи к демпферамMR 27 и (iv) фактической генерацией силы самими демпферами MR28. Такие временные задержки могут привести к расхождениям между создаваемой силой управления и силой, ожидаемой конструкцией, что значительно снижает эффективность управления29. К сожалению, большинство существующих алгоритмов управления для заслонок MR не учитывают эти задержки.
Кроме того, из-за присущей катастрофическим событиям случайности, любой эффективный полуактивный алгоритм управления должен быть способен поддерживать производительность при стохастических возбуждениях. Метод линейного квадратичного гауссова управления (LQG), являющийся классическим методом стохастической оптимизации, был исследован для смягчения вибраций в конструкциях, оснащенных гасителями MR. Например, Dyke et al. предложили оптимальную стратегию управления LQG для улучшения сейсмической реакции конструкций, оснащенных демпферами MR, с использованием обратной связи по ускорению30. Ying et al. представили неклипированную полуактивную стохастическую оптимальную стратегию управления для нелинейных структур с MR-демпферами, включающую методы стохастического усреднения и динамического программирования31. В других исследованиях применялось модальное управление LQG для повышения сейсмических характеристик зданий с изоляцией основания19 и анализировалась его эффективность для снижения вибрации в башнях ветряных турбин32. Тем не менее, классические методы LQG, которые предполагают белый гауссов шум, не очень хорошо подходят для моделирования нестационарной, негауссовской природы реальных возбуждений, таких как землетрясения или сильные ветры. Для решения этой проблемы была разработана концепция физически обоснованного стохастического оптимального управления (PSO)33,34, которая преодолевает ограничения традиционных методов LQG и предлагает более точную основу для управления различными стохастическими возбуждениями35. Исследования показали, что полуактивное стохастическое оптимальное управление на основе PSO значительно улучшает подавление вибрации как для линейных, так и для нелинейных конструкций, подвергающихся воздействию стохастических сейсмических сил36.
Таким образом, существует острая потребность в робастном полуактивном методе управления, который компенсирует временные задержки, повышая надежность конструкций, управляемых гасителями MR25,37. Кроме того, для обеспечения оптимальных характеристик управления при стохастических возбуждениях важно оптимизировать критические параметры предлагаемого метода управления с использованием подхода, основанного на надежности. Поэтому в данной работе предлагается метод стохастического оптимального полуактивного управления с компенсацией временной задержки (SOSC-PSO) для повышения надежности конструкций с MR-демпферами.
протокол
1. Стохастический оптимальный метод полуактивного управления
Поскольку на управляющий эффект демпфера MR существенно влияет неизбежная временная задержка, для повышения производительности управляемой конструкции разработан полуактивный метод управления с алгоритмом компенсации временной задержки. Кроме того, случайность, присущая внешним возбуждениям, обуславливает очевидную неопределенность динамических реакций. Управление ПСО введено для оптимизации критических параметров предложенного метода обеспечения надежности системы управления сооружением.
1.1 Алгоритм компенсации полуактивного управления
Без потери общности рассмотрим структуру n-Degree-Of-Freedoms (n-DOF), управляемую МР-демпферами с временной задержкой, уравнение движения которой под действием стохастических возбуждений определяется как:
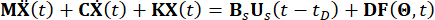 (1)
(1)
Где  — матрицы массы n x n, демпфирования и жесткости конструкции соответственно; n — количество степеней свободы управляемой конструкции. Векторы перемещения, скорости и ускорения конструкции представлены как
— матрицы массы n x n, демпфирования и жесткости конструкции соответственно; n — количество степеней свободы управляемой конструкции. Векторы перемещения, скорости и ускорения конструкции представлены как 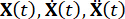 , соответственно. Маленькие одна и две точки над символами представляют собой производные первого и второго раза. Us (t - tD) представляет собой r-мерный вектор силы управления задержкой по времени для заслонок MR, а r представляет количество демпферов; t обозначает время; t D обозначает временную задержку, которая предполагается равномерной для всех демпферов в данном исследовании, где
, соответственно. Маленькие одна и две точки над символами представляют собой производные первого и второго раза. Us (t - tD) представляет собой r-мерный вектор силы управления задержкой по времени для заслонок MR, а r представляет количество демпферов; t обозначает время; t D обозначает временную задержку, которая предполагается равномерной для всех демпферов в данном исследовании, где 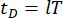 , где здесь целое число
, где здесь целое число 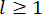 , и
, и 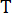 обозначающее период дискретизации.
обозначающее период дискретизации. 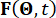 представляет собой p-мерный вектор стохастических возбуждений и
представляет собой p-мерный вектор стохастических возбуждений и  представляет собой вектор стохастических параметров, характеризующих случайность, связанную с внешними возбуждениями. Размерность
представляет собой вектор стохастических параметров, характеризующих случайность, связанную с внешними возбуждениями. Размерность  зависит от модели, используемой для внешних возбуждений, но не связана с механическими степенями свободы конструкции. Bs и D представляют собой матрицы n x r и n x p, которые определяют расположение демпферов и внешних возбуждений соответственно. В представлении пространства состояний уравнение (1) записывается как:
зависит от модели, используемой для внешних возбуждений, но не связана с механическими степенями свободы конструкции. Bs и D представляют собой матрицы n x r и n x p, которые определяют расположение демпферов и внешних возбуждений соответственно. В представлении пространства состояний уравнение (1) записывается как:
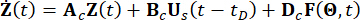 (2)
(2)
Где 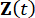 представляет собой 2n-мерный вектор состояния;
представляет собой 2n-мерный вектор состояния; 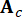 представляет матрицу системы 2n x 2n;
представляет матрицу системы 2n x 2n; 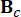 представляет матрицу расположения 2n x r демпферов MR;
представляет матрицу расположения 2n x r демпферов MR; 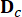 представляет собой матрицу расположения внешних возбуждений размером 2n x p. Эти параметры выражаются следующим образом:
представляет собой матрицу расположения внешних возбуждений размером 2n x p. Эти параметры выражаются следующим образом:
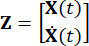 ,
, 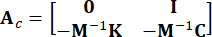 ,
,  ,
, 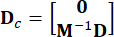 (3)
(3)
Где 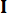 обозначает матрицу тождества с тем же порядком
обозначает матрицу тождества с тем же порядком 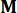 . Для удобства вычислений уравнение пространства непрерывных состояний уравнение (2) может быть выражено в дискретном виде как:
. Для удобства вычислений уравнение пространства непрерывных состояний уравнение (2) может быть выражено в дискретном виде как:
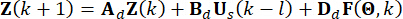 (4)
(4)
Где временная точка 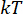 упрощается как
упрощается как 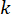 . А
. А  ,
, 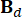 ,
, 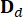 обозначают матрицы 2n x 2n, 2n x r и 2n x p, которые выражаются как:
обозначают матрицы 2n x 2n, 2n x r и 2n x p, которые выражаются как:
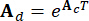 ,
,  ,
, 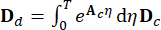 (5)
(5)
Где 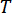 обозначает период выборки.
обозначает период выборки.
Для достижения эффективности, аналогичной активному контролю, предложен простой и эффективный метод управления на основе алгоритма Гровата38 для управления на основе демпфера MR с временной задержкой:
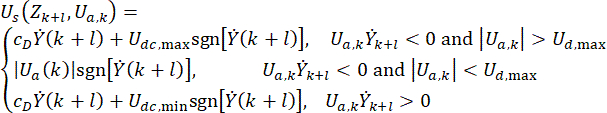 (6)
(6)
где  представляет собой полуактивный сигнал управляющей силы в момент времени\
представляет собой полуактивный сигнал управляющей силы в момент времени\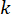 для демпфера MR;
для демпфера MR; 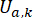 представляет собой опорную активную силу управления с компенсацией временной задержки;
представляет собой опорную активную силу управления с компенсацией временной задержки;  представляет собой максимальную силу демпфирования демпфера MR, которая является изменяемой;
представляет собой максимальную силу демпфирования демпфера MR, которая является изменяемой; 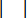 представляет собой символ операции с абсолютным значением;
представляет собой символ операции с абсолютным значением; 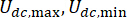 представляют максимальные и минимальные кулоновские силы демпфера MR;
представляют максимальные и минимальные кулоновские силы демпфера MR;  представляет собой коэффициент вязкого демпфирования;
представляет собой коэффициент вязкого демпфирования; 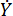 представляет собой вход скорости в демпфер MR, который представляет собой скорость движения поршня относительно цилиндра демпфера. В уравнении (6)
представляет собой вход скорости в демпфер MR, который представляет собой скорость движения поршня относительно цилиндра демпфера. В уравнении (6)  представлены расчетные параметры демпфера MR.
представлены расчетные параметры демпфера MR.
Уравнение (6) показывает расчет полуактивной управляющей силы демпфера MR с временной задержкой. Видно, что полуактивная управляющая сила  на временном шаге
на временном шаге  в уравнении (4) рассчитывается на основе активной управляющей силы
в уравнении (4) рассчитывается на основе активной управляющей силы  на временном шаге
на временном шаге  и переменной
и переменной 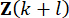 состояния на временном шаге
состояния на временном шаге  с момента
с момента 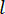 задержки временных шагов. Для получения активной управляющей силы
задержки временных шагов. Для получения активной управляющей силы  условная стоимостная функция устанавливается по формуле
условная стоимостная функция устанавливается по формуле
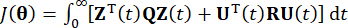 (7)
(7)
Где  представляет собой симметричную положительную полуопределенную весовую матрицу состояния системы размером 2n x 2n;
представляет собой симметричную положительную полуопределенную весовую матрицу состояния системы размером 2n x 2n;  представляет собой симметричную положительную определенную весовую матрицу управляющей силы r x r. Видно, что внешнее возбуждение пренебрежимо мало. Фактически, основываясь на уравнении (7), система управления структурой может достичь оптимального эффекта управления независимо от вида внешнего возбуждения. В качестве дискретной формы уравнение (7) выражается как39:
представляет собой симметричную положительную определенную весовую матрицу управляющей силы r x r. Видно, что внешнее возбуждение пренебрежимо мало. Фактически, основываясь на уравнении (7), система управления структурой может достичь оптимального эффекта управления независимо от вида внешнего возбуждения. В качестве дискретной формы уравнение (7) выражается как39:
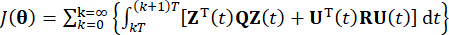 (8)
(8)
Минимизация функции  стоимости приводит к проблеме условного экстремального значения, и активная сила
стоимости приводит к проблеме условного экстремального значения, и активная сила  управления вычисляется как25:
управления вычисляется как25:
 (9)
(9)
Где 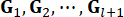 обозначают выигрыши управления для переменной
обозначают выигрыши управления для переменной 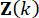 состояния на временном шаге
состояния на временном шаге  и активной управляющей силы
и активной управляющей силы 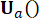 на временном шаге
на временном шаге 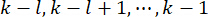 , которая определяется весовыми матрицами
, которая определяется весовыми матрицами 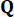 и
и 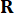 37. С неизбежной временной задержкой, полученная управляющая сила
37. С неизбежной временной задержкой, полученная управляющая сила 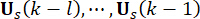 воздействует на конструкцию в моменты
воздействует на конструкцию в моменты 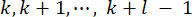 времени. Следовательно, активная управляющая сила в уравнении (9) рассчитывается по формуле:
времени. Следовательно, активная управляющая сила в уравнении (9) рассчитывается по формуле:
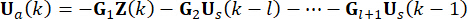 (10)
(10)
Для ясности понятия полуактивная управляющая сила в уравнении (10) выражается следующим образом, исходя из уравнения (6):
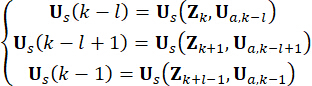 (11)
(11)
Где  обозначает активную управляющую силу в момент
обозначает активную управляющую силу в момент  времени . Подставляем уравнение (11) в уравнение (10),
времени . Подставляем уравнение (11) в уравнение (10),
 (12)
(12)
ПРИМЕЧАНИЕ: Все значения состояния  от момента
от момента  времени до
времени до 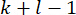 необходимы для расчета
необходимы для расчета  . Таким образом, вводится следующий метод прогнозирования состояния40.
. Таким образом, вводится следующий метод прогнозирования состояния40.
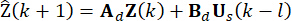 (13)
(13)
Где  обозначает прогнозируемую переменную. С помощью итерации уравнения (13) вычисляется состояние
обозначает прогнозируемую переменную. С помощью итерации уравнения (13) вычисляется состояние  at
at  . Активная сила управления Ua(k) выражается как:
. Активная сила управления Ua(k) выражается как:
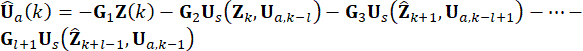 (14)
(14)
Полуактивная управляющая сила может быть получена путем комбинирования уравнений. (6), (12) и (13).
1.2 Анализ надежности системы управления конструкцией
В соответствии с принципом сохранения вероятности, дополненная система 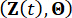 и
и 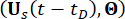 структура с МР-демпферами являются вероятностно-консервативными и управляются следующими обобщенными уравнениями эволюции плотности вероятностей (GDEE)38:
структура с МР-демпферами являются вероятностно-консервативными и управляются следующими обобщенными уравнениями эволюции плотности вероятностей (GDEE)38:
 (15)
(15)
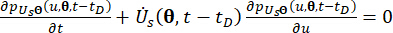 (16)
(16)
Где  ,
,  обозначают соответствующие компоненты состояния системы и полуактивной управляющей силы с временной задержкой, соответственно;
обозначают соответствующие компоненты состояния системы и полуактивной управляющей силы с временной задержкой, соответственно; 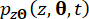 и
и  обозначают совместные функции плотности вероятности систем дополненных выборок
обозначают совместные функции плотности вероятности систем дополненных выборок 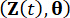 и
и 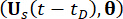 , соответственно;
, соответственно; 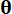 обозначают выборку в пределах пространства
обозначают выборку в пределах пространства 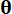 выборки ;
выборки ;  и
и  ) обозначают частичные производные первого порядка по времени компонент состояния системы и полуактивной управляющей силы, соответственно. Общая плотность вероятности функционирует
) обозначают частичные производные первого порядка по времени компонент состояния системы и полуактивной управляющей силы, соответственно. Общая плотность вероятности функционирует 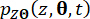 и
и  может быть достигнута путем решения уравнений. (15) и (16) со следующими начальными условиями:
может быть достигнута путем решения уравнений. (15) и (16) со следующими начальными условиями:
 (17)
(17)
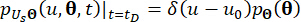 (18)
(18)
Где 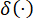 обозначает дельта-функцию Дирака;
обозначает дельта-функцию Дирака; 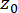 и
и 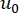 обозначают детерминированные начальные
обозначают детерминированные начальные  значения и
значения и 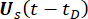 , соответственно;
, соответственно; 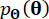 обозначают функцию плотности вероятности выборки
обозначают функцию плотности вероятности выборки 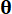 .
.
Мгновенные функции  плотности вероятности и могут быть получены путем одномерного интегрирования
плотности вероятности и могут быть получены путем одномерного интегрирования 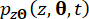 области пространства выборок и
области пространства выборок и 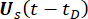
 над ней:
над ней:
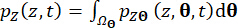 (19)
(19)
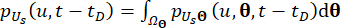 (20)
(20)
Где 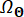 обозначает область распространения домена
обозначает область распространения домена  .
.
На основе уравнений. (19) и (20) видно, что полная вероятностная информация о соответствующих физических величинах легко выводится, если определить их отношения, связанные с параметрами алгоритма. Надежность рассматриваемых физических величин может быть рассчитана с помощью следующей соответствующей функции производительности:
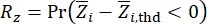 (21)
(21)
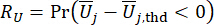 (22)
(22)
где 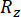 и
и 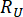 обозначают расчетную надежность величины соответствующего состояния и полуактивной управляющей силы, соответственно;
обозначают расчетную надежность величины соответствующего состояния и полуактивной управляющей силы, соответственно;  обозначают эквивалентный вектор экстремальных значений i-й рассматриваемой физической величины управляемой конструкции;
обозначают эквивалентный вектор экстремальных значений i-й рассматриваемой физической величины управляемой конструкции; 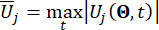 обозначают эквивалентный вектор экстремальных значений j-й управляющей силы; шляпа '-' на символах указывает на эквивалентный вектор экстремальных значений41;
обозначают эквивалентный вектор экстремальных значений j-й управляющей силы; шляпа '-' на символах указывает на эквивалентный вектор экстремальных значений41;  обозначает i-ю заинтересованную физическую величину k-й степени свободы управляемой структуры;
обозначает i-ю заинтересованную физическую величину k-й степени свободы управляемой структуры; 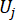 обозначает j-ю управляющую силу;
обозначает j-ю управляющую силу; 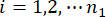 ,
, 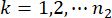 ,
,  ,
, ,
,  и
и  обозначают количество соответствующих физических величин и степень свободы конструкции и MR-демпферов, установленных в конструкции, соответственно.
обозначают количество соответствующих физических величин и степень свободы конструкции и MR-демпферов, установленных в конструкции, соответственно.  и
и 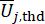 обозначают пороговые
обозначают пороговые  значения и
значения и  ;
;  обозначает вероятность случайного события.
обозначает вероятность случайного события.
1.3 Оптимизация параметров
Соотношение амплитуд  и
и  сильно влияет на эффективность управления38 в режиме управления с обратной связью. Поэтому для достижения наилучшей эффективности контроля,
сильно влияет на эффективность управления38 в режиме управления с обратной связью. Поэтому для достижения наилучшей эффективности контроля, так и
так и  нужно проводить оптимизацию. Кроме того, в качестве метода управления на основе МРТ-демпфера эффективность управления также зависит от параметров
нужно проводить оптимизацию. Кроме того, в качестве метода управления на основе МРТ-демпфера эффективность управления также зависит от параметров  устройства (уравнение (6). Для достижения оптимальной надежности системы управления конструкцией в уравнении (25) предложен критерий, основанный на надежности.
устройства (уравнение (6). Для достижения оптимальной надежности системы управления конструкцией в уравнении (25) предложен критерий, основанный на надежности.
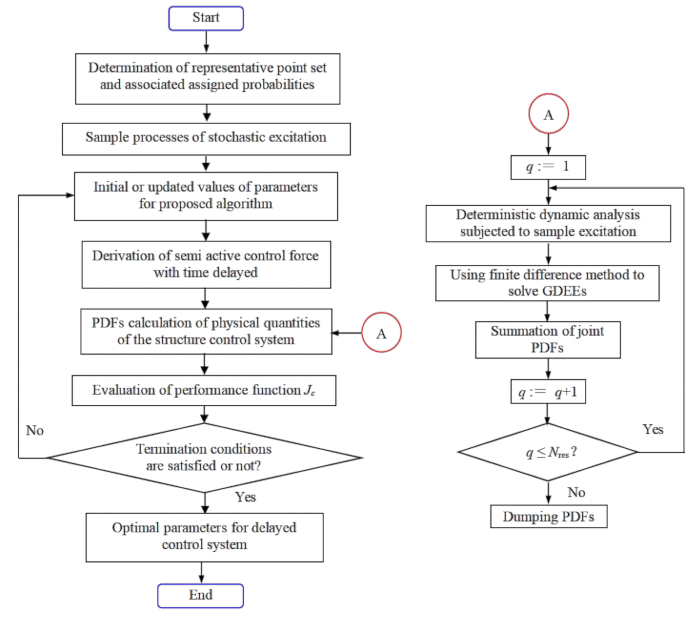
Рисунок 1: Блок-схема оптимизации параметров для стохастического оптимального управления полуактивной структурой с компенсацией временной задержки. Сокращения: GDEE = обобщенное дифференциальное уравнение события; PDF = функция плотности вероятности. Пожалуйста, нажмите здесь, чтобы просмотреть увеличенную версию этой цифры.
Таким образом, для проведения стохастического оптимального полуактивного управления структурой на основе МР-демпферов с компенсацией временной задержки требуется два этапа:
1.3.1 Минимизируя функцию  стоимости, показанную в уравнении (7), достигается логика обратной связи по состоянию в смысле выборок, т.е. уравнение 12.
стоимости, показанную в уравнении (7), достигается логика обратной связи по состоянию в смысле выборок, т.е. уравнение 12.
1.3.2 Минимизация функции  производительности, основанной на надежности, достигается достижение оптимальных параметров в смысле статистики. На рисунке 1 представлена блок-схема оптимизации параметров контроллера на шаге 1.3.2.
производительности, основанной на надежности, достигается достижение оптимальных параметров в смысле статистики. На рисунке 1 представлена блок-схема оптимизации параметров контроллера на шаге 1.3.2.
Следующие шаги на шаге 1.3.2, которые включают в себя два слоя петель, следующие:
1.3.2.1 Разбиение вероятностного пространства стохастических возбуждений, которое характеризуется вектором  стохастических параметров, позволяет идентифицировать множество репрезентативных точек
стохастических параметров, позволяет идентифицировать множество репрезентативных точек 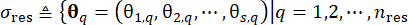 вместе с связанными с ними присвоенными вероятностями Pq. Этот подход позволяет эффективно генерировать процессы выборки для легкого получения стохастического возбуждения, обозначаемого как
вместе с связанными с ними присвоенными вероятностями Pq. Этот подход позволяет эффективно генерировать процессы выборки для легкого получения стохастического возбуждения, обозначаемого как 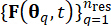 ,
,
1.3.2.2 Для оптимизации параметров системы управления полуактивной конструкцией инициализируйте или обновите значения весов  стоимость-функция и
стоимость-функция и  . Затем вычисляется связанная с этим сила управления состоянием с временной задержкой, см. уравнение (12).
. Затем вычисляется связанная с этим сила управления состоянием с временной задержкой, см. уравнение (12).
1.3.2.3 Получение функций плотности вероятности (PDF) структурных реакций и управляющей силы путем решения GDEE, показанных в уравнениях. (17)–(20):
Оптимизация выполняется в автономном режиме, но не в режиме онлайн. При применении предложенного метода в реальных структурных системах управления, оптимальные  и
и  достигнуты, а оптимизация в реальном применимом процессе не требуется.
достигнуты, а оптимизация в реальном применимом процессе не требуется.
Детерминированный динамический анализ полуактивной системы управления структурой при воздействии образца, с помощью которого рассчитываются соответствующие физические величины 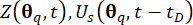
 и их производные.
и их производные.
Используя метод конечных разностей, такой как модифицированная схема Лакса-Вендроффа со свойствами уменьшения полной вариации (TVD), можно решить обобщенные дифференциальные уравнения (GDEE) и вывести численные решения для совместных функций 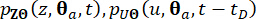 плотности вероятности.
плотности вероятности.
Повторяя два предыдущих шага детерминированного динамического анализа и метода конечных разностей и проходя по всем репрезентативным точкам 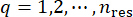 , функции плотности вероятности могут быть получены путем суммирования:
, функции плотности вероятности могут быть получены путем суммирования:
 (23)
(23)
 (24)
(24)
Где  представляет собой меру площади подобласти, связанной с опорной точкой
представляет собой меру площади подобласти, связанной с опорной точкой 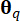 . Метод, используемый для решения обобщенного дифференциального уравнения события (GDEE), известен как метод эволюции плотности вероятности (PDEM)42.
. Метод, используемый для решения обобщенного дифференциального уравнения события (GDEE), известен как метод эволюции плотности вероятности (PDEM)42.
1.3.2.4 Для оценки их надежности используются PDF-файлы соответствующих физических величин, которые затем включаются в функцию  рабочих характеристик вероятностного критерия.
рабочих характеристик вероятностного критерия.
1.3.2.5 Оцените, были ли соблюдены критерии завершения процесса оптимизации параметров. Если условия не выполнены, вернуться к Шагу 1.3.2.2; Если они есть, то можно определить оптимальные параметры для системы управления с задержкой по времени. В этой работе набор инструментов генетического алгоритма (GA) в MATLAB используется для оптимизации параметров, что облегчает обновление параметров и определяет условия завершения. С помощью генетического алгоритма оптимальные значения могут быть достигнуты в течение десяти итераций, а сходимость стабильна без проблем локальных минимумов. Несмотря на то, что вычислительные затраты на ГА выше, чем на оптимизацию роя частиц или методы на основе градиента, ГА хорошо справляется со сложными и недифференцируемыми задачами, подобными той, что описана в этой рукописи. Поэтому применяется ГА. А поскольку свойство быстрой сходимости является таковым, вычислительные затраты GA приемлемы.
1.3.2.6 Для достижения оптимального контроля надежности формулируется следующая эксплуатационная функция  . Сворачиваем
. Сворачиваем  для определения оптимальных значений параметров
для определения оптимальных значений параметров  и
и  :
:
 } (25)
} (25)
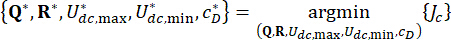 (26)
(26)
Как упоминалось ранее, весовые матрицы контроллера симметричны, где элементы в матрице  соответствуют весам, назначенным перемещению, скорости и их взаимодействию, в то время как элементы в матрице
соответствуют весам, назначенным перемещению, скорости и их взаимодействию, в то время как элементы в матрице  представляют веса, связанные с управляющей силой. Основываясь на выводах более ранних исследований38, было замечено, что изменение конфигураций весов «стоимость-функция»
представляют веса, связанные с управляющей силой. Основываясь на выводах более ранних исследований38, было замечено, что изменение конфигураций весов «стоимость-функция»  оказывает
оказывает  минимальное влияние на эффективность контроля. Следовательно, в данном исследовании принята упрощенная конфигурация, как указано ниже:
минимальное влияние на эффективность контроля. Следовательно, в данном исследовании принята упрощенная конфигурация, как указано ниже:
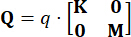 ,
, 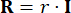 (27)
(27)
Где 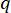 обозначает коэффициент матрицы взвешивания состояния, подлежащей определению;
обозначает коэффициент матрицы взвешивания состояния, подлежащей определению; 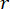 обозначает коэффициент контрольной матрицы взвешивания, подлежащей определению;
обозначает коэффициент контрольной матрицы взвешивания, подлежащей определению; 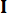 обозначает матрицу тождества. На эффект управления влияет отношение
обозначает матрицу тождества. На эффект управления влияет отношение 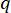 до,
до, 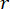 но не сами значения. Кроме того,
но не сами значения. Кроме того, 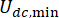 в уравнении (6) обозначает минимальную кулоновскую силу демпфера MR, что означает, что
в уравнении (6) обозначает минимальную кулоновскую силу демпфера MR, что означает, что  при входе тока в демпфер равен нулю. Тогда уравнение (26) может быть дополнительно выражено как: T
при входе тока в демпфер равен нулю. Тогда уравнение (26) может быть дополнительно выражено как: T
 (28)
(28)
Где 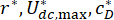 находятся оптимальные коэффициенты беспокойства. Чтобы сделать их разумными в инженерном отношении, оптимальные диапазоны их основаны на производственных мощностях заводов по производству демпферов MR.
находятся оптимальные коэффициенты беспокойства. Чтобы сделать их разумными в инженерном отношении, оптимальные диапазоны их основаны на производственных мощностях заводов по производству демпферов MR.
Очевидно, что оптимальные параметры, полученные с помощью уравнения (28), поддерживают оптимальную эффективность управления предложенным полуактивным алгоритмом управления с временной задержкой, что позволяет системе управления структурой достичь сбалансированной оптимальной надежности при воздействии стохастических возбуждений.
2. Пример из практики
Для анализа эффективности предложенного метода полуактивного управления с компенсацией временной задержки для демпфера MR плоская одноэтажная каркасная конструкция сдвига, прикрепленная к демпферу MR, была подвергнута горизонтальному стохастическому сейсмическому движению грунта, как показано на рисунке 2. Параметры полуактивно управляемой системы конструкций следующие: масса 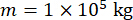 конструкции, собственная круговая частота
конструкции, собственная круговая частота  , коэффициент
, коэффициент 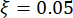 демпфирования. Согласно прошлому опыту и существующим на рынке шкалам демпферов, пороговые значения структурного смещения, скорости, ускорения и управляющей силы составляют 10 мм, 100 мм/с, 1 500 мм/с2 и 150 кН соответственно. Для представления стохастического сейсмического движения грунта была использована физически мотивированная модель стохастического движения грунта43:
демпфирования. Согласно прошлому опыту и существующим на рынке шкалам демпферов, пороговые значения структурного смещения, скорости, ускорения и управляющей силы составляют 10 мм, 100 мм/с, 1 500 мм/с2 и 150 кН соответственно. Для представления стохастического сейсмического движения грунта была использована физически мотивированная модель стохастического движения грунта43:
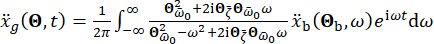 (29)
(29)
Where 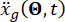 обозначает движение грунта во временной области на инженерной площадке и
обозначает движение грунта во временной области на инженерной площадке и 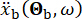 обозначает движение грунта в частотной области в коренной породе. Вектор
обозначает движение грунта в частотной области в коренной породе. Вектор  характеризует стохастический характер движения грунта на поверхности инженерного участка. Параметры
характеризует стохастический характер движения грунта на поверхности инженерного участка. Параметры 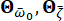 представляют собой стохастические переменные, которые описывают характеристики почвы участка, включая преобладающую частоту
представляют собой стохастические переменные, которые описывают характеристики почвы участка, включая преобладающую частоту  и эквивалентное демпфирование
и эквивалентное демпфирование  . Вектор
. Вектор 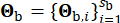 представляет стохастический характер движения грунта в коренной породе, на который влияют свойства источника и траектория распространения, с
представляет стохастический характер движения грунта в коренной породе, на который влияют свойства источника и траектория распространения, с 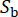 указанием количества стохастических переменных, задействованных на этом этапе.
указанием количества стохастических переменных, задействованных на этом этапе.  относится к круговой частоте, а i является мнимой единицей.
относится к круговой частоте, а i является мнимой единицей.
Преобладающая частота  и эквивалентный коэффициент
и эквивалентный коэффициент  демпфирования инженерного участка являются ключевыми параметрами, характеризующими динамические свойства грунта участка. Вероятностное распределение и статистические параметры этих величин могут быть определены на основе данных о сейсмических ускорениях, собранных на определенном классе инженерных площадок. В иллюстративных целях рассмотрен класс площадки с диапазоном скоростей сдвиговой волны [150, 250] м/с, а расчетный характеристический период движения грунта был установлен равным 0,45 с.
демпфирования инженерного участка являются ключевыми параметрами, характеризующими динамические свойства грунта участка. Вероятностное распределение и статистические параметры этих величин могут быть определены на основе данных о сейсмических ускорениях, собранных на определенном классе инженерных площадок. В иллюстративных целях рассмотрен класс площадки с диапазоном скоростей сдвиговой волны [150, 250] м/с, а расчетный характеристический период движения грунта был установлен равным 0,45 с.
Критические параметры 
 рассматривались как взаимно независимые стохастические переменные, оба из которых следовали логнормальному распределению для идентификации параметров. Статистические параметры были следующими: средние
рассматривались как взаимно независимые стохастические переменные, оба из которых следовали логнормальному распределению для идентификации параметров. Статистические параметры были следующими: средние  значения составили
значения составили  12 рад/с и 0,1 соответственно. Коэффициенты вариации
12 рад/с и 0,1 соответственно. Коэффициенты вариации  и
и  составили 0,42 и 0,35 соответственно. Движение грунта в коренной породе было смоделировано как гауссов процесс белого шума с амплитудой Фурье 0,20 м/с2, что соответствует пиковому ускорению грунта 0,11 g. Фазовый угол, используемый для создания движения коренной породы, был обозначен как
составили 0,42 и 0,35 соответственно. Движение грунта в коренной породе было смоделировано как гауссов процесс белого шума с амплитудой Фурье 0,20 м/с2, что соответствует пиковому ускорению грунта 0,11 g. Фазовый угол, используемый для создания движения коренной породы, был обозначен как 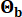 . Следовательно, Sb =1 и
. Следовательно, Sb =1 и 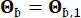 . Этот подход можно рассматривать как моделирование условных стохастических движений грунта с заданной вероятностью превышения44. Предположение о логнормальном распределении широко используется при моделировании движения грунта из-за его способности фиксировать асимметрию наблюдаемых параметров движения грунта.
. Этот подход можно рассматривать как моделирование условных стохастических движений грунта с заданной вероятностью превышения44. Предположение о логнормальном распределении широко используется при моделировании движения грунта из-за его способности фиксировать асимметрию наблюдаемых параметров движения грунта.
Для оценки чувствительности этого предположения в другихисследованиях были проведены дополнительные анализы с использованием альтернативных вероятностных распределений, включая нормальное и гамма-распределения. Полученные данные показывают, что, хотя общие тенденции остаются последовательными, логнормальное распределение обеспечивает наилучшее соответствие наблюдаемым данным, особенно для фиксации поведения хвоста измерений интенсивности движения грунта
С помощью метода касательных сфер47 была выбрана коллекция из 221 репрезентативной точки с соответствующими присвоенными вероятностями и синтезированы репрезентативные ускорения грунта. Частота дискретизации составила 50 Гц, а продолжительность движений грунта — 20,48 с. Для присвоения нестационарной интенсивности моделируемому движению грунта была использована функция равномерной модуляции, которая была сформулирована следующимобразом:
 (30)
(30)
Где  занимают 2 и 16 с соответственно.
занимают 2 и 16 с соответственно.
Среднее и стандартное отклонение стохастического сейсмического движения грунта, а также временная история репрезентативного сейсмического движения грунта показаны на рисунке 3. Амплитуда среднего значения (0,06 м/с2) составила ~8% от амплитуды стандартного отклонения (0,8 м/с2), что указывает на то, что физически мотивированная стохастическая модель движения грунта обладает свойством нулевого среднего. Между тем, сейсмическое движение грунта продемонстрировало замечательное нестационарное поведение как во временной, так и в частотной областях.
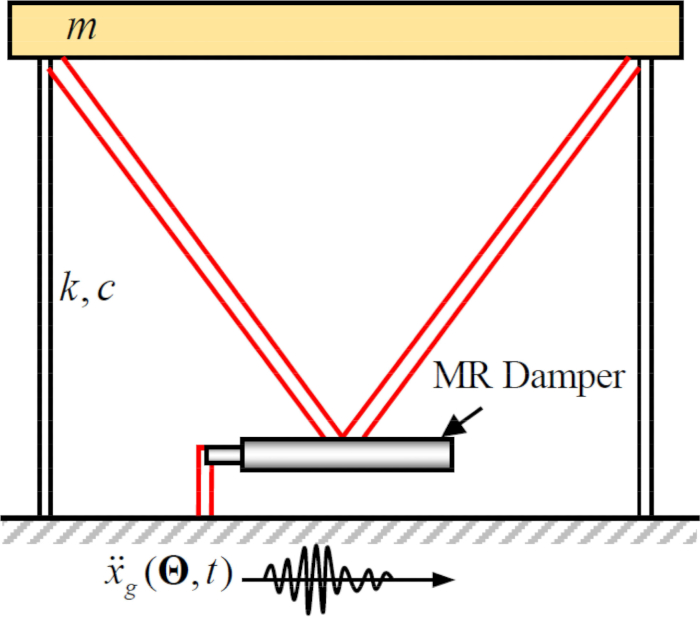
Рисунок 2: Эскиз одноэтажной срезной рамы с магнитореологическим демпфером. 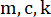 обозначают массу конструкции, коэффициент демпфирования и жесткость;
обозначают массу конструкции, коэффициент демпфирования и жесткость; 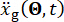 обозначает стохастическое сейсмическое возбуждение. Пожалуйста, нажмите здесь, чтобы просмотреть увеличенную версию этой цифры.
обозначает стохастическое сейсмическое возбуждение. Пожалуйста, нажмите здесь, чтобы просмотреть увеличенную версию этой цифры.
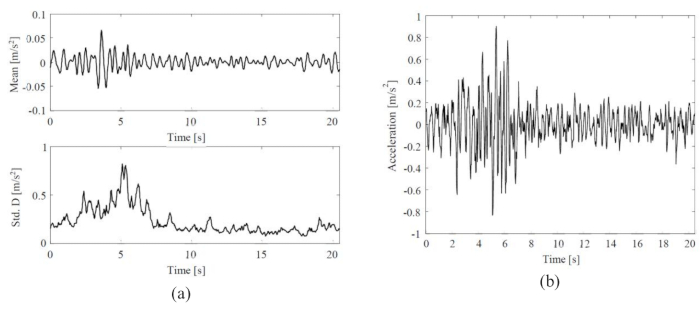
Рисунок 3: Статистические данные и репрезентативные выборки выбранных сейсмических движений грунта. (А) Среднее и стандартное отклонение стохастического сейсмического движения грунта; (B) Временная история репрезентативного сейсмического движения грунта. Пожалуйста, нажмите здесь, чтобы просмотреть увеличенную версию этой цифры.
2.1 Анализ влияния временной задержки
Для анализа влияния временной задержки на эффективность полуактивного управления МР-демпфером на рисунке 4 показаны среднеквадратичные характеристики перемещения, скорости и ускорения управляемой конструкции. Отношение матрицы взвешивания и параметры демпфера были равны 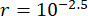 ,
, 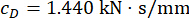 , и
, и 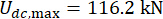 , которые являются оптимизированными результатами без временной задержки38. Реакции управляемой структуры с временной задержкой были больше, чем управляемой структуры без временной задержки, а влияние временной задержки на управляющий эффект представляло собой периодичность наряду с увеличением временной задержки. Поскольку метод полуактивного контроля с МР-демпфером является разновидностью метода обратной связи, было сочтено, что периодичность воздействия связана с естественным периодом контролируемой структуры (T = 0,56 с).
, которые являются оптимизированными результатами без временной задержки38. Реакции управляемой структуры с временной задержкой были больше, чем управляемой структуры без временной задержки, а влияние временной задержки на управляющий эффект представляло собой периодичность наряду с увеличением временной задержки. Поскольку метод полуактивного контроля с МР-демпфером является разновидностью метода обратной связи, было сочтено, что периодичность воздействия связана с естественным периодом контролируемой структуры (T = 0,56 с).
По сравнению с реакцией неуправляемой конструкции, из которых максимальное перемещение, скорость и ускорение MRS составляли 24,6 мм, 270,0 мм/с и 3111,3 мм/с2, управляемая конструкция MR с демпфером достигла заметного эффекта. В отличие от неустойчивости активной управляемой структуры с временной задержкой25, метод полуактивного управления на основе МР-демпфера все же давал некоторый эффект даже при временном запаздывании.
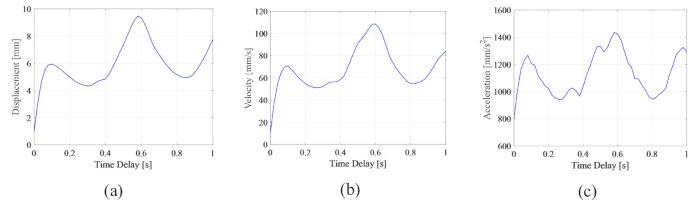
Рисунок 4: Максимальные среднеквадратичные реакции управляемой структуры с течением времени. а) перемещение; b) скорость; (c) Ускорение. Пожалуйста, нажмите здесь, чтобы просмотреть увеличенную версию этой цифры.
Для анализа влияния временного запаздывания на надежность полуактивно управляемой конструкции на рисунке 5 показана надежность перемещения, скорости и ускорения с увеличением временного запаздывания. Надежность реакции управляемой структуры при любом временном запаздывании была ниже, чем значения без временного запаздывания, а это означает, что надежность управляемой структуры снижалась на временное запаздывание. Между тем, как и в случае с максимальным среднеквадратичным значением, эффект контроля надежности проявлял периодичность с увеличением временной задержки. При этом надежность управляемой конструкции, с задержкой по времени или без нее, была выше, чем значения неуправляемых конструкций с надежностью перемещения, скорости и ускорения 0,0954, 0,1058 и 0,1111.
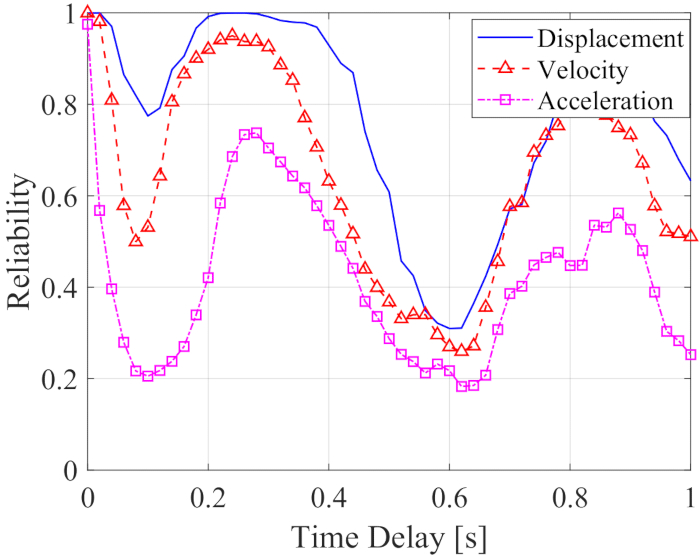
Рисунок 5: Надежность откликов управляемой структуры с возрастающей временной задержкой. Пожалуйста, нажмите здесь, чтобы просмотреть увеличенную версию этой цифры.
Таким образом, реакция структуры была смягчена с помощью метода полуактивного контроля. Однако эффективность управления, независимо от СКО или надежности, полуактивного метода управления снижалась из-за временной задержки. Поэтому необходимо компенсировать временную задержку.
2.1.1 Анализ метода компенсации временной задержки
Для анализа эффективности предложенного метода компенсации временной задержки на рисунке 6 сравниваются среднеквадратичные временные истории перемещения, скорости и ускорения для неконтролируемой (Unc), системы с временной задержкой с некомпенсационным управлением (TDN-SAC-PSO) и системы с временной задержкой с компенсационным управлением (TDC-SAC-PSO), где временная задержка составила 0,1 с. Параметры весовой матрицы и метода полуактивного контроля такие же, как и на шаге 2.1.
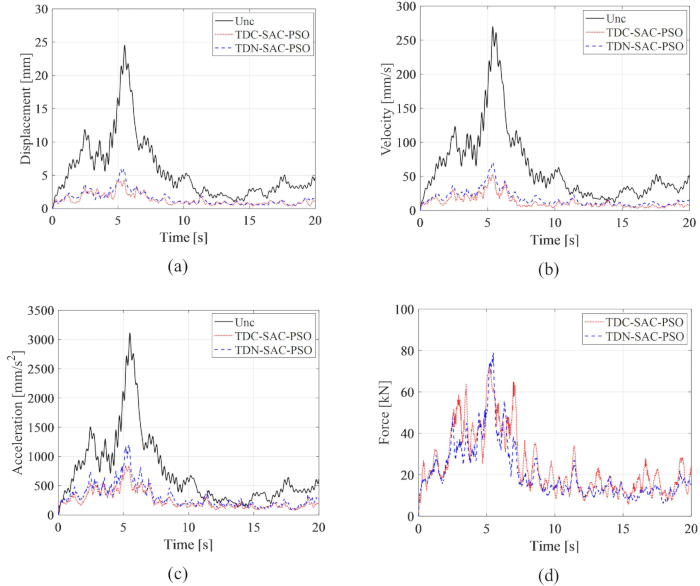
Рисунок 6: Среднеквадратичное сравнение динамики по времени структур, контролируемых различными методами. а) перемещение; b) скорость; с) ускорение; (D) Управляющая сила. Сокращения: Unc = неконтролируемый; TDC-SAC-PSO = система с задержкой по времени с контролируемой компенсацией; TDN -SAC-PSO = система с задержкой по времени с управлением без компенсации. Пожалуйста, нажмите здесь, чтобы просмотреть увеличенную версию этой цифры.
Оба метода контроля значительно снизили реакцию конструкции по сравнению с неконтролируемой структурой, что выявило преимущества метода управления на основе МР-демпфера. По сравнению с неуправляемой конструкцией максимальные среднеквадратичные значения перемещения, скорости и ускорения уменьшаются на 75,79%, 73,75% и 61,22% при использовании метода TDN-SAC-PSO. Далее, с компенсацией временной задержки, отклики управляемой структуры уменьшаются на 82,59%, 80,40% и 73,04% при методе TDC-SAC-PSO. Максимальное среднеквадратичное значение управляющей силы при использовании метода TDC-SAC-PSO уменьшилось на 8,43% по сравнению с методом TDN-SAC-PSO, хотя вибрационные отклики первого метода были меньше, чем при втором. Приведенный выше анализ показывает, что влияние временной задержки на метод управления на основе заслонки MR было эффективно снижено с помощью метода компенсации, что показывает необходимость компенсации временной задержки для полуактивного метода управления заслонкой MR.
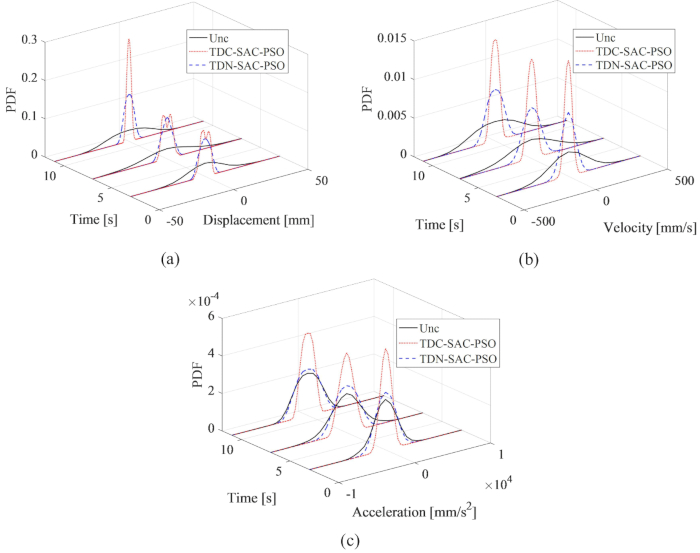
Рисунок 7: Сравнение в формате PDF в типичное время реакции структуры. а) перемещение; b) скорость; (c) Ускорение. Сокращения: PDF = функция плотности вероятности; Unc = неконтролируемый; TDC-SAC-PSO = система с задержкой по времени с контролируемой компенсацией; TDN -SAC-PSO = система с задержкой по времени с управлением без компенсации. Пожалуйста, нажмите здесь, чтобы просмотреть увеличенную версию этой цифры.
Чтобы всесторонне раскрыть влияние предложенного метода компенсации на неопределенность реакций управляемой конструкции, на рисунке 7 показаны сравнения смещения, скорости и ускорения с помощью функции плотности вероятности (PDF) в типичные моменты времени 3, 7 и 11 с. PDF-файлы для метода TDN-SAC-PSO были уже, чем для неконтролируемой структуры, что означает, что неопределенность реакций структуры снижалась при использовании метода полуактивного управления даже с временной задержкой. Когда временная задержка была компенсирована, PDF-файлы ответов были еще больше сужены. Таким образом, предложенный метод компенсации необходим для улучшения полуактивного контрольного эффекта.
| Метод управления | Смещение | Скорость | Ускорение | Сила управления | Минимальное значение |
| Unc | 0.0954 | 0.1058 | 0.1111 | -- | 0.1111 |
| TDC-SAC-PSO | 0.9565 | 0.8107 | 0.7654 | 0.9845 | 0.7654 |
| ТДН-САК-ПСО | 0.7747 | 0.531 | 0.2054 | 0.884 | 0.2054 |
Таблица 1: Вибрационные отклики и надежность регулирующей силы конструкций, контролируемых различными методами. Сокращения: Unc = неконтролируемый; TDC-SAC-PSO = система с задержкой по времени с контролируемой компенсацией; TDN -SAC-PSO = система с задержкой по времени с управлением без компенсации.
Вибрационные отклики и надежность управляющей силы неуправляемых конструкций, управляемых методами TDC-SAC-PSO и TDN-SAC-PSO, приведены в таблице 1. С помощью метода управления TDN-SAC-PSO надежность конструкции была значительно повышена по сравнению с неконтролируемой структурой, что подтверждает эффективность метода управления на основе демпфера MR, даже со временем. Тем не менее, с компенсацией временной задержки надежность была значительно повышена по сравнению с без компенсации, особенно для ускорения. Следует также отметить, что достоверность различных откликов и управляющей силы показали существенные различия для метода TDC-SAC-PSO. Это указывает на то, что оптимальные значения критических параметров для управления без временного запаздывания не являются оптимальными для управления с временным запаздыванием. Для достижения оптимального эффекта управления вибрационными откликами и управляющей силой при влиянии временной задержки необходимо дополнительно оптимизировать параметры. На основании приведенного выше анализа сделан вывод о том, что полуактивный метод управления с помощью МР-демпфера может эффективно снижать вибрационные реакции конструкции, при этом параметры нуждаются в оптимизации из-за влияния временной задержки.
2.2 Оптимизация параметров
Для достижения оптимальных значений параметров применен метод комплексной оптимизации на основе критерия надежности38. Оптимизация критических параметров проводилась с , 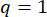
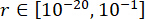 ,
,  ,
, 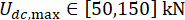 , и перестраиваемыми временами силы демпфера MR s = 8. Для реализации оптимизации был использован набор инструментов GA в MATLAB.
, и перестраиваемыми временами силы демпфера MR s = 8. Для реализации оптимизации был использован набор инструментов GA в MATLAB.
Результаты оптимизации параметров равны  ,
, 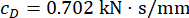 , а
, а  для временной задержки
для временной задержки 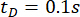 . На рисунке 8 показана среднеквадратичная временная история перемещения, скорости, ускорения и управляющей силы для неуправляемых (Unc) структур, управляемых методом TDC-SAC-PSO и SOSC-PSO. Метод SOSC-PSO обозначает полуактивный метод управления с компенсацией временной задержки и оптимизированными значениями критических параметров.
. На рисунке 8 показана среднеквадратичная временная история перемещения, скорости, ускорения и управляющей силы для неуправляемых (Unc) структур, управляемых методом TDC-SAC-PSO и SOSC-PSO. Метод SOSC-PSO обозначает полуактивный метод управления с компенсацией временной задержки и оптимизированными значениями критических параметров.
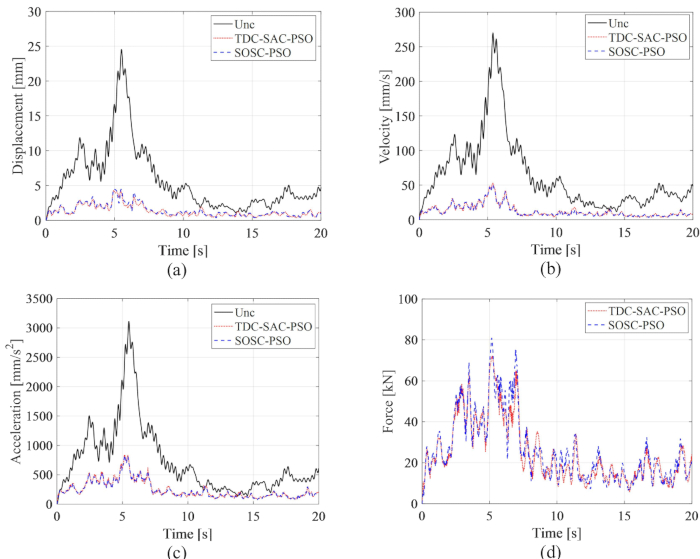
Рисунок 8: Среднеквадратичные временные данные о перемещении, скорости, ускорении и управляющей силе для неуправляемых конструкций и конструкций методом TDC-SAC-PSO и SOSC-PSO. а) перемещение; b) скорость; с) ускорение; (D) Управляющая сила. Сокращения: Unc = неконтролируемый; TDC-SAC-PSO = система с задержкой по времени с контролируемой компенсацией; SOSC-PSO = Стохастический метод оптимального полуактивного управления с компенсацией временной задержки. Пожалуйста, нажмите здесь, чтобы просмотреть увеличенную версию этой цифры.
Из рисунка 8 видно, что контрольные эффекты методов TDC-SAC-PSO и SOSC-PSO показали незначительную разницу. Максимальные среднеквадратичные значения скорости и ускорения перемещения для первого метода составили 81,60%, 81,21%, 73,62% для неуправляемой конструкции и 82,59%, 80,40%, 73,04% для второго метода. Для всестороннего анализа вероятностных характеристик реакций для обоих методов управления на рисунке 9 показаны PDF-файлы перемещения, скорости и ускорения для неконтролируемых структур, управляемых методом TDC-SAC-PSO и SOSC-PSO. Оба метода управления имели почти одинаковые PDF-файлы смещения и скорости в типичное время. PDF-коэффициенты ускорения метода SOSC-PSO были уже, чем у метода TDC-SAC-PSO, что означает, что неопределенность ускорения достигала лучшего эффекта управления при использовании первого метода.
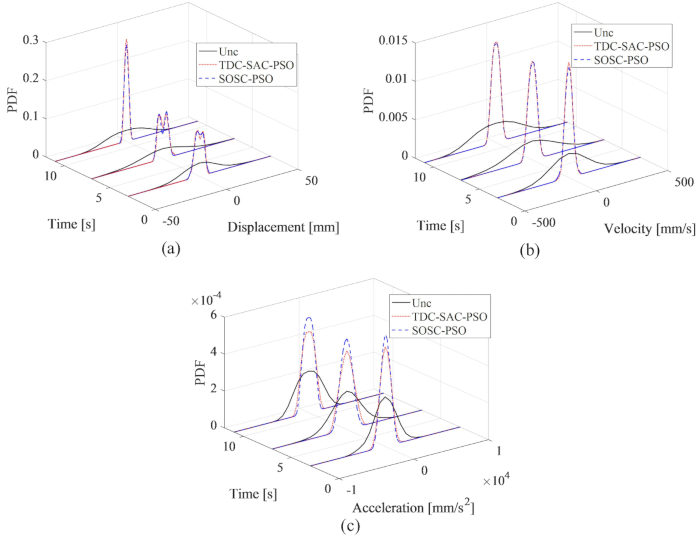
Рисунок 9: Сравнение перемещения, скорости и ускорения в формате PDF для различных управляемых конструкций. а) перемещение; b) скорость; (c) Ускорение. Сокращения: PDF-файлы = функции плотности вероятности; Unc = неконтролируемый; TDC-SAC-PSO = система с задержкой по времени с контролируемой компенсацией; SOSC-PSO = Стохастический метод оптимального полуактивного управления с компенсацией временной задержки. Пожалуйста, нажмите здесь, чтобы просмотреть увеличенную версию этой цифры.
Надежность перемещения, скорости, ускорения и управляющей силы для неуправляемых и управляемых по методу TDC-SAC-PSO- и SOSC-PSO конструкций приведена в таблице 2. Оба метода контроля позволили добиться значительного повышения надежности по сравнению с неуправляемой конструкцией. Достоверность смещения показала незначительную разницу между методами TDC-SAC-PSO и SOSC-PSO. При этом надежность разгона, самая низкая надежность управляемой конструкции, достигала заметного увеличения. Это означает, что метод SOSC-PSO позволяет достичь оптимального эффекта управления балансом.
| Метод управления | Смещение | Скорость | Ускорение | Сила управления | Минимальное значение |
| Unc | 0.0954 | 0.1058 | 0.1111 | -- | 0.1111 |
| TDC-SAC-PSO | 0.9565 | 0.8107 | 0.7654 | 0.9845 | 0.7654 |
| СОСК-ПСО | 0.953 | 0.8704 | 0.8934 | 0.9586 | 0.8934 |
Таблица 2: Надежность конструкций, контролируемых различными методами. Сокращения: Unc = неконтролируемый; TDC-SAC-PSO = система с задержкой по времени с контролируемой компенсацией; SOSC-PSO = Стохастический метод оптимального полуактивного управления с компенсацией временной задержки.
Проанализирована эффективность предложенного метода SOSC-PSO с временным запаздыванием 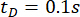 . Для дальнейшей верификации предложенного метода для различных временных задержек в таблице 3 приведены оптимальные значения параметров и соответствующая надежность для диапазона
. Для дальнейшей верификации предложенного метода для различных временных задержек в таблице 3 приведены оптимальные значения параметров и соответствующая надежность для диапазона 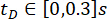 временных задержек.
временных задержек.
| тД(ы) | lg(r*) | CD(кН·с/мм) | Udc, max (кН) | Смещение | Скорость | Ускорение | Сила управления |
| 0 | -2.524 | 1.44 | 116.163 | 0.9997 | 0.9998 | 0.9752 | 1 |
| 0.02 | -4.413 | 0.414 | 144.066 | 0.9989 | 0.9988 | 0.872 | 0.9011 |
| 0.04 | -4.416 | 0.25 | 141.759 | 0.9998 | 0.9846 | 0.8881 | 0.9135 |
| 0.06 | -3.226 | 0.203 | 145.613 | 0.993 | 0.9318 | 0.8756 | 0.9556 |
| 0.08 | -5.207 | 0.345 | 133.692 | 0.9646 | 0.8998 | 0.8998 | 0.953 |
| 0.1 | -4.669 | 0.702 | 130.739 | 0.9531 | 0.8704 | 0.8934 | 0.9586 |
| 0.12 | -4.895 | 0.833 | 69.72 | 0.9526 | 0.863 | 0.888 | 0.9686 |
| 0.14 | -4.231 | 0.921 | 75.221 | 0.9531 | 0.8681 | 0.8697 | 0.9671 |
| 0.16 | -5.594 | 0.662 | 138.922 | 0.9529 | 0.8461 | 0.8262 | 0.931 |
| 0.18 | -4.262 | 0.882 | 76.335 | 0.9516 | 0.7873 | 0.7614 | 0.9618 |
| 0.2 | -3.926 | 0.783 | 67.951 | 0.904 | 0.7277 | 0.7116 | 0.9653 |
| 0.22 | -5.965 | 1.071 | 52.554 | 0.8377 | 0.6411 | 0.6205 | 0.965 |
| 0.24 | -4.481 | 1.216 | 128.148 | 0.7567 | 0.474 | 0.474 | 0.9687 |
| 0.26 | -3.53 | 0.672 | 53.706 | 0.53 | 0.4096 | 0.4158 | 0.9921 |
| 0.28 | -4.433 | 0.638 | 64.225 | 0.3547 | 0.3745 | 0.3464 | 0.9928 |
| 0.3 | -3.536 | 0.459 | 57.705 | 0.2735 | 0.316 | 0.2736 | 0.9929 |
| Unc | -- | -- | -- | 0.0954 | 0.1058 | 0.1111 | -- |
Таблица 3: Оптимальные значения параметров и соответствующие им значения надежности для различных временных задержек. 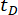 обозначает временную задержку;
обозначает временную задержку;  обозначает оптимальную логарифмическую величину r,r обозначает коэффициент управляющей весовой матрицы;
обозначает оптимальную логарифмическую величину r,r обозначает коэффициент управляющей весовой матрицы; 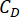 обозначает коэффициент вязкостного демпфера MR;
обозначает коэффициент вязкостного демпфера MR; 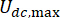 обозначают максимальные и минимальные кулоновские силы демпфера MR.
обозначают максимальные и минимальные кулоновские силы демпфера MR.
Можно заметить, что надежность перемещения, скорости и ускорения была улучшена по сравнению с неконтролируемой конструкцией, даже при наличии временной задержки, что демонстрирует устойчивость предложенного метода к таким задержкам. Тем не менее, надежность структурных реакций при использовании предложенного метода контроля снижалась по мере увеличения временной задержки, что указывает на то, что, хотя влияние временной задержки на эффективность управления можно смягчить, оно не может быть полностью устранено. Примечательно, что надежность силы управления оставалась выше 90% при различных временных задержках.
3. Числовой пример
Для верификации предложенного метода SOSC-PSO в структуре MDOF была проанализирована шестиэтажная конструкция с двумя заслонками MR, установленными на первом и третьем этажах, как показано на рисунке 10. Были применены сейсмические образцы, полученные с помощью стохастической сейсмической модели в разделе 2, а пороги надежности смещения, скорости, ускорения и управляющей силы составили 20 мм, 200 мм/с, 3 000 мм/с2 и 200 кН. Уравнения. (27) были использованы в качестве матрицы взвешивания с 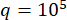 . Набор инструментов GA MATLAB был использован для оптимизации
. Набор инструментов GA MATLAB был использован для оптимизации 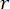 ,, и
,, и  , с оптимальными диапазонами
, с оптимальными диапазонами 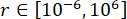 ,
,  , и
, и 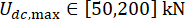
 .
.
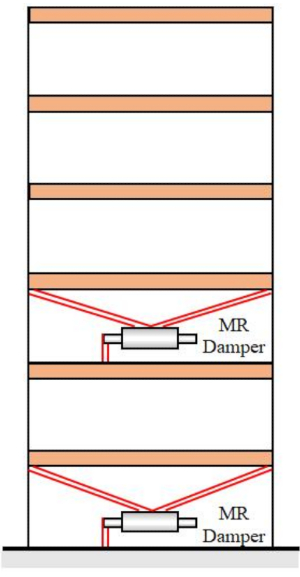
Рисунок 10: Шестиэтажная конструкция с двумя заслонками MR. Сокращение: MR = магнитореологический. Пожалуйста, нажмите здесь, чтобы просмотреть увеличенную версию этой цифры.
3.1 Анализ влияния временной задержки
Для анализа влияния временной задержки на эффективность управления демпфером MR в структуре MDOF на рисунке 11 показаны максимальные среднеквадратичные значения смещения (межэтажного перемещения), скорости (межэтажной скорости) и ускорения (ускорения этажа) вместе с временной задержкой для метода TDC-SAC-PSO. Параметры были ,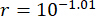
 , и
, и  для заслонки MR на 1-м этаже,
для заслонки MR на 1-м этаже,  и
и  для заслонки MR на 3-м этаже, которые представляют собой оптимизированные результаты без задержки по времени. Максимальные среднеквадратичные значения реакций управляемой структуры демонстрировали флуктуации периода вместе с временной задержкой. Максимальные СКО смещения и скорости были на 1 этаже, максимальное ускорение на 6 этаже. Кроме того, все максимальные MRS откликов с любым временным запаздыванием были больше, чем значения без временного запаздывания, а это означает, что временное запаздывание снижает управляющий эффект MR-демпфера.
для заслонки MR на 3-м этаже, которые представляют собой оптимизированные результаты без задержки по времени. Максимальные среднеквадратичные значения реакций управляемой структуры демонстрировали флуктуации периода вместе с временной задержкой. Максимальные СКО смещения и скорости были на 1 этаже, максимальное ускорение на 6 этаже. Кроме того, все максимальные MRS откликов с любым временным запаздыванием были больше, чем значения без временного запаздывания, а это означает, что временное запаздывание снижает управляющий эффект MR-демпфера.
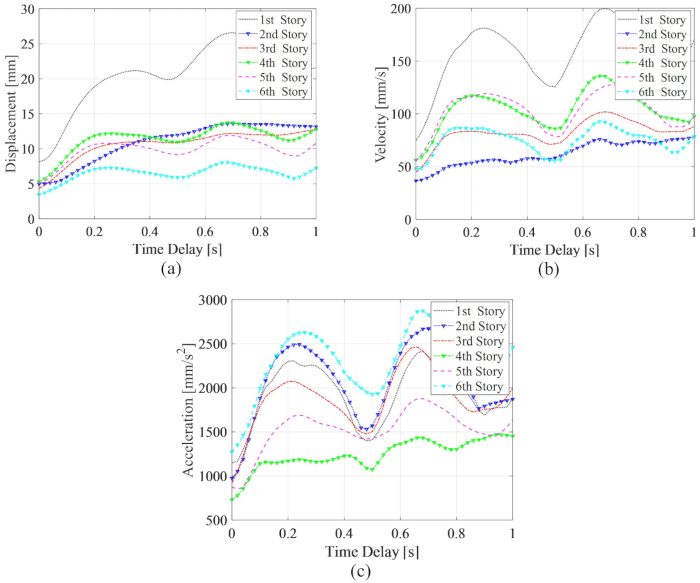
Рисунок 11: Максимальное среднеквадратичное значение откликов вместе с временной задержкой для структуры, управляемой методом TDC-SAC-PSO. а) перемещение; b) скорость; (c) Ускорение. Сокращения: RMS = среднеквадратичный; TDC-SAC-PSO = система с задержкой по времени с контролируемой компенсацией. Пожалуйста, нажмите здесь, чтобы просмотреть увеличенную версию этой цифры.
Надежность перемещения, скорости и ускорения вместе с временной задержкой показана на рисунке 12. Надежность скорости и ускорения показывает флуктуацию периода вместе с временной задержкой, в то время как надежность смещения резко снижается вместе с временной задержкой; Все значения надежности при любой временной задержке были меньше, чем без временной задержки. Таким образом, метод компенсации временной задержки необходим для снижения влияния временной задержки на надежность конструкции, управляемой заслонкой MR.
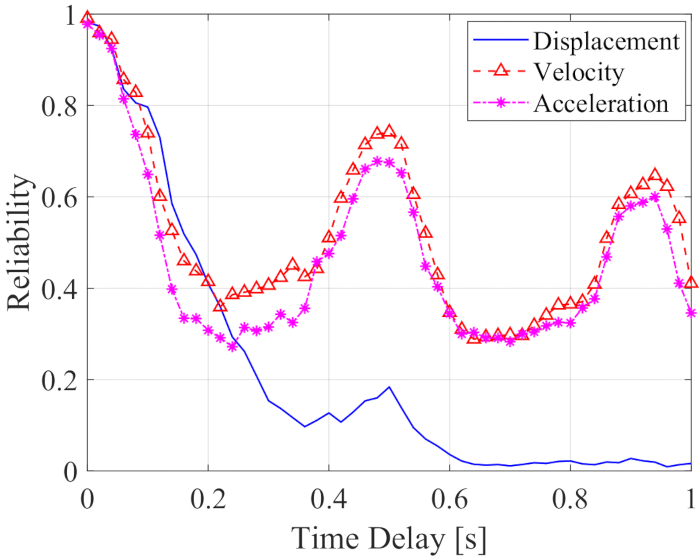
Рисунок 12: Надежность управляемых реакций конструкции наряду с временной задержкой. Пожалуйста, нажмите здесь, чтобы просмотреть увеличенную версию этой цифры.
3.2 Управляющий эффект компенсации задержки по времени
На основе предложенного метода TDC-SAC-PSO была проанализирована структура 6-DOF с двумя MR-демпферами. На рисунке 13 показана среднеквадратичная временная история смещения и ускорения на 1-м и 3-м этажах для неконтролируемых (Unc), управляемых методом TDC-SAC-PSO и управляемых методом TDN-SAC-PSO. Временная задержка была равна 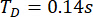 , а отношение
, а отношение 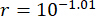 матрицы взвешивания ; параметры демпфера MR были , для
матрицы взвешивания ; параметры демпфера MR были , для 
 1-го этажа
1-го этажа  и
и  для 3-го этажа.
для 3-го этажа.

Рисунок 13: Среднеквадратичные временные истории смещения и ускорения на 1-м и 3-м этажах для конструкций, контролируемых различными методами. (А) Смещение на 1-м этаже; (B) Смещение на 3-м этаже; (C) Ускорение на 1-м этаже; (D) Ускорение на 3-м этаже. Сокращения: RMS = среднеквадратичный; Unc = неконтролируемый; TDC-SAC-PSO = система с задержкой по времени с контролируемой компенсацией; TDN -SAC-PSO = система с задержкой по времени с управлением без компенсации. Пожалуйста, нажмите здесь, чтобы просмотреть увеличенную версию этой цифры.
Максимальные СКО смещения на 1 и 3 этажах снижены на 35,42% и 30,44% методом TDN-SAC-PSO, где временная задержка не компенсировалась. В то время как с компенсацией максимальные СКО смещения на 1 и 3 этажах снижены на 49,33% и 53,39% соответственно. Без учета компенсации максимальное СКО ускорения на 1 и 3 этажах увеличилось на 16,22% и 2,88%, но снизилось на 25,77% и 36,00% соответственно с компенсацией. Таким образом, компенсация временной задержки в методе управления демпфером MR необходима для снижения реакции конструкции, особенно на ускорение.
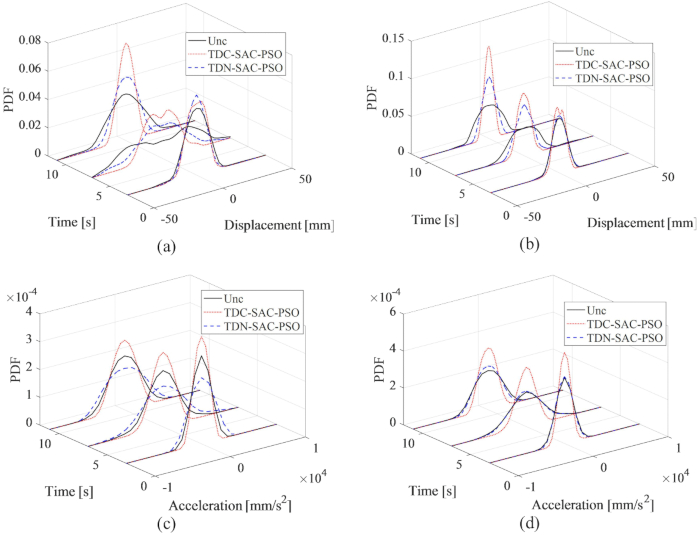
Рисунок 14: PDF-файлы смещения и ускорения на 1-м и 3-м этажах для различных методов управления. (А) Смещение на 1-м этаже; (B) Смещение на 3-м этаже; (C) Ускорение на 1-м этаже; (D) Ускорение на 3-м этаже. Сокращения: PDF-файлы = функции плотности вероятности; Unc = неконтролируемый; TDC-SAC-PSO = система с задержкой по времени с контролируемой компенсацией; TDN -SAC-PSO = система с задержкой по времени с управлением без компенсации. Пожалуйста, нажмите здесь, чтобы просмотреть увеличенную версию этой цифры.
На рисунке 14 показаны PDF-файлы смещения и ускорения на 1-м и 3-м этажах, показывающие различные управляющие эффекты методов TDC-SAC-PSO и TDN-SAC-PSO по сравнению с неконтролируемой структурой. Без компенсации ДСП смещения на 1-м и 3-м этажах были еще уже, чем у неконтролируемой конструкции. Кроме того, с компенсацией временной задержки, PDF-файлы смещения стали уже, чем у структуры с управлением методом TDN-SAC-PSO. В отличие от смещения, без компенсации, ДПС ускорения на 1-м этаже по методу TDN-SAC-PSO были шире, чем у неуправляемой конструкции. Однако, с учетом компенсации, PDF-файлы ускорения как на 1-м, так и на 3-м этажах оказались уже, чем у неуправляемой конструкции. Таким образом, проверяется необходимость компенсации временного запаздывания для повышения достоверности реакций конструкции, особенно на ускорение.
| Метод управления | Смещение | Скорость | Ускорение | Управляющее усилие на1-м этаже | Управляющее усилие на3-м этаже |
| Unc | 0.0114 | 0.5822 | 0.6372 | -- | -- |
| ТДН-САК-ПСО | 0.5851 | 0.5258 | 0.398 | 1 | 1 |
| TDC-SAC-PSO | 0.806 | 0.8674 | 0.8037 | 1 | 1 |
Таблица 4: Надежность конструкций, контролируемых различными методами. Сокращения: Unc = неконтролируемый; TDC-SAC-PSO = система с задержкой по времени с контролируемой компенсацией; TDN -SAC-PSO = система с задержкой по времени с управлением без компенсации.
Значения надежности перемещения, скорости, ускорения и управляющей силы при управлении структурными системами различными методами приведены в таблице 4. Значения надежности реакций конструкции рассчитывали с использованием метода эквивалентных экстремальных значений25. При управлении методом TDN-SAC-PSO надежность перемещения увеличивалась по сравнению с неуправляемой конструкцией, при этом надежность скорости и ускорения снижалась. При компенсации временной задержки в методе TDC-SAC-PSO достоверность перемещения, скорости и ускорения значительно возрастала. Кроме того, в достаточной степени поддерживаются значения надежности регулирующего усилия для обоих методов TDN-SAC-PSO и TDN-SAC-PSO. Таким образом, предложенный метод управления с компенсацией временного запаздывания позволяет достичь благоприятного управляющего эффекта для управляемой МР демпферной конструкции.
3.3 Оптимизация параметров
Для достижения оптимального эффекта управления параметры предложенного метода управления были оптимизированы на основе критерия надежности. С задержкой 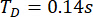 по времени оптимальный результат был
по времени оптимальный результат был  ;
; 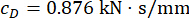 , и
, и 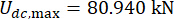 для 1-го этажа MR демпфера;
для 1-го этажа MR демпфера; 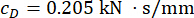 и
и  для 3-го MR демпфера.
для 3-го MR демпфера.
Среднеквадратичные временные истории смещения и ускорения на 1-м и 3-м этажах показаны на рисунке 15 , где сравниваются управляющие эффекты методов TDC-SAC-PSO и SOSC-PSO и неуправляемой конструкции. При управлении амортизаторами MR, с компенсацией задержки по времени или без нее, среднеквадратичное значение смещения и ускорения значительно снизилось. При использовании метода SOSC-PSO максимальная среднеквадратичность смещения на 1 и 3 этажах снизилась на 65,15% и 63,16% относительно неуправляемой конструкции соответственно. По сравнению с методом TDC-SAC-PSO реакция на смещение была дополнительно снижена. Максимальные СКЗ ускорения на 1 и 3 этажах снижены на 23,39% и на 35,60% для метода SOSC-PSO. Наблюдалась незначительная разница в управляющем эффекте ускорения для методов SOSC-PSO и TDC-SAC-PSO, что указывает на то, что управляющий эффект компенсации временной задержки был различным для смещения и ускорения.
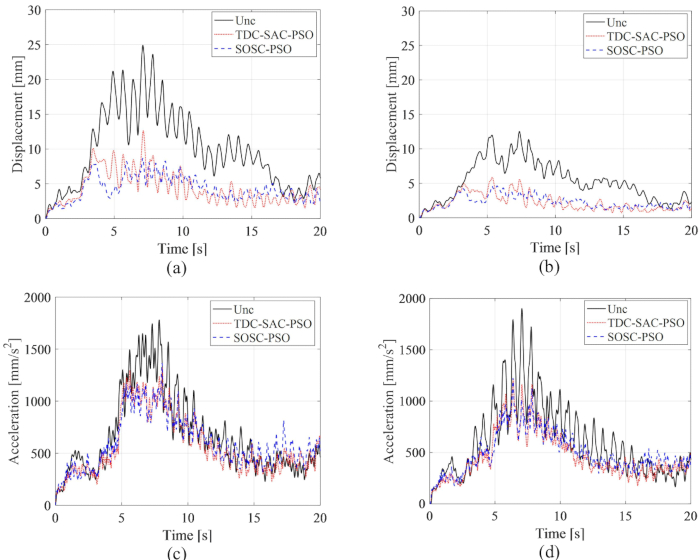
Рисунок 15: Среднеквадратичные временные истории смещения и ускорения на 1-м и 3-м этажах для различных методов управления. (А) Смещение на 1-м этаже; (B) Смещение на 3-м этаже; (C) Ускорение на 1-м этаже; (D) Ускорение на 3-м этаже. Сокращения: RMS = среднеквадратичный; Unc = неконтролируемый; TDC-SAC-PSO = система с задержкой по времени с контролируемой компенсацией; SOSC-PSO = Стохастический метод оптимального полуактивного управления с компенсацией временной задержки. Пожалуйста, нажмите здесь, чтобы просмотреть увеличенную версию этой цифры.
PDF-файлы смещения и ускорения на 1-м и 3-м этажах представлены на рисунке 16; Методы TDC-SAC-PSO и SOSC-PSO сузили PDF-смещения и ускорения по сравнению с неуправляемой структурой. Кроме того, PDF-файлы смещения и ускорения для метода SOSC-PSO были дополнительно сужены по сравнению с структурой, управляемой методом TDC-SAC-PSO. Таким образом, при оптимизации параметров предложенный метод управления с компенсацией временной задержки достиг лучшего эффекта управления, чем без оптимизации.
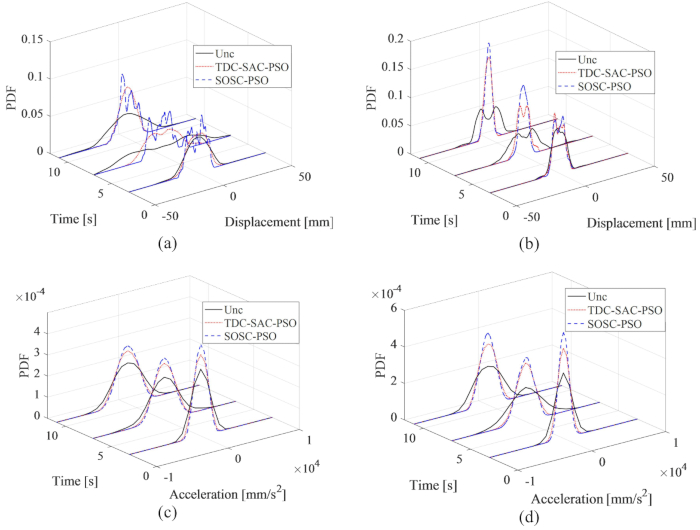
Рисунок 16: PDF-файлы смещения и ускорения на 1-м и 3-м этажах для различных методов управления. (А) Смещение на 1-м этаже; (B) Смещение на 3-м этаже; (C) Ускорение на 1-м этаже; (D) Ускорение на 3-м этаже. Сокращения: PDF-файлы = функции плотности вероятности; Unc = неконтролируемый; TDC-SAC-PSO = система с задержкой по времени с контролируемой компенсацией; SOSC-PSO = Стохастический метод оптимального полуактивного управления с компенсацией временной задержки Нажмите здесь, чтобы просмотреть увеличенную версию этого рисунка.
Значения надежности перемещения, скорости, ускорения и силы управления приведены в таблице 5. Значения надежности для метода SOSC-PSO были выше, чем для метода TDC-SAC-PSO. Между тем, сила управления еще сохраняла достаточную надежность. Таким образом, оптимизация параметров необходима для достижения наилучшего эффекта управления для метода управления на основе демпфера MR.
| Метод управления | Смещение | Скорость | Ускорение | Управляющее усилие на1-м этаже | Управляющее усилие на3-м этаже |
| Unc | 0.0114 | 0.5822 | 0.6372 | -- | -- |
| TDC-SAC-PSO | 0.806 | 0.8674 | 0.8037 | 1 | 1 |
| СОСК-ПСО | 0.9544 | 0.9314 | 0.8788 | 1 | 1 |
Таблица 5: Надежность конструкций, контролируемых различными методами. Сокращения: Unc = неконтролируемый; TDC-SAC-PSO = система с задержкой по времени с контролируемой компенсацией; SOSC-PSO = Стохастический метод оптимального полуактивного управления с компенсацией временной задержки.
Результаты
С целью изучения влияния временной задержки на эффективность управления методом на основе МР-демпфера в данной работе предложен полуактивный метод управления с компенсацией временной задержки. В предложенном методе критические параметры оптимизированы на основе к...
Обсуждение
С введением теории физического стохастического оптимального управления (PSO) в данной работе предложен метод стохастического оптимального полуактивного управления с компенсацией временной задержки (SOSC-PSO), который предназначен для поддержания надежности конструкци?...
Раскрытие информации
У всех авторов нет конфликта интересов, о котором можно было бы заявить.
Благодарности
Авторы выражают благодарность за поддержку Фонду естественных наук провинции Хэбэй (грант No E2023210007).
Материалы
| Name | Company | Catalog Number | Comments |
| MATLAB | MathWorks | 2016 | Using for the calculation of the proposed method |
Ссылки
- Yao, J. T. P. Concept of structural control. J Struct Div. 98 (7), 1567-1574 (1972).
- Liu, J., Silva, C. E., Dyke, S. J., Wu, Y., Liu, H. Using real-time hybrid simulation for active mass damper experimentation and validation. Mech Mach Theory. 191, 105474 (2024).
- Pan, H., Li, C., Cao, L. Bidirectional pendulum-type tuned tendem mass dampers-inerters for integrated control of alongwind and crosswind responses in super-tall buildings. J Build Eng. 100, 111676 (2025).
- Housner, G. W. et al. Structural control: past, present, and future. J Eng Mech. 123 (9), 897-971 (1997).
- Rahman, M., Ong, Z. C., Chong, W. T., Julai, S. Smart Semi-active PID-ACO control strategy for tower vibration reduction in Wind Turbines with MR damper. Earthq Eng Eng Vib. 18 (4), 887-902 (2019).
- Morales-Beltran, M., Paul, J. Active and semi-active strategies to control building structures under large earthquake motion. J Earthquake Eng. 19 (7), 1086-1111 (2015).
- Shu, Z., You, R., Xie, Y. Viscoelastic dampers for vibration control of building structures: A state-of-art review. J Earthq Eng. 28 (12), 3558-3585 (2024).
- Soong, T. T. Active structural control: Theory and practice. Longman Scientific & Technical. New York (1990).
- Wan, H. P., Ma, Q., Dong, G. S., Luo, Y., Ni, Y. Q. Data-driven model reduction approach for active vibration control of cable-strut structures. Eng Struct. 302, 117434 (2024).
- Cao, L., Li, X., Huang, Y., Li, C., Pan, H. High robust eddy current tuned tandem mass dampers-inerters for structures under the ground acceleration. Soil Dyn Earthq Eng. 188, 109040 (2025).
- Chha, H., Peng, Y. Adaptive semiactive control of structure with magnetorheological dampers using wavelet packet transform. Adv Struct Eng. 27 (9), 1509-1527 (2024).
- Zeng, X., Peng, Y., Chen, J. Serviceability-based damping optimization of randomly wind-excited high-rise buildings. Struct Des Tall Spec. 26 (11), e1371 (2017).
- Li, C., Chang, K., Cao, L., Huang, Y. Performance of a nonlinear hybrid base isolation system under the ground motions. Soil Dyn Earthq Eng. 143, 106589 (2021).
- Cao, L., Li, C. A high performance hybrid passive base-isolated system. Struct Control Health Monitoring. 29 (3), e2887 (2022).
- Zareie, S., Issa, A. S., Seethaler, R., Zabihollah, A., Ahmad, R. A novel SMA-magnetorheological hybrid bracing system for seismic control. Eng Struct. 244, 112709 (2021).
- Chu, S. Y., Soong, T. T., Reinhorn, A. M. Active, hybrid and semi-active structural control. John Wiley & Sons, New York (2005).
- Danielian, S. A., Jabbari, F., Zareian, F. Effects and distribution of semi-active resettable springs on the seismic response of asymmetric structures. Earthq Eng Struct D. 52 (10). 2966-2982 (2023).
- Shuang, Z., Wenliuhan, H. S., Liu, Y. H., Inoue, N., Zhai, Z. P. Seismic response control for bridge piers with semi-active MR damper based on displacement feedback. J Earthq Eng. 28 (3). 849-865 (2024).
- Wang, Y., Dyke, S. Modal-based LQG for smart base isolation system design in seismic response control. Struct Control Health Monitoring. 20 (5), 753-768 (2013).
- Desai, R. M. et al. Performance evaluation of a single sensor control scheme using a twin-tube MR damper based semi-active suspension. J Vib Eng Technol. 9, 1193-1210 (2021).
- Abdi, M. S., Nekooei, M. Jafari, M. A. Seismic control of multi-degrees-of-freedom structures by vertical mass isolation method using MR dampers. Earthq Eng Eng Vib. 23 (2), 503-510 (2024).
- Bhowmik, K., Debnath, N. Semi-active vibration control of soft-storey building with magnetorheological damper under seismic excitation. J Vib Eng Technol. 12 (4), 6943-6961 (2024).
- Yang, J. N., Akbarpour, A., Askar, G. Effect of time delay on control of seismic-excited buildings. J Struct Eng. 116 (10), 2801-2814 (1990).
- Temimi, H., Ben-Romdhane, M., El-Borgi, S., Cha, Y. Time-delay effects on controlled seismically excited linear and nonlinear structures. Int J Struct Stab Dyn. 16 (7), 1550031 (2016).
- Peng, J., Wang, L., Zhao, Y., Lenci, S. Time-delay dynamics of the MR damper-cable system with one-to-one internal resonances. Nonlinear Dynamics. 105 (2), 1343-1356 (2021).
- Cha, Y. J., Agrawal, A. K., Dyke, S. J. Time delay effects on large-scale MR damper based semi-active control strategies. Smart Mater Struct. 22 (1), 015011 (2013).
- Yu, Y. et al. Experimental study of wireless structural vibration control considering different time delays. Smart Mater Struct. 24, 045005 (2015).
- Ahmadizadeh, M., Mosqueda, G., Reinhorn, A. M. Compensation of actuator delay and dynamics for real-time hybrid structural simulation. Earthq Eng Struct Dyn. 37 (1), 21-42 (2008).
- Bathaei, A., Zahrai, S. M. Compensating time delay in semi-active control of a SDOF structure with MR damper using predictive control. Struc Eng Mech. 82 (4), 445-458 (2022).
- Dyke, S. J., Spencer, Jr, B. F., Sain, M. K., Carlson, J. D. Modeling and control of magnetorheological dampers for seismic response reduction. Smart Mater Struct. 5 (5), 565-575 (1996).
- Ying, Z. G., Ni, Y. Q., Ko, J. M. A semi-active stochastic optimal control strategy for nonlinear structural systems with MR dampers. Smart Struct Syst. 5 (1), 69-79 (2009).
- Rosol, M., Martynowicz, P. Implementation of the LQG controller for a wind turbine tower-nacelle model with a MR tuned vibration absorber. J Theor App Mech-Pol. 54 (4), 1109-1123 (2016).
- Lyu, M. Z., Feng, D. C., Chen, J. B., Li, J. A decoupled approach for determination of the joint probability density function of a high-dimensional nonlinear stochastic dynamical system via the probability density evolution method. Comput Method Appl M. 418 (A), 116443 (2024).
- Chha, H., Peng, Y. Multiscale stochastic optimal control of hysteretic structures based on wavelet transform and probability density evolution method. Eng Computation. 41 (4), 865-896 (2024).
- Li, J., Peng, Y. B., Chen, J. B. A physical approach to structural stochastic optimal controls. Probabilist Eng Mech. 25 (1), 127-141 (2010).
- Peng, Y. B., Yang, J. G., Li, J. Seismic risk-based stochastic optimal control of structures using magnetorheological dampers. Nat Hazards Rev. 18 (1), B4016001 (2017).
- Dong, X. M., Yu, M., Li, Z., Liao, C., Chen, W. Neural network compensation of semi-active Control for magneto-rheological suspension with time delay uncertainty. Smart Mater Struct. 18 (1), 015014 (2008).
- Peng, Y. B., Zhang, Z. Optimal MR damper-based semiactive control scheme for strengthening seismic capacity and structural reliability. J Eng Mech. 146 (6), 04020045 (2020).
- Luo, M. X., Gao, M. Cai, G. Delayed full-state feedback control of airfoil flutter using sliding mode control method. J Fluid Struct. 61, 262-273 (2016).
- Xu, J., Chung, K. W., Chan, C. L. An efficient method for studying weak resonant double Hopf bifurcation in nonlinear systems with delayed feedbacks. Siam J Appl Dyn Syst. 6 (1), 29-60 (2007).
- Yang, J. S., Jensen, H., Chen, J. B. Structural optimization under dynamic reliability constraints utilizing probability density evolution method and metamodels in augmented input space. Struct Multidiscip Optimization. 65, 107 (2022).
- Li, J., Chen, J. B. Stochastic dynamics of structures. John Wiley & Sons, Singapore (2009).
- Peng, Y. B., Li, J. Stochastic optimal control of structures. Springer (2019).
- Dowrick, C. Beyond depression: A new approach to understanding and management. Oxford University Press (2009).
- Wang, D., Li, J. Physical random function model of ground motions for engineering purposes. Sci China Technol Sci. 54 (1), 175-182 (2011).
- Wang, D., Li, J. A random physical model of seismic ground motion field on local engineering site. Sci China Technol Sci. 55 (7), 2057-2065 (2012).
- Chen, J. B., Li, J. Strategy for selecting representative points via tangent spheres in the probability density evolution method. Int J Numer Meth Eng. 74 (13), 1988-2014 (2008).
Перепечатки и разрешения
Запросить разрешение на использование текста или рисунков этого JoVE статьи
Запросить разрешениеThis article has been published
Video Coming Soon
Авторские права © 2025 MyJoVE Corporation. Все права защищены