需要订阅 JoVE 才能查看此. 登录或开始免费试用。
Research Article
考虑时滞的基于磁流变阻尼器的结构随机半主动控制方法
摘要
该文提出了一种具有时滞补偿的随机最优半主动控制方法(SOSC-PSO),旨在保持MR阻尼器控制结构的可靠性。
摘要
在半主动控制系统中使用磁流变 (MR) 阻尼器面临一个关键挑战:反馈过程引起的时间延迟,这会降低土木工程结构在随机激励下的可靠性。该文提出了一种具有时滞补偿的随机最优半主动控制方法(SOSC-PSO),利用物理随机最优控制理论(PSO)来解决这一问题并保持结构可靠性。所提出的方法将半主动控制力作为当前和先前状态的函数推导出来,补偿控制过程中的时间延迟。为了优化控制效果,根据系统的可靠性标准调整关键参数。在随机地震激励下对单自由度和多自由度结构的验证分析表明,时间延迟会显著损害 MR 阻尼器的性能。然而,具有时滞补偿的 SOSC-PSO 方法显著提高了控制效果,并且通过优化参数,它增强了结构控制系统的可靠性,超越了没有参数优化的方法。
引言
在面对灾难性事件(如地震和极端大风)时,提高工程结构的性能仍然是土木工程界的主要关注点。结构控制是一种减少振动的有效技术,已被证明可以提高此类结构的安全性和功能性 1,2,3。在过去的几十年里,为此目的开发了各种先进的方法和技术。根据用于驱动控制设备的能量类型,这些方法大致可分为四类:主动、半主动、被动和混合控制系统 4,5,6,7。
在主动控制中,所需的控制力直接通过控制装置施加,这需要大量的能量 8,9,10。另一方面,半主动控制涉及根据控制信号调整控制设备的特性(例如阻尼或刚度),与主动系统相比,需要的能量要少得多11。相比之下,被动控制依赖于能量耗散,无需任何外部能量输入到系统中 12,13,14。混合动力系统结合了主动/半主动和被动控制策略的特点,以实现更有效的性能15。在这些方法中,半主动控制被认为特别有前途,因为它在低能耗和高效率之间取得了平衡 16,17,18。磁流变 (MR) 阻尼器具有卓越的动态阻尼特性,被认为是最有效的半主动控制装置之一 19,20,21,22。
然而,使用 MR 阻尼器的半主动控制系统出现了一个挑战,因为反馈逻辑不可避免地会引入时间延迟。这些延迟通常是由几个因素引起的 23,24,25,包括:(i) 传感器数据的采集和处理,(ii) 控制器计算所需的控制力 26,(iii) 通过传感器向 MR 阻尼器传输信号27,以及 (iv) MR 阻尼器本身产生的实际力28.这种时间延迟会导致产生的控制力与结构预期的力之间存在差异,从而严重影响控制效果29。遗憾的是,大多数现有的 MR 阻尼器控制算法都没有考虑这些延迟。
此外,由于灾难性事件的固有随机性,任何有效的半主动控制算法都必须能够在随机激励下保持性能。线性二次高斯 (LQG) 控制方法是一种经典的随机优化技术,已被探索用于减轻配备 MR 阻尼器的结构中的振动。例如,Dyke 等人提出了一种 LQG 裁剪最优控制策略,用于使用加速度反馈30 改善装有 MR 阻尼器的结构的地震响应。Ying 等人介绍了一种具有 MR 阻尼器的非线性结构的非剪辑半主动随机最优控制策略,结合了随机平均和动态规划技术31。其他研究应用基于模态的 LQG 控制来提高基础隔振建筑物的抗震性能19,并分析了其对风力涡轮机塔架减振的有效性32。然而,假设高斯白噪声的经典 LQG 方法不太适合对地震或强风等真实世界激励的非平稳、非高斯性质进行建模。为了解决这个问题,已经开发了基于物理的随机最优 (PSO) 控制的概念33,34,它克服了传统 LQG 方法的局限性,并为处理各种随机激发提供了更准确的框架35。研究表明,基于 PSO 的半主动随机最优控制显著改善了受随机地震力作用的线性和非线性结构的减振效果36。
因此,迫切需要一种强大的半主动控制方法来补偿时间延迟,从而提高 MR 阻尼器控制结构的可靠性25,37。此外,为了确保在随机激励下的最佳控制性能,必须使用基于可靠性的方法优化所提出的控制方法的关键参数。因此,该文提出了一种具有时间延迟补偿的随机最优半主动控制方法(SOSC-PSO),以提高具有MR阻尼器的结构的可靠性。
研究方案
1. 随机最优半主动控制方法
由于 MR 阻尼器的控制效果受到不可避免的时间延迟的显着影响,因此开发了一种带有时间延迟补偿算法的半主动控制方法,以提高受控结构的性能。此外,外部激励固有的随机性导致了动态响应的明显不确定性。引入 PSO 控制来优化所提方法的关键参数,以保证结构控制系统的可靠性。
1.1 半主动控制的补偿算法
在不损失通用性的情况下,考虑一个由 MR 阻尼器控制的 n 自由度 (n-DOF) 结构,具有时间延迟,其中受到随机激励的运动方程由下式给出:
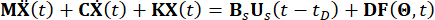 (1)
(1)
其中  分别表示结构的质量、阻尼和刚度矩阵 n x n;n 表示受控结构的自由度数。结构体的位移、速度和加速度矢量分别用
分别表示结构的质量、阻尼和刚度矩阵 n x n;n 表示受控结构的自由度数。结构体的位移、速度和加速度矢量分别用 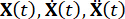 表示。符号上方的小 1 和 2 点代表第一次和第二次导数。 Us (t - tD) 表示 MR 阻尼器时滞控制力的 r 维向量,r 表示阻尼器的数量;t 表示时间;tD 表示时间延迟,假设在本研究中所有阻尼器上都是均匀的,其中
表示。符号上方的小 1 和 2 点代表第一次和第二次导数。 Us (t - tD) 表示 MR 阻尼器时滞控制力的 r 维向量,r 表示阻尼器的数量;t 表示时间;tD 表示时间延迟,假设在本研究中所有阻尼器上都是均匀的,其中 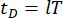 ,这里是整数
,这里是整数 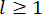 ,
, 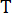 表示采样周期。
表示采样周期。 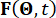 表示随机激励的 p 维向量,并
表示随机激励的 p 维向量,并  表示表征与外部激励相关的随机性的随机参数向量。的尺寸
表示表征与外部激励相关的随机性的随机参数向量。的尺寸  取决于用于外部激励的模型,但与结构的机械自由度无关。 Bs 和 D 是 n x r 和 n x p 矩阵,分别指定了阻尼器和外部激励的位置。在状态空间表示中,方程 (1) 写为:
取决于用于外部激励的模型,但与结构的机械自由度无关。 Bs 和 D 是 n x r 和 n x p 矩阵,分别指定了阻尼器和外部激励的位置。在状态空间表示中,方程 (1) 写为:
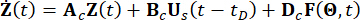 (2)
(2)
其中 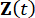 表示 2n 维状态向量;
表示 2n 维状态向量; 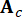 表示 2n x 2n 系统矩阵;
表示 2n x 2n 系统矩阵; 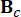 表示 MR 阻尼器的 2n x r 位置矩阵;
表示 MR 阻尼器的 2n x r 位置矩阵; 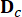 表示外部激励的 2N x P 位置矩阵。这些参数表示为:
表示外部激励的 2N x P 位置矩阵。这些参数表示为:
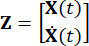 、
、 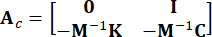 、 、
、 、 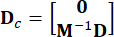
 (3)
(3)
其中 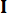 表示具有相同 阶数的
表示具有相同 阶数的 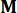 单位矩阵。为了便于计算,连续状态空间方程 (2) 可以用离散形式表示为:
单位矩阵。为了便于计算,连续状态空间方程 (2) 可以用离散形式表示为:
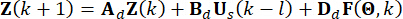 (4)
(4)
其中,时间点 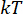 简化为
简化为 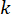 。和
。和  ,
, 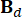 ,
, 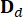 表示 2n x 2n、2n x r 和 2n x p 矩阵,它们表示为:
表示 2n x 2n、2n x r 和 2n x p 矩阵,它们表示为:
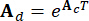 、
、  、
、 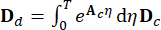 (5)
(5)
其中 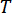 表示采样周期。
表示采样周期。
为了实现与主动控制类似的效果,针对基于 MR 阻尼器的具有时间延迟的控制,提出了一种基于 Hrovat 算法38的简单高效的控制方法:
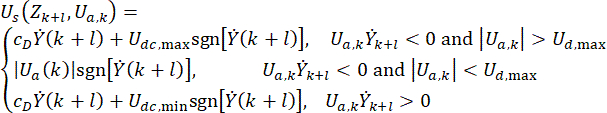 (6)
(6)
其中  ,表示 MR 阻尼器在时间点的
,表示 MR 阻尼器在时间点的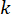 半主动控制力信号;
半主动控制力信号; 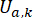 表示具有时间延迟补偿的参考主动控制力;
表示具有时间延迟补偿的参考主动控制力;  表示 MR 阻尼器的最大阻尼力,是可变的;
表示 MR 阻尼器的最大阻尼力,是可变的; 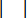 表示绝对值作符号;
表示绝对值作符号; 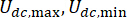 表示 MR 阻尼器的最大和最小库仑力;
表示 MR 阻尼器的最大和最小库仑力;  表示粘性阻尼系数;
表示粘性阻尼系数; 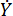 表示 MR 阻尼器中输入的速度,即活塞相对于阻尼器气缸的运动速度。在方程 (6) 中,
表示 MR 阻尼器中输入的速度,即活塞相对于阻尼器气缸的运动速度。在方程 (6) 中,  表示 MR 阻尼器的设计参数。
表示 MR 阻尼器的设计参数。
方程 (6) 显示了 MR 阻尼器的半主动控制力随时间延迟的计算。可以看出,方程 (4) 中时间步 的半主动控制力
的半主动控制力  是根据时间步
是根据时间步 的主动控制力
的主动控制力 和由于时间步延迟以来
和由于时间步延迟以来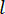 的时间步
的时间步 的状态变量
的状态变量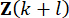 计算的。为了获得主动控制力
计算的。为了获得主动控制力  ,常规成本函数由
,常规成本函数由
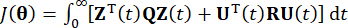 (7)
(7)
其中  表示系统状态的 2n x 2n 对称正半定加权矩阵;
表示系统状态的 2n x 2n 对称正半定加权矩阵;  表示控制力的 r x r 对称正定加权矩阵。可以看出,外部激励可以忽略不计。实际上,基于方程 (7),无论外部激励类型如何,结构控制系统都可以实现最佳控制效果。作为离散形式,方程 (7) 表示为39:
表示控制力的 r x r 对称正定加权矩阵。可以看出,外部激励可以忽略不计。实际上,基于方程 (7),无论外部激励类型如何,结构控制系统都可以实现最佳控制效果。作为离散形式,方程 (7) 表示为39:
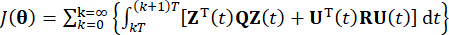 (8)
(8)
成本函数  的最小化导致一个条件极值问题,主动控制力
的最小化导致一个条件极值问题,主动控制力  由25 计算:
由25 计算:
 (9)
(9)
其中 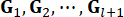 表示时间步
表示时间步 长处状态变量
长处状态变量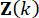 的控制增益和时间步
的控制增益和时间步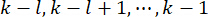 长处的主动控制力
长处的主动控制力 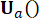 ,由加权矩阵
,由加权矩阵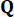 和
和 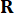 37 确定。由于不可避免的时间延迟,获得的控制力
37 确定。由于不可避免的时间延迟,获得的控制力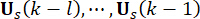 在时间点
在时间点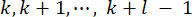 作用在结构上。因此,方程 (9) 中的主动控制力计算如下:
作用在结构上。因此,方程 (9) 中的主动控制力计算如下:
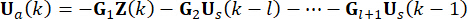 (10)
(10)
为了概念清晰,方程 (10) 中的半主动控制力根据方程 (6) 表示如下:
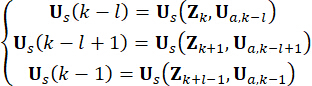 (11)
(11)
其中  表示时间点
表示时间点  的主动控制力。将方程(11)代入方程(10),
的主动控制力。将方程(11)代入方程(10),
 (12)
(12)
注意:计算  需要从时间点
需要从时间点 到
到 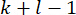 的所有状态
的所有状态 值。因此,引入了以下状态预测方法40.
值。因此,引入了以下状态预测方法40.
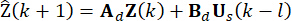 (13)
(13)
其中  表示预测变量。通过方程 (13) 的迭代,
表示预测变量。通过方程 (13) 的迭代,  计算状态 at
计算状态 at  。主动控制力 Ua(k) 表示为:
。主动控制力 Ua(k) 表示为:
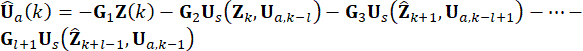 (14)
(14)
半主动控制力可以通过组合 Eqs 来获得。(6)、(12) 和 (13)。
1.2 结构控制系统的可靠性分析
根据概率守恒原理,增强系统和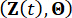
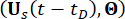 带有 MR 阻尼器的结构是概率守恒的,它们受以下广义概率密度演化方程 (GDEEs) 控制38:
带有 MR 阻尼器的结构是概率守恒的,它们受以下广义概率密度演化方程 (GDEEs) 控制38:
 (15)
(15)
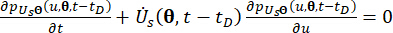 (16)
(16)
其中 ,,分别
,,分别  表示系统状态和具有时间延迟的半主动控制力的相应分量;
表示系统状态和具有时间延迟的半主动控制力的相应分量;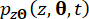 分别
分别 表示增强样本系统的
表示增强样本系统的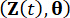 联合概率密度函数 和
联合概率密度函数 和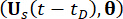 ;
;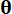 表示样本空间
表示样本空间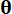 内的样本;
内的样本; 和
和  )分别表示系统状态和半主动控制力分量的一阶时间偏导数。联合概率密度函数
)分别表示系统状态和半主动控制力分量的一阶时间偏导数。联合概率密度函数 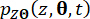 ,
, 可以通过求解 Eqs 来实现。(15) 和 (16) 具有以下初始条件:
可以通过求解 Eqs 来实现。(15) 和 (16) 具有以下初始条件:
 (17)
(17)
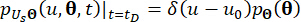 (18)
(18)
其中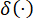 表示 Dirac delta 函数;
表示 Dirac delta 函数; 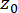 和
和 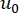 分别表示 和
分别表示 和 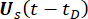 的确定性初始值
的确定性初始值 ;
;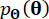 表示样本
表示样本 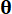 的概率密度函数 。
的概率密度函数 。
和 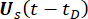 的瞬时概率密度函数
的瞬时概率密度函数 可以通过 和
可以通过 和  在样本空间域上的一维积分
在样本空间域上的一维积分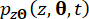 来获得:
来获得:
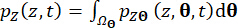 (19)
(19)
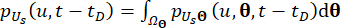 (20)
(20)
其中 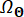 表示 的
表示 的  分发域。
分发域。
基于 Eqs。(19) 和 (20) 中,如果定义了与算法参数相关的关系,则可以很容易地推导出相关物理量的完整概率信息。相关物理量的可靠性可以通过以下相关性能函数来计算:
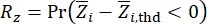 (21)
(21)
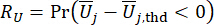 (22)
(22)
其中 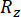 和
和 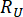 分别表示相关状态量和半主动控制力的计算可靠性;
分别表示相关状态量和半主动控制力的计算可靠性; 表示受控结构的第 i 个相关物理量的等效极值向量;
表示受控结构的第 i 个相关物理量的等效极值向量;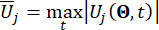 表示第 j 个控制力的等效极值向量;符号上的帽子 '-' 表示等效极值向量41;
表示第 j 个控制力的等效极值向量;符号上的帽子 '-' 表示等效极值向量41;  表示受控结构的第 k 个 DOF 的第 i 个相关物理量;
表示受控结构的第 k 个 DOF 的第 i 个相关物理量; 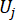 表示第 j 个控制力;
表示第 j 个控制力;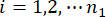 、
、 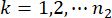 、 、
、 、

 和
和  分别表示结构中安装的结构和 MR 阻尼器的相关物理量和 DOF 的数量。
分别表示结构中安装的结构和 MR 阻尼器的相关物理量和 DOF 的数量。 和
和 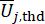 表示 和
表示 和  的阈值;
的阈值;
 表示随机事件的概率。
表示随机事件的概率。
1.3 参数优化
在反馈控制模态中,振幅 和  的比
的比 值对控制效果38 有很大影响。因此,要达到最佳的控制效果,
值对控制效果38 有很大影响。因此,要达到最佳的控制效果, 需要
需要 进行优化。此外,作为一种基于 MR 阻尼器的控制方法,控制效果也受到器件参数的影响,
进行优化。此外,作为一种基于 MR 阻尼器的控制方法,控制效果也受到器件参数的影响,  如方程 (6) 所示。为了实现结构控制系统的最佳可靠性,方程 (25) 中提出了基于可靠性的标准。
如方程 (6) 所示。为了实现结构控制系统的最佳可靠性,方程 (25) 中提出了基于可靠性的标准。
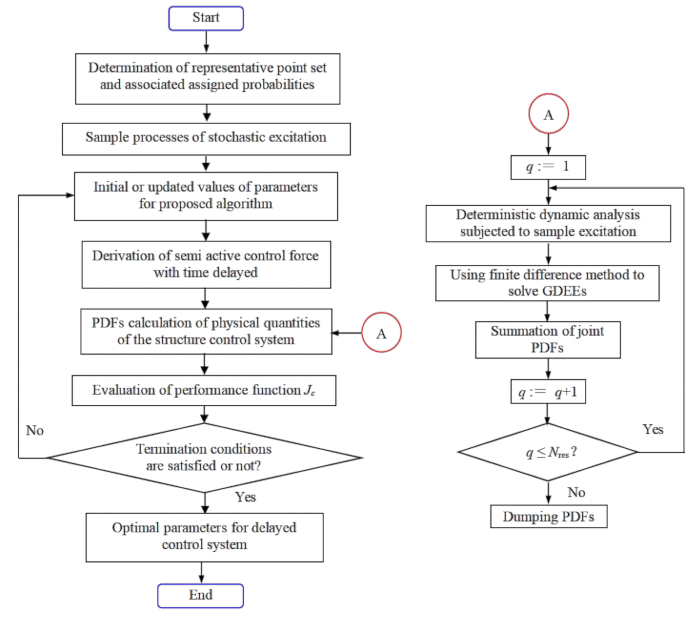
图 1:具有时间延迟补偿的随机最优半主动结构控制的参数优化流程图。 缩写: GDEE = 事件的广义微分方程 ;PDF = 概率密度函数。 请单击此处查看此图的较大版本。
总之,执行基于具有时间延迟补偿的 MR 阻尼器的随机最优半主动结构控制需要两个阶段:
1.3.1 最小化方程 (7) 所示的代价函数 ,实现了样本意义上的状态反馈逻辑,即方程 12)
,实现了样本意义上的状态反馈逻辑,即方程 12)
1.3.2 最小化基于可靠性的性能函数  ,得到统计意义上的最优参数。图 1 显示了步骤 1.3.2 中控制器参数的优化流程图。
,得到统计意义上的最优参数。图 1 显示了步骤 1.3.2 中控制器参数的优化流程图。
步骤 1.3.2 中的以下步骤涉及两层循环,如下所示:
1.3.2.1 对随机激励的概率分配空间进行分区,其特征是随机参数向量  ,可以识别一组代表点
,可以识别一组代表点 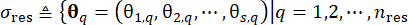 及其相关的分配概率 Pq。这种方法能够有效地生成随机激发的样品过程,表示为
及其相关的分配概率 Pq。这种方法能够有效地生成随机激发的样品过程,表示为 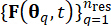 ,很容易获得。
,很容易获得。
1.3.2.2 对于半主动结构控制系统的参数优化,初始化或更新成本函数权重  和
和  的值。然后计算与时间延迟相关的状态反馈控制力,参见方程 (12)。
的值。然后计算与时间延迟相关的状态反馈控制力,参见方程 (12)。
1.3.2.3 通过求解方程中所示的 GDEE 来获得结构响应和控制力的概率密度函数 (PDF)。(17)–(20):
优化是离线完成,而不是在线完成。在实际结构控制系统中所提出的方法的适用中,最优  和
和  已经实现,而在实际适用的过程中不需要优化。
已经实现,而在实际适用的过程中不需要优化。
在样品激发下对半主动结构控制系统进行确定性动力学分析,通过该分析计算相关的物理量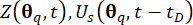 及其导数
及其导数 。
。
通过采用有限差分方法,例如具有总变分递减 (TVD) 属性的改进 Lax-Wendroff 方案,可以求解广义微分方程 (GDEE),并可以推导出联合概率密度函数 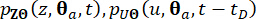 的数值解。
的数值解。
重复上述确定性动态分析和有限差分法的两个步骤,遍历所有代表点 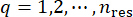 ,通过求和可以得到概率密度函数:
,通过求和可以得到概率密度函数:
 (23)
(23)
 (24)
(24)
其中  表示与采样点
表示与采样点 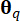 关联的子域的面积度量 。用于求解事件广义微分方程 (GDEE) 的方法称为概率密度演化法 (PDEM)42。
关联的子域的面积度量 。用于求解事件广义微分方程 (GDEE) 的方法称为概率密度演化法 (PDEM)42。
1.3.2.4 使用相关物理量的 PDF 来评估其可靠性,然后将其纳入概率标准的性能函数  中。
中。
1.3.2.5 评估是否满足参数优化过程的终止标准。如果不满足条件,请返回步骤 1.3.2.2;如果是,则可以确定延时控制系统的最佳参数。在这项工作中,MATLAB 中的遗传算法 (GA) 工具箱用于参数优化,这有助于参数更新并定义终止条件。通过遗传算法,可以在 10 次迭代内实现最优值,并且收敛稳定,没有局部最小值问题。尽管 GA 的计算成本大于粒子群优化或基于梯度的方法,但 GA 擅长处理复杂且不可微分的问题,例如本手稿中的问题。因此,将应用 GA。由于快速收敛特性,GA 的计算成本是可以接受的。
1.3.2.6 为了实现最优的可靠性控制,制定了以下性能函数  。Minimize
。Minimize  确定参数
确定参数  的最佳值,以及
的最佳值,以及  :
:
 } (25)
} (25)
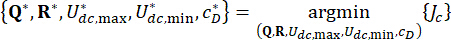 (26)
(26)
如前所述,控制器的加权矩阵是对称的,其中矩阵  中的单元对应于分配给位移、速度及其相互作用的权重,而矩阵
中的单元对应于分配给位移、速度及其相互作用的权重,而矩阵  中的单元表示与控制力相关的权重。根据早期研究的结果38,已经观察到改变成本函数权重
中的单元表示与控制力相关的权重。根据早期研究的结果38,已经观察到改变成本函数权重  的配置,
的配置,  并且对控制效果的影响最小。因此,本研究采用了简化的配置,如下所述:
并且对控制效果的影响最小。因此,本研究采用了简化的配置,如下所述:
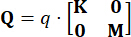 、
、 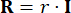 (27)
(27)
其中 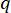 表示要定义的状态加权矩阵的系数;
表示要定义的状态加权矩阵的系数;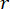 表示要定义的控制加权矩阵的系数;
表示要定义的控制加权矩阵的系数;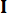 表示单位矩阵。控制效果受 的
表示单位矩阵。控制效果受 的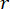 比率
比率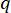 影响,但受值本身的影响。此外,
影响,但受值本身的影响。此外,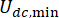 在方程 (6) 中表示 MR 阻尼器的最小库仑力,这意味着
在方程 (6) 中表示 MR 阻尼器的最小库仑力,这意味着 阻尼器中的电流输入为零。那么,方程(26)可以进一步表示为:T
阻尼器中的电流输入为零。那么,方程(26)可以进一步表示为:T
 (28)
(28)
最佳关注系数在哪里 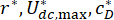 。为了在工程设计上合理,它们的最佳范围基于 MR 减振器工厂的生产能力。
。为了在工程设计上合理,它们的最佳范围基于 MR 减振器工厂的生产能力。
显然,方程(28)得到的最优参数保持了所提出的具有时间延迟的半主动控制算法的最优控制效果,这使得结构控制系统在随机激励下实现了平衡的最优可靠性。
2. 案例研究
为了分析所提出的具有时间延迟补偿的半主动控制方法对 MR 阻尼器的有效性,连接到 MR 阻尼器的平面单层剪力框架结构受到了水平随机地震地震动,如图 2 所示。半主动控制结构系统的参数如下:结构质量 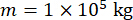 、固有圆频率
、固有圆频率  、阻尼比
、阻尼比 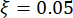 。根据过去的经验和市场上现有的阻尼器刻度,结构位移、速度、加速度和控制力的阈值分别为 10 mm、100 mm/s、1,500 mm/s2 和 150 kN。为了表示随机地震地震动,采用了物理驱动的随机地震动模型43:
。根据过去的经验和市场上现有的阻尼器刻度,结构位移、速度、加速度和控制力的阈值分别为 10 mm、100 mm/s、1,500 mm/s2 和 150 kN。为了表示随机地震地震动,采用了物理驱动的随机地震动模型43:
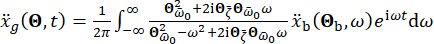 (29)
(29)
其中 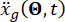 表示工程现场时域中的地震动,
表示工程现场时域中的地震动, 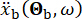 表示基岩频域中的地震动。该矢量
表示基岩频域中的地震动。该矢量  描述了工程现场表面地震动的随机性质。参数
描述了工程现场表面地震动的随机性质。参数 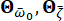 是描述场地土壤特性的随机变量,包括主频率
是描述场地土壤特性的随机变量,包括主频率  和等效阻尼
和等效阻尼  。该向量
。该向量 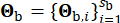 表示基岩上地震动的随机性质,它受源属性和传播路径的影响,并
表示基岩上地震动的随机性质,它受源属性和传播路径的影响,并 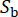 指示此阶段涉及的随机变量的数量。
指示此阶段涉及的随机变量的数量。  指圆周频率,i 是虚数单位。
指圆周频率,i 是虚数单位。
工程场地的主要频率  和等效阻尼比
和等效阻尼比  是表征场地土壤动力特性的关键参数。这些量的概率分布和统计参数可以根据从特定类别的工程现场收集的地震加速度记录来确定。为了便于说明,考虑了剪切波速度范围为 [150, 250] m/s 的站点类别,并将地震动的设计特征周期设置为 0.45 s。
是表征场地土壤动力特性的关键参数。这些量的概率分布和统计参数可以根据从特定类别的工程现场收集的地震加速度记录来确定。为了便于说明,考虑了剪切波速度范围为 [150, 250] m/s 的站点类别,并将地震动的设计特征周期设置为 0.45 s。
关键参数  被视为
被视为 相互独立的随机变量,均服从对数正态分布以进行参数识别。统计参数如下:的
相互独立的随机变量,均服从对数正态分布以进行参数识别。统计参数如下:的 平均值
平均值 分别为 12 rad/s 和 0.1。和
分别为 12 rad/s 和 0.1。和  的变异
的变异 系数分别为 0.42 和 0.35。基岩的地震动被建模为高斯白噪声过程,傅里叶振幅为 0.20 m/s2,对应于 0.11 g 的峰值地震动加速度。用于产生基岩运动的相位角表示为
系数分别为 0.42 和 0.35。基岩的地震动被建模为高斯白噪声过程,傅里叶振幅为 0.20 m/s2,对应于 0.11 g 的峰值地震动加速度。用于产生基岩运动的相位角表示为 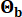 。因此,Sb =1 和
。因此,Sb =1 和 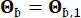 。这种方法可以被认为是对具有给定超标概率44 的条件随机地震动进行建模。对数正态分布的假设在地震动建模中被广泛使用,因为它能够捕获观察到的地震动参数的偏斜性质。
。这种方法可以被认为是对具有给定超标概率44 的条件随机地震动进行建模。对数正态分布的假设在地震动建模中被广泛使用,因为它能够捕获观察到的地震动参数的偏斜性质。
为了评估这一假设的敏感性,其他研究45,46 中使用替代概率分布(包括正态分布和 gamma 分布)进行了额外的分析。研究结果表明,虽然总体趋势保持一致,但对数正态分布为观测数据提供了最佳拟合,特别是对于捕获地震动强度测量的尾部行为
通过切线球体方法47,选择了 221 个具有相关分配概率的代表性点的集合,并合成了代表性的地面加速度。采样频率为 50 Hz,地震动持续时间为 20.48 s。为了给模拟的地震动分配非平稳强度,使用了均匀调制函数,其公式如下42:
 (30 页)
(30 页)
其中  分别需要 2 秒和 16 秒。
分别需要 2 秒和 16 秒。
随机地震地震动的平均值和标准差,以及代表性地震地震动的时间历程如图 3 所示。平均值的振幅 (0.06 m/s2) 是标准差振幅 (0.8 m/s2) 的 ~8%,表明物理驱动的随机地震动模型表现出零均值的特性。同时,地震地震动在时域和频域中都表现出显著的非平稳行为。
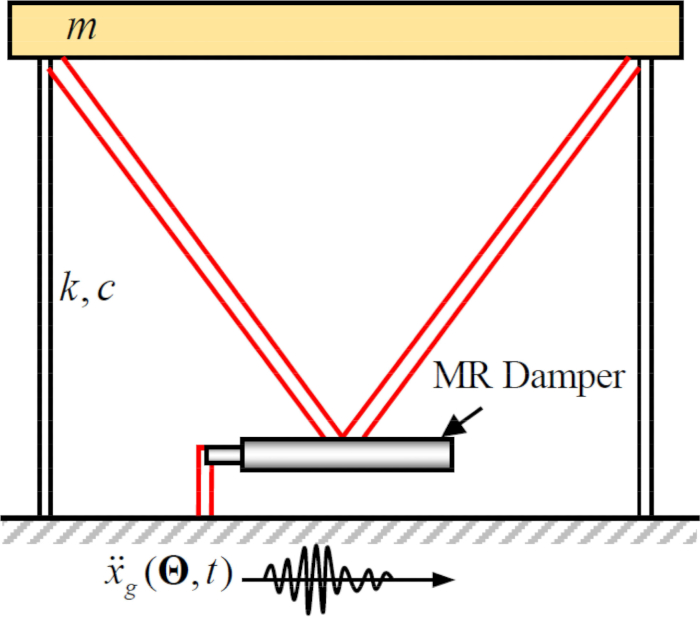
图 2:带有磁流变阻尼器的单层剪切框架草图。 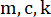 表示结构质量、阻尼比和刚度;
表示结构质量、阻尼比和刚度;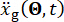 表示随机地震激励。请单击此处查看此图的较大版本。
表示随机地震激励。请单击此处查看此图的较大版本。
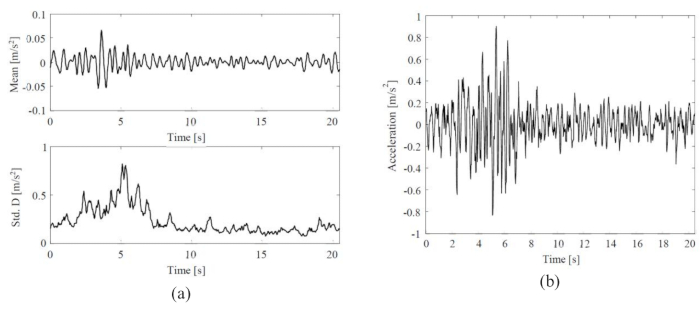
图 3:选定地震地震动的统计数据和代表性样本。 (A) 随机地震地震动的平均值和标准差;(B) 代表性地震地震动的时间历程。 请单击此处查看此图的较大版本。
2.1 时延影响分析
为了分析时间延迟对 MR 阻尼器半主动控制效果的影响, 图 4 显示了受控结构的位移、速度和加速度 RMS(均方根响应)。加权矩阵比率和阻尼器参数分别为 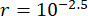 、
、 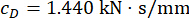 和
和 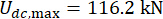 ,它们是无时间延迟的优化结果38。有时间延迟的受控结构的响应大于无时间延迟的受控结构,时间延迟对控制效果的影响表现为随着时间延迟的增加而具有周期性。由于 MR 阻尼器的半主动控制方法是一种反馈方法,因此认为影响的周期性与受控结构的自然周期 (T = 0.56 s) 有关。
,它们是无时间延迟的优化结果38。有时间延迟的受控结构的响应大于无时间延迟的受控结构,时间延迟对控制效果的影响表现为随着时间延迟的增加而具有周期性。由于 MR 阻尼器的半主动控制方法是一种反馈方法,因此认为影响的周期性与受控结构的自然周期 (T = 0.56 s) 有关。
与最大 MRS 位移、速度和加速度分别为 24.6 mm、270.0 mm/s 和 3111.3 mm/s2 的非受控结构的响应相比,MR 阻尼器控制结构取得了显著的效果。与时延25 的主动控制结构的不稳定性不同,基于 MR 阻尼器的半主动控制方法即使在时间延迟下仍然获得了一定的效果。
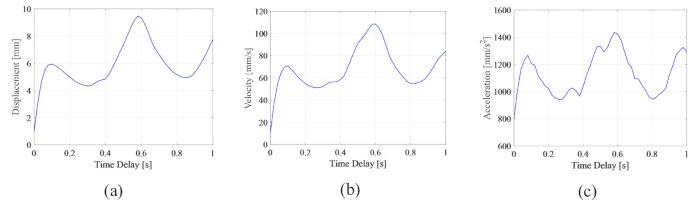
图 4:受控结构响应随时间变化的最大均方根。(a) 流离失所;(B) 速度;(C) 加速。请单击此处查看此图的较大版本。
为了分析时间延迟对半主动控制结构可靠性的影响, 图 5 显示了位移、速度和加速度随时间延迟的增加而的可靠性。具有任何时间延迟的受控结构响应的可靠性都低于没有时间延迟的值,这意味着受控结构的可靠性会因时间延迟而降低。同时,与最大 RMS 相似,可靠性控制效果表现出随着时间延迟的增加而具有周期性。此外,受控结构的可靠性(有或没有时间延迟)高于位移、速度和加速度可靠性为 0.0954、0.1058 和 0.1111 的非受控结构的值。
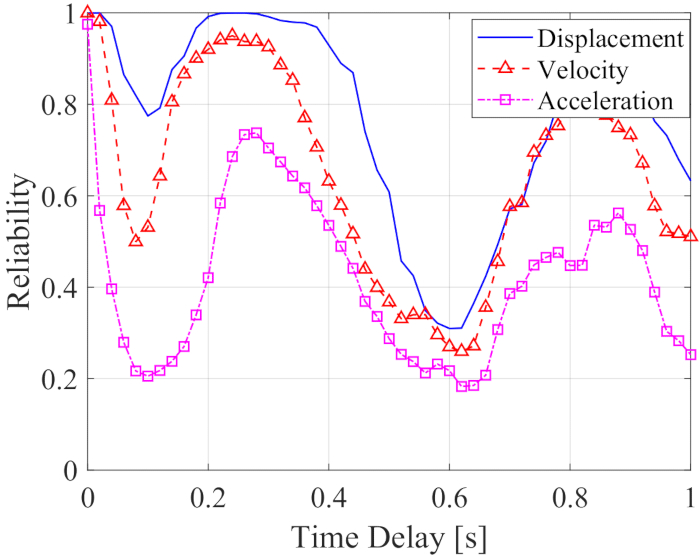
图 5:受控结构的响应可靠性随时间延迟的增加。请单击此处查看此图的较大版本。
综上所述,半主动控制方法减轻了结构的响应。然而,无论 RMS 或可靠性如何,半主动控制方法的控制效果都因时间延迟而降低。因此,有必要补偿时间延迟。
2.1.1 时延补偿方法解析
为了分析所提出的时间延迟补偿方法的有效性, 图6比较了非受控(Unc)、非补偿控制的时间延迟系统(TDN-SAC-PSO)和补偿控制的时间延迟系统(TDC-SAC-PSO)的位移、速度和加速度的RMS时间历程,其中时间延迟为0.1 s。加权矩阵和半主动控制方法的参数与步骤 2.1 中的相同。
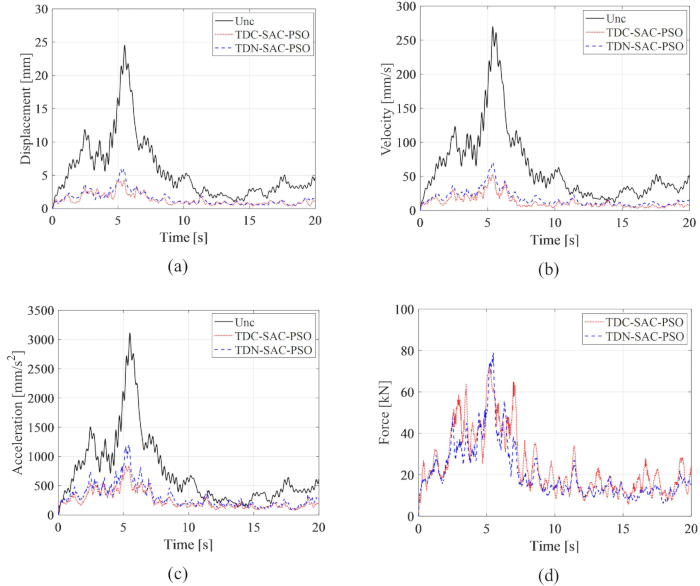
图 6:由不同方法控制的结构的均方根时间历史比较。 (a) 流离失所;(B) 速度;(c) 加速度;(D) 控制力。缩写: unc = 不受控制;TDC-SAC-PSO = 带补偿控制的时间延迟系统;TDN -SAC-PSO = 非补偿控制的时间延迟系统。 请单击此处查看此图的较大版本。
与非受控结构相比,两种控制方法都显著降低了结构的响应,揭示了基于 MR 阻尼器的控制方法的优势。与非受控结构相比,TDN-SAC-PSO方法的位移、速度和加速度的最大RMS分别降低了75.79%、73.75%和61.22%。此外,在时间延迟补偿下,TDC-SAC-PSO方法对受控结构的响应分别降低了82.59%、80.40%和73.04%。与 TDN-SAC-PSO 方法相比,TDC-SAC-PSO 方法的控制力最大 RMS 降低了 8.43%,但前一种方法的振动响应小于后者。以上分析表明,补偿方法有效降低了时滞对基于 MR 阻尼器的控制方法的影响,这表明了 MR 阻尼器半主动控制方法进行时滞补偿的必要性。
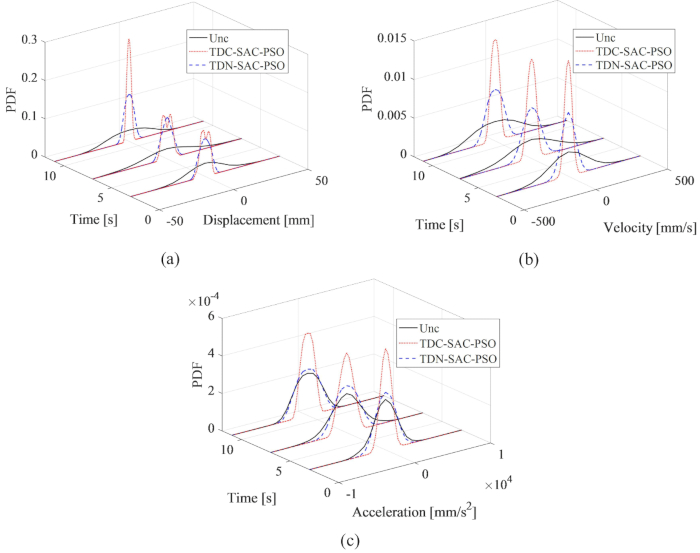
图 7:结构响应典型时间的 PDF 比较。(a) 流离失所;(B) 速度;(C) 加速。缩写: PDF = 概率密度函数;unc = 不受控制;TDC-SAC-PSO = 带补偿控制的时间延迟系统;TDN -SAC-PSO = 非补偿控制的时间延迟系统。 请单击此处查看此图的较大版本。
为了全面揭示所提出的补偿方法对受控结构响应不确定性的影响, 图 7 显示了典型时间 3、7 和 11s 的位移、速度和加速度的概率密度函数 (PDF) 比较。TDN-SAC-PSO 方法的 PDF 比非受控结构的 PDF 窄,这意味着即使有时间延迟,半主动控制方法也降低了结构响应的不确定性。补偿时间延迟后,响应的 PDF 进一步缩小。因此,所提出的补偿方法对于提高半主动控制效果是必要的。
| 控制方式 | 位移 | 速度 | 加速度 | 控制力 | 最小值 |
| 蜻蜓 | 0.0954 | 0.1058 | 0.1111 | -- | 0.1111 |
| TDC-SAC-PSO | 0.9565 | 0.8107 | 0.7654 | 0.9845 | 0.7654 |
| TDN-SAC-PSO 协议 | 0.7747 | 0.531 | 0.2054 | 0.884 | 0.2054 |
表 1:由不同方法控制的结构的振动响应和控制力可靠性。 缩写: unc = 不受控制;TDC-SAC-PSO = 带补偿控制的时间延迟系统;TDN -SAC-PSO = 非补偿控制的时间延迟系统。
表 1 显示了 Uncontrolled、TDC-SAC-PSO 和 TDN-SAC-PSO 方法控制结构的振动响应和控制力可靠性。与 Uncontrolled 结构相比,使用 TDN-SAC-PSO 方法控制,结构的可靠性显著提高,这验证了基于 MR 阻尼器的控制方法的有效性,即使随着时间的推移也是如此。然而,与无补偿相比,有时间延迟补偿的可靠性显著提高,尤其是加速。同样值得注意的是,TDC-SAC-PSO 方法不同响应的可靠性和控制力显示出显著差异。这表明无时间延迟的控制的关键参数的最优值对于有时间延迟的控制不是最优的。为了实现振动响应和控制力的最佳控制效果,需要进一步优化参数。基于上述分析,得出结论:采用MR阻尼器的半主动控制方法可以有效降低结构的振动响应,但由于时间延迟的影响,参数需要优化。
2.2 参数优化
为了实现参数的最优值,应用了基于可靠性准则的集成优化方法38.关键参数的优化是通过 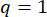 、
、 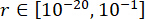

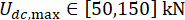 和 MR 阻尼力 s = 8 的可调时间进行的。MATLAB 中的 GA 工具箱用于实现优化。
和 MR 阻尼力 s = 8 的可调时间进行的。MATLAB 中的 GA 工具箱用于实现优化。
参数的优化结果为  , , 和
, , 和  对于 time delay
对于 time delay 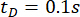
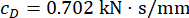 。图 8 显示了非受控 (Unc)、TDC-SAC-PSO 方法和 SOSC-PSO 方法控制结构的位移、速度、加速度和控制力的 RMS 时间历程。SOSC-PSO 方法表示具有时间延迟补偿和优化的关键参数值的半主动控制方法。
。图 8 显示了非受控 (Unc)、TDC-SAC-PSO 方法和 SOSC-PSO 方法控制结构的位移、速度、加速度和控制力的 RMS 时间历程。SOSC-PSO 方法表示具有时间延迟补偿和优化的关键参数值的半主动控制方法。
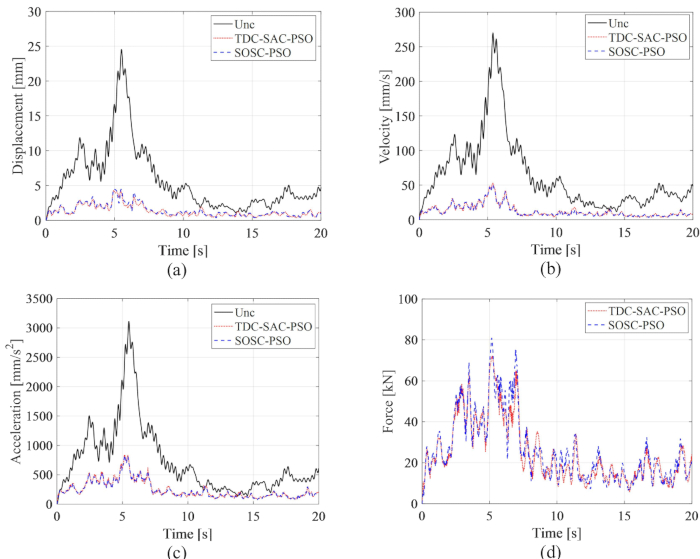
图 8:非受控和 TDC-SAC-PSO 方法和 SOSC-PSO 方法控制结构的位移、速度、加速度和控制力的 RMS 时间历程。 (a) 流离失所;(B) 速度;(c) 加速度;(D) 控制力。缩写: unc = 不受控制;TDC-SAC-PSO = 带补偿控制的时间延迟系统;SOSC-PSO = 具有时间延迟补偿的随机最优半主动控制方法。 请单击此处查看此图的较大版本。
从 图 8 中可以看出,TDC-SAC-PSO 和 SOSC-PSO 方法的控制效果差异不大。前一种方法的位移速度和加速度的最大 RMS 分别为非受控结构的 81.60%、81.21%、73.62% 和后一种方法的 82.59%、80.40%、73.04%。为了全面分析两种控制方法的响应概率特征, 图 9 显示了不受控、TDC-SAC-PSO 方法和 SOSC-PSO 方法控制结构的位移、速度和加速度的 PDF。在典型时间,两种控制方法的位移和速度 PDF 几乎相同。SOSC-PSO 方法的加速度 PDF 比 TDC-SAC-PSO 方法窄,这意味着加速度的不确定性比前一种方法获得了更好的控制效果。
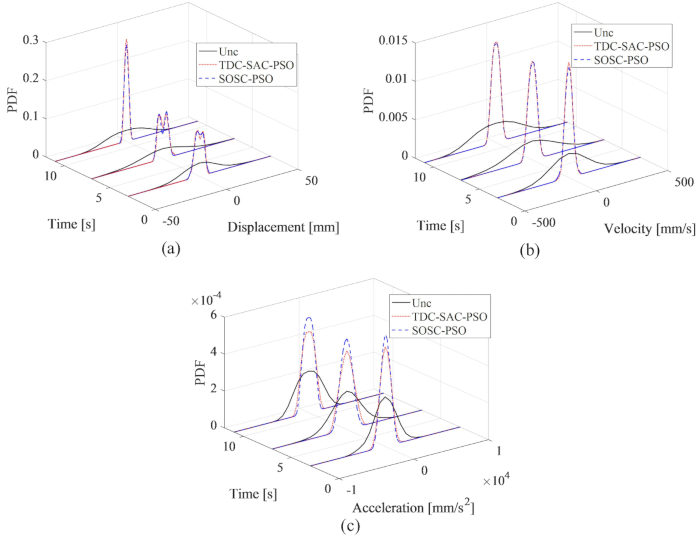
图 9:不同受控结构的位移、速度和加速度的 PDF 比较。 (a) 流离失所;(B) 速度;(C) 加速。缩写: PDFs = 概率密度函数;unc = 不受控制;TDC-SAC-PSO = 带补偿控制的时间延迟系统;SOSC-PSO = 具有时间延迟补偿的随机最优半主动控制方法。 请单击此处查看此图的较大版本。
表 2 显示了非受控和 TDC-SAC-PSO 和 SOSC-PSO 方法控制结构的位移、速度、加速度和控制力的可靠性。与非受控结构相比,两种控制方法的可靠性都得到了显著提高。TDC-SAC-PSO和SOSC-PSO方法之间的位移可靠性差异不大。而加速度可靠性(受控结构的最低可靠性)实现了显着提高。这意味着 SOSC-PSO 方法实现了平衡最优控制效果。
| 控制方式 | 位移 | 速度 | 加速度 | 控制力 | 最小值 |
| 蜻蜓 | 0.0954 | 0.1058 | 0.1111 | -- | 0.1111 |
| TDC-SAC-PSO | 0.9565 | 0.8107 | 0.7654 | 0.9845 | 0.7654 |
| SOSC-PSO | 0.953 | 0.8704 | 0.8934 | 0.9586 | 0.8934 |
表 2:由不同方法控制的结构的可靠性。 缩写: unc = 不受控制;TDC-SAC-PSO = 带补偿控制的时间延迟系统;SOSC-PSO = 具有时间延迟补偿的随机最优半主动控制方法。
分析了所提出的 SOSC-PSO 方法在时间延迟 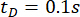 方面的有效性。为了进一步验证所提出的方法对不同的时间延迟, 表 3 显示了时间延迟范围
方面的有效性。为了进一步验证所提出的方法对不同的时间延迟, 表 3 显示了时间延迟范围 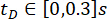 的最佳参数值和相应的可靠性。
的最佳参数值和相应的可靠性。
| 吨D(s) | lg(r*) | CD(kN·s/mm) | U直流,最大值 (kN) | 位移 | 速度 | 加速度 | 控制力 |
| 0 | -2.524 | 1.44 | 116.163 | 0.9997 | 0.9998 | 0.9752 | 1 |
| 0.02 | -4.413 | 0.414 | 144.066 | 0.9989 | 0.9988 | 0.872 | 0.9011 |
| 0.04 | -4.416 | 0.25 | 141.759 | 0.9998 | 0.9846 | 0.8881 | 0.9135 |
| 0.06 | -3.226 | 0.203 | 145.613 | 0.993 | 0.9318 | 0.8756 | 0.9556 |
| 0.08 | -5.207 | 0.345 | 133.692 | 0.9646 | 0.8998 | 0.8998 | 0.953 |
| 0.1 | -4.669 | 0.702 | 130.739 | 0.9531 | 0.8704 | 0.8934 | 0.9586 |
| 0.12 | -4.895 | 0.833 | 69.72 | 0.9526 | 0.863 | 0.888 | 0.9686 |
| 0.14 | -4.231 | 0.921 | 75.221 | 0.9531 | 0.8681 | 0.8697 | 0.9671 |
| 0.16 | -5.594 | 0.662 | 138.922 | 0.9529 | 0.8461 | 0.8262 | 0.931 |
| 0.18 | -4.262 | 0.882 | 76.335 | 0.9516 | 0.7873 | 0.7614 | 0.9618 |
| 0.2 | -3.926 | 0.783 | 67.951 | 0.904 | 0.7277 | 0.7116 | 0.9653 |
| 0.22 | -5.965 | 1.071 | 52.554 | 0.8377 | 0.6411 | 0.6205 | 0.965 |
| 0.24 | -4.481 | 1.216 | 128.148 | 0.7567 | 0.474 | 0.474 | 0.9687 |
| 0.26 | -3.53 | 0.672 | 53.706 | 0.53 | 0.4096 | 0.4158 | 0.9921 |
| 0.28 | -4.433 | 0.638 | 64.225 | 0.3547 | 0.3745 | 0.3464 | 0.9928 |
| 0.3 | -3.536 | 0.459 | 57.705 | 0.2735 | 0.316 | 0.2736 | 0.9929 |
| 蜻蜓 | -- | -- | -- | 0.0954 | 0.1058 | 0.1111 | -- |
表 3:不同时间延迟的最佳参数值和相应的可靠性值。 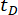 表示时间延迟;
表示时间延迟;  表示 r 的最佳对数值,r 表示控制加权矩阵的系数;
表示 r 的最佳对数值,r 表示控制加权矩阵的系数; 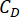 表示 MR 阻尼器的粘性阻尼系数;
表示 MR 阻尼器的粘性阻尼系数; 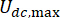 表示 MR 阻尼器的最大和最小库仑力。
表示 MR 阻尼器的最大和最小库仑力。
可以观察到,与非受控结构相比,即使在存在时间延迟的情况下,位移、速度和加速度的可靠性也有所提高,这表明所提出的方法对此类延迟的稳健性。然而,随着时间延迟的增加,所提出的控制方法的结构响应可靠性降低,表明虽然可以减轻时间延迟对控制效果的影响,但不能完全消除。值得注意的是,在不同的时间延迟下,控制力的可靠性保持在 90% 以上。
3. 数值示例
为了在 MDOF 结构中验证所提出的 SOSC-PSO 方法,分析了一个六层结构,在一楼和三楼安装了两个 MR 阻尼器,如图 10 所示。采用第 2 节随机地震模型生成的地震样本,位移、速度、加速度和控制力的可靠性阈值分别为 20 mm、200 mm/s、3 000 mm/s2 和 200 kN。方程。(27) 用作加权矩阵,其中 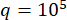 。使用 MATLAB 的 GA 工具箱来优化
。使用 MATLAB 的 GA 工具箱来优化 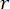 、
、 和
和  、 和最优范围
、 和最优范围 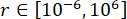 、
、  和
和 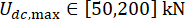 。
。
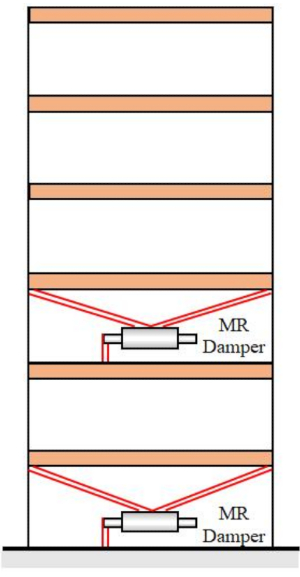
图 10:带有两个 MR 阻尼器的六层结构。 缩写:MR = 磁流变。 请单击此处查看此图的较大版本。
3.1 时延影响分析
为了分析时间延迟对 MDOF 结构中 MR 阻尼器控制效果的影响, 图 11 显示了 TDC-SAC-PSO 方法的位移(层间位移)、速度(层间速度)和加速度(层加速度)的最大 RMS 以及时间延迟。参数为 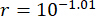 ,
, ,
,  对于 1 楼的 MR 阻尼器;
对于 1 楼的 MR 阻尼器;  和
和  3 楼的 MR 阻尼器,它们是无时间延迟的优化结果。受控结构响应的最大 RMS 表现出周期波动和时间延迟。位移和速度的最大 RMS 在 1 楼,最大加速度在 6 楼。此外,所有具有任何时间延迟的响应的最大 MRS 都大于没有时间延迟的值,这意味着时间延迟降低了 MR 阻尼器的控制效果。
3 楼的 MR 阻尼器,它们是无时间延迟的优化结果。受控结构响应的最大 RMS 表现出周期波动和时间延迟。位移和速度的最大 RMS 在 1 楼,最大加速度在 6 楼。此外,所有具有任何时间延迟的响应的最大 MRS 都大于没有时间延迟的值,这意味着时间延迟降低了 MR 阻尼器的控制效果。
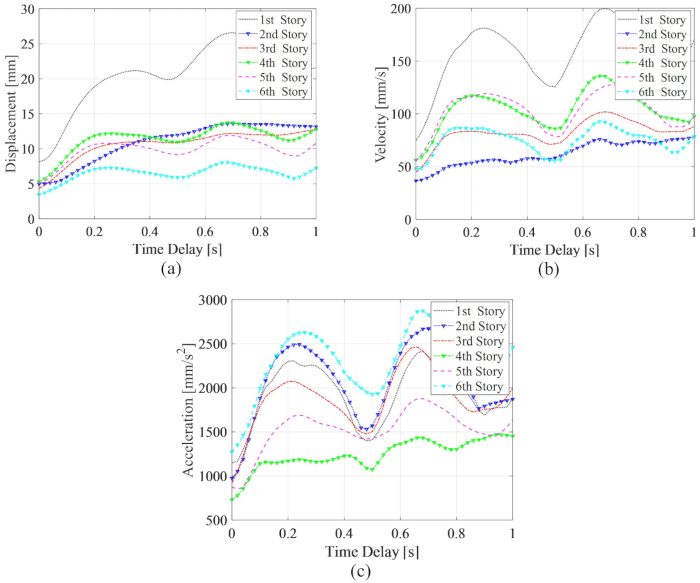
图 11:TDC-SAC-PSO 方法控制结构的最大响应 RMS 和时间延迟。 (a) 流离失所;(B) 速度;(C) 加速。缩写: RMS = 均方根;TDC-SAC-PSO = 带补偿控制的时间延迟系统。 请单击此处查看此图的较大版本。
位移、速度和加速度以及时间延迟的可靠性如图 12 所示。速度和加速度的可靠性随时间延迟呈周期波动,而位移的可靠性随时间延迟而急剧降低;所有 Accuracy 值在任何时间延迟时均小于无时间延迟的可靠性值。因此,为了减少时滞对MR阻尼器控制结构可靠性的影响,必须采用时延补偿方法。
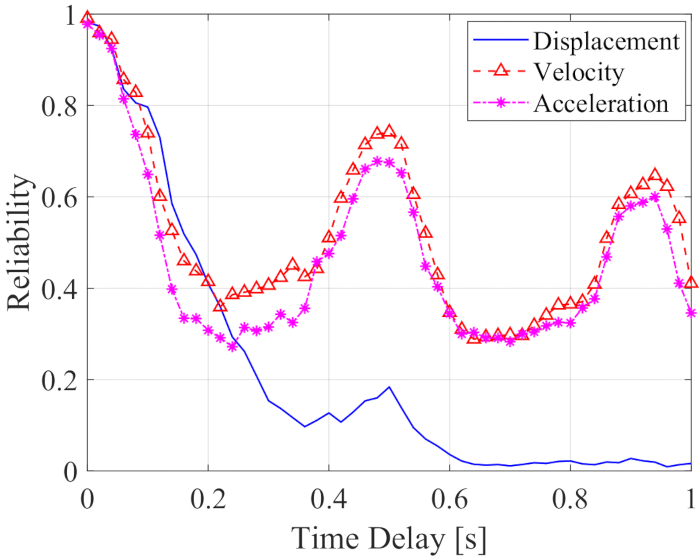
图 12:受控结构响应的可靠性以及时间延迟。请单击此处查看此图的较大版本。
3.2 时延补偿的控制效果
基于所提出的 TDC-SAC-PSO 方法,分析了具有两个 MR 阻尼器的 6-DOF 结构。 图 13 显示了非受控 (Unc)、TDC-SAC-PSO 方法控制和 TDN-SAC-PSO 方法控制结构在 1 楼和 3 楼的位移和加速度的 RMS 时间历程。时间延迟为 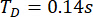 ,加权矩阵比率
,加权矩阵比率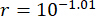 ;MR 阻尼器参数为
;MR 阻尼器参数为  ,
,  用于 1 楼;
用于 1 楼;  和
和  3 楼。
3 楼。

图 13:由不同方法控制的结构在 1 楼和 3 楼的位移和加速度的 RMS 时间历程。 (A) 一楼的位移;(B) 3 楼的流离失所;(C) 1 楼的加速;(D) 3 楼的加速度。缩写: RMS = 均方根;unc = 不受控制;TDC-SAC-PSO = 带补偿控制的时间延迟系统;TDN -SAC-PSO = 非补偿控制的时间延迟系统。 请单击此处查看此图的较大版本。
TDN-SAC-PSO方法将1楼和3楼位移的最大RMS降低了35.42%和30.44%,其中时间延迟没有得到补偿。而补偿后,1 层和 3 层位移的最大 RMS 分别降低了 49.33% 和 53.39%。在没有补偿的情况下,1 层和 3 层的最大加速度 RMS 增加了 16.22% 和 2.88%,但分别减少了 25.77% 和 36.00%,补偿后。因此,MR 阻尼器控制方法中对时间延迟的补偿对于降低结构的响应是必要的,尤其是对于加速度。
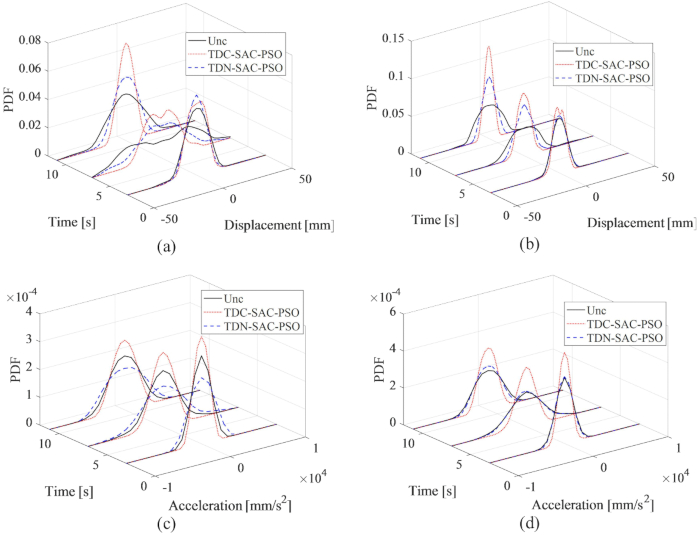
图 14:不同控制方法的 1 楼和 3 楼位移和加速度的 PDF。 (A) 一楼的位移;(B) 3 楼的流离失所;(C) 1 楼的加速;(D) 3 楼的加速度。缩写: PDFs = 概率密度函数;unc = 不受控制;TDC-SAC-PSO = 带补偿控制的时间延迟系统;TDN -SAC-PSO = 非补偿控制的时间延迟系统。 请单击此处查看此图的较大版本。
图 14 显示了 1 楼和 3 楼的位移和加速度的 PDF,揭示了 TDC-SAC-PSO 和 TDN-SAC-PSO 方法与非受控结构相比的不同控制效果。在没有补偿的情况下,1 楼和 3 楼的位移 PDF 仍然比不受控制的结构的 PDF 窄。此外,在补偿时间延迟的情况下,位移的 PDF 变得比 TDN-SAC-PSO 方法控制结构的 PDF 更窄。与无补偿的位移不同,TDN-SAC-PSO 方法在 1 楼的加速度 PDF 比非受控结构的 PDF 宽。然而,在补偿的情况下,1 楼和 3 楼的加速度 PDF 都比非受控结构的 PDF 窄。因此,验证了时间延迟补偿的必要性,以提高结构响应的确定性,特别是对于加速度。
| 控制方式 | 位移 | 速度 | 加速度 | 1楼 的控制力 | 3楼 的控制力 |
| 蜻蜓 | 0.0114 | 0.5822 | 0.6372 | -- | -- |
| TDN-SAC-PSO 协议 | 0.5851 | 0.5258 | 0.398 | 1 | 1 |
| TDC-SAC-PSO | 0.806 | 0.8674 | 0.8037 | 1 | 1 |
表 4:由不同方法控制的结构的可靠性。 缩写: unc = 不受控制;TDC-SAC-PSO = 带补偿控制的时间延迟系统;TDN -SAC-PSO = 非补偿控制的时间延迟系统。
表 4 显示了由不同方法控制的结构系统的位移、速度、加速度和控制力的可靠性值。使用等效极值法25 计算结构响应的可靠性值。采用 TDN-SAC-PSO 方法控制,位移的可靠性较非受控结构增加,而速度和加速度的可靠性降低。使用 TDC-SAC-PSO 方法进行时间延迟补偿后,位移、速度和加速度的可靠性显著提高。此外,TDN-SAC-PSO 和 TDN-SAC-PSO 方法的控制力的可靠性值都得到了充分的维持。因此,所提出的时滞补偿控制方法对 MR 阻尼器控制结构取得了良好的控制效果。
3.3 参数优化
为达到最优控制效果,基于可靠性准则对所提控制方法的参数进行了优化。使用时间延迟 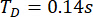 ,最佳结果是
,最佳结果是  ;
; 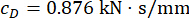 ,
, 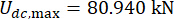 对于 1st floor MR 阻尼器;
对于 1st floor MR 阻尼器; 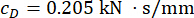 和
和  3rd MR 阻尼器。
3rd MR 阻尼器。
图 15 显示了 1 楼和 3 楼位移和加速度的 RMS 时间历史,其中比较了 TDC-SAC-PSO 和 SOSC-PSO 方法与非受控结构的控制效果。使用 MR 阻尼器控制,无论有没有时间延迟补偿,位移和加速度的 RMS 显着降低。采用 SOSC-PSO 方法时,相对于非受控结构,1 层和 3 层的最大位移 RMS 分别降低了 65.15% 和 63.16%。与 TDC-SAC-PSO 方法相比,位移响应进一步降低。对于 SOSC-PSO 方法,1 楼和 3 楼的最大加速度 RMS 降低了 23.39% 和 35.60%。SOSC-PSO 和 TDC-SAC-PSO方法的加速度控制效果差异不大,表明时滞补偿对位移和加速度的控制效果不同。
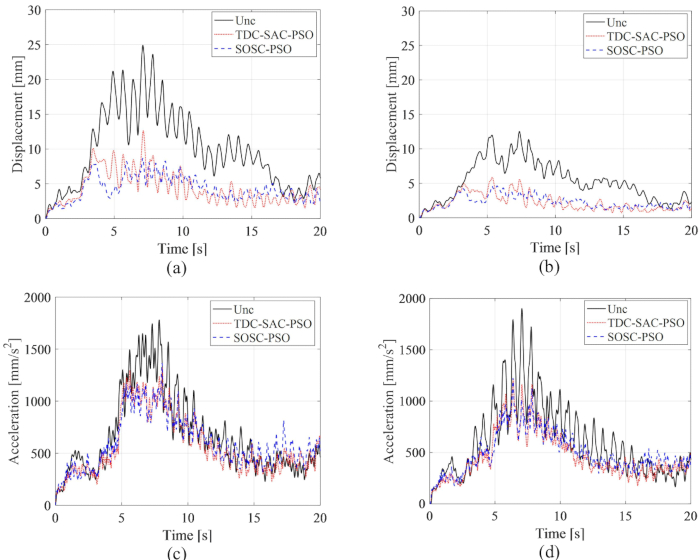
图 15:不同控制方法下 1 楼和 3 楼位移和加速度的 RMS 时间历史。 (A) 一楼的位移;(B) 3 楼的流离失所;(C) 1 楼的加速;(D) 3 楼的加速度。缩写: RMS = 均方根;unc = 不受控制;TDC-SAC-PSO = 带补偿控制的时间延迟系统;SOSC-PSO = 具有时间延迟补偿的随机最优半主动控制方法。 请单击此处查看此图的较大版本。
图 16 显示了 1 楼和 3 楼的位移和加速度的 PDF;与非受控结构相比,TDC-SAC-PSO 和 SOSC-PSO 方法缩小了位移和加速度的 PDF。此外,与 TDC-SAC-PSO 方法控制结构相比,SOSC-PSO 方法的位移和加速度 PDF 进一步缩小。因此,在参数优化的情况下,所提出的时滞补偿控制方法取得了比未优化更好的控制效果。
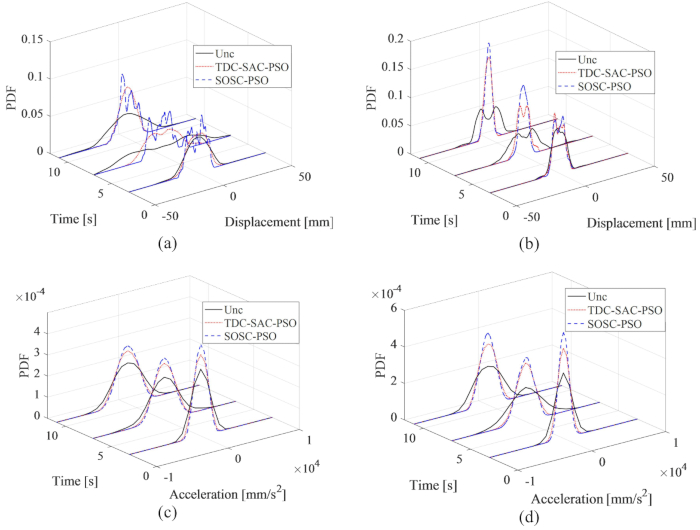
图 16:不同控制方法的 1 楼和 3 楼位移和加速度的 PDF。 (A) 一楼的位移;(B) 3 楼的流离失所;(C) 1 楼的加速;(D) 3 楼的加速度。缩写: PDFs = 概率密度函数;unc = 不受控制;TDC-SAC-PSO = 带补偿控制的时间延迟系统;SOSC-PSO = 带时间延迟补偿的随机最优半主动控制方法 请单击此处查看此图的较大版本。
位移、速度、加速度和控制力的可靠性值如 表 5 所示。SOSC-PSO 方法的可靠性值高于 TDC-SAC-PSO 方法。同时,控制力仍然保持了足够的可靠性。因此,参数的优化对于实现基于 MR 阻尼器的控制方法的最佳控制效果是必要的。
| 控制方式 | 位移 | 速度 | 加速度 | 1楼 的控制力 | 3楼 的控制力 |
| 蜻蜓 | 0.0114 | 0.5822 | 0.6372 | -- | -- |
| TDC-SAC-PSO | 0.806 | 0.8674 | 0.8037 | 1 | 1 |
| SOSC-PSO | 0.9544 | 0.9314 | 0.8788 | 1 | 1 |
表 5:由不同方法控制的结构的可靠性。 缩写: unc = 不受控制;TDC-SAC-PSO = 带补偿控制的时间延迟系统;SOSC-PSO = 具有时间延迟补偿的随机最优半主动控制方法。
结果
针对时滞对基于 MR 阻尼器的方法控制效果的影响,该文提出了一种具有时滞补偿的半主动控制方法。在所提出的方法中,基于可靠性准则对关键参数进行了优化。通过比较控制效果,得出以下结论:
(1) 基于 MR 阻尼器的半主动控制方法比主动控制方法更鲁棒。即使有时间延迟,半主动控制系统仍然达到一定的控制效果,但不会产生不稳定。
讨论
随着物理随机最优控制理论(PSO)的引入,该文提出了一种具有时滞补偿的随机最优半主动控制方法(SOSC-PSO),旨在保持MR阻尼器控制结构的可靠性。为了补偿所提出的方法中的时间延迟,半主动控制力不仅推导出为当前状态的函数,而且推导出离散状态空间中先前时间步中的状态和控制力的函数。为了实现可靠性的最优控制效果,基于结构控制系统的可靠性准则对 SOSC...
披露声明
所有作者都没有需要声明的利益冲突。
致谢
作者衷心感谢河北省自然科学基金(第 E2023210007 号)的支持。
材料
| Name | Company | Catalog Number | Comments |
| MATLAB | MathWorks | 2016 | Using for the calculation of the proposed method |
参考文献
- Yao, J. T. P. Concept of structural control. J Struct Div. 98 (7), 1567-1574 (1972).
- Liu, J., Silva, C. E., Dyke, S. J., Wu, Y., Liu, H. Using real-time hybrid simulation for active mass damper experimentation and validation. Mech Mach Theory. 191, 105474 (2024).
- Pan, H., Li, C., Cao, L. Bidirectional pendulum-type tuned tendem mass dampers-inerters for integrated control of alongwind and crosswind responses in super-tall buildings. J Build Eng. 100, 111676 (2025).
- Housner, G. W. et al. Structural control: past, present, and future. J Eng Mech. 123 (9), 897-971 (1997).
- Rahman, M., Ong, Z. C., Chong, W. T., Julai, S. Smart Semi-active PID-ACO control strategy for tower vibration reduction in Wind Turbines with MR damper. Earthq Eng Eng Vib. 18 (4), 887-902 (2019).
- Morales-Beltran, M., Paul, J. Active and semi-active strategies to control building structures under large earthquake motion. J Earthquake Eng. 19 (7), 1086-1111 (2015).
- Shu, Z., You, R., Xie, Y. Viscoelastic dampers for vibration control of building structures: A state-of-art review. J Earthq Eng. 28 (12), 3558-3585 (2024).
- Soong, T. T. Active structural control: Theory and practice. Longman Scientific & Technical. New York (1990).
- Wan, H. P., Ma, Q., Dong, G. S., Luo, Y., Ni, Y. Q. Data-driven model reduction approach for active vibration control of cable-strut structures. Eng Struct. 302, 117434 (2024).
- Cao, L., Li, X., Huang, Y., Li, C., Pan, H. High robust eddy current tuned tandem mass dampers-inerters for structures under the ground acceleration. Soil Dyn Earthq Eng. 188, 109040 (2025).
- Chha, H., Peng, Y. Adaptive semiactive control of structure with magnetorheological dampers using wavelet packet transform. Adv Struct Eng. 27 (9), 1509-1527 (2024).
- Zeng, X., Peng, Y., Chen, J. Serviceability-based damping optimization of randomly wind-excited high-rise buildings. Struct Des Tall Spec. 26 (11), e1371 (2017).
- Li, C., Chang, K., Cao, L., Huang, Y. Performance of a nonlinear hybrid base isolation system under the ground motions. Soil Dyn Earthq Eng. 143, 106589 (2021).
- Cao, L., Li, C. A high performance hybrid passive base-isolated system. Struct Control Health Monitoring. 29 (3), e2887 (2022).
- Zareie, S., Issa, A. S., Seethaler, R., Zabihollah, A., Ahmad, R. A novel SMA-magnetorheological hybrid bracing system for seismic control. Eng Struct. 244, 112709 (2021).
- Chu, S. Y., Soong, T. T., Reinhorn, A. M. Active, hybrid and semi-active structural control. John Wiley & Sons, New York (2005).
- Danielian, S. A., Jabbari, F., Zareian, F. Effects and distribution of semi-active resettable springs on the seismic response of asymmetric structures. Earthq Eng Struct D. 52 (10). 2966-2982 (2023).
- Shuang, Z., Wenliuhan, H. S., Liu, Y. H., Inoue, N., Zhai, Z. P. Seismic response control for bridge piers with semi-active MR damper based on displacement feedback. J Earthq Eng. 28 (3). 849-865 (2024).
- Wang, Y., Dyke, S. Modal-based LQG for smart base isolation system design in seismic response control. Struct Control Health Monitoring. 20 (5), 753-768 (2013).
- Desai, R. M. et al. Performance evaluation of a single sensor control scheme using a twin-tube MR damper based semi-active suspension. J Vib Eng Technol. 9, 1193-1210 (2021).
- Abdi, M. S., Nekooei, M. Jafari, M. A. Seismic control of multi-degrees-of-freedom structures by vertical mass isolation method using MR dampers. Earthq Eng Eng Vib. 23 (2), 503-510 (2024).
- Bhowmik, K., Debnath, N. Semi-active vibration control of soft-storey building with magnetorheological damper under seismic excitation. J Vib Eng Technol. 12 (4), 6943-6961 (2024).
- Yang, J. N., Akbarpour, A., Askar, G. Effect of time delay on control of seismic-excited buildings. J Struct Eng. 116 (10), 2801-2814 (1990).
- Temimi, H., Ben-Romdhane, M., El-Borgi, S., Cha, Y. Time-delay effects on controlled seismically excited linear and nonlinear structures. Int J Struct Stab Dyn. 16 (7), 1550031 (2016).
- Peng, J., Wang, L., Zhao, Y., Lenci, S. Time-delay dynamics of the MR damper-cable system with one-to-one internal resonances. Nonlinear Dynamics. 105 (2), 1343-1356 (2021).
- Cha, Y. J., Agrawal, A. K., Dyke, S. J. Time delay effects on large-scale MR damper based semi-active control strategies. Smart Mater Struct. 22 (1), 015011 (2013).
- Yu, Y. et al. Experimental study of wireless structural vibration control considering different time delays. Smart Mater Struct. 24, 045005 (2015).
- Ahmadizadeh, M., Mosqueda, G., Reinhorn, A. M. Compensation of actuator delay and dynamics for real-time hybrid structural simulation. Earthq Eng Struct Dyn. 37 (1), 21-42 (2008).
- Bathaei, A., Zahrai, S. M. Compensating time delay in semi-active control of a SDOF structure with MR damper using predictive control. Struc Eng Mech. 82 (4), 445-458 (2022).
- Dyke, S. J., Spencer, Jr, B. F., Sain, M. K., Carlson, J. D. Modeling and control of magnetorheological dampers for seismic response reduction. Smart Mater Struct. 5 (5), 565-575 (1996).
- Ying, Z. G., Ni, Y. Q., Ko, J. M. A semi-active stochastic optimal control strategy for nonlinear structural systems with MR dampers. Smart Struct Syst. 5 (1), 69-79 (2009).
- Rosol, M., Martynowicz, P. Implementation of the LQG controller for a wind turbine tower-nacelle model with a MR tuned vibration absorber. J Theor App Mech-Pol. 54 (4), 1109-1123 (2016).
- Lyu, M. Z., Feng, D. C., Chen, J. B., Li, J. A decoupled approach for determination of the joint probability density function of a high-dimensional nonlinear stochastic dynamical system via the probability density evolution method. Comput Method Appl M. 418 (A), 116443 (2024).
- Chha, H., Peng, Y. Multiscale stochastic optimal control of hysteretic structures based on wavelet transform and probability density evolution method. Eng Computation. 41 (4), 865-896 (2024).
- Li, J., Peng, Y. B., Chen, J. B. A physical approach to structural stochastic optimal controls. Probabilist Eng Mech. 25 (1), 127-141 (2010).
- Peng, Y. B., Yang, J. G., Li, J. Seismic risk-based stochastic optimal control of structures using magnetorheological dampers. Nat Hazards Rev. 18 (1), B4016001 (2017).
- Dong, X. M., Yu, M., Li, Z., Liao, C., Chen, W. Neural network compensation of semi-active Control for magneto-rheological suspension with time delay uncertainty. Smart Mater Struct. 18 (1), 015014 (2008).
- Peng, Y. B., Zhang, Z. Optimal MR damper-based semiactive control scheme for strengthening seismic capacity and structural reliability. J Eng Mech. 146 (6), 04020045 (2020).
- Luo, M. X., Gao, M. Cai, G. Delayed full-state feedback control of airfoil flutter using sliding mode control method. J Fluid Struct. 61, 262-273 (2016).
- Xu, J., Chung, K. W., Chan, C. L. An efficient method for studying weak resonant double Hopf bifurcation in nonlinear systems with delayed feedbacks. Siam J Appl Dyn Syst. 6 (1), 29-60 (2007).
- Yang, J. S., Jensen, H., Chen, J. B. Structural optimization under dynamic reliability constraints utilizing probability density evolution method and metamodels in augmented input space. Struct Multidiscip Optimization. 65, 107 (2022).
- Li, J., Chen, J. B. Stochastic dynamics of structures. John Wiley & Sons, Singapore (2009).
- Peng, Y. B., Li, J. Stochastic optimal control of structures. Springer (2019).
- Dowrick, C. Beyond depression: A new approach to understanding and management. Oxford University Press (2009).
- Wang, D., Li, J. Physical random function model of ground motions for engineering purposes. Sci China Technol Sci. 54 (1), 175-182 (2011).
- Wang, D., Li, J. A random physical model of seismic ground motion field on local engineering site. Sci China Technol Sci. 55 (7), 2057-2065 (2012).
- Chen, J. B., Li, J. Strategy for selecting representative points via tangent spheres in the probability density evolution method. Int J Numer Meth Eng. 74 (13), 1988-2014 (2008).
转载和许可
请求许可使用此 JoVE 文章的文本或图形
请求许可探索更多文章
This article has been published
Video Coming Soon
版权所属 © 2025 MyJoVE 公司版权所有,本公司不涉及任何医疗业务和医疗服务。