È necessario avere un abbonamento a JoVE per visualizzare questo. Accedi o inizia la tua prova gratuita.
Research Article
Metodo di controllo stocastico semi-attivo della struttura basato su smorzatori magnetoreologici considerando il ritardo
In questo articolo
Riepilogo
In questo documento viene proposto un metodo di controllo semiattivo ottimale stocastico con compensazione del ritardo (SOSC-PSO), progettato per mantenere l'affidabilità delle strutture controllate dagli smorzatori MR.
Abstract
L'uso di smorzatori magnetoreologici (MR) nei sistemi di controllo semi-attivi affronta una sfida fondamentale: il ritardo causato dai processi di feedback, che riduce l'affidabilità delle strutture di ingegneria civile sotto eccitazioni stocastiche. Questo articolo propone un metodo di controllo semi-attivo ottimale stocastico con compensazione del ritardo (SOSC-PSO), sfruttando la teoria del controllo ottimale stocastico fisico (PSO) per affrontare questo problema e mantenere l'affidabilità strutturale. Il metodo proposto deriva la forza di controllo semi-attiva in funzione sia dello stato attuale che di quello precedente, compensando i ritardi nel processo di controllo. Per ottimizzare l'efficacia del controllo, i parametri chiave vengono regolati in base a un criterio di affidabilità del sistema. Le analisi di validazione su strutture a singolo grado di libertà e multigrado di libertà sotto eccitazioni sismiche stocastiche mostrano che i ritardi temporali compromettono significativamente le prestazioni degli smorzatori MR. Tuttavia, il metodo SOSC-PSO con compensazione del ritardo migliora significativamente l'efficacia del controllo e, con parametri ottimizzati, migliora l'affidabilità del sistema di controllo strutturale oltre i metodi senza ottimizzazione dei parametri.
Introduzione
Migliorare le prestazioni delle strutture ingegneristiche di fronte a eventi catastrofici, come terremoti e venti estremi, rimane una preoccupazione primaria all'interno della comunità dell'ingegneria civile. È stato dimostrato che il controllo strutturale, una tecnica efficace per ridurre le vibrazioni, migliora sia la sicurezza che la funzionalità di tali strutture 1,2,3. Negli ultimi decenni, a questo scopo sono stati sviluppati vari metodi e tecnologie avanzate. Questi metodi possono essere classificati in quattro categorie in base al tipo di energia utilizzata per azionare i dispositivi di controllo: sistemi di controllo attivi, semi-attivi, passivi e ibridi 4,5,6,7.
Nel controllo attivo, la forza di controllo richiesta viene applicata direttamente attraverso i dispositivi di controllo, il che richiede una notevole quantità di energia 8,9,10. Il controllo semiattivo, d'altra parte, comporta la regolazione delle proprietà dei dispositivi di controllo (come lo smorzamento o la rigidità) in base ai segnali di controllo, richiedendo molta meno energia rispetto ai sistemi attivi11. Il controllo passivo, al contrario, si basa sulla dissipazione di energia senza alcun input di energia esterna nel sistema 12,13,14. I sistemi ibridi combinano le caratteristiche delle strategie di controllo attivo/semi-attivo e passivo per ottenere prestazioni più efficaci15. Tra questi approcci, il controllo semi-attivo è considerato particolarmente promettente grazie al suo equilibrio tra basso consumo energetico e alta efficienza 16,17,18. L'ammortizzatore magnetoreologico (MR), con le sue caratteristiche di smorzamento dinamico superiori, è considerato uno dei dispositivi di controllo semi-attivo più efficaci 19,20,21,22.
Tuttavia, sorge una sfida nei sistemi di controllo semi-attivi che utilizzano smorzatori MR, poiché la logica di retroazione introduce inevitabilmente ritardi temporali. Questi ritardi sono tipicamente causati da diversi fattori 23,24,25, tra cui: (i) l'acquisizione e l'elaborazione dei dati del sensore, (ii) il calcolo della forza di controllo richiesta dal controller26, (iii) la trasmissione del segnale attraverso trasduttori agli smorzatori MR27 e (iv) l'effettiva generazione di forza da parte degli stessi smorzatori MR 28. Tali ritardi temporali possono portare a discrepanze tra la forza di controllo prodotta e la forza attesa dalla struttura, compromettendo in modo significativo l'efficacia del controllo29. Sfortunatamente, la maggior parte degli algoritmi di controllo esistenti per gli smorzatori RM non tiene conto di questi ritardi.
Inoltre, a causa della casualità intrinseca degli eventi catastrofici, qualsiasi algoritmo di controllo semi-attivo efficace deve essere in grado di mantenere le prestazioni in condizioni di eccitazioni stocastiche. Il metodo di controllo Linear Quadratic Gaussian (LQG), una classica tecnica di ottimizzazione stocastica, è stato esplorato per mitigare le vibrazioni in strutture dotate di smorzatori MR. Ad esempio, Dyke et al. hanno proposto una strategia di controllo ottimale con clipping LQG per migliorare la risposta sismica delle strutture dotate di smorzatori MR, utilizzando il feedback di accelerazione30. Ying et al. hanno introdotto una strategia di controllo ottimale stocastico semi-attivo non clippato per strutture non lineari con smorzatori MR, incorporando tecniche di media stocastica e programmazione dinamica31. Altri studi hanno applicato il controllo LQG su base modale per migliorare le prestazioni sismiche degli edifici isolati alla base19 e ne hanno analizzato l'efficacia per la mitigazione delle vibrazioni nelle torri delle turbine eoliche32. Tuttavia, i metodi LQG classici, che presuppongono il rumore gaussiano bianco, non sono adatti per modellare la natura non stazionaria e non gaussiana delle eccitazioni del mondo reale come terremoti o venti forti. Per affrontare questo problema, è stato sviluppato il concetto di controllo stocastico ottimale (PSO) su base fisica33,34, che supera i limiti dei metodi tradizionali LQG e offre un quadro più accurato per la gestione di diverse eccitazioni stocastiche35. Gli studi hanno dimostrato che il controllo ottimale stocastico semi-attivo basato su PSO migliora significativamente la mitigazione delle vibrazioni per strutture lineari e non lineari soggette a forze sismiche stocastiche36.
Pertanto, c'è un urgente bisogno di un robusto metodo di controllo semi-attivo che compensi i ritardi, migliorando l'affidabilità delle strutture controllate da smorzatori MR 25,37. Inoltre, per garantire prestazioni di controllo ottimali in condizioni di eccitazioni stocastiche, è essenziale ottimizzare i parametri critici del metodo di controllo proposto utilizzando un approccio basato sull'affidabilità. Pertanto, in questo articolo viene proposto un metodo di controllo semi-attivo ottimale stocastico con compensazione del ritardo (SOSC-PSO) per migliorare l'affidabilità delle strutture con smorzatori MR.
Protocollo
1. Metodo di controllo semi-attivo stocastico ottimale
Poiché l'effetto di controllo di uno smorzatore MR è significativamente influenzato dall'inevitabile ritardo, viene sviluppato un metodo di controllo semi-attivo con un algoritmo di compensazione del ritardo per aumentare le prestazioni della struttura controllata. Inoltre, la casualità insita nelle eccitazioni esterne causa le evidenti incertezze delle risposte dinamiche. Il controllo PSO viene introdotto per ottimizzare i parametri critici del metodo proposto per garantire l'affidabilità del sistema di controllo della struttura.
1.1 Algoritmo di compensazione del controllo semi-attivo
Senza perdita di generalità, si consideri una struttura n-Degree-Of-Freedoms (n-DOF) controllata da smorzatori MR con ritardo temporale, di cui l'equazione del moto soggetta a eccitazioni stocastiche è data da:
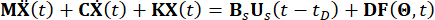 (1)
(1)
Dove  rappresentano rispettivamente le matrici n x n di massa, smorzamento e rigidezza della struttura; n rappresenta il numero di gradi di libertà della struttura controllata. I vettori di spostamento, velocità e accelerazione della struttura sono rappresentati rispettivamente da
rappresentano rispettivamente le matrici n x n di massa, smorzamento e rigidezza della struttura; n rappresenta il numero di gradi di libertà della struttura controllata. I vettori di spostamento, velocità e accelerazione della struttura sono rappresentati rispettivamente da 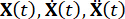 , . I piccoli punti uno e due sopra i simboli rappresentano la prima e la seconda derivata. Us (t - tD) rappresenta il vettore r-dimensionale della forza di controllo ritardata nel tempo degli smorzatori MR e r rappresenta il numero di smorzatori; t rappresenta il tempo; tD denota il ritardo temporale, assunto come uniforme in tutti gli smorzatori in questo studio, dove
, . I piccoli punti uno e due sopra i simboli rappresentano la prima e la seconda derivata. Us (t - tD) rappresenta il vettore r-dimensionale della forza di controllo ritardata nel tempo degli smorzatori MR e r rappresenta il numero di smorzatori; t rappresenta il tempo; tD denota il ritardo temporale, assunto come uniforme in tutti gli smorzatori in questo studio, dove 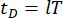 , con qui il numero
, con qui il numero 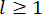 integrale , e
integrale , e 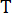 denota il periodo di campionamento.
denota il periodo di campionamento. 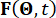 rappresenta il vettore p-dimensionale delle eccitazioni stocastiche e
rappresenta il vettore p-dimensionale delle eccitazioni stocastiche e  rappresenta il vettore del parametro stocastico che caratterizza la casualità associata alle eccitazioni esterne. La dimensione di
rappresenta il vettore del parametro stocastico che caratterizza la casualità associata alle eccitazioni esterne. La dimensione di  dipende dal modello utilizzato per le eccitazioni esterne ma non è correlata ai gradi di libertà meccanica della struttura. Bs e D sono matrici n x r e n x p che specificano rispettivamente le posizioni degli smorzatori e delle eccitazioni esterne. Nella rappresentazione nello spazio degli stati, l'Eq. (1) è scritta come:
dipende dal modello utilizzato per le eccitazioni esterne ma non è correlata ai gradi di libertà meccanica della struttura. Bs e D sono matrici n x r e n x p che specificano rispettivamente le posizioni degli smorzatori e delle eccitazioni esterne. Nella rappresentazione nello spazio degli stati, l'Eq. (1) è scritta come:
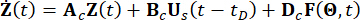 (2)
(2)
Dove 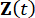 rappresenta il vettore di stato 2n-dimensionale;
rappresenta il vettore di stato 2n-dimensionale; 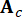 rappresenta la matrice del sistema 2n x 2n;
rappresenta la matrice del sistema 2n x 2n; 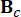 rappresenta la matrice di localizzazione 2n x r degli smorzatori MR;
rappresenta la matrice di localizzazione 2n x r degli smorzatori MR; 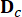 Rappresenta la matrice di localizzazione 2N x P delle eccitazioni esterne. Questi parametri sono espressi come:
Rappresenta la matrice di localizzazione 2N x P delle eccitazioni esterne. Questi parametri sono espressi come:
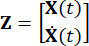 ,
, 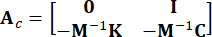 ,
,  ,
, 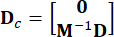 (3)
(3)
Dove 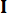 denota una matrice identità con lo stesso ordine di
denota una matrice identità con lo stesso ordine di 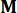 . Per comodità di calcolo, l'equazione dello spazio degli stati continui Eq. (2) può essere espressa in forma discreta come:
. Per comodità di calcolo, l'equazione dello spazio degli stati continui Eq. (2) può essere espressa in forma discreta come:
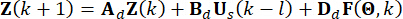 (4)
(4)
Dove il punto 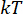 temporale viene semplificato come
temporale viene semplificato come 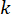 . E
. E  ,
, 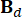 ,
, 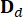 denotano matrici 2n x 2n, 2n x r e 2n x p, che sono espresse come:
denotano matrici 2n x 2n, 2n x r e 2n x p, che sono espresse come:
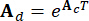 ,
,  ,
, 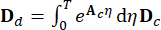 (5)
(5)
Dove 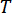 indica il periodo di campionamento.
indica il periodo di campionamento.
Per ottenere un'efficacia simile a quella del controllo attivo, viene proposto un metodo di controllo semplice ed efficiente basato sull'algoritmo Hrovat38 per il controllo MR basato su serrande con ritardo:
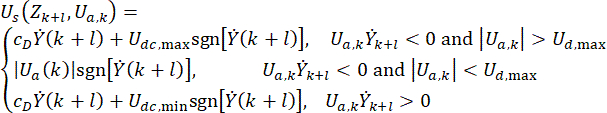 (6)
(6)
dove  rappresenta il segnale della forza di controllo semi-attivo al punto temporale\
rappresenta il segnale della forza di controllo semi-attivo al punto temporale\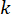 per lo smorzatore MR;
per lo smorzatore MR; 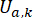 rappresenta la forza di controllo attiva di riferimento con compensazione del ritardo;
rappresenta la forza di controllo attiva di riferimento con compensazione del ritardo;  rappresenta la forza massima di smorzamento dell'ammortizzatore MR, che è variabile;
rappresenta la forza massima di smorzamento dell'ammortizzatore MR, che è variabile; 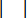 rappresenta il simbolo dell'operazione di valore assoluto;
rappresenta il simbolo dell'operazione di valore assoluto; 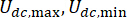 rappresentano le forze coulombiane massime e minime dello smorzatore MR;
rappresentano le forze coulombiane massime e minime dello smorzatore MR;  rappresenta il coefficiente di smorzamento viscoso;
rappresenta il coefficiente di smorzamento viscoso; 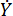 rappresenta l'input di velocità nello smorzatore MR, che è la velocità di movimento del pistone rispetto al cilindro dello smorzatore. Nell'Eq. (6),
rappresenta l'input di velocità nello smorzatore MR, che è la velocità di movimento del pistone rispetto al cilindro dello smorzatore. Nell'Eq. (6),  rappresentano i parametri progettati dello smorzatore MR.
rappresentano i parametri progettati dello smorzatore MR.
L'eq. (6) mostra il calcolo della forza di controllo semiattiva dello smorzatore MR con ritardo. Si è visto che la forza  di controllo semi-attiva, al passo
di controllo semi-attiva, al passo  temporale nell'Eq. (4), è calcolata in base alla forza
temporale nell'Eq. (4), è calcolata in base alla forza  di controllo attiva al passo
di controllo attiva al passo  temporale e alla variabile
temporale e alla variabile 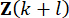 di stato al passo
di stato al passo  temporale dal ritardo dei
temporale dal ritardo dei 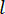 passi temporali. Per ottenere la forza
passi temporali. Per ottenere la forza  di controllo attiva, la funzione di costo convenzionale è stabilita da
di controllo attiva, la funzione di costo convenzionale è stabilita da
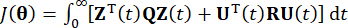 (7)
(7)
Dove  rappresenta la matrice di ponderazione semidefinita positiva simmetrica 2n x 2n dello stato del sistema;
rappresenta la matrice di ponderazione semidefinita positiva simmetrica 2n x 2n dello stato del sistema;  rappresenta la matrice di ponderazione definita positiva simmetrica r x r della forza di controllo. Si vede che l'eccitazione esterna è trascurabile. In realtà, sulla base dell'Eq. (7), il sistema di controllo della struttura può ottenere l'effetto di controllo ottimale qualunque sia il tipo di eccitazione esterna. Come forma discreta, l'Eq. (7) è espressa come39:
rappresenta la matrice di ponderazione definita positiva simmetrica r x r della forza di controllo. Si vede che l'eccitazione esterna è trascurabile. In realtà, sulla base dell'Eq. (7), il sistema di controllo della struttura può ottenere l'effetto di controllo ottimale qualunque sia il tipo di eccitazione esterna. Come forma discreta, l'Eq. (7) è espressa come39:
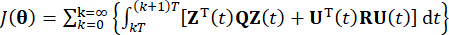 E 8
E 8
La minimizzazione della funzione  di costo porta a un problema di valori estremi condizionali e la forza
di costo porta a un problema di valori estremi condizionali e la forza  di controllo attiva viene calcolata da25:
di controllo attiva viene calcolata da25:
 (9)
(9)
Dove 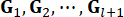 denotano i guadagni di controllo per la variabile
denotano i guadagni di controllo per la variabile 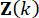 di stato al passo
di stato al passo  temporale e la forza
temporale e la forza 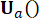 di controllo attiva al passo
di controllo attiva al passo 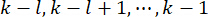 temporale , che è determinata dalle matrici
temporale , che è determinata dalle matrici 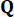 di ponderazione e
di ponderazione e 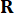 37. Poiché l'inevitabile ritardo temporale, la forza
37. Poiché l'inevitabile ritardo temporale, la forza 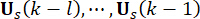 di controllo ottenuta viene agita sulla struttura in punti
di controllo ottenuta viene agita sulla struttura in punti 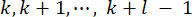 temporali. Pertanto, la forza di controllo attiva nell'Eq. (9) è calcolata da:
temporali. Pertanto, la forza di controllo attiva nell'Eq. (9) è calcolata da:
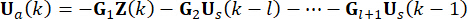 (10)
(10)
Per chiarezza di concezione, la forza di controllo semi-attiva nell'Eq. (10) è espressa come segue sulla base dell'Eq. (6):
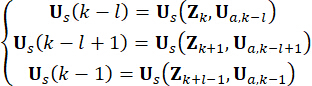 (11)
(11)
Dove  denota la forza di controllo attiva nel punto
denota la forza di controllo attiva nel punto  temporale . Sostituendo l'Eq. (11) con l'Eq. (10),
temporale . Sostituendo l'Eq. (11) con l'Eq. (10),
 (12)
(12)
NOTA: Tutti i valori di stato  dal punto temporale
dal punto temporale  a
a 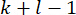 sono necessari per il calcolo .
sono necessari per il calcolo .  Pertanto, viene introdotto il seguente metodo di previsione dello stato40.
Pertanto, viene introdotto il seguente metodo di previsione dello stato40.
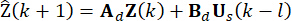 (13)
(13)
Dove  indica la variabile prevista. Con l'iterazione dell'Eq. (13), viene calcolato lo stato
indica la variabile prevista. Con l'iterazione dell'Eq. (13), viene calcolato lo stato  a
a  . La forza di controllo attiva Ua(k) è espressa come:
. La forza di controllo attiva Ua(k) è espressa come:
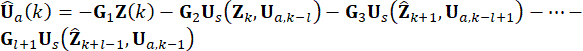 (14)
(14)
La forza di controllo semi-attiva può essere ottenuta combinando le Eq. (6), (12) e (13).
1.2 Analisi dell'affidabilità del sistema di controllo della struttura
Secondo il principio di conservazione della probabilità, il sistema 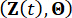 aumentato e
aumentato e 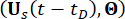 la struttura con smorzatori MR sono conservati in probabilità e sono governati dalle seguenti equazioni generalizzate di evoluzione della densità di probabilità (GDEE)38:
la struttura con smorzatori MR sono conservati in probabilità e sono governati dalle seguenti equazioni generalizzate di evoluzione della densità di probabilità (GDEE)38:
 E 15
E 15
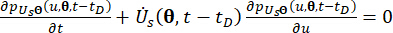 E 16
E 16
Dove  ,
,  denotano le componenti corrispondenti dello stato del sistema e della forza di controllo semi-attiva con ritardo, rispettivamente;
denotano le componenti corrispondenti dello stato del sistema e della forza di controllo semi-attiva con ritardo, rispettivamente; 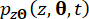 e
e  denotano le funzioni di densità di probabilità congiunte dei sistemi
denotano le funzioni di densità di probabilità congiunte dei sistemi 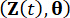 campionari aumentati e
campionari aumentati e 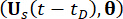 , rispettivamente;
, rispettivamente; 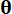 denota il campione all'interno dello spazio campionario di
denota il campione all'interno dello spazio campionario di 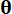 ;
;  e
e  ) denotano le derivate parziali temporali del primo ordine delle componenti dello stato del sistema e della forza di controllo semi-attiva, rispettivamente. Le funzioni
) denotano le derivate parziali temporali del primo ordine delle componenti dello stato del sistema e della forza di controllo semi-attiva, rispettivamente. Le funzioni 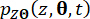 di densità di probabilità congiunte e
di densità di probabilità congiunte e  possono essere ottenute risolvendo le Eq. (15) e (16) con le seguenti condizioni iniziali:
possono essere ottenute risolvendo le Eq. (15) e (16) con le seguenti condizioni iniziali:
 (17)
(17)
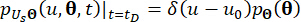 (18)
(18)
Dove 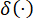 denota la funzione delta di Dirac;
denota la funzione delta di Dirac; 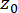 e
e 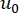 denotano i valori iniziali deterministici di
denotano i valori iniziali deterministici di  e
e 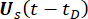 , rispettivamente;
, rispettivamente; 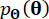 denota la funzione di densità di probabilità del campione
denota la funzione di densità di probabilità del campione 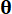 .
.
Le funzioni di densità di probabilità istantanea di  e
e 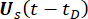 possono essere ottenute dall'integrazione unidimensionale di
possono essere ottenute dall'integrazione unidimensionale di 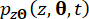 e
e  sul dominio dello spazio campionario:
sul dominio dello spazio campionario:
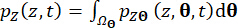 (19)
(19)
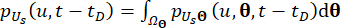 E 20
E 20
Dove 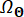 indica il dominio di distribuzione di
indica il dominio di distribuzione di  .
.
Sulla base delle Eq. (19) e (20), si vede che l'informazione probabilistica completa delle grandezze fisiche interessate è facilmente derivabile, se le loro relazioni associate con i parametri dell'algoritmo sono definite. L'affidabilità delle grandezze fisiche interessate può essere calcolata dalla seguente funzione di prestazione pertinente:
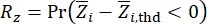 E 21
E 21
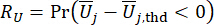 (22)
(22)
Dove 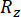 e
e 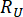 denotano l'affidabilità calcolata rispettivamente della quantità di stato e della forza di controllo semiattiva in questione;
denotano l'affidabilità calcolata rispettivamente della quantità di stato e della forza di controllo semiattiva in questione;  denota il vettore di valori estremi equivalenti della i-esima quantità fisica interessata della struttura controllata;
denota il vettore di valori estremi equivalenti della i-esima quantità fisica interessata della struttura controllata; 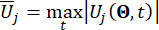 denota il vettore di valori estremi equivalenti della j-esima forza di controllo; il cappello '-' sui simboli indica il vettore di valori estremi equivalenti41;
denota il vettore di valori estremi equivalenti della j-esima forza di controllo; il cappello '-' sui simboli indica il vettore di valori estremi equivalenti41;  denota l'i-esima quantità fisica interessata del k-esimo DOF di struttura controllata;
denota l'i-esima quantità fisica interessata del k-esimo DOF di struttura controllata; 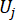 denota la j-esima forza di controllo;
denota la j-esima forza di controllo; 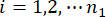 ,
, 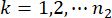 ,
,  ,
, ,
,  e
e  denotano rispettivamente il numero di grandezze fisiche interessate e la DOF della struttura e degli smorzatori MR installati nella struttura.
denotano rispettivamente il numero di grandezze fisiche interessate e la DOF della struttura e degli smorzatori MR installati nella struttura.  e
e 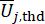 denota le soglie di
denota le soglie di  e
e  ;
;  denota la probabilità dell'evento casuale.
denota la probabilità dell'evento casuale.
1.3 Ottimizzazione dei parametri
Il rapporto tra le ampiezze e  influenza fortemente l'efficacia del
influenza fortemente l'efficacia del  controllo38 nella modalità di controllo in retroazione. Pertanto, per ottenere la migliore efficacia del controllo,
controllo38 nella modalità di controllo in retroazione. Pertanto, per ottenere la migliore efficacia del controllo, e
e  devono essere ottimizzati. Inoltre, come metodo di controllo basato su serrande RM, l'efficacia del controllo è influenzata anche dai parametri del dispositivo,
devono essere ottimizzati. Inoltre, come metodo di controllo basato su serrande RM, l'efficacia del controllo è influenzata anche dai parametri del dispositivo,  nell'Eq. (6). Per ottenere l'affidabilità ottimale del sistema di controllo della struttura, il criterio basato sull'affidabilità è proposto nell'Eq. (25).
nell'Eq. (6). Per ottenere l'affidabilità ottimale del sistema di controllo della struttura, il criterio basato sull'affidabilità è proposto nell'Eq. (25).
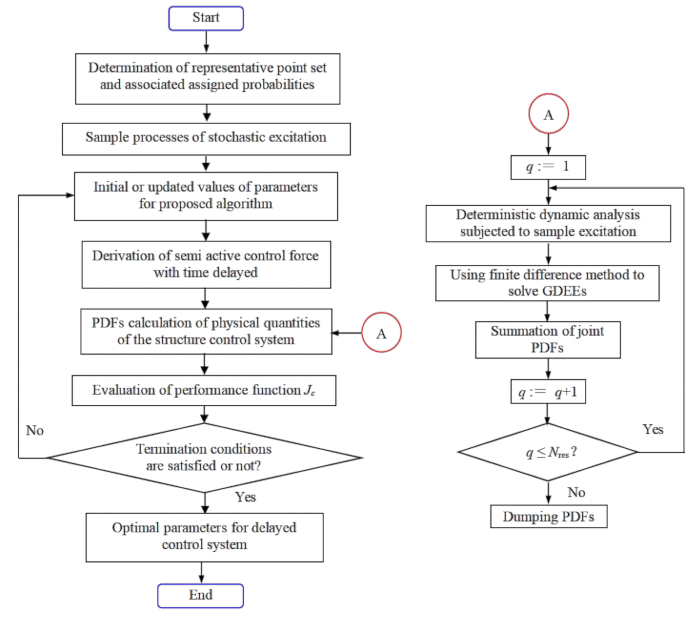
Figura 1: Diagramma di flusso dell'ottimizzazione dei parametri per il controllo stocastico ottimale della struttura semi-attiva con compensazione del ritardo. Abbreviazioni: GDEE = Equazione differenziale generalizzata dell'evento; PDF = Funzione di densità di probabilità. Clicca qui per visualizzare una versione più grande di questa figura.
In sintesi, sono necessari due stadi per eseguire il controllo stocastico ottimale della struttura semi-attiva basato su smorzatori MR con compensazione del ritardo:
1.3.1 Minimizzando la funzione  di costo mostrata nell'Eq. (7), si ottiene la logica di retroazione di stato nel senso dei campioni, cioè Eq. 12)
di costo mostrata nell'Eq. (7), si ottiene la logica di retroazione di stato nel senso dei campioni, cioè Eq. 12)
1.3.2 Riducendo al minimo la funzione  di prestazione basata sull'affidabilità, si ottengono i parametri ottimali nel senso della statistica. La Figura 1 presenta il diagramma di flusso di ottimizzazione dei parametri del controllore nel passaggio 1.3.2.
di prestazione basata sull'affidabilità, si ottengono i parametri ottimali nel senso della statistica. La Figura 1 presenta il diagramma di flusso di ottimizzazione dei parametri del controllore nel passaggio 1.3.2.
I passaggi seguenti nel passaggio 1.3.2, che coinvolgono due livelli di cicli, sono i seguenti:
1.3.2.1 Il partizionamento dello spazio assegnato alla probabilità delle eccitazioni stocastiche, che è caratterizzato dal vettore  del parametro stocastico , consentel'identificazione di un insieme di punti
del parametro stocastico , consentel'identificazione di un insieme di punti 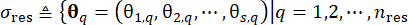 rappresentativi insieme alle probabilità assegnate ad essi associate. Questo approccio consente di ottenere facilmente la generazione efficiente di processi di campionamento per l'eccitazione stocastica, indicata come
rappresentativi insieme alle probabilità assegnate ad essi associate. Questo approccio consente di ottenere facilmente la generazione efficiente di processi di campionamento per l'eccitazione stocastica, indicata come 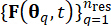 .
.
1.3.2.2 Per l'ottimizzazione dei parametri del sistema di controllo della struttura semi-attivo, inizializzare o aggiornare i valori dei pesi  costo-funzione e
costo-funzione e  . Viene quindi calcolata la forza di controllo del feedback di stato associata con il ritardo, vedi Eq. (12).
. Viene quindi calcolata la forza di controllo del feedback di stato associata con il ritardo, vedi Eq. (12).
1.3.2.3 Ottenere le funzioni di densità di probabilità (PDF) delle risposte strutturali e della forza di controllo risolvendo le GDEE mostrate nelle Eq. (17)–(20):
L'ottimizzazione è il completamento offline, ma non online. Nell'applicazione del metodo proposto nei sistemi di controllo della struttura reale, l'ottimale  e
e  sono stati raggiunti, e l'ottimizzazione non è necessaria nel processo reale applicabile.
sono stati raggiunti, e l'ottimizzazione non è necessaria nel processo reale applicabile.
Analisi dinamica deterministica del sistema di controllo della struttura semi-attiva sottoposto ad eccitazione campionaria, mediante la quale vengono calcolate le grandezze 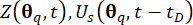 fisiche interessate e le loro derivate
fisiche interessate e le loro derivate  .
.
Impiegando un metodo alle differenze finite, come lo schema di Lax-Wendroff modificato con proprietà di variazione totale decrescente (TVD), le equazioni differenziali generalizzate (GDEE) possono essere risolte e possono essere derivate soluzioni numeriche per le funzioni 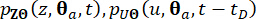 di densità di probabilità congiunte.
di densità di probabilità congiunte.
Ripetendo i due passaggi precedenti dell'analisi dinamica deterministica e del metodo delle differenze finite, e passando su tutti i punti 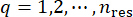 rappresentativi, le funzioni di densità di probabilità possono essere ottenute per sommatoria:
rappresentativi, le funzioni di densità di probabilità possono essere ottenute per sommatoria:
 (23)
(23)
 (24)
(24)
Dove  rappresenta la misura dell'area del sottodominio associato al punto
rappresenta la misura dell'area del sottodominio associato al punto 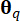 di campionamento . Il metodo utilizzato per risolvere l'equazione differenziale generalizzata dell'evento (GDEE) è noto come metodo di evoluzione della densità di probabilità (PDEM)42.
di campionamento . Il metodo utilizzato per risolvere l'equazione differenziale generalizzata dell'evento (GDEE) è noto come metodo di evoluzione della densità di probabilità (PDEM)42.
1.3.2.4 Per valutarne l'affidabilità vengono utilizzati i PDF delle grandezze fisiche rilevanti, che vengono poi incorporate nella funzione  di prestazione del criterio probabilistico.
di prestazione del criterio probabilistico.
1.3.2.5 Valutare se i criteri di terminazione per il processo di ottimizzazione dei parametri sono stati soddisfatti. Se le condizioni non sono soddisfatte, tornare al passaggio 1.3.2.2; In caso affermativo, è possibile determinare i parametri ottimali per il sistema di controllo ritardato. In questo lavoro, il toolbox dell'algoritmo genetico (GA) in MATLAB viene utilizzato per l'ottimizzazione dei parametri, che facilita gli aggiornamenti dei parametri e definisce le condizioni di terminazione. Con l'algoritmo genetico, i valori ottimali possono essere raggiunti entro dieci iterazioni e la convergenza è stabile senza problemi di minimi locali. Sebbene il costo computazionale del GA sia maggiore dell'ottimizzazione dello sciame di particelle o dei metodi basati sul gradiente, il GA è in grado di affrontare problemi complessi e non differenziabili, come quello in questo manoscritto. Pertanto, viene applicato l'AG. E poiché la proprietà di convergenza rapida, il costo computazionale di GA è accettabile.
1.3.2.6 Per ottenere un controllo ottimale dell'affidabilità, viene formulata la seguente funzione  di prestazione. Minimizza
di prestazione. Minimizza  per determinare i valori ottimali dei parametri
per determinare i valori ottimali dei parametri  e
e  :
:
 } (25)
} (25)
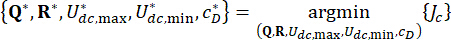 E 26
E 26
Come accennato in precedenza, le matrici di ponderazione del controller sono simmetriche, dove gli elementi in matrice  corrispondono ai pesi assegnati allo spostamento, alla velocità e alla loro interazione, mentre gli elementi in matrice
corrispondono ai pesi assegnati allo spostamento, alla velocità e alla loro interazione, mentre gli elementi in matrice  rappresentano i pesi relativi alla forza di controllo. Sulla base dei risultati di studi precedenti38, è stato osservato che variare le configurazioni dei pesi
rappresentano i pesi relativi alla forza di controllo. Sulla base dei risultati di studi precedenti38, è stato osservato che variare le configurazioni dei pesi  costo-funzione e
costo-funzione e  ha un impatto minimo sull'efficacia del controllo. Di conseguenza, in questo studio viene adottata una configurazione semplificata, come descritto di seguito:
ha un impatto minimo sull'efficacia del controllo. Di conseguenza, in questo studio viene adottata una configurazione semplificata, come descritto di seguito:
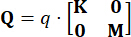 ,
, 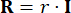 (27)
(27)
Dove 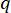 indica il coefficiente della matrice di ponderazione dello stato da definire;
indica il coefficiente della matrice di ponderazione dello stato da definire; 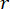 indica il coefficiente della matrice di ponderazione del controllo da definire;
indica il coefficiente della matrice di ponderazione del controllo da definire; 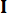 indica la matrice identità. L'effetto di controllo è influenzato dal rapporto tra
indica la matrice identità. L'effetto di controllo è influenzato dal rapporto tra 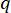 a
a 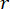 ma non dai valori stessi. Inoltre,
ma non dai valori stessi. Inoltre, 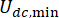 nell'Eq. (6) denota la forza coulombica minima dello smorzatore MR, il che significa che
nell'Eq. (6) denota la forza coulombica minima dello smorzatore MR, il che significa che  con l'ingresso di corrente nello smorzatore pari a zero. Quindi, l'Eq. (26) può essere ulteriormente espressa come:T
con l'ingresso di corrente nello smorzatore pari a zero. Quindi, l'Eq. (26) può essere ulteriormente espressa come:T
 (28)
(28)
Dove 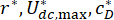 sono i coefficienti ottimali di preoccupazione. Per renderli ragionevoli in ingegneria, le gamme ottimali si basano sulla capacità produttiva delle fabbriche di ammortizzatori MR.
sono i coefficienti ottimali di preoccupazione. Per renderli ragionevoli in ingegneria, le gamme ottimali si basano sulla capacità produttiva delle fabbriche di ammortizzatori MR.
Ovviamente, i parametri ottimali ottenuti dall'Eq. (28) mantengono l'efficacia di controllo ottimale dell'algoritmo di controllo semi-attivo proposto con ritardo, che consente al sistema di controllo della struttura di raggiungere l'affidabilità ottimale bilanciata soggetta a eccitazioni stocastiche.
2. Caso di studio
Per analizzare l'efficacia del metodo di controllo semi-attivo proposto con compensazione del ritardo temporale per uno smorzatore MR, una struttura a telaio di taglio planare a un piano collegata a uno smorzatore MR è stata sottoposta al movimento sismico stocastico orizzontale del suolo, come mostrato nella Figura 2. I parametri del sistema di struttura semi-attivamente controllato sono i seguenti: massa 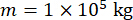 della struttura, frequenza
della struttura, frequenza  circolare naturale, rapporto
circolare naturale, rapporto 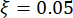 di smorzamento. In base all'esperienza passata e alle scale degli smorzatori esistenti sul mercato, i valori soglia di spostamento strutturale, velocità, accelerazione e forza di controllo sono rispettivamente 10 mm, 100 mm/s, 1.500 mm/s2 e 150 kN. Per rappresentare il moto stocastico sismico del suolo, è stato impiegato il modello stocastico del movimento del suolo fisicamente motivato43:
di smorzamento. In base all'esperienza passata e alle scale degli smorzatori esistenti sul mercato, i valori soglia di spostamento strutturale, velocità, accelerazione e forza di controllo sono rispettivamente 10 mm, 100 mm/s, 1.500 mm/s2 e 150 kN. Per rappresentare il moto stocastico sismico del suolo, è stato impiegato il modello stocastico del movimento del suolo fisicamente motivato43:
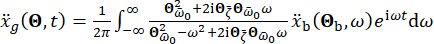 (29)
(29)
Dove 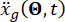 rappresenta il movimento del suolo nel dominio del tempo nel sito di ingegneria e
rappresenta il movimento del suolo nel dominio del tempo nel sito di ingegneria e 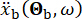 denota il movimento del suolo nel dominio della frequenza al substrato roccioso. Il vettore
denota il movimento del suolo nel dominio della frequenza al substrato roccioso. Il vettore  caratterizza la natura stocastica del movimento del suolo sulla superficie del sito di ingegneria. I parametri
caratterizza la natura stocastica del movimento del suolo sulla superficie del sito di ingegneria. I parametri 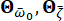 sono variabili stocastiche che descrivono le caratteristiche del suolo del sito, tra cui la frequenza
sono variabili stocastiche che descrivono le caratteristiche del suolo del sito, tra cui la frequenza  predominante e lo smorzamento
predominante e lo smorzamento  equivalente. Il vettore
equivalente. Il vettore 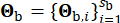 rappresenta la natura stocastica del movimento del suolo sul substrato roccioso, che è influenzato dalle proprietà della sorgente e dal percorso di propagazione, indicando
rappresenta la natura stocastica del movimento del suolo sul substrato roccioso, che è influenzato dalle proprietà della sorgente e dal percorso di propagazione, indicando 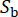 il numero di variabili stocastiche coinvolte in questa fase.
il numero di variabili stocastiche coinvolte in questa fase.  si riferisce alla frequenza circolare e i è l'unità immaginaria.
si riferisce alla frequenza circolare e i è l'unità immaginaria.
La frequenza  predominante e il rapporto
predominante e il rapporto  di smorzamento equivalente del sito di ingegneria sono parametri chiave che caratterizzano le proprietà dinamiche del terreno del sito. La distribuzione probabilistica e i parametri statistici di queste grandezze possono essere determinati sulla base delle registrazioni di accelerazione sismica raccolte da una specifica classe di siti di ingegneria. A scopo illustrativo, è stata presa in considerazione una classe di sito con un intervallo di velocità delle onde trasversali di [150, 250] m/s e il periodo caratteristico di progetto del movimento del suolo è stato impostato a 0,45 s.
di smorzamento equivalente del sito di ingegneria sono parametri chiave che caratterizzano le proprietà dinamiche del terreno del sito. La distribuzione probabilistica e i parametri statistici di queste grandezze possono essere determinati sulla base delle registrazioni di accelerazione sismica raccolte da una specifica classe di siti di ingegneria. A scopo illustrativo, è stata presa in considerazione una classe di sito con un intervallo di velocità delle onde trasversali di [150, 250] m/s e il periodo caratteristico di progetto del movimento del suolo è stato impostato a 0,45 s.
I parametri  critici sono
critici sono  stati trattati come variabili stocastiche reciprocamente indipendenti, entrambi seguendo una distribuzione log-normale per l'identificazione dei parametri. I parametri statistici erano i seguenti: le medie di
stati trattati come variabili stocastiche reciprocamente indipendenti, entrambi seguendo una distribuzione log-normale per l'identificazione dei parametri. I parametri statistici erano i seguenti: le medie di  ,
,  erano rispettivamente 12 rad/s e 0,1. I coefficienti di variazione di
erano rispettivamente 12 rad/s e 0,1. I coefficienti di variazione di  e
e  erano rispettivamente 0,42 e 0,35. Il movimento del suolo sul substrato roccioso è stato modellato come un processo di rumore bianco gaussiano con un'ampiezza di Fourier di 0,20 m/s2, corrispondente a un picco di accelerazione del suolo di 0,11 g. L'angolo di fase utilizzato per generare il movimento del substrato roccioso è stato indicato come
erano rispettivamente 0,42 e 0,35. Il movimento del suolo sul substrato roccioso è stato modellato come un processo di rumore bianco gaussiano con un'ampiezza di Fourier di 0,20 m/s2, corrispondente a un picco di accelerazione del suolo di 0,11 g. L'angolo di fase utilizzato per generare il movimento del substrato roccioso è stato indicato come 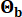 . Pertanto, Sb = 1 e
. Pertanto, Sb = 1 e 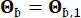 . Questo approccio può essere considerato come la modellazione di movimenti stocastici condizionali del terreno con una data probabilità di superamento44. L'ipotesi della distribuzione log-normale è ampiamente utilizzata nella modellazione del movimento del suolo grazie alla sua capacità di catturare la natura distorta dei parametri di movimento del suolo osservati.
. Questo approccio può essere considerato come la modellazione di movimenti stocastici condizionali del terreno con una data probabilità di superamento44. L'ipotesi della distribuzione log-normale è ampiamente utilizzata nella modellazione del movimento del suolo grazie alla sua capacità di catturare la natura distorta dei parametri di movimento del suolo osservati.
Per valutare la sensibilità di questa ipotesi, le analisi aggiuntive che utilizzano distribuzioni probabilistiche alternative, comprese le distribuzioni normali e gamma, sono state condotte in altre ricerche 45,46. I risultati indicano che, mentre le tendenze generali rimangono coerenti, la distribuzione log-normale fornisce il miglior adattamento ai dati osservati, in particolare per catturare il comportamento della coda delle misure di intensità del movimento al suolo
In virtù del metodo47 delle sfere tangenti, è stata selezionata una raccolta di 221 punti rappresentativi con probabilità assegnate associate e sono state sintetizzate accelerazioni di terra rappresentative. La frequenza di campionamento era di 50 Hz e la durata dei movimenti del suolo era di 20,48 s. Per assegnare un'intensità non stazionaria al movimento simulato del suolo, è stata utilizzata una funzione di modulazione uniforme e la sua formulazione è stata la seguente:42:
 (30)
(30)
Dove  prendere 2 e 16 s, rispettivamente.
prendere 2 e 16 s, rispettivamente.
La media e la deviazione standard del movimento sismico stocastico del suolo e una storia temporale del movimento sismico rappresentativo del suolo sono mostrate nella Figura 3. L'ampiezza della media (0,06 m/s2) era ~8% dell'ampiezza della deviazione standard (0,8 m/s2), indicando che il modello stocastico del movimento del suolo fisicamente motivato mostrava la proprietà della media zero. Nel frattempo, il movimento sismico del suolo ha mostrato notevoli comportamenti non stazionari sia nel dominio temporale che in quello della frequenza.
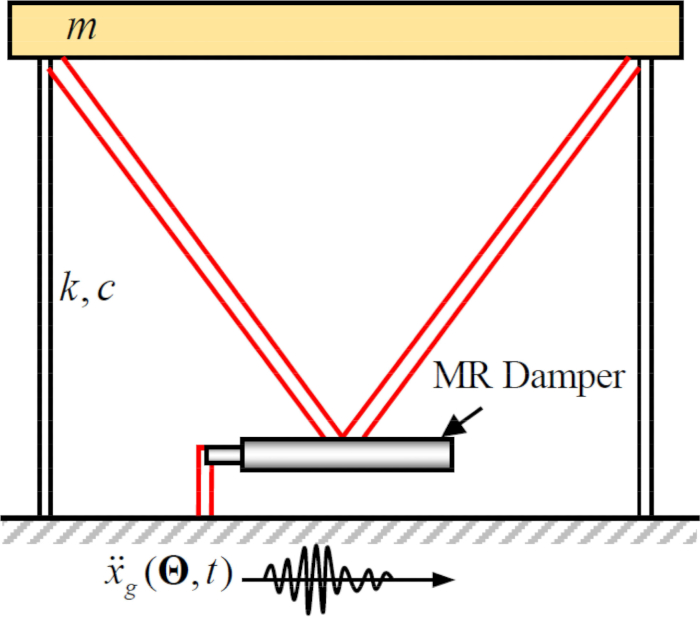
Figura 2: Schizzo di un telaio a taglio a un piano con uno smorzatore magnetoreologico. 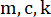 denotare la massa della struttura, il rapporto di smorzamento e la rigidità;
denotare la massa della struttura, il rapporto di smorzamento e la rigidità; 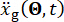 denota l'eccitazione sismica stocastica. Clicca qui per visualizzare una versione più grande di questa figura.
denota l'eccitazione sismica stocastica. Clicca qui per visualizzare una versione più grande di questa figura.
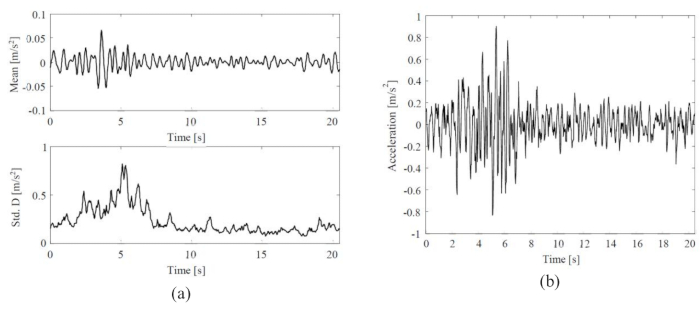
Figura 3: Statistiche e campioni rappresentativi di moti sismici selezionati del suolo. (A) Media e deviazione standard del moto sismico stocastico del suolo; (B) Storia temporale del movimento sismico rappresentativo del suolo. Clicca qui per visualizzare una versione più grande di questa figura.
2.1 Analisi dell'influenza del ritardo
Per analizzare l'influenza del ritardo sull'efficacia del controllo semi-attivo di uno smorzatore RM, la Figura 4 mostra lo spostamento, la velocità e l'accelerazione RMS (radice quadrata media) della struttura controllata. Il rapporto della matrice di ponderazione e i parametri dello smorzatore erano 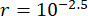 ,
, 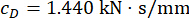 , e
, e 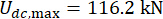 , che sono i risultati ottimizzati senza ritardo38. Le risposte della struttura controllata con ritardo temporale erano maggiori della struttura controllata senza ritardo temporale e l'influenza del ritardo temporale sull'effetto del controllo rappresentava la periodicità insieme all'aumento del ritardo temporale. Poiché il metodo di controllo semi-attivo con uno smorzatore MR è una sorta di metodo di feedback, la periodicità dell'influenza è stata considerata correlata al periodo naturale della struttura controllata (T = 0,56 s).
, che sono i risultati ottimizzati senza ritardo38. Le risposte della struttura controllata con ritardo temporale erano maggiori della struttura controllata senza ritardo temporale e l'influenza del ritardo temporale sull'effetto del controllo rappresentava la periodicità insieme all'aumento del ritardo temporale. Poiché il metodo di controllo semi-attivo con uno smorzatore MR è una sorta di metodo di feedback, la periodicità dell'influenza è stata considerata correlata al periodo naturale della struttura controllata (T = 0,56 s).
Rispetto alle risposte della struttura non controllata, di cui lo spostamento, la velocità e l'accelerazione MRS massimi erano 24,6 mm, 270,0 mm/s e 3111,3 mm/s2, la struttura controllata dallo smorzatore MR ha ottenuto un effetto notevole. A differenza dell'instabilità della struttura controllata attiva con ritardo25, il metodo di controllo semi-attivo basato su smorzatore MR ha comunque ottenuto un certo effetto anche con ritardo temporale.
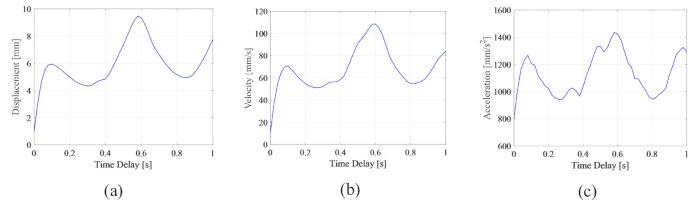
Figura 4: Il massimo quadratico medio delle risposte della struttura controllata nel tempo. (A) Spostamento; (b) velocità; (c) Accelerazione. Clicca qui per visualizzare una versione più grande di questa figura.
Per analizzare l'influenza del ritardo sull'affidabilità di una struttura controllata semi-attivamente, la Figura 5 mostra l'affidabilità dello spostamento, della velocità e dell'accelerazione con l'aumentare del ritardo. L'affidabilità delle risposte della struttura controllata con qualsiasi ritardo temporale era inferiore ai valori senza ritardo, il che significa che l'affidabilità della struttura controllata era diminuita dal ritardo. Nel frattempo, in modo simile all'RMS massimo, l'effetto del controllo dell'affidabilità ha mostrato periodicità con l'aumentare del ritardo. Inoltre, l'affidabilità della struttura controllata, con o senza ritardo, era superiore ai valori delle strutture non controllate con affidabilità di spostamento, velocità e accelerazione 0,0954, 0,1058 e 0,1111.
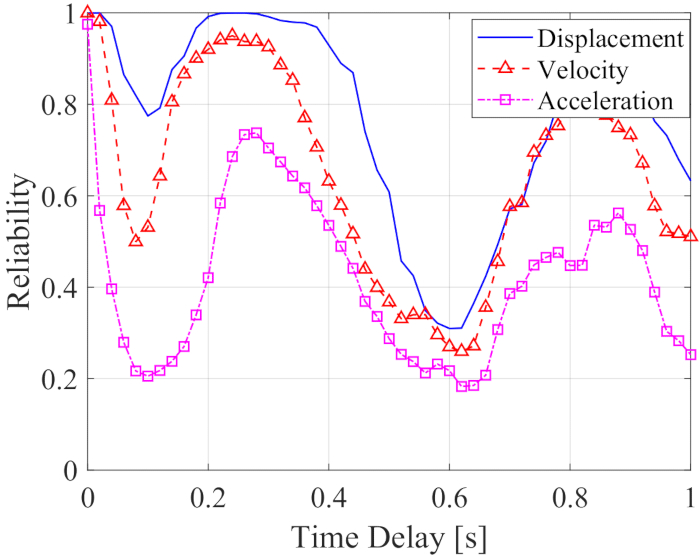
Figura 5: Affidabilità delle risposte della struttura controllata con ritardo crescente. Clicca qui per visualizzare una versione più grande di questa figura.
In sintesi, le risposte della struttura sono state mitigate dal metodo del controllo semi-attivo. Tuttavia, l'efficacia del controllo, indipendentemente dall'RMS o dall'affidabilità, del metodo di controllo semi-attivo è diminuita dal ritardo. Pertanto, è necessario compensare il ritardo.
2.1.1 Analisi del metodo di compensazione del ritardo
Per analizzare l'efficacia del metodo di compensazione del ritardo temporale proposto, le storie temporali RMS di spostamento, velocità e accelerazione per sistemi non controllati (Unc), ritardati con controllo senza compensazione (TDN-SAC-PSO) e sistemi ritardati con controllo della compensazione (TDC-SAC-PSO) sono confrontati nella Figura 6, dove il ritardo è stato di 0,1 s. I parametri della matrice di ponderazione e del metodo di controllo semi-attivo sono gli stessi del passaggio 2.1.
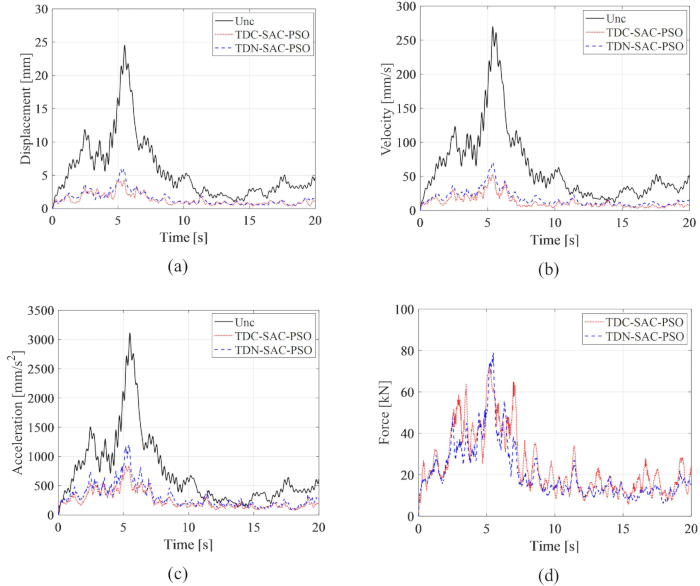
Figura 6: Confronto storico della radice quadrata media di strutture controllate con metodi diversi. (A) Spostamento; (b) velocità; c) accelerazione; (D) Forza di controllo. Abbreviazioni: Unc = non controllato; TDC-SAC-PSO = sistema ritardato con compensazione controllata; TDN -SAC-PSO = sistema ritardato con controllo di non compensazione. Clicca qui per visualizzare una versione più grande di questa figura.
Entrambi i metodi di controllo hanno ridotto significativamente le risposte della struttura rispetto alla struttura non controllata, rivelando i vantaggi del metodo di controllo basato su ammortizzatori MR. Rispetto alla struttura incontrollata, l'RMS massimo di spostamento, velocità e accelerazione è diminuito del 75,79%, 73,75% e 61,22% con il metodo TDN-SAC-PSO. Inoltre, con la compensazione del ritardo, le risposte della struttura controllata sono diminuite dell'82,59%, 80,40% e 73,04% con il metodo TDC-SAC-PSO. L'RMS massimo della forza di controllo con il metodo TDC-SAC-PSO è diminuito dell'8,43% rispetto al metodo TDN-SAC-PSO, sebbene le risposte alle vibrazioni del primo metodo fossero inferiori rispetto al secondo. L'analisi di cui sopra indica che l'influenza del ritardo sul metodo di controllo basato sull'ammortizzatore MR è stata effettivamente ridotta dal metodo di compensazione, che mostra la necessità della compensazione del ritardo per il metodo di controllo semi-attivo dell'ammortizzatore MR.
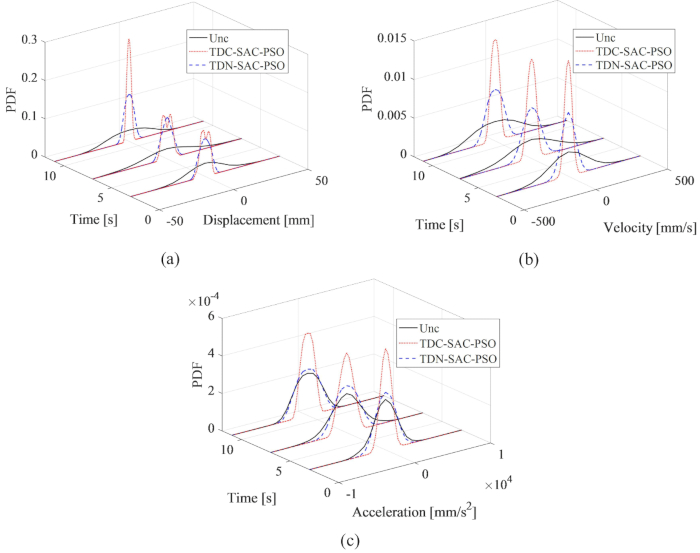
Figura 7: Confronto PDF in tempi tipici delle risposte della struttura. (A) Spostamento; (b) velocità; (c) Accelerazione. Abbreviazioni: PDF = funzione di densità di probabilità; Unc = non controllato; TDC-SAC-PSO = sistema ritardato con compensazione controllata; TDN -SAC-PSO = sistema ritardato con controllo di non compensazione. Clicca qui per visualizzare una versione più grande di questa figura.
Per rivelare in modo completo l'effetto del metodo di compensazione proposto sull'incertezza delle risposte della struttura controllata, i confronti della funzione di densità di probabilità (PDF) di spostamento, velocità e accelerazione in tempi tipici, 3, 7 e 11s, sono mostrati nella Figura 7. I PDF per il metodo TDN-SAC-PSO erano più stretti di quelli della struttura non controllata, il che significa che l'incertezza delle risposte della struttura è stata diminuita dal metodo di controllo semi-attivo anche con ritardo temporale. Quando il ritardo è stato compensato, i PDF delle risposte sono stati ulteriormente ristretti. Pertanto, il metodo di compensazione proposto è necessario per migliorare l'effetto di controllo semiattivo.
| Metodo di controllo | Spostamento | Velocità | Accelerazione | Forza di controllo | Valore minimo |
| Unc | 0.0954 | 0.1058 | 0.1111 | -- | 0.1111 |
| TDC-SAC-PSO | 0.9565 | 0.8107 | 0.7654 | 0.9845 | 0.7654 |
| TDN-SAC-PSO | 0.7747 | 0.531 | 0.2054 | 0.884 | 0.2054 |
Tabella 1: Risposte alle vibrazioni e affidabilità della forza di controllo di strutture controllate con diversi metodi. Abbreviazioni: Unc = non controllato; TDC-SAC-PSO = sistema ritardato con compensazione controllata; TDN -SAC-PSO = sistema ritardato con controllo di non compensazione.
Le risposte alle vibrazioni e l'affidabilità della forza di controllo delle strutture controllate con metodo non controllato, TDC-SAC-PSO e TDN-SAC-PSO sono mostrate nella Tabella 1. Con il controllo del metodo TDN-SAC-PSO, l'affidabilità della struttura è stata notevolmente aumentata rispetto alla struttura non controllata, che convalida l'efficacia del metodo di controllo basato su ammortizzatori MR, anche nel tempo. Tuttavia, con la compensazione del ritardo, l'affidabilità è stata notevolmente aumentata rispetto a senza compensazione, soprattutto per l'accelerazione. È anche degno di nota il fatto che l'affidabilità delle diverse risposte e la forza di controllo hanno mostrato differenze significative per il metodo TDC-SAC-PSO. Ciò indica che i valori ottimali dei parametri critici per il controllo senza ritardo non sono ottimali per il controllo con ritardo. Per ottenere l'effetto di controllo ottimale delle risposte alle vibrazioni e della forza di controllo con l'influenza del ritardo, i parametri devono essere ulteriormente ottimizzati. Sulla base dell'analisi di cui sopra, si conclude che il metodo di controllo semi-attivo con uno smorzatore MR può ridurre efficacemente le risposte alle vibrazioni della struttura, mentre i parametri devono essere ottimizzati a causa dell'influenza del ritardo.
2.2 Ottimizzazione dei parametri
Per ottenere i valori ottimali dei parametri, è stato applicato il metodo di ottimizzazione integrato basato sul criterio di affidabilità38. L'ottimizzazione dei parametri critici è stata effettuata con 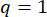 ,
, 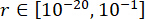 ,
,  ,
, 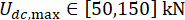 , e i tempi regolabili della forza dello smorzatore MR s = 8. Per implementare l'ottimizzazione è stato utilizzato il toolbox GA all'interno di MATLAB.
, e i tempi regolabili della forza dello smorzatore MR s = 8. Per implementare l'ottimizzazione è stato utilizzato il toolbox GA all'interno di MATLAB.
I risultati dell'ottimizzazione dei parametri sono  , , e
, , e  per il ritardo
per il ritardo 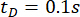
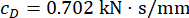 . La Figura 8 mostra le storie temporali RMS di spostamento, velocità, accelerazione e forza di controllo per le strutture controllate dal metodo Uncontrolled (Unc), TDC-SAC-PSO e SOSC-PSO. Il metodo SOSC-PSO denota il metodo di controllo semi-attivo con compensazione del ritardo e valori dei parametri critici ottimizzati.
. La Figura 8 mostra le storie temporali RMS di spostamento, velocità, accelerazione e forza di controllo per le strutture controllate dal metodo Uncontrolled (Unc), TDC-SAC-PSO e SOSC-PSO. Il metodo SOSC-PSO denota il metodo di controllo semi-attivo con compensazione del ritardo e valori dei parametri critici ottimizzati.
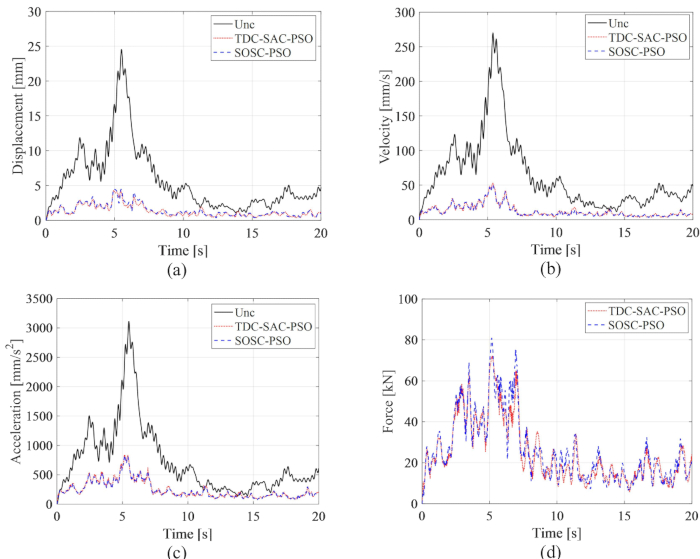
Figura 8: Storie temporali RMS di spostamento, velocità, accelerazione e forza di controllo per strutture incontrollate e controllate dal metodo TDC-SAC-PSO e dal metodo SOSC-PSO. (A) Spostamento; (b) velocità; c) accelerazione; (D) Forza di controllo. Abbreviazioni: Unc = non controllato; TDC-SAC-PSO = sistema ritardato con compensazione controllata; SOSC-PSO = Metodo di controllo semi-attivo ottimale stocastico con compensazione del ritardo. Clicca qui per visualizzare una versione più grande di questa figura.
Dalla Figura 8, si vede che gli effetti di controllo dei metodi TDC-SAC-PSO e SOSC-PSO hanno mostrato poche differenze. L'RMS massimo della velocità di spostamento e dell'accelerazione per il primo metodo era dell'81,60%, 81,21%, 73,62% della struttura non controllata e 82,59%, 80,40%, 73,04% per il secondo metodo. Per analizzare in modo completo le caratteristiche di probabilità delle risposte per entrambi i metodi di controllo, la Figura 9 mostra i PDF di spostamento, velocità e accelerazione per le strutture controllate dal metodo TDC-SAC-PSO e SOSC-PSO. Entrambi i metodi di controllo avevano quasi gli stessi PDF di spostamento e velocità in tempi tipici. I PDF di accelerazione del metodo SOSC-PSO erano più stretti di quelli del metodo TDC-SAC-PSO, il che significa che l'incertezza dell'accelerazione ha ottenuto un migliore effetto di controllo con il primo metodo.
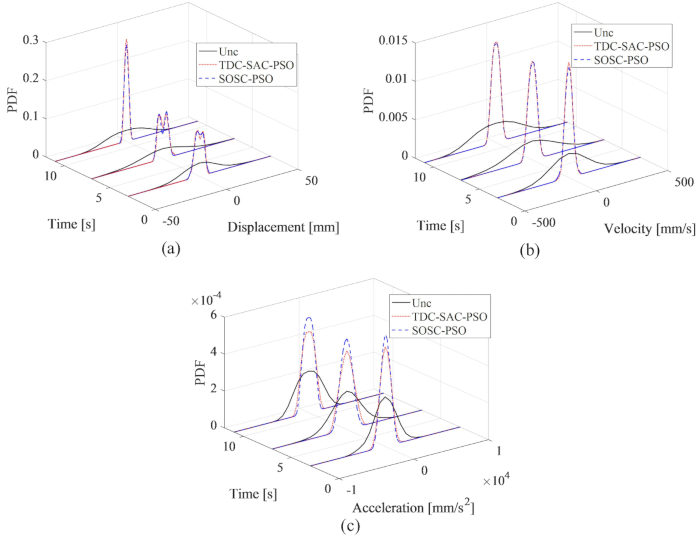
Figura 9: Confronto in PDF di spostamento, velocità e accelerazione per diverse strutture controllate. (A) Spostamento; (b) velocità; (c) Accelerazione. Abbreviazioni: PDF = funzioni di densità di probabilità; Unc = non controllato; TDC-SAC-PSO = sistema ritardato con compensazione controllata; SOSC-PSO = Metodo di controllo semi-attivo ottimale stocastico con compensazione del ritardo. Clicca qui per visualizzare una versione più grande di questa figura.
L'affidabilità dello spostamento, della velocità, dell'accelerazione e della forza di controllo per le strutture non controllate e controllate con i metodi TDC-SAC-PSO e SOSC-PSO sono mostrate nella Tabella 2. Entrambi i metodi di controllo hanno ottenuto un notevole aumento dell'affidabilità rispetto alla struttura non controllata. L'affidabilità dello spostamento ha mostrato poca differenza tra i metodi TDC-SAC-PSO e SOSC-PSO. Mentre l'affidabilità dell'accelerazione, la più bassa affidabilità della struttura controllata, ha ottenuto un notevole aumento. Ciò significa che il metodo SOSC-PSO raggiunge l'effetto di controllo ottimale dell'equilibrio.
| Metodo di controllo | Spostamento | Velocità | Accelerazione | Forza di controllo | Valore minimo |
| Unc | 0.0954 | 0.1058 | 0.1111 | -- | 0.1111 |
| TDC-SAC-PSO | 0.9565 | 0.8107 | 0.7654 | 0.9845 | 0.7654 |
| SOSC-PSO | 0.953 | 0.8704 | 0.8934 | 0.9586 | 0.8934 |
Tabella 2: Affidabilità per strutture controllate con metodi diversi. Abbreviazioni: Unc = non controllato; TDC-SAC-PSO = sistema ritardato con compensazione controllata; SOSC-PSO = Metodo di controllo semi-attivo ottimale stocastico con compensazione del ritardo.
È stata analizzata l'efficacia del metodo SOSC-PSO proposto con ritardo temporale 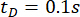 . Per verificare ulteriormente il metodo proposto per diversi ritardi temporali, la Tabella 3 mostra i valori ottimali dei parametri e la corrispondente affidabilità per l'intervallo
. Per verificare ulteriormente il metodo proposto per diversi ritardi temporali, la Tabella 3 mostra i valori ottimali dei parametri e la corrispondente affidabilità per l'intervallo 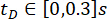 di ritardo temporale.
di ritardo temporale.
| tD(s) | lg(r*) | CD(kN·s/mm) | Uc.c., max (kN) | Spostamento | Velocità | Accelerazione | Forza di controllo |
| 0 | -2.524 | 1.44 | 116.163 | 0.9997 | 0.9998 | 0.9752 | 1 |
| 0.02 | -4.413 | 0.414 | 144.066 | 0.9989 | 0.9988 | 0.872 | 0.9011 |
| 0.04 | -4.416 | 0.25 | 141.759 | 0.9998 | 0.9846 | 0.8881 | 0.9135 |
| 0.06 | -3.226 | 0.203 | 145.613 | 0.993 | 0.9318 | 0.8756 | 0.9556 |
| 0.08 | -5.207 | 0.345 | 133.692 | 0.9646 | 0.8998 | 0.8998 | 0.953 |
| 0.1 | -4.669 | 0.702 | 130.739 | 0.9531 | 0.8704 | 0.8934 | 0.9586 |
| 0.12 | -4.895 | 0.833 | 69.72 | 0.9526 | 0.863 | 0.888 | 0.9686 |
| 0.14 | -4.231 | 0.921 | 75.221 | 0.9531 | 0.8681 | 0.8697 | 0.9671 |
| 0.16 | -5.594 | 0.662 | 138.922 | 0.9529 | 0.8461 | 0.8262 | 0.931 |
| 0.18 | -4.262 | 0.882 | 76.335 | 0.9516 | 0.7873 | 0.7614 | 0.9618 |
| 0.2 | -3.926 | 0.783 | 67.951 | 0.904 | 0.7277 | 0.7116 | 0.9653 |
| 0.22 | -5.965 | 1.071 | 52.554 | 0.8377 | 0.6411 | 0.6205 | 0.965 |
| 0.24 | -4.481 | 1.216 | 128.148 | 0.7567 | 0.474 | 0.474 | 0.9687 |
| 0.26 | -3.53 | 0.672 | 53.706 | 0.53 | 0.4096 | 0.4158 | 0.9921 |
| 0.28 | -4.433 | 0.638 | 64.225 | 0.3547 | 0.3745 | 0.3464 | 0.9928 |
| 0.3 | -3.536 | 0.459 | 57.705 | 0.2735 | 0.316 | 0.2736 | 0.9929 |
| Unc | -- | -- | -- | 0.0954 | 0.1058 | 0.1111 | -- |
Tabella 3: I valori ottimali dei parametri e i corrispondenti valori di affidabilità per diversi ritardi temporali. 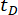 denota un ritardo;
denota un ritardo;  denota il valore logaritmico ottimale di r,r denota la matrice di ponderazione del coefficiente di controllo;
denota il valore logaritmico ottimale di r,r denota la matrice di ponderazione del coefficiente di controllo; 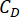 denota il coefficiente di smorzamento viscoso dello smorzatore MR;
denota il coefficiente di smorzamento viscoso dello smorzatore MR; 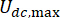 denotare le forze coulombiane massime e minime dello smorzatore MR.
denotare le forze coulombiane massime e minime dello smorzatore MR.
Si può osservare che l'affidabilità dello spostamento, della velocità e dell'accelerazione è stata migliorata rispetto alla struttura incontrollata, anche in presenza di ritardo, dimostrando la robustezza del metodo proposto nei confronti di tali ritardi. Tuttavia, l'affidabilità delle risposte strutturali con il metodo di controllo proposto è diminuita all'aumentare del ritardo, indicando che, sebbene l'impatto del ritardo sull'efficacia del controllo possa essere mitigato, non può essere completamente eliminato. In particolare, l'affidabilità della forza di controllo è rimasta superiore al 90% in diversi ritardi.
3. Esempio numerico
Per verificare il metodo SOSC-PSO proposto nella struttura MDOF, è stata analizzata una struttura a sei piani con due smorzatori MR installati nel primo e nel terzo piano, come mostrato nella Figura 10. Sono stati applicati i campioni sismici prodotti dal modello sismico stocastico nella Sezione 2 e le soglie di affidabilità di spostamento, velocità, accelerazione e forza di controllo erano 20 mm, 200 mm/s, 3.000 mm/s2 e 200 kN. Eqs. (27) sono stati utilizzati come matrice di ponderazione con 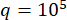 . Il toolbox GA di MATLAB è stato utilizzato per ottimizzare
. Il toolbox GA di MATLAB è stato utilizzato per ottimizzare 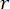 ,
, , e
, e  , con intervalli
, con intervalli 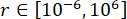 ottimali ,
ottimali ,  , e
, e 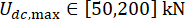 .
.
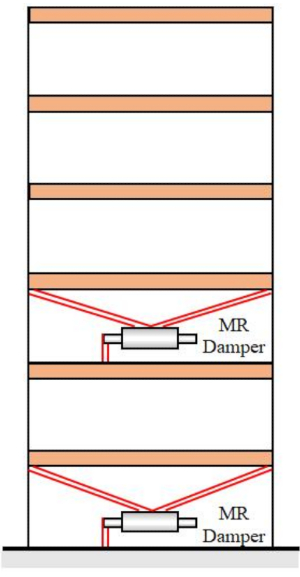
Figura 10: Struttura a sei piani con due smorzatori MR. Abbreviazione: MR = magnetoreologico. Clicca qui per visualizzare una versione più grande di questa figura.
3.1 Analisi dell'influenza del ritardo
Per analizzare l'influenza del ritardo sull'efficacia del controllo dello smorzatore MR nella struttura MDOF, la Figura 11 mostra l'RMS massimo di spostamento (spostamento tra piani), velocità (velocità tra piani) e accelerazione (accelerazione del piano) insieme al ritardo temporale per il metodo TDC-SAC-PSO. I parametri erano 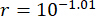 ,
, , e
, e  per la serranda MR al 1° piano;
per la serranda MR al 1° piano;  e
e  per la serranda MR al 3° piano, che sono i risultati ottimizzati senza ritardo. L'RMS massimo delle risposte della struttura controllata ha mostrato fluttuazioni di periodo insieme a ritardo temporale. L'RMS massimo di spostamento e velocità era al 1° piano, l'accelerazione massima al 6° piano. Inoltre, tutti i valori MRS massimi delle risposte con qualsiasi ritardo erano maggiori dei valori senza ritardo, il che significa che il ritardo diminuisce l'effetto di controllo dello smorzatore RM.
per la serranda MR al 3° piano, che sono i risultati ottimizzati senza ritardo. L'RMS massimo delle risposte della struttura controllata ha mostrato fluttuazioni di periodo insieme a ritardo temporale. L'RMS massimo di spostamento e velocità era al 1° piano, l'accelerazione massima al 6° piano. Inoltre, tutti i valori MRS massimi delle risposte con qualsiasi ritardo erano maggiori dei valori senza ritardo, il che significa che il ritardo diminuisce l'effetto di controllo dello smorzatore RM.
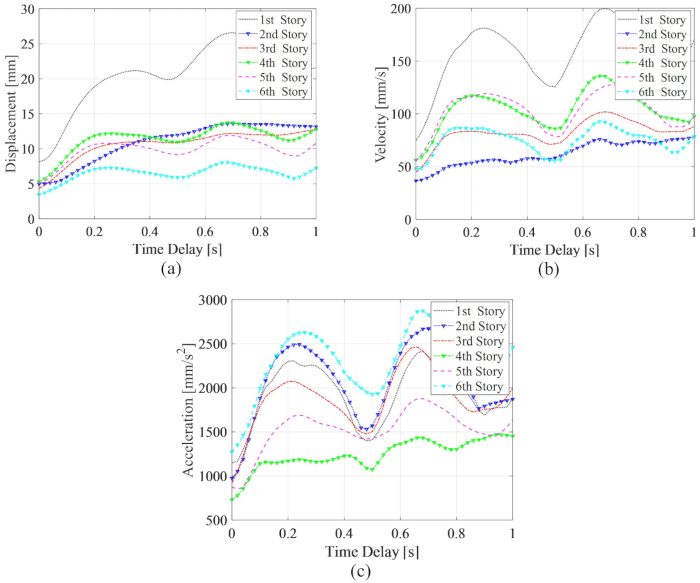
Figura 11: RMS massimo delle risposte insieme al ritardo per la struttura controllata dal metodo TDC-SAC-PSO. (A) Spostamento; (b) velocità; (c) Accelerazione. Abbreviazioni: RMS = radice-media-quadrato; TDC-SAC-PSO = sistema ritardato con compensazione controllata. Clicca qui per visualizzare una versione più grande di questa figura.
L'affidabilità dello spostamento, della velocità e dell'accelerazione insieme al ritardo è mostrata nella Figura 12. L'affidabilità della velocità e dell'accelerazione mostra fluttuazioni di periodo insieme al ritardo temporale, mentre l'affidabilità dello spostamento è diminuita drasticamente insieme al ritardo temporale; Tutti i valori di affidabilità in qualsiasi ritardo erano inferiori a quelli senza ritardo. Pertanto, il metodo di compensazione del ritardo è necessario per ridurre l'influenza del ritardo sull'affidabilità della struttura controllata dallo smorzatore MR.
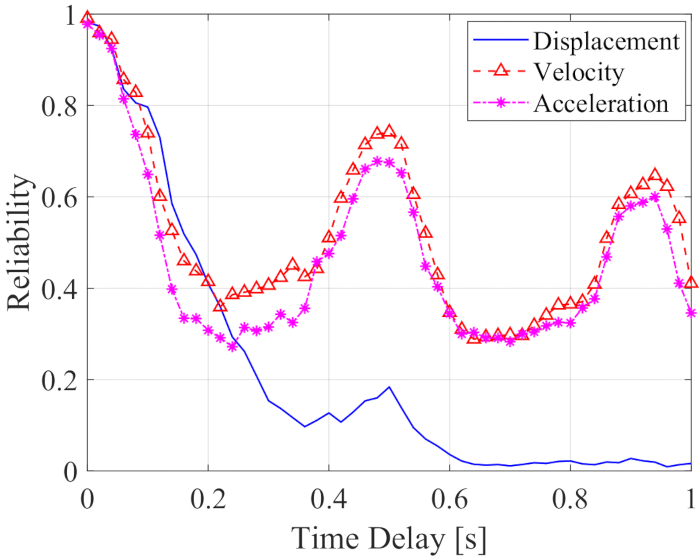
Figura 12: Affidabilità delle risposte della struttura controllata insieme al ritardo temporale. Clicca qui per visualizzare una versione più grande di questa figura.
3.2 Effetto di controllo della compensazione del ritardo
Sulla base del metodo TDC-SAC-PSO proposto, è stata analizzata la struttura 6-DOF con due smorzatori RM. La Figura 13 mostra le storie temporali RMS di spostamento e accelerazione al 1° e 3° piano per le strutture controllate con metodo Uncontrolled (Unc), TDC-SAC-PSO e TDN-SAC-PSO. Il ritardo era 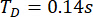 , e il rapporto
, e il rapporto 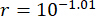 della matrice di ponderazione; i parametri dello smorzatore MR erano
della matrice di ponderazione; i parametri dello smorzatore MR erano  ,
,  per il 1° piano;
per il 1° piano;  e
e  per il 3° piano.
per il 3° piano.

Figura 13: Storie temporali RMS di spostamento e accelerazione al 1° e 3° piano per strutture controllate con metodi diversi. (A) Spostamento al 1° piano; (B) Spostamento al 3° piano; (C) Accelerazione al 1° piano; (D) Accelerazione al 3° piano. Abbreviazioni: RMS = radice-media-quadrato; Unc = non controllato; TDC-SAC-PSO = sistema ritardato con compensazione controllata; TDN -SAC-PSO = sistema ritardato con controllo di non compensazione. Clicca qui per visualizzare una versione più grande di questa figura.
L'RMS massimo di spostamento al 1° e al 3° piano è stato ridotto del 35,42% e del 30,44% con il metodo TDN-SAC-PSO, dove il ritardo non è stato compensato. Mentre con la compensazione, l'RMS massimo di spostamento al 1° e al 3° piano è stato ridotto rispettivamente del 49,33% e del 53,39%. Senza compensazione, l'RMS massimo di accelerazione al 1° e al 3° piano è aumentato del 16,22% e del 2,88%, ma è diminuito rispettivamente del 25,77% e del 36,00%, con la compensazione. Pertanto, la compensazione del ritardo nel metodo di controllo dell'ammortizzatore MR è necessaria per ridurre le risposte della struttura, in particolare per l'accelerazione.
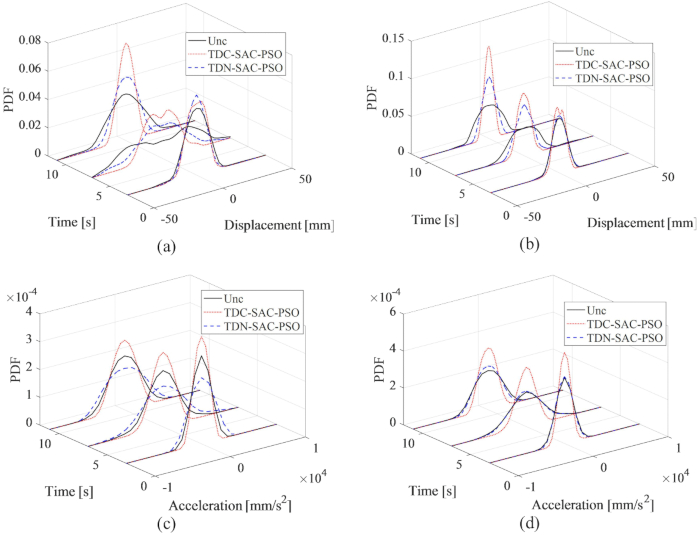
Figura 14: PDF di spostamento e accelerazione al 1° e 3° piano per diversi metodi di controllo. (A) Spostamento al 1° piano; (B) Spostamento al 3° piano; (C) Accelerazione al 1° piano; (D) Accelerazione al 3° piano. Abbreviazioni: PDF = funzioni di densità di probabilità; Unc = non controllato; TDC-SAC-PSO = sistema ritardato con compensazione controllata; TDN -SAC-PSO = sistema ritardato con controllo di non compensazione. Clicca qui per visualizzare una versione più grande di questa figura.
I PDF di spostamento e accelerazione al 1° e 3° piano sono mostrati nella Figura 14, rivelando i diversi effetti di controllo dei metodi TDC-SAC-PSO e TDN-SAC-PSO rispetto alla struttura non controllata. Senza compensazione, i PDF di spostamento al 1° e al 3° piano erano ancora più stretti di quelli della struttura non controllata. Inoltre, con la compensazione del ritardo, i PDF di spostamento sono diventati più stretti di quelli della struttura controllata dal metodo TDN-SAC-PSO. A differenza dello spostamento, senza compensazione, i PDF di accelerazione al 1° piano per il metodo TDN-SAC-PSO erano più larghi di quelli della struttura non controllata. Tuttavia, con la compensazione, i PDF di accelerazione sia al 1° che al 3° piano erano più stretti di quelli della struttura non controllata. Pertanto, viene verificata la necessità della compensazione del ritardo per aumentare la certezza delle risposte della struttura, in particolare per l'accelerazione.
| Metodo di controllo | Spostamento | Velocità | Accelerazione | Forza di controllo al 1° piano | Forza di controllo al 3° piano |
| Unc | 0.0114 | 0.5822 | 0.6372 | -- | -- |
| TDN-SAC-PSO | 0.5851 | 0.5258 | 0.398 | 1 | 1 |
| TDC-SAC-PSO | 0.806 | 0.8674 | 0.8037 | 1 | 1 |
Tabella 4: Affidabilità per strutture controllate con metodi diversi. Abbreviazioni: Unc = non controllato; TDC-SAC-PSO = sistema ritardato con compensazione controllata; TDN -SAC-PSO = sistema ritardato con controllo di non compensazione.
I valori di affidabilità di spostamento, velocità, accelerazione e forza di controllo con i sistemi di struttura controllati dai diversi metodi sono mostrati nella Tabella 4. I valori di affidabilità delle risposte della struttura sono stati calcolati utilizzando il metodo dei valori estremi equivalenti25. Con il controllo del metodo TDN-SAC-PSO, l'affidabilità dello spostamento è aumentata rispetto alla struttura incontrollata, mentre l'affidabilità della velocità e dell'accelerazione è diminuita. Con la compensazione del ritardo nel metodo TDC-SAC-PSO, l'affidabilità di spostamento, velocità e accelerazione è aumentata in modo significativo. Inoltre, i valori di affidabilità della forza di controllo per entrambi i metodi TDN-SAC-PSO e TDN-SAC-PSO sono sufficientemente mantenuti. Pertanto, il metodo di controllo della compensazione del ritardo proposto raggiunge un effetto di controllo favorevole per la struttura controllata dall'ammortizzatore MR.
3.3 Ottimizzazione dei parametri
Per ottenere l'effetto di controllo ottimale, i parametri del metodo di controllo proposto sono stati ottimizzati in base al criterio di affidabilità. Con il ritardo 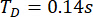 , il risultato ottimale era
, il risultato ottimale era  ;
; 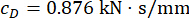 , e
, e 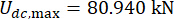 per la serranda MR del 1° piano;
per la serranda MR del 1° piano; 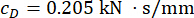 e
e  per la serranda MR del 3°.
per la serranda MR del 3°.
Le storie temporali RMS di spostamento e accelerazione al 1° e 3° piano sono mostrate nella Figura 15 dove vengono confrontati gli effetti di controllo dei metodi TDC-SAC-PSO e SOSC-PSO e della struttura non controllata. Con il controllo dell'ammortizzatore MR, con o senza compensazione del ritardo, l'RMS di spostamento e accelerazione è diminuito in modo significativo. Con il metodo SOSC-PSO, l'RMS massimo di spostamento al 1° e al 3° piano è diminuito rispettivamente del 65,15% e del 63,16% rispetto alla struttura non controllata. Rispetto al metodo TDC-SAC-PSO, la risposta allo spostamento è stata ulteriormente ridotta. L'RMS massimo di accelerazione al 1° e 3° piano è diminuito del 23,39% e del 35,60% per il metodo SOSC-PSO. C'era poca differenza nell'effetto di controllo dell'accelerazione per i metodi SOSC-PSO e TDC-SAC-PSO, indicando che l'effetto di controllo della compensazione del ritardo era diverso per lo spostamento e l'accelerazione.
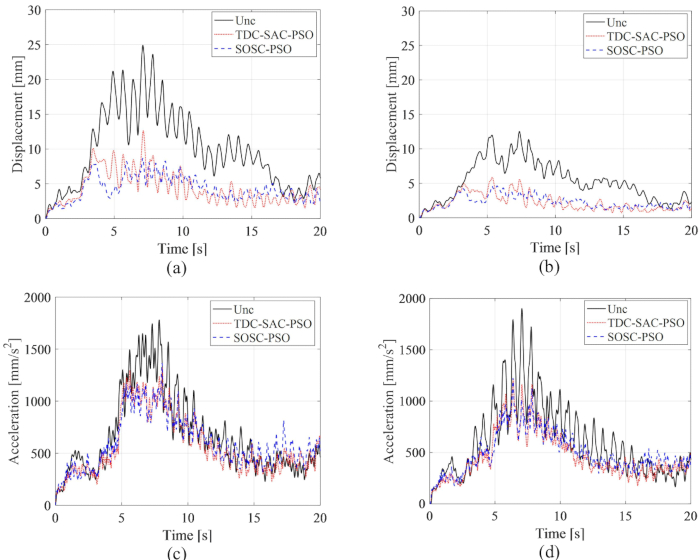
Figura 15: Cronologie RMS di spostamento e accelerazione al 1° e 3° piano per diversi metodi di controllo. (A) Spostamento al 1° piano; (B) Spostamento al 3° piano; (C) Accelerazione al 1° piano; (D) Accelerazione al 3° piano. Abbreviazioni: RMS = radice-media-quadrato; Unc = non controllato; TDC-SAC-PSO = sistema ritardato con compensazione controllata; SOSC-PSO = Metodo di controllo semi-attivo ottimale stocastico con compensazione del ritardo. Clicca qui per visualizzare una versione più grande di questa figura.
I PDF di spostamento e accelerazione al 1° e 3° piano sono presentati nella Figura 16; i PDF di spostamento e accelerazione sono stati ristretti dai metodi TDC-SAC-PSO e SOSC-PSO rispetto alla struttura incontrollata. Inoltre, i PDF di spostamento e accelerazione per il metodo SOSC-PSO sono stati ulteriormente ristretti rispetto a quelli della struttura controllata dal metodo TDC-SAC-PSO. Pertanto, con l'ottimizzazione dei parametri, il metodo di controllo della compensazione del ritardo proposto ha ottenuto un effetto di controllo migliore rispetto a senza ottimizzazione.
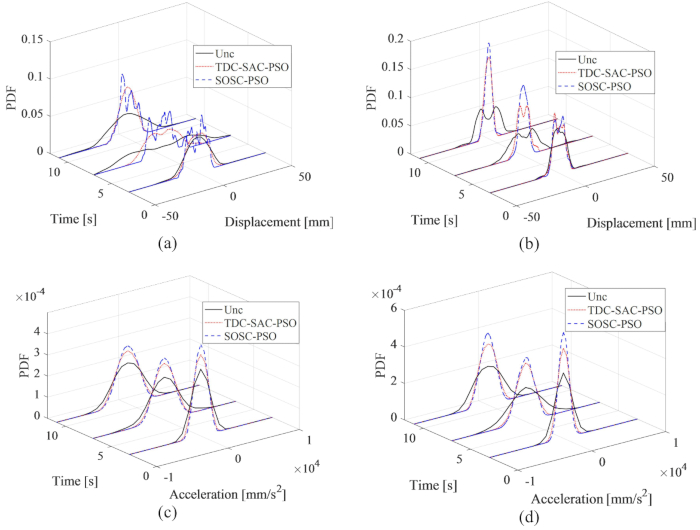
Figura 16: PDF di spostamento e accelerazione al 1° e 3° piano per diversi metodi di controllo. (A) Spostamento al 1° piano; (B) Spostamento al 3° piano; (C) Accelerazione al 1° piano; (D) Accelerazione al 3° piano. Abbreviazioni: PDF = funzioni di densità di probabilità; Unc = non controllato; TDC-SAC-PSO = sistema ritardato con compensazione controllata; SOSC-PSO = Metodo di controllo semiattivo ottimale stocastico con compensazione del ritardo Fare clic qui per visualizzare una versione più grande di questa figura.
I valori di affidabilità di spostamento, velocità, accelerazione e forza di controllo sono mostrati nella Tabella 5. I valori di affidabilità per il metodo SOSC-PSO erano superiori a quelli per il metodo TDC-SAC-PSO. Nel frattempo, la forza di controllo manteneva ancora un'affidabilità sufficiente. Pertanto, l'ottimizzazione dei parametri è necessaria per ottenere il miglior effetto di controllo per il metodo di controllo basato su ammortizzatori MR.
| Metodo di controllo | Spostamento | Velocità | Accelerazione | Forza di controllo al 1° piano | Forza di controllo al 3° piano |
| Unc | 0.0114 | 0.5822 | 0.6372 | -- | -- |
| TDC-SAC-PSO | 0.806 | 0.8674 | 0.8037 | 1 | 1 |
| SOSC-PSO | 0.9544 | 0.9314 | 0.8788 | 1 | 1 |
Tabella 5: Affidabilità per strutture controllate con metodi diversi. Abbreviazioni: Unc = non controllato; TDC-SAC-PSO = sistema ritardato con compensazione controllata; SOSC-PSO = Metodo di controllo semi-attivo ottimale stocastico con compensazione del ritardo.
Risultati
Con l'obiettivo di influenzare il ritardo sull'efficacia del controllo del metodo basato su smorzatori RM, in questo articolo viene proposto un metodo di controllo semi-attivo con compensazione del ritardo. Nel metodo proposto, i parametri critici sono ottimizzati in base al criterio di affidabilità. Confrontando l'efficacia del controllo, si giunge alle seguenti conclusioni:
(1) Il metodo di controllo semi-attivo basato su uno smorzatore MR è più robusto d...
Discussione
Con l'introduzione della teoria del controllo ottimale stocastico fisico (PSO), in questo articolo viene proposto un metodo di controllo semiattivo ottimale stocastico con compensazione del ritardo temporale (SOSC-PSO), progettato per mantenere l'affidabilità delle strutture controllate dagli smorzatori MR. Per compensare il ritardo temporale nel metodo proposto, la forza di controllo semi-attiva è derivata in funzione non solo degli stati presenti, ma anche degli stati e delle forze d...
Divulgazioni
Tutti gli autori non hanno conflitti di interesse da dichiarare.
Riconoscimenti
Gli autori riconoscono con gratitudine il sostegno della Fondazione per le Scienze Naturali della Provincia di Hebei (Grant No. E2023210007).
Materiali
| Name | Company | Catalog Number | Comments |
| MATLAB | MathWorks | 2016 | Using for the calculation of the proposed method |
Riferimenti
- Yao, J. T. P. Concept of structural control. J Struct Div. 98 (7), 1567-1574 (1972).
- Liu, J., Silva, C. E., Dyke, S. J., Wu, Y., Liu, H. Using real-time hybrid simulation for active mass damper experimentation and validation. Mech Mach Theory. 191, 105474 (2024).
- Pan, H., Li, C., Cao, L. Bidirectional pendulum-type tuned tendem mass dampers-inerters for integrated control of alongwind and crosswind responses in super-tall buildings. J Build Eng. 100, 111676 (2025).
- Housner, G. W. et al. Structural control: past, present, and future. J Eng Mech. 123 (9), 897-971 (1997).
- Rahman, M., Ong, Z. C., Chong, W. T., Julai, S. Smart Semi-active PID-ACO control strategy for tower vibration reduction in Wind Turbines with MR damper. Earthq Eng Eng Vib. 18 (4), 887-902 (2019).
- Morales-Beltran, M., Paul, J. Active and semi-active strategies to control building structures under large earthquake motion. J Earthquake Eng. 19 (7), 1086-1111 (2015).
- Shu, Z., You, R., Xie, Y. Viscoelastic dampers for vibration control of building structures: A state-of-art review. J Earthq Eng. 28 (12), 3558-3585 (2024).
- Soong, T. T. Active structural control: Theory and practice. Longman Scientific & Technical. New York (1990).
- Wan, H. P., Ma, Q., Dong, G. S., Luo, Y., Ni, Y. Q. Data-driven model reduction approach for active vibration control of cable-strut structures. Eng Struct. 302, 117434 (2024).
- Cao, L., Li, X., Huang, Y., Li, C., Pan, H. High robust eddy current tuned tandem mass dampers-inerters for structures under the ground acceleration. Soil Dyn Earthq Eng. 188, 109040 (2025).
- Chha, H., Peng, Y. Adaptive semiactive control of structure with magnetorheological dampers using wavelet packet transform. Adv Struct Eng. 27 (9), 1509-1527 (2024).
- Zeng, X., Peng, Y., Chen, J. Serviceability-based damping optimization of randomly wind-excited high-rise buildings. Struct Des Tall Spec. 26 (11), e1371 (2017).
- Li, C., Chang, K., Cao, L., Huang, Y. Performance of a nonlinear hybrid base isolation system under the ground motions. Soil Dyn Earthq Eng. 143, 106589 (2021).
- Cao, L., Li, C. A high performance hybrid passive base-isolated system. Struct Control Health Monitoring. 29 (3), e2887 (2022).
- Zareie, S., Issa, A. S., Seethaler, R., Zabihollah, A., Ahmad, R. A novel SMA-magnetorheological hybrid bracing system for seismic control. Eng Struct. 244, 112709 (2021).
- Chu, S. Y., Soong, T. T., Reinhorn, A. M. Active, hybrid and semi-active structural control. John Wiley & Sons, New York (2005).
- Danielian, S. A., Jabbari, F., Zareian, F. Effects and distribution of semi-active resettable springs on the seismic response of asymmetric structures. Earthq Eng Struct D. 52 (10). 2966-2982 (2023).
- Shuang, Z., Wenliuhan, H. S., Liu, Y. H., Inoue, N., Zhai, Z. P. Seismic response control for bridge piers with semi-active MR damper based on displacement feedback. J Earthq Eng. 28 (3). 849-865 (2024).
- Wang, Y., Dyke, S. Modal-based LQG for smart base isolation system design in seismic response control. Struct Control Health Monitoring. 20 (5), 753-768 (2013).
- Desai, R. M. et al. Performance evaluation of a single sensor control scheme using a twin-tube MR damper based semi-active suspension. J Vib Eng Technol. 9, 1193-1210 (2021).
- Abdi, M. S., Nekooei, M. Jafari, M. A. Seismic control of multi-degrees-of-freedom structures by vertical mass isolation method using MR dampers. Earthq Eng Eng Vib. 23 (2), 503-510 (2024).
- Bhowmik, K., Debnath, N. Semi-active vibration control of soft-storey building with magnetorheological damper under seismic excitation. J Vib Eng Technol. 12 (4), 6943-6961 (2024).
- Yang, J. N., Akbarpour, A., Askar, G. Effect of time delay on control of seismic-excited buildings. J Struct Eng. 116 (10), 2801-2814 (1990).
- Temimi, H., Ben-Romdhane, M., El-Borgi, S., Cha, Y. Time-delay effects on controlled seismically excited linear and nonlinear structures. Int J Struct Stab Dyn. 16 (7), 1550031 (2016).
- Peng, J., Wang, L., Zhao, Y., Lenci, S. Time-delay dynamics of the MR damper-cable system with one-to-one internal resonances. Nonlinear Dynamics. 105 (2), 1343-1356 (2021).
- Cha, Y. J., Agrawal, A. K., Dyke, S. J. Time delay effects on large-scale MR damper based semi-active control strategies. Smart Mater Struct. 22 (1), 015011 (2013).
- Yu, Y. et al. Experimental study of wireless structural vibration control considering different time delays. Smart Mater Struct. 24, 045005 (2015).
- Ahmadizadeh, M., Mosqueda, G., Reinhorn, A. M. Compensation of actuator delay and dynamics for real-time hybrid structural simulation. Earthq Eng Struct Dyn. 37 (1), 21-42 (2008).
- Bathaei, A., Zahrai, S. M. Compensating time delay in semi-active control of a SDOF structure with MR damper using predictive control. Struc Eng Mech. 82 (4), 445-458 (2022).
- Dyke, S. J., Spencer, Jr, B. F., Sain, M. K., Carlson, J. D. Modeling and control of magnetorheological dampers for seismic response reduction. Smart Mater Struct. 5 (5), 565-575 (1996).
- Ying, Z. G., Ni, Y. Q., Ko, J. M. A semi-active stochastic optimal control strategy for nonlinear structural systems with MR dampers. Smart Struct Syst. 5 (1), 69-79 (2009).
- Rosol, M., Martynowicz, P. Implementation of the LQG controller for a wind turbine tower-nacelle model with a MR tuned vibration absorber. J Theor App Mech-Pol. 54 (4), 1109-1123 (2016).
- Lyu, M. Z., Feng, D. C., Chen, J. B., Li, J. A decoupled approach for determination of the joint probability density function of a high-dimensional nonlinear stochastic dynamical system via the probability density evolution method. Comput Method Appl M. 418 (A), 116443 (2024).
- Chha, H., Peng, Y. Multiscale stochastic optimal control of hysteretic structures based on wavelet transform and probability density evolution method. Eng Computation. 41 (4), 865-896 (2024).
- Li, J., Peng, Y. B., Chen, J. B. A physical approach to structural stochastic optimal controls. Probabilist Eng Mech. 25 (1), 127-141 (2010).
- Peng, Y. B., Yang, J. G., Li, J. Seismic risk-based stochastic optimal control of structures using magnetorheological dampers. Nat Hazards Rev. 18 (1), B4016001 (2017).
- Dong, X. M., Yu, M., Li, Z., Liao, C., Chen, W. Neural network compensation of semi-active Control for magneto-rheological suspension with time delay uncertainty. Smart Mater Struct. 18 (1), 015014 (2008).
- Peng, Y. B., Zhang, Z. Optimal MR damper-based semiactive control scheme for strengthening seismic capacity and structural reliability. J Eng Mech. 146 (6), 04020045 (2020).
- Luo, M. X., Gao, M. Cai, G. Delayed full-state feedback control of airfoil flutter using sliding mode control method. J Fluid Struct. 61, 262-273 (2016).
- Xu, J., Chung, K. W., Chan, C. L. An efficient method for studying weak resonant double Hopf bifurcation in nonlinear systems with delayed feedbacks. Siam J Appl Dyn Syst. 6 (1), 29-60 (2007).
- Yang, J. S., Jensen, H., Chen, J. B. Structural optimization under dynamic reliability constraints utilizing probability density evolution method and metamodels in augmented input space. Struct Multidiscip Optimization. 65, 107 (2022).
- Li, J., Chen, J. B. Stochastic dynamics of structures. John Wiley & Sons, Singapore (2009).
- Peng, Y. B., Li, J. Stochastic optimal control of structures. Springer (2019).
- Dowrick, C. Beyond depression: A new approach to understanding and management. Oxford University Press (2009).
- Wang, D., Li, J. Physical random function model of ground motions for engineering purposes. Sci China Technol Sci. 54 (1), 175-182 (2011).
- Wang, D., Li, J. A random physical model of seismic ground motion field on local engineering site. Sci China Technol Sci. 55 (7), 2057-2065 (2012).
- Chen, J. B., Li, J. Strategy for selecting representative points via tangent spheres in the probability density evolution method. Int J Numer Meth Eng. 74 (13), 1988-2014 (2008).
Ristampe e Autorizzazioni
Richiedi autorizzazione per utilizzare il testo o le figure di questo articolo JoVE
Richiedi AutorizzazioneThis article has been published
Video Coming Soon