É necessária uma assinatura da JoVE para visualizar este conteúdo. Faça login ou comece sua avaliação gratuita.
Research Article
Método de controle semi-ativo estocástico da estrutura baseado em amortecedores magnetoreológicos considerando o atraso de tempo
Neste Artigo
Resumo
Um método de controle semi-ativo ótimo estocástico com compensação de atraso de tempo (SOSC-PSO) é proposto neste artigo, projetado para manter a confiabilidade de estruturas controladas por amortecedores de RM.
Resumo
O uso de amortecedores magnetoreológicos (MR) em sistemas de controle semi-ativos enfrenta um desafio importante: atraso de tempo causado por processos de feedback, o que reduz a confiabilidade das estruturas de engenharia civil sob excitações estocásticas. Este artigo propõe um método de Controle Semi-ativo Ótimo Estocástico com compensação de atraso de tempo (SOSC-PSO), aproveitando a teoria de controle Ótimo Estocástico Físico (PSO) para resolver esse problema e manter a confiabilidade estrutural. O método proposto deriva a força de controle semi-ativa em função dos estados atual e anterior, compensando os atrasos no processo de controle. Para otimizar a eficácia do controle, os principais parâmetros são ajustados com base em um critério de confiabilidade para o sistema. Análises de validação em estruturas de grau único de liberdade e multigrau de liberdade sob excitações sísmicas estocásticas mostram que atrasos de tempo prejudicam significativamente o desempenho dos amortecedores de RM. No entanto, o método SOSC-PSO com compensação de atraso de tempo melhora significativamente a eficácia do controle e, com parâmetros otimizados, aumenta a confiabilidade do sistema de controle estrutural além dos métodos sem otimização de parâmetros.
Introdução
Melhorar o desempenho das estruturas de engenharia diante de eventos catastróficos, como terremotos e ventos extremos, continua sendo uma preocupação primordial na comunidade de engenharia civil. O controle estrutural, uma técnica eficaz para reduzir vibrações, provou aumentar a segurança e a funcionalidade de tais estruturas 1,2,3. Nas últimas décadas, vários métodos e tecnologias avançadas foram desenvolvidos para esse fim. Esses métodos podem ser amplamente classificados em quatro categorias com base no tipo de energia usada para acionar os dispositivos de controle: sistemas de controle ativos, semiativos, passivos e híbridos 4,5,6,7.
No controle ativo, a força de controle necessária é aplicada diretamente através dos dispositivos de controle, o que requer uma quantidade significativa de energia 8,9,10. O controle semiativo, por outro lado, envolve o ajuste das propriedades dos dispositivos de controle (como amortecimento ou rigidez) com base nos sinais de controle, exigindo muito menos energia em comparação com os sistemas ativos11. O controle passivo, por outro lado, depende da dissipação de energia sem qualquer entrada de energia externa no sistema12 , 13 , 14 . Os sistemas híbridos combinam as características das estratégias de controle ativo/semiativo e passivo para alcançar um desempenho mais eficaz15. Dentre essas abordagens, o controle semiativo é considerado particularmente promissor devido ao seu equilíbrio entre baixo consumo de energia e alta eficiência 16,17,18. O amortecedor magnetoreológico (MR), com suas características superiores de amortecimento dinâmico, é considerado um dos dispositivos de controle semi-ativo mais eficazes 19,20,21,22.
No entanto, surge um desafio em sistemas de controle semi-ativos que utilizam amortecedores de RM, pois a lógica de feedback inevitavelmente introduz atrasos de tempo. Esses atrasos são normalmente causados por vários fatores 23,24,25, incluindo: (i) a aquisição e processamento de dados do sensor, (ii) o cálculo da força de controle necessária pelo controlador 26, (iii) transmissão de sinal através de transdutores para os amortecedores MR27 e (iv) a geração de força real pelos próprios amortecedores MR28. Tais atrasos podem levar a discrepâncias entre a força de controle produzida e a força esperada pela estrutura, comprometendo significativamente a eficácia do controle29. Infelizmente, a maioria dos algoritmos de controle existentes para amortecedores de RM não leva em conta esses atrasos.
Além disso, devido à aleatoriedade inerente de eventos catastróficos, qualquer algoritmo de controle semi-ativo eficaz deve ser capaz de manter o desempenho sob excitações estocásticas. O método de controle Gaussiano Quadrático Linear (LQG), uma técnica clássica de otimização estocástica, tem sido explorado para mitigar vibrações em estruturas equipadas com amortecedores MR. Por exemplo, Dyke et al. propuseram uma estratégia de controle ideal de corte LQG para melhorar a resposta sísmica de estruturas equipadas com amortecedores MR, usando feedback de aceleração30. Ying et al. introduziram uma estratégia de controle ótimo estocástico semi-ativo não cortado para estruturas não lineares com amortecedores MR, incorporando técnicas de média estocástica e programação dinâmica31. Outros estudos aplicaram o controle LQG baseado em modal para melhorar o desempenho sísmico de edifícios isolados na base19 e analisaram sua eficácia para mitigação de vibração em torres de turbinas eólicas32. No entanto, os métodos clássicos de LQG, que assumem ruído gaussiano branco, não são adequados para modelar a natureza não estacionária e não gaussiana de excitações do mundo real, como terremotos ou ventos fortes. Para resolver isso, o conceito de controle estocástico ótimo (PSO) baseado em física foi desenvolvido33 , 34 , que supera as limitações dos métodos LQG tradicionais e oferece uma estrutura mais precisa para lidar com diversas excitações estocásticas35 . Estudos mostraram que o controle ótimo estocástico semi-ativo baseado em PSO melhora significativamente a mitigação de vibrações para estruturas lineares e não lineares sujeitas a forças sísmicas estocásticas36.
Assim, há uma necessidade urgente de um método de controle semi-ativo robusto que compense os atrasos, aumentando a confiabilidade das estruturas controladas por amortecedores de RM25,37. Além disso, para garantir o desempenho ideal do controle sob excitações estocásticas, é essencial otimizar os parâmetros críticos do método de controle proposto usando uma abordagem baseada em confiabilidade. Portanto, um método de controle semi-ativo ótimo estocástico com compensação de atraso de tempo (SOSC-PSO) é proposto neste artigo para melhorar a confiabilidade de estruturas com amortecedores de RM.
Protocolo
1. Método de controle semi-ativo ótimo estocástico
Como o efeito de controle de um amortecedor MR é significativamente influenciado pelo inevitável atraso de tempo, um método de controle semi-ativo com um algoritmo de compensação de atraso de tempo é desenvolvido para aumentar o desempenho da estrutura controlada. Além disso, a aleatoriedade inerente às excitações externas causa as incertezas óbvias das respostas dinâmicas. O controle PSO é introduzido para otimizar os parâmetros críticos do método proposto para garantir a confiabilidade do sistema de controle da estrutura.
1.1 Algoritmo de compensação de controle semi-ativo
Sem perda de generalidade, considere uma estrutura n-Degree-Of-Freedoms (n-DOF) controlada por amortecedores MR com atraso de tempo, da qual a equação de movimento submetida a excitações estocásticas é dada por:
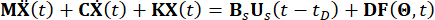 Características (1)
Características (1)
Onde  representam as matrizes de massa, amortecimento e rigidez n x n da estrutura, respectivamente; n representa o número de graus de liberdade da estrutura controlada. Os vetores de deslocamento, velocidade e aceleração da estrutura são representados por
representam as matrizes de massa, amortecimento e rigidez n x n da estrutura, respectivamente; n representa o número de graus de liberdade da estrutura controlada. Os vetores de deslocamento, velocidade e aceleração da estrutura são representados por 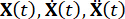 , respectivamente. O pequeno e os dois pontos acima dos símbolos representam a primeira e a segunda derivadas. Us (t - tD) representa o vetor r-dimensional da força de controle retardada no tempo dos amortecedores MR e r representa o número de amortecedores; t representa o tempo; tD denota atraso de tempo, assumido como uniforme em todos os amortecedores neste estudo, onde
, respectivamente. O pequeno e os dois pontos acima dos símbolos representam a primeira e a segunda derivadas. Us (t - tD) representa o vetor r-dimensional da força de controle retardada no tempo dos amortecedores MR e r representa o número de amortecedores; t representa o tempo; tD denota atraso de tempo, assumido como uniforme em todos os amortecedores neste estudo, onde 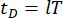 , com aqui o número
, com aqui o número 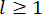 integral , e
integral , e 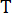 denotando o período de amostragem.
denotando o período de amostragem. 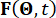 representa o vetor p-dimensional de excitações estocásticas e
representa o vetor p-dimensional de excitações estocásticas e  representa o vetor de parâmetro estocástico que caracteriza a aleatoriedade associada a excitações externas. A dimensão de
representa o vetor de parâmetro estocástico que caracteriza a aleatoriedade associada a excitações externas. A dimensão de  depende do modelo usado para as excitações externas, mas não está relacionada aos graus de liberdade mecânicos da estrutura. Bs e D são matrizes n x r e n x p que especificam as localizações dos amortecedores e excitações externas, respectivamente. Na representação do espaço de estados, a Eq. (1) é escrita como:
depende do modelo usado para as excitações externas, mas não está relacionada aos graus de liberdade mecânicos da estrutura. Bs e D são matrizes n x r e n x p que especificam as localizações dos amortecedores e excitações externas, respectivamente. Na representação do espaço de estados, a Eq. (1) é escrita como:
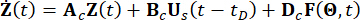 (2)
(2)
Onde 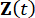 representa o vetor de estado 2n-dimensional;
representa o vetor de estado 2n-dimensional; 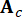 representa a matriz do sistema 2n x 2n;
representa a matriz do sistema 2n x 2n; 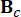 representa a matriz de localização 2n x r dos amortecedores MR;
representa a matriz de localização 2n x r dos amortecedores MR; 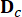 Representa a matriz de localização 2n x p de excitações externas. Esses parâmetros são expressos como:
Representa a matriz de localização 2n x p de excitações externas. Esses parâmetros são expressos como:
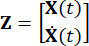 ,
, 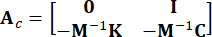 ,
, 
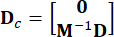 , (3)
, (3)
Onde 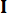 denota uma matriz de identidade com a mesma ordem de
denota uma matriz de identidade com a mesma ordem de 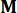 . Para facilitar o cálculo, a equação de espaço de estados contínuos Eq. (2) pode ser expressa de forma discreta como:
. Para facilitar o cálculo, a equação de espaço de estados contínuos Eq. (2) pode ser expressa de forma discreta como:
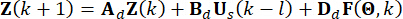 Eletrônicos (4)
Eletrônicos (4)
Onde o ponto de 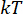 tempo é simplificado como
tempo é simplificado como 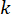 . E
. E  ,
, 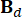 ,
, 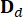 denotam matrizes 2n x 2n, 2n x r e 2n x p, que são expressas como:
denotam matrizes 2n x 2n, 2n x r e 2n x p, que são expressas como:
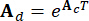 ,
,  ,
, 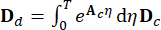 (5)
(5)
Onde 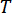 denota o período de amostragem.
denota o período de amostragem.
Para alcançar uma eficácia semelhante à do controle ativo, um método de controle simples e eficiente baseado no algoritmo Hrovat 38 é proposto para o controle baseado em amortecedor MR com atraso de tempo:
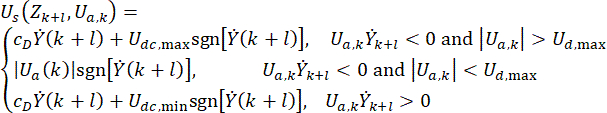 Eletrônicos (6)
Eletrônicos (6)
onde  representa o sinal de força de controle semi-ativo no ponto de tempo\
representa o sinal de força de controle semi-ativo no ponto de tempo\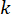 para o amortecedor MR;
para o amortecedor MR; 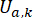 representa a força de comando activa de referência com compensação de atraso de tempo;
representa a força de comando activa de referência com compensação de atraso de tempo;  representa a força máxima de amortecimento do amortecedor MR, que é mutável;
representa a força máxima de amortecimento do amortecedor MR, que é mutável; 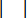 representa o símbolo de operação de valor absoluto;
representa o símbolo de operação de valor absoluto; 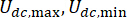 representam as forças coulombianas máximas e mínimas do amortecedor MR;
representam as forças coulombianas máximas e mínimas do amortecedor MR;  representa o coeficiente de amortecimento viscoso;
representa o coeficiente de amortecimento viscoso;  representa a entrada de velocidade no amortecedor MR, que é a velocidade de movimento do pistão em relação ao cilindro do amortecedor. Na Eq. (6),
representa a entrada de velocidade no amortecedor MR, que é a velocidade de movimento do pistão em relação ao cilindro do amortecedor. Na Eq. (6),  representam os parâmetros dimensionados do amortecedor MR.
representam os parâmetros dimensionados do amortecedor MR.
A Eq. (6) mostra o cálculo da força de controle semi-ativa do amortecedor MR com atraso de tempo. Vê-se que a força  de controle semi-ativa, no intervalo
de controle semi-ativa, no intervalo  de tempo na Eq. (4), é calculada com base na força
de tempo na Eq. (4), é calculada com base na força  de controle ativa no intervalo
de controle ativa no intervalo  de tempo e na variável
de tempo e na variável 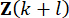 de estado no intervalo
de estado no intervalo  de tempo desde o atraso dos
de tempo desde o atraso dos 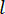 intervalos de tempo. Para obter a força
intervalos de tempo. Para obter a força  de controle ativa, a função de custo convencional é estabelecida por
de controle ativa, a função de custo convencional é estabelecida por
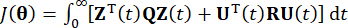 (7)
(7)
Onde  representa a matriz de ponderação semidefinida positiva simétrica 2n x 2n do estado do sistema;
representa a matriz de ponderação semidefinida positiva simétrica 2n x 2n do estado do sistema;  representa a matriz de ponderação definida positiva simétrica r x r da força de controle. Vê-se que a excitação externa é insignificante. Na verdade, com base na Eq. (7), o sistema de controle da estrutura pode alcançar o efeito de controle ideal, seja qual for o tipo de excitação externa. Como forma discreta, a Eq. (7) é expressa como39:
representa a matriz de ponderação definida positiva simétrica r x r da força de controle. Vê-se que a excitação externa é insignificante. Na verdade, com base na Eq. (7), o sistema de controle da estrutura pode alcançar o efeito de controle ideal, seja qual for o tipo de excitação externa. Como forma discreta, a Eq. (7) é expressa como39:
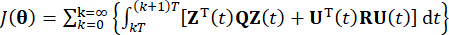 (8)
(8)
A minimização da função  de custo leva a um problema de valor extremo condicional, e a força
de custo leva a um problema de valor extremo condicional, e a força  de controle ativa é calculada por25:
de controle ativa é calculada por25:
 Telefone (9)
Telefone (9)
Onde 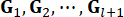 denotam os ganhos de controle para a variável
denotam os ganhos de controle para a variável 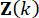 de estado no intervalo
de estado no intervalo  de tempo e força
de tempo e força 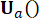 de controle ativa no intervalo
de controle ativa no intervalo 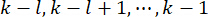 de tempo , que é determinado pelas matrizes
de tempo , que é determinado pelas matrizes 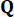 de ponderação e
de ponderação e 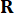 37. Desde o inevitável atraso de tempo, a força
37. Desde o inevitável atraso de tempo, a força 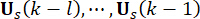 de controle obtida é atuada na estrutura em pontos
de controle obtida é atuada na estrutura em pontos 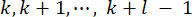 de tempo . Portanto, a força de controle ativo na Eq. (9) é calculada por:
de tempo . Portanto, a força de controle ativo na Eq. (9) é calculada por:
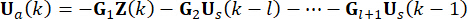 Eletrônicos (10)
Eletrônicos (10)
Para maior clareza de concepção, a força de controle semi-ativa na Eq. (10) é expressa da seguinte forma com base na Eq. (6):
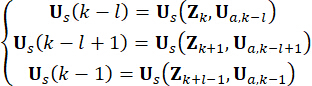 Artigos (11)
Artigos (11)
Onde  denota a força de controle ativa no ponto de
denota a força de controle ativa no ponto de  tempo . Substituindo a Eq. (11) na Eq. (10),
tempo . Substituindo a Eq. (11) na Eq. (10),
 Acessórios (12)
Acessórios (12)
NOTA: Todos os valores de estado  do ponto
do ponto  de tempo até são
de tempo até são 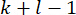 necessários para calcular
necessários para calcular  . Portanto, o seguinte método de previsão de estado é introduzido40.
. Portanto, o seguinte método de previsão de estado é introduzido40.
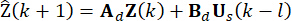 Acessórios (13)
Acessórios (13)
Onde  denota a variável prevista. Pela iteração da Eq. (13), o estado
denota a variável prevista. Pela iteração da Eq. (13), o estado  em
em  é calculado. A força ativa de comando Ua(k) é expressa como:
é calculado. A força ativa de comando Ua(k) é expressa como:
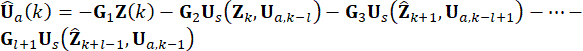 Telefone (14)
Telefone (14)
A força de controle semi-ativa pode ser obtida combinando as Eqs. (6), (12) e (13).
1.2 Análise de confiabilidade do sistema de controle da estrutura
De acordo com o princípio da preservação da probabilidade, o sistema  aumentado e
aumentado e 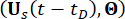 a estrutura com amortecedores de RM são conservados em probabilidade e são governados pelas seguintes equações de evolução de densidade de probabilidade generalizada (GDEEs)38:
a estrutura com amortecedores de RM são conservados em probabilidade e são governados pelas seguintes equações de evolução de densidade de probabilidade generalizada (GDEEs)38:
 Eletrônicos (15)
Eletrônicos (15)
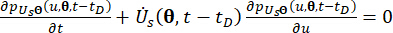 Acessórios (16)
Acessórios (16)
Onde  ,
,  denotam os componentes correspondentes do estado do sistema e da força de controle semi-ativa com atraso de tempo, respectivamente;
denotam os componentes correspondentes do estado do sistema e da força de controle semi-ativa com atraso de tempo, respectivamente; 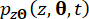 e
e  denotam as funções de densidade de probabilidade conjunta de sistemas
denotam as funções de densidade de probabilidade conjunta de sistemas 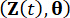 de amostra aumentada e
de amostra aumentada e 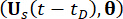 , respectivamente;
, respectivamente; 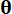 denota a amostra dentro do espaço amostral de
denota a amostra dentro do espaço amostral de 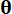 ;
;  e
e  ) denotam as derivadas parciais de tempo de primeira ordem do estado do sistema e componentes de força de controle semi-ativos, respectivamente. A densidade de probabilidade conjunta funciona
) denotam as derivadas parciais de tempo de primeira ordem do estado do sistema e componentes de força de controle semi-ativos, respectivamente. A densidade de probabilidade conjunta funciona 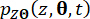 e
e  pode ser alcançada resolvendo as Eqs. (15) e (16) com as seguintes condições iniciais:
pode ser alcançada resolvendo as Eqs. (15) e (16) com as seguintes condições iniciais:
 Acessórios (17)
Acessórios (17)
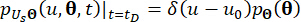 Acessórios (18)
Acessórios (18)
Onde 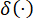 denota a função delta de Dirac;
denota a função delta de Dirac; 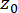 e
e 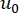 denotam os valores iniciais determinísticos de
denotam os valores iniciais determinísticos de  e
e 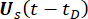 , respectivamente;
, respectivamente; 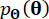 denota a função de densidade de probabilidade da amostra
denota a função de densidade de probabilidade da amostra 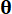 .
.
As funções de densidade de probabilidade instantânea de  e
e  podem ser obtidas pela integração unidimensional de
podem ser obtidas pela integração unidimensional de 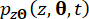 e
e  sobre o domínio do espaço amostral:
sobre o domínio do espaço amostral:
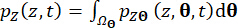 (19)
(19)
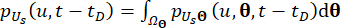 (20)
(20)
Onde 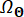 denota o domínio de distribuição de
denota o domínio de distribuição de  .
.
Com base nas Eqs. (19) e (20), vê-se que as informações probabilísticas completas das grandezas físicas em questão são prontamente derivadas, se suas relações associadas aos parâmetros do algoritmo forem definidas. A confiabilidade das grandezas físicas em questão pode ser calculada pela seguinte função de desempenho pertinente:
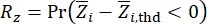 Acessórios (21)
Acessórios (21)
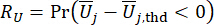 Acessórios (22)
Acessórios (22)
Onde 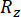 e
e 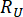 denota a confiabilidade calculada da quantidade de estado em questão e da força de controle semi-ativa, respectivamente;
denota a confiabilidade calculada da quantidade de estado em questão e da força de controle semi-ativa, respectivamente;  denota o vetor de valor extremo equivalente da i-ésima quantidade física em questão da estrutura controlada;
denota o vetor de valor extremo equivalente da i-ésima quantidade física em questão da estrutura controlada; 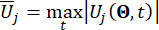 denota o vetor de valor extremo equivalente da j-ésima força de controle; o chapéu '-' nos símbolos indica o vetor de valor extremo equivalente41;
denota o vetor de valor extremo equivalente da j-ésima força de controle; o chapéu '-' nos símbolos indica o vetor de valor extremo equivalente41;  denota a i-ésima quantidade física em questão do k-ésimo DOF da estrutura controlada;
denota a i-ésima quantidade física em questão do k-ésimo DOF da estrutura controlada; 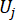 denota a j-ésima força de controle;
denota a j-ésima força de controle; 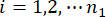 ,
, 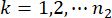 ,
,  ,
, ,
,  e
e  denota o número de grandezas físicas em questão e DOF da estrutura e amortecedores MR instalados na estrutura, respectivamente.
denota o número de grandezas físicas em questão e DOF da estrutura e amortecedores MR instalados na estrutura, respectivamente.  e
e 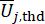 denota os limiares de
denota os limiares de  e
e  ;
;  denota a probabilidade do evento aleatório.
denota a probabilidade do evento aleatório.
1.3 Otimização de parâmetros
A razão das amplitudes e 
 influencia fortemente a eficácia do controle38 na modalidade de controle de feedback. Portanto, para alcançar a melhor eficácia de controle,
influencia fortemente a eficácia do controle38 na modalidade de controle de feedback. Portanto, para alcançar a melhor eficácia de controle, e
e  precisa ser otimizado. Além disso, como um método de controle baseado em amortecedor de RM, a eficácia do controle também é afetada pelos parâmetros do dispositivo,
precisa ser otimizado. Além disso, como um método de controle baseado em amortecedor de RM, a eficácia do controle também é afetada pelos parâmetros do dispositivo,  na Eq. (6). Para alcançar a confiabilidade ideal do sistema de controle da estrutura, o critério baseado em confiabilidade é proposto na Eq. (25).
na Eq. (6). Para alcançar a confiabilidade ideal do sistema de controle da estrutura, o critério baseado em confiabilidade é proposto na Eq. (25).
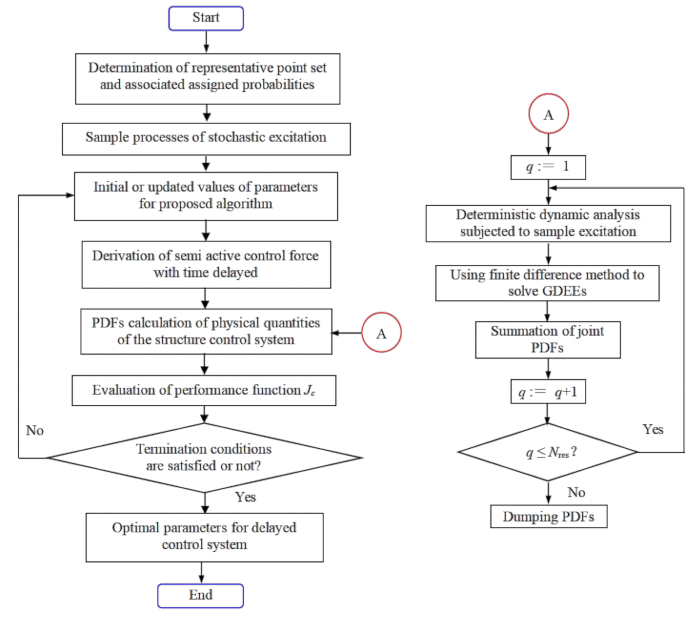
Figura 1: Fluxograma de otimização de parâmetros para controle de estrutura semi-ativa ótima estocástica com compensação de atraso de tempo. Abreviaturas: GDEE = Equação Diferencial Generalizada do Evento; PDF = Função de densidade de probabilidade. Clique aqui para ver uma versão maior desta figura.
Em resumo, são necessárias duas etapas para realizar o controle estocástico da estrutura semiativa ótima com base em amortecedores MR com compensação de atraso de tempo:
1.3.1 Minimizando a função  de custo mostrada na Eq. (7), a lógica de feedback de estado no sentido de amostras é alcançada, ou seja, Eq. 12)
de custo mostrada na Eq. (7), a lógica de feedback de estado no sentido de amostras é alcançada, ou seja, Eq. 12)
1.3.2 Minimizando a função  de desempenho baseada em confiabilidade, os parâmetros ideais no sentido de estatísticas são alcançados. A Figura 1 apresenta o fluxograma de otimização dos parâmetros do controlador na etapa 1.3.2.
de desempenho baseada em confiabilidade, os parâmetros ideais no sentido de estatísticas são alcançados. A Figura 1 apresenta o fluxograma de otimização dos parâmetros do controlador na etapa 1.3.2.
As etapas a seguir na etapa 1.3.2, que envolvem duas camadas de loops, são as seguintes:
1.3.2.1 O particionamento do espaço atribuído à probabilidade de excitações estocásticas, que é caracterizado pelo vetor  de parâmetro estocástico , permite a identificação de um conjunto de pontos
de parâmetro estocástico , permite a identificação de um conjunto de pontos 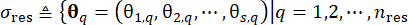 representativos junto com suas probabilidades atribuídas associadasPq's. Essa abordagem permite a geração eficiente de processos de amostra para a excitação estocástica, denotada como
representativos junto com suas probabilidades atribuídas associadasPq's. Essa abordagem permite a geração eficiente de processos de amostra para a excitação estocástica, denotada como 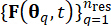 , a ser prontamente obtida.
, a ser prontamente obtida.
1.3.2.2 Para a otimização de parâmetros do sistema de controle de estrutura semi-ativa, inicialize ou atualize os valores dos pesos  da função de custo e
da função de custo e  . A força de controle de realimentação de estado associada com atraso de tempo, consulte a Eq. (12), é então calculada.
. A força de controle de realimentação de estado associada com atraso de tempo, consulte a Eq. (12), é então calculada.
1.3.2.3 Obtenção das funções de densidade de probabilidade (PDFs) de respostas estruturais e força de controle resolvendo os GDEEs mostrados nas Eqs. (17)–(20):
A otimização é a conclusão offline, mas não online. Na aplicação do método proposto em sistemas de controle de estrutura real, o ótimo  e
e  foram alcançados, e a otimização não é necessária no processo real aplicável.
foram alcançados, e a otimização não é necessária no processo real aplicável.
Análise dinâmica determinística do sistema de controle de estrutura semi-ativa submetido à excitação da amostra, pela qual as grandezas 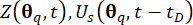 físicas em questão e seus derivados
físicas em questão e seus derivados  são calculados.
são calculados.
Empregando um método de diferenças finitas, como o esquema de Lax-Wendroff modificado com propriedades de Variação Total Diminuindo (TVD), as Equações Diferenciais Generalizadas (GDEEs) podem ser resolvidas e soluções numéricas para as funções 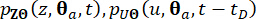 de densidade de probabilidade conjunta , podem ser derivadas.
de densidade de probabilidade conjunta , podem ser derivadas.
Repetindo as duas etapas acima da análise dinâmica determinística e do método das diferenças finitas, e percorrendo todos os pontos 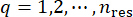 representativos, as funções de densidade de probabilidade podem ser obtidas por soma:
representativos, as funções de densidade de probabilidade podem ser obtidas por soma:
 Acessórios (23)
Acessórios (23)
 Eletrônicos (24)
Eletrônicos (24)
Onde  representa a medida de área do subdomínio associado ao ponto
representa a medida de área do subdomínio associado ao ponto 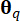 amostral . O método utilizado para resolver a Equação Diferencial Generalizada do Evento (GDEE) é conhecido como método de evolução da densidade de probabilidade (PDEM)42.
amostral . O método utilizado para resolver a Equação Diferencial Generalizada do Evento (GDEE) é conhecido como método de evolução da densidade de probabilidade (PDEM)42.
1.3.2.4 Os PDFs das grandezas físicas relevantes são usados para avaliar sua confiabilidade, que são então incorporados à função  de desempenho do critério probabilístico.
de desempenho do critério probabilístico.
1.3.2.5 Avaliar se os critérios de terminação para o processo de otimização de parâmetros foram atendidos. Se as condições não forem satisfeitas, retorne à Etapa 1.3.2.2; Se forem, os parâmetros ideais para o sistema de controle retardado podem ser determinados. Neste trabalho, a caixa de ferramentas do algoritmo genético (GA) no MATLAB é utilizada para otimização de parâmetros, o que facilita as atualizações de parâmetros e define as condições de terminação. Por algoritmo genético, os valores ótimos podem ser alcançados em dez iterações, e a convergência é estável sem problemas mínimos locais. Embora o custo computacional do GA seja maior do que a otimização por enxame de partículas ou métodos baseados em gradiente, o GA é bom para lidar com problemas complexos e não diferenciáveis, como o deste manuscrito. Portanto, o GA é aplicado. E como a propriedade de convergência rápida, o custo computacional do GA é aceitável.
1.3.2.6 Para obter um controle de confiabilidade ideal, a seguinte função  de desempenho é formulada. Minimize
de desempenho é formulada. Minimize  para determinar os valores ideais dos parâmetros
para determinar os valores ideais dos parâmetros  e
e  :
:
 } (25)
} (25)
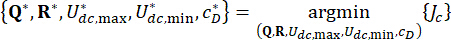 Acessórios (26)
Acessórios (26)
Como mencionado anteriormente, as matrizes de ponderação do controlador são simétricas, onde os elementos na matriz  correspondem aos pesos atribuídos ao deslocamento, velocidade e sua interação, enquanto os elementos na matriz
correspondem aos pesos atribuídos ao deslocamento, velocidade e sua interação, enquanto os elementos na matriz  representam os pesos relacionados à força de controle. Com base nos achados de estudos anteriores38, observou-se que a variação das configurações dos pesos
representam os pesos relacionados à força de controle. Com base nos achados de estudos anteriores38, observou-se que a variação das configurações dos pesos  da função de custo e
da função de custo e  tem impacto mínimo na eficácia do controle. Consequentemente, adota-se uma configuração simplificada neste estudo, conforme descrito a seguir:
tem impacto mínimo na eficácia do controle. Consequentemente, adota-se uma configuração simplificada neste estudo, conforme descrito a seguir:
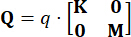 ,
, 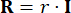 (27)
(27)
Onde 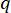 denota o coeficiente da matriz de ponderação de estado a ser definida;
denota o coeficiente da matriz de ponderação de estado a ser definida; 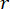 denota o coeficiente da matriz de ponderação de controle a ser definida;
denota o coeficiente da matriz de ponderação de controle a ser definida; 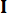 denota a matriz de identidade. O efeito de controle é influenciado pela proporção de
denota a matriz de identidade. O efeito de controle é influenciado pela proporção de 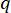 para
para 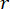 , mas não pelos valores em si. Além disso,
, mas não pelos valores em si. Além disso, 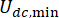 na Eq. (6) denota a força Coulombica mínima do amortecedor MR, o que significa que
na Eq. (6) denota a força Coulombica mínima do amortecedor MR, o que significa que  com a entrada de corrente no amortecedor sendo zero. Então, a Eq. (26) pode ser expressa como:T
com a entrada de corrente no amortecedor sendo zero. Então, a Eq. (26) pode ser expressa como:T
 Acessórios (28)
Acessórios (28)
Onde 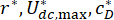 estão os coeficientes ideais de preocupação. Para torná-los razoáveis em engenharia, as faixas ideais deles são baseadas na capacidade de produção das fábricas de amortecedores MR.
estão os coeficientes ideais de preocupação. Para torná-los razoáveis em engenharia, as faixas ideais deles são baseadas na capacidade de produção das fábricas de amortecedores MR.
Obviamente, os parâmetros ótimos obtidos pela Eq. (28) mantêm a eficácia de controle ideal do algoritmo de controle semi-ativo proposto com atraso de tempo, o que permite que o sistema de controle da estrutura atinja a confiabilidade ideal equilibrada sujeita a excitações estocásticas.
2. Estudo de caso
Para analisar a eficácia do método de controle semi-ativo proposto com compensação de atraso de tempo para um amortecedor de RM, uma estrutura plana de cisalhamento de um andar presa a um amortecedor de RM foi submetida ao movimento sísmico estocástico horizontal do solo, conforme mostrado na Figura 2. Os parâmetros do sistema de estrutura semi-ativamente controlada são os seguintes: massa 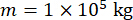 da estrutura, frequência
da estrutura, frequência  circular natural, taxa
circular natural, taxa 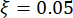 de amortecimento. De acordo com a experiência passada e as escalas de amortecedores existentes no mercado, os valores limite de deslocamento estrutural, velocidade, aceleração e força de controle são 10 mm, 100 mm/s, 1.500 mm/s2 e 150 kN, respectivamente. Para representar o movimento sísmico estocástico do solo, o modelo de movimento do solo estocástico fisicamente motivado foi empregado43:
de amortecimento. De acordo com a experiência passada e as escalas de amortecedores existentes no mercado, os valores limite de deslocamento estrutural, velocidade, aceleração e força de controle são 10 mm, 100 mm/s, 1.500 mm/s2 e 150 kN, respectivamente. Para representar o movimento sísmico estocástico do solo, o modelo de movimento do solo estocástico fisicamente motivado foi empregado43:
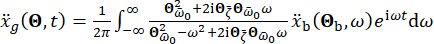 Acessórios (29)
Acessórios (29)
Onde 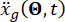 representa o movimento do solo no domínio do tempo no local de engenharia e
representa o movimento do solo no domínio do tempo no local de engenharia e 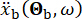 denota o movimento do solo no domínio da frequência no leito rochoso. O vetor
denota o movimento do solo no domínio da frequência no leito rochoso. O vetor  caracteriza a natureza estocástica do movimento do solo na superfície do local de engenharia. Os parâmetros
caracteriza a natureza estocástica do movimento do solo na superfície do local de engenharia. Os parâmetros 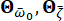 são variáveis estocásticas que descrevem as características do solo do local, incluindo a frequência
são variáveis estocásticas que descrevem as características do solo do local, incluindo a frequência  predominante e o amortecimento
predominante e o amortecimento  equivalente. O vetor
equivalente. O vetor 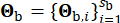 representa a natureza estocástica do movimento do solo no leito rochoso, que é influenciado pelas propriedades da fonte e pelo caminho de propagação, indicando
representa a natureza estocástica do movimento do solo no leito rochoso, que é influenciado pelas propriedades da fonte e pelo caminho de propagação, indicando 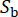 o número de variáveis estocásticas envolvidas neste estágio.
o número de variáveis estocásticas envolvidas neste estágio.  refere-se à frequência circular e i é a unidade imaginária.
refere-se à frequência circular e i é a unidade imaginária.
A frequência  predominante e a taxa
predominante e a taxa  de amortecimento equivalente do canteiro de obras são parâmetros-chave que caracterizam as propriedades dinâmicas do solo do sítio. A distribuição probabilística e os parâmetros estatísticos dessas grandezas podem ser determinados com base em registros de aceleração sísmica coletados de uma classe específica de locais de engenharia. Para fins ilustrativos, uma classe de local com uma faixa de velocidade de onda de cisalhamento de [150, 250] m / s foi considerada, e o período característico de projeto do movimento do solo foi definido como 0,45 s.
de amortecimento equivalente do canteiro de obras são parâmetros-chave que caracterizam as propriedades dinâmicas do solo do sítio. A distribuição probabilística e os parâmetros estatísticos dessas grandezas podem ser determinados com base em registros de aceleração sísmica coletados de uma classe específica de locais de engenharia. Para fins ilustrativos, uma classe de local com uma faixa de velocidade de onda de cisalhamento de [150, 250] m / s foi considerada, e o período característico de projeto do movimento do solo foi definido como 0,45 s.
Os parâmetros  críticos ,
críticos ,  foram tratados como variáveis estocásticas mutuamente independentes, ambos seguindo uma distribuição log-normal para identificação dos parâmetros. Os parâmetros estatísticos foram os seguintes: as médias de ,
foram tratados como variáveis estocásticas mutuamente independentes, ambos seguindo uma distribuição log-normal para identificação dos parâmetros. Os parâmetros estatísticos foram os seguintes: as médias de ,  foram de
foram de  12 rad/s e 0,1, respectivamente. Os coeficientes de variação de
12 rad/s e 0,1, respectivamente. Os coeficientes de variação de  e
e  foram de 0,42 e 0,35, respectivamente. O movimento do solo no leito rochoso foi modelado como um processo de ruído branco gaussiano com uma amplitude de Fourier de 0,20 m/s2, correspondendo a um pico de aceleração do solo de 0,11 g. O ângulo de fase usado para gerar o movimento do leito rochoso foi denotado como
foram de 0,42 e 0,35, respectivamente. O movimento do solo no leito rochoso foi modelado como um processo de ruído branco gaussiano com uma amplitude de Fourier de 0,20 m/s2, correspondendo a um pico de aceleração do solo de 0,11 g. O ângulo de fase usado para gerar o movimento do leito rochoso foi denotado como 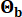 . Portanto, Sb = 1 e
. Portanto, Sb = 1 e 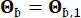 . Essa abordagem pode ser considerada como modelagem de movimentos de solo estocásticos condicionais com uma determinada probabilidade de excedência44. A suposição de distribuição log-normal é amplamente utilizada na modelagem do movimento do solo devido à sua capacidade de capturar a natureza distorcida dos parâmetros de movimento do solo observados.
. Essa abordagem pode ser considerada como modelagem de movimentos de solo estocásticos condicionais com uma determinada probabilidade de excedência44. A suposição de distribuição log-normal é amplamente utilizada na modelagem do movimento do solo devido à sua capacidade de capturar a natureza distorcida dos parâmetros de movimento do solo observados.
Para avaliar a sensibilidade dessa suposição, as análises adicionais usando distribuições probabilísticas alternativas, incluindo as distribuições normal e gama, foram realizadas em outras pesquisas45,46. Os resultados indicam que, embora as tendências gerais permaneçam consistentes, a distribuição log-normal fornece o melhor ajuste aos dados observados, particularmente para capturar o comportamento da cauda das medidas de intensidade do movimento do solo
Em virtude do método das esferas tangentes47, uma coleção de 221 pontos representativos com probabilidades atribuídas associadas foi selecionada e as acelerações representativas do solo foram sintetizadas. A frequência de amostragem foi de 50 Hz e a duração dos movimentos do solo foi de 20,48 s. Para atribuir uma intensidade não estacionária ao movimento simulado do solo, uma função de modulação uniforme foi utilizada e sua formulação foi a seguinte42:
 (30)
(30)
Onde  tomar 2 e 16 s, respectivamente.
tomar 2 e 16 s, respectivamente.
A média e o desvio padrão do movimento sísmico estocástico do solo e um histórico de tempo do movimento sísmico representativo do solo são mostrados na Figura 3. A amplitude da média (0,06 m/s2) foi ~8% da amplitude do desvio padrão (0,8 m/s2), indicando que o modelo de movimento do solo estocástico fisicamente motivado exibiu a propriedade de média zero. Enquanto isso, o movimento sísmico do solo exibiu comportamentos não estacionários notáveis nos domínios temporal e de frequência.
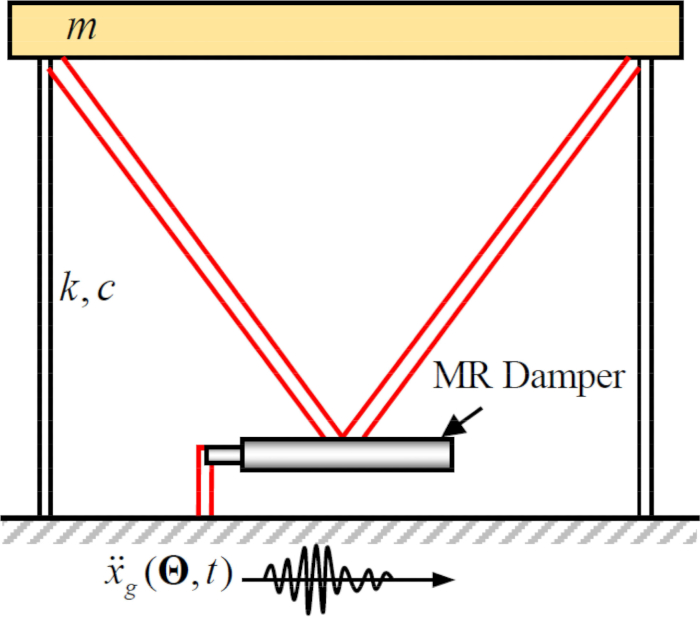
Figura 2: Esboço de uma estrutura de cisalhamento de um andar com um amortecedor magnetoreológico. 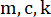 denotam massa da estrutura, taxa de amortecimento e rigidez;
denotam massa da estrutura, taxa de amortecimento e rigidez; 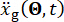 denota a excitação sísmica estocástica. Clique aqui para ver uma versão maior desta figura.
denota a excitação sísmica estocástica. Clique aqui para ver uma versão maior desta figura.
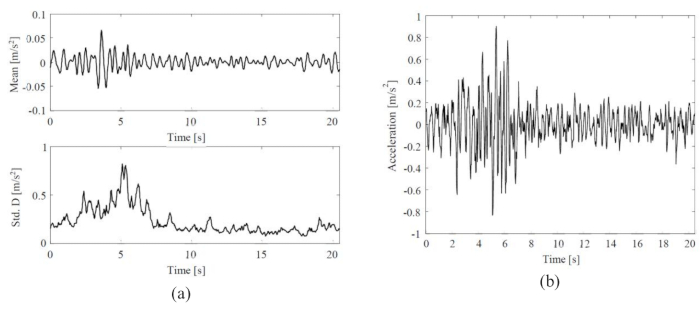
Figura 3: Estatísticas e amostras representativas de movimentos sísmicos selecionados do solo. (A) Média e desvio padrão do movimento sísmico estocástico do solo; (B) Histórico de tempo do movimento sísmico representativo do solo. Clique aqui para ver uma versão maior desta figura.
2.1 Análise de influência do atraso de tempo
Para analisar a influência do atraso de tempo na eficácia de controle semi-ativo de um amortecedor de RM, a Figura 4 mostra o deslocamento, a velocidade e a aceleração RMS (resposta quadrática média da raiz) da estrutura controlada. A razão da matriz de ponderação e os parâmetros do amortecedor foram 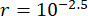 ,
, 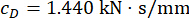 , e
, e 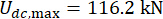 , que são os resultados otimizados sem atrasode tempo 38. As respostas da estrutura controlada com atraso de tempo foram maiores do que a estrutura controlada sem atraso de tempo, e a influência do atraso de tempo no efeito de controle representou periodicidade junto com o aumento do atraso de tempo. Como o método de controle semi-ativo com amortecedor MR é um tipo de método de feedback, a periodicidade da influência foi considerada relacionada ao período natural da estrutura controlada (T = 0,56 s).
, que são os resultados otimizados sem atrasode tempo 38. As respostas da estrutura controlada com atraso de tempo foram maiores do que a estrutura controlada sem atraso de tempo, e a influência do atraso de tempo no efeito de controle representou periodicidade junto com o aumento do atraso de tempo. Como o método de controle semi-ativo com amortecedor MR é um tipo de método de feedback, a periodicidade da influência foi considerada relacionada ao período natural da estrutura controlada (T = 0,56 s).
Em comparação com as respostas da estrutura descontrolada, das quais o deslocamento máximo de MRS, velocidade e aceleração foram de 24,6 mm, 270,0 mm/s e 3111,3 mm/s2, a estrutura controlada por amortecedor MR alcançou um efeito notável. Ao contrário da instabilidade da estrutura controlada ativa com atraso de tempo25, o método de controle semi-ativo baseado em amortecedor MR ainda obteve algum efeito mesmo com atraso de tempo.
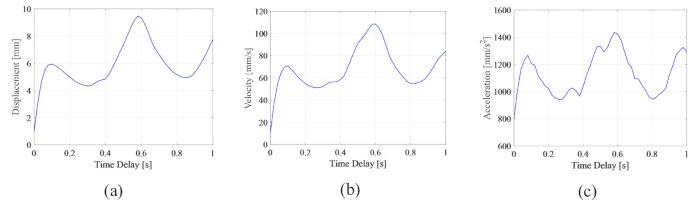
Figura 4: Os quadrados médios máximos das respostas da estrutura controlada com o tempo. (A) Deslocamento; (B) Velocidade; (C) Aceleração. Clique aqui para ver uma versão maior desta figura.
Para analisar a influência do atraso de tempo na confiabilidade de uma estrutura controlada semiativamente, a Figura 5 mostra a confiabilidade do deslocamento, velocidade e aceleração com o aumento do atraso de tempo. A confiabilidade das respostas da estrutura controlada com qualquer atraso de tempo foi menor do que os valores sem atraso de tempo, o que significa que a confiabilidade da estrutura controlada foi diminuída pelo atraso de tempo. Enquanto isso, semelhante ao RMS máximo, o efeito do controle de confiabilidade apresentou periodicidade com o aumento do atraso de tempo. Além disso, a confiabilidade da estrutura controlada, com ou sem atraso de tempo, foi maior do que os valores de estruturas não controladas com confiabilidade de deslocamento, velocidade e aceleração 0,0954, 0,1058 e 0,1111.
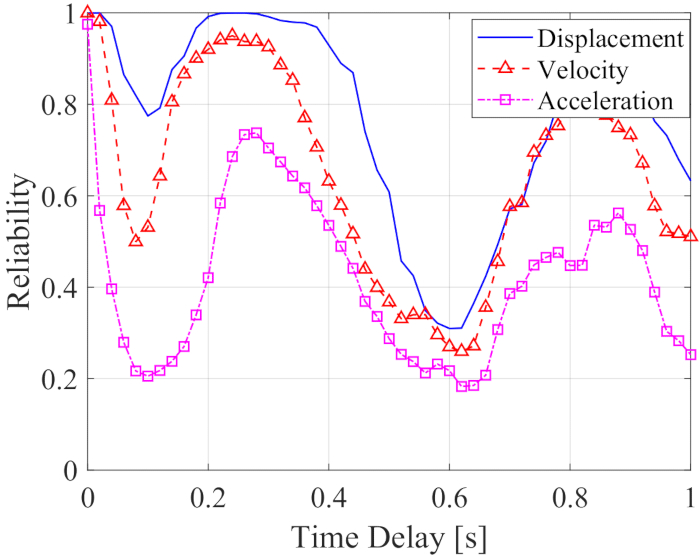
Figura 5: Confiabilidade das respostas da estrutura controlada com atraso de tempo crescente. Clique aqui para ver uma versão maior desta figura.
Em resumo, as respostas da estrutura foram mitigadas pelo método de controle semi-ativo. No entanto, a eficácia do controle, independentemente do RMS ou confiabilidade, do método de controle semi-ativo foi diminuída pelo atraso no tempo. Portanto, é necessário compensar o atraso.
2.1.1 Análise do método de compensação de atraso de tempo
Para analisar a eficácia do método de compensação de atraso de tempo proposto, os históricos de tempo RMS de deslocamento, velocidade e aceleração para sistema não controlado (Unc), de atraso de tempo com não compensação controlada (TDN-SAC-PSO) e de tempo de atraso com compensação controlada (TDC-SAC-PSO) são comparados na Figura 6, onde o atraso de tempo foi de 0,1 s. Os parâmetros da matriz de ponderação e do método de controlo semi-activo são os mesmos que na etapa 2.1.
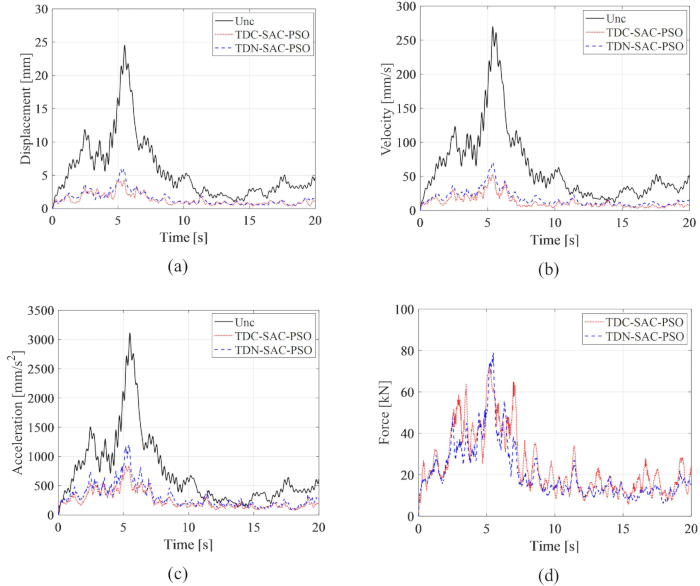
Figura 6: Comparação do histórico de tempo quadrático médio de estruturas controladas por diferentes métodos. (A) Deslocamento; (B) Velocidade; (c) aceleração; (D) Força de controle. Abreviaturas: Unc = não controlado; TDC-SAC-PSO = sistema de retardo de tempo com compensação controlada; TDN -SAC-PSO = sistema de retardo de tempo com não compensação controlada. Clique aqui para ver uma versão maior desta figura.
Ambos os métodos de controle diminuíram significativamente as respostas da estrutura em comparação com a estrutura não controlada, revelando as vantagens do método de controle baseado em amortecedores MR. Em comparação com a estrutura não controlada, o RMS máximo de deslocamento, velocidade e aceleração é reduzido em 75,79%, 73,75% e 61,22% com o método TDN-SAC-PSO. Além disso, com a compensação de atraso de tempo, as respostas da estrutura controlada são diminuídas em 82,59%, 80,40% e 73,04% com o método TDC-SAC-PSO. O RMS máximo da força de controle com o método TDC-SAC-PSO diminuiu 8,43% em comparação com o método TDN-SAC-PSO, embora as respostas de vibração do primeiro método tenham sido menores do que o segundo. A análise acima indica que a influência do atraso de tempo no método de controle baseado em amortecedor MR foi efetivamente diminuída pelo método de compensação, que mostra a necessidade de compensação de atraso de tempo para o método de controle semi-ativo do amortecedor MR.
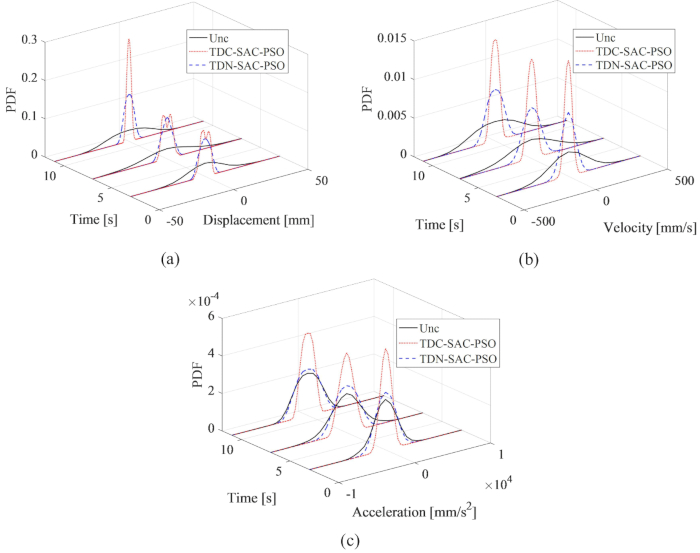
Figura 7: Comparação em PDF em momentos típicos de respostas de estrutura. (A) Deslocamento; (B) Velocidade; (C) Aceleração. Abreviaturas: PDF = função de densidade de probabilidade; Unc = não controlado; TDC-SAC-PSO = sistema de retardo de tempo com compensação controlada; TDN -SAC-PSO = sistema de retardo de tempo com não compensação controlada. Clique aqui para ver uma versão maior desta figura.
Para revelar de forma abrangente o efeito do método de compensação proposto na incerteza das respostas da estrutura controlada, as comparações da função de densidade de probabilidade (PDF) de deslocamento, velocidade e aceleração em tempos típicos, 3, 7 e 11s, são mostradas na Figura 7. Os PDFs para o método TDN-SAC-PSO foram mais estreitos do que os da estrutura não controlada, o que significa que a incerteza das respostas da estrutura foi diminuída pelo método de controle semi-ativo, mesmo com atraso de tempo. Quando o atraso foi compensado, os PDFs das respostas foram reduzidos ainda mais. Portanto, o método de compensação proposto é necessário para melhorar o efeito de controle semi-ativo.
| Método de controle | Deslocamento | Velocidade | Aceleração | Força de controle | Valor mínimo |
| Unc | 0.0954 | 0.1058 | 0.1111 | -- | 0.1111 |
| TDC-SAC-PSO | 0.9565 | 0.8107 | 0.7654 | 0.9845 | 0.7654 |
| TDN-SAC-PSO | 0.7747 | 0.531 | 0.2054 | 0.884 | 0.2054 |
Tabela 1: Respostas de vibração e confiabilidade da força de controle de estruturas controladas por diferentes métodos. Abreviaturas: Unc = não controlado; TDC-SAC-PSO = sistema de retardo de tempo com compensação controlada; TDN -SAC-PSO = sistema de retardo de tempo com não compensação controlada.
As respostas de vibração e a confiabilidade da força de controle de estruturas controladas por métodos não controladas, TDC-SAC-PSO e TDN-SAC-PSO são mostradas na Tabela 1. Com o controle do método TDN-SAC-PSO, a confiabilidade da estrutura foi drasticamente aumentada em comparação com a estrutura não controlada, que valida a eficácia do método de controle baseado em amortecedores MR, mesmo com o tempo. No entanto, com a compensação de atraso de tempo, a confiabilidade foi significativamente aumentada em comparação com sem compensação, especialmente para a aceleração. Destaca-se também que a confiabilidade das diferentes respostas e a força de controle apresentaram diferenças significativas para o método TDC-SAC-PSO. Isso indica que os valores ideais de parâmetros críticos para o controle sem atraso de tempo não são ideais para o controle com atraso de tempo. Para obter o efeito de controle ideal das respostas de vibração e da força de controle com influência de atraso de tempo, os parâmetros precisam ser otimizados ainda mais. Com base na análise acima, conclui-se que o método de controle semi-ativo com um amortecedor MR pode efetivamente diminuir as respostas de vibração da estrutura, enquanto os parâmetros precisam ser otimizados devido à influência do atraso de tempo.
2.2 Otimização de parâmetros
Para atingir os valores ótimos dos parâmetros, foi aplicado o método de otimização integrado baseado no critério de confiabilidade38. A otimização dos parâmetros críticos foi realizada com 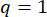 ,
, 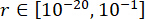 ,
,  ,
, 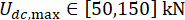 , e os tempos sintonizáveis da força do amortecedor MR s = 8. A caixa de ferramentas GA dentro do MATLAB foi usada para implementar a otimização.
, e os tempos sintonizáveis da força do amortecedor MR s = 8. A caixa de ferramentas GA dentro do MATLAB foi usada para implementar a otimização.
Os resultados de otimização dos parâmetros são  ,
, 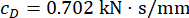 , e
, e  para o atraso
para o atraso 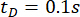 de tempo . A Figura 8 mostra os históricos de tempo RMS de deslocamento, velocidade, aceleração e força de controle para as estruturas controladas pelo método Uncontrolled (Unc), TDC-SAC-PSO e SOSC-PSO. O método SOSC-PSO denota o método de controle semi-ativo com compensação de atraso de tempo e valores de parâmetros críticos otimizados.
de tempo . A Figura 8 mostra os históricos de tempo RMS de deslocamento, velocidade, aceleração e força de controle para as estruturas controladas pelo método Uncontrolled (Unc), TDC-SAC-PSO e SOSC-PSO. O método SOSC-PSO denota o método de controle semi-ativo com compensação de atraso de tempo e valores de parâmetros críticos otimizados.
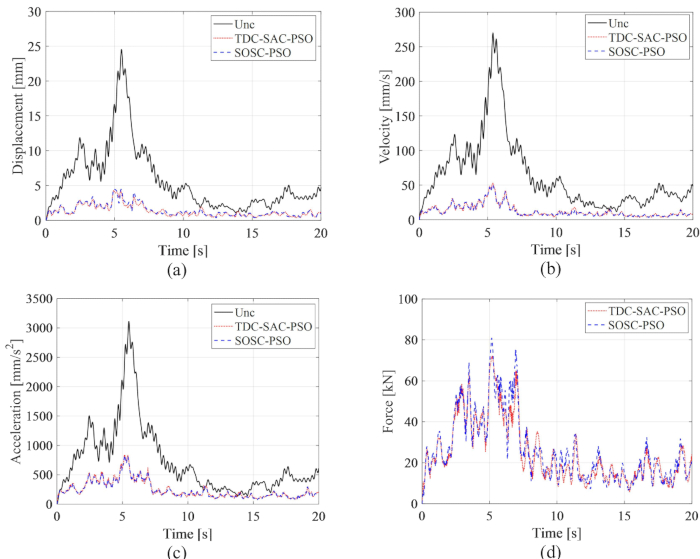
Figura 8: Históricos de tempo RMS de deslocamento, velocidade, aceleração e força de controle para estruturas controladas pelo método não controlado e TDC-SAC-PSO e SOSC-PSO. (A) Deslocamento; (B) Velocidade; (c) aceleração; (D) Força de controle. Abreviaturas: Unc = não controlado; TDC-SAC-PSO = sistema de retardo de tempo com compensação controlada; SOSC-PSO = Método de controle semi-ativo ótimo estocástico com compensação de atraso de tempo. Clique aqui para ver uma versão maior desta figura.
A partir da Figura 8, observa-se que os efeitos de controle dos métodos TDC-SAC-PSO e SOSC-PSO apresentaram pouca diferença. O RMS máximo da velocidade de deslocamento e aceleração para o primeiro método foi de 81,60%, 81,21%, 73,62% da estrutura não controlada e 82,59%, 80,40%, 73,04% para o segundo método. Para analisar de forma abrangente as características de probabilidade das respostas para ambos os métodos de controle, a Figura 9 mostra os PDFs de deslocamento, velocidade e aceleração para as estruturas controladas pelo método não controlado, TDC-SAC-PSO e SOSC-PSO. Ambos os métodos de controle tinham quase os mesmos PDFs de deslocamento e velocidade em momentos típicos. Os PDFs de aceleração do método SOSC-PSO foram mais estreitos do que os do método TDC-SAC-PSO, o que significa que a incerteza da aceleração alcançou um melhor efeito de controle pelo método anterior.
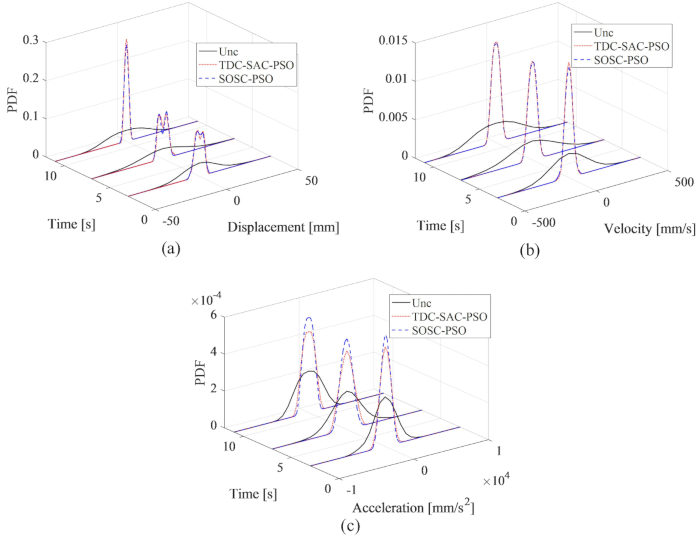
Figura 9: Comparação de PDFs de deslocamento, velocidade e aceleração para diferentes estruturas controladas. (A) Deslocamento; (B) Velocidade; (C) Aceleração. Abreviaturas: PDFs = funções de densidade de probabilidade; Unc = não controlado; TDC-SAC-PSO = sistema de retardo de tempo com compensação controlada; SOSC-PSO = Método de controle semi-ativo ótimo estocástico com compensação de atraso de tempo. Clique aqui para ver uma versão maior desta figura.
A confiabilidade do deslocamento, velocidade, aceleração e força de controle para as estruturas controladas pelos métodos TDC-SAC-PSO e SOSC-PSO não controladas são mostradas na Tabela 2. Ambos os métodos de controle alcançaram aumento significativo na confiabilidade em comparação com a estrutura não controlada. A confiabilidade do deslocamento mostrou pouca diferença entre os métodos TDC-SAC-PSO e SOSC-PSO. Enquanto a confiabilidade da aceleração, a menor confiabilidade da estrutura controlada, alcançou um aumento notável. Isso significa que o método SOSC-PSO atinge o efeito de controle ideal do equilíbrio.
| Método de controle | Deslocamento | Velocidade | Aceleração | Força de controle | Valor mínimo |
| Unc | 0.0954 | 0.1058 | 0.1111 | -- | 0.1111 |
| TDC-SAC-PSO | 0.9565 | 0.8107 | 0.7654 | 0.9845 | 0.7654 |
| SOSC-PSO | 0.953 | 0.8704 | 0.8934 | 0.9586 | 0.8934 |
Tabela 2: Confiabilidade para estruturas controladas por diferentes métodos. Abreviaturas: Unc = não controlado; TDC-SAC-PSO = sistema de retardo de tempo com compensação controlada; SOSC-PSO = Método de controle semi-ativo ótimo estocástico com compensação de atraso de tempo.
A eficácia do método SOSC-PSO proposto com atraso 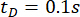 de tempo foi analisada. Para verificar ainda mais o método proposto para diferentes atrasos de tempo, a Tabela 3 mostra os valores ideais dos parâmetros e a confiabilidade correspondente para o intervalo de
de tempo foi analisada. Para verificar ainda mais o método proposto para diferentes atrasos de tempo, a Tabela 3 mostra os valores ideais dos parâmetros e a confiabilidade correspondente para o intervalo de 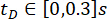 atraso.
atraso.
| tD(s) | lg(r*) | CD (kN · s / mm) | U dc,max (kN) | Deslocamento | Velocidade | Aceleração | Força de controle |
| 0 | -2.524 | 1.44 | 116.163 | 0.9997 | 0.9998 | 0.9752 | 1 |
| 0.02 | -4.413 | 0.414 | 144.066 | 0.9989 | 0.9988 | 0.872 | 0.9011 |
| 0.04 | -4.416 | 0.25 | 141.759 | 0.9998 | 0.9846 | 0.8881 | 0.9135 |
| 0.06 | -3.226 | 0.203 | 145.613 | 0.993 | 0.9318 | 0.8756 | 0.9556 |
| 0.08 | -5.207 | 0.345 | 133.692 | 0.9646 | 0.8998 | 0.8998 | 0.953 |
| 0.1 | -4.669 | 0.702 | 130.739 | 0.9531 | 0.8704 | 0.8934 | 0.9586 |
| 0.12 | -4.895 | 0.833 | 69.72 | 0.9526 | 0.863 | 0.888 | 0.9686 |
| 0.14 | -4.231 | 0.921 | 75.221 | 0.9531 | 0.8681 | 0.8697 | 0.9671 |
| 0.16 | -5.594 | 0.662 | 138.922 | 0.9529 | 0.8461 | 0.8262 | 0.931 |
| 0.18 | -4.262 | 0.882 | 76.335 | 0.9516 | 0.7873 | 0.7614 | 0.9618 |
| 0.2 | -3.926 | 0.783 | 67.951 | 0.904 | 0.7277 | 0.7116 | 0.9653 |
| 0.22 | -5.965 | 1.071 | 52.554 | 0.8377 | 0.6411 | 0.6205 | 0.965 |
| 0.24 | -4.481 | 1.216 | 128.148 | 0.7567 | 0.474 | 0.474 | 0.9687 |
| 0.26 | -3.53 | 0.672 | 53.706 | 0.53 | 0.4096 | 0.4158 | 0.9921 |
| 0.28 | -4.433 | 0.638 | 64.225 | 0.3547 | 0.3745 | 0.3464 | 0.9928 |
| 0.3 | -3.536 | 0.459 | 57.705 | 0.2735 | 0.316 | 0.2736 | 0.9929 |
| Unc | -- | -- | -- | 0.0954 | 0.1058 | 0.1111 | -- |
Tabela 3: Os valores ideais dos parâmetros e os valores de confiabilidade correspondentes para diferentes atrasos de tempo. 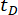 denota atraso de tempo;
denota atraso de tempo;  denotar o valor logarítmico ótimo de r,r denota o coeficiente da matriz de ponderação de controle;
denotar o valor logarítmico ótimo de r,r denota o coeficiente da matriz de ponderação de controle; 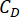 denota o coeficiente de amortecimento viscoso do amortecedor MR;
denota o coeficiente de amortecimento viscoso do amortecedor MR; 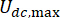 denotam as forças Coulombic máximas e mínimas do amortecedor MR.
denotam as forças Coulombic máximas e mínimas do amortecedor MR.
Pode-se observar que a confiabilidade do deslocamento, velocidade e aceleração foi melhorada em comparação com a estrutura não controlada, mesmo na presença de atraso de tempo, demonstrando a robustez do método proposto em relação a tais atrasos. No entanto, a confiabilidade das respostas estruturais com o método de controle proposto diminuiu à medida que o atraso aumentava, indicando que, embora o impacto do atraso na eficácia do controle possa ser mitigado, ele não pode ser totalmente eliminado. Notavelmente, a confiabilidade da força de controle permaneceu acima de 90% em diferentes atrasos de tempo.
3. Exemplo numérico
Para verificar o método SOSC-PSO proposto na estrutura MDOF, foi analisada uma estrutura de seis pavimentos com dois amortecedores MR instalados no primeiro e terceiro pavimentos, conforme mostrado na Figura 10. As amostras sísmicas produzidas pelo modelo sísmico estocástico na Seção 2 foram aplicadas, e os limiares de confiabilidade de deslocamento, velocidade, aceleração e força de controle foram de 20 mm, 200 mm/s, 3.000 mm/s2 e 200 kN. Eqs. (27) foram utilizados como matriz de ponderação com 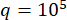 . A caixa de ferramentas GA do MATLAB foi usada para otimizar
. A caixa de ferramentas GA do MATLAB foi usada para otimizar 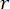 ,
, , e
, e  , com intervalos
, com intervalos 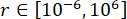 ótimos ,
ótimos ,  , e
, e 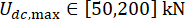 .
.
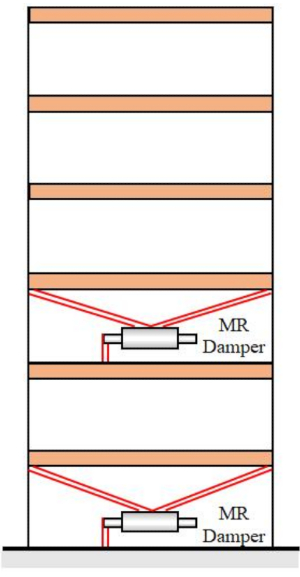
Figura 10: Estrutura de seis andares com dois amortecedores MR. Abreviatura: MR = magnetorreológico. Clique aqui para ver uma versão maior desta figura.
3.1 Análise de influência do atraso de tempo
Para analisar a influência do atraso de tempo na eficácia de controle do amortecedor MR na estrutura MDOF, a Figura 11 mostra o RMS máximo de deslocamento (deslocamento entre andares), velocidade (velocidade entre andares) e aceleração (aceleração de andar) junto com o atraso de tempo para o método TDC-SAC-PSO. Os parâmetros foram 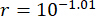 ,
, , e
, e  para o amortecedor MR no 1º andar;
para o amortecedor MR no 1º andar;  e
e  para o amortecedor MR no 3º andar, que são os resultados otimizados sem atraso de tempo. O RMS máximo das respostas da estrutura controlada exibiu flutuação do período junto com o atraso de tempo. O RMS máximo de deslocamento e velocidade estava no 1º andar, a aceleração máxima no 6º andar. Além disso, todas as respostas máximas de MRS com qualquer atraso de tempo foram maiores do que os valores sem atraso de tempo, o que significa que o atraso de tempo diminui o efeito de controle do amortecedor de RM.
para o amortecedor MR no 3º andar, que são os resultados otimizados sem atraso de tempo. O RMS máximo das respostas da estrutura controlada exibiu flutuação do período junto com o atraso de tempo. O RMS máximo de deslocamento e velocidade estava no 1º andar, a aceleração máxima no 6º andar. Além disso, todas as respostas máximas de MRS com qualquer atraso de tempo foram maiores do que os valores sem atraso de tempo, o que significa que o atraso de tempo diminui o efeito de controle do amortecedor de RM.
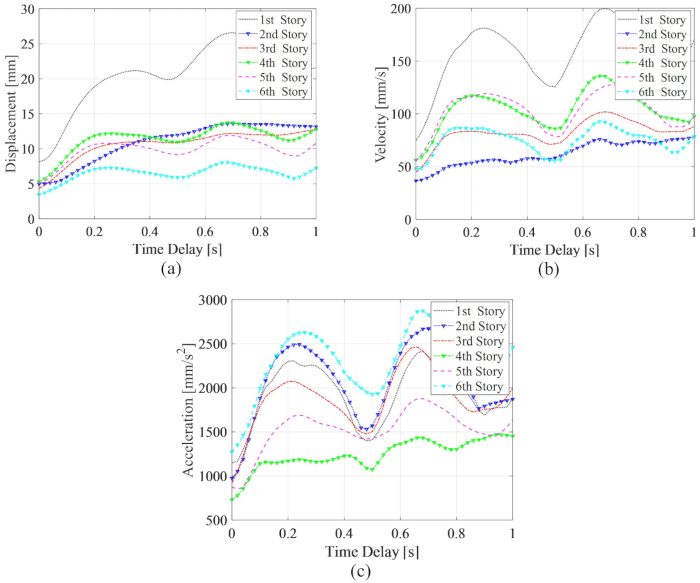
Figura 11: RMS máximo de respostas junto com atraso de tempo para a estrutura controlada pelo método TDC-SAC-PSO. (A) Deslocamento; (B) Velocidade; (C) Aceleração. Abreviaturas: RMS = raiz quadrada média; TDC-SAC-PSO = sistema de retardo de tempo com compensação controlada. Clique aqui para ver uma versão maior desta figura.
A confiabilidade do deslocamento, velocidade e aceleração, juntamente com o atraso de tempo, é mostrada na Figura 12. A confiabilidade da velocidade e da aceleração mostra flutuação do período junto com o atraso de tempo, enquanto a confiabilidade do deslocamento diminuiu drasticamente junto com o atraso de tempo; Todos os valores de confiabilidade em qualquer atraso de tempo foram menores do que aqueles sem atraso de tempo. Portanto, o método de compensação de atraso de tempo é necessário para reduzir a influência do atraso de tempo na confiabilidade da estrutura controlada pelo amortecedor MR.
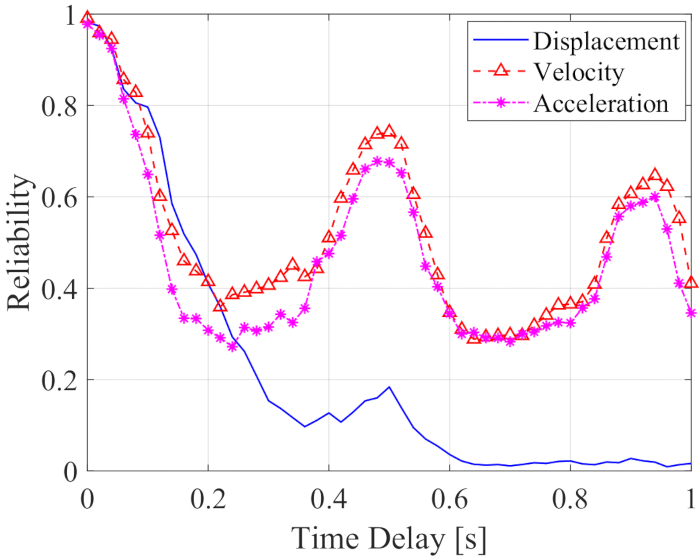
Figura 12: Confiabilidade das respostas da estrutura controlada junto com o atraso de tempo. Clique aqui para ver uma versão maior desta figura.
3.2 Efeito de controle da compensação de atraso de tempo
Com base no método TDC-SAC-PSO proposto, foi analisada a estrutura de 6 graus de profundidade com dois amortecedores de RM. A Figura 13 mostra os históricos de tempo RMS de deslocamento e aceleração no 1º e 3º andares para as estruturas controladas pelo método TDC-SAC-PSO (Unc), controladas pelo método TDC-SAC-PSO e controladas pelo método TDN-SAC-PSO. O atraso de tempo foi 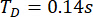 , e a razão
, e a razão 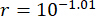 da matriz de ponderação; os parâmetros do amortecedor de RM foram
da matriz de ponderação; os parâmetros do amortecedor de RM foram  ,
,  para o 1º andar;
para o 1º andar;  e
e  para o 3º andar.
para o 3º andar.

Figura 13: Históricos de tempo RMS de deslocamento e aceleração no 1º e 3º andares para estruturas controladas por diferentes métodos. (A) Deslocamento no 1º andar; (B) Deslocamento no 3º andar; (C) Aceleração no 1º andar; (D) Aceleração no 3º andar. Abreviaturas: RMS = raiz quadrada média; Unc = não controlado; TDC-SAC-PSO = sistema de retardo de tempo com compensação controlada; TDN -SAC-PSO = sistema de retardo de tempo com não compensação controlada. Clique aqui para ver uma versão maior desta figura.
As RMS máximas de deslocamento no 1º e 3º andares foram reduzidas em 35,42% e 30,44% pelo método TDN-SAC-PSO, onde o atraso de tempo não foi compensado. Já com a compensação, o RMS máximo de deslocamento no 1º e 3º andares foi reduzido em 49,33% e 53,39%, respectivamente. Sem compensação, o RMS máximo de aceleração no 1º e 3º andares aumentou 16,22% e 2,88%, mas diminuiu 25,77% e 36,00%, respectivamente, com compensação. Portanto, a compensação do atraso de tempo no método de controle do amortecedor MR é necessária para reduzir as respostas da estrutura, especialmente para a aceleração.
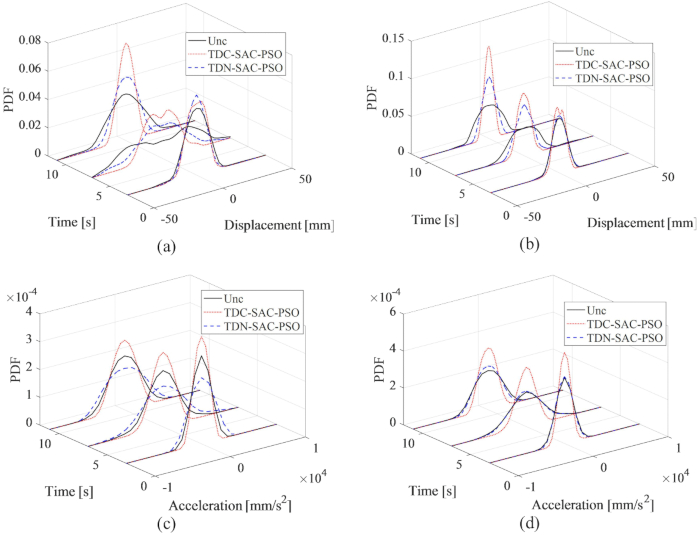
Figura 14: PDFs de deslocamento e aceleração no 1º e 3º andares para diferentes métodos de controle. (A) Deslocamento no 1º andar; (B) Deslocamento no 3º andar; (C) Aceleração no 1º andar; (D) Aceleração no 3º andar. Abreviaturas: PDFs = funções de densidade de probabilidade; Unc = não controlado; TDC-SAC-PSO = sistema de retardo de tempo com compensação controlada; TDN -SAC-PSO = sistema de retardo de tempo com não compensação controlada. Clique aqui para ver uma versão maior desta figura.
Os PDFs de deslocamento e aceleração no 1º e 3º pavimentos são mostrados na Figura 14, revelando os diferentes efeitos de controle dos métodos TDC-SAC-PSO e TDN-SAC-PSO em comparação com a estrutura não controlada. Sem compensação, os PDFs de deslocamento no 1º e 3º andares ainda eram mais estreitos do que os da estrutura não controlada. Além disso, com a compensação do atraso de tempo, os PDFs de deslocamento tornaram-se mais estreitos do que os da estrutura controlada pelo método TDN-SAC-PSO. Ao contrário do deslocamento, sem compensação, os PDFs de aceleração no 1º pavimento para o método TDN-SAC-PSO foram mais largos do que os da estrutura não controlada. No entanto, com compensação, os PDFs de aceleração no 1º e 3º andares foram mais estreitos do que os da estrutura não controlada. Assim, verifica-se a necessidade de compensação de atraso de tempo para aumentar a certeza das respostas da estrutura, especialmente para a aceleração.
| Método de controle | Deslocamento | Velocidade | Aceleração | Força de controle no1º andar | Força de controle no3º andar |
| Unc | 0.0114 | 0.5822 | 0.6372 | -- | -- |
| TDN-SAC-PSO | 0.5851 | 0.5258 | 0.398 | 1 | 1 |
| TDC-SAC-PSO | 0.806 | 0.8674 | 0.8037 | 1 | 1 |
Tabela 4: Confiabilidade para estruturas controladas por diferentes métodos. Abreviaturas: Unc = não controlado; TDC-SAC-PSO = sistema de retardo de tempo com compensação controlada; TDN -SAC-PSO = sistema de retardo de tempo com não compensação controlada.
Os valores de confiabilidade de deslocamento, velocidade, aceleração e força de controle com os sistemas de estrutura controlados pelos diferentes métodos são mostrados na Tabela 4. Os valores de confiabilidade das respostas da estrutura foram calculados usando o método dos valores extremos equivalentes25. Pelo controle do método TDN-SAC-PSO, a confiabilidade do deslocamento aumentou em comparação com a estrutura não controlada, enquanto a confiabilidade da velocidade e aceleração diminuiu. Com a compensação de atraso de tempo no método TDC-SAC-PSO, a confiabilidade do deslocamento, velocidade e aceleração aumentou significativamente. Além disso, os valores de confiabilidade da força de controle para os métodos TDN-SAC-PSO e TDN-SAC-PSO são suficientemente mantidos. Assim, o método de controle de compensação de atraso de tempo proposto alcança um efeito de controle favorável para a estrutura controlada por amortecedor MR.
3.3 Otimização de parâmetros
Para alcançar o efeito de controle ideal, os parâmetros do método de controle proposto foram otimizados com base no critério de confiabilidade. Com o atraso 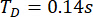 de tempo, o resultado ótimo foi
de tempo, o resultado ótimo foi  ;
; 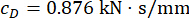 , e
, e 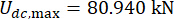 para o amortecedor MR do 1º andar;
para o amortecedor MR do 1º andar; 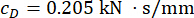 e
e  para o amortecedor MR do 3º andar.
para o amortecedor MR do 3º andar.
Os históricos de tempo RMS de deslocamento e aceleração no 1º e 3º andares são mostrados na Figura 15 , onde os efeitos de controle dos métodos TDC-SAC-PSO e SOSC-PSO e a estrutura não controlada são comparados. Com o controle do amortecedor MR, com ou sem compensação de atraso de tempo, o RMS de deslocamento e aceleração diminuiu significativamente. Com o método SOSC-PSO, o RMS máximo de deslocamento no 1º e 3º andares diminuiu 65,15% e 63,16% em relação à estrutura não controlada, respectivamente. Em comparação com o método TDC-SAC-PSO, a resposta de deslocamento foi ainda mais reduzida. O RMS máximo de aceleração no 1º e 3º andares é reduzido em 23,39% e 35,60% para o método SOSC-PSO. Houve pouca diferença no efeito de controle da aceleração para os métodos SOSC-PSO e TDC-SAC-PSO, indicando que o efeito de controle da compensação do atraso de tempo foi diferente para deslocamento e aceleração.
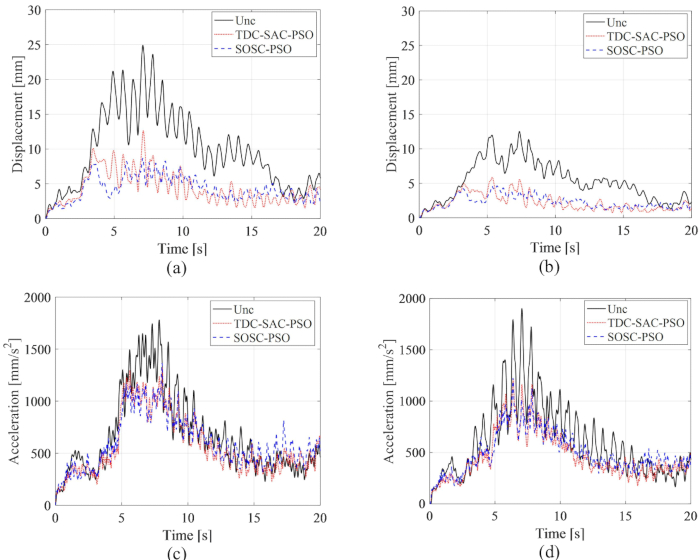
Figura 15: Históricos de tempo RMS de deslocamento e aceleração no 1º e 3º andares para diferentes métodos de controle. (A) Deslocamento no 1º andar; (B) Deslocamento no 3º andar; (C) Aceleração no 1º andar; (D) Aceleração no 3º andar. Abreviaturas: RMS = raiz quadrada média; Unc = não controlado; TDC-SAC-PSO = sistema de retardo de tempo com compensação controlada; SOSC-PSO = Método de controle semi-ativo ótimo estocástico com compensação de atraso de tempo. Clique aqui para ver uma versão maior desta figura.
Os PDFs de deslocamento e aceleração no 1º e 3º andares são apresentados na Figura 16; os PDFs de deslocamento e aceleração foram reduzidos pelos métodos TDC-SAC-PSO e SOSC-PSO em comparação com a estrutura não controlada. Além disso, os PDFs de deslocamento e aceleração para o método SOSC-PSO foram ainda mais reduzidos em comparação com os da estrutura controlada pelo método TDC-SAC-PSO. Portanto, com a otimização de parâmetros, o método de controle de compensação de atraso de tempo proposto alcançou um efeito de controle melhor do que sem otimização.
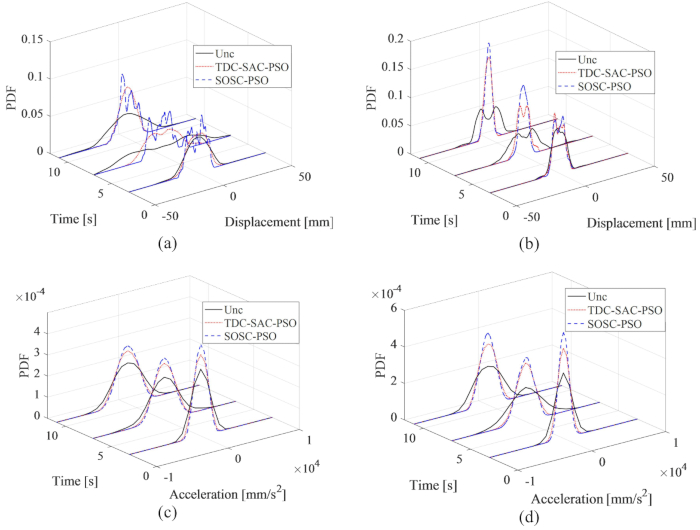
Figura 16: PDFs de deslocamento e aceleração no 1º e 3º andares para diferentes métodos de controle. (A) Deslocamento no 1º andar; (B) Deslocamento no 3º andar; (C) Aceleração no 1º andar; (D) Aceleração no 3º andar. Abreviaturas: PDFs = funções de densidade de probabilidade; Unc = não controlado; TDC-SAC-PSO = sistema de retardo de tempo com compensação controlada; SOSC-PSO = Método de controle semi-ativo ótimo estocástico com compensação de atraso de tempo Clique aqui para ver uma versão maior desta figura.
Os valores de confiabilidade de deslocamento, velocidade, aceleração e força de controle são mostrados na Tabela 5. Os valores de confiabilidade para o método SOSC-PSO foram maiores do que para o método TDC-SAC-PSO. Enquanto isso, a força de controle ainda mantinha confiabilidade suficiente. Assim, a otimização dos parâmetros é necessária para obter o melhor efeito de controle para o método de controle baseado em amortecedor MR.
| Método de controle | Deslocamento | Velocidade | Aceleração | Força de controle no1º andar | Força de controle no3º andar |
| Unc | 0.0114 | 0.5822 | 0.6372 | -- | -- |
| TDC-SAC-PSO | 0.806 | 0.8674 | 0.8037 | 1 | 1 |
| SOSC-PSO | 0.9544 | 0.9314 | 0.8788 | 1 | 1 |
Tabela 5: Confiabilidade para estruturas controladas por diferentes métodos. Abreviaturas: Unc = não controlado; TDC-SAC-PSO = sistema de retardo de tempo com compensação controlada; SOSC-PSO = Método de controle semi-ativo ótimo estocástico com compensação de atraso de tempo.
Resultados
Visando a influência do atraso de tempo na eficácia de controle do método baseado em amortecedores de RM, um método de controle semi-ativo com compensação de atraso de tempo é proposto neste artigo. No método proposto, os parâmetros críticos são otimizados com base no critério de confiabilidade. Ao comparar a eficácia do controle, as seguintes conclusões são abordadas:
(1) O método de controle semi-ativo baseado em um amortecedor MR é mais rob...
Discussão
Com a introdução da teoria de controle ótimo estocástico físico (PSO), um método de controle semi-ativo ótimo estocástico com compensação de atraso de tempo (SOSC-PSO) é proposto neste artigo, projetado para manter a confiabilidade das estruturas controladas por amortecedores de RM. Para compensar o atraso de tempo no método proposto, a força de controle semi-ativa é derivada como a função não apenas dos estados presentes, mas também dos estados e forças de controle em...
Divulgações
Todos os autores não têm conflitos de interesse a declarar.
Agradecimentos
Os autores agradecem o apoio da Fundação de Ciências Naturais da Província de Hebei (Concessão nº E2023210007).
Materiais
| Name | Company | Catalog Number | Comments |
| MATLAB | MathWorks | 2016 | Using for the calculation of the proposed method |
Referências
- Yao, J. T. P. Concept of structural control. J Struct Div. 98 (7), 1567-1574 (1972).
- Liu, J., Silva, C. E., Dyke, S. J., Wu, Y., Liu, H. Using real-time hybrid simulation for active mass damper experimentation and validation. Mech Mach Theory. 191, 105474 (2024).
- Pan, H., Li, C., Cao, L. Bidirectional pendulum-type tuned tendem mass dampers-inerters for integrated control of alongwind and crosswind responses in super-tall buildings. J Build Eng. 100, 111676 (2025).
- Housner, G. W. et al. Structural control: past, present, and future. J Eng Mech. 123 (9), 897-971 (1997).
- Rahman, M., Ong, Z. C., Chong, W. T., Julai, S. Smart Semi-active PID-ACO control strategy for tower vibration reduction in Wind Turbines with MR damper. Earthq Eng Eng Vib. 18 (4), 887-902 (2019).
- Morales-Beltran, M., Paul, J. Active and semi-active strategies to control building structures under large earthquake motion. J Earthquake Eng. 19 (7), 1086-1111 (2015).
- Shu, Z., You, R., Xie, Y. Viscoelastic dampers for vibration control of building structures: A state-of-art review. J Earthq Eng. 28 (12), 3558-3585 (2024).
- Soong, T. T. Active structural control: Theory and practice. Longman Scientific & Technical. New York (1990).
- Wan, H. P., Ma, Q., Dong, G. S., Luo, Y., Ni, Y. Q. Data-driven model reduction approach for active vibration control of cable-strut structures. Eng Struct. 302, 117434 (2024).
- Cao, L., Li, X., Huang, Y., Li, C., Pan, H. High robust eddy current tuned tandem mass dampers-inerters for structures under the ground acceleration. Soil Dyn Earthq Eng. 188, 109040 (2025).
- Chha, H., Peng, Y. Adaptive semiactive control of structure with magnetorheological dampers using wavelet packet transform. Adv Struct Eng. 27 (9), 1509-1527 (2024).
- Zeng, X., Peng, Y., Chen, J. Serviceability-based damping optimization of randomly wind-excited high-rise buildings. Struct Des Tall Spec. 26 (11), e1371 (2017).
- Li, C., Chang, K., Cao, L., Huang, Y. Performance of a nonlinear hybrid base isolation system under the ground motions. Soil Dyn Earthq Eng. 143, 106589 (2021).
- Cao, L., Li, C. A high performance hybrid passive base-isolated system. Struct Control Health Monitoring. 29 (3), e2887 (2022).
- Zareie, S., Issa, A. S., Seethaler, R., Zabihollah, A., Ahmad, R. A novel SMA-magnetorheological hybrid bracing system for seismic control. Eng Struct. 244, 112709 (2021).
- Chu, S. Y., Soong, T. T., Reinhorn, A. M. Active, hybrid and semi-active structural control. John Wiley & Sons, New York (2005).
- Danielian, S. A., Jabbari, F., Zareian, F. Effects and distribution of semi-active resettable springs on the seismic response of asymmetric structures. Earthq Eng Struct D. 52 (10). 2966-2982 (2023).
- Shuang, Z., Wenliuhan, H. S., Liu, Y. H., Inoue, N., Zhai, Z. P. Seismic response control for bridge piers with semi-active MR damper based on displacement feedback. J Earthq Eng. 28 (3). 849-865 (2024).
- Wang, Y., Dyke, S. Modal-based LQG for smart base isolation system design in seismic response control. Struct Control Health Monitoring. 20 (5), 753-768 (2013).
- Desai, R. M. et al. Performance evaluation of a single sensor control scheme using a twin-tube MR damper based semi-active suspension. J Vib Eng Technol. 9, 1193-1210 (2021).
- Abdi, M. S., Nekooei, M. Jafari, M. A. Seismic control of multi-degrees-of-freedom structures by vertical mass isolation method using MR dampers. Earthq Eng Eng Vib. 23 (2), 503-510 (2024).
- Bhowmik, K., Debnath, N. Semi-active vibration control of soft-storey building with magnetorheological damper under seismic excitation. J Vib Eng Technol. 12 (4), 6943-6961 (2024).
- Yang, J. N., Akbarpour, A., Askar, G. Effect of time delay on control of seismic-excited buildings. J Struct Eng. 116 (10), 2801-2814 (1990).
- Temimi, H., Ben-Romdhane, M., El-Borgi, S., Cha, Y. Time-delay effects on controlled seismically excited linear and nonlinear structures. Int J Struct Stab Dyn. 16 (7), 1550031 (2016).
- Peng, J., Wang, L., Zhao, Y., Lenci, S. Time-delay dynamics of the MR damper-cable system with one-to-one internal resonances. Nonlinear Dynamics. 105 (2), 1343-1356 (2021).
- Cha, Y. J., Agrawal, A. K., Dyke, S. J. Time delay effects on large-scale MR damper based semi-active control strategies. Smart Mater Struct. 22 (1), 015011 (2013).
- Yu, Y. et al. Experimental study of wireless structural vibration control considering different time delays. Smart Mater Struct. 24, 045005 (2015).
- Ahmadizadeh, M., Mosqueda, G., Reinhorn, A. M. Compensation of actuator delay and dynamics for real-time hybrid structural simulation. Earthq Eng Struct Dyn. 37 (1), 21-42 (2008).
- Bathaei, A., Zahrai, S. M. Compensating time delay in semi-active control of a SDOF structure with MR damper using predictive control. Struc Eng Mech. 82 (4), 445-458 (2022).
- Dyke, S. J., Spencer, Jr, B. F., Sain, M. K., Carlson, J. D. Modeling and control of magnetorheological dampers for seismic response reduction. Smart Mater Struct. 5 (5), 565-575 (1996).
- Ying, Z. G., Ni, Y. Q., Ko, J. M. A semi-active stochastic optimal control strategy for nonlinear structural systems with MR dampers. Smart Struct Syst. 5 (1), 69-79 (2009).
- Rosol, M., Martynowicz, P. Implementation of the LQG controller for a wind turbine tower-nacelle model with a MR tuned vibration absorber. J Theor App Mech-Pol. 54 (4), 1109-1123 (2016).
- Lyu, M. Z., Feng, D. C., Chen, J. B., Li, J. A decoupled approach for determination of the joint probability density function of a high-dimensional nonlinear stochastic dynamical system via the probability density evolution method. Comput Method Appl M. 418 (A), 116443 (2024).
- Chha, H., Peng, Y. Multiscale stochastic optimal control of hysteretic structures based on wavelet transform and probability density evolution method. Eng Computation. 41 (4), 865-896 (2024).
- Li, J., Peng, Y. B., Chen, J. B. A physical approach to structural stochastic optimal controls. Probabilist Eng Mech. 25 (1), 127-141 (2010).
- Peng, Y. B., Yang, J. G., Li, J. Seismic risk-based stochastic optimal control of structures using magnetorheological dampers. Nat Hazards Rev. 18 (1), B4016001 (2017).
- Dong, X. M., Yu, M., Li, Z., Liao, C., Chen, W. Neural network compensation of semi-active Control for magneto-rheological suspension with time delay uncertainty. Smart Mater Struct. 18 (1), 015014 (2008).
- Peng, Y. B., Zhang, Z. Optimal MR damper-based semiactive control scheme for strengthening seismic capacity and structural reliability. J Eng Mech. 146 (6), 04020045 (2020).
- Luo, M. X., Gao, M. Cai, G. Delayed full-state feedback control of airfoil flutter using sliding mode control method. J Fluid Struct. 61, 262-273 (2016).
- Xu, J., Chung, K. W., Chan, C. L. An efficient method for studying weak resonant double Hopf bifurcation in nonlinear systems with delayed feedbacks. Siam J Appl Dyn Syst. 6 (1), 29-60 (2007).
- Yang, J. S., Jensen, H., Chen, J. B. Structural optimization under dynamic reliability constraints utilizing probability density evolution method and metamodels in augmented input space. Struct Multidiscip Optimization. 65, 107 (2022).
- Li, J., Chen, J. B. Stochastic dynamics of structures. John Wiley & Sons, Singapore (2009).
- Peng, Y. B., Li, J. Stochastic optimal control of structures. Springer (2019).
- Dowrick, C. Beyond depression: A new approach to understanding and management. Oxford University Press (2009).
- Wang, D., Li, J. Physical random function model of ground motions for engineering purposes. Sci China Technol Sci. 54 (1), 175-182 (2011).
- Wang, D., Li, J. A random physical model of seismic ground motion field on local engineering site. Sci China Technol Sci. 55 (7), 2057-2065 (2012).
- Chen, J. B., Li, J. Strategy for selecting representative points via tangent spheres in the probability density evolution method. Int J Numer Meth Eng. 74 (13), 1988-2014 (2008).
Reimpressões e Permissões
Solicitar permissão para reutilizar o texto ou figuras deste artigo JoVE
Solicitar PermissãoThis article has been published
Video Coming Soon
Copyright © 2025 MyJoVE Corporation. Todos os direitos reservados