基于增益频谱工程优化布里渊光学时域分析仪

摘要

提出了一种基于增益频谱工程的 Brillouin 光学时域分析仪协议。实现了传感性能的增强，包括传感距离和被测分辨率，并研究了过量的布里渊强度噪声。该协议引入了一种增强分布式布里渊传感性能的新方法。

摘要

演示的是提高布里渊光学时域分析仪 （BOTDA） 传感性能的独特方法。一个布里渊增益谱 （BGS） 与两个对称的布里渊损耗谱 （BLS） 叠加。这导致了复杂的工程频谱形状，对传感系统噪声的抵抗力更强。与传统的 BOTDA 设置中只有一个泵浦和探头相互作用不同，它利用了三个光学探头波，其中一个探头位于 BGS 中，另外两个探头对称位于 BLS 中。由于工程光谱形状对噪声的抵抗力和不敏感性，传感性能提高了 60%，被测分辨率提高了一倍。

引言

分布式光纤传感 （DFS） 是一种独特的机制，它使用整根光纤作为传感介质。由于光纤损耗低，它引起了很多兴趣;体积小;以及能够轻松嵌入各种结构中，例如水坝、桥梁和建筑物，以作为人工神经系统执行环境监测。与应用光纤布拉格光栅 （FBG） 等众多传统点传感器相比，它在广泛的大规模传感任务（如基础设施和结构健康监测）中提供了更高效、更具成本效益的解决方案¹。

电流分布式传感器利用光纤内部的不同散射机制来测量温度和应变分布。其中，基于布里渊散射的 DFS 最具吸引力，因为受激布里渊散射 （SBS） 具有高信噪比 （SNR）、低阈值以及对温度² 和应变³ 的敏感性。SBS 可以经典地描述为入射光连续波 （CW）（即泵浦）与通过声波反向传播的 CW 探测波之间的相互作用。根据能量守恒和动量守恒，探测波的频率降频到泵浦。这种偏移称为布里渊频移 （BFS）。考虑到 10 ns 声波的有限寿命，折射波的光谱分布有限，也称为布里渊增益谱 （BGS），其中 BFS 是泵浦波与峰值中心频率之间的频率差。波之间的相互作用导致频率下移增益区域和频率上移损耗区域，探针波分别被放大和衰减。对于 C 波段的标准单模光纤 （SSMF），BFS 约为 11 GHz，BGS 具有洛伦兹形状，具有 10-30 MHz 的超窄半峰全宽 （FWHM），可以通过特定技术进一步降低到 3.4 MHz 4,5,6,7。基于这些特性，SBS 还可以应用于微波光子学滤光片 ^8,9,10、光学滤光片¹¹、慢速和快光 12,13,14 以及高分辨率光谱 ^7,15。

最有前途的 SBS 应用之一是分布式布里渊传感。这些传感器利用了 BFS 对温度和应变的依赖性。首先演示的是布里渊光学时域分析仪 （BOTDA）¹⁶，这是最整合的时域分布式布里渊传感技术。它与传统的 CW-SBS 交互不同，因为它利用脉冲泵浦波和探针 CW 之间的 SBS 交互，以便在每个光纤截面上本地查询环境信息。泵浦或探头频率通常是固定的，而探头或泵浦频率在 BFS 附近进行扫描。记录探头功率用于 BGS 重建，理想情况下，BFS 是每个光纤段本地 BGS 的峰值频率。然而，由于不可避免的系统噪声，BGS 峰通常是模棱两可的，必须采用拟合算法¹⁷，这会导致频率¹⁸ 存在一定的估计误差，并影响被测分辨率。

从统计学上讲，BFS 估计误差与系统信噪比 （SNR） 成反比。提高 SNR 的最直接方法是增加泵浦和探头的功率。然而，这些受到调制不稳定性 （MI）¹⁹ 和非局部效应 （NLE） ^20,21 至 ~20 dBm 和 -14 dBm 的限制。已经提出了许多技术，例如编码²² 和基于拉曼的在线扩增²³ 来打破这些限制。最近，据报道，通过选择合适的拟合算法²⁴ 可以最大限度地减少这种频率误差。与此相关的是，据报道，利用布里渊相位和线性拟合算法的测量也降低了频率误差²⁵，这表明设计精良的 BGS 有可能提高传感性能。增强 SNR 的另一种选择是降噪。但是，根据传统观点，传感系统噪声主要来自探测器（即共模噪声，包括暗噪声、散粒噪声等）^26,27 和改善的可能性较小。

本文的基本思想是通过传统 BGS 与两个对称布里渊损失谱 （BLS） 的叠加来设计 BGS（见 图 1）。与遵循洛伦兹形状的传统 BGS 谱相比，在相同水平的系统噪声下，工程谱更清晰、更稳健。因此，噪声对峰值频率的确定影响较小。这可以通过收集和拟合具有统计学意义的 BGS 测量数据次数来验证。由于这种更好的抗噪声能力，传感性能得到了增强，包括感应距离增加了 60%，被测分辨率翻了一番，即频率误差降低了 50%。由于工程 BGS 的一部分涉及布里渊损耗相互作用的测量，因此可以直接比较有和没有布里渊相互作用的痕量噪声。由于规避了过多的布里渊噪声，工程 BGS 的轨迹更加清晰。

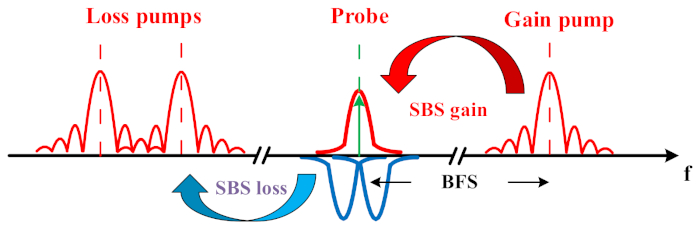
图 1：一个布里渊增益和两个对称布里渊损耗谱叠加的工程 BGS 示意图。请单击此处查看此图的较大版本。

研究方案

1. 通过仿真为频谱工程选择优化参数

1. 用方程^28,29 对工程 BGS g_SBS（ν，z） 进行建模
   
   例如，由补充 MATLAB 脚本实现。
   注：此处，G（ν） 是复数增益系数，在脚本中计算为 SBS_g 函数（对于常规 BGS）或 SBS_gl 函数（对于工程 BGS）中的 G_complex;g（ν，z） 是局部复布里渊增益;g_SBS 和 φ_SBS 是 g（ν，z） 的实部和虚部，分别表示从泵发射端开始的 z 位置 BGS 和 SBS 的相位响应。在脚本中，g_SBS 分别由对数刻度的传统和工程 BGS 的变量 SBS_g_log 和 SBS_gl_log 表示。P_p = 20 dBm（脚本中的P_pump）是光纤发射端的泵浦脉冲峰值功率;ν_B 是 BFS（在脚本中标准化）;g₀ = 0.2 ^{W-1 m-1} （脚本中的 g₀） 是布里渊增益系数;Δν_B = 50 MHz（脚本中为 gamma_B）是 BGS 的 FWHM;α = 0.2 dB/km 是光纤损耗系数，分别用 alpha_log 和 alpha_lin 表示为脚本中对数和线性刻度的值;ν 是探测波频率，因此泵浦和探头频率偏移 ν_{- ν B} 在 -250 MHz 到 250 MHz 范围内扫描。泵浦和探针的频率偏移在脚本中表示为全局矢量 f。项 g₁ = mg₀ 是损失因子;2d∙Δν_B 是两个损耗之间的频率偏移;L_eff = 10 m （脚本中为 L_eff）是 100 ns 脉冲宽度的布里渊相互作用长度。通过调整两个归一化因子 m 和 d，可以很容易地调整工程光谱形状。传统的 BGS 可以简单地用 m = 0 建模。
2. 添加在传统 BGS 和工程 BGS 上具有相同水平的随机噪声（即加性高斯白噪声）。调整脚本中的参数 noise_level 可以更改噪声级别。
3. 将传统的噪声 BGS 与洛伦兹函数（脚本中的 Lorentz_g_gain_fun 函数）拟合，将工程噪声 BGS 与叠加的洛伦兹函数（脚本中的 Lorentz_gl_gain_fun 函数）拟合（参见 图 2A）。
4. 确定传统和工程 BGS 的噪声引起的峰值频率偏移（图 2B）。
5. 对 N = 500 重复步骤 1.2-1.4，并分别收集^{第 i 个}过程中常规和工程 BGS 的所有峰值频率偏移 Δf_ci 和 Δf_pi（分别由 delta_g_g 和 delta_g_gl 表示）。

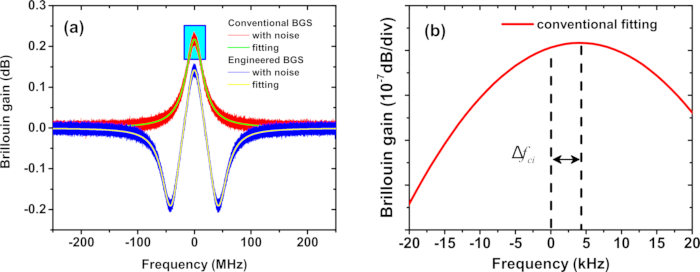
图 2：模拟 BGS。（A） 模拟中典型洛伦兹（红色）和工程（蓝色）BGS 的拟合演示。（B） （A） 的洛伦兹 BGS 峰。Δf_ci 表示^{第 i 次}测量中常规 BGS 的 BFS 估计误差。请单击此处查看此图的较大版本。

6. 计算噪声诱导的 BFS 估计误差的标准差之比，如下所示：
   
7. 将 η 绘制为 m 和 d 的函数（参见图 3A）。找到最小值 _{η min} 以及相应的 m 和 d。估计精度的优势将在整个纤维²⁸ 上保持。
8. 将等式 （2） 中的 z （即纤维长度，也是脚本中的 z ）的值从 0 公里调整到 60 公里，步长 50 米，然后用一些选定的 m 和 d 值重复步骤 1.1-1.7。然后可以获得标准偏差与纤维长度的函数之比（参见 图 3B）。

2. 准备和测试常规 BOTDA 设置（ 图 4B 中突出显示的块）

1. 打开半导体激光管 （LD） 并使用光谱分析仪 （OSA） 检查 LD 的功能。通常，使用 1,550 nm 左右的波长。
2. 将 LD 与 10：90 光耦合器 （OC） 连接。检查 10% OC 输出的功率。如果功率高于 13 dBm（偏振扰码器 [Pol.S.） 的最大输入功率]），则通过降低 LD 电流来降低 LD 输出功率。
3. 将 10% OC 输出与 Pol.S 连接。为避免极化衰落¹，请将加扰频率设置为 1 kHz。
4. 检查 Pol.S 输出的电源。如果功率高于 -3 dBm（半导体光放大器 [SOA] 的最大输入功率限制），请添加衰减器，直到满足功率要求。连接 Pol.S.与 SOA 一起使用。
5. 在 SOA 上应用来自脉冲发生器 （PG） 的 100 ns 脉冲宽度和 4 kHz 重复率的电脉冲序列信号。确保脉冲信号的幅度高于 SOA 的晶体管-晶体管逻辑 （TTL） 阈值（即 4 dBm），并且重复频率满足往返要求³⁰。
6. 将 SOA 的输出与掺铒光纤放大器 （EDFA 1） 连接，并在自动电流控制 （ACC） 模式下运行 EDFA。将 EDFA 1 的输出连接到环行器 （Cir） 的端口 1。
7. 通过将 Cir 端口与光电二极管 （PD） 连接，检查来自数字化仪中 Cir 端口 2 的光脉冲信号。为了避免对 PD 造成任何损坏，需要足够的衰减。
8. 通过在数字化仪中测量的波形计算光脉冲峰值功率。光峰值功率 P_o 的估计依据
   
   其中 VE 是电脉冲峰值电压，R 和 R_f 是 PD 响应度和跨阻。在此计算中考虑保护衰减，以便评估进入被测光纤的正确输入泵浦功率 （FUT， 10.6 km）。
9. 请注意，当计算的光脉冲峰值功率达到 20 dBm（MI 阈值¹⁹）时，EDFA 电流值 I₁₉。光脉冲序列的消光比 （ER） 可以根据能量守恒来评估：
   
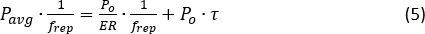
   其中 P_avg 是脉冲序列的光平均功率;f_rep 是重复率;τ 是脉冲宽度。SOA 的 ER 通常超过 30 dBm，有效避免了 NLE^31,32。
   注意：在断开 PD 并继续构建系统之前，请关闭 EDFA。
10. 将 Cir 的端口 2 与 FUT 的一端连接，完成泵支路的设置。通过检查 OSA 中 FUT 另一端的频谱并将 EDFA 设置为恒定电流值 I₂₀，检查系统是否会出现 MI。如果检测到的频谱与步骤 2.1 中测得的频谱相同（形状，不一定是振幅），则系统没有 MI。否则，当观察到明显的频谱展宽或峰分裂³³ 时，减小 EDFA 1 电流以保持频谱形状。
11. 将 OC 的 90% 输出连接到 50：50 OC 1，并通过极化控制器 （PC） 将其中一个 OC 1 输出连接到马赫-曾德尔调制器 （MZM 1）。正确设置极化，以便 MZM 1 的输出最大化（极化对准）。
12. 将来自 RF 发生器 （RFG 1） 的射频 （RF） 信号与 FUT 的 BFS（对于 11 GHz 左右的 SSMF）和 16 dBm 幅度施加到 MZM 1。设置 MZM 1 的直流偏置电压，以便将载波抑制到最小。
13. 将 MZM 1 的输出端与光纤布拉格光栅 （FBG 1） 连接。检查 OSA 中 FBG 1 的输出频谱，以便将 FBG 1 设置为阻止高频边带和载波。
14. 将 FBG 1 的输出连续连接到 EDFA 2、另一个 50：50 OC 2 和隔离器 （ISO）。
15. 在 ACC 模式下也运行 EDFA 2 并将电流值设置为 I_g，使 ISO 的输出功率低于 -14 dBm，从而最小化 NLE²⁰。在断开功率计之前关闭 EDFA，然后继续构建系统。将 ISO 输出连接到 FUT 的另一端，以完成增益探针分支的设置构建。
16. 将 Cir 端口 3 连接到 EDFA 4（用于预放大³⁴）和 PD。将 EDFA 设置为 ACC 模式。电流值 I₄ 应让 EDFA 的输出功率小于 PD 的输入限值 4。将 PD 射频输出连接到 10 MHz 射频低通滤波器^35,36。将滤波器输出连接到数字化器。
17. 将数字化器的触发器与脉冲发生器的同步（或反向）输出连接起来。按如下方式设置数字化器参数：采样率：500 MSa/s;平均：4,096 次;样本数量：10,000。
18. 将 EDFA 1、EDFA 2 和 EDFA 4 的当前值分别设置为 I₂₀、 I_g 和 I₄。运行跟踪记录程序。检查在数字化器中测量的轨迹。如果迹线幅度跟随指数衰减，则传感系统无 MI。否则，请减小 EDFA 1 的当前值。

3. 使用传统的 BOTDA 设置和数据处理进行测量

1. 将 EDFA 1 和 EDFA 2 的值分别设置为 I₂₀ 和 I_g。在 BFS ± 90 MHz 范围内以 1 MHz 的步长扫描 RFG 1 的频率。在每个扫描步骤之后，记录来自录制程序的跟踪。
2. 通过将迹线幅度（在布里渊相互作用周期中）除以每个直流偏移（非布里渊相互作用周期）来计算局部布里渊增益。
3. 通过将测得的噪声 BGS 与洛伦兹拟合来检索每个光纤截面的 BGS。从接头中确定常规 BGS Δν_B0 的 FWHM。
4. 对 N = 48 次重复步骤 3.1 和 3.2，并在^{第 i 个}过程中沿光纤 ν_Bci（z） 收集所有估计的峰值 （BFS） 频率分布（参见图 5A）。
5. 将 BFS 估计误差计算为 48 次测量中每个纤维截面的拟合 BFS 的标准差（参见 图 5B）。

4. 准备其余的设置

注意：在这种情况下，根据仿真结果，使用了 m = 1 和 d = 1.24（参见第 1 节和 图 3）。

1. 将探头分支中 50：50 OC 1 的另一个输出与 EDFA 3 和 50：50 OC 3 连接。
2. 将 50：50 OC 3 的一个输出连接到 PC 和 MZM 2。调整极化，使 MZM 2 的输出最大化。
3. 在 MZM 2 上以 BFS - d∙Δν_B0 和 16 dBm 幅度施加来自 RFG 2 的射频信号。检查 OSA 中的调制频谱并调整偏置电压以最小化载波幅度。
4. 将 MZM 2 的输出连接到光开关 （OS 1） 的输入端（50：50 OC 4 的输入之一）和 FBG 2。
5. 检查 OSA 中的光信号并调整 FBG 2 中心波长，以便阻挡载波和较低频率的边带（参见 图 4A）。然后，loss 1 探针分支的设置将完成。
6. 将 50：50 OC 3 的另一个输出连接到 PC 和 MZM 3。调整极化，使 MZM 3 的输出最大化。
7. 在 MZM 3 上以 BFS + d∙Δν_B0 和 16 dBm 幅度施加来自 RFG 3 的射频信号。检查 OSA 中的调制频谱并调整偏置电压以最小化载波幅度。
8. 将 MZM 3 的输出连接到具有开关功能 （OS 2） 的可变光衰减器 （VOA） 和另一个 50：50 OC 4 输入。考虑到与 FBG 2 传输窗口（几 GHz）相比，损耗探针频率之间的偏移相对较小，MZM 3 的载波和较低频率边带也将被 FBG 2 阻挡。然后，loss 2 探针分支的设置将完成。
9. 关闭 OS 1，打开 OS 2，并将 EDFA 3 电流值设置为 I_l ，使损失 1 探头的功率等于 -14 dBm （m = 1）。
10. 打开 OS 1，关闭 OS 2，并调整 VOA 的衰减，使 loss 2 探头的功率也等于 -14 dBm。

5. 使用完整的 BOTDA 设置和数据处理进行测量

1. 关闭 OS 1，关闭 OS 2，将 EDFA 1、EDFA 2、EDFA 3 和 EDFA 4 的当前值分别设置为 I₂₀、 I_g、 I_l 和 I₄。在 BFS ± 90 MHz 范围内以 1 MHz 的步长扫描 RFG 1 的频率。来自 RFG 2 和 RFG 3 的频率相应地扫描。在每个扫描步骤之后记录程序中的跟踪。
2. 如步骤 3.2 所示计算局部布里渊增益，并通过将测得的噪声 BGS 与叠加的洛伦兹函数拟合来检索每个光纤截面的工程 BGS。
3. 对 N = 48 次重复步骤 5.1 和 5.2，并在^{第 i 个}过程中收集沿光纤 ν_Bpi（z） 的所有估计峰值 （BFS） 频率分布（参见图 5A）。
4. 将 BFS 估计误差计算为 48 次测量中每个纤维截面的拟合 BFS 的标准差（参见 图 5B）。

结果

图 3 显示了仿真结果。图 3A 中 η < 1 的点表示工程 BGS 的频率误差较小（被测分辨率更高）。值越低，优势越大。最小比率为 m = 1，表明可以执行多探针而不是多泵方案（参见讨论）。图 3B 显示了频率误差比 η 沿光纤的分布，并为

讨论

实验过程中最关键的一步是均衡三个探针功率，使 m = 1 并实现两个布里渊损失光谱之间的对称性。除了如步骤 4.9 和 4.10 所示，使用 Cir 端口 2 的功率计进行单独的功率检查外，还可以在数字化仪中更精确地检查功率均衡。通过将 RF 1 频率设置为 ~11 GHz（光纤 BFS）并关闭 EDFA 3，可以在数字化仪（迹线 I）中记录具有峰值增益的常规迹线。然后将 RF 2 和 RF 3 频率分别?...

材料

Name	Company	Catalog Number	Comments
Current controller for laser diode	ILX Lightwave	LDX3220
Digitizer	Acqiris SA	U5309A-1039
Erbium doped fiber amplifier 1	Photop	PTEDFA-A-PA-C-SCH-15
Erbium doped fiber amplifier 2	LiComm	OFA-TCH
Erbium doped fiber amplifier 3	Calmar Optcom	AMP-ST30
Erbium doped fiber amplifier 4	Photop	PTEDFA-A-PA-C-SCH-15
Fiber Bragg grating 1	Advanced Optics Solutions	T-FBG
Fiber Bragg grating 2	Advanced Optics Solutions	T-FBG
Fiber under test	ofs
Isolator	General Photonics	S-15-NTSS
Laser diode	3SP Group	A1905 LMI
Mach-Zehnder modulator 1	Avanex	IM10
Mach-Zehnder modulator 2	Avanex	IM10
Mach-Zehnder modulator 3	Avanex	IM10
Nanosecond driving board for semiconductor optical amplifier	Highland Technology	T160-9 (28A160-9C)
Optical coupler 10:90	Newport		Benchtop coupler/WDM
Optical coupler 50:50	Newport		Benchtop coupler/WDM
Optical spectrum analyzer	Hewlett Packard	86145A
Optical switch 1	JDSU	SN12-1075NC
Photodiode	Thorlabs	D400FC
Polarization scrambler	General Photonics	PSY-101
Pulase generator	Hewlett Packard	8082A
Radio function generator 1	Anritsu	MG3692C
Radio function generator 2	Agilent Technology	E8257D
Radio function generator 3	HTM	T2100
Semiconductor optical amplifier	Thorlabs	SOA1013SXS
Temperature controller for laser diode	ILX Lightwave	LDT5948
Temperature controller for semiconductor optical amplifier	Tektronix	TED200
Variable optical attenuator	JDSU	mVOA-A1	With optical switch function