Optimierung von optischen Zeitbereichsanalysatoren von Brillouin auf Basis von Gain Spectrum Engineering

Zusammenfassung

Es wird ein Protokoll für optische Zeitbereichsanalysatoren von Brillouin vorgestellt, das auf Gain Spectrum Engineering basiert. Verbesserungen der Sensorleistung, einschließlich des Schaltabstands und der Messgrößenauflösung, werden erreicht und das übermäßige Brillouin-Intensitätsrauschen wird untersucht. Das Protokoll führt eine neue Methode zur Verbesserung der Leistung der verteilten Brillouin-Sensorik ein.

Zusammenfassung

Demonstriert wird eine einzigartige Methode zur Verbesserung der Messleistung in optischen Zeitbereichsanalysatoren (BOTDA) von Brillouin. Ein Brillouin-Verstärkungsspektrum (BGS) wird mit zwei symmetrischen Brillouin-Verlustspektren (BLS) überlagert. Dies führt zu einer komplexen, konstruierten Spektrumsform, die widerstandsfähiger gegen das Rauschen des Sensorsystems ist. Anstelle von nur einer Pump-Sonden-Wechselwirkung wie beim herkömmlichen BOTDA-Aufbau werden drei optische Sondenwellen genutzt, wobei sich eine Sonde im BGS und die beiden anderen symmetrisch im BLS befinden. Aufgrund des Widerstands und der Unempfindlichkeit der konstruierten Spektrumform gegenüber dem Rauschen wird die Erfassungsleistung um 60 % gesteigert und die Messwertauflösung verdoppelt.

Einleitung

Distributed Fiber Sensing (DFS) ist ein einzigartiger Mechanismus, bei dem eine ganze Faser als Sensormedium verwendet wird. Aufgrund des geringen Faserverlusts hat es großes Interesse geweckt. Kleinformat; und die Fähigkeit, sich leicht in verschiedene Strukturen wie Dämme, Brücken und Gebäude einbetten zu lassen, um die Umgebungsüberwachung als künstliches Nervensystem durchzuführen. Im Vergleich zur Anwendung zahlreicher herkömmlicher Punktsensoren, wie z. B. Faser-Bragg-Gitter (FBG), bietet es eine effizientere und kostengünstigere Lösung für eine Vielzahl von groß angelegten Sensoraufgaben, wie z. B. Infrastruktur- und Structural Health Monitoring¹.

Stromverteilte Sensoren nutzen verschiedene Streumechanismen innerhalb der Faser, um die Temperatur- und Dehnungsverteilung zu messen. Unter ihnen ist die auf Brillouin-Streuung basierende DFS aufgrund der markanten Vorteile der stimulierten Brillouin-Streuung (SBS), wie z. B. ein hohes Signal-Rausch-Verhältnis (SNR), eine niedrige Schwelle und die Empfindlichkeit sowohl gegenüber Temperatur² als auch gegenüber Stamm³, am attraktivsten. SBS kann klassisch als Wechselwirkung zwischen den einfallenden optischen Dauerwellen (CW), d.h. der Pumpe, und der gegenläufigen CW-Sondenwelle über eine akustische Welle beschrieben werden. Entsprechend der Energie- und Impulserhaltung wird die Sondenwelle frequenzmäßig zur Pumpe herunterverschoben. Diese Verschiebung wird als Brillouin-Frequenzverschiebung (BFS) bezeichnet. Unter Berücksichtigung der endlichen Lebensdauer einer akustischen Welle von 10 ns gibt es eine endliche spektrale Verteilung der gebrochenen Welle, auch Brillouin-Verstärkungsspektrum (BGS) genannt, bei der die BFS die Frequenzdifferenz zwischen der Pumpwelle und der Spitzenmittenfrequenz ist. Die Wechselwirkung zwischen den Wellen führt zu einem frequenzherunterverschobenen Verstärkungsbereich und einem frequenzhochverschobenen Verlustbereich, in dem die Sondenwelle verstärkt bzw. gedämpft wird. Für eine Standard-Singlemode-Faser (SSMF) im C-Band beträgt die BFS ca. 11 GHz und die BGS hat eine Lorentz-Form mit einer ultraschmalen vollen Breite bei halbem Maximum (FWHM) von 10-30 MHz, die mit spezifischen Techniken weiter auf 3,4 MHz reduziert werden kann 4,5,6,7. Basierend auf diesen Eigenschaften kann SBS auch in Mikrowellen-Photonik-Filtern ^8,9,10, optischen Filtern¹¹, langsamem und schnellem Licht 12,13,14 und hochauflösender optischer Spektroskopie ^7,15 eingesetzt werden.

Eine der vielversprechendsten SBS-Anwendungen ist die verteilte Brillouin-Sensorik. Diese Sensoren nutzen die BFS-Abhängigkeit von Temperatur und Dehnung aus. Die erste, die demonstriert wurde, war der Brillouin Optical Time-Domain Analyzer (BOTDA)¹⁶, die am stärksten konsolidierte zeitbereichsverteilte Brillouin-Sensortechnik. Sie unterscheidet sich von der herkömmlichen CW-SBS-Wechselwirkung dadurch, dass sie die SBS-Wechselwirkung zwischen einer gepulsten Pumpwelle und einer Sonde CW ausnutzt, so dass die Umgebungsinformationen lokal auf jedem Faserabschnitt abgefragt werden. Die Pump- oder Sondenfrequenz ist in der Regel festgelegt, während die Sonde oder die Pumpenfrequenz in der Nähe des BFS abgetastet wird. Die Sondenleistung wird für die BGS-Rekonstruktion aufgezeichnet und der BFS ist idealerweise die Spitzenfrequenz des lokalen BGS an jedem Faserabschnitt. Aufgrund des unvermeidlichen Systemrauschens ist der BGS-Peak jedoch in der Regel mehrdeutig und es muss ein Anpassungsalgorithmus¹⁷ angewendet werden, der zu einem gewissen Schätzfehler in der Frequenz¹⁸ führt und die Messgrößenauflösung beeinflusst.

Statistisch gesehen ist der BFS-Schätzfehler umgekehrt proportional zum Signal-Rausch-Verhältnis (SNR) des Systems. Der einfachste Weg, das SNR zu verbessern, besteht darin, die Leistung von Pumpe und Sonde zu erhöhen. Diese sind jedoch durch die Modulationsinstabilität (MI)¹⁹ und nicht-lokale Effekte (NLE)^20,21 bis ~20 dBm bzw. -14 dBm begrenzt. Zahlreiche Techniken, wie die Codierung²² und die Raman-basierte Inline-Amplifikation²³, wurden vorgeschlagen, um diese Grenzen zu durchbrechen. Kürzlich wurde berichtet, dass dieser Frequenzfehler durch die Wahl eines geeigneten Anpassungsalgorithmus²⁴ minimiert werden kann. In diesem Zusammenhang wird auch berichtet, dass Messungen, die die Brillouin-Phase und einen linearen Anpassungsalgorithmus nutzen, einen reduzierten Frequenzfehler²⁵ aufweisen, was auf das Potenzial eines ausgereiften BGS zur Verbesserung der Messleistung hinweist. Eine weitere Option zur Verbesserung des SNR ist die Rauschunterdrückung. Nach traditioneller Sichtweise kommt das Rauschen des Sensorsystems jedoch hauptsächlich vom Detektor (d. h. Gleichtaktrauschen, einschließlich Dunkelrauschen, Schrotrauschen usw.)^26,27 und eine Verbesserung ist weniger wahrscheinlich.

Die Grundidee dieser Arbeit besteht darin, das BGS durch die Überlagerung eines konventionellen BGS mit zwei symmetrischen Brillouin-Verlustspektren (BLS) zu konstruieren (siehe Abbildung 1). Im Vergleich zu einem herkömmlichen BGS-Spektrum, das einer Lorentzschen Form folgt, ist das technische Spektrum bei gleichem Rauschen schärfer und robuster. Somit hat das Rauschen weniger Einfluss auf die Bestimmung der Spitzenfrequenz. Dies kann überprüft werden, indem die BGS-Messdaten eine statistisch signifikante Anzahl von Malen gesammelt und angepasst werden. Aufgrund dieser besseren Beständigkeit gegen Rauschen werden Verbesserungen der Sensorleistung erreicht, einschließlich des Schaltabstands um 60 % und einer verdoppelten Messgrößenauflösung, d. h. eines um 50 % reduzierten Frequenzfehlers. Aufgrund der Einbeziehung der Messung mit Brillouin-Verlustwechselwirkung in einen Teil des technischen BGS wird ein direkter Vergleich des Spurenrauschens mit und ohne Brillouin-Wechselwirkung durchgeführt. Durch die Umgehung des übermäßigen Brillouin-Rauschens ist die Spur mit dem konstruierten BGS viel klarer.

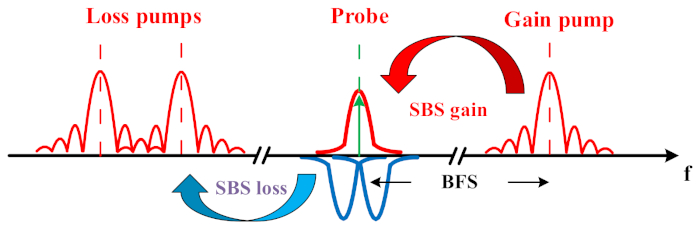
Abbildung 1: Schematische Darstellung eines konstruierten BGS durch Überlagerung eines Brillouin-Verstärkungs- und zweier symmetrischer Brillouin-Verlustspektren. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.

Protokoll

1. Auswahl optimierter Parameter für das Spectrum Engineering mittels Simulation

1. Modellieren Sie den konstruierten BGS g_SBS(ν,z) mit den Gleichungen^28,29
   
   wie z. B. durch das ergänzende MATLAB-Skript implementiert.
   HINWEIS: Hier ist G(ν) der komplexe Verstärkungskoeffizient, der im Skript als G_complex innerhalb der Funktion SBS_g für das konventionelle BGS oder der Funktion SBS_gl für das technische BGS berechnet wird; g(ν,z) ist der lokale Komplex Brillouin-Gewinn; und g_SBS und φ_SBS sind der reale und der imaginäre Teil von g(ν,z) und symbolisieren den BGS- bzw. SBS-Phasengang an der Stelle z vom Pumpenstartende aus. Im Skript wird g_SBS durch die Variablen SBS_g_log und SBS_gl_log für das konventionelle bzw. konstruierte BGS in logarithmischer Skala symbolisiert. P_p = 20 dBm (P_pump im Skript) ist die Spitzenleistung des Pumpimpulses am Faserstartende; ν_B ist die BFS (im Skript normiert); g₀ = 0,2 ^{W-1 m-1} (g₀ im Skript) ist der Brillouin-Verstärkungskoeffizient; Δν_B = 50 MHz (gamma_B im Skript) ist die FWHM des BGS; α = 0,2 dB/km ist der Faserverlustkoeffizient und wird durch alpha_log und alpha_lin als Wert in logarithmischer bzw. linearer Skala im Skript dargestellt. ν ist die Sondenwellenfrequenz, so dass der Frequenzversatz von Pumpe und Sonde ν - ν_B von -250 MHz bis 250 MHz abgetastet wird. Der Frequenzversatz von Pumpe und Sonde wird im Skript als globaler Vektor f dargestellt. Der Term g₁ = mg₀ ist der Verlustfaktor; 2d∙Δν_B ist der Frequenzversatz zwischen den beiden Verlusten; und L_eff = 10 m (L_eff im Skript) ist die Brillouin-Wechselwirkungslänge für 100 ns Pulsbreite. Die konstruierte spektrale Form kann leicht angepasst werden, indem zwei normierte Faktoren, m und d, abgestimmt werden. Der konventionelle BGS kann einfach mit m = 0 modelliert werden.
2. Fügen Sie zufälliges Rauschen (d. h. additives weißes Gaußsches Rauschen) mit dem gleichen Pegel sowohl auf dem konventionellen als auch auf dem technischen BGS hinzu. Durch Anpassen des Parameters noise_level im Skript kann sich der Geräuschpegel ändern.
3. Passen Sie das konventionelle verrauschte BGS mit der Lorentzschen Funktion (Lorentz_g_gain_fun Funktion im Skript) und das konstruierte verrauschte BGS mit der überlagerten Lorentzschen Funktion (Lorentz_gl_gain_fun Funktion im Skript) an (siehe Abbildung 2A).
4. Bestimmen Sie den Spitzenfrequenzversatz aufgrund des Rauschens für das konventionelle und technische BGS (Abbildung 2B).
5. Wiederholen Sie die Schritte 1.2-1.4 für N = 500 und erfassen Sie alle Spitzenfrequenz-Offsets Δf_ci und Δf_pi (dargestellt durch delta_g_g bzw. delta_g_gl im Skript) für das konventionelle bzw. technische BGS im ^i-ten Prozess.

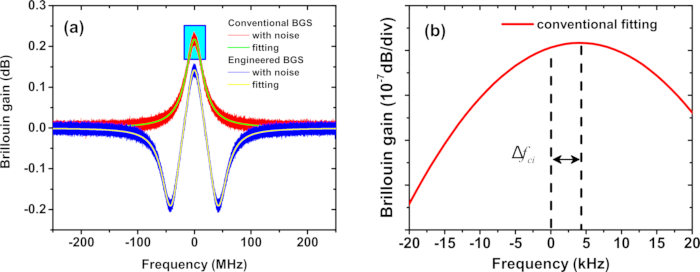
Abbildung 2: Simuliertes BGS. (A) Demonstration der Anpassung eines typischen Lorentzschen (rot) und konstruierten (blau) BGS in der Simulation. (B) Der Lorentzsche BGS-Peak aus (A). Δf_ci stellt den BFS-Schätzfehler für den konventionellen BGS in der ^i-ten Messung dar. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.

6. Berechnen Sie das Verhältnis der Standardabweichung der lärminduzierten BFS-Schätzfehler wie folgt:
   
7. Plotten Sie η als Funktion von m und d (siehe Abbildung 3A). Ermitteln Sie den Minimalwert η_min und die entsprechenden m und d. Der Vorteil der Schätzgenauigkeit wird entlang der gesamten Faser²⁸ beibehalten.
8. Optimieren Sie den Wert von z (d.h. die Faserlänge, im Skript auch z ) in Gleichung (2) von 0 km auf 60 km, Schritt 50 m und wiederholen Sie die Schritte 1.1-1.7 mit einigen ausgewählten m - und d-Werten . Dann kann das Verhältnis der Standardabweichung in Abhängigkeit von der Faserlänge ermittelt werden (siehe Abbildung 3B).

2. Bereiten Sie das konventionelle BOTDA-Setup vor und testen Sie es (hervorgehobener Block in Abbildung 4B)

1. Schalten Sie die Laserdiode (LD) ein und überprüfen Sie die Funktionalität der LD mit dem optischen Spektrumanalysator (OSA). In der Regel wird eine Wellenlänge um 1.550 nm verwendet.
2. Verbinden Sie den LD mit dem optischen Koppler (OC) im Verhältnis 10:90. Überprüfen Sie die Leistung des 10% OC-Ausgangs. Wenn die Leistung höher als 13 dBm ist (die maximale Eingangsleistung des Polarisations-Scramblers [Pol.S.]), verringern Sie die LD-Ausgangsleistung, indem Sie den LD-Strom verringern.
3. Verbinden Sie den 10% OC-Ausgang mit dem Pol.S. Um ein Polarisationsfading¹ zu vermeiden, stellen Sie die Scrambling-Frequenz auf 1 kHz ein.
4. Überprüfen Sie die Stromversorgung am Ausgang des Pol.S. Wenn die Leistung höher als -3 dBm ist (die maximale Eingangsleistungsgrenze des optischen Halbleiterverstärkers [SOA]), fügen Sie Dämpfungsglieder hinzu, bis die Leistungsanforderung erfüllt ist. Verbinden Sie die Pol.S. mit der SOA.
5. Legen Sie das elektrische Impulsfolgesignal mit 100 ns Impulsbreite und 4 kHz Wiederholrate vom Impulsgenerator (PG) an den SOA an. Es ist sicherzustellen, dass die Amplitude des Impulssignals höher ist als die TTL-Schwelle (Transistor-Transistor-Logik) des SOA (d. h. 4 dBm) und die Wiederholrate die Round-Trip-Anforderung³⁰ erfüllt.
6. Verbinden Sie den Ausgang des SOA mit dem Erbium-dotierten Faserverstärker (EDFA 1) und betreiben Sie den EDFA im ACC-Modus (Automatic Current Control). Verbinden Sie den Ausgang von EDFA 1 mit Anschluss 1 der Umwälzpumpe (Cir).
7. Überprüfen Sie das optische Impulssignal von Anschluss 2 von Cir im Digitizer, indem Sie ihn mit der Fotodiode (PD) verbinden. Um eine Beschädigung der TE zu vermeiden, ist eine ausreichende Dämpfung erforderlich.
8. Berechnen Sie die Spitzenleistung des optischen Impulses anhand der im Digitizer gemessenen Wellenform. Die optische Spitzenleistung P_o wird geschätzt nach
   
   wobei V_E die elektrische Impulsspitzenspannung und R und R_f die TE-Empfindlichkeit und der Transwiderstand sind. Berücksichtigen Sie bei dieser Berechnung die Schutzdämpfung, so dass eine korrekte Eingangspumpleistung in die zu testende Faser (FUT, 10,6 km) ausgewertet wird.
9. Notieren Sie den EDFA-Stromwert I₂₀ , wenn die berechnete Spitzenleistung des optischen Impulses 20 dBm erreicht (MI-Schwellenwert¹⁹). Das Extinktionsverhältnis (ER) der optischen Pulsfolge kann anhand der Energieerhaltung ausgewertet werden:
   
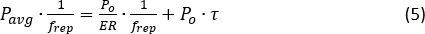
   wobei P_avg die optische Durchschnittsleistung der Impulsfolge ist; f_rep ist die Wiederholungsrate; und τ ist die Impulsbreite. Die ER des SOA beträgt in der Regel mehr als 30 dBm, wodurch NLE^31,32 effizient vermieden wird.
   HINWEIS: Schalten Sie die EDFA aus, bevor Sie den PD trennen und mit dem Aufbau des Systems fortfahren.
10. Verbinden Sie Port 2 des Cir mit einem Ende des FUT, um die Einrichtung des Pumpenzweigs abzuschließen. Überprüfen Sie, ob das System unter MI leidet, indem Sie das Spektrum vom anderen Ende der FUT in der OSA überprüfen und die EDFA auf einen konstanten Stromwert I₂₀ einstellen. Wenn das detektierte Spektrum mit dem in Schritt 2.1 gemessenen Spektrum identisch ist (in der Form, nicht notwendigerweise in der Amplitude), dann ist das System frei von MI. Andernfalls, wenn eine offensichtliche Spektrumverbreiterung oder Peak-Splitting³³ beobachtet wird, wird der EDFA 1-Strom reduziert, um die Spektrumsform beizubehalten.
11. Verbinden Sie den 90%-Ausgang des OC mit einem 50:50 OC 1 und verbinden Sie einen der OC 1-Ausgänge über einen Polarisationsregler (PC) mit dem Mach-Zehnder-Modulator (MZM 1). Stellen Sie die Polarisation richtig ein, so dass die Leistung von MZM 1 maximiert wird (Polarisationsausrichtung).
12. Legt das Hochfrequenzsignal (RF) des HF-Generators (RFG 1) mit dem BFS des FUT (für SSMF ca. 11 GHz) und 16 dBm Amplitude an den MZM 1 an. Stellen Sie die DC-Vorspannung des MZM 1 so ein, dass der Träger auf ein Minimum unterdrückt wird.
13. Verbinden Sie den Ausgang des MZM 1 mit einem Glasfaser-Bragg-Gitter (FBG 1). Überprüfen Sie das Ausgangsspektrum von FBG 1 in der OSA, so dass das FBG 1 so eingestellt ist, dass es das obere Frequenzseitenband und den Träger blockiert.
14. Verbinden Sie den Ausgang des FBG 1 nacheinander mit dem EDFA 2, einem weiteren 50:50 OC 2 und einem Isolator (ISO).
15. Betreiben Sie EDFA 2 auch im ACC-Modus und stellen Sie den Stromwert auf I_g, so dass die Ausgangsleistung von ISO kleiner als -14 dBm ist, wodurch NLE²⁰ minimiert wird. Schalten Sie die EDFA aus, bevor Sie den Stromzähler abklemmen, und fahren Sie mit dem Aufbau des Systems fort. Verbinden Sie den ISO-Ausgang mit dem anderen Ende des FUT, um die Einrichtung des Gain-Probe-Zweigs abzuschließen.
16. Verbinden Sie den Cir-Anschluss 3 mit dem EDFA 4 (für Vorverstärkung³⁴) und PD. Stellen Sie den EDFA auf den ACC-Modus. Der Stromwert I₄ sollte die Ausgangsleistung von EDFA um 4 kleiner als die Eingangsgrenze des PD sein lassen. Der PD-HF-Ausgang wird an einen 10 MHz HF-Tiefpassfilter^35,36 angeschlossen. Verbinden Sie den Filterausgang mit dem Digitizer.
17. Verbinden Sie den Trigger des Digitizers mit dem synchronisierten (oder inversen) Ausgang des Impulsgenerators. Stellen Sie die Digitizer-Parameter wie folgt ein: Abtastrate: 500 MSa/s; Mittelwert: 4.096 mal; Anzahl der Proben: 10.000.
18. Legen Sie den aktuellen Wert von EDFA 1, EDFA 2 und EDFA 4 auf I₂₀, I_g bzw. I₄ fest. Führen Sie ein Trace-Aufzeichnungsprogramm aus. Überprüfen Sie die im Digitalisierer gemessene Spur. Wenn die Flankenamplitude dem exponentiellen Zerfall folgt, ist das Sensorsystem MI-frei. Andernfalls verringern Sie den aktuellen Wert von EDFA 1.

3. Messung mit dem herkömmlichen BOTDA-Setup und Datenverarbeitung

1. Legen Sie die Werte von EDFA 1 und EDFA 2 auf I₂₀ bzw. I_g fest. Die Frequenz von RFG 1 wird im Bereich von BFS ± 90 MHz in 1 MHz-Schritten abgetastet. Zeichnen Sie die Spur aus dem Aufnahmeprogramm nach jedem Scanschritt auf.
2. Berechnen Sie die lokale Brillouin-Verstärkung, indem Sie die Leiterbahnamplitude (in der Brillouin-Wechselwirkungsperiode) durch jeden DC-Offset (Nicht-Brillouin-Wechselwirkungsperiode) dividieren.
3. Rufen Sie das BGS an jedem Faserabschnitt ab, indem Sie das gemessene verrauschte BGS mit dem Lorentz-Fitting anpassen. Ermitteln Sie den FWHM des herkömmlichen BGS Δν_B0 aus der Armatur.
4. Wiederholen Sie die Schritte 3.1 und 3.2 für N = 48 Mal und erfassen Sie im ^i-ten Prozess alle geschätzten Peak-Häufigkeitsverteilungen (BFS) entlang der Faser ν_Bci(z) (siehe Abbildung 5A).
5. Berechnen Sie den BFS-Schätzfehler als Standardabweichung des angepassten BFS an jedem Faserabschnitt in den 48 Messungen (siehe Abbildung 5B).

4. Vorbereiten des restlichen Setups

HINWEIS: In diesem Fall wurde m = 1 und d = 1,24 pro Simulationsergebnis verwendet (siehe Abschnitt 1 und Abbildung 3).

1. Verbinden Sie den anderen Ausgang des 50:50 OC 1 im Tastkopfzweig mit dem EDFA 3 und dem 50:50 OC 3.
2. Verbinden Sie einen der Ausgänge von 50:50 OC 3 mit einem PC und MZM 2. Stellen Sie die Polarisation so ein, dass die Leistung von MZM 2 maximiert wird.
3. Das HF-Signal von RFG 2 mit BFS - d∙Δν_B0 und 16 dBm Amplitude auf MZM 2 anlegen. Überprüfen Sie das Modulationsspektrum in der OSA und stellen Sie die Bias-Spannung ein, um die Trägeramplitude zu minimieren.
4. Verbinden Sie den Ausgang von MZM 2 mit dem Eingang eines optischen Schalters (OS 1), einem der Eingänge von 50:50 OC 4 und dem FBG 2.
5. Überprüfen Sie das optische Signal in der OSA und stellen Sie die Mittenwellenlänge des FBG 2 so ein, dass der Träger und das unterfrequente Seitenband blockiert sind (siehe Abbildung 4A). Die Einrichtung des Sondenzweigs Verlust 1 ist dann abgeschlossen.
6. Verbinden Sie den anderen Ausgang des 50:50 OC 3 mit einem PC und MZM 3. Stellen Sie die Polarisation so ein, dass die Leistung von MZM 3 maximiert wird.
7. Das HF-Signal vom RFG 3 mit BFS + d∙Δν_B0 und 16 dBm Amplitude auf MZM 3 anlegen. Überprüfen Sie das Modulationsspektrum in der OSA und stellen Sie die Bias-Spannung ein, um die Trägeramplitude zu minimieren.
8. Verbinden Sie den Ausgang von MZM 3 mit einem variablen optischen Abschwächer (VOA) mit Schaltfunktion (OS 2) und dem anderen Eingang von 50:50 OC 4. Wenn man bedenkt, dass der Offset zwischen den Dämpfungssondenfrequenzen im Vergleich zum FBG 2-Übertragungsfenster (mehrere GHz) relativ klein ist, werden auch der Träger und das niederfrequente Seitenband von MZM 3 durch FBG 2 blockiert. Die Einrichtung des Sondenzweigs Verlust 2 ist dann abgeschlossen.
9. Schließen Sie OS 1, öffnen Sie OS 2, und stellen Sie den Stromwert von EDFA 3 auf I_l ein, sodass die Leistung der Sonde für Verlust 1 -14 dBm (m = 1) beträgt.
10. Öffnen Sie OS 1, schließen Sie OS 2 und stellen Sie die Dämpfung von VOA so ein, dass die Leistung der Loss-2-Sonde ebenfalls -14 dBm beträgt.

5. Messung mit dem vollständig vorgeschlagenen BOTDA-Setup und der Datenverarbeitung

1. Schließen Sie OS 1, schließen Sie OS 2, und legen Sie den aktuellen Wert von EDFA 1, EDFA 2, EDFA 3 und EDFA 4 auf I₂₀, I_g, _{I l} bzw. I₄ fest. Tasten Sie die Frequenz des RFG 1 im Bereich von BFS ± 90 MHz in 1 MHz Schritten ab. Frequenzen aus RFG 2 und RFG 3 werden entsprechend abgetastet. Zeichnen Sie die Ablaufverfolgung aus dem Programm nach jedem Scanschritt auf.
2. Berechnen Sie die lokale Brillouin-Verstärkung wie in Schritt 3.2 und rufen Sie das konstruierte BGS an jedem Faserabschnitt ab, indem Sie das gemessene verrauschte BGS mit der überlagerten Lorentz-Funktion anpassen.
3. Wiederholen Sie die Schritte 5.1 und 5.2 für N = 48 Mal und erfassen Sie im ^i-ten Prozess alle geschätzten Peak-Häufigkeitsverteilungen (BFS) entlang der Faser ν_Bpi(z) (siehe Abbildung 5A).
4. Berechnen Sie den BFS-Schätzfehler als Standardabweichung des angepassten BFS an jedem Faserabschnitt in den 48 Messungen (siehe Abbildung 5B).

Ergebnisse

Abbildung 3 zeigt die Simulationsergebnisse. Punkte mit η < 1 in Abbildung 3A weisen auf einen kleineren Frequenzfehler (höhere Messgrößenauflösung) mit dem entwickelten BGS hin. Je niedriger der Wert war, desto größer war der Vorteil. Das minimale Verhältnis lag bei m = 1, was darauf hindeutet, dass ein Multisonden- anstelle eines Multipumpenschemas dur...

Diskussion

Der kritischste Schritt während des Experiments ist die Entzerrung der drei Sondenleistungen, so dass m = 1 und eine Symmetrie zwischen den beiden Brillouin-Verlustspektren erreicht wird. Neben der separaten Leistungskontrolle mit dem Leistungsmesser an Cir-Anschluss 2, wie in den Schritten 4.9 und 4.10 beschrieben, kann der Leistungsausgleich im Digitizer genauer überprüft werden. Durch das Einstellen der Frequenz von RF 1 auf ~11 GHz (die Glasfaser BFS) und das Ausschalten ...

Materialien

Name	Company	Catalog Number	Comments
Current controller for laser diode	ILX Lightwave	LDX3220
Digitizer	Acqiris SA	U5309A-1039
Erbium doped fiber amplifier 1	Photop	PTEDFA-A-PA-C-SCH-15
Erbium doped fiber amplifier 2	LiComm	OFA-TCH
Erbium doped fiber amplifier 3	Calmar Optcom	AMP-ST30
Erbium doped fiber amplifier 4	Photop	PTEDFA-A-PA-C-SCH-15
Fiber Bragg grating 1	Advanced Optics Solutions	T-FBG
Fiber Bragg grating 2	Advanced Optics Solutions	T-FBG
Fiber under test	ofs
Isolator	General Photonics	S-15-NTSS
Laser diode	3SP Group	A1905 LMI
Mach-Zehnder modulator 1	Avanex	IM10
Mach-Zehnder modulator 2	Avanex	IM10
Mach-Zehnder modulator 3	Avanex	IM10
Nanosecond driving board for semiconductor optical amplifier	Highland Technology	T160-9 (28A160-9C)
Optical coupler 10:90	Newport		Benchtop coupler/WDM
Optical coupler 50:50	Newport		Benchtop coupler/WDM
Optical spectrum analyzer	Hewlett Packard	86145A
Optical switch 1	JDSU	SN12-1075NC
Photodiode	Thorlabs	D400FC
Polarization scrambler	General Photonics	PSY-101
Pulase generator	Hewlett Packard	8082A
Radio function generator 1	Anritsu	MG3692C
Radio function generator 2	Agilent Technology	E8257D
Radio function generator 3	HTM	T2100
Semiconductor optical amplifier	Thorlabs	SOA1013SXS
Temperature controller for laser diode	ILX Lightwave	LDT5948
Temperature controller for semiconductor optical amplifier	Tektronix	TED200
Variable optical attenuator	JDSU	mVOA-A1	With optical switch function