Optimización de los analizadores ópticos en el dominio del tiempo de Brillouin basados en la ingeniería del espectro de ganancia

Resumen

Se presenta un protocolo para analizadores ópticos en el dominio del tiempo de Brillouin basado en ingeniería de espectro de ganancia. Se logran mejoras en el rendimiento de detección, incluido el rango de detección y la resolución del mensurando, y se estudia el exceso de ruido de intensidad de Brillouin. El protocolo presenta una nueva forma de mejorar el rendimiento de la detección distribuida de Brillouin.

Resumen

Se ha demostrado un método único para la mejora del rendimiento de detección en los analizadores ópticos de dominio del tiempo (BOTDA) de Brillouin. Un espectro de ganancia de Brillouin (BGS) se superpone con dos espectros de pérdida de Brillouin (BLS) simétricos. Esto conduce a una forma de espectro compleja que es más resistente al ruido del sistema de detección. En lugar de una sola interacción entre la bomba y la sonda como en la configuración BOTDA convencional, se explotan tres ondas de sonda óptica, con una sonda ubicada en el BGS y las otras dos simétricamente en el BLS. Debido a la resistencia e insensibilidad de la forma del espectro diseñado al ruido, el rendimiento de detección se mejora en un 60% y la resolución del mensurando se duplica.

Introducción

La detección de fibra distribuida (DFS) es un mecanismo único que emplea una fibra completa como medio de detección. Ha atraído mucho interés debido a la baja pérdida de fibra; tamaño pequeño; y la capacidad de integrarse fácilmente en diversas estructuras, como presas, puentes y edificios, para realizar la vigilancia del entorno como un sistema nervioso artificial. En comparación con la aplicación de numerosos sensores puntuales tradicionales, como las rejillas de Bragg de fibra (FBG), proporciona una solución más eficiente y rentable en una amplia gama de tareas de detección a gran escala, como el monitoreo de la infraestructura y la salud estructural¹.

Los sensores distribuidos de corriente explotan diferentes mecanismos de dispersión dentro de la fibra para medir la temperatura y la distribución de la deformación. Entre ellos, el DFS basado en la dispersión de Brillouin es el más atractivo debido a las sorprendentes ventajas de la dispersión de Brillouin estimulada (SBS), como la alta relación señal-ruido (SNR), el bajo umbral y la sensibilidad tanto a la temperatura² como a la deformación³. SBS puede describirse clásicamente como una interacción entre las ondas ópticas continuas (CW) incidentes, es decir, la bomba, y la onda de sonda CW contrapropagante a través de una onda acústica. De acuerdo con la conservación de la energía y el momento, la onda de la sonda se desplaza a la frecuencia a la bomba. Este cambio se denomina cambio de frecuencia de Brillouin (BFS). Teniendo en cuenta la vida útil finita de una onda acústica de 10 ns, existe una distribución espectral finita de la onda refractada, también llamada espectro de ganancia de Brillouin (BGS), en la que el BFS es la diferencia de frecuencia entre la onda de bombeo y la frecuencia central máxima. La interacción entre las ondas conduce a una región de ganancia con desplazamiento de frecuencia hacia abajo y una región de pérdida con desplazamiento de frecuencia hacia arriba donde la onda de la sonda se amplifica y atenúa, respectivamente. Para una fibra monomodo estándar (SSMF) en banda C, el BFS es de aproximadamente 11 GHz y el BGS tiene una forma lorentziana con un ancho completo ultraestrecho a la mitad del máximo (FWHM) de 10-30 MHz, que se puede reducir aún más a 3,4 MHz con técnicas específicas 4,5,6,7. Sobre la base de estas características, SBS también se puede aplicar en filtros fotónicos de microondas ^8,9,10, filtros ópticos¹¹, luz lenta y rápida 12,13,14 y espectroscopía óptica de alta resolución ^7,15.

Una de las aplicaciones SBS más prometedoras es la detección distribuida de Brillouin. Estos sensores aprovechan la dependencia del BFS de la temperatura y la deformación. El primero en demostrarse fue el analizador óptico en el dominio del tiempo de Brillouin (BOTDA)¹⁶, que es la técnica de detección de Brillouin distribuida en el dominio del tiempo más consolidada. Se diferencia de la interacción convencional CW-SBS en que explota la interacción SBS entre una onda de bomba pulsada y una onda CW de sonda, de modo que la información ambiental se interroga localmente en cada sección de fibra. La frecuencia de la bomba o de la sonda suele ser fija mientras que la sonda o la frecuencia de la bomba se escanean en las proximidades del BFS. La potencia de la sonda se registra para la reconstrucción de BGS y el BFS es idealmente la frecuencia máxima del BGS local en cada sección de fibra. Sin embargo, debido al inevitable ruido del sistema, el pico BGS suele ser ambiguo y se debe aplicar un algoritmo de ajuste¹⁷, lo que conduce a un cierto error de estimación en la frecuencia¹⁸ e influye en la resolución del mensurando.

Estadísticamente, el error de estimación de BFS es inversamente proporcional a la relación señal/ruido (SNR) del sistema. La forma más sencilla de mejorar la SNR es aumentar la potencia de la bomba y la sonda. Sin embargo, estos están limitados por la inestabilidad de modulación (MI)¹⁹ y los efectos no locales (NLE)^20,21 a ~20 dBm y -14 dBm, respectivamente. Se han propuesto numerosas técnicas, como la codificación²² y la amplificación en línea basada en Raman²³ para romper estos límites. Recientemente, se ha informado de que este error de frecuencia puede minimizarse eligiendo un algoritmo de ajuste adecuado²⁴. En relación con esto, también se ha informado de que las mediciones que explotan la fase de Brillouin y un algoritmo de ajuste lineal tienen un error de frecuencia reducido²⁵, lo que indica el potencial de un BGS bien diseñado para mejorar el rendimiento de la detección. Otra opción para mejorar la SNR es la reducción de ruido. Sin embargo, de acuerdo con el punto de vista tradicional, el ruido del sistema de detección proviene principalmente del detector (es decir, ruido de modo común, incluido el ruido oscuro, el ruido de disparo, etc.)^26,27 y la mejoría es menos probable.

La idea básica de este artículo es diseñar el BGS mediante la superposición de un BGS convencional con dos espectros de pérdida de Brillouin (BLS) simétricos (ver Figura 1). En comparación con un espectro BGS convencional, que sigue una forma lorentziana, el espectro diseñado es más nítido y robusto con el mismo nivel de ruido del sistema. Por lo tanto, el ruido tiene menos influencia en la determinación de la frecuencia de pico. Esto se puede verificar recopilando y ajustando los datos de medición de BGS un número estadísticamente significativo de veces. Debido a esta mejor resistencia al ruido, se logran mejoras en el rendimiento de la detección, incluido el rango de detección en un 60% y la resolución del mensurando duplicada, es decir, un error de frecuencia reducido en un 50%. Debido a la implicación de la medición con la interacción de pérdida de Brillouin en parte del BGS diseñado, se realiza una comparación directa del ruido de traza con y sin interacción de Brillouin. Debido a la elusión del exceso de ruido de Brillouin, el rastro con el BGS diseñado es mucho más claro.

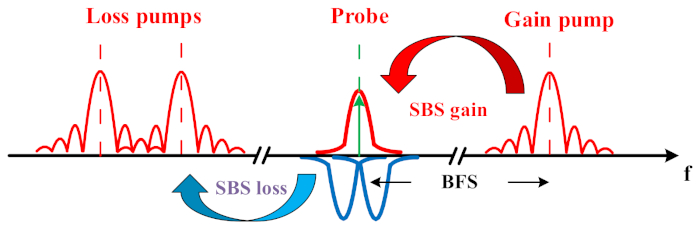
Figura 1: Esquema de un BGS diseñado por la superposición de un espectro de ganancia de Brillouin y dos espectros simétricos de pérdida de Brillouin. Haga clic aquí para ver una versión más grande de esta figura.

Protocolo

1. Selección de parámetros optimizados para la ingeniería del espectro mediante simulación

1. Modele el BGS g_SBS(ν,z) con las ecuaciones^28,29
   
   tal como se implementa, por ejemplo, en el script complementario de MATLAB.
   NOTA: Aquí, G(ν) es el coeficiente de ganancia complejo, calculado en el script como G_complex dentro de la función SBS_g para el BGS convencional o la función SBS_gl para el BGS diseñado; g(ν,z) es la ganancia de Brillouin del complejo local; y g_SBS y φ_SBS son la parte real e imaginaria de g(ν,z) y simbolizan la respuesta de fase BGS y SBS en la ubicación z desde el extremo de lanzamiento de la bomba, respectivamente. En el script, g_SBS se simboliza mediante las variables SBS_g_log y SBS_gl_log para el BGS convencional y diseñado en escala logarítmica, respectivamente. P_p = 20 dBm (P_pump en el script) es la potencia máxima del pulso de la bomba en el extremo de lanzamiento de la fibra; ν_B es el BFS (normalizado en el script); g₀ = 0,2 ^{W-1 m-1} (g₀ en el script) es el coeficiente de ganancia de Brillouin; Δν_B = 50 MHz (gamma_B en el alfabeto) es el FWHM del BGS; α = 0,2 dB/km es el coeficiente de pérdida de fibra y se representa mediante alpha_log y alpha_lin como el valor en escala logarítmica y lineal en el script, respectivamente; ν es la frecuencia de onda de la sonda, de modo que el desplazamiento de frecuencia de la bomba y la sonda ν - ν_B se escanea de -250 MHz a 250 MHz. El desplazamiento de frecuencia de la bomba y la sonda se representa en el script como el vector global f. El término g₁ = mg₀ es el factor de pérdida; 2d∙Δν_B es el desplazamiento de frecuencia entre las dos pérdidas; y L_eff = 10 m (L_eff en el script) es la longitud de interacción de Brillouin para un ancho de pulso de 100 ns. La forma espectral diseñada se puede ajustar fácilmente ajustando dos factores normalizados, m y d. El BGS convencional se puede modelar simplemente por m = 0.
2. Agregue ruido aleatorio (es decir, ruido gaussiano blanco aditivo) con el mismo nivel tanto en el BGS convencional como en el de ingeniería. El ajuste de los parámetros noise_level en el script puede cambiar el nivel de ruido.
3. Ajuste el BGS ruidoso convencional con la función Lorentziana (función Lorentz_g_gain_fun en el script) y el BGS ruidoso diseñado con la función Lorentziana superpuesta (función Lorentz_gl_gain_fun en el script) (consulte la Figura 2A).
4. Determine el desplazamiento de frecuencia máxima debido al ruido para el BGS convencional y diseñado (Figura 2B).
5. Repita los pasos 1.2-1.4 para N = 500 y recoja todos los desplazamientos de frecuencia de pico Δf_ci y Δf_pi (representados por delta_g_g y delta_g_gl en el script, respectivamente) para el BGS convencional y el BGS diseñado en el ^i-ésimo proceso, respectivamente.

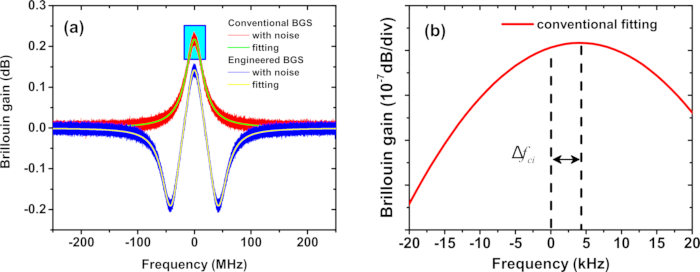
Figura 2: BGS simulado. (A) Demostración de la instalación de un BGS típicamente Lorentziano (rojo) y de ingeniería (azul) en la simulación. (B) El pico Lorentziano BGS desde (A). Δf_ci representa el error de estimación del BFS para el BGS convencional en la ^i-ésima medición. Haga clic aquí para ver una versión más grande de esta figura.

6. Calcule la relación entre la desviación típica de los errores de estimación del BFS inducidos por el ruido como:
   
7. Grafique η en función de m y d (véase la figura 3A). Encuentre el valor mínimo η_min y los valores m y d correspondientes. La ventaja de la precisión de la estimación se mantendrá a lo largo de toda la fibra²⁸.
8. Ajuste el valor de z (es decir, la longitud de la fibra, también z en el script) en la ecuación (2) de 0 km a 60 km, paso 50 m y repita los pasos 1.1-1.7 con algunos valores m y d seleccionados. A continuación, se puede obtener la relación de la desviación estándar en función de la longitud de la fibra (véase la Figura 3B).

2. Prepare y pruebe la configuración convencional de BOTDA (bloque resaltado en la Figura 4B)

1. Encienda el diodo láser (LD) y compruebe el funcionamiento del LD con el analizador de espectro óptico (OSA). Por lo general, se utiliza una longitud de onda de alrededor de 1.550 nm.
2. Conecte el LD con el acoplador óptico 10:90 (OC). Compruebe la potencia de la salida OC del 10%. Si la potencia es superior a 13 dBm (la potencia de entrada máxima del codificador de polarización [Pol.S.]), reduzca la potencia de salida LD disminuyendo la corriente LD.
3. Conecte la salida OC del 10% con el Pol.S. Para evitar el desvanecimiento de la polarización¹, ajuste la frecuencia de aleatorización a 1 kHz.
4. Compruebe la potencia de la salida del Pol.S. Si la potencia es superior a -3 dBm (el límite máximo de potencia de entrada del amplificador óptico semiconductor [SOA]), agregue atenuadores hasta que se satisfaga el requisito de energía. Conecte el Pol.S. con la SOA.
5. Aplique la señal de tren de pulsos eléctricos con un ancho de pulso de 100 ns y una tasa de repetición de 4 kHz desde el generador de pulsos (PG) en el SOA. Asegúrese de que la amplitud de la señal de impulso sea superior al umbral de la lógica de transistor-transistor (TTL) de la SOA (es decir, 4 dBm) y que la tasa de repetición satisfaga el requisito de ida y vuelta³⁰.
6. Conecte la salida del SOA con el amplificador de fibra dopada con erbio (EDFA 1) y opere el EDFA en modo de control automático de corriente (ACC). Conecte la salida de EDFA 1 al puerto 1 del circulador (Cir).
7. Compruebe la señal de pulso óptico del puerto 2 de Cir en el digitalizador conectándolo con el fotodiodo (PD). Para evitar cualquier daño a la DP, es necesaria una atenuación suficiente.
8. Calcule la potencia máxima del pulso óptico mediante la forma de onda medida en el digitalizador. La potencia máxima óptica P_o se estima de acuerdo con
   
   donde V_E es el voltaje máximo del pulso eléctrico, y R y R_f son la respuesta y la transresistencia de DP. Tenga en cuenta la atenuación de protección en este cálculo para que se evalúe una potencia de bomba de entrada correcta en la fibra bajo prueba (FUT, 10,6 km).
9. Obsérvese el valor de corriente EDFA I₂₀ cuando la potencia máxima del pulso óptico calculada alcanza los 20 dBm (umbral MI¹⁹). La relación de extinción (ER) del tren de pulsos ópticos se puede evaluar de acuerdo con la conservación de la energía:
   
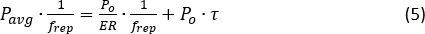
   donde P_avg es la potencia media óptica del tren de impulsos; f_rep es la tasa de repetición; y τ es el ancho de pulso. El ER de la SOA suele ser superior a 30 dBm, evitando eficientemente el NLE^31,32.
   NOTA: Apague el EDFA antes de desconectar el PD y continuar con la construcción del sistema.
10. Conecte el puerto 2 del Cir con un extremo del FUT para completar la configuración de la rama de la bomba. Compruebe si el sistema sufrirá de MI comprobando el espectro desde el otro extremo del FUT en el OSA y ajustando el EDFA a un valor de corriente constante, I₂₀. Si el espectro detectado es el mismo (en forma, no necesariamente en amplitud) al medido en el paso 2.1, entonces el sistema está libre de IM. De lo contrario, cuando se observe un ensanchamiento evidente del espectro o una división de crestas³³ , reduzca la corriente EDFA 1 para mantener la forma del espectro.
11. Conecte la salida del 90% del OC a un OC 1 50:50 y conecte una de las salidas OC 1 al modulador Mach-Zehnder (MZM 1) a través de un controlador de polarización (PC). Ajuste la polarización correctamente, de modo que la salida de MZM 1 se maximice (alineación de polarización).
12. Aplique la señal de radiofrecuencia (RF) del generador de RF (RFG 1) con el BFS del FUT (para SSMF alrededor de 11 GHz) y una amplitud de 16 dBm al MZM 1. Ajuste el voltaje de polarización de CC del MZM 1 para que la portadora se suprima al mínimo.
13. Conecte la salida del MZM 1 con rejilla de Bragg de fibra (FBG 1). Verifique el espectro de salida de FBG 1 en el OSA para que el FBG 1 esté configurado para bloquear la banda lateral de frecuencia superior y la portadora.
14. Conecte la salida del FBG 1 al EDFA 2, otro 50:50 OC 2 y un aislador (ISO) consecutivamente.
15. Opere EDFA 2 también en modo ACC y establezca el valor actual en I_g, de modo que la potencia de salida del ISO sea inferior a -14 dBm, minimizando NLE²⁰. Apague el EDFA antes de desconectar el medidor de potencia y continúe con la construcción del sistema. Conecte la salida ISO al otro extremo del FUT para completar la configuración de la rama de la sonda de ganancia.
16. Conecte el puerto Cir 3 al EDFA 4 (para preamplificación³⁴) y PD. Configure el EDFA en modo ACC. El valor de corriente I₄ debe permitir que la potencia de salida de EDFA sea 4 menor que el límite de entrada del PD. Conecte la salida de RF PD a un filtro de paso bajo de RF de 10 MHz^35,36. Conecte la salida del filtro al digitalizador.
17. Conecte el disparador del digitalizador con la salida sincronizada (o inversa) del generador de pulsos. Configure los parámetros del digitalizador de la siguiente manera: Frecuencia de muestreo: 500 MSa/s; promedio: 4.096 veces; Número de muestras: 10.000.
18. Establezca el valor actual de EDFA 1, EDFA 2 y EDFA 4 en I₂₀, I_g e I₄, respectivamente. Ejecute un programa de registro de rastreo. Compruebe la traza medida en el digitalizador. Si la amplitud de la traza sigue el decaimiento exponencial, entonces el sistema de detección está libre de MI. De lo contrario, reduzca el valor actual de EDFA 1.

3. Medición mediante la configuración convencional de BOTDA y procesamiento de datos

1. Establezca los valores de EDFA 1 y EDFA 2 en I₂₀ e I_g, respectivamente. Escanee la frecuencia de RFG 1 en el rango de BFS ± 90 MHz con pasos de 1 MHz. Registre el rastro del programa de grabación después de cada paso de escaneo.
2. Calcule la ganancia local de Brillouin dividiendo la amplitud de la traza (en el período de interacción de Brillouin) por cada desplazamiento de CC (período de interacción no Brillouin).
3. Recupere el BGS en cada sección de fibra ajustando el BGS ruidoso medido con el accesorio Lorentziano. Determine el FWHM del BGS convencional Δν_B0 desde el accesorio.
4. Repita los pasos 3.1 y 3.2 para N = 48 veces y recoja todas las distribuciones de frecuencia de pico estimadas (BFS) a lo largo de la fibra ν_Bci(z) en el ^i-ésimo proceso (véase la Figura 5A).
5. Calcule el error de estimación del BFS como la desviación estándar del BFS ajustado en cada sección de fibra en las 48 mediciones (consulte la Figura 5B).

4. Preparando el resto de la configuración

NOTA: En este caso, se utilizaron m = 1 y d = 1,24, según los resultados de la simulación (ver sección 1 y Figura 3).

1. Conecte la otra salida del 50:50 OC 1 en la rama de la sonda con el EDFA 3 y el 50:50 OC 3.
2. Conecte una de las salidas de 50:50 OC 3 a un PC y MZM 2. Ajuste la polarización para que se maximice la salida de MZM 2.
3. Aplique la señal de RF de RFG 2 con BFS - d∙Δν_B0 y amplitud de 16 dBm en MZM 2. Verifique el espectro de modulación en el OSA y ajuste el voltaje de polarización para minimizar la amplitud de la portadora.
4. Conecte la salida de MZM 2 a la entrada de un interruptor óptico (OS 1), una de las entradas de 50:50 OC 4, y el FBG 2.
5. Verifique la señal óptica en el OSA y ajuste la longitud de onda central FBG 2 para que la portadora y la banda lateral de frecuencia más baja estén bloqueadas (consulte la Figura 4A). A continuación, se completará la configuración de la rama de sondeo de pérdida 1.
6. Conecte la otra salida del 50:50 OC 3 a un PC y MZM 3. Ajuste la polarización para que se maximice la salida de MZM 3.
7. Aplique la señal de RF del RFG 3 con BFS + d∙Δν_B0 y 16 dBm de amplitud en MZM 3. Verifique el espectro de modulación en el OSA y ajuste el voltaje de polarización para minimizar la amplitud de la portadora.
8. Conecte la salida de MZM 3 a un atenuador óptico variable (VOA) con función de conmutación (OS 2) y la otra entrada de 50:50 OC 4. Teniendo en cuenta que el desplazamiento entre las frecuencias de la sonda de pérdida es relativamente pequeño en comparación con la ventana de transmisión FBG 2 (varios GHz), la portadora y la banda lateral de frecuencia más baja de MZM 3 también serán bloqueadas por FBG 2. A continuación, se completará la configuración de la rama de sondeo de pérdida 2.
9. Cierre el OS 1, abra el OS 2 y establezca el valor de corriente de EDFA 3 en I_l para que la potencia de la sonda de pérdida 1 sea igual a -14 dBm (m = 1).
10. Abra el OS 1, cierre el OS 2 y ajuste la atenuación de VOA para que la potencia de la sonda de pérdida 2 también sea igual a -14 dBm.

5. Medición utilizando la configuración completa propuesta de BOTDA y el procesamiento de datos

1. Cierre el sistema operativo 1, cierre el sistema operativo 2 y establezca el valor actual de EDFA 1, EDFA 2, EDFA 3 y EDFA 4 en I₂₀, I_g, I_l e I₄, respectivamente. Escanee la frecuencia del RFG 1 en el rango de BFS ± 90 MHz en pasos de 1 MHz. Las frecuencias de RFG 2 y RFG 3 se escanean en consecuencia. Registre el rastro del programa después de cada paso de escaneo.
2. Calcule la ganancia local de Brillouin como en el paso 3.2 y recupere el BGS diseñado en cada sección de fibra ajustando el BGS ruidoso medido con la función lorentziana superpuesta.
3. Repita los pasos 5.1 y 5.2 para N = 48 veces y recoja todas las distribuciones de frecuencia de cresta estimadas (BFS) a lo largo de la fibra ν_Bpi(z) en el ^i-ésimo proceso (véase la Figura 5A).
4. Calcule el error de estimación del BFS como la desviación estándar del BFS ajustado en cada sección de fibra en las 48 mediciones (consulte la Figura 5B).

Resultados

La Figura 3 muestra los resultados de la simulación. Los puntos con η < 1 en la Figura 3A indican un error de frecuencia menor (mayor resolución de medición) con el BGS diseñado. Cuanto menor sea el valor, mayor será la ventaja. La relación mínima fue de m = 1, lo que indica que se puede llevar a cabo un esquema de multisonda en lugar de multibomba (ver ...

Discusión

El paso más crítico durante el experimento es la ecualización de las tres potencias de la sonda para que m = 1 y se logre la simetría entre los dos espectros de pérdida de Brillouin. Además de la comprobación de potencia por separado utilizando el medidor de potencia en el puerto Cir 2, como se presenta en los pasos 4.9 y 4.10, la ecualización de potencia se puede comprobar con mayor precisión en el digitalizador. Al ajustar la frecuencia RF 1 a ~11 GHz (la fibra BFS) y...

Materiales

Name	Company	Catalog Number	Comments
Current controller for laser diode	ILX Lightwave	LDX3220
Digitizer	Acqiris SA	U5309A-1039
Erbium doped fiber amplifier 1	Photop	PTEDFA-A-PA-C-SCH-15
Erbium doped fiber amplifier 2	LiComm	OFA-TCH
Erbium doped fiber amplifier 3	Calmar Optcom	AMP-ST30
Erbium doped fiber amplifier 4	Photop	PTEDFA-A-PA-C-SCH-15
Fiber Bragg grating 1	Advanced Optics Solutions	T-FBG
Fiber Bragg grating 2	Advanced Optics Solutions	T-FBG
Fiber under test	ofs
Isolator	General Photonics	S-15-NTSS
Laser diode	3SP Group	A1905 LMI
Mach-Zehnder modulator 1	Avanex	IM10
Mach-Zehnder modulator 2	Avanex	IM10
Mach-Zehnder modulator 3	Avanex	IM10
Nanosecond driving board for semiconductor optical amplifier	Highland Technology	T160-9 (28A160-9C)
Optical coupler 10:90	Newport		Benchtop coupler/WDM
Optical coupler 50:50	Newport		Benchtop coupler/WDM
Optical spectrum analyzer	Hewlett Packard	86145A
Optical switch 1	JDSU	SN12-1075NC
Photodiode	Thorlabs	D400FC
Polarization scrambler	General Photonics	PSY-101
Pulase generator	Hewlett Packard	8082A
Radio function generator 1	Anritsu	MG3692C
Radio function generator 2	Agilent Technology	E8257D
Radio function generator 3	HTM	T2100
Semiconductor optical amplifier	Thorlabs	SOA1013SXS
Temperature controller for laser diode	ILX Lightwave	LDT5948
Temperature controller for semiconductor optical amplifier	Tektronix	TED200
Variable optical attenuator	JDSU	mVOA-A1	With optical switch function