Optimisation des analyseurs optiques dans le domaine temporel Brillouin basée sur l’ingénierie du spectre de gain

Résumé

Un protocole pour les analyseurs optiques Brillouin dans le domaine temporel basé sur l’ingénierie du spectre de gain est présenté. Des améliorations des performances de détection, y compris la portée de détection et la résolution de mesure, sont obtenues et le bruit d’intensité Brillouin excédentaire est étudié. Le protocole introduit une nouvelle façon d’améliorer les performances de détection Brillouin distribuée.

Résumé

La démonstration d’une méthode unique d’amélioration des performances de détection dans les analyseurs optiques dans le domaine temporel (BOTDA) Brillouin. Un spectre de gain Brillouin (BGS) est superposé à deux spectres symétriques de perte Brillouin (BLS). Cela conduit à une forme de spectre complexe qui est plus résistante au bruit du système de détection. Au lieu d’une seule interaction entre la pompe et la sonde comme dans la configuration BOTDA conventionnelle, trois ondes de sonde optiques sont exploitées, une sonde étant située dans le BGS et les deux autres symétriquement dans le BLS. En raison de la résistance et de l’insensibilité de la forme du spectre au bruit, les performances de détection sont améliorées de 60 % et la résolution du mesurande est doublée.

Introduction

La détection distribuée par fibre (DFS) est un mécanisme unique qui utilise une fibre entière comme support de détection. Il a suscité beaucoup d’intérêt en raison de la faible perte de fibre ; petite taille ; et la capacité d’être facilement intégré dans diverses structures, telles que des barrages, des ponts et des bâtiments, pour effectuer une surveillance de l’environnement en tant que système nerveux artificiel. Par rapport à l’application de nombreux capteurs ponctuels traditionnels, tels que les réseaux de Bragg à fibre (FBG), il offre une solution plus efficace et plus rentable dans un large éventail de tâches de détection à grande échelle, telles que la surveillance de l’infrastructure et de l’état des^structures1.

Les capteurs distribués en courant exploitent différents mécanismes de diffusion à l’intérieur de la fibre pour mesurer la température et la distribution de la déformation. Parmi eux, le DFS basé sur la diffusion Brillouin est le plus attrayant en raison des avantages frappants de la diffusion Brillouin stimulée (SBS), tels que le rapport signal/bruit (SNR) élevé, le seuil bas et la sensibilité à la fois à la température² et à la déformation³. La SBS peut être classiquement décrite comme une interaction entre les ondes optiques continues (CW) incidentes, c’est-à-dire la pompe, et l’onde de sonde CW à contre-propagation via une onde acoustique. En fonction de la conservation de l’énergie et de la quantité de mouvement, la fréquence de l’onde de la sonde est rétrogradée à la pompe. Ce décalage est appelé décalage de fréquence de Brillouin (BFS). Si l’on considère la durée de vie finie d’une onde acoustique de 10 ns, il existe une distribution spectrale finie de l’onde réfractée, également appelée spectre de gain de Brillouin (BGS), dans laquelle le BFS est la différence de fréquence entre l’onde de pompe et la fréquence centrale de crête. L’interaction entre les ondes conduit à une région de gain décalée en fréquence et à une région de perte décalée en fréquence où l’onde de sonde est amplifiée et atténuée, respectivement. Pour une fibre monomode standard (SSMF) en bande C, le BFS est d’environ 11 GHz et le BGS a une forme lorentzienne avec une largeur totale ultra-étroite à mi-hauteur (FWHM) de 10-30 MHz, qui peut être encore réduite à 3,4 MHz avec des techniques spécifiques 4,5,6,7. Sur la base de ces caractéristiques, le SBS peut également être appliqué dans les filtres photoniques à micro-ondes ^8,9,10, les filtres optiques¹¹, la lumière lente et rapide 12,13,14 et la spectroscopie optique à haute résolution ^7,15.

L’une des applications les plus prometteuses de la SBS est la détection Brillouin distribuée. Ces capteurs exploitent la dépendance du BFS à la température et à la déformation. Le premier à avoir été présenté a été l’analyseur optique dans le domaine temporel Brillouin (BOTDA)¹⁶, qui est la technique de détection Brillouin distribuée dans le domaine temporel la plus consolidée. Elle diffère de l’interaction conventionnelle CW-SBS en ce qu’elle exploite l’interaction SBS entre une onde de pompe pulsée et une sonde CW de sorte que les informations environnementales sont interrogées localement sur chaque section de fibre. La fréquence de la pompe ou de la sonde est généralement fixe pendant que la fréquence de la sonde ou de la pompe est balayée à proximité du BFS. La puissance de la sonde est enregistrée pour la reconstruction du BGS et le BFS est idéalement la fréquence de crête du BGS local à chaque section de fibre. Cependant, en raison de l’inévitable bruit du système, le pic BGS est généralement ambigu et un algorithme d’ajustement doit être appliqué¹⁷, ce qui conduit à une certaine erreur d’estimation de la fréquence¹⁸ et influence la résolution du mesure.

Statistiquement, l’erreur d’estimation BFS est inversement proportionnelle au rapport signal/bruit (SNR) du système. La façon la plus simple d’améliorer le SNR est d’augmenter la puissance de la pompe et de la sonde. Cependant, ceux-ci sont limités par l’instabilité de modulation (MI)¹⁹ et les effets non locaux (NLE)^20,21 à ~20 dBm et -14 dBm, respectivement. De nombreuses techniques, telles que le codage²² et l’amplification en ligne basée sur Raman²³, ont été proposées pour briser ces limites. Récemment, il a été rapporté que cette erreur de fréquence peut être minimisée en choisissant un algorithme d’ajustement approprié²⁴. De même, les mesures exploitant la phase Brillouin et un algorithme d’ajustement linéaire présentent également une erreur de fréquence réduite^{de 25}, ce qui indique le potentiel d’un BGS bien conçu pour l’amélioration des performances de détection. Une autre option pour améliorer le SNR est la réduction du bruit. Cependant, selon le point de vue traditionnel, le bruit du système de détection provient principalement du détecteur (c’est-à-dire le bruit de mode commun, y compris le bruit sombre, le bruit de tir, etc.)^26,27 et l’amélioration est moins probable.

L’idée de base de cet article est de concevoir le BGS par la superposition d’un BGS conventionnel avec deux spectres de perte de Brillouin (BLS) symétriques (voir Figure 1). Par rapport à un spectre BGS conventionnel, qui suit une forme lorentzienne, le spectre conçu est plus net et plus robuste avec le même niveau de bruit du système. Ainsi, le bruit a moins d’influence sur la détermination de la fréquence de crête. Cela peut être vérifié en collectant et en ajustant les données de mesure BGS un nombre statistiquement significatif de fois. En raison de cette meilleure résistance au bruit, des améliorations des performances de détection sont obtenues, notamment la portée de détection de 60 % et une résolution de mesure doublée, c’est-à-dire une erreur de fréquence réduite de 50 %. En raison de l’implication de la mesure avec l’interaction de perte de Brillouin dans une partie du BGS conçu, une comparaison directe du bruit à l’état de traces avec et sans interaction de Brillouin est effectuée. En raison du contournement de l’excès de bruit Brillouin, la trace avec le BGS conçu est beaucoup plus claire.

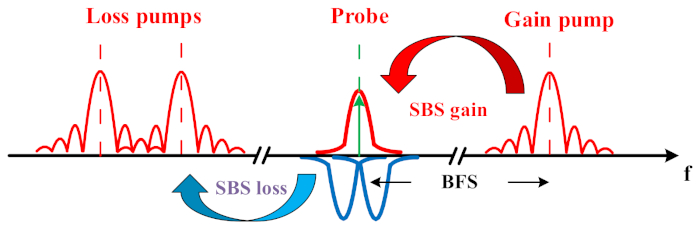
Figure 1 : Schéma d’un BGS conçu par la superposition d’un gain de Brillouin et de deux spectres de perte de Brillouin symétriques. Veuillez cliquer ici pour voir une version agrandie de cette figure.

Protocole

1. Sélection de paramètres optimisés pour l’ingénierie spectrale par simulation

1. Modélisez le BGS g_SBS(ν,z) avec les équations^28,29
   
   tel qu’implémenté, par exemple, par le script MATLAB supplémentaire.
   REMARQUE : Ici, G(ν) est le coefficient de gain complexe, calculé dans le script comme G_complex dans la fonction SBS_g pour le BGS conventionnel ou SBS_gl fonction pour le BGS conçu ; g(ν,z) est le gain de Brillouin complexe local ; et g_SBS et φ_SBS sont la partie réelle et imaginaire de g(ν,z) et symbolisent la réponse de phase BGS et SBS à l’emplacement z de l’extrémité de lancement de la pompe, respectivement. Dans le script, g_SBS est symbolisé par les variables SBS_g_log et SBS_gl_log pour le BGS conventionnel et le BGS d’ingénierie sur une échelle logarithmique, respectivement. P_p = 20 dBm (P_pump dans le script) est la puissance de crête de l’impulsion de la pompe à l’extrémité de lancement de la fibre ; ν_B est le BFS (normalisé dans le script) ; g₀ = 0,2 ^{W-1 m-1} (g₀ dans le script) est le coefficient de gain de Brillouin ; Δν_B = 50 MHz (gamma_B dans le script) est le FWHM du BGS ; α = 0,2 dB/km est le coefficient de perte de fibre et est représenté par alpha_log et alpha_lin comme valeur à l’échelle logarithmique et linéaire dans le script, respectivement ; ν est la fréquence de l’onde de la sonde de sorte que le décalage de fréquence de la pompe et de la sonde ν - ν_B est balayé de -250 MHz à 250 MHz. Le décalage de fréquence de la pompe et de la sonde est représenté dans le script par le vecteur global f. Le terme g₁ = mg₀ est le facteur de perte ; 2d∙Δν_B est le décalage de fréquence entre les deux affaiblissements ; et L_eff = 10 m (L_eff dans le script) est la longueur d’interaction de Brillouin pour une largeur d’impulsion de 100 ns. La forme spectrale conçue peut être facilement ajustée en ajustant deux facteurs normalisés, m et d. Le BGS conventionnel peut être modélisé simplement par m = 0.
2. Ajoutez du bruit aléatoire (c’est-à-dire un bruit blanc gaussien additif) avec le même niveau sur le BGS conventionnel et technique. Le réglage du paramètre noise_level dans le script peut modifier le niveau de bruit.
3. Ajustez le BGS bruyant conventionnel avec la fonction lorentzienne (fonction Lorentz_g_gain_fun dans le script) et le BGS bruyant conçu avec la fonction lorentzienne superposée (fonction Lorentz_gl_gain_fun dans le script) (voir Figure 2A).
4. Déterminez le décalage de fréquence de crête dû au bruit pour le BGS conventionnel et technique (Figure 2B).
5. Répétez les étapes 1.2 à 1.4 pour N = 500 et collectez tous les décalages de fréquence de crête Δf_ci et Δf_pi (représentés par delta_g_g et delta_g_gl dans le script, respectivement) pour le BGS conventionnel et le BGS d’ingénierie dans le ^ième processus, respectivement.

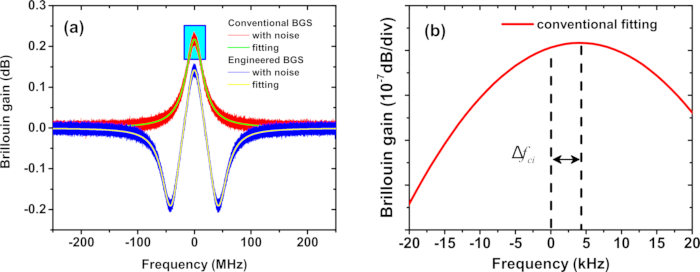
Figure 2 : BGS simulé. (A) Démonstration de l’ajustement d’un BGS typique de Lorentz (rouge) et d’ingénierie (bleu) dans la simulation. (B) Le pic Lorentzien BGS de (A). Δf_ci représente l’erreur d’estimation BFS pour le BGS conventionnel dans la ^ième mesure. Veuillez cliquer ici pour voir une version agrandie de cette figure.

6. Calculer le rapport de l’écart-type des erreurs d’estimation de la BFS induites par le bruit comme suit :
   
7. Tracer η en fonction de m et d (voir figure 3A). Trouvez la valeur minimale η_min et les m et d correspondants. L’avantage de la précision de l’estimation sera maintenu sur l’ensemble de la fibre²⁸.
8. Réglez la valeur de z (c’est-à-dire la longueur de la fibre, également z dans le script) dans l’équation (2) de 0 km à 60 km, pas 50 m et répétez les étapes 1.1 à 1.7 avec certaines valeurs m et d sélectionnées. Ensuite, le rapport de l’écart-type en fonction de la longueur de la fibre peut être acquis (voir Figure 3B).

2. Préparez et testez la configuration BOTDA conventionnelle (bloc mis en évidence sur la figure 4B)

1. Allumez la diode laser (LD) et vérifiez le fonctionnement de la LD avec l’analyseur de spectre optique (OSA). Habituellement, une longueur d’onde d’environ 1 550 nm est utilisée.
2. Connectez le LD avec le coupleur optique 10:90 (OC). Vérifiez l’alimentation à partir de la sortie OC de 10 %. Si la puissance est supérieure à 13 dBm (la puissance d’entrée maximale du brouilleur de polarisation [Pol.S.]), réduisez la puissance de sortie LD en baissant le courant LD.
3. Connectez la sortie OC 10 % avec le Pol.S. Afin d’éviter l’évanouissement de polarisation^{de 1}, réglez la fréquence d’embrouillage sur 1 kHz.
4. Vérifiez la puissance de la sortie du Pol.S. Si la puissance est supérieure à -3 dBm (la limite de puissance d’entrée maximale de l’amplificateur optique à semi-conducteur [SOA]), ajoutez des atténuateurs jusqu’à ce que la puissance requise soit satisfaite. Connectez le Pol.S. avec la SOA.
5. Appliquez le signal du train d’impulsions électriques avec une largeur d’impulsion de 100 ns et un taux de répétition de 4 kHz à partir du générateur d’impulsions (PG) sur le SOA. Assurez-vous que l’amplitude du signal d’impulsion est supérieure au seuil logique transistor-transistor (TTL) du SOA (c’est-à-dire 4 dBm) et que le taux de répétition satisfait à l’exigence d’aller-retour³⁰.
6. Connectez la sortie du SOA avec l’amplificateur à fibre dopé à l’erbium (EDFA 1) et faites fonctionner l’EDFA en mode de contrôle automatique du courant (ACC). Connectez la sortie de l’EDFA 1 au port 1 du circulateur (Cir).
7. Vérifiez le signal d’impulsion optique du port 2 de Cir dans le numériseur en le connectant à la photodiode (). Afin d’éviter tout dommage à la, une atténuation suffisante est nécessaire.
8. Calculez la puissance de crête de l’impulsion optique par la forme d’onde mesurée dans le numériseur. La puissance de crête optique P_o est estimée en fonction de
   
   où V_E est la tension de crête de l’impulsion électrique, et R et R_f sont la réactivité et la transrésistance. Tenez compte de l’atténuation de protection dans ce calcul afin d’évaluer une puissance de pompe d’entrée correcte dans la fibre testée (FUT, 10,6 km).
9. Notez la valeur du courant EDFA I₂₀ lorsque la puissance de crête de l’impulsion optique calculée atteint 20 dBm (seuil MI¹⁹). Le taux d’extinction (RE) du train d’impulsions optiques peut être évalué en fonction de la conservation de l’énergie :
   
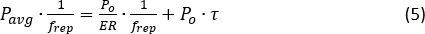
   où P_moy est la puissance moyenne optique du train d’impulsions ; f_rep est le taux de redoublement ; et τ est la largeur de l’impulsion. Le RE du SOA est généralement supérieur à 30 dBm, ce qui permet d’éviter efficacement le NLE^31,32.
   REMARQUE : Éteignez l’EDFA avant de déconnecter le et de continuer à construire le système.
10. Connectez le port 2 du Cir avec une extrémité du FUT pour terminer la configuration de la branche de la pompe. Vérifiez si le système souffrira d’IM en vérifiant le spectre de l’autre extrémité du FUT dans l’OSA et en réglant l’EDFA à une valeur de courant constant, I₂₀. Si le spectre détecté est le même (en forme, pas nécessairement en amplitude) que celui mesuré à l’étape 2.1, alors le système est exempt de MI. Sinon, lorsqu’un élargissement du spectre ou un fractionnement des crêtes³³ évidents sont observés, réduisez le courant EDFA 1 pour maintenir la forme du spectre.
11. Connectez la sortie à 90 % de l’OC à un OC 1 50:50 et connectez l’une des sorties OC 1 au modulateur de Mach-Zehnder (MZM 1) via un contrôleur de polarisation (PC). Réglez correctement la polarisation, de sorte que la sortie de MZM 1 soit maximisée (alignement de polarisation).
12. Appliquez le signal de radiofréquence (RF) du générateur RF (RFG 1) avec le BFS du FUT (pour SSMF autour de 11 GHz) et une amplitude de 16 dBm au MZM 1. Réglez la tension de polarisation CC du MZM 1 de manière à ce que la porteuse soit supprimée au minimum.
13. Connectez la sortie du MZM 1 avec le réseau de Bragg fibre (FBG 1). Vérifiez le spectre de sortie du FBG 1 dans l’OSA afin que le FBG 1 soit réglé pour bloquer la bande latérale de fréquence supérieure et la porteuse.
14. Connectez la sortie du FBG 1 à l’EDFA 2, un autre 50:50 OC 2 et un isolateur (ISO) consécutivement.
15. Faites fonctionner EDFA 2 également en mode ACC et réglez la valeur de courant sur I_g, de sorte que la puissance de sortie de l’ISO soit inférieure à -14 dBm, minimisant ainsi NLE²⁰. Éteignez l’EDFA avant de débrancher le wattmètre et poursuivez la construction du système. Connectez la sortie ISO à l’autre extrémité du FUT pour terminer la construction de la configuration de la branche de la sonde de gain.
16. Connectez le port Cir 3 à l’EDFA 4 (pour la pré-amplification³⁴) et au. Réglez l’EDFA sur le mode ACC. La valeur de courant I₄ doit laisser la puissance de sortie de l’EDFA être inférieure de 4 à la limite d’entrée du. Connectez la sortie RF à un filtre passe-bas RF 10 MHz^35,36. Connectez la sortie du filtre au numériseur.
17. Connectez le déclencheur du numériseur avec la sortie synchronisée (ou inverse) du générateur d’impulsions. Réglez les paramètres du numériseur comme suit : Fréquence d’échantillonnage : 500 MSa/s ; moyenne : 4 096 fois ; Nombre d’échantillons : 10 000.
18. Définissez la valeur actuelle de EDFA 1, EDFA 2 et EDFA 4 sur I₂₀, I_g et I₄, respectivement. Exécutez un programme d’enregistrement de traces. Vérifiez la trace mesurée dans le numériseur. Si l’amplitude de la trace suit la décroissance exponentielle, alors le système de détection est exempt de MI. Sinon, réduisez la valeur actuelle d’EDFA 1.

3. Mesure à l’aide de la configuration conventionnelle BOTDA et traitement des données

1. Définissez les valeurs de EDFA 1 et EDFA 2 sur I₂₀ et I_g, respectivement. Scannez la fréquence de RFG 1 dans la gamme BFS ± 90 MHz avec des pas de 1 MHz. Enregistrez la trace du programme d’enregistrement après chaque étape de numérisation.
2. Calculez le gain local de Brillouin en divisant l’amplitude de trace (en période d’interaction Brillouin) par chaque décalage DC (période d’interaction non Brillouin).
3. Récupérez le BGS à chaque section de fibre en ajustant le BGS bruyant mesuré avec le raccord lorentzien. Déterminez le FWHM du BGS conventionnel Δν_B0 à partir du raccord.
4. Répétez les étapes 3.1 et 3.2 pour N = 48 fois et collectez toutes les distributions de fréquence de crête estimées (BFS) le long de la fibre ν_Bci(z) dans le ^ième processus (voir Figure 5A).
5. Calculez l’erreur d’estimation BFS comme l’écart-type du BFS ajusté à chaque section de fibre dans les 48 mesures (voir Figure 5B).

4. Préparation du reste de la configuration

REMARQUE : Dans ce cas, m = 1 et d = 1,24 ont été utilisés, selon les résultats de la simulation (voir la section 1 et la figure 3).

1. Connectez l’autre sortie de l’OC 1 50:50 dans la branche de la sonde avec l’EDFA 3 et l’OC 3 50:50.
2. Connectez l’une des sorties de 50:50 OC 3 à un PC et à MZM 2. Ajustez la polarisation de manière à ce que la sortie de MZM 2 soit maximisée.
3. Appliquez le signal RF de RFG 2 avec BFS - d∙Δν_B0 et une amplitude de 16 dBm sur MZM 2. Vérifiez le spectre de modulation dans l’OSA et ajustez la tension de polarisation pour minimiser l’amplitude de la porteuse.
4. Connectez la sortie de MZM 2 à l’entrée d’un commutateur optique (OS 1), à l’une des entrées de 50:50 OC 4 et au FBG 2.
5. Vérifiez le signal optique dans l’OSA et ajustez la longueur d’onde centrale FBG 2 de sorte que la porteuse et la bande latérale de fréquence inférieure soient bloquées (voir Figure 4A). La configuration de la branche de sonde de perte 1 sera alors terminée.
6. Connectez l’autre sortie de l’OC 3 50:50 à un PC et à MZM 3. Ajustez la polarisation de manière à ce que la sortie de MZM 3 soit maximisée.
7. Appliquez le signal RF du RFG 3 avec BFS + d∙Δν_B0 et une amplitude de 16 dBm sur MZM 3. Vérifiez le spectre de modulation dans l’OSA et ajustez la tension de polarisation pour minimiser l’amplitude de la porteuse.
8. Connectez la sortie de MZM 3 à un atténuateur optique variable (VOA) avec une fonction de commutation (OS 2) et l’autre entrée de 50:50 OC 4. Étant donné que le décalage entre les fréquences de la sonde de perte est relativement faible par rapport à la fenêtre de transmission du FBG 2 (plusieurs GHz), la porteuse et la bande latérale de fréquence inférieure de MZM 3 seront également bloquées par le FBG 2. La configuration de la branche de sonde loss 2 sera alors terminée.
9. Fermez le système d’exploitation 1, ouvrez le système d’exploitation 2 et réglez la valeur de courant EDFA 3 sur I_l de sorte que la puissance de la sonde de perte 1 soit égale à -14 dBm (m = 1).
10. Ouvrez le système d’exploitation 1, fermez le système d’exploitation 2 et ajustez l’atténuation de la VOA de sorte que la puissance de la sonde de perte 2 soit également égale à -14 dBm.

5. Mesure à l’aide de la configuration et du traitement des données BOTDA

1. Fermez le système d’exploitation 1, fermez le système d’exploitation 2 et définissez la valeur actuelle de EDFA 1, EDFA 2, EDFA 3 et EDFA 4 sur I₂₀, I_g, I_l et I₄, respectivement. Scannez la fréquence du RFG 1 dans la plage de BFS ± 90 MHz par pas de 1 MHz. Les fréquences de RFG 2 et RFG 3 sont balayées en conséquence. Enregistrez la trace du programme après chaque étape de numérisation.
2. Calculez le gain de Brillouin local comme à l’étape 3.2 et récupérez le BGS technique à chaque section de fibre en ajustant le BGS bruyant mesuré avec la fonction lorentzienne superposée.
3. Répétez les étapes 5.1 et 5.2 pour N = 48 fois et collectez toutes les distributions de fréquence de crête estimées (BFS) le long de la fibre ν_Bpi(z) dans le ^ième processus (voir Figure 5A).
4. Calculez l’erreur d’estimation BFS comme l’écart-type du BFS ajusté à chaque section de fibre dans les 48 mesures (voir Figure 5B).

Résultats

La figure 3 montre les résultats de la simulation. Les points η < 1 dans la figure 3A indiquent une erreur de fréquence plus faible (résolution de mesure plus élevée) avec le BGS conçu. Plus la valeur était faible, plus l’avantage était grand. Le rapport minimum était à m = 1, ce qui indique qu’il est possible d’utiliser un schéma multisonde au...

Discussion

L’étape la plus critique de l’expérience est l’égalisation des trois puissances de la sonde de sorte que m = 1 et la symétrie entre les deux spectres de perte de Brillouin soit atteinte. Outre la vérification séparée de l’alimentation à l’aide du capteur de puissance sur le port Cir 2, comme présenté aux étapes 4.9 et 4.10, l’égalisation de puissance peut être vérifiée plus précisément dans le numériseur. En réglant la fréquence RF 1 sur ~11 GHz (...

matériels

Name	Company	Catalog Number	Comments
Current controller for laser diode	ILX Lightwave	LDX3220
Digitizer	Acqiris SA	U5309A-1039
Erbium doped fiber amplifier 1	Photop	PTEDFA-A-PA-C-SCH-15
Erbium doped fiber amplifier 2	LiComm	OFA-TCH
Erbium doped fiber amplifier 3	Calmar Optcom	AMP-ST30
Erbium doped fiber amplifier 4	Photop	PTEDFA-A-PA-C-SCH-15
Fiber Bragg grating 1	Advanced Optics Solutions	T-FBG
Fiber Bragg grating 2	Advanced Optics Solutions	T-FBG
Fiber under test	ofs
Isolator	General Photonics	S-15-NTSS
Laser diode	3SP Group	A1905 LMI
Mach-Zehnder modulator 1	Avanex	IM10
Mach-Zehnder modulator 2	Avanex	IM10
Mach-Zehnder modulator 3	Avanex	IM10
Nanosecond driving board for semiconductor optical amplifier	Highland Technology	T160-9 (28A160-9C)
Optical coupler 10:90	Newport		Benchtop coupler/WDM
Optical coupler 50:50	Newport		Benchtop coupler/WDM
Optical spectrum analyzer	Hewlett Packard	86145A
Optical switch 1	JDSU	SN12-1075NC
Photodiode	Thorlabs	D400FC
Polarization scrambler	General Photonics	PSY-101
Pulase generator	Hewlett Packard	8082A
Radio function generator 1	Anritsu	MG3692C
Radio function generator 2	Agilent Technology	E8257D
Radio function generator 3	HTM	T2100
Semiconductor optical amplifier	Thorlabs	SOA1013SXS
Temperature controller for laser diode	ILX Lightwave	LDT5948
Temperature controller for semiconductor optical amplifier	Tektronix	TED200
Variable optical attenuator	JDSU	mVOA-A1	With optical switch function