JoVE Logo
著者
お問い合わせ

サインイン

このコンテンツを視聴するには、JoVE 購読が必要です。 サインイン又は無料トライアルを申し込む。

この記事について

  • 要約
  • 要約
  • 概要
  • プロトコル
  • 結果
  • ディスカッション
  • 開示事項
  • 謝辞
  • 資料
  • 参考文献
  • 転載および許可

要約

ゲインスペクトルエンジニアリングに基づくBrillouin光時間領域アナライザのプロトコルが提示されます。センシング範囲や測定分解能などのセンシング性能の向上が達成され、過剰なブリルアン強度ノイズが研究されます。このプロトコルは、分散型Brillouinセンシング性能を向上させる新しい方法を導入しています。

要約

Brillouin光時間領域アナライザ(BOTDA)のセンシング性能向上のためのユニークな方法を実証します。ブリルアンゲインスペクトル(BGS)は、2つの対称ブリルアン損失スペクトル(BLS)と重ね合わせられます。これにより、センシングシステムのノイズに対してより耐性のある、複雑に設計されたスペクトル形状が得られます。従来のBOTDAセットアップのように1つのポンプとプローブの相互作用だけでなく、3つの光学プローブ波が利用され、1つのプローブがBGSに配置され、他の2つのプローブがBLSに対称に配置されます。設計されたスペクトル形状のノイズに対する抵抗と非感度により、センシング性能は60%向上し、測定分解能は2倍になります。

概要

分散型ファイバーセンシング(DFS)は、ファイバー全体をセンシング媒体として採用する独自のメカニズムです。繊維損失が少ないため、多くの関心を集めています。小さいサイズ;また、ダムや橋梁、建物など様々な構造物に手軽に埋め込むことができ、人工神経システムとして環境監視を行うことができること。ファイバブラッググレーティング(FBG)など、従来の多数のポイントセンサを適用するのと比較して、インフラや構造ヘルスモニタリング1など、幅広い大規模センシングタスクにおいて、より効率的で費用対効果の高いソリューションを提供します。

電流分布センサは、ファイバ内のさまざまな散乱メカニズムを利用して、温度とひずみ分布を測定します。その中でも、ブリルアン散乱に基づくDFSは、高い信号対雑音比(SNR)、低い閾値、温度2とひずみ3の両方に対する感度など、刺激ブリルアン散乱(SBS)の顕著な利点により、最も魅力的です。SBSは、古典的には、入射光連続波(CW)、すなわちポンプと、音波を介して逆伝播するCWプローブ波との間の相互作用として説明できます。エネルギーと運動量の保存則に従って、プローブ波はポンプに周波数ダウンシフトされます。このシフトはブリルアン周波数シフト(BFS)と呼ばれます。10nsの音波の有限寿命を考慮すると、屈折波には有限のスペクトル分布があり、ブリルアンゲインスペクトル(BGS)とも呼ばれ、BFSはポンプ波とピーク中心周波数の周波数差です。波間の相互作用により、周波数がダウンシフトしたゲイン領域と、プローブ波が増幅および減衰する周波数アップシフト損失領域がそれぞれ生じます。Cバンドの標準的なシングルモードファイバー(SSMF)の場合、BFSは約11GHzで、BGSはローレンツ形状で、半値(FWHM)は10〜30MHzの超狭全幅(FWHM)で、特定の手法4,5,6,7でさらに3.4MHzに縮小できます。これらの特性に基づいて、SBSは、マイクロ波フォトニクスフィルタ8,9,10、光学フィルタ11、低速および高速光12,13,14、および高分解能光学分光法7,15にも適用できます。

最も有望なSBSアプリケーションの1つは、分散型ブリルアンセンシングです。これらのセンサーは、BFSの温度とひずみ依存性を利用しています。最初に実証されたのは、ブリルアン光学時間領域アナライザー(BOTDA)16であり、これは最も統合された時間領域分布ブリルアンセンシング技術です。従来のCW-SBS相互作用とは異なり、パルスポンプ波とプローブCWとの間のSBS相互作用を利用し、環境情報を各繊維セクションについて局所的に調査します。通常、ポンプまたはプローブの周波数は固定され、プローブまたはポンプの周波数はBFSの近くでスキャンされます。プローブの電力はBGS再構成のために記録され、BFSは理想的には各ファイバーセクションのローカルBGSのピーク周波数です。しかし、避けられないシステムノイズのために、BGSピークは通常曖昧であり、フィッティングアルゴリズム17を適用する必要があり、これは周波数18 に一定の推定誤差をもたらし、測定および分解能に影響を与える。

統計的には、BFS 推定誤差はシステムの信号対雑音比 (SNR) に反比例します。SNRを向上させる最も簡単な方法は、ポンプとプローブの出力を上げることです。ただし、これらは変調不安定性(MI)19および非局所効果(NLE)20,21によってそれぞれ~20dBmおよび-14dBmに制限されます。これらの限界を打破するために、コーディング22やラマンベースのインライン増幅23など、数多くの技術が提案されている。最近、この周波数誤差は、適切な適合アルゴリズム24を選択することによって最小化できることが報告されている。これに関連して、ブリルアン相と線形フィッティングアルゴリズムを利用した測定では、周波数誤差が減少することが報告されており25、これは、適切に設計されたBGSがセンシング性能を向上させる可能性を示しています。SNRを向上させるもう一つの選択肢は、ノイズリダクションです。しかし、従来の見方によれば、センシングシステムのノイズは主に検出器から発生します(つまり、ダークノイズ、ショットノイズなどのコモンモードノイズ)26,27 そして改善の可能性は低いです。

この論文の基本的な考え方は、2つの対称的なブリルアン損失スペクトル(BLS)を持つ従来のBGSの重ね合わせによってBGSを設計することです( 図1を参照)。ローレンツ形状をたどる従来のBGSスペクトルと比較して、設計されたスペクトルは、同じレベルのシステムノイズでよりシャープで堅牢です。したがって、ノイズはピーク周波数の決定にあまり影響を与えません。これは、BGS測定データを統計的に有意な回数収集してフィッティングすることで検証できます。このノイズに対する耐性の向上により、検出範囲が60%、測定分解能が2倍になる(周波数誤差が50%減少する)など、検出性能の向上が達成されます。エンジニアリングされたBGSの一部では、測定がブリルアン損失相互作用に関与しているため、ブリルアン相互作用がある場合とない場合のトレースノイズの直接比較が行われます。過剰なブリルアンノイズを回避するため、エンジニアリングされたBGSのトレースははるかにクリアになります。

figure-introduction-3282
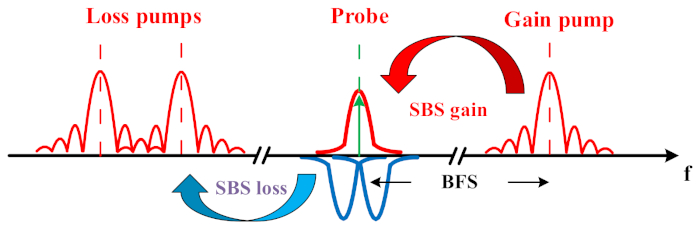
図1:1つのブリルアンゲインと2つの対称ブリルアン損失スペクトルの重ね合わせによるエンジニアリングBGSの概略図。この図の拡大版を表示するには、ここをクリックしてください。

プロトコル

1. シミュレーションによるスペクトルエンジニアリングに最適なパラメータの選択

  1. 工学的な BGS gSBS(ν,z) を式28,29 でモデル化します。
    figure-protocol-250
    たとえば、補足的な MATLAB スクリプトによって実装されます。
    注:ここで、G(ν)は複素ゲイン係数であり、スクリプトでは従来のBGSのSBS_g関数内または設計されたBGSのSBS_gl関数内でG_complexとして計算されます。g(ν,z) は局所複素ブリルアン利得です。gSBSとφSBSはg(ν,z)の実数部と虚数部であり、それぞれポンプ発射端からの位置zでのBGSとSBSの位相応答を象徴しています。このスクリプトでは、gSBS は、従来の BGS と工学的な BGS の変数 SBS_g_log と SBS_gl_log によってそれぞれ対数スケールでシンボル化されます。Pp = 20 dBm(スクリプトのP_pump)は、ファイバーの発射端でのポンプ パルスのピーク電力です。νB は BFS です (スクリプトでは正規化されています)。g0 = 0.2 W-1 m-1 (スクリプトの g0) はブリルアンのゲイン係数です。ΔνB = 50 MHz (スクリプトでは gamma_B) は BGS の FWHM です。α = 0.2 dB/km はファイバー損失係数で、スクリプトではそれぞれ alpha_log と alpha_lin で対数スケールと線形スケールの値で表されます。ν はプローブ波の周波数であるため、ポンプとプローブの周波数オフセット ν - νB が -250 MHz から 250 MHz までスキャンされます。ポンプとプローブの周波数オフセットは、スクリプトではグローバル ベクトル f として表されます。項g1 = mg0は損失係数です。2d・ΔνB は、2 つの損失間の周波数オフセットです。Leff = 10 m (スクリプトではL_eff) は、100 ns のパルス幅に対するブリルアン相互作用の長さです。設計されたスペクトル形状は、2つの正規化された係数mとdを調整することで簡単に調整できます。従来のBGSは、m = 0で簡単にモデル化できます。
  2. ランダムノイズ(つまり、加法的なホワイトガウスノイズ)を従来のBGSとエンジニアリングされたBGSの両方で同じレベルで追加します。スクリプトでパラメータ noise_level を調整すると、ノイズレベルを変更できます。
  3. 従来のノイズの多い BGS をローレンツ関数 (スクリプトの Lorentz_g_gain_fun 関数) に適合させ、設計されたノイズの多い BGS にローレンツ関数 (スクリプトの Lorentz_gl_gain_fun 関数) を重ね合わせます ( 図 2A を参照)。
  4. 従来型BGSとエンジニアリングBGSのノイズによるピーク周波数オフセットを求めます(図2B)。
  5. N = 500 に対して手順 1.2 から 1.4 を繰り返し、i 番目のプロセスで従来の BGS と工学的な BGS のすべてのピーク周波数オフセット Δfci と Δfpi (スクリプトではそれぞれ delta_g_g と delta_g_gl で表されます) を収集します。

figure-protocol-2407
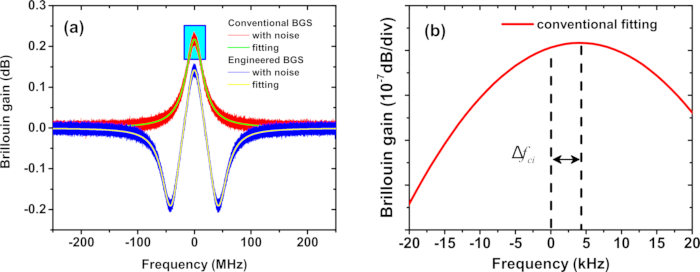
図2:シミュレートされたBGS。 (A)シミュレーションにおける典型的なローレンツ(赤)BGSと工学(青)BGSのフィッティングのデモンストレーション。(B)(A)からのローレンツBGSピーク。Δfci は、 i番目の 測定における従来の BGS の BFS 推定誤差を表します。 この図の拡大版を表示するには、ここをクリックしてください。

  1. ノイズに起因するBFS推定誤差の標準偏差の比を次のように計算します。
    figure-protocol-2932
  2. η を m と d の関数としてプロットします (図 3A を参照)。最小値 ηmin と対応する m と d を見つけます。推定精度の利点は、全繊維28に沿って維持されることになる。
  3. 式 (2) の z の値 (つまり、繊維の長さ、スクリプトの z も) を 0 km から 60 km、ステップ 50 m に調整し、選択した m 値と d 値でステップ 1.1 から 1.7 を繰り返します。次に、繊維長の関数としての標準偏差の比を取得できます(図3Bを参照)。

2. 従来のBOTDAセットアップ(図4Bで強調表示されているブロック)を準備してテストします

  1. レーザーダイオード(LD)をオンにし、光スペクトラムアナライザー(OSA)でLDの機能を確認します。通常、1,550nm前後の波長が使用されます。
  2. LDを10:90光カプラー(OC)で接続します。10%OC出力からの電力を確認してください。電力が 13 dBm(偏波スクランブラ [Pol.S.] の最大入力電力)よりも高い場合は、LD 電流を下げて LD 出力電力を下げます。
  3. 10% OC 出力を Pol.S に接続します。偏波フェージング1を避けるために、スクランブル周波数を1kHzに設定してください。
  4. Pol.Sの出力から電力を確認してください。電力が -3 dBm(半導体光増幅器(SOA)の最大入力電力制限)よりも高い場合は、電力要件が満たされるまで減衰器を追加します。Pol.S.を接続するSOAと。
  5. パルス発生器(PG)からのパルス幅100ns、繰り返し周波数4kHzの電気パルス列信号をSOAに適用します。パルス信号の振幅がSOAのトランジスタ-トランジスタロジック(TTL)しきい値(つまり、4dBm)よりも高く、繰り返しレートが往復要件30を満たしていることを確認します。
  6. SOAからの出力をエルビウムドープファイバアンプ(EDFA 1)に接続し、EDFAを自動電流制御(ACC)モードで操作します。EDFA 1 からの出力をサーキュレーター (Cir) のポート 1 に接続します。
  7. Cirのポート2からの光パルス信号をフォトダイオード(PD)に接続して、デジタイザーで確認します。PDへの損傷を避けるためには、十分な減衰が必要です。
  8. デジタイザで測定された波形によって光パルスのピークパワーを計算します。光ピークパワーPOは、次式に従って推定されます。
    figure-protocol-4480
    ここで、VEは電気パルスのピーク電圧、RとRFはPDの応答性とトランスレジスタンスです。この計算では、テスト対象のファイバーへの正しい入力ポンプ電力(FUT、10.6 km)が評価されるように、保護減衰を考慮に入れます。
  9. 計算された光パルスのピーク電力が 20 dBm(MI しきい値19)に達したときの EDFA 電流値 I20 に注意してください。光パルス列の消光比(ER)は、エネルギー保存則に応じて評価できます。
    figure-protocol-4851
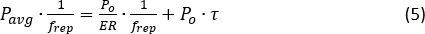
    ここで、Pavgはパルス列の光学平均パワーです。frep は繰り返し率です。τ はパルス幅です。SOA の ER は通常 30 dBm を超え、NLE31,32 を効率的に回避します。
    注: PD を取り外してシステムの構築を続行する前に、EDFA の電源を切ってください。
  10. Cirのポート2をFUTの一方の端に接続して、ポンプブランチのセットアップを完了します。システムがMIに問題を引き起こすかどうかを確認するには、OSAのFUTのもう一方の端からのスペクトルをチェックし、EDFAを定電流値I20に設定します。検出されたスペクトルがステップ2.1で測定されたものと同じ(形状において、振幅において必ずしもそうではない)場合、システムはMIから解放される。
  11. OCの90%出力を50:50のOC1に接続し、OC1出力の1つを偏波コントローラー(PC)を介してマッハツェンダー変調器(MZM1)に接続します。MZM 1からの出力が最大になるように、偏光を正しく設定してください(偏光アライメント)。
  12. RF ジェネレータ(RFG 1)からの無線周波数(RFG 1)信号を、FUT の BFS(約 11 GHz SSMF の場合)と 16 dBm の振幅で MZM 1 に適用します。MZM1のDCバイアス電圧は、キャリアが最小になるように設定してください。
  13. MZM 1の出力をファイバーブラッググレーティング(FBG 1)に接続します。FBG 1 が上限周波数の側波帯と搬送波をブロックするように設定されているよう、OSA で FBG 1 からの出力スペクトルを確認します。
  14. FBG 1 からの出力を EDFA 2、別の 50:50 OC 2、アイソレータ (ISO) に連続して接続します。
  15. EDFA 2 を ACC モードでも動作させ、電流値を I g に設定して、ISO からの出力電力が -14 dBm より低くなるようにし、NLE20 を最小限に抑えます。電源メーターを取り外す前に EDFA の電源を切り、システムの構築を続行します。ISO出力をFUTのもう一方の端に接続して、ゲインプローブブランチのセットアップ構築を完了します。
  16. Cirポート3をEDFA4(プレアンプ34用)とPDに接続し、EDFAをACCモードに設定します。電流値I4は、EDFAからの出力電力がPDの入力制限より4小さくなるようにすべきである。フィルター出力をデジタイザーに接続します。
  17. デジタイザのトリガをパルス発生器の同期(または逆)出力に接続します。デジタイザパラメータを次のように設定します:サンプリングレート:500 MSa / s;平均:4,096回;サンプル数:10,000。
  18. EDFA 1、EDFA 2、および EDFA 4 の電流値をそれぞれ I20、 Ig、 および I4 に設定します。トレース記録プログラムを実行します。デジタイザで測定されたトレースを確認します。トレース振幅が指数関数的減衰に従う場合、センシングシステムはMIフリーです。それ以外の場合は、EDFA 1 の現行値を小さくします。

3. 従来のBOTDAセットアップによる計測とデータ処理

  1. EDFA 1 と EDFA 2 の値をそれぞれ I20 と Ig に設定します。BFS ± 90 MHz の範囲で RFG 1 の周波数を 1 MHz ステップでスキャンします。各スキャンステップの後に、記録プログラムからのトレースを記録します。
  2. トレース振幅 (ブリルアン相互作用周期) を各 DC オフセット (非ブリルアン相互作用周期) で割ることにより、ローカル・ブリルアン・ゲインを計算します。
  3. 測定されたノイズの多いBGSをローレンツフィッティングにフィッティングすることにより、各ファイバーセクションでBGSを取り出します。フィッティングから従来のBGSのFWHMδνB0を求めます。
  4. N = 48 に対して手順 3.1 と 3.2 を繰り返し、i番目のプロセスでファイバー νBci(z) に沿った推定ピーク (BFS) 周波数分布をすべて収集します (図 5A を参照)。
  5. BFS推定誤差を、48回の測定で各繊維セクションにおける適合BFSの標準偏差として計算します(図5Bを参照)。

4. 残りのセットアップの準備

注:この場合、シミュレーション結果ごとに 、m = 1および d = 1.24が使用されました(セクション1および 図3を参照)。

  1. プローブブランチの50:50 OC 1の他の出力をEDFA3および50:50OC3に接続します。
  2. 50:50 OC 3の出力の1つをPCとMZM2に接続します。MZM2からの出力が最大になるように偏光を調整します。
  3. RFG 2 からの RF 信号を BFS ( d・ΔνB0 と MZM 2 の 16 dBm 振幅) で印加します。OSAの変調スペクトルを確認し、バイアス電圧を調整してキャリア振幅を最小化します。
  4. MZM2からの出力を光スイッチ(OS1)の入力、50:50 OC4の入力の1つ、FBG2に接続します。
  5. OSA の光信号を確認し、FBG 2 の中心波長を調整して、キャリアと低周波数の側波帯がブロックされるようにします ( 図 4A を参照)。これで、loss 1プローブブランチのセットアップが完了します。
  6. 50:50 OC 3 のもう一方の出力を PC と MZM 3 に接続します。MZM3からの出力が最大になるように偏光を調整します。
  7. RFG 3 からの RF 信号を BFS + d・δνB0 で MZM 3 に 16 dBm の振幅で印加します。OSAの変調スペクトルを確認し、バイアス電圧を調整してキャリア振幅を最小化します。
  8. MZM3からの出力をスイッチ機能付き可変光減衰器(VOA)に接続(OS2)し、もう1つの入力である50:50OC4を接続します。損失プローブ周波数間のオフセットがFBG2の伝送ウィンドウに比べて比較的小さい(数GHz)ことを考えると、MZM3からのキャリアと低周波数の側波帯もFBG2によってブロックされます。これで、loss 2プローブブランチのセットアップが完了します。
  9. OS 1 を閉じ、OS 2 を開き、損失 1 プローブの電力が -14 dBm (m = 1) に等しくなるように、EDFA 3 の電流値を Il に設定します。
  10. OS 1 を開き、OS 2 を閉じて、損失 2 プローブの電力も -14 dBm に等しくなるように VOA の減衰を調整します。

5. BOTDAの提案型セットアップとデータ処理一式による測定

  1. OS 1 を閉じ、OS 2 を閉じ、EDFA 1、EDFA 2、EDFA 3、および EDFA 4 の現在値をそれぞれ I20、 Ig、 Il、 および I4 に設定します。BFS±90MHzの範囲のRFG1の周波数を1MHzステップでスキャンします。RFG 2 と RFG 3 の周波数は、対応するようにスキャンされます。各スキャンステップの後にプログラムからのトレースを記録します。
  2. ステップ 3.2 のようにローカルなブリルアン ゲインを計算し、測定されたノイズの多い BGS に重ね合わせたローレンツ関数を当てはめることにより、各ファイバー セクションで設計された BGS を取得します。
  3. N = 48 に対して手順 5.1 と 5.2 を繰り返し、i番目のプロセスでファイバー νBpi(z) に沿った推定ピーク (BFS) 周波数分布をすべて収集します (図 5A を参照)。
  4. BFS推定誤差を、48回の測定で各繊維セクションにおける適合BFSの標準偏差として計算します(図5Bを参照)。

結果

図3にシミュレーション結果を示します。図3Aのη<1の点は、設計されたBGSの周波数誤差が小さい(測定分解能が高い)ことを示しています。値が低ければ低いほど、利点は大きくなります。最小比はm = 1であり、マルチポンプ方式の代わりにマルチプローブ方式を実行できる?...

ディスカッション

実験中の最も重要なステップは、 m = 1 と 2 つのブリルアン損失スペクトル間の対称性が達成されるように、3 つのプローブ出力を均等化することです。ステップ 4.9 と 4.10 で示したように、Cir ポート 2 のパワー メーターを使用した個別のパワー チェックに加えて、デジタイザでパワー イコライゼーションをより正確にチェックできます。RF 1 の周波数を ~11 GH...

開示事項

著者らは、競合する金銭的利益がないことを宣言します。トーマス・シュナイダーは、ブラウンシュヴァイク工科大学の従業員です。Cheng Fengは、ドイツ研究財団とNiedersächsisches Vorabから資金提供を受けています。

謝辞

Cheng Fengは、ドイツ研究財団(SCHN 716/13-1, 716/15-2, 716/18-1, 716/26-1)とNiedersächsisches Vorab(NL-4プロジェクト「QUANOMET」)からの財政支援に感謝の意を表したいと思います。

資料

NameCompanyCatalog NumberComments
Current controller for laser diodeILX LightwaveLDX3220
DigitizerAcqiris SAU5309A-1039
Erbium doped fiber amplifier 1PhotopPTEDFA-A-PA-C-SCH-15
Erbium doped fiber amplifier 2LiCommOFA-TCH
Erbium doped fiber amplifier 3Calmar OptcomAMP-ST30
Erbium doped fiber amplifier 4PhotopPTEDFA-A-PA-C-SCH-15
Fiber Bragg grating 1Advanced Optics SolutionsT-FBG
Fiber Bragg grating 2Advanced Optics SolutionsT-FBG
Fiber under testofs
IsolatorGeneral PhotonicsS-15-NTSS
Laser diode3SP GroupA1905 LMI
Mach-Zehnder modulator 1AvanexIM10
Mach-Zehnder modulator 2AvanexIM10
Mach-Zehnder modulator 3AvanexIM10
Nanosecond driving board for semiconductor optical amplifierHighland TechnologyT160-9 (28A160-9C)
Optical coupler 10:90NewportBenchtop coupler/WDM
Optical coupler 50:50NewportBenchtop coupler/WDM
Optical spectrum analyzerHewlett Packard86145A
Optical switch 1JDSUSN12-1075NC
PhotodiodeThorlabsD400FC
Polarization scramblerGeneral PhotonicsPSY-101
Pulase generatorHewlett Packard8082A
Radio function generator 1AnritsuMG3692C
Radio function generator 2Agilent TechnologyE8257D
Radio function generator 3HTMT2100
Semiconductor optical amplifierThorlabsSOA1013SXS
Temperature controller for laser diodeILX LightwaveLDT5948
Temperature controller for semiconductor optical amplifierTektronixTED200
Variable optical attenuatorJDSUmVOA-A1With optical switch function

参考文献

  1. Motil, A., Bergman, A., Tur, M. [INVITED] State of the art of Brillouin fiber-optic distributed sensing. Optics & Laser Technology. 78, 81-103 (2016).
  2. Kurashima, T., Tateda, M. Thermal effects on the Brillouin frequency shift in jacketed optical silica fibers. Applied Optics. 29 (15), 2219-2222 (1990).
  3. Horiguchi, T., Kurashima, T., Tateda, M. Tensile strain dependence of Brillouin frequency shift in silica optical fibers. IEEE Photonics Technology Letters. 1 (5), 107-108 (1989).
  4. Preussler, S., Wiatrek, A., Jamshidi, K., Schneider, T. Brillouin scattering gain bandwidth reduction down to 3.4MHz. Optics Express. 19 (9), 8565-8570 (2011).
  5. Wiatrek, A., Preußler, S., Jamshidi, K., Schneider, T. Frequency domain aperture for the gain bandwidth reduction of stimulated Brillouin scattering. Optics Letters. 37 (5), 930-932 (2012).
  6. Preussler, S., Schneider, T. Bandwidth reduction in a multistage Brillouin system. Optics Letters. 37 (19), 4122-4124 (2012).
  7. Preussler, S., Schneider, T. Stimulated Brillouin scattering gain bandwidth reduction and applications in microwave photonics and optical signal processing. Optical Engineering. 55 (3), 031110 (2015).
  8. Wei, W., Yi, L., Jaouen, Y., Morvan, M., Hu, W. Brillouin Rectangular Optical Filter with Improved Selectivity and Noise Performance. IEEE Photonics Technology Letters. 27 (15), 1593-1596 (2015).
  9. Feng, C., Preussler, S., Schneider, T. The Influence of Dispersion on Stimulated Brillouin Scattering Based Microwave Photonic Notch Filters. Journal of Lightwave Technology. 36 (22), 5145-5151 (2018).
  10. Feng, C., Preussler, S., Schneider, T. Investigation of the Dispersion Effect on Stimulated Brillouin Scattering based Microwave Photonic Notch Filters. 2018 International Topical Meeting on Microwave Photonics (MWP). , 1-4 (2018).
  11. Feng, C., Preussler, S., Schneider, T. Sharp tunable and additional noise-free optical filter based on Brillouin losses. Photonics Research. 6 (2), 132-137 (2018).
  12. Henker, R., et al. Gain enhancement in multiple-pump-line Brillouin-based slow light systems by using fiber segments and filter stages. Applied Optics. 48 (29), 5583-5588 (2009).
  13. Zhang, L., et al. Superluminal propagation at negative group velocity in optical fibers based on Brillouin lasing oscillation. Physical Review Letters. 107 (9), 93903 (2011).
  14. Xing, L., Zhan, L., Xia, Y. Large delay tunable slow-light based on high-gain stimulated-Brillouin-scattering amplification in optical fibers. Chinese Science Bulletin. 54 (21), 3947-3952 (2009).
  15. Preussler, S., Wiatrek, A., Jamshidi, K., Schneider, T. Ultrahigh-resolution spectroscopy based on the bandwidth reduction of stimulated brillouin scattering. IEEE Photonics Technology Letters. 23 (16), 1118-1120 (2011).
  16. Horiguchi, T., Tateda, M. Optical-fiber-attenuation investigation using stimulated Brillouin scattering between a pulse and a continuous wave. Optics Letters. 14 (8), 408-410 (1989).
  17. Feng, C., Emad Kadum, J., Schneider, T. The State-of-the-Art of Brillouin Distributed Fiber Sensing. Brillouin Distributed and Fiber-bragg-grating-based Fiber Sensing - Principle, Measurement and Applications. , (2019).
  18. Soto, M. A., Thévenaz, L. Modeling and evaluating the performance of Brillouin distributed optical fiber sensors. Optics Express. 21 (25), 31347-31366 (2013).
  19. Alem, M., Soto, M. A., Thévenaz, L. Analytical model and experimental verification of the critical power for modulation instability in optical fibers. Optics Express. 23 (23), 29514-29532 (2015).
  20. Thévenaz, L., Mafang, S. F., Lin, J. Effect of pulse depletion in a Brillouin optical time-domain analysis system. Optics Express. 21 (12), 14017-14035 (2013).
  21. Iribas, H., Urricelqui, J., Mompó, J. J., Mariñelarena, J., Loayssa, A. Non-Local Effects in Brillouin Optical Time-Domain Analysis Sensors. Applied Sciences. 7 (8), 761 (2017).
  22. Soto, M. A., Le Floch, S., Thévenaz, L. Bipolar optical pulse coding for performance enhancement in BOTDA sensors. Optics Express. 21 (14), 16390-16397 (2013).
  23. Angulo-Vinuesa, X., Martin-Lopez, S., Corredera, P., Gonzalez-Herraez, M. Raman-assisted Brillouin optical time-domain analysis with sub-meter resolution over 100 km. Optics Express. 20 (11), 12147 (2012).
  24. Haneef, S. M., Yang, Z., Thévenaz, L., Venkitesh, D., Srinivasan, B. Performance analysis of frequency shift estimation techniques in Brillouin distributed fiber sensors. Optics Express. 26 (11), 14661-14677 (2018).
  25. Lopez-Gil, A., et al. Evaluation of the accuracy of BOTDA systems based on the phase spectral response. Optics Express. 24 (15), 17200-17214 (2016).
  26. Urricelqui, J., Soto, M. A., Thévenaz, L. Sources of noise in Brillouin optical time-domain analyzers. 24th International Conference on Optical Fibre Sensors. 9634, 963434 (2015).
  27. Zornoza, A., Sagues, M., Loayssa, A. Self-heterodyne detection for SNR improvement and distributed phase-shift measurements in BOTDA. Journal of Lightwave Technology. 30 (8), 1066-1072 (2012).
  28. Feng, C., Lu, X., Preussler, S., Schneider, T. Gain Spectrum Engineering in Distributed Brillouin Fiber Sensors. Journal of Lightwave Technology. 37 (20), 5231-5237 (2019).
  29. Feng, C., Lu, X., Preussler, S., Schneider, T. Measurement accuracy enhancement of distributed Brillouin sensors based on gain spectrum engineering. Seventh European Workshop on Optical Fibre Sensors. 11199, 9 (2019).
  30. Peled, Y., Motil, A., Tur, M. Fast Brillouin optical time domain analysis for dynamic sensing. Optics Express. 20 (8), 8584-8591 (2012).
  31. Feng, C., Iribas, H., Marinelaerña, J., Schneider, T., Loayssa, A. Detrimental Effects in Brillouin Distributed Sensors Caused By EDFA Transient. Conference on Lasers and Electro-Optics. , JTu5A.85 (2017).
  32. Iribas, H., et al. Effects of pump pulse extinction ratio in Brillouin optical time-domain analysis sensors. Optics Express. 25 (22), 27896-27911 (2017).
  33. Tai, K., Hasegawa, A., Tomita, A. Observation of modulational instability in optical fibers. Physical Review Letters. 56 (2), 135-138 (1986).
  34. De Souza, K., Newson, T. P. Brillouin-based fiber-optic distributed temperature sensor with optical preamplification. Optics Letters. 25 (18), 1331 (2000).
  35. Feng, C., Preussler, S., Emad Kadum, J., Schneider, T. Measurement Accuracy Enhancement via Radio Frequency Filtering in Distributed Brillouin Sensing. Sensors. 19 (13), 2878 (2019).
  36. Kadum, J., Feng, C., Preussler, S., Schneider, T. Improvement of the measurement accuracy of distributed Brillouin sensing via radio frequency filtering. Seventh European Workshop on Optical Fibre Sensors. 19 (13), 3 (2019).

転載および許可

このJoVE論文のテキスト又は図を再利用するための許可を申請します

許可を申請

さらに記事を探す

BOTDA

This article has been published

Video Coming Soon

JoVE Logo

個人情報保護方針

利用規約

一般データ保護規則

お問い合わせ

図書館への推薦

JoVE ニュースレター

研究

教育

著者

図書館員

JoVEについて

Copyright © 2023 MyJoVE Corporation. All rights reserved